概率论与数理统计第14节全概及逆概公式

合集下载

高考数学知识点解析全概率公式与逆概率公式

高考数学知识点解析全概率公式与逆概率公式高考数学知识点解析：全概率公式与逆概率公式在高考数学中，概率是一个重要的考点，而全概率公式与逆概率公式更是其中的难点和重点。

理解并熟练运用这两个公式，对于解决复杂的概率问题具有关键作用。

首先，我们来认识一下什么是全概率公式。

假设事件B 可以在多种不同的情况下发生，而这些情况分别为A1，A2，A3，……，An ，且这些情况两两互斥，并且它们的并集构成了整个样本空间。

同时，已知在每种情况 Ai 下事件 B 发生的概率为P(B|Ai) ，以及每种情况 Ai 本身发生的概率 P(Ai) 。

那么事件 B 发生的概率 P(B) 就可以通过全概率公式来计算：P(B) ＝ P(A1)×P(B|A1) ＋ P(A2)×P(B|A2) ＋… ＋ P(An)×P(B|An)为了更好地理解全概率公式，我们来看一个具体的例子。

假设某学校有三个年级，高一年级有 500 名学生，高二年级有 600名学生，高三年级有 400 名学生。

在某次考试中，高一年级学生的优秀率为 30%，高二年级学生的优秀率为 40%，高三年级学生的优秀率为 50%。

现在随机抽取一名学生，求这名学生考试优秀的概率。

在这里，事件 B 就是抽取的学生考试优秀，情况 A1、A2、A3 分别是抽取到高一年级、高二年级、高三年级的学生。

P(A1) ＝ 500 ／（500 ＋ 600 ＋ 400) ＝ 5 ／ 15，P(B|A1) ＝ 30% ＝ 03 ；P(A2) ＝ 600／ 1500 ＝ 6 ／ 15 ，P(B|A2) ＝ 04 ；P(A3) ＝ 400 ／ 1500 ＝ 4 ／ 15 ，P(B|A3) ＝ 05 。

根据全概率公式，P(B) ＝（5 ／ 15)×03 ＋（6 ／ 15)×04 ＋（4 ／15)×05 ＝ 04 。

接下来，我们再看看逆概率公式，也称为贝叶斯公式。

全概率公式和逆概率公式

新乡医学院教案首页单位：计算机教研室基本内容备注 1.4 全概率公式和逆概率公式一、全概率公式例1 现有10个阄，其中两阄为“有”，其余均为“无”。

试判断第一个抓阄者是否比第二个更合算。

解：设B={第一个抓得“有”}，A={第二个抓得“有”}，则P(B)=0.2,P(A|B)=1/9，(|)2/9.P A B =而,A AB AB =+ 于是()()()()P A P AB AB P AB P AB =+=+()(|)()(|)P B P A B P B P A B =+120.20.80.299=⨯+⨯=故先后抓阄者获得“有”的机会是相等的。

定理1 如果事件A 能且只能与互不相容事件B 1,B 2,…,B n 之一同时发生，则1()()(|)niii P A P B P A B ==∑证令12,n C B B B =+++则12n B B B C U ++++=1212()n n A AU A B B B C AB AB AB AC ==++++=++++因为A 能且只能与B 1,B 2,…,B n 之一同时发生，故,AC V =即1,nii A AB ==∑且AB 1,AB 2,…,AB n 互不相容.于是由加法公式和乘法公式可得111()()()()(|).nnni i i i i i i P A P AB P AB P B P A B ======∑∑∑1()()(|).ni i i P A P B P A B ==∑在实际问题中，当计算P(A)比较困难，而计算P(B i )和P(A|B i )比较容易时，可用全概率公式求P(A).全概率公式,)n B)j。

概率论与数理统计完整公式以及各知识点梳理

的次数是随机变量，设为 X ，则 X 可能取值为 0,1,2,, n 。
P( X

k)

Pn(k )

C
k n
p k q ，
其中
则称随机变量 X 服从参数为 n ， p 的二项分布。记为
X ~ B(n, p) 。
当 n 1时， P( X k) p k q1k ， k 0.1，这就是（0-1）分
1567014781.doc
概率论与数理统计完整版公式
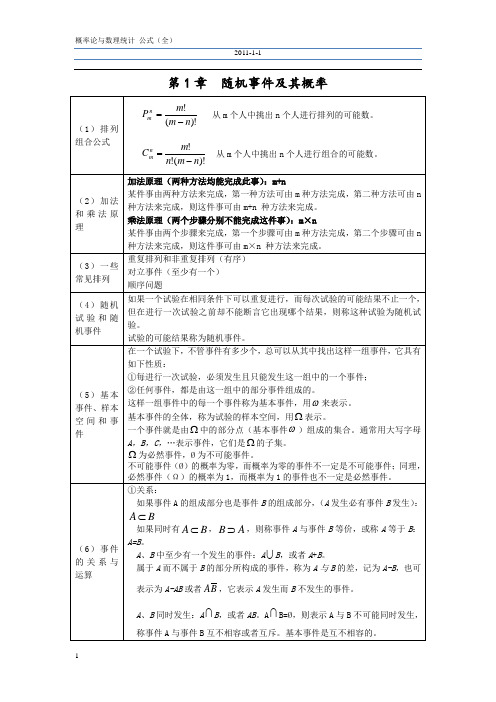
第 1 章随机事件及其概率
（1）排列组合公式
Pmn

m! (m n)!
从 m 个人中挑出 n 个人进行排列的可能数。
Cmn

m! n!(m n)!
从 m 个人中挑出 n 个人进行组合的可能数。
加法原理（两种方法均能完成此事）：m+n
（2）加法和乘法原理
5° P(X x) F(x) F(x 0) 。
对于离散型随机变量， F(x) pk ； xk x
x
对于连续型随机变量， F (x) f (x)dx 。
0-1 分布
P(X=1)=p, P(X=0)=q
二项分布
（5）八大分布
在 n 重贝努里试验中，设事件 A 发生的概率为 p 。事件 A 发生
1° 0 F(x) 1, x ；
（4）分布函数
2° F(x) 是单调不减的函数，即 x1 x2 时，有 F(x1) F (x2) ；
3° F() lim F(x) 0， F() lim F(x) 1；
x
x
4° F(x 0) F(x) ，即 F(x) 是右连续的；

概率论与数理统计超全公式总结

E (X )=∑∑x i p i jijxxn+∞ n n−λλkP (X = k ) = e ， (k = 0,1,...)k !(a ≤ x ≤ b )1b − af (x ) =概率论与数理统计公式总结F (x ) = P (X ≤ x ) = ∑P (X = k )k ≤x分布函数对离散型随机变量F ' (x ) = f (x )第一章P(A+B)=P(A)+P(B)- P(AB)特别地，当 A 、B 互斥时， P(A+B)=P(A)+P(B)对连续型随机变量F (x ) = P (X ≤ x ) =∫−∞f (t )dt条件概率公式分布函数与密度函数的重要关系：P (A | B ) =P (AB )P (B )F (x ) = P (X ≤ x ) =∫−∞f (t )dt概率的乘法公式P (AB ) = P (B )P (A | B )= P (A )P (B | A )二元随机变量及其边缘分布分布规律的描述方法全概率公式：从原因计算结果P (A ) = ∑ P (B k )P (A | B k )k =1联合密度函数联合分布函数f (x , y ) ≥ 0f (x , y ) F (x , y )+∞ +∞Bayes 公式：从结果找原因∫−∞ ∫−∞f (x , y )dx dy = 1 0 ≤ F (x , y ) ≤ 1P (B k| A ) = P (B i )P (A | B i ) ∑P (B )P (A | B )F (x , y ) = P {X ≤ x ,Y ≤ y }f (x ) = ∫ f (x , y )d y 联合密度与边缘密度第二章kkk =1Xf Y (y ) = −∞+∞−∞f (x , y )dx二项分布（Bernoulli 分布）——X~B(n,p)P (X =k )=C k p k (1−p)n −k，(k =0,1,...n , ) 泊松分布——X~P(λ)概率密度函数离散型随机变量的独立性P {X = i ,Y = j } = P {X = i }P {Y = j }连续型随机变量的独立性f (x , y ) = f X (x ) f Y (y ) 第三章数学期望离散型随机变量，数学期望定义怎样计算概率P (a ≤ X ≤ b )b连续型随机变量，数学期望定义� E(a)=a ，其中 a 为常数P (a ≤ X ≤ b ) = ∫af (x )d x均匀分布 X~U(a,b)指数分布 X~Exp (θ)• E(a+bX)=a+bE(X)，其中 a 、b 为常数 � E(X+Y)=E(X)+E(Y)，X 、Y 为任意随机变量随机变量 g(X)的数学期望常用公式+∞∫−∞ f (x )dx = 1+∞E (X ) = ∑x k ⋅P kk =−∞+∞E (X ) = ∫−∞x ⋅ f (x )dxE (g (X )) = ∑ g (x k ) p kk∫Y / nD (X +Y ) = D (X ) + D (Y ) + 2E {(X − E (X ))(Y − E (Y ))} X ~ N (µ,σ2 )i σ 12 σ E (X Y ) = ∑∑x i y j p i jij2σ22−(x −µ) e 12πσf (x ) =不相关不一定独立第四章正态分布E (X ) = µ,D (X ) = σ2方差定义式常用计算式常用公式当 X 、Y 相互独立时：标准正态分布的概率计算标准正态分布的概率计算公式P (Z ≤ a ) = P (Z < a ) = Φ(a )P (Z ≥ a ) = P (Z > a ) = 1− Φ(a )P (a ≤ Z ≤ b ) = Φ(b ) − Φ(a )P (−a ≤ Z ≤ a ) = Φ(a ) − Φ(−a ) = 2Φ(a ) −1一般正态分布的概率计算一般正态分布的概率计算公式 P (X ≤ a ) = P (X < a ) = Φ(a − µσ ) a − µ方差的性质P (X ≥ a ) = P (X > a ) = 1− Φ( σ)D(a)=0，其中 a 为常数P (a ≤ X ≤ b ) = Φ(b − µ− Φ(a − µD(a+bX)=b2D(X)，其中 a 、b 为常数当 X 、Y 相互独立时，D(X+Y)=D(X)+D(Y) 协方差与相关系数E {[X − E (X )][Y − E (Y )]}= E (XY ) − E (X )E (Y )第五章卡方分布σ ) σ)n若X ~ N (0,1)，则∑ X 2 ~ χ2(n )i =121n2 2协方差的性质若Y ~ N (µ,σ ),t 分布则 2 ∑(Y i− µ) i =1 ~ χ (n )若X ~ N (0,1), Y ~ χ2(n ),则X ~ t (n )独立与相关独立必定不相关 Cov (aX ,bY ) = abCov (X ,Y )若U ~ χ2 (n ), F 分布正态总体条件下样本均值的分布：V ~ χ2(n ),则U / n 1 V / n 2~ F (n 1,n 2 )相关必定不独立2X ~ N (µ,)nX − µ~ N (0,1)σ/ n 2− E (X )) ⋅ f (x )dx x +∞−∞∫ D (X ) =( E (XY ) = ∫ ∫ xyf (x , y )dxdy σX ~ N (µ,σ2 ) ⇔ Z = X − µ~ N (0,1)D (X )D (Y )XY ρ =C ov (X ,Y )Cov (X +Y , Z ) = Cov (X , Z ) + Cov (Y , Z )C ov (X , X ) = E (X 2 ) − (E (X ))2 =D (X )Cov (X ,Y ) = E (XY ) − E (X )E (Y )D (X +Y ) = D (X ) + D (Y )D (X ) =E (X 2 ) − [E (X )]2当X 与Y 独立时,E (XY ) = E (X )E (Y )Φ(a ) = 1− Φ(−a ) E (X +Y ) = E (X ) + E (Y )E (X ) = ∫ ∫ xf (x , y )dxdyn ⎠ n ⎠ n ⎠σ2 1 + 2 n 1 n 2 σ2 σ / n(x 1 − x 2 )± z α/ 2 2 2 ⎜ χ χ ⎛ ⎜ ⎟12x ± z样本方差的分布：正态总体方差的区间估计两个正态总体均值差的置信区间(n −1)S 2 ~ χ2 (n −1) X − µ~ t (n −1) 大样本或正态小样本且方差已知σ2两个正态总体的方差之比⎛⎜ ⎜ ⎝S 2 / S 2两个正态总体方差比的置信区间1 2~ F (n 1 −1,σ2 /σ2n 2 −1)2 / S 2 , 2 / S 2⎞ ⎝ F α/ 2 (n 1 −1,n 2 −1) F α/ 2 (n 1 −1,n 2 −1) ⎠第六章点估计：参数的估计值为一个常数矩估计最大似然估计n似然函数第七章假设检验的步骤1 根据具体问题提出原假设 H0 和备择假设 H12 根据假设选择检验统计量，并计算检验统计值3 看检验统计值是否落在拒绝域，若落在拒绝域则L = Π i =1f (x i ;θ)L = Π i =1p (x i ;θ)拒绝原假设，否则就不拒绝原假设。

概率论与数理统计公式整理(超全免费版)

（6）事件的关系与运算
AB 属于 A 而不属于 B 的部分所构成的事件，称为 A 与 B 的差，记为 A-B，也可表示为 A-AB 或者
，它表
示 A 发生而 B 不发生的事件。
A、B 同时发生：A B，或者 AB。A B=Ø，则表示 A 与 B 不可能同时发生，称事件 A 与事件 B 互不相容
分布是二项分布的特例。
设随机变量 X 的分布律为
P( X k) k e ， 0 ， k 0,1,2， k!
则称随机变量 X 服从参数为的泊松分布，记为 X ~ () 或者 P( )。
泊松分布为二项分布的极限分布（np=λ，n→∞）。
P( X
k)
CMk
•
C
nk N M
C
n N
k 0,1,2,l , l min(M , n)
即
f
(x)
b
1
a
,
0,
a≤x≤b
其他，
指数分布
则称随机变量 X 在[a，b]上服从均匀分布，记为 X~U(a，b)。
分布函数为
0，
x<a，
x
F(x) f (x)dx
xa, ba
1，
a≤x≤b x>b。
x , x 当 a≤x1<x2≤b 时，X 落在区间（ 1 2 ）内的概率为
P( x1
X
如果一个试验在相同条件下可以重复进行，而每次试验的可能结果不止一个，但在进行一次试验之前却不能断言它出现哪个结果，则称这种试验为随机试验。试验的可能结果称为随机事件。
在一个试验下，不管事件有多少个，总可以从其中找出这样一组事件，它具有如下性质：
①每进行一次试验，必须发生且只能发生这一组中的一个事件；

(完整版)概率论与数理统计公式整理(超全版)

，（，，…，），通常叫先验概率。，（，，…，），通常称为后验概率。贝叶斯公式反映了“因果”的概率规律，并作出了“由果朔因”的推断。
（17）伯努利概型
我们作了次试验，且满足
每次试验只有两种可能结果，发生或不发生；
次试验是重复进行的，即发生的概率每次均一样；
每次试验是独立的，即每次试验发生与否与其他次试验发生与否是互不影响的。
并且同时满足P(ABC)=P(A)P(B)P(C)
那么A、B、C相互独立。
对于n个事件类似。
（15）全概公式
设事件满足
1° 两两互不相容，，
2° ，
则有
。
（16）贝叶斯公式
设事件，，…，及满足
1° ，，…，两两互不相容， >0， 1，2，…，，
2° ，，
则
，i=1，2，…n。
此公式即为贝叶斯公式。
条件概率是概率的一种，所有概率的性质都适合于条件概率。
例如P(Ω/B)=1 P( /A)=1-P(B/A)
（13）乘法公式
乘法公式：
更一般地，对事件A1，A2，…An，若P(A1A2…An-1)>0，则有
… …… … 。
（14）独立性
①两个事件的独立性
设事件、满足，则称事件、是相互独立的。
则称上式为离散型随机变量的概率分布或分布律。有时也用分布列的形式给出：
。
显然分布律应满足下列条件：
（1），，（2）。
（2）连续型随机变量的分布密度
设是随机变量的分布函数，若存在非负函数，对任意实数，有
，
则称为连续型随机变量。称为的概率密度函数或密度函数，简称概率密度。

概率论与数理统计公式整理(超全版)

P(A+B)=P(A)+P(B)-P(AB) 当 P(AB)＝0 时，P(A+B)=P(A)+P(B) P(A-B)=P(A)-P(AB) 当 B A 时，P(A-B)=P(A)-P(B) 当 A=Ω 时，P( B )=1- P(B) 定义设 A、B 是两个事件，且 P(A)>0，则称 P( AB) 为事件 A 发生条件下，事件 B 发生的条件概率，记为 P( A)
1 , 2 n ，
P(1 ) P( 2 ) P( n ) 1 。 n
A 的概率。
（8）古典概型
设任一事件
P(A)=
(1 ) ( 2 ) ( m ) = P(1 ) P( 2 ) P( m )
A ，它是由 1 , 2 m 组成的，则有
A B ，它
A、B 同时发生：A B，或者 AB。A B=Ø，则表示 A 与 B 不可能同时发生，称事件 A 与事件 B 互不相
（6）事件的关系与运算容或者互斥。基本事件是互不相容的。
-A 称为事件 A 的逆事件，或称 A 的对立事件，记为 A 。它表示 A 不发生的事件。互斥未必对立。

f ( x)dx 1
。
P( X x) P( x X x dx) f ( x)dx
积分元似。
f ( x)dx 在连续型随机变量理论中所起的作用与 P( X xk ) pk 在离散型随机变量理论中所起的作用相类
（4）分布函数
设 X 为随机变量， x 是任意实数，则函数
来表示。
A，B，C，„表示事件，它
基本事件的全体，称为试验的样本空间，用表示。
）组成的集合。通常用大写字母

1.4全概逆概公式

定义
设A1，A2， An为n个随机事件，如果对其中的任意k个事件Ai1，Ai 2， Aik ( k 2,3, n, i 1,2, n)都有 P( Ai1 Ai 2 Aik ) P( Ai1 ) P( Ai 2 ) P( Aik ) 成立，则称事件A1，A2， An 相互独立。
P ( A| B ) 90%
机器调整得良好 B
B 机器发生某一故障
P ( A| B ) 30%
产品合格 A
解：
P (B | A)
P( A | B)P(B) P( A | B)P(B) P( A | B )P(B )

0 .9 0 .7 5 0 .9 0 .7 5 0 .3 0 .2 5
0 .9 3 %
问题1 虽然此检验方法很精确。真阳性率(又称检验方法的灵敏性) P(B|A)=0.94 真阴性率(又称检验方法的特异性) P(B |A )=0.96 两者都很高，且诊断价值
LR P (B | A) P (B | A) 0 .9 4 0 .0 4 2 3 .5
也很高（一般诊断价值 LR>20就认为是高的），但 P(A|B) 值却不大，为什么？因为发病率P(A)=0.0004，大大小于检测方法的错误率 P(B| A )=0.04 P( B |A)=0.06。
由题意可知
P( A1 ) 50%, P( A2 ) P( A3 ) 25%
P( B A ) P( B A2 ) 2%, P( B A3 ) 4% 1
则 P( B) P( Ai ) P( B | Ai )
i 1 3
= 5 0 % 2 % 2 5 % 2 % 2 5 % 4 % = 2 .5 %

概率论与数理统计公式(完整精华版)

（5）基本事件、样本空间和事件
（6）事件的关系与运算
加法原理（两种方法均能完成此事：）m+ n 某件事由两种方法来完成，第一种方法可由 m 种方法完成，第二种方法可由 n 种方法来完成，则这件事可由 m+n 种方法来完成。乘法原理（两个步骤分别不能完成这件事：）m× n 某件事由两个步骤来完成，第一个步骤可由 m 种方法完成，第二个步骤可由 n 种方法来完成，则这件事可由 m× n 种方法来完成。重复排列和非重复排列（有序）
1° f (x) 0。
2°
+¥ -¥
f
(
x)dx
=
1。
4
概率论与数理统计公式（全）
知识点总结
（3）离散与连续型随机变量的关系（4）分布函数
P(X = x) » P(x < X £ x + dx) » f (x)dx
积分元 f (x)dx 在连续型随机变量理论中所起的作用与 P(X = xk) = pk 在离散型随机变量理论中所起的作用相类似。
②任何事件，都是由这一组中的部分事件组成的。
这样一组事件中的每一个事件称为基本事件，用w 来表示。
基本事件的全体，称为试验的样本空间，用 W 表示。
一个事件就是由 W 中的部分点（基本事件 w ）组成的集合。通常用
大写字母 A，B，C，„表示事件，它们是 W 的子集。
W 为必然事件，Ø为不可能事件。不可能事件（Ø）的概率为零，而概率为零的事件不一定是不可能事件；同理，必然事件（Ω ）的概率为 1，而概率为 1 的事件也不一定是必然事件。
①关系：如果事件 A的组成部分也是事件 B 的组成部分，（A 发生必有事件
B 发生）： A Ì B 如果同时有 A Ì B ， B A ，则称事件 A 与事件 B 等价，或称 A

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1.4 全概率公式与逆概率公式
1.4.1 全概率公式 1.4.2 逆概率公式
样本空间的分割（P38）
定义设A1,A2,,An为一个随机事件且序满列足，
(1 )P (A i)0 ,i1 ,2 , n
A2
(2)
A1,A2,,An两
两
互
斥
A3
(3 )A 1 A 2 A n
A1
An1
An
那么，A1称 ,A2,,An为一个完备事件组也称为的一个分割
P ( A 1 ) P ( B A 1 ) P ( A 2 ) P ( B A 2 ) P ( A n ) P ( B A n )
全概率公式的主要用处在于它可以将一个复杂事件的概率计算问题,分解为若干个简单事件的概率计算问题,最后应用概率的可加性求出最终结果.
全概率公式的使用P(B) n P(Ai)P(BAi) i1
由全概率 P(B)公式 P(Ai得 )P(B|Ai) i1
例1 有一批同一型号的产品，已知其中由一厂生产的占 30% ，二厂生产的占 50% ，三厂生产的占 20%，又知这三个厂的产品次品率分别为2% ， 1%，1%，问从这批产品中任取一件是次品的概率是多少?
解设事件 B 为“任取一件为次品”,
解代:入记数A据i =计{算球得取：自Pi(号B)罐}1i2=13, 2,13, A21, A32, A3是样本空间的一个分割; B ={3取3得红4球2} 36 依 P因(B题为|A意B1):发=2P生/(3A,总i P)是=(B1伴|/A3随2(i)=着=13,/A24,3 ,13,)A,P2(,BA|A3 3之)=一1/2同, 时发生．
P ( B ) P ( A 1 ) P ( B A 1 ) P ( A 2 ) P ( B A 2 ) P ( A 3 ) P ( B A 3 )
0 . 0 0 . 3 0 2 . 0 0 . 5 0 1 . 0 0 . 2 0 1 . 0 .
例2
飞机有三个不同的部分遭到射击,在第一部分被击中一弹,或第二部分被击中2 弹,或第3部分被击中3弹飞机才会被击落,其命中率和每一部分面积成正比,三部分面积之比为0.1:0.2:0.7.若已知飞机中两弹（两弹独立）,求飞机被击落的概率.
我们把事件B看作某一过程的结果，把A1, A2,, An看作该过程的若干因个，原
根据历史资料，每一原因发生的概率已知，
即 PAn已知
而且每一原因对结果的影响程度已知，
即 PBA n已知
则我们可用全概率公式计算结果发生的概率．
即P 求 B
再看引例1
1
23
有三个罐子,1号装有 2 红 1 黑球 , 2号装有 3 红 1 黑球，3号装有 2 红 2 黑球. 某人从中随机取一罐，再从中任意取出一球，求取得红球的概率.
P(B) P(A1)P(BA1)P(A2)P(BA2) P(An)P(BAn)
全概率公式
证明 BΩB (A 1 A 2 A n ) B
A 1 B A 2B A n B .
A1B,A2B,,AnB两两互斥 P ( B ) P ( A 1 B ) P ( A 2 B ) P ( A n B )
0.10.110.10.210.10.710.20.11
事 A i为件 “ 任取 i厂一的 ” 件 ,i 1 产 ,2 为 ,3 . 品
A1A2A3, A iA j , i j i,j 1 ,2 ,3 .
P(A1)0.3, P(A2)0.5, P(A3)0.2,
30% A1
20% A2
50%
A3
例1 有一批同一型号的产品，已知其中由一厂生产的占 30% ，二厂生产的占 50% ，三厂生产的占 20%，又知这三个厂的产品次品率分别为2% ， 1%，1%，问从这批产品中任取一件是次品的概率是多少?
事件 B 为“任取一件为次品”,
P(BA1)0.0,2 P(BA2)0.01, P(BA3)0.01,
30% A1
2% 1% 50%
1%
20% A2 A 3
P ( A 1 ) 0 . 3 ,P ( A 2 ) 0 . 5 ,P ( A 3 ) 0 . 2 ,
P ( B A 1 ) 0 .0 ,P ( 2 B A 2 ) 0 .0 ,P ( 1 B A 3 ) 0 .0 , 1 由全概率公式得
引例1：有三个罐子,1号装有 2 红 1 黑球 , 2号装有 3 红 1 黑球，3号装有 2 红 2 黑球. 某人从中随机取一罐，再从中任意取出一球，求？？
一、全概率公式（P38）定理设试验 E的样本空间 ,为 B为E的事件 , A1, A2,, An为的一个完备事,则件组
P (A 3B 3)P (C |A 3B 3)
A1 A2 A3
B1 1 B2 1 B3 1
B1 1 B2 1 B3 0
B1 1 B2 0 B3 0
C C C
C C C
C C C
P (C ) P (A 1 B 1 )P (C |A 1 B 1 ) P (A 1 B 2)P (C |A 1 B 2) P (A 1B 3)P (C |A 1B 3) P (A 2B 1)P (C |A 2B 1) P (A 2 B 2 )P (C |A 2 B 2 )P (A 2B 3)P (C |A 2B 3) P (A 3B 1)P (C |A 3B 1)P (A 3B 2)P (C |A 3B 2) P (A 3B 3)P (C |A 3B 3)
解: 将中的两弹分出先后次序
设Ai为第一弹击中i部第分 Bi为第二弹击中i部第分
i
1,2,3
设C为飞机被击落 P (C ) P (A 1 B 1 )P (C |A 1 B 1 )
P (A 1 B 2)P (C |A 1 B 2) P (A 1B 3)P (C |A 1B 3) P (A 2B 1)P (C |A 2B 1) P (A 2 B 2 )P (C |A 2 B 2 ) P (A 2B 3)P (C |A 2B 3) P (A 3B 1)P (C |A 3B 1) P (A 3 B 2)P (C | A 3 B 2)