小升初奥数知识点讲解 比和比例
六年级下小升初典型奥数之比例问题

六年级下小升初典型奥数之比例问题在六年级下学期的小升初备考中,比例问题是一个非常重要的知识点,也是奥数中常常出现的题型。
掌握好比例问题,不仅能够提升我们的数学思维能力,还能在考试中取得更好的成绩。
首先,我们来了解一下什么是比例。
比例就是表示两个比相等的式子。
比如,2:3 = 4:6,这就是一个比例。
在比例中,两个内项的积等于两个外项的积,这就是比例的基本性质。
那么,比例问题在奥数中会以哪些形式出现呢?让我们一起来看看。
一、简单的比例计算比如这样一道题:已知甲、乙两个数的比是 3:5,甲数是 12,求乙数是多少。
我们可以设乙数为 x ,根据比例的性质,3:5 = 12:x ,通过交叉相乘得到 3x = 60 ,解得 x = 20 。
再比如:如果 a:b = 4:7 ,且 a + b = 66 ,求 a 和 b 分别是多少。
我们可以把 a 看作 4 份,b 看作 7 份,那么一共是 11 份,11 份是66 ,一份就是 6 。
所以 a = 4×6 = 24 ,b = 7×6 = 42 。
二、比例中的分数问题有这样一道题:已知甲、乙两数的比是 3:4 ,乙数比甲数多几分之几?我们先求出乙数比甲数多的部分,即 4 3 = 1 。
然后用多的部分除以甲数,1÷3 = 1/3 ,所以乙数比甲数多 1/3 。
反过来,如果问甲数比乙数少几分之几,同样先求出少的部分 1 ,再除以乙数,1÷4 = 1/4 ,甲数比乙数少 1/4 。
三、比例的应用比如:工厂要生产一批零件,原计划每天生产 60 个,20 天完成。
实际每天生产的零件数与原计划每天生产的零件数的比是 6:5 ,实际多少天完成?我们先算出这批零件的总数,60×20 = 1200 (个)因为实际每天生产的零件数与原计划每天生产的零件数的比是6:5 ,原计划每天生产 60 个,所以实际每天生产 60÷5×6 = 72 (个)最后用总数除以实际每天生产的个数,1200÷72 = 50/3 (天)四、比例中的图形问题例如:一个长方形的长和宽的比是 5:3 ,周长是 80 厘米,求这个长方形的面积。
小学奥数比和比例

1、比例的基本性质2、熟练掌握比例式的恒等变形及连比问题3、能够进行各种条件下比例的转化,有目的的转化;4、单位“1”变化的比例问题5、方程解比例应用题知识点拨比例与百分数作为一种数学工具在人们日常生活中处理多组数量关系非常有用,这一部 分内容也是小升初考试的重要内容.通过本讲需要学生掌握的内容有: 一、比和比例的性质性质 1 :若 a : b=c : d ,则(a + c) : (b + d)= a : b=c : d ;性质 2 :若 a: b=c : d ,则(a - c) : (b - d)= a : b=c : d ;性质 3 :若 a : b=c : d ,则(a +x c) : (b +x d)=a : b=c : d ; (x 为常数)性质4 :若a : b=c : d ,则axd = bxc ;(即外项积等于内项积)正比例:如果a :b=k (k 为常数),则称a 、b 成正比;反比例:如果axb=k (k 为常数),则称a 、b 成反比.二、主要比例转化实例ma=(其中m 丰0);mb x a y c x ac ④ 一二一,—=— n —=——;% : y : z — ac : bc : bd ; y b z d z bd教学 目标mxmy x — a —b⑤%的c等于y的d,则%是y的㈣,y是%的吃.a b bc ad三、按比例分配与和差关系⑴按比例分配例如:将%个物体按照a: b的比例分配给甲、乙两个人,那么实际上甲、乙两个人各自分配到的物体数量与%的比分别为a: (a + b)和b: (a + b),所以甲分配到至个,乙分配到回a +b a + b 个.⑵已知两组物体的数量比和数量差,求各个类别数量的问题例如:两个类别A、B,元素的数量比为a: b (这里a> b),数量差为%,那么A的元素数量为三,B的元素数量为反,所以解题的关键是求出(a - b)与a或b的比值.a -b a - b四、比例题目常用解题方式和思路解答分数应用题关键是正确理解、运用单位“1”。
六年级下册数学知识点解析:比和比例

小升初数学知识点解析:比和比例两个数相除又叫做两个数的比.一、比和比例的性质性质1:若a: b=c:d,则(a + c):(b + d)= a:b=c:d;性质2:若a: b=c:d,则(a - c):(b - d)= a:b=c:d;性质3:若a: b=c:d,则(a +x c):(b +x d)=a:b=c:d;(x为常数)性质4:若a: b=c:d,则a×d = b×c;(即外项积等于内项积)正比例:如果a÷b=k(k为常数),则称a、b成正比;反比例:如果a×b=k(k为常数),则称a、b成反比.二、比和比例在行程问题中的体现在行程问题中,因为有速度=路程时间,所以:当一组物体行走速度相等,那么行走的路程比等于对应时间的反比;当一组物体行走路程相等,那么行走的速度比等于对应时间的反比;当一组物体行走时间相等,那么行走的速度比等于对应路程的正比.1.A和B两个数的比是8:5,每一数都减少34后,A是B的2倍,试求这两个数.【分析与解】方法一:设A为8x,则B为5x,于是有(8x-34):(5x-34)=2:1,x=17,所以A为136,B为85.方法二:因为减少的数相同,所以前后A 、B的差不变,开始时差占3份,后来差占1份且与B 一样多,也就是说减少的34,占开始的3-1=2份,所以开始的1份为34÷2=17,所以A为17×8=136,B为17×5=85.2.近年来火车大提速,1427次火车自北京西站开往安庆西站,行驶至全程的511再向前56千米处所用时间比提速前减少了60分钟,而到达安庆西站比提速前早了2小时.问北京西站、安庆西站两地相距多少千米?【分析与解】设北京西站、安庆西站相距多少千米?(511x+56):x=60:120,即(511x+56):x=1:2,即x=1011x+112,解得x=1232.即北京西站、安庆西站两地相距1232千米,3.两座房屋A和B各被分成两个单元.若干只猫和狗住在其中.已知:A房第一单元内猫的比率(即住在该单元内猫的数目与住在该单元内猫狗总数之比)大于B房第一单元内猫的比率;并且A房第二单元内猫的比率也大于B房第二单元内猫的比率.试问是否整座房屋A内猫的比率必定大于整座房屋B内猫的比率?【分析与解】如下表给出的反例指出:对所提出问题的回答应该是否定的.表中具体写出了各个单元及整座房屋中的宠物情况和猫占宠物总数的比率.4.家禽场里鸡、鸭、鹅三种家禽中公篱与母篱数量之比是2:3,已知鸡、鸭、鹅数量之比是8:7:5,公鸡、母鸡数量之比是1:3,公鸭、母鸭数量之比是3:4.试求公鹅、母鹅的数量比.【分析与解】公鸡占家禽场家禽总数的=21124615:(3544)45:46:(3544)46:47.333345⨯⨯+⨯⨯=⨯⨯+⨯⨯=8118751310⨯=+++,母鸡占总数的3 10;公鸭占总数的8338753420⨯=+++,母鸭占总数的420;公鹅占总数的213332102020-+=+(),母鹅占总数的234232102020-+=+(),公鹅、母鹅数量之比为322020::3:2.5.在古巴比伦的金字塔旁,其朝西下降的阶梯旁6m的地方树立有1根走子,其影子的前端正好到达阶梯的第3阶(箭头).另外,此时树立l根长70cm自杆子,其影子的长度为175cm,设阶梯各阶的高度与深度都是50cm,求柱子的高度为多少?【分析与解】70cm的杆子产生影子的长度为175cm;所以影子的长度与杆子的长度比为:175:70=2.5倍.于是,影子的长度为6+1.5+1.5×2.5=11.25,所以杆子的长度为11.25÷2.5=4.5m.6.已知三种混合物由三种成分A、B、C组成,第一种仅含成分A和B,重量比为3:5;第二种只含成分B和C,重量比为I:2;第三种只含成分A和C,重量之比为2:3.以什么比例取这些混合物,才能使所得的混合物中A,B和C,这三种成分的重量比为3:5:2 ?【分析与解】注意到第一种混合物种A、B重量比与最终混合物的A、B重量比相同,均为3:5.所以,先将第二种、第三种混合物的A 、B 重量比调整到 3:5,再将第二种、第三种混合物中A 、B 与第一种混合物中A 、B 视为单一物质.第二种混合物不含A ,第三种混合物不含B ,所以1.5倍第三种混合物含A 为3,5倍第二种混合物含B 为5,即第二种、第三种混合物的重量比为5:1.5.于是此时含有C 为5×2+1.5×3=14.5,在最终混合物中C 的含量为3A /5B 含量的2倍.有14.5÷2-1=6.25,所以含有第一种混合物6.25.即第一、二、三这三种混合物的比例为6.25:5:1.5=25:20:6.7.现有男、女职工共1100人,其中全体男工和全体女工可用同样天数完成同样的工作;若将男工人数和女工人数对调一下,则全体男25天完成的工作,全体女工需36天才能完成,问:男、女工各多少人?【分析与解】 直接设出男、女工人数,然后在通过方程求解,过程会比较繁琐.设开始男工为“1”,此时女工为“k ”,有1名男工相当k 名女工.男工、女工人数对调以后,则男工为“k ”,相当于女工“k 2”,女工为“I”.有k 2:1=36:25,所以k=65. 于是,开始有男工数为11k +×1100=500人,女工600人.8.有甲乙两个钟,甲每天比标准时间慢5分钟,而乙每天比标准时间快5分钟,在3月15日的零点零分的时候两钟正好对准.若已知在某一时刻,乙钟和甲钟时针与分针都分别重合,且在从3月15日开始到这个时候,乙钟时针与分针重合的次数比甲钟多10次,那么这个时候的标准时间是多少?【分析与解】 标准的时钟每隔56511分钟重合一次. 假设经历了x 分钟. 于是,甲钟每隔52460651124605⨯⨯⨯-分钟重合一次,甲钟重合了246052460⨯-⨯×x 次; 同理,乙钟重合了246052460⨯+⨯×x 次; 于是,需要乙钟比甲钟多重合 246052460⨯+⨯×x-246052460⨯-⨯×x=102460⨯×x=10; 所以,x=24×60;所以要经历24×60×65511分钟,则为524606551165246011⨯⨯=⨯天. 于是为65天510(24)10()1111⨯=小时106(60)541111⨯=分钟.9.一队和二队两个施工队的人数之比为3:4,每人工作效率之比为5:4,两队同时分别接受两项工作量与条件完全相同的工程,结果二队比一队早完工9天.后来,由一队工人23与二队工人13组成新一队,其余的工人组成新二队.两支新队又同时分别接受两项工作量与条件完全相同的工程,结果新二队比新一队早完工6天.试求前后两次工程的工作量之比?【分析与解】一队与二队的工作效率之比为:(3×5):(4×4)=15:16.一队干前一个工程需9÷116=144天.新一队与新二队的工作效率之比为:2112(3544):(3544)46:47.3333⨯⨯+⨯⨯⨯⨯+⨯⨯=新一队干后一个工程需6÷147=282天.一队与新一队的工作效率之比为2115:(3544)45:46 33⨯⨯+⨯⨯=所以一队干后一个工程需282×4645天.前后两次工程的工作量之比是144:(282×4645)=(144×45):(282×46)=540:1081.。
小升初数学比和比例的知识点

小升初数学比和比例的知识点小升初数学比和比例的知识点上学的时候,大家都背过不少知识点,肯定对知识点非常熟悉吧!知识点就是学习的重点。
你知道哪些知识点是真正对我们有帮助的吗?下面是店铺精心整理的小升初数学比和比例的知识点,希望能够帮助到大家。
1比和比例:比和比例一直是学数学容易弄混的几大问题之一,其实它们之间的问题完全可以用一句话概括:比,等同于算式中等号左边的式子,是式子的一种(如:a:b);比例,由至少两个称为比的式子由等号连接而成,且这两个比的比值是相同(如:a:b=c:d)。
所以,比和比例的联系就可以说成是:比是比例的一部分;而比例是由至少两个比值相等的比组合而成的。
表示两个比相等的式子叫做比例,是比的意义。
比例有4项,前项后项各2个.2.比的基本性质:比的前项和后项都乘以或除以一个不为零的数。
比值不变。
比的性质用于化简比。
比表示两个数相除;只有两个项:比的前项和后项。
比例是一个等式,表示两个比相等;有四个项:两个外项和两个内项。
3.比例的性质:在比例里,两个外项的乘积等于两个内项的乘积。
比例的性质用于解比例。
4.比和比例的区别(1)意义、项数、各部分名称不同。
比表示两个数相除;只有两个项:比的前项和后项。
如:a:b这是比比例是一个等式,表示两个比相等;有四个项:两个外项和两个内项。
a:b=3:4这是比例。
(2)比的基本性质和比例的基本性质意义不同、应用不同。
比的性质:比的前项和后项都乘或除以一个不为零的数。
比值不变。
比例的性质:在比例里,两个外项的乘积等于两个内项的乘积相等。
比例的性质用于解比例。
联系:比例是由两个相等的比组成。
5比和比例的意义比的意义是两个数的除又叫做两个数的比,而比例的意义是表示两个比相等的式子是叫做比例。
比是表示两个数相除,有两项;比例是一个等式,表示两个比相等,有四项。
因此,比和比例的意义也有所不同。
而且,比号没有括号的.含义而另一种形式,分数有括号的含义!6比和比例的联系:比和比例有着密切联系。
比和比例—小升初复习讲义(通用版 含详解)17页

2021-2022学年小升初数学精讲精练专题汇编讲义第5讲比和比例知识点一:比1.比的意义:两个数相除又叫作两个数的比。
2.比的各部分名称及比的读法:4 : 5=4÷5=0.8↓↓↓↓前项比号后项比值3.比的基本性质:比的前项和后项同时乘以或除以相同的数(0除外),比值不变4.求比值与化简比(1)求比值:前项除以后项所得的商是比的结果,叫比值。
同类量的比,其比值没有单位名称; 不同类量的比,其比值有单位名称。
例如:100千米:5时=20千米/时(2)化简比:比的前项和后项都是整数,并且是互质数,这样的比就是最简整数比。
把两个数的比化成最简整数比的,称为化简比或比的化简。
5.比与分数、除法的关系关系:比与分数相比,比的前项相当于分子,比的后项相当于分母,比值相当于分数值,比号相当于分数线;比与除法比较,比的前项相当于除法中的被除数,比的后项相当于除法中的除数,比值相当于商,比号相当于除号。
(1)比、分数和除法之间的联系与区别如下表所示:由比与分数、除法各部分间的关系可知,比的基本性质、分数的基本性质以及商不变的规律三者只是说法不同,其实质是一样的。
6.按比分配:(1)在工农业生产和日常生活中,常常需要把一个数量按照一定的比来进行分配,这种分配方法通常叫作按比分配。
(2)按比分配应用题的特征:已知总数量和部分数量的比,求各部分数量。
(3)常用的解题方法有两种:一种是先求总份数,再求各部分量占总量的几分之几,最后求各部分数量;另一种是先求每份是多少,再求几份是多少。
知识点二:比例1.比例的意义:表示两个比相等的式子叫做比例。
2.比例的各部分名称:组成比例的四个数,叫做比例的项。
两端的两项叫做外项,中间的两项叫做内项。
3.比例的基本性质:在比例里,两个外项的积等于两个内项的积。
这叫做比例的基本性质。
4.比和比例的区别(1)比表示两个量相除的关系,它有两项(即前、后项);比例表示两个比相等的式子,它有四项(即两个内项和两个外项)。
小升初数学3.5比和比例

小升初数学3.5比和比例五比和比例1.比的意义和性质(1) 比的意义两个数相除又叫做两个数的比。
“:”是比号,读作“比”。
比号前面的数叫做比的前项,比号后面的数叫做比的后项。
比的前项除以后项所得的商,叫做比值。
同除法比较,比的前项相当于被除数,后项相当于除数,比值相当于商。
比值通常用分数表示,也可以用小数表示,有时也可能是整数。
比的后项不能是零。
根据分数与除法的关系,可知比的前项相当于分子,后项相当于分母,比值相当于分数值。
(2)比的性质比的前项和后项同时乘上或者除以相同的数(0除外),比值不变,这叫做比的基本性质。
(3) 求比值和化简比求比值的方法:用比的前项除以后项,它的结果是一个数值可以是整数,也可以是小数或分数。
根据比的基本性质可以把比化成最简单的整数比。
它的结果必须是一个最简比,即前、后项是互质的数。
(4)比例尺图上距离:实际距离=比例尺要求会求比例尺;已知图上距离和比例尺求实际距离;已知实际距离和比例尺求图上距离。
线段比例尺:在图上附有一条注有数目的线段,用来表示和地面上相对应的实际距离。
(5)按比例分配在农业生产和日常生活中,常常需要把一个数量按照一定的比来进行分配。
这种分配的方法通常叫做按比例分配。
方法:首先求出各部分占总量的几分之几,然后求出总数的几分之几是多少。
2 比例的意义和性质(1) 比例的意义表示两个比相等的式子叫做比例。
组成比例的四个数,叫做比例的项。
两端的两项叫做外项,中间的两项叫做内项。
(2)比例的性质在比例里,两个外项的积等于两个两个内向的积。
这叫做比例的基本性质。
(3)解比例根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个数比例中的另外一个未知项。
求比例中的未知项,叫做解比例。
3 正比例和反比例(1) 成正比例的量两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,他们的关系叫做正比例关系。
小升初讲座 比和比例

【风雨数学小升初讲座】比和比例比是两个量相除的关系,例如男女生人数比是3:4,我们通常理解成男生有3份,女生有4份,他们的每份都相同。
比例包括正比例和反比例,正比例是比值相同,反比例是积相等,并且构成比的前项后项都是变量。
根据比和比例的定义,我们可以把它转化成份数计算,也可以转化成分数计算。
当然,用方程来计算也是不错的。
【题目1】圆珠笔和铅笔的价格比是4:3,20支圆珠笔和21支铅笔共用71.5元。
问圆珠笔的单价是每支多少元。
【解法一】用份数法来解答。
假设圆珠笔的单价是4份,铅笔的单价是4份,20支圆珠笔是20×4=80份,21支铅笔21×3=63份,80+63=143份共71.5元,每份71.5÷143=0.5元,圆珠笔的单价是4份,那么就是0.5×4=2元。
【解法二】用分数的方法解答。
铅笔的单价是圆珠笔的3/4,把圆珠笔的单价看作单位1,铅笔的单价就是3/4,那么21支圆珠笔相当于3/4×21=63/4,那么总共相当于20+63/4=143/4,圆珠笔的单价是71.5÷143/4=2元【解法三】用方程解答。
有两种设未知数的方法,设圆珠笔的单价是x元,或者设圆珠笔的单价是4x元。
前者用分数形式列方程,后面用整数的形式列方程。
3如果以圆珠笔的单价是x元来列方程,那么铅笔的单价就是x,则43可以列出方程20x+x×21=71.5元,解得x=24如果以圆珠笔的单价是4x来列方程,那么铅笔的单价是3x,则可列出方程4x×20+3x×21=71.5【题目2】加工一个零件,甲要2分钟,乙要3分钟,丙要4分钟。
现有1170个零件,甲乙丙三人各加工几个零件,才能使他们同时完成任务?【解答】先算出工作效率的比,然后按照工作效率的比来分配任务。
(1)甲每分钟加工1/2个零件,乙每分钟加工1/3个零件,丙每分钟加工1/4个零件。
小学六年级数学小升初珍藏版复习资料第5讲 比和比例(解析)
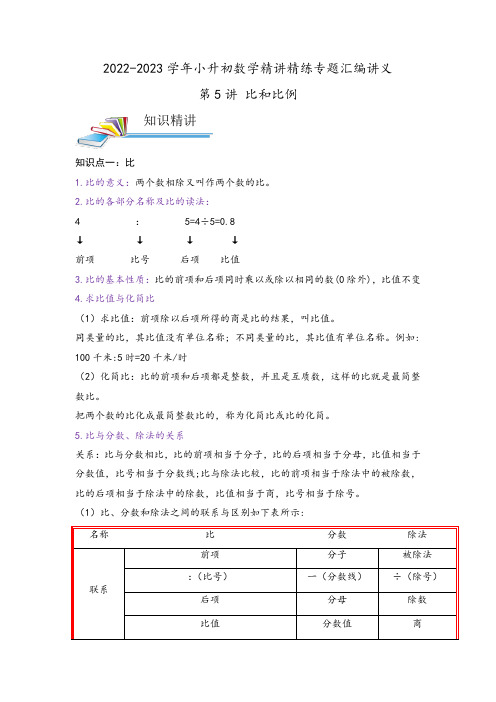
2022-2023学年小升初数学精讲精练专题汇编讲义第5讲比和比例知识点一:比1.比的意义:两个数相除又叫作两个数的比。
2.比的各部分名称及比的读法:4 : 5=4÷5=0.8↓↓↓↓前项比号后项比值3.比的基本性质:比的前项和后项同时乘以或除以相同的数(0除外),比值不变4.求比值与化简比(1)求比值:前项除以后项所得的商是比的结果,叫比值。
同类量的比,其比值没有单位名称; 不同类量的比,其比值有单位名称。
例如: 100千米:5时=20千米/时(2)化简比:比的前项和后项都是整数,并且是互质数,这样的比就是最简整数比。
把两个数的比化成最简整数比的,称为化简比或比的化简。
5.比与分数、除法的关系关系:比与分数相比,比的前项相当于分子,比的后项相当于分母,比值相当于分数值,比号相当于分数线;比与除法比较,比的前项相当于除法中的被除数,比的后项相当于除法中的除数,比值相当于商,比号相当于除号。
(1)比、分数和除法之间的联系与区别如下表所示:名称比分数除法联系前项分子被除法:(比号)一(分数线)÷(除号)后项分母除数比值分数值商知识精讲除法各部分间的关系可知,比的基本性质、分数的基本性质以及商不变的规律三者只是说法不同,其实质是一样的。
6.按比分配:(1)在工农业生产和日常生活中,常常需要把一个数量按照一定的比来进行分配,这种分配方法通常叫作按比分配。
(2)按比分配应用题的特征:已知总数量和部分数量的比,求各部分数量。
(3)常用的解题方法有两种:一种是先求总份数,再求各部分量占总量的几分之几,最后求各部分数量;另一种是先求每份是多少,再求几份是多少。
知识点二:比例1.比例的意义:表示两个比相等的式子叫做比例。
2.比例的各部分名称:组成比例的四个数,叫做比例的项。
两端的两项叫做外项,中间的两项叫做内项。
3.比例的基本性质:在比例里,两个外项的积等于两个内项的积。
这叫做比例的基本性质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【小升初奥数知识点讲解】比和比例
比和比例
比:两个数相除又叫两个数的比。
比号前面的数叫比的前项,比号后面的数叫比的后项。
比值:比的前项除以后项的商,叫做比值。
比的性质:比的前项和后项同时乘以或除以相同的数(零除外),比值不变。
比例:表示两个比相等的式子叫做比例。
a:b=c:d或
比例的性质:两个外项积等于两个内项积(交叉相乘),ad=bc。
正比例:若A扩大或缩小几倍,B也扩大或缩小几倍(AB的商不变时),则A与B成正比。
反比例:若A扩大或缩小几倍,B也缩小或扩大几倍(AB的积不变时),则A与B成反比。
比例尺:图上距离与实际距离的比叫做比例尺。
按比例分配:把几个数按一定比例分成几份,叫按比例分配。
