机载设备随机振动疲劳寿命分析-曹立帅
振动疲劳试验寿命确定方法研究_杨万均

振动疲劳试验寿命确定方法研究_杨万均DOI:10.13952/ki.jofmdr.2019.02.022第28卷第2期2019年4月机械设计与研究MachineDesignandResearchVol.28No.2Apr.,20192343(2019)02-071-02文章编号:1006-振动疲劳试验寿命确定方法研究杨万均,施荣明(沈阳飞机设计研究所,E-mail:yangwanjun2019@sohu.com)沈阳110035,摘要:提出了一种确定振动疲劳试验寿命的方法,首先基于有限元分析获得2A12铝合金简支梁试件的裂纹长度与试件固有频率的关系曲线,借助断裂力学失效准则,计算试件在试验载荷下疲劳失效时的临界裂纹长度,根据临界裂纹长度对应的固有频率能够确定试件疲劳失效时固有频率下降的幅度,从而根据振动疲劳试停机时所经历的循环数即为振动疲劳的试验寿命。
该方法结合理论验固有频率跟踪控制技术确定停机标准,与实际,为振动疲劳试验寿命的确定提供了理论依据,统一了试验标准,并且在实际操作试验过程中容易操作,所得的结果安全可靠。
关键词:振动疲劳;裂纹扩展动应力强度因子;试验寿命中图分类号:V215.5文献标识码:AResearchontheConfirmationMethodofVibrationFatigueExperimentLifeYANGWan-jun,SHIRong-ming(ShenyangAircraftDesignandResearchInstitute,Shenyang110035,China)Abstract:Anovelmethodofdeterminingthevibrationfatigueexperimentlifewasproposedinthispap er.Firsttherelationshipbetweenthecracklengthandthemodalfrequencyofthealuminiu malloy2A12modelwasacquiredbyfiniteelementanalysis.Accordingtothefracturefailu rerule,thecriticalcracklengththespecimencanbecomputedatexperimentloadspectrum,thedecreasesoftheinherentfrequencywhenthespecimenfailuredcanbedetermined.Then thestoppingcriterionofvibrationfatigueexperimentscanbeconfirmedbytheinherentfrequencytrackingandcontrol-lingtechnology,andthetimeorcirclesexperiencedwhenstoppingisrightthevibrationfatigueexperiment life.Themethodprovidedtheoreticalcriterionfordetermingthevibrationfatigueexpe rimentlifebycombiningthetheoriesandapplications,andthecriterionofthevibrationfatigueexperimentwasunified.Itisalsoeasytooperat eandtheresultswasreliable.Keywords:vibrationfatigue;crackpropagation;dynamicstressintensityfactor;experimentlife9]提出以结构固有频率下降人员带来很大的困难。
Fluent 资料集合(续)

流体动力学的并行计算(EN)
流体动力学的有限元法(EN) 流体动力学的有限元法(卷3)(EN) 流体动力学和流体机械手册卷1(EN)
10.Fluent动网格教程分享
fluent动荡讲座
fluent动态网讲座 fluent动态网教程1—8
11.Fluent软件知多少
相当水力直径进行计算?
A:1.如果不画边界层的计算结果与实验值的误差在工程精度范围内,是 可以接受的;但是,正如贴主所说,有边界层算的更准,那保证网格质 量就没有多大意义了。 2.如果不画边界层网格,建议采用k-epsilon Realizable湍流模型。
3.计算水力直径,应当是计算域流体入口的水力直径:H=4A/C(A为入口
7.2014 ANSYS技术大会讲义集--系统
ANSYS SBU视觉从三维到嵌入式软件 UGM V2
Ansys_基于模型的系统和软件工程_傅金泉_v2.0
UGM V1的SCADE创新 先进的UGM V7系统设计 张国明-云时代的中国仿真 - 2014 ANSYS中国UGM演讲V2
8.FLUENT超级学习手册
Fluent 14.5 Eulerian Wall Film Defogging官方教程
Fluent 14.5自定义输入参数官方教程
Fluent_14.5meshing官方教程 Fluent 14.5 FSI官方教程 Fluent 14.5 built-in tutorials Fluent 14.5传热 官方教程
3.之前利用fluent计算敞水时舵的水动力,采用SST湍流模型,分别用有
边界层和无边界层进行计算,无边界层计算的升力、阻力比有边界层的 大10%左右,有边界层更接近实验值。不过失速角和变化趋势还是一致的
机载设备随机振动疲劳寿命分析-曹立帅

3σ的概率为0.27%。可以看出,随机变量超出3σ量级的可能性已很小,采用
3σ已可以满足工程要求。
由上可知,大于3σ的应力仅仅发生在0.27%的时间内,假定其不造成任何损
伤。在利用Miner线性累积损伤理论进行疲劳计算时,将应力处理成上述3个水平,
总体损伤的计算公式就可以写成:
D = n1σ + n2σ + n3σ
(4)
N1σ N2σ N3σ
n1σ :等于或低于1σ水平的实际循环数目(0.6831); n2σ :等于或低于2σ水平的实际循环数目(0.271); n3σ :等于或低于3σ水平的实际循环数(0.0433)。
N1σ , N2σ , N3σ 分别为根据疲劳曲线计算求得的1σ、2σ和3σ应力水平对 应的许可循环的次数。 2.3 随机振动疲劳寿命分析流程
次对材料的损伤为 D/N1,经 n1 次循环作用后,σ1 对材料的总损伤为 n1D/N1,如此
类推,当各级应力对材料的损伤综合达到临界值 D 时,材料发生破坏。用公式表
示为
n1D + n2D + n3D +... = D
(1)
N1 N2 N3
推广到更普遍的情况,即有
∑∞ ni = 1
(2)
N i=1 i
约束:试验台的底面设为固定约束; 载荷:在 X、Y、Z 三个方向上分别施加功率谱密度。
图 4 功率谱密度曲线
3.3 疲劳寿命评估 通过对计算结果的分析,得到控制壳体上危险部位出现在耳片位置上,同时
分别得到该部位三个方向上 1σ、2σ和 3σ应力。
图 5 X 方向加载时耳片危险部位最大 1σ应力图
材料抗拉强度σb =490MPa
7
N3σ=5.44×10 。
随机振动疲劳寿命预测方法研究

随机振动疲劳寿命预测方法研究随机振动是在振动研究中一个重要的方面,它不仅可以模拟复杂的工程问题,而且可以用于预测疲劳寿命的预测。
本文将介绍随机振动疲劳寿命预测方法的原理、主要方法及其应用,并对研究进展进行概述。
一、随机振动疲劳寿命预测方法原理随机振动疲劳寿命预测是根据测试发生在机械结构中的振动情况,通过数值方法和实验方法来估算结构的寿命。
振动通常是实际的受力原因,从而导致结构的早期疲劳和衰减,从而影响结构的使用寿命。
随机振动是一种不可预测的振动,它可能来自外部的环境或加载,也可能来自机械结构自身的动态特性。
一般来说,随机振动可以分为低频和高频两种。
低频随机振动来自恶劣的环境或罕见的加载,而高频随机振动则来自结构自身的动态特性。
通过将随机振动信号分解,其中的各个分量构成随机振动疲劳寿命预测的基础。
二、主要方法(1)加速度空间灰色关联分析法加速度空间灰色关联分析法是一种基于加速度信号(能量空间模型)的灰色预测技术。
根据监测加速度信号的空间相关性,本方法可以有效地提取其中的振动特征,并预测结构疲劳寿命。
它是一种分步灰色预测法,采用灰色关联数据变换(GCDT)算法来实现信号的分类,提取足够的特征向量,再采用灰色预测技术来估算疲劳寿命。
(2)加速度时域参数方法加速度时域参数方法是一种基于加速度信号的动态参数分析方法。
根据监测加速度信号,研究者从时间和频率上提取相关参数,如“振幅”、“峰值”、“峰值因子”、“保守系数”等,从而得到疲劳寿命的预测值。
本方法采用的参数较多,预测结果更加准确,但是计算复杂,要求更高。
三、应用随机振动疲劳寿命预测方法主要应用于汽车的发动机和传动系统的预测,同时也应用于船舶柴油机、发电机组、齿轮箱及其他链条系统的疲劳寿命预测。
在发动机和传动系统中,汽车设计者要求通过对随机振动进行分析和综合,来估算设计寿命,以实现安全可靠的汽车使用。
因此,结合动态负荷分布、结构比重和疲劳材料强度计算,此类测试结果常用于分析汽车动力总成和传动系统的疲劳设计要求,以实现安全可靠的设计寿命。
离心通风机结构随机振动下的疲劳分析
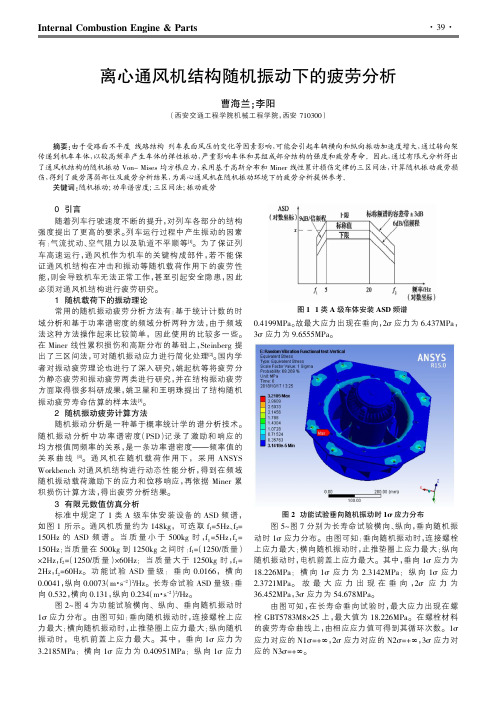
Internal Combustion Engine&Parts0引言随着列车行驶速度不断的提升,对列车各部分的结构强度提出了更高的要求。
列车运行过程中产生振动的因素有:气流扰动、空气阻力以及轨道不平顺等[1]。
为了保证列车高速运行,通风机作为机车的关键构成部件,若不能保证通风机结构在冲击和振动等随机载荷作用下的疲劳性能,则会导致机车无法正常工作,甚至引起安全隐患,因此必须对通风机结构进行疲劳研究。
1随机载荷下的振动理论常用的随机振动疲劳分析方法有:基于统计计数的时域分析和基于功率谱密度的频域分析两种方法,由于频域法这种方法操作起来比较简单,因此使用的比较多一些。
在Miner线性累积损伤和高斯分布的基础上,Steinberg提出了三区间法,可对随机振动应力进行简化处理[2]。
国内学者对振动疲劳理论也进行了深入研究,姚起杭等将疲劳分为静态疲劳和振动疲劳两类进行研究,并在结构振动疲劳方面取得很多科研成果,姚卫星和王明珠提出了结构随机振动疲劳寿命估算的样本法[3]。
2随机振动疲劳计算方法随机振动分析是一种基于概率统计学的谱分析技术。
随机振动分析中功率谱密度(PSD)记录了激励和响应的均方根值同频率的关系,是一条功率谱密度———频率值的关系曲线[4]。
通风机在随机载荷作用下,采用ANSYS Workbench对通风机结构进行动态性能分析,得到在频域随机振动载荷激励下的应力和位移响应,再依据Miner累积损伤计算方法,得出疲劳分析结果。
3有限元数值仿真分析标准中规定了1类A级车体安装设备的ASD频谱,如图1所示。
通风机质量约为148kg,可选取f1=5Hz、f2= 150Hz的ASD频谱。
当质量小于500kg时,f1=5Hz,f2= 150Hz;当质量在500kg到1250kg之间时:f1=(1250/质量)×2Hz,f2=(1250/质量)×60Hz;当质量大于1250kg时,f1= 2Hz,f2=60Hz。
随机振动载荷下机械零部件疲劳寿命预测研究

随机振动载荷下机械零部件疲劳寿命预测研究
杜卫丹;顾昌铃;李修旋
【期刊名称】《机械与电子》
【年(卷),期】2024(42)6
【摘要】针对机械零部件疲劳寿命预测准度较低的问题,提出一种随机振动载荷下机械零部件疲劳寿命预测方法。
对随机振动载荷下机械零部件开展疲劳分析,根据机械零部件的应力/应变响应,获取一定范围内的机械零部件疲劳部位应力功率谱密度函数。
基于累计损伤理论和S-N曲线,进一步估算出随机振动载荷下机械零部件疲劳寿命,实现机械零部件寿命预测研究。
实验结果表明,该方法的应力功率谱密度与实际结果一致,在不同振幅及预压量下的机械零部件疲劳寿命预测结果均较为准确,验证了该方法的可靠性高。
【总页数】5页(P65-69)
【作者】杜卫丹;顾昌铃;李修旋
【作者单位】上海烟草机械有限责任公司
【正文语种】中文
【中图分类】TH113.1
【相关文献】
1.随机振动载荷下大直径薄壁球形结构疲劳寿命分析
2.随机载荷循环作用下的机械结构疲劳寿命预测模型
3.随机振动载荷下塑封球栅阵列含铅焊点疲劳寿命模型
4.
随机振动载荷下电子箱PCBA焊点疲劳寿命分析5.浅析干涉量对随机振动载荷作用下航空液压管路疲劳寿命的影响
因版权原因,仅展示原文概要,查看原文内容请购买。
某机载雷达天馈伺系统结构疲劳寿命评估

某机载雷达天馈伺系统结构疲劳寿命评估杨志刚;房凯【摘要】机载雷达作为重要的航空电子设备,要求其结构在一定寿命周期内必须能够承受载机特有的随机振动环境,且不发生破坏.随机振动是造成机载雷达结构发生疲劳损坏的关键因素,如何找出结构的薄弱部位,并对薄弱部位进行疲劳寿命评估是在机载雷达研发阶段的重要工作.本文基于有限元法及Miner线性累积损伤理论系统阐述了进行结构疲劳寿命评估的理论依据及详细的工程实践方法,并对某机载雷达天馈伺系统结构进行了疲劳寿命评估.【期刊名称】《火控雷达技术》【年(卷),期】2018(047)004【总页数】5页(P90-93,98)【关键词】机载雷达;天馈伺系统;疲劳寿命;累积损伤;有限元【作者】杨志刚;房凯【作者单位】南京电子技术研究所南京210039;中国人民解放军驻南京电子技术研究所军事代表室南京210039【正文语种】中文【中图分类】TP391.90 引言机载雷达作为重要的航空电子设备,要求其结构能够承受载机平台特有的振动环境,并且在一定寿命周期内不发生结构破坏[1-2]。
随机振动是造成结构破坏的关键因素,也是振动工程领域研究的一个重点问题[3-5]。
随机振动对结构造成损坏的过程与机理相当复杂,最直接的方法是采用试验方法对结构进行验证,试验方法虽然直接有效,但不利于从开始的设计阶段就发现结构的薄弱环节,以及不能有效避免可能破坏的发生,且重复地修改设计-试验将使研发周期变得很长,高成本但效率低下。
有限元法作为现代飞速发展起来的一种工程分析方法,有效解决了此问题,我们不再需要重复修改设计与试验,可以通过有限元分析,事先知道我们想了解的信息,并对设计进行评估,而使研发变得更高效、低成本。
有限元法不但能给出整体的详细信息,还能给出局部的详细信息,如加速度、应力、应变响应等,目前,在工程领域较多地采用有限元法用于随机振动分析。
通过随机振动响应分析可找出结构的危险部位,再对结构危险部位进行疲劳分析,进而对整体的结构疲劳寿命进行评估[6-7]。
随机振动疲劳寿命预测方法研究

随机振动疲劳寿命预测方法研究随机振动疲劳寿命预测方法研究随机振动是指在一定时间内,不同时刻上所发生的振动信号之间存在差异性的振动。
由于许多机械结构都会遭受到不可预测的外界环境干扰,这些外界环境干扰的特性通常被抽象为随机振动。
因此,要准确地预测机械结构的寿命,就必须对其受到的随机振动进行有效的分析和预测。
随机振动分析中的疲劳寿命预测是一个重要的研究内容。
疲劳寿命是指机械结构在设计使用条件下,能够耐受的最大的疲劳应力循环次数或者疲劳应力循环时间。
疲劳寿命预测是指根据机械结构的设计参数和受到的振动信号,预测该机械结构的疲劳寿命。
疲劳寿命预测的方法主要包括:静态疲劳预测方法、静动态耦合疲劳预测方法、单峰值疲劳预测方法和随机振动疲劳预测方法。
由于随机振动疲劳预测方法能更好地反映实际环境,因此,随机振动疲劳预测方法也是最常用的疲劳预测方法之一。
随机振动疲劳寿命预测方法主要依赖于随机振动理论,该理论可以将随机振动过程分解为三个独立的过程:功率谱密度函数、相位移动函数和幅度变化函数。
功率谱密度函数描述了振动的能量分布情况;相位移动函数描述了振动的相位变化;而幅度变化函数则描述了振动的幅度变化。
随机振动疲劳寿命预测的基本原理是:将受到的振动信号转换为功率谱密度函数、相位移动函数和幅度变化函数,然后根据疲劳理论,以及功率谱密度函数、相位移动函数和幅度变化函数作为输入参数,计算出机械结构受到的疲劳应力和应变,从而确定其疲劳寿命。
随机振动疲劳寿命预测可以更加准确地反映机械结构实际的疲劳寿命,尤其是在受到非常复杂的随机振动时,其预测结果更为可靠。
然而,随机振动疲劳寿命预测的计算量较大,而且需要准确的功率谱密度函数、相位移动函数和幅度变化函数,因此,随机振动疲劳寿命预测的可靠性取决于这些函数的准确性。
随机振动疲劳寿命预测方法也可以改进,例如采用改进的功率谱密度函数,改进的相位移动函数,改进的幅度变化函数,以及改进的疲劳理论,以期提高疲劳寿命预测的准确性和可靠性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机载设备随机振动疲劳寿命分析
作者姓名:曹立帅,李刚,顾卫平 作者单位:庆安集团有限公司航空设备研究所 联系方式:029-84636527
机载设备随机振动疲劳寿命分析
1
曹立帅 ,李刚,顾卫平
(庆安集团有限公司航空设备研究所,陕西 西安 710077)
摘要:机载设备在使用过程中会面临恶劣的随机振动环境,容易出现振动疲 劳问题。本文应用Miner线性累积损伤理论和三区间技术,阐述了随机振动疲劳 寿命仿真分析方法,并以某机载设备控制壳体为例,得到宽带振动环境下与试验 结果相吻合的仿真结果,证明在研发过程中可运用此方法预测产品的随机振动疲 劳寿命并进行结构的改进优化。
次对材料的损伤为 D/N1,经 n1 次循环作用后,σ1 对材料的总损伤为 n1D/N1,如此
类推,当各级应力对材料的损伤综合达到临界值 D 时,材料发生破坏。用公式表
示为
n1D + n2D + n3D +... = D
(1)
N1 N2 N3
推广到更普遍的情况,即有
∑∞ ni = 1
Hale Waihona Puke (2)N i=1 i关键词:随机振动;三区间技术;疲劳寿命
Random Vibration Fatigue Life Analysis on Airborne Equipment Cao Lishuai1, Li Gang, Gu Weiping
(Aviation Equipment Institute,Qingan Group Co. Ltd, Xi’an 710077, Shaanxi Province, China)
3σ的概率为0.27%。可以看出,随机变量超出3σ量级的可能性已很小,采用
3σ已可以满足工程要求。
由上可知,大于3σ的应力仅仅发生在0.27%的时间内,假定其不造成任何损
伤。在利用Miner线性累积损伤理论进行疲劳计算时,将应力处理成上述3个水平,
总体损伤的计算公式就可以写成:
D = n1σ + n2σ + n3σ
式(3)中:x为瞬态随机变量;σ为均方根值(如加速度、应力和位移等)。
概率曲线见图1。由图1可知:瞬态随机变量落入-σ~σ之间的概率为68.3%,即
超出σ的概率为31.7%;瞬态随机变量落入-2σ~2σ之间的概率为95.4%,即超
出2σ的概率为4.6%;瞬态随机变量落入-3σ~3σ之间的概率为99.73%,即超出
1 前言
机载设备在飞机使用过程中各阶段均经历不同振动环境的考验,在研制过程 中为保证高可靠性要进行严酷的振动试验。机载设备随机振动仿真分析过程中, 对于复杂的模型,通常将计算模型合理简化,其他部件等效为集中质量,然后将 振动试验功率谱作为输入条件进行应力分析,最后根据线性累积损伤理论及三区 间技术进行结构的疲劳寿命计算。
2 线性疲劳累积损伤理论与随机振动
2.1 Miner 线性疲劳累积损伤理论
线性累积损伤理论认为,材料在各个应力下的疲劳损伤是独立进行的,并且
[1]
总损伤可以进行线性累加 。
应力作用σ1 作用 n1 次,该应力水平下材料达到破坏的总循环次数为 N1。设
D 为最终断裂时的损伤临界值,根据线性疲劳累加损伤理论,应力σ1 每作用一
心极限定理,若随机现象由众多随机因素引起,且每个因素在总的变化里不起显
著作用,就可认为描述该随机现象的随机变量近似服从Gaussian分布,一般各态
历经平稳随机过程服从Gaussian分布。均值为0的Gaussian分布概率密度可用式
(3)表示。
P(x) =
1
e−
x2 2σ 2
σ 2π
(3)
图 1 Gaussian 分布曲线
2.2 随机振动及三区间技术
当应力历程是随机过程时,疲劳计算相对比较复杂,Steinberg 提出了更加
[2]
简单的基于高斯分布和 Miner 线性累计损伤定律的三区间法 ,该技术假设瞬态
随机变量以σ,2σ和 3σ量级的发生概率分别为 68.3%,27.1%和 4.33%。
Gaussian分布又被称为正态分布,是一种常见的重要分布,依据概率论的中
(4)
N1σ N2σ N3σ
n1σ :等于或低于1σ水平的实际循环数目(0.6831); n2σ :等于或低于2σ水平的实际循环数目(0.271); n3σ :等于或低于3σ水平的实际循环数(0.0433)。
N1σ , N2σ , N3σ 分别为根据疲劳曲线计算求得的1σ、2σ和3σ应力水平对 应的许可循环的次数。 2.3 随机振动疲劳寿命分析流程
