第一章-空间几何体的表面积和体积练习题
高一数学空间几何体的表面积与体积试题答案及解析

高一数学空间几何体的表面积与体积试题答案及解析1. 已知正方体的棱长为1,且其顶点都在一个球面上,则该球的表面积为( ) A .π B .2π C .3π D .4π【答案】C.【解析】正方体的对角线长为外接球的直径,因此,,因此.【考点】球的表面积公式.2. 如图,在四边形ABCD 中,∠DAB =90°,∠ADC =135°,AB =5,CD =2,AD =2,求四边形ABCD 绕AD 旋转一周所成几何体的表面积及体积.【答案】S 表面=(60+4)π.V =π.【解析】该图形旋转后是一个圆台除去一个倒放的圆锥, 则S 表面=S 下底面+S 台侧面+S 锥侧面 , 设圆台上,下地面半径是r 1,r 2,则 S 表面=π×r 22+π×(r 2+r 1)×5+π×r 1×CDV =V 台-V 锥=π(+r 1r 2+)AE -πr 2DE ,将数据代入计算即可。
试题解析:如图,设圆台上,下地面半径是r 1,r 2,过C 点作CF ⊥AB ,由∠ADC =135°,CE ⊥AD, CD=2得∠EDC =45°,r 1=" CE=" 2,则CF=4,BF=3,CF ⊥AB ,得BC=5,r 2=" AB=" 5, ∴S 表面=S 下底面+S 台侧面+S 锥侧面 =π×r 22+π×(r 2+r 1)×5+π×r 1×CD =π×52+π×(2+5)×5+π×2×2 =(60+4)π. V =V 台-V 锥=π(+r 1r 2+)AE -πDE =π(+2×5+)4-π×2=π.【考点】圆台,圆锥的表面积和体积.3.如图,在长方体ABCD—A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点,连结ED,EC,EB和DB.(1)求证:ED⊥平面EBC;(2)求三棱锥E-DBC的体积.【答案】(1)见解析;(2)【解析】(1)易得△DD1E为等腰直角三角形DE⊥EC,BC⊥平面 BC⊥DE,所以DE⊥平面EBC平面DEB⊥平面EBC.(2)需要做辅助线,取CD中点M,连接EM∥,DCB(这个证明很关键),然后根据公式.试题解析:(1)在长方体ABCD-A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点.∴△DD1E为等腰直角三角形,∠D1ED=45°.同理∠C1EC=45°.∴,即DE⊥EC.在长方体ABCD-中,BC⊥平面,又DE平面,∴BC⊥DE.又,∴DE⊥平面EBC.又∴平面DEB⊥平面EBC.(2)取CD中点M,连接EM,E为D1C1的中点,∥,且,又DCB.【考点】线面垂直,三棱锥的体积.4.设甲、乙两个圆柱的底面积分别为,体积分别为,若它们的侧面积相等,且,则的值是.【答案】【解析】设甲、乙两个圆柱的底面半径为,母线长,由于侧面积相等,,,,.【考点】圆柱的体积公式应用.5.如果两个球的体积之比为8:27,那么两个球的表面积之比为()A.8:27B.2:3C.4:9D.2:9【答案】C【解析】由题意,故选C【考点】球的体积和表面积6.棱长为4的正方体的八个顶点都在同一个球面上,则此球的表面积为_____________.【答案】48【解析】正方体的外接球的球心为正方体的中心,球的直径为正方体的对角线,所以球的表面积为【考点】正方体的外接球7.如图是从上下底面处在水平状态下的棱长为的正方体中分离出来的.有如下结论:①在图中的度数和它表示的角的真实度数都是;②;③与所成的角是;④若,则用图示中这样一个装置盛水,最多能盛的水.其中正确的结论是(请填上你所有认为正确结论的序号).【答案】①④【解析】①∵在正视图的等腰直角中,在图中的度数和它表示的角的真实度数都是,故①正确;②补全正方体如图所示:连接.∵,∴是正三角形,故.而==,故②错;③连接、,∵,∴是正三角形,所以与所成的角是,故③错;④用图示中这样一个装置来盛水,那么盛最多体积的水时应是三棱锥的体积.又===,故④正确,故填①④.【考点】1、正方体的性质;2、异面直线所成角;3、三棱锥的体积.8.已知一个正三棱锥的三条侧棱两两垂直且相等,底面边长为,则该三棱锥的外接球的表面积是()A.B.C.D.【答案】A【解析】设该正三棱锥为,依题意两两垂直且,所以,且该正三棱锥的外接球与以为邻边的正方体的外接球是相同的,正方体的边长为,体对角线长为,故球的半径为,所以球的表面积为,故选A.【考点】1.三棱锥的外接球;2.球的表面积公式.9.如图,已知直三棱柱中,,,,D为BC的中点.(1)求证:∥面;(2)求三棱锥的体积.【答案】(1)略(2)【解析】(1)连接交于点O,连接OD,在中可根据中位线证得∥,再根据线面平行的性质定理可证得∥面。
高二数学空间几何体的表面积与体积试题答案及解析

高二数学空间几何体的表面积与体积试题答案及解析1.正四棱锥的五个顶点在同一个球面上,若其底面边长为4,侧棱长为,则此球的表面积为()A.B.C.D.【答案】B【解析】设球的半径为,正方形的ABCD的对角线的交点 M,则球心在直线PM上.,由勾股定理得,再由射影定理得即∴此球的表面积为.【考点】球的表面积.2.一个圆柱形的罐子半径是4米,高是9米,将其平放,并在其中注入深2米的水,截面如图所示,水的体积是()平方米.A.B.C.D.【答案】D.【解析】所求几何体的体积为阴影部分的面积与高的乘积,在中,,则,,体积.【考点】组合体的体积.3.一个四棱锥的侧棱长都相等,底面是正方形,其正视图如图所示,则该四棱锥的侧面积是_________.【答案】【解析】由正视图可知四棱锥的底面边长为2,高为2,可求出斜高为,因此四棱锥的侧面积,答案为.【考点】1.几何体的三视图;2.锥体的侧面积计算4.已知球的直径SC=4,A.,B是该球球面上的两点,AB=2,∠ASC=∠BSC=45°,则棱锥S-ABC的体积为_________【答案】【解析】设AB的中点为D,球心为O,连结SD,CD,OD,由SC=4为球的直径知,∠SBC=∠SAC=90o,因为∠ASC=∠BSC=45°,所以SA=BC=SB=AC=,所以SD⊥AB,DC⊥AB,所以AB⊥面SDC,因为AB=2,所以SD=DC==,所以DO= =,所以= ===.考点:球的性质,线面垂直判定,三棱锥的体积公式,转化思想5.如图,一个盛满水的三棱锥容器,不久发现三条侧棱上各有一个小洞,且知,若仍用这个容器盛水,则最多可盛水的体积是原来的 .【答案】【解析】过作截面平行于平面,可得截面下体积为原体积的,若过点F,作截面平行于平面,可得截面上的体积为原体积的,若C为最低点,以平面为水平上面,则体积为原体积的,此时体积最大.【考点】体积相似计算.6.一个半径为1的小球在一个内壁棱长为的正四面体封闭容器内可向各个方向自由运动,则该小球表面永远不可能接触到的容器内壁的面积是.【答案】【解析】如图甲,考虑小球挤在一个角时的情况,记小球半径为,作平面//平面,与小球相切于点,则小球球心为正四面体的中心,,垂足为的中心.因,故,从而.记此时小球与面的切点为,连接,则.考虑小球与正四面体的一个面(不妨取为)相切时的情况,易知小球在面上最靠近边的切点的轨迹仍为正三角形,记为,如图乙.记正四面体的棱长为,过作于.因,有,故小三角形的边长.小球与面不能接触到的部分的面积为(如答图2中阴影部分).又,,所以.由对称性,且正四面体共4个面,所以小球不能接触到的容器内壁的面积共为.【考点】(1)三棱锥的体积公式;(2)分情况讨论及割补思想的应用。
高三高考数学复习练习82空间几何体的表面积与体积

821.一个球的表面积是16π,那么这个球的体积为( )A.163π B.323π C .16π D .24π【解析】 设球的半径为R ,因为表面积是16π,所以4πR 2=16π,解得R =2,所以体积为43πR 3=32π3. 【答案】 B2.某几何体的三视图如图所示,则其表面积为( )A .πB .2πC .3πD .4π【解析】 由三视图可知,该几何体为半径为r =1的半球体,表面积为底面圆面积加上半球面的面积,所以S =πr 2+12×4πr 2=π×12+12×4π×12=3π.故选C. 【答案】 C3.在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2.将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.2π3B.4π3C.5π3 D .2π【解析】 过点C 作CE 垂直AD 所在直线于点E ,梯形ABCD 绕AD 所在直线旋转一周而形成的旋转体是由以线段AB 的长为底面圆半径,线段BC 为母线的圆柱挖去以线段CE 的长为底面圆半径,ED 为高的圆锥,如图所示,该几何体的体积为V =V圆柱-V 圆锥=π·AB 2·BC -13·π·CE 2·DE =π×12×2-13π×12×1=5π3,故选C. 【答案】 C4.一个四面体的三视图如图所示,则该四面体的表面积是( )A .1+ 3B .2+ 3C .1+2 2D .2 2 【解析】 由空间几何体的三视图可得该空间几何体的直观图,如图所示,∴该四面体的表面积为S 表=2×12×2×1+2×34×(2)2=2+3,故选B. 【答案】 B5.(2018·太原一模)某几何体的三视图如图所示,则该几何体的表面积为( )A .6π+1B.(24+2)π4+1C.(23+2)π4+12D.(23+2)π4+1 【解析】 由几何体的三视图知,该几何体为一个组合体,其中下部是底面直径为2,高为2的圆柱,上部是底面直径为2,高为1的圆锥的四分之一,所以该几何体的表面积为4π+π+3π4+2π4+1=(23+2)π4+1,故选D. 【答案】 D6.甲几何体(上)与乙几何体(下)的组合体的三视图如图所示,甲、乙几何体的体积分别为V 1,V 2,则V 1∶V 2等于( )A .1∶4B .1∶3C .2∶3D .1∶π【解析】 由三视图知,甲几何体是半径为1的球,乙几何体是底面半径为2,高为3的圆锥,所以球的体积V 1=43π,V 2=13π×22×3=4π,所以V 1∶V 2=1∶3.故选B. 【答案】 B7.(2017·全国Ⅲ卷)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A .πB.3π4C.π2D.π4【解析】 设圆柱的底面半径为r ,球的半径为R ,且R =1,由圆柱两个底面的圆周在同一个球的球面上可知,r ,R 及圆柱的高的一半构成直角三角形.∴r = 12-⎝⎛⎭⎫122=32.∴圆柱的体积为V =πr 2h =34π×1=3π4. 故选B.【答案】 B8.(2017·襄阳调研)如图是一个空间几何体的三视图,则该几何体的表面积为________.【解析】 由三视图可知,该几何体是一个正四棱柱挖掉一个半球所得的几何体,其中半球的底面就是正四棱柱上底面的内切圆,正四棱柱的底面边长为4,高为2,半球所在球的半径为2.所以该几何体的表面由正四棱柱的表面与半球的表面积之和减去半球的底面构成,故其表面积为(4×4×2+2×4×4)+12×(4π×22)-π×22=64+4π. 【答案】 64+4π9.(2018·乌鲁木齐二诊)已知四面体ABCD 满足AB =CD =6,AC =AD =BC =BD =2,则四面体ABCD 的外接球的表面积是________.【解析】 (图略)在四面体ABCD 中,取线段CD 的中点为E ,连接AE ,BE .∵AC =AD =BC =BD =2,∴AE ⊥CD ,BE ⊥C D.在Rt △AED 中,CD =6,∴AE =102.同理BE =102.取AB 的中点为F ,连接EF .由AE =BE ,得EF ⊥A B.在Rt △EF A 中,∵AF =12AB =62,AE =102,∴EF =1.取EF 的中点为O ,连接OA ,则OF =12.在Rt △OF A 中,OA =72.∵OA =OB =OC =OD ,∴该四面体的外接球的半径是72,∴外接球的表面积是7π. 【答案】 7π10.(2018·贵州适应性考试)已知球O 的表面积是36π,A ,B 是球面上的两点,∠AOB =60°,C 是球面上的动点,则四面体OABC 体积V 的最大值为________.【解析】 设球的半径为R ,由4πR 2=36π,得R =3.显然在四面体OABC 中,△OAB 的面积为定值,S △OAB =12×R ×32R =34R 2=934.要使三棱锥的体积最大,只需球上的点到平面OAB 的距离最大,显然,到平面OAB 距离的最大值为球的半径,所以四面体OABC 的体积的最大值V =13×934×R =934. 【答案】 93411.(2016·全国丙卷)如图,四棱锥P -ABCD 中,P A ⊥底面ABCD ,AD ∥BC ,AB =AD =AC =3,P A =BC =4,M 为线段AD 上一点,AM =2MD ,N 为PC 的中点.(1)证明:MN ∥平面P AB ;(2)求四面体N -BCM 的体积.【解析】 (1)证明 由已知得AM =23AD =2. 如图,取BP 的中点T ,连接AT ,TN ,由N 为PC 中点知TN ∥BC ,TN =12BC =2. 又AD ∥BC ,故TN 綊AM ,所以四边形AMNT 为平行四边形,于是MN ∥AT .因为AT ⊂平面P AB ,MN ⊄平面P AB ,所以MN ∥平面P AB .(2)因为P A ⊥平面ABCD ,N 为PC 的中点,所以N 到平面ABCD 的距离为12P A. 取BC 的中点E ,连接AE .由AB =AC =3得AE ⊥BC ,AE =AB 2-BE 2= 5.由AM ∥BC 得M 到BC 的距离为5,故S △BCM =12×4×5=2 5. 所以四面体N -BCM 的体积V N -BCM =13×S △BCM ×P A 2=453. 12.如图所示,在空间几何体ADE -BCF 中,四边形ABCD 是梯形,四边形CDEF 是矩形,且平面ABCD ⊥平面CDEF ,AD ⊥DC ,AB =AD =DE =2,EF =4,M 是线段AE 上的动点.(1)试确定点M 的位置,使AC ∥平面MDF ,并说明理由;(2)在(1)的条件下,平面MDF 将几何体ADE -BCF 分成两部分,求空间几何体M -DEF 与空间几何体ADM -BCF 的体积之比.【解析】(1)当M 是线段AE 的中点时,AC ∥平面MDF .理由如下:连接CE 交DF 于点N ,连接MN .因为M ,N 分别是AE ,CE 的中点,所以MN ∥AC .又因为MN ⊂平面MDF ,AC ⊄平面MDF ,所以AC ∥平面MDF .(2)将几何体ADE -BCF 补成三棱柱ADE -B ′CF ,如图所示,三棱柱ADE -B ′CF 的体积为V =S △ADE ·CD =12×2×2×4=8,则几何体ADE -BCF 的体积V ADE BCF =V ADE B ′CF -V F BB ′C=8-13×⎝⎛⎭⎫12×2×2×2=203. 因为三棱锥M -DEF 的体积V M DEF =13×⎝⎛⎭⎫12×2×4×1=43, 所以V ADM BCF =203-43=163, 所以两几何体的体积之比为43∶163=1∶4.。
空间几何体的表面积与体积习题附答案

空间几何体的表面积与体积习题附答案1.圆柱的侧面积可以通过展开图计算,展开图是一个正方形,边长为2πr,所以侧面积为4πr^2,即4πS,因此选项为A。
2.根据三视图可以看出该几何体由两个同底的半圆锥组成,底面半径为1,高为3,因此体积为2×(1/3)πr^2h=π,因此选项为D。
3.根据三视图可以看出该几何体是一个组合体,由一个底面为等腰直角三角形的直三棱柱和一个底面为等腰直角三角形的三棱锥组成。
直三棱柱的高为2,三棱锥的高为2,因此梯形的高为2,底边为2和4,面积为(2+4)×2/2=6,共有2个梯形,因此梯形的面积之和为12,因此选项为B。
4.根据三视图可以看出该几何体为一个圆柱挖去一个同底的圆锥,圆锥的高为圆柱高的一半,因此圆锥的高为2,圆柱的底面积为π,侧面积为4π,圆锥的侧面积为2π×5/2=5π,因此表面积为π+4π+5π=9π+5π,因此选项为A。
5.根据三视图可以看出该几何体为一个直三棱柱削去一个同底的三棱锥,三棱柱的高为5,三棱锥的高为3,三棱锥与三棱柱的底面均为两直角边分别为3和4的直角三角形,因此三棱柱的体积为底面积×高=3×4×5=60,三棱锥的体积为1/3×底面积×高=1/3×3×4×3=4,因此该几何体的体积为60-4=56,因此选项为C。
C1F=4,连接EF,交AD于点G,求三角形AEF和四边形ABCG的面积和长方体ABCD-A1B1C1D1的体积.解:首先可以求出AE=BF=6,EF=8,再根据三角形相似可以求出AG=12,GD=4,因此AD=16,AGD为等腰直角三角形,所以GD=DG=4,因此CG=10,BG=AB-AG =4,所以ABCG为梯形,其面积为(AB+CG)×4=56.三角形AEF的面积为1/2×AE×EF=24.长方体ABCD-A1B1C1D1的体积为16×10×8=1280.题目1:一长方体被平面α分成两个高为10的直棱柱,求平面α把该长方体分成的两部分体积的比值。
几何体的体积与表面积试题

几何体的体积与表面积试题一、选择题1. 下面关于体积和表面积的说法,正确的是:A. 体积是指几何体的外部空间,表面积是指几何体的内部空间。
B. 箱子的体积和表面积一定是相等的。
C. 体积和表面积都是用立方单位来计量的。
D. 几何体的体积是几何体的表面积的两倍。
2. 一个长方体的长、宽、高分别为3cm、4cm、5cm,它的体积是:A. 60cm³B. 48cm³C. 40cm³D. 20cm³3. 一个正方体的表面积是96平方厘米,它的边长是:A. 8厘米B. 12厘米C. 16厘米D. 24厘米4. 一个圆柱体的底面半径为2cm,高为6cm,它的表面积是:A. 24π平方厘米B. 28π平方厘米C. 32π平方厘米D. 36π平方厘米5. 一个球体的表面积是100π平方厘米,它的半径是:A. 2厘米B. 4厘米C. 6厘米D. 8厘米二、解答题1. 计算一个直方体的体积和表面积,并给出结果的单位。
解答:设直方体的长、宽、高分别为a、b、c,则直方体的体积V为 V = a * b * c,表面积S为 S = 2(a * b + a * c + b * c)。
根据具体的数值,计算出V和S,并注明单位。
2. 已知一个圆柱体的表面积为48π平方厘米,底面半径为3厘米,求圆柱体的高。
解答:设圆柱体的底面半径为r,高为h。
根据题意,可列出方程:2πr^2 + 2πrh = 48π化简得 r^2 + rh = 24代入r=3,解方程得 h = 6厘米。
3. 一个球体的表面积是200π平方厘米,求它的体积。
解答:设球体的半径为r。
根据题意,可列出方程:4πr^2 = 200π化简得 r^2 = 50代入r=√50,计算得体积V = (4/3)πr^3。
三、应用题1. 小明家的水缸是一个圆柱体,底面半径为50厘米,高为120厘米。
他要知道这个水缸最多可以盛多少升水。
解答:水缸的体积为圆柱体的体积V = πr^2h。
(完整版)空间几何体的表面积与体积练习题.及答案

For personal use only in study and research; not forcommercial use空间几何体的表面积与体积专题一、选择题1.棱长为2的正四面体的表面积是( C ).A. 3 B .4 C .4 3 D .16解析 每个面的面积为:12×2×2×32= 3.∴正四面体的表面积为:4 3.2.把球的表面积扩大到原来的2倍,那么体积扩大到原来的 ( B ). A .2倍 B .22倍 C.2倍 D.32倍解析 由题意知球的半径扩大到原来的2倍,则体积V =43πR 3,知体积扩大到原来的22倍.3.如图是一个长方体截去一个角后所得多面体的三视图,则该多面体的体积为( B ). A.1423 B.2843 C.2803D.1403解析 根据三视图的知识及特点,可画出多面体 的形状,如图所示.这个多面体是由长方体截去 一个正三棱锥而得到的,所以所求多面体的体积 V =V 长方体-V 正三棱锥=4×4×6-13×⎝ ⎛⎭⎪⎫12×2×2×2=2843. 4.某几何体的三视图如下,则它的体积是( A) A .8-2π3 B .8-π3C .8-2π D.2π3解析 由三视图可知该几何体是一个边长为2的正方体内部挖去一个底面半径为1,高为2的圆锥,所以V =23-13×π×2=8-2π3.5.已知某几何体的三视图如图,其中正视图中半圆的半径为1,则该几何体的体积为( A)A .24-32π B .24-π3 C .24-π D .24-π2据三视图可得几何体为一长方体内挖去一个半圆柱,其中长方体的棱长分别为:2,3,4,半圆柱的底面半径为1,母线长为3,故其体积V =2×3×4-12×π×12×3=24-3π2.6.某品牌香水瓶的三视图如图 (单位:cm),则该几何体的表面积为( C )A.⎝ ⎛⎭⎪⎫95-π2 cm 2B.⎝ ⎛⎭⎪⎫94-π2 cm 2C.⎝ ⎛⎭⎪⎫94+π2 cm 2D.⎝⎛⎭⎪⎫95+π2 cm 2解析 这个空间几何体上面是一个四棱柱、中间部分是一个圆柱、下面是一个四棱柱.上面四棱柱的表面积为2×3×3+12×1-π4=30-π4;中间部分的表面积为2π×12×1=π,下面部分的表面积为2×4×4+16×2-π4=64-π4.故其表面积是94+π2.7.已知球的直径SC =4,A ,B 是该球球面上的两点,AB =3,∠ASC =∠BSC =30°,则棱锥S-ABC 的体积为( C).A .3 3B .2 3 C. 3 D .1解析 由题可知AB 一定在与直径SC 垂直的小圆面上,作过AB 的小圆交直径SC 于D ,设SD =x ,则DC =4-x ,此时所求棱锥即分割成两个棱锥S-ABD 和C-ABD ,在△SAD 和△SBD 中,由已知条件可得AD =BD =33x ,又因为SC 为直径,所以∠SBC =∠SAC =90°,所以∠DCB =∠DCA =60°,在△BDC 中 ,BD =3(4-x ),所以33x =3(4-x ),所以x =3,AD =BD =3,所以三角形ABD 为正三角形,所以V =13S △ABD ×4= 3.二、填空题8.三棱锥PABC 中,PA ⊥底面ABC ,PA =3,底面ABC 是边长为2的正三角形,则三棱锥PABC 的体积等于__3______.解析 依题意有,三棱锥PABC 的体积V =13S △ABC ·|PA |=13×34×22×3= 3.9.一个圆柱的轴截面是正方形,其侧面积与一个球的表面积相等,那么这个圆柱的体积与这个球的体积之比为_ 3∶2_______.解析 设圆柱的底面半径是r ,则该圆柱的母线长是2r ,圆柱的侧面积是2πr ·2r =4πr 2,设球的半径是R ,则球的表面积是4πR 2,根据已知4πR 2=4πr 2,所以R =r .所以圆柱的体积是πr 2·2r=2πr 3,球的体积是43πr 3,所以圆柱的体积和球的体积的比是2πr 343πr 3=3∶2.10.如图所示,已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成,则该多面体的体积是___26_____. 解析 由题知该多面体为正四棱锥,底面边长为1,侧棱长为1,斜高为32,连接顶点和底面中心即为高,可求得高为22,所以体积V =13×1×1×22=26. 11.如图,半径为R 的球O 中有一内接圆柱.当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是____2πR 2____.解析 由球的半径为R ,可知球的表面积为4πR 2.设内接圆柱底面半径为r ,高为2h ,则h 2+r 2=R 2.而圆柱的侧面积为2πr ·2h =4πrh ≤4πr 2+h 22=2πR 2(当且仅当r =h 时等号成立),即内接圆柱的侧面积最大值为2πR 2,此时球的表面积与内接圆柱的侧面积之差为2πR 2.12.如图,已知正三棱柱ABCA 1B 1C 1的底面边长为2 cm ,高为5 cm ,则一质点自点A 出发,沿着三棱柱的侧面绕行两周到达点A 1的最短路线的长为___13_____cm. 解析 根据题意,利用分割法将原三棱柱分割为两个相同的三棱柱,然后将其展开为如图所示的实线部分,则可知所求最短路线的长为52+122=13 (cm). 三、解答题13.某高速公路收费站入口处的安全标识墩如图1所示,墩的上半部分是正四棱锥PEFGH ,下半部分是长方体ABCDEFGH .图2、图3分别是该标识墩的正视图和俯视图. (1)请画出该安全标识墩的侧视图; (2)求该安全标识墩的体积.解析 (1)侧视图同正视图,如图所示:(2)该安全标识墩的体积为V =V PEFGH +V ABCDEFGH =13×402×60+402×20=64 000(cm 3).14 .一个几何体的三视图如图所示.已知正视图是底边长为1的平行四边形,侧视图是一个长为3,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.(1)求该几何体的体积V ;(2)求该几何体的表面积S.解析 (1)由三视图可知,该几何体是一个平行六面体(如图),其底面是边长为1的正方形,高为3,所以V =1×1×3= 3.(2)由三视图可知,该平行六面体中,A1D ⊥平面ABCD ,CD ⊥平面BCC1B1, 所以AA1=2,侧面ABB1A1,CDD1C1均为矩形, S =2×(1×1+1×3+1×2)=6+2 3.15.已知某几何体的俯视图是如右图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.(1)求该几何体的体积V ;(2)求该几何体的侧面积S .解析 由题设可知,几何体是一个高为4的四棱锥,其底面是长、宽分别为8和6的矩形,正侧面及其相对侧面均为底边长为8,高为h 1的等腰三角形,左、 右侧面均为底边长为6,高为h 2的等腰三角形,如右图所示. (1)几何体的体积为:V =13·S 矩形·h =13×6×8×4=64.(2)正侧面及相对侧面底边上的高为:h 1=42+32=5.左、右侧面的底边上的高为:h 2=42+42=4 2.故几何体的侧面面积为:S =2×⎝ ⎛⎭⎪⎫12×8×5+12×6×42=40+24 2. 1.一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是( ). .解:设展开图的正方形边长为a ,圆柱的底面半径为r ,则2πr =a ,2ar π=,底面圆的面积是24a π,于是全面积与侧面积的比是2221222a a a πππ++=, 2.在棱长为 1 的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去与8个顶点相关的8个三棱锥后 ,剩下的几何体的体积是( ).2.解:正方体的体积为1,过共顶点的三条棱中点的平面截该正方体截得的三棱锥的体积是111111()3222248⨯⨯⨯⨯=,于是8个三棱锥的体积是61,剩余部分的体积是65, 3.一个直棱柱(侧棱垂直于底面的棱柱)的底面是菱形,对角线长分别是6cm 和8cm ,高是5cm ,则这个直棱柱的全面积是 。
几何体的表面积及体积习题及答案
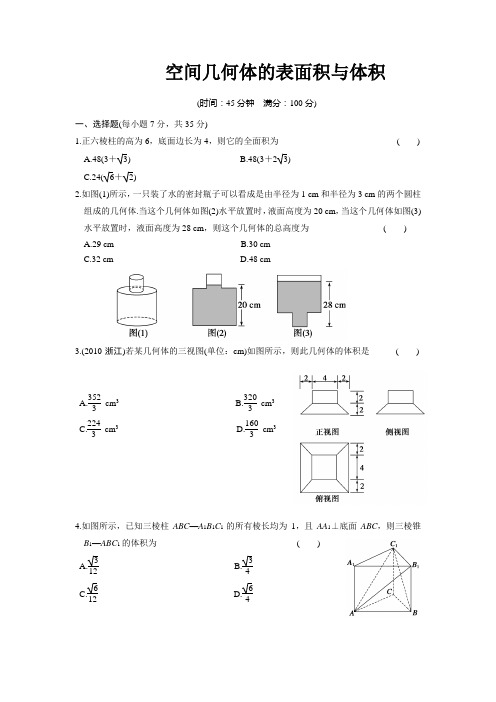
空间几何体的表面积与体积(时间:45分钟 满分:100分)一、选择题(每小题7分,共35分)1.正六棱柱的高为6,底面边长为4,则它的全面积为 ( )A.48(3+3)B.48(3+23)C.24(6+2)2.如图(1)所示,一只装了水的密封瓶子可以看成是由半径为1 cm 和半径为3 cm 的两个圆柱组成的几何体.当这个几何体如图(2)水平放置时,液面高度为20 cm ,当这个几何体如图(3)水平放置时,液面高度为28 cm ,则这个几何体的总高度为 ( )A.29 cmB.30 cmC.32 cmD.48 cm3.(2010·浙江)若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是 ( )A.3523 cm 3B.3203cm 3 C.2243 cm 3 D.1603cm 34.如图所示,已知三棱柱ABC —A 1B 1C 1的所有棱长均为1,且AA 1⊥底面ABC ,则三棱锥B 1—ABC 1的体积为 ( )A.312 B.34 C.612 D.645.(2010·辽宁)已知S,A,B,C是球O表面上的点,SA⊥平面ABC,AB⊥BC,SA=AB=1,BC=2,则球O的表面积等于()二、填空题(每小题6分,共24分)6.(2010·天津)一个几何体的三视图如图所示,则这个几何体的体积为.7.(2011·湖州模拟)如图所示,已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成,则该多面体的体积是.8.(2010·抚顺六校第二次模拟)把边长为1的正方形ABCD沿对角线BD折起形成三棱锥C—ABD,其正视图与俯视图如图所示,则其侧视图的面积为.9.(2011·南京第一次调研)如图,已知正三棱柱ABC—A1B1C1的底面边长为2 cm,高为5 cm,则一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为cm.三、解答题(共41分)10.(13分)已知正方体AC 1的棱长为a ,E ,F 分别为棱AA 1与CC 1的中点,求四棱锥A 1—EBFD 1的体积.11.(14分)如图,已知某几何体的三视图如下(单位:cm).(1)画出这个几何体的直观图(不要求写画法);(2)求这个几何体的表面积及体积.12.(14分)(2011·广州调研)如图1,在直角梯形ABCD 中,∠ADC =90°,CD ∥AB ,AB =4,AD =CD =2,将△ADC 沿AC 折起,使平面ADC ⊥平面ABC ,得到几何体D —ABC ,如图2所示.图1 图2(1)求证:BC ⊥平面ACD ;(2)求几何体D —ABC 的体积.答案7.26 8.1410. 解 因为EB =BF =FD 1=D 1E =a 2+⎝⎛⎭⎫a 22=52a , 所以四棱锥A 1—EBFD 1的底面是菱形,连接EF ,则△EFB ≌△EFD 1,由于三棱锥A 1—EFB 与三棱锥A 1—EFD 1等底同高,所以111122A EBFD A EFB F EBA V V V ---===2·13·1EBA S ∆·a =16a 3. 11. 解 (1)这个几何体的直观图如图所示.(2)这个几何体可看成是正方体AC 1及直三棱柱B 1C 1Q —A 1D 1P 的组合体.由P A 1=PD 1=2,A 1D 1=AD =2,可得P A 1⊥PD 1.故所求几何体的表面积S =5×22+2×2×2+2×12×(2)2=22+42(cm 2),体积V =23+12×(2)2×2=10 (cm 3).12. (1)证明 在图中,可得AC =BC =22,从而AC 2+BC 2=AB 2,故AC ⊥BC ,取AC 的中点O ,连接DO ,则DO ⊥AC ,又平面ADC ⊥平面ABC ,平面ADC ∩平面ABC =AC ,DO ⊂平面ADC ,从而DO ⊥平面ABC ,∴DO ⊥BC ,又AC ⊥BC ,AC ∩DO =O ,∴BC ⊥平面ACD .(2)解 由(1)可知BC 为三棱锥B —ACD 的高,BC =22,S △ACD =2,∴V B —ACD =13S △ACD ·BC =13×2×22=423,由等体积性可知,几何体D —ABC 的体积为423.几何作图(作业)1.如图,按要求作图:(1)连接CE ;(2)延长CE 到点D ,使ED =CE ;(3)作直线AD ,作射线DB .B2.如图,已知线段AB,按要求作图:(1)分别以点A和点B为圆心、以AB的长为半径作弧,两弧相交于点C和点D;(2)作直线CD,交线段AB于点E.A3.如图,一辆汽车在公路上由A向B行驶,M、N分别为位于AB两侧的学校.(1)汽车在公路上行驶时会对学校的教学造成影响,当汽车行驶到点P的位置时对学校M的影响最大,行驶到点Q的位置时对学校N的影响最大.请在图中分别作出点P,Q的位置.(2)当汽车从A向B行驶,哪一段上对两个学校的影响越来越大?哪一段上对学校M的影响逐渐减小,而对学校N的影响逐渐增大?NMB A4.(1)如图1,在一条笔直的公路两侧,分别有A ,B 两个村庄,现在要在公路l 上建一座火力发电厂,向A ,B 两个村庄供电,为使所用电线最短,请问发电厂P 应建在何处?简要说明理由.(2)如图2,若要向4个村庄A ,B ,C ,D 供电,发电厂Q 应该建在何处使发电厂到四个村庄的距离之和最小?l A BDC B A图1 图25.下列四个生活、生产现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要定出两棵树的位置,就能确定同一行所在的直线;③从A 地到B 地,架设电线,总是尽可能沿着线段AB 架设;④把弯曲的公路改直就能缩短路程.其中可用定理“两点之间,线段最短”来解释的现象有______(填序号).6.在直线l 上任取一点A ,截取AB =10cm ,再截取AC =6cm ,则线段BC 的长为__________.B A B A7.在直线l 上任取一点A ,截取AB =20cm ,再截取AC=50cm ,则AB 的中点D 与AC 的中点E 之间的距离为__________.B A B A8.已知线段AB =15cm ,C 点在直线AB 上,BC =2AB ,则AC 的长为__________.B A B A9.从O 点出发的三条射线OA ,OB ,OC ,若∠AOB =60°,∠AOC =40°,则∠BOC 的度数为__________.O B A 60° O B A60°10.已知∠AOB 为直角,∠BOC =40°,OM 平分∠AOB ,ON 平分∠BOC ,则∠MON 的度数为__________.B O A B OA【参考答案】1.(1)作图略;(2)作图略;(3)作图略;2.作图略;3.(1)作图略(提示:过点M作AB的垂线,垂足即为所求的点P,过点N作AB的垂线,垂足即为Q 点);(2)AP段,PQ段;4.(1)作图略(连接AB交直线l的交点即为P点);(2)作图略(提示:连接AD,BC,AD与BC的交点即为Q点)5.③④;6.4 cm或16 cm;7.15 cm或35 cm;8.15cm或45cm;9.20°或100°;10.20°或100°;11.25°或65°.。
2020高中数学 第一章 空间几何体 1..1 柱体、锥体、台体的表面积与体积(含解析)2

1.3.1 柱体、锥体、台体的表面积与体积[基础巩固](25分钟,60分)一、选择题(每小题5分,共25分)1.如图所示,圆锥的底面半径为1,高为错误!,则该圆锥的表面积为( )A.πB.2πC.3π D.4π解析:设圆锥的母线长为l,则l=错误!=2,所以圆锥的表面积为S=π×1×(1+2)=3π.答案:C2.若棱台的上、下底面面积分别为4,16,高为3,则该棱台的体积为()A.26 B.28C.30 D.32解析:所求棱台的体积V=错误!×(4+16+错误!)×3=28.答案:B3.若圆柱的底面半径为1,其侧面展开图是一个正方形,则这个圆柱的侧面积是( )A.4π2B.3π2C.2π2D.π2解析:依题意,圆柱的母线长l=2πr,故S侧=2πrl=4π2r2=4π2。
答案:A4.正方体ABCD-A1B1C1D1中,以顶点A、C、B1、D1为顶点的正三棱锥的全面积为4错误!,则该正方体的棱长为( )A.错误!B.2C.4 D.2错误!解析:设正方体棱长为a,侧面的对角线长为错误!a,所以正三棱锥A-CB1D1的棱长为错误!a,其表面积为4×错误!×(错误!a)2=4错误!,可得a2=2,即a=错误!.答案:A5.在△ABC中,AB=2,BC=错误!,∠ABC=120°,将△ABC绕直线BC旋转一周,所形成的几何体的体积是( )A 。
92π B。
错误!π C.错误!π D.错误!π解析:如图,△ABC 绕直线BC 旋转一周,所形成的几何体是以△ACD 为轴截面的圆锥中挖去一个以△ABD 为轴截面的圆锥后剩余的部分.因为AB =2,BC =32,∠ABC =120°, 所以AE =AB sin60°=3,BE =AB ·cos60°=1,CE =错误!。
V 1=13π·AE 2·CE =错误!,V 2=错误!π·AE 2·BE =π, 所以V =V 1-V 2=错误!π.故选D 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间几何体的表面积和体积练习题
题1 一个圆锥与一个球的体积相等,圆锥的底面半径是球的半径的3倍,则圆锥的高与底面
半径之比为( ) A.49
B.94
C.427
D.274
题2 正四棱锥P —ABCD 的五个顶点在同一个球面上,若该正四棱锥的底面边长为2,侧棱长
为6,则此球的体积为________.
题3 一空间几何体的三视图如图所示,则该几何体的体积为( )
A .2π+2 3
B .4π+2 3
C .2π+23
3
D .4π+23
3
题4 如图,正方体ABCD -A 1B 1C 1D 1的棱长为2.动点E ,F 在棱A 1B 1上,点Q 是棱CD 的中
点,动点P 在棱AD 上.若EF =1,DP =x ,A 1E =y (x ,y 大于零),则三棱锥P -EFQ 的体积.( )
A .与x ,y 都有关
B .与x ,y 都无关
C .与x 有关,与y 无关
D .与y 有关,与x 无关
题5 直角梯形的一个底角为45°,下底长为上底长的3
2
,这个梯形绕下底所在直线旋转一周所
成的旋转体的表面积是(5+2)π,求这个旋转体的体积.
题6 设三棱柱的侧棱垂直于底面,所有棱的长都为a ,顶点都在一个球面上,则该球的表面
积为( ) A .πa 2
B.7
3
πa 2
C.11
3
πa 2
D .5πa 2
题7 在球心同侧有相距9 cm 的两个平行截面,它们的面积分别为49π cm 2和400π cm 2,求
球的表面积.
题8 正四棱台的高为12cm ,两底面的边长分别为2cm 和12cm .(Ⅰ)求正四棱台的全面
积;(Ⅱ)求正四棱台的体积.
题9 如图,已知几何体的三视图(单位:cm).(1)画出这个几何体的直观图(不要求写画法);
(2)求这个几何体的表面积及体积.
题10 如图,在长方体ABCD A B C D ''''-中,用截面截下一个棱锥C A DD ''-,求棱锥
C A D
D ''-的体积与剩余部分的体积之比.
题11已知一个棱长为2的正方体,被一个平面截后所得几何体的三视图如图所示,求该几何体的体积.
题12如图所示,在直三棱柱ABC-A1B1C1中,底面为直角三角形,∠ACB=90°,AC=6,BC=CC1= 2,P是BC1上一动点,则CP+P A1的最小值是__________.
课后练习详解
题1 答案:C
详解:设圆锥底面半径为1R ,高为h ,球的半径为2R
,则圆锥体积为
2113R h π,球的体积为3243
R π.由题意知圆锥的底面半径是球的半径的3倍,即1R
=32R .由圆锥与球的体积相等有
2113R h π=3
243
R π,将2R =1
3
R
代入,有2
1R h =31
3
43
R ⨯
,故1
h
R =433=427
. 题2 答案:9
2
π
详解:如图所示,设底面中心为O ′,球心为O ,设球半径为R ,∵AB =2,则AO ′=2,PO ′=P A 2-AO ′2=2,OO ′=PO ′-PO =2-R .在Rt △AOO ′中,AO 2=AO ′2+OO ′2⇒R 2=(2)2+(2-R )2,∴R =32,∴V 球=4
3πR 3=
9
2
π.
题3 答案:C
详解:由几何体的三视图可知,该几何体是由一个底面直径和高都是2的圆柱和一个底面边长为2,侧棱长为2的正四棱锥叠放而成.故该几何体的体积为 V =π×12×2+13×(2)2×3=2π+2
33,故选C.
题4 答案:C
详解:设P 到平面EFQ 的距离为h ,则V P -EFQ =1
3×S △EFQ ·h ,由于Q 为CD 的中点,∴点Q 到直线EF 的距
离为定值2,又EF =1,∴S △EFQ 为定值,而P 点到平面EFQ 的距离,即P 点到平面A 1B 1CD 的距离,显然与x 有关、与y 无关,故选C. 题5 答案:7
3π.
详解:
如图所示,在梯形ABCD 中,AB ∥CD ,∠A =90°,∠B =45°,绕AB 边旋转一周后形成一圆柱和一圆锥的组合体.
设CD =x ,则AB =32x ,AD =AB -CD =x 2,BC =22
x .
S 表=S 柱底圆+S 柱圆侧+S 圆锥侧=π·AD 2+2π·AD ·CD +π·AD ·BC
=π·x 24+2π·x 2·x +π·x 2·22x =5+24πx 2
.
根据题设,5+24πx 2=(5+2)π,则x =2.
所以旋转体体积
V =π·AD 2·CD +π3AD 2·(AB -CD )=π×12×2+π3×12×(3-2)=7
3π.
题6 答案:B 详解:
如图,O 1,O 分别为上、下底面的中心,D 为O 1O 的中点,则DB 为球的半径,有 r =DB =
OD 2+OB 2=
a 24+a 23
=7a 2
12
, ∴S 表=4πr 2=4π×7a 212=7
3πa 2.
题7 答案:2500πcm 2
.
详解:如图为球的轴截面,由球的截面性质知,AO 1∥BO 2,且O 1、O 2分别为两截面圆的圆心,则
OO 1⊥AO 1,OO 2⊥BO 2
.设球的半径为R .
∵π·O 2B 2=49π,∴O 2B =7 cm ,同理π·O 1A 2=400π,∴O 1A =20 cm .
设OO 1=x cm ,则OO 2=(x +9) cm.在Rt △OO 1
A 中,R 2=x 2+202,
在Rt △OO 2B 中,R 2=(x +9)2+72,∴x 2+202=72+(x +9)2
,解得x =15.
∴R 2=x 2+202=252
,∴R =25 cm .∴S 球
=4πR 2=2500π cm 2.
∴球的表面积为2500π cm 2
. 题8 答案:512 cm 2; 688 cm 3
详解:(Ⅰ)斜高2
2
122'12132h -⎛⎫
=+= ⎪⎝⎭
cm
S 正四棱台=S 上+S 下+S 侧=22+122+ 12×(2+12)×13=512 cm 2 (Ⅱ)V= 13(S+
'SS +S′)h= 13(22+22
212++122)×12=688 cm 3
题9 答案:(1)见详解.
(2) 表面积22+4 2 cm 2,体积10 cm 3. 详解: (1)这个几何体的直观图如图所示.
(2)这个几何体可看成是由正方体AC 1及直三棱柱B 1C 1Q —A 1D 1P 的组合体. 由P A 1=PD 1=2,A 1D 1=AD =2,可得P A 1⊥PD 1. 故所求几何体的表面积为:
S =5×22+2×2×2+2×12×(2)2=22+4 2 cm 2,所求几何体的体积V =23+1
2×(2)2×2
=10 cm 3. 题10 答案:15∶
详解: 已知长方体可以看成直四棱柱
ADD A BCC B ''''-.
设它的底面ADD A ''面积为S ,高为h ,则它的体积为V Sh =.
而棱锥C A DD ''-的底面面积为1
2
S ,高是h ,
因此棱锥C A DD ''-的体积111326
C AD
D V Sh Sh -=⨯=''
. 余下的体积是15
66
Sh Sh Sh -=.
所以棱锥C A DD ''-的体积与剩余部分的体积之比为1:5.
题11 答案:17
3
详解:由三视图知,此几何体可以看作是一个边长为2的正方体被截去了一个棱台而得到,此棱台的
高为2,一底为直角边长为2的等腰直角三角形,一底为直角边长为1的等腰直角三角形,棱台的
两底面的面积分别为
111
222,11
222
⨯⨯=⨯⨯=
该几何体的体积是
111717 2222228
32233
⎛⎫
⨯⨯-⨯⨯++⨯=-=
⎪
⎪
⎝⎭
题12答案:52.
详解:
将△BCC1沿直线BC1折到面A1C1B上,如图,连接A1C,即为CP+P A1的最小值,过点C作CD⊥C1D于D 点,△BCC1为等腰直角三角形,
∴CD=1,C1D=1,A1D=A1C1+C1D=7,
22 1149152
AC A D CD
∴=+=+=。
