第四章 单元测试题(二)
人教版八年级地理上册第四章中国的经济发展单元测试(含答案)

第四章中国的经济发展单元测试题(含答案)一.选择题(4*15=60分)1.目前,我国最重要的运输方式是()A.铁路 B.公路 C.航空 D.水运2.下列各种交通运输方式中,哪些属于现代交通运输方式?()①牛马拉车②风帆行船③公路运输④铁路运输⑤航空运输⑥管道运输⑦手提肩扛A.①②③④⑤⑦ B.③④⑤⑥⑦ C.②③④⑤⑥⑦ D.③④⑤⑥3.运输速度最快的运输方式是A. 航空运输B. 公路运输C. 水路运输D. 铁路运输4.有一沙漠探险队经过京沪线,陇海线和兰新线来到南疆,这支探险队最有可能来自()A.上海 B.北京 C.武汉 D.广州5.甲、乙、丙、丁四位同学选择的交通运输方式,你认为合适的是()A.甲同学从石家庄到香港旅游,选择铁路运输B.乙同学从重庆到武汉观赏三峡风光,选择空运C.上海的丙同学急需骨髓移植,台北有捐献的骨髓要运到上海,选择水运D.丁同学爸爸将500公斤活鱼从郊区水库运到城区市场,丁同学帮爸爸选择铁路运输6.我国农业在国民经济中的地位是()A. 国民经济的主导B. 国民经济的基础C. 国民经济的关键D. 经济发展的先行官7.下列地区中,油菜开花最早的是()A. 藏南谷地B. 四川盆地C. 长江三角洲D. 珠江三角洲8.精准扶贫,园地制宜,适合湘西山区种植的经济作物有A. 柑橘、茶叶B. 荔枝、核桃C. 甘蔗、芒果D. 甜菜、菠萝9.我国北方地区在农业生产中流传着这样的话:“春耕、夏种、秋收、冬藏”,你认为形成这种农业生产模式的主要影响因素是()A. 纬度位置B. 海陆位置C. 地形D. 气候变化10.在某超市的农产品销售处的标签上,产品原产地的标注错误..的是()A. 蔗糖——广西B. 花生油——山东C. 茶叶——新疆D. 面粉——河北11.下列生产过程,不属于工业生产过程的是()A.开采铁矿B.将大米加工成雪米饼 C.生产化肥、农药D.人工养殖珍珠12.发展和建立新兴高新技术产业的最重要条件是()A.自然资源丰富 B.科技力量雄厚 C.劳动力充足 D.位置优越13.“互联网+”就是互联网+各个传统行业,是利用通信信息技术以及互联网平台,让互联网与传统行业进行深度融合,创造新的发展生态。
高中地理第四章区域发展战略单元测试含解析2

单元测试4一、选择题(每小题2分,共50分)如图示意某岛国城市、铁路与河流分布,该国中北部地区是其重要的甘蔗种植和蔗糖工业基地.读图完成1~3题。
1.该国铁路发展较晚,推测该国铁路选线时考虑的主导因素是()A.地形状况B.河流状况C.耕地资源D.城市分布2.该国甲-乙—丙段铁路以货运为主,运输的货物主要是() A.咖啡B.蔗糖C.水稻D.香蕉3.该国铁路未沿着海岸地带选线的主要原因是海岸带() A.沼泽湿地广布B.地质构造复杂C.耕地面积较广D.高山、峡谷众多向塘镇隶属于江西省南昌市南昌县,是江西省最大的建制镇。
京九铁路、沪昆铁路、向莆铁路在向塘镇形成“大”字型交会,如下图所示,向塘西站是江南地区最大的货运编组站,此外,105、320、316三条国道也在此交会。
据此完成4~5题。
4.向塘镇不断发展壮大,主要得益于()A.交通区位优势B.丰富的矿产资源C.劳动力丰富廉价D.地处鱼米之乡5.依据当地的区位优势,向塘镇适宜发展的产业类型为() A.现代物流业B.煤炭工业C.钢铁工业D.电子工业爪哇岛为印度尼西亚的政治、经济与文化中心地区,是世界上人口最多,也是人口密度最高的岛屿之一,近来规划建设雅加达——泗水高速铁路,其中2015年11月率先开工建设的雅加达——万隆段由中印两国合作建设。
读图完成6~7题。
6.雅泗高铁建设中可能遇到的最大自然障碍是()A.气候湿热B.河网稠密C.植被茂密D.地形复杂7.雅万高铁开工建设,率先受益的产业是()A.旅游业B.电子工业C.石油化工D.机械设备制造2016年9月,《长江经济带发展规划纲要》正式印发,确立了长江经济带“一轴、两翼、三极、多点”的发展新格局。
读图,完成8~9题。
8.与长江下游经济圈相比,长江上游经济圈发展的地理优势是()A.土地广阔,价格高B.水能资源丰富C.人口众多,素质高D.交通设施完善9.目前,云、贵、川、渝等地区承接产业转移采取的合理措施是()A.大量吸纳劳动力移民B.大力开发区域资源C.投资一批重大工程建设D.加强基础设施建设长江经济带既是我国综合实力最强、战略支撑作用最大的区域之一,也是一条面向国内外开放合作的重要走廊。
2021学年北师大版小学五年级数学下册《第四章长方体(二)》单元测试题(含解析)

2021学年北师大版小学五年级数学下册《第四章长方体(二)》单元测试题一.选择题(共10小题)1.下面容器中,()的容量最接近2升。
A.玻璃杯B.水桶C.热水瓶2.一瓶消毒洗手液标着“500mL”,500mL是指洗手液的()A.体积B.容积C.质量3.我们家里的洗碗池大约能盛水()A.12升B.50毫升C.500升4.一团橡皮泥,淘气第一次把它捏成正方体,第二次把它成长方体,捏成的两个物体()A.正方体大B.长方体太C.一样大5.4瓶250毫升的饮料正好是()升.A.1B.100C.10006.如图(单位:cm),西红柿的体积是()cm3.A.640B.760C.1207.下图是测量一颗铁球体积的过程:①将300ml的水倒进一个容量为500ml的杯子中;②将四颗相同的铁球放入水中,结果水没有满;③再加一颗同样的铁球放入水中,结果水满溢出.根据以上过程,推测这样一颗铁球的体积大约在()A.60cm3以上,70cm3以下B.50cm3以上,60cm3以下C.40cm3以上,50cm3以下D.30cm3以上,403以下8.把一盒1.5升的果汁倒进容积为250毫升的杯子里,能倒满()杯.A.0.6B.6C.60D.6009.一个长是5dm、宽是3dm、高是5dm的长方体鱼缸,倒入水后量得水深是3.5dm,倒入的水是()升.A.60B.52.5C.4210.如图把一根长10分米的长方体木料横截成两个小长方体,表面积增加了6平方分米,原来这根木料的体积是()立方分米.A.10B.20C.30D.60二.填空题(共10小题)11.20000毫升=升8升=毫升毫升>4升.12.升用字母表示,毫升用字母表示.13.在横杠上填上“升”或“毫升”.一个热水瓶的容量大约是2;一瓶墨水大约是50;小华今天早晨喝牛奶250;浴缸的容量大约是400.14.从里面测量,棱长为米的正方体盒子的容积是1立方米,可以容纳升的液体。
15.“0.78升、780毫升、780立方分米、780立方厘米”四个数量中,与其它数量不相等。
大学生心理健康教育章节测试题与答案

大学生心理健康教育章节测试题与答案第一章单元测试1、真正的大学教育不是传授有限的知识和技能,而是令人胜任任何学科和职业。
A:错B:对答案:【对】2、联合国教科文组织把大学生的主要任务界定为“四个学会”,包括:A:学会学习B:学会与人相处C:学会做事D:学会做人答案:【学会学习;学会与人相处;学会做事;学会做人】3、大学与中学相比,会有哪些方面的变化?A:人际关系变化B:自身角色变化C:生活上的变化D:学习上的变化答案:【人际关系变化;自身角色变化;生活上的变化;学习上的变化】4、自律学习是大学学习的主要特点。
A:对B:错答案:【对】5、学业规划和生涯规划是每一位大学生都必须思考的问题。
A:对B:错答案:【对】第二章单元测试1、学习是指通过阅读、听讲、思考、研究、实践等途径获得知识或技能的过程。
A:对B:错答案:【对】2、在中国古人看来,学习可以分为()个阶段。
A:4个B:3个C:1个D:2个答案:【2个】3、在苛勒看来,学习是个体利用自身的智慧与理解力对情境及情境与自身关系的反思。
A:错B:对答案:【错】4、桑代克通过“抓狂的饿猫”实验认为学习的本质是不断试误。
A:错B:对答案:【对】5、根据动机理论,学习动机与学习成绩的关系是()。
A:倒U型B:W型C:倒V型D:线性关系答案:【倒U型】第三章单元测试1、关于自我认识,以下表述中错误的是()A:不同的人自我意识整合的结果与类型也不同B:自我意识的矛盾冲突常常会令人心理痛苦。
C:很少有人会出现自我冲突D:一个人自我意识的发展越好,人格越完善答案:【很少有人会出现自我冲突】2、一个人如果想要悦纳自己,以下不正确的是()A:追求完美。
B:目标合理恰当。
C:建立合理的评价参照系和立足点。
D:接纳自己的不完美。
答案:【追求完美。
】3、胆汁质的同学可以采取以下哪种方法来进行自我调节。
()A:目标管理和奖惩法B:活动法和自我暗C:及时反应法和改变思考角度D:延迟发火和转移法答案:【延迟发火和转移法】4、悦纳自我就是:我什么都是好的,不准别人说我的缺点。
2020-2021学年 北师大版五年级数学下册《第四章 长方体(二)》单元测试卷 (有答案)

2020-2021学年北师大版小学五年级数学下册《第四章长方体(二)》单元测试题一.选择题(共10小题)1.求一个水桶能装多少升水,就是求这个水桶的()A.面积B.体积C.表面积D.容积2.一个水池能蓄水260m3,我们就说,这个水池的()是260m3.A.重量B.容积C.体积3.下面说法正确的是()A.1000毫升水比10升水多B.升、毫升、毫米都是容量单位C.毫升是比升小的容量单位4.求一个油桶能装油多少升,是求油桶的()A.表面积B.体积C.容积D.占地面积5.把1升的水倒入容量为200毫升的纸杯中,可倒()杯.A.1B.4C.56.一个量杯中装有200mL水;把一个土豆放入其中(完全浸没,水未溢出),水面上升至456mL这个土豆的体积是()A.456cm3 B.456dm3C.256 cm3D.256 dm37.准备一个有刻度的容器先注入一些水,然后把土豆放入水中,观察水面高度上升的情况,通过以上方法测量土豆的体积,运用了()的数学思想方法.A.统计B.倒推C.转化D.假设8.把50cm3改写成用”dm3”作单位,下面选项错误的是()A.0.05dm3 B.5%dm3 C.dm3 D.dm39.正方体的棱长扩大到原来的2倍,它的体积就扩大到原来的()倍.A.2B.4C.6D.810.将一个长9cm,宽5cm,高4cm的长方体截成一个体积最大的正方体,这个正方体的体积是()cm3.A.25B.64C.80二.填空题(共10小题)11.3.85立方米=立方分米4升40毫升=升.12.一瓶果汁大约有500,一箱果汁(12瓶装)大约有升.13.在横线里填上“升”或“亳升”.一桶油2.5一瓶果汁330一瓶眼药水4一脸盆水6一桶纯净水19一汤勺水1014.棱长为1分米的正方体的容积是,用字母表示为;棱长为1厘米的正方体的容积是,用字母表示为.15.在横线上填上“L”或“mL”.一瓶洗衣液大约有3;一瓶绿茶是500.16.如图中大球体积是mL.17.一个底面半径为5厘米的圆锥形金属铸件,浸没在棱长15厘米的正方体盛着水的容器中后,水面比原来升高1.5厘米(没有溢出).这个圆锥体的体积是.18.6.4L=dm3=cm3850mL=L12000cm3=dm3=m38.63m2=dm2350mL=cm319.一个商品盒是正方体形状,棱长为6厘米,这个商品盒的体积是立方厘米,在这个盒的四周贴上商标,贴商标的面积是平方厘米.20.用10个棱长为1厘米的小正方体搭成一个大长方体,这个长方体的体积是立方厘米.三.判断题(共5小题)21.容器的高是指容器外面的高.(判断对错)22.一个保温杯的体积是2立方分米,瓶里一定能装2升水.(判断对错)23.可以用排水法测量不规则物体的体积.(判断对错)24.3000ml和3升一样多。
人教版八年级物理上册第四章《光现象》单元测试

第四章《光现象》单元测试人教版八年级物理上册(含答案)时间:60分钟满分70分一、填空题(每空1分,共14分)1.小明站在竖直的玻璃幕墙前20m处,他在玻璃幕墙上的像距他的距离为m,当他走近玻璃幕墙时,所成像的大小(选填“变大”、“不变”或“变小”)。
2.小明上学前站在穿衣镜前2m处整理仪表,他与镜中自己像的距离是m;当小明向后退了60cm时,镜中所成像的大小(选填“变大”、“不变”或“变小”)。
3.小芳站在平面镜前2m处,镜中的像与她相距m;当她走近平面镜时,她在镜中的像的大小(选填“变小”、“不变”或“变大”)。
她在镜中成的像是(“虚”或“实”)像。
4.小明从汽车的后视镜里看见驾驶员的眼睛,此时驾驶员通过车内后视镜(填“一定”“不一定”或“一定不”)能看见小明;小明在后视镜里看到的驾驶员的像是(填“虚”或“实”)像.5.①岸边树在水中的倒影、②自己在阳光下的影子、③池水映明月、④海市蜃楼、⑤中午树荫下的亮斑。
属于光的反射是,属于光的折射是,属于光的直线传播是。
(填序号)6.光与镜面成30°角射在平面镜上,反射角为;如果入射角减小,则反射角会。
(选填“增大”、“减小”或“不变”)二、选择题(每题2分,共24分)7.近些年来,潜水颇受年轻人的青睐,潜入水中的潜水者看到岸上的树木位置变高了。
下图中的四幅光路图中,那一幅能正确说明产生这一现象的原因()A.B.C.D.8.一束光线射到平面镜上,当入射角增大20º时,反射光线与入射光线恰好成直角,则原来的入射角是()A.20ºB.25ºC.30ºD.45º9.在平静的水面上空,一只鱼鹰正在斜向下俯冲捕鱼,下列说法正确的是()A.鱼鹰在水中的自己像是由光的折射形成的虚像B.鱼鹰看到的鱼是由光的反射形成的虚像C.鱼鹰在俯冲过程中,它在水中的像变大D.鱼鹰应向它看到的鱼的下方俯冲才可能捕捉到鱼10.如图所示,小梦用激光笔对准看到的小鱼照射,以下说法正确的是()A.能照亮小鱼,因为激光照到了鱼身上B.不能照亮小鱼,因为激光照到鱼身的上方C.不能照亮小鱼,因为激光照到鱼身的下方D.能照亮小鱼,因为激光照到鱼的像上,使像反射的光变强11.小明同学在课外用直径不同的纸筒制成如图所示的装置做小孔成像实验,如果外筒左侧中央有一个很小的三角形小孔,点燃蜡烛并置于小孔前一段距离,贴在内筒左侧半透明纸上能看到清晰的像。
北师大版八年级上册数学第四章《一次函数》单元测试卷(含答案)

北师大版八年级上册数学第四章《一次函数》单元测试卷(含答案)一、选择题(每题3分,共30分)1.下列两个变量之间不存在函数关系的是( )A.圆的面积S和半径r B.某地一天的气温T与时间t C.某班学生的身高y与学生的学号x D.一个正数的平方根与这个数2.一个正比例函数的图象经过点(-2,-4),则它的表达式为( )A.y=-2x B.y=2x C.y=-12x D.y=12x3.【教材P88习题T4改编】正比例函数y=x的图象向上平移2个单位长度,所得函数为( )A.y=x+2 B.y=x-2 C.y=2x D.y=x 24.一次函数y=mx+n的图象如图所示,则关于x的方程mx+n=0的解为( ) A.x=3B.x=-3C.x=4D.x=-45.已知点P(a,-3)在一次函数y=2x+9的图象上,则a的值为( ) A.-3 B.-6 C.15 D.36.关于函数y=-x2-1,下列说法错误的是( )A.当x=2时,y=-2B.y随x的增大而减小C.若(x1,y1),(x2,y2)为该函数图象上两点,x1>x2,则y1>y2D.图象经过第二、三、四象限7.【教材P98复习题T3变式】弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂物体质量x(kg)间有如下关系(其中x≤12).下列说法不正确的是( )A.x与y都是变量,且x是自变量B.弹簧不挂物体时的长度为10 cmC.物体质量每增加1 kg,弹簧长度增加0.5 cmD.所挂物体质量为7 kg,弹簧长度为14.5 cm8.若直线y=-3x+m与两坐标轴所围成的三角形的面积是6,则m的值为( ) A.6 B.-6 C.±6 D.±39.【教材P99复习题T8变式】已知一次函数y=kx+b,y随着x的增大而减小,且kb>0,则这个函数的大致图象是( )10.【2020·铜仁】如图,在长方形ABCD中,AB=3,BC=4,动点P沿折线BCD 从点B开始运动到点D,设点P运动的路程为x,△ADP的面积为y,那么y与x 之间的函数关系的图象大致是( )二、填空题(每题3分,共24分)11.【2021·黑龙江】在函数y =1x -5中,自变量x 的取值范围是__________.12.若函数y =(m +1)x |m |是关于x 的正比例函数,则m =________. 13.直线y =3x +1与y 轴的交点坐标是__________.14.点⎝ ⎛⎭⎪⎫-12,m 和点(2,n )在直线y =2x +1上,则m 与n 的大小关系是__________.15.拖拉机油箱中有54 L 油,拖拉机工作时,每小时平均耗油6 L ,则油箱里剩下的油量Q (L)与拖拉机的工作时间t (h)之间的函数关系式是________________(写出自变量的取值范围).16.【教材P 90习题T 2改编】一次函数y =-2x +m 的图象经过点P (-2,3),且与x 轴、y 轴分别交于点A ,B ,则△AOB 的面积是________.17.如图,过A 点的一次函数的图象与正比例函数y =2x 的图象相交于点B ,则这个一次函数的表达式是____________.(第17题) (第18题)18.甲、乙两地之间是一条直路,在全民健身活动中,赵明阳跑步从甲地往乙地,王浩月骑自行车从乙地往甲地,两人同时出发,王浩月先到达目的地,两人之间的距离s(km)与运动时间t(h)的函数关系大致如图所示,下列说法:①两人出发1小时后相遇;②赵明阳跑步的速度为8 km/h;③王浩月到达目的地时两人相距10 km;④王浩月比赵明阳提前1.5 h到目的地.其中错误的序号是________.三、解答题(每题11分,共66分)19.已知y-2与x成正比例,且x=2时,y=4.(1)求y与x之间的函数关系式;(2)若点M(m,3)在这个函数的图象上,求点M的坐标.20.已知一次函数y=(m-3)x+m-8中,y随x的增大而增大.(1)求m的取值范围;(2)如果这个一次函数又是正比例函数,求m的值;(3)如果这个一次函数的图象经过第一、三、四象限,试写一个m的值,不用写理由.21.如图,一次函数y=2x+b的图象与x轴交于点A(2,0),与y轴交于点B.(1)求b的值,(2)若直线AB上的点C在第一象限,且S△AOC=4,求点C的坐标.22.如图,一次函数y=kx+5的图象与y轴交于点B,与正比例函数y=32x的图象交于点P(2,a).(1)求k的值;(2)求△POB的面积.23.水龙头关闭不紧会持续不断地滴水,小明用可以显示水量的容器做实验,并根据实验数据绘制出容器内盛水量y(L)与滴水时间t(h)之间的函数关系图象(如图).请结合图象解答下面的问题:(1)容器内原有水多少升?(2)求y与t之间的函数表达式,并计算在这种滴水状态下一天的滴水量是多少升.24.某通信公司推出①②两种通信收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的收费金额y (元)与通信时间x (分钟)之间的函数关系如图所示.(1)有月租费的收费方式是________(填“①”或“②”),月租费是________元; (2)分别求出①②两种收费方式中,收费金额y (元)与通信时间x (分钟)之间的函数表达式;(3)请你根据用户通信时间的多少,给出经济实惠的选择建议.参考答案一、1.D 2.B 3.A 4.D 5.B 6.C 7.D 8.C 9.B 10.D二、11.x ≠5 12.1 13.(0,1) 14.m <n15.Q =54-6t (0≤t ≤9) 16.14 17.y =-x +3 18.③三、19.解:(1)设y -2=kx (k ≠0).把x =2,y =4代入,得k =1.故y 与x 之间的函数关系式是y =x +2. (2)因为点M (m ,3)在这个函数的图象上, 所以3=m +2,解得m =1.所以点M 的坐标为(1,3).20.解:(1)因为一次函数y =(m -3)x +m -8中,y 随x 的增大而增大,所以m -3>0. 所以m >3.(2)因为这个一次函数是正比例函数, 所以m -8=0,即m =8. (3)答案不唯一,如m =4.21.解:将A (2,0)的坐标代入y =2x +b ,得2×2+b =0,解得b =-4.(2)因为S △AOC =4,点A (2,0), 所以OA =2.所以12OA ·y c =4,解得y c =4.把y =4代入y =2x -4,得2x -4=4, 解得x =4.所以点C 的坐标为(4,4).22.解:(1)把点P (2,a )的坐标代入y =32x ,得a =3,所以点P 的坐标为(2,3).把点P (2,3)的坐标代入y =kx +5,得2k +5=3, 解得k =-1.(2)由(1)知一次函数表达式为y =-x +5. 把x =0代入y =-x +5,得y =5,所以点B的坐标为(0,5).所以S△POB=12×5×2=5.23.解:(1)根据图象可知,当t=0时,y=0.3,即容器内原有水0.3 L.(2)设y与t之间的函数表达式为y=kt+b.将点(0,0.3),(1.5,0.9)的坐标分别代入,得b=0.3,1.5k+b=0.9,解得k=0.4.所以y与t之间的函数表达式为y=0.4t+0.3.当t=24时,y=0.4×24+0.3=9.9,所以在这种滴水状态下一天的滴水量是9.9-0.3=9.6(L).24.解:(1)①;30(2)记有月租费的收费金额为y1(元),无月租费的收费金额为y2(元),则设y1=k1x+30,y2=k2x.将点(500,80)的坐标代入y1=k1x+30,得500k1+30=80,所以k1=0.1,则y1=0.1x+30.将点(500,100)的坐标代入y2=k2x,得500k2=100,所以k2=0.2,则y2=0.2x.所以①②两种收费方式中,收费金额y(元)与通信时间x(分钟)之间的函数表达式分别为y1=0.1x+30,y2=0.2x.(3)当收费相同,即y1=y2时,0.1x+30=0.2x,解得x=300.结合图象,可知当通信时间少于300分钟时,选择收费方式②更实惠;当通信时间超过300分钟时,选择收费方式①更实惠;当通信时间等于300分钟时,选择收费方式①②一样实惠.。
七年级数学第四章《几何图形初步》单元测试卷(含答案) (2)
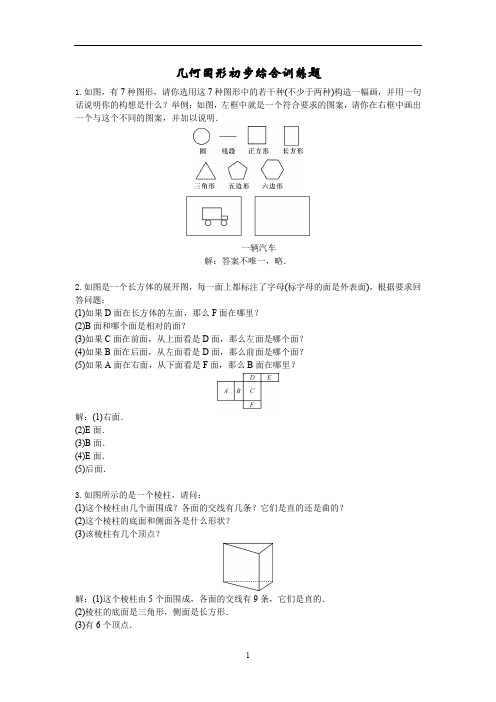
几何图形初步综合训练题1.如图,有7种图形,请你选用这7种图形中的若干种(不少于两种)构造一幅画,并用一句话说明你的构想是什么?举例:如图,左框中就是一个符合要求的图案,请你在右框中画出一个与这个不同的图案,并加以说明.一辆汽车解:答案不唯一,略.2.如图是一个长方体的展开图,每一面上都标注了字母(标字母的面是外表面),根据要求回答问题:(1)如果D面在长方体的左面,那么F面在哪里?(2)B面和哪个面是相对的面?(3)如果C面在前面,从上面看是D面,那么左面是哪个面?(4)如果B面在后面,从左面看是D面,那么前面是哪个面?(5)如果A面在右面,从下面看是F面,那么B面在哪里?解:(1)右面.(2)E面.(3)B面.(4)E面.(5)后面.3.如图所示的是一个棱柱,请问:(1)这个棱柱由几个面围成?各面的交线有几条?它们是直的还是曲的?(2)这个棱柱的底面和侧面各是什么形状?(3)该棱柱有几个顶点?解:(1)这个棱柱由5个面围成,各面的交线有9条,它们是直的.(2)棱柱的底面是三角形,侧面是长方形.(3)有6个顶点.4.下面图1是正方体木块,若用不同的方法,把它切去一块,可以得到如图2、图3、图4、图5不同形状的木块.图1图2图3图4图5(1)我们知道,图1的正方体木块有8个顶点,12条棱,6个面.请你观察,将图2、图3、图4、图5中木块的顶点数a、棱数b、面数c填入下表:(2)观察这张表,请你归纳出上述各种木块的顶点数a、棱数b、面数c之间的数量关系,这种数量关系是:a+c-b=2(用含a、b、c的一个等式表示).5.如图,直线有多少条?把他们分别表示出来;线段有多少条?把他们分别表示出来;射线有多少条?可以表示的射线有多少条?把他们表示出来.解:直线有3条,直线AB、直线AC、直线BC;线段有6条,分别为线段AB,线段AC,线段AD,线段BD,线段CD,线段BC;射线有14条,可以表示的射线有8条,分别为射线AB,射线AC,射线BA,射线BC,射线CA,射线CB,射线DB,射线DC.6.如图,已知数轴上的原点为O,点A表示3,点B表示-1,回答下列问题:(1)数轴在原点O左边的部分(包括原点)是一条什么线?怎样表示?(2)射线OB上的点表示什么数?(3)数轴上表示不大于3且不小于-1的部分的数是什么图形?怎样表示?解:(1)是一条射线,表示为射线OB.(2)负数和零(非正数).(3)线段,线段AB.7.如图:(1)试验观察:如果每过两点可以画一条直线,那么: 第①组最多可以画3条直线; 第②组最多可以画6条直线; 第③组最多可以画10条直线; (2)探索归纳:如果平面上有n(n ≥3)个点,且任意3个点均不在一条直线上,那么最多可以画n (n -1)2条直线;(用含n 的式子表示) (3)解决问题:某班45名同学在毕业后的一次聚会中,如果每两人握1次手问好,那么共握990次手.8.如图,点C 是线段AB 上的点,点D 是线段BC 的中点.(1)若AB =10,AC =6,求CD 的长; (2)若AC =30,BD =10,求AB 的长. 解:(1)因为点D 是线段BC 的中点, 所以CD =12BC.因为AB =10,AC =6,所以BC =AB -AC =10-6=4. 所以CD =12BC =2.(2)因为点D 是线段BC 的中点, 所以BC =2BD. 因为BD =10,所以BC =2×10=20. 因为AB =AC +BC , 所以AB =30+20=50.9.如图,已知线段AB =20 cm ,点M 是线段AB 的中点,点C 是AB 延长线上一点,AC =3BC ,点D 是线段BA 延长线上一点,AD =12AB.(1)求线段BC 的长; (2)求线段DC 的长;(3)点M 还是哪些线段的中点?解:(1)因为AC =AB +BC ,AC =3BC , 所以3BC =AB +BC ,即AB =2BC. 因为AB =20 cm ,所以BC =10 cm.(2)因为AD =12AB ,AB =20 cm ,所以AD =10 cm.所以DC =AD +AB +BC =10+20+10=40(cm). (3)因为点M 是线段AB 的中点, 所以AM =MB =10 cm.所以DM =20 cm ,MC =20 cm. 所以点M 还是线段DC 的中点.10.线段AB 上有两点P 、Q ,点P 将AB 分成两部分,AP ∶PB =2∶3.点Q 将AB 也分成两部分,AQ ∶QB =4∶1,且PQ =3 cm.求AP 、QB 的长. 解:画出图形,如图:设AP =2x cm ,PB =3x cm ,则AB =5x cm. 因为AQ ∶QB =4∶1,所以AQ =4x cm ,QB =x cm. 所以PQ =PB -QB =2x cm. 因为PQ =3 cm , 所以2x =3. 所以x =1.5.所以AP =3 cm ,QB =1.5 cm.11.如图所示,有一个圆柱形纸筒,一只虫子在点B 处,一只蜘蛛在点A 处,蜘蛛沿着纸筒表面准备偷袭虫子,那么蜘蛛想要最快地捉住虫子,应怎样走? 解:如图所示,蜘蛛沿线段AB 爬行,能最快地捉住虫子.12.如图,已知点C ,D 为线段AB 上顺次两点,M 、N 分别是AC 、BD 的中点.(1)若AB =24,CD =10,求MN 的长;(2)若AB =a ,CD =b ,请用含a 、b 的式子表示出MN 的长. 解:(1)因为AB =24,CD =10, 所以得出AC +DB =14.因为M 、N 分别为AC ,BD 的中点, 所以CM =12AC ,DN =12BD.所以MC +DN =12(AC +DB)=7.所以MN =MC +DN +CD =17.(2)因为AB =a ,CD =b ,所以得出AC +DB =a -b ,所以MC +DN =12(AC +DB)=12(a -b).所以MN =MC +DN +CD =12(a -b)+b =12(a +b).13.课间休息时小明拿两根木棒玩,小明说:“较短木棒AB 长40 cm ,较长木棒CD 长60 cm ,将它们的一端重合,放在同一条直线上,此时两根木棒的中点分别是点E 和点F ,则点E 和点F 间的距离是多少?你说对了我就给你玩.”聪明的你请帮小华求出此时两根木棒的中点E 和F 间的距离是多少?解:如图1,当AB 在CD 的左侧且点B 和点C 重合时,图1因为点E 是AB 的中点, 所以BE =12AB =12×40=20(cm).因为点F 是CD 的中点, 所以CF =12CD =12×60=30(cm).所以EF =BE +CF =20+30=50(cm).如图2,当AB 在CD 上且点B 和点C 重合时,图2因为点E 是AB 的中点, 所以BE =12AB =12×40=20(cm).因为点F 是CD 的中点, 所以CF =12CD =12×60=30(cm).所以EF =CF -BE =30-20=10(cm).所以此时两根木棒的中点E 和F 间的距离是50 cm 或10 cm.14.请解答下面有关钟面上的角的问题. (1)8点15分,时针与分针的夹角是157.5°;(2)从12点整始,至少再经过多长时间,分针与时针能再一次重合? 解:设至少再过x 分钟分针与时针再一次重合, 根据题意,得0.5x +360=6x , 解得x =72011.所以从12点整始,至少再过72011分钟,分针与时针再一次重合.15.已知在同一平面内,∠AOB =90°,∠AOC =60°. (1)∠COB =30°或150°;(2)若OD 平分∠BOC ,OE 平分∠AOC ,则∠DOE 的度数为45°;(3)在(2)的条件下,将题目中的∠AOC =60°改成∠AOC =2α(α<45°),其他条件不变,你能求出∠DOE 的度数吗?若能,请写出求解过程,若不能,说明理由.解:需要分两种情况讨论: 当OC 在∠AOB 内部时,因为OD 平分∠BOC ,OE 平分∠AOC , 所以∠COD =12∠BOC ,∠COE =12∠AOC.所以∠DOE =∠COD +∠COE =12∠BOC +12∠AOC =12(90°-2α)+12·2α =45°;当OC 在∠AOB 外部时,因为OD 平分∠BOC ,OE 平分∠AOC , 所以∠COD =12∠BOC ,∠COE =12∠AOC.所以∠DOE =∠COD -∠COE =12∠BOC -12∠AOC =12(90°+2α)- 12·2α =45°.16.如图,O 是直线AB 上的一点,∠AOD =∠BOD =∠EOC =90°,∠BOC ∶∠AOE =3∶1. (1)求∠COD 的度数;(2)图中有哪几对角互为余角? (3)图中有哪几对角互为补角?解:(1)根据题意, 得∠BOC +∠AOE =90°. 因为∠BOC ∶∠AOE =3∶1, 所以∠BOC =34×90°=67.5°.所以∠COD =90°-67.5°=22.5°.(2)∠COB 与∠COD ,∠COB 与∠AOE ,∠DOE 与∠COD ,∠DOE 与∠AOE.(3)∠COB 与∠COA ,∠DOE 与∠COA ,∠AOE 与∠EOB ,∠COD 与∠EOB ,∠AOD 与∠BOD ,∠EOC 与∠AOD ,∠EOC 与∠BOD.18.如图1所示,将一副三角尺的直角顶点重合在点O 处.(1)①∠AOD 和∠BOC 相等吗?说明理由;②∠AOC 和∠BOD 在数量上有何关系?说明理由; (2)若将等腰的三角尺绕点O 旋转到如图2的位置. ①∠AOD 和∠BOC 相等吗?说明理由;②∠AOC 和∠BOD 的以上关系还成立吗?说明理由. 解:(1)①∠AOD =∠BOC.理由略. ②∠AOC 和∠BOD 互补.理由略. (2)①∠AOD =∠BOC.理由略.②∠AOC 和∠BOD 互补.理由略.19.如图,已知∠AOB 内部有顺次的四条射线:OE 、OC 、OD 、OF ,OE 平分∠AOC ,OF 平分∠BOD.(1)若∠AOB =160°,∠COD =40°,则∠EOF 的度数为100°; (2)若∠AOB =α,∠COD =β,求∠EOF 的度数; (3)从(1)、(2)的结果,你能看出什么规律吗?解:(2)因为OE 平分∠AOC ,OF 平分∠BOD , 所以∠COE =12∠AOC ,∠DOF =12∠BOD.因为∠EOF =∠COE +∠COD +∠FOD =12∠AOC +∠COD +12∠BOD =12(∠AOC +∠COD +∠BOD)+12∠COD =12∠AOB +12∠COD , 又∠AOB =α,∠COD =β, 所以∠EOF =12α+12β=12(α+β).(3)若∠AOB 内部有顺次的四条射线:OE 、OC 、OD 、OF ,OE 平分∠AOC ,OF 平分∠BOD , 则∠EOF =12(∠AOB +∠COD).20.如图,点D ,C 是线段AB 上任意两点,根据图形填空:(1)AD +CD =AC ;(2)AC +BC =AB ;(3)DB -BC =DC ;(4)AB -BD =AD. 21.如图:(1)试验观察:如果每过两点可以画一条直线,那么: 第①组最多可以画3条直线; 第②组最多可以画6条直线; 第③组最多可以画10条直线; (2)探索归纳:如果平面上有n(n ≥3)个点,且任意3个点均不在一条直线上,那么最多可以画n (n -1)2条直线;(用含n 的式子表示) (3)解决问题:某班45名同学在毕业后的一次聚会中,如果每两人握1次手问好,那么共握990次手. 21.如图,点C 是线段AB 上的点,点D 是线段BC 的中点.(1)若AB =10,AC =6,求CD 的长; (2)若AC =30,BD =10,求AB 的长. 解:(1)因为点D 是线段BC 的中点, 所以CD =12BC.因为AB =10,AC =6,所以BC =AB -AC =10-6=4. 所以CD =12BC =2.(2)因为点D 是线段BC 的中点, 所以BC =2BD. 因为BD =10,所以BC =2×10=20. 因为AB =AC +BC , 所以AB =30+20=50.22.在一次数学活动课上,王老师给学生发了一张长40 cm ,宽30 cm 的长方形纸片(如图),要求折成一个高为5 cm 的无盖的长方体盒子. (1)该如何裁剪呢?请画出示意图,并标出尺寸; (2)求该盒子的容积.解:(1)如图:(2)该盒子的容积为30×20×5=3 000(cm3).23.已知m、n满足等式(m-6)2+2|n-m+4|=0.(1)求m、n的值;(2)已知线段AB=m,在直线AB上取一点P,恰好使AP=nPB,点Q为PB的中点,求线段AQ的长.解:(1)由题意,得m-6=0,n-m+4=0,解得m=6,n=2.(2)如图,当点P在线段AB上时,因为AP=2PB,所以AP=4,PB=2.因为点Q为PB的中点,所以PQ=1.所以AQ=AP+PQ=4+1=5;如图,当点P在AB的延长线上时,AP-PB=AB,即2PB-PB=6,所以PB=6.因为点Q为PB的中点,所以BQ=3.所以AQ=AB+BQ=6+3=9.综上所述,线段AQ的长为5或9.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 单元测试题(二)一、选择题1.关于物体的惯性,下列说法中正确的是( )A .质量相同的两个物体,在阻力相同的情况下,速度大的不容易停下来,所以速度大的物体惯性大B .质量相同的物体惯性相同C .推动地面上静止的物体,比保持这个物体匀速运动时所需的力大,所以静止的物体惯性大D .在月球上举重比在地球上举重容易,所以同一物体2.一个人站在封闭的升降机中。
某段时间内这个人发现他处于超重状态,则在这段时间内( )A .他只能判断出升降机的加速度方向B .他只能判断出升降机的速度方向C .他既可以判断出升降机的加速度方向,也能判断出升降机的速度方向D .他既不能判断出升降机的加速度方向,也不能判断出升降机的速度方向3.下列说法正确的是( )A.有的物体只对别的物体施力而本身不受力B.牛顿第三定律对各种性质的力都适用C.当相互作用的两个物体做加速运动时,牛顿第三定律不适用D.当相互作用的两个物体没有直接接触时,牛顿第三定律也适用4. 如图1所示,物体M 位于升降机内的斜面上,升降机在上升的过程中,M 与斜面保持相对静止,突然悬挂升降机的绳子P 断裂,升降机在空中运动的过程中( )A.M 处于失重状态,不受任何力的作用B.M 处于失重状态,对斜面没有力的作用C.M 处于失重状态,它相对于斜面将有滑动D .M 不处于失重状态,它受力情况与断裂前相比没有发生变化5.如图2甲所示,小车上固定着硬质支架,杆的端点固定着一个质量为m 的小球。
杆对小球的作用力的变化如图乙所示,则关于小车的运动,下列说法中正确的图1是(杆对小球的作用力由F 1变化至F 4)( )A .小车可能向左做加速度增大的运动B .小车由静止开始向右做匀加速运动C .小车的速度越来越大D .小车的加速度越来越小 6.如图3所示,圆柱形的仓库内有三块长度不同的滑板ao 、bo,co ,其下端都固定于底部圆心O ,而上端则搁在仓库侧壁上,三块滑板与水平面的夹角依次是30O 、45O 、60O 。
若有三个小孩同时从a 、b 、c 处开始下滑(忽略阻力),则( )A .a 处小孩最后到0点B .b 处小孩最后到0点C .c 处小孩最先到0点D .a 、C 处小孩同时到0点 7.如图4所示,ab 、cd 是竖直平面内两根固定的细杆,a 、b 、c 、d 位于同一圆周上,圆周半径为R ,b 点为圆周的最低点,c 点为圆周的最高点。
现有两个小滑环A 、B 分别从a 、c 处由静止释放,滑环A 经时间t 1从a 点到达b 点,滑环B 经时间t 2从c 点到达d 点;另有一小球C 从c 点自由下落,到达b 点时间为t 3,不计一切阻力与摩擦,且A 、B 、C 都可视为质点,则t 1、t 2、t 3的大小关系为( )A .t 1=t 2=t 3B .t 1=t 2>t 3C .t 2>t 1>t 3D .A 、B 、C 三物体的质量未知,因此无法比较8.一条不可伸长的轻绳跨过质量可忽略不计的定滑轮,绳的一端系一质量M=15kg 的重物,重物静止于地面上,有一质量m=10kg 的猴子,从绳子的另一端沿绳向上爬,如图5所示,不计滑轮摩擦,在重物不离开地面条件下,猴子向上爬的最大加速度为(g=10m /s 2)( )A. 25 m /s 2B. 5 m /s 2C. 10 m /s 2D. 15 m /s 29.如图6所示、一个质量为m 的圆环套在一根固定的水平长直杆上、环与杆图3 图5 图2c a R 图4的摩擦因数为μ,现给环一个向右的初速度0v ,同时对环加一个竖直向上的作用力F ,并使F 的大小随v 的大小变化,两者关系为F kv =,其中k 为常数,则环运动过程中的速度图像可能是图中的( )二、填空与实验题10.如图7所示,质量为m 的小球用水平弹簧系住,并用倾角为︒30的光滑木板AB 托住,小球恰好处于静止状态.当木板AB 突然向下撤离的瞬间,小球的加速度大小为,方向为。
11. “探究加速度与物体质量、物体受力的关系”的实验装置如图8甲所示。
(1)在平衡小车与桌面之间摩擦力的过程中,打出了一条纸带如图8乙所示。
计时器打点的时间间隔为0.02 s 。
从比较清晰的点起,每5个点取一个计数点,量出相邻计数点之间的距离。
该小车的加速度a = m /s 2。
(结果保留两位有效数字)(2)平衡摩擦力后,将5个相同的砝码都放在小车上。
挂上砝码盘,然后每次从小车上取一个砝码添加到砝码盘中,测量小车的加速度。
小车的加速度a 与砝码盘中砝码总重力F 的实验数据如下表:请根据实验数据作出a -F 的关系图象。
(3)根据提供的实验数据作出的a —F 图线不通过原点,请说明主要原因。
图6 甲乙图7三、计算题12.一游客在峨眉山滑雪时,由静止开始沿倾角为37°的山坡匀加速滑下。
下滑过程中从A 点开始给游客抓拍一张连续曝光的照片如图9所示。
经测量游客从起点到本次曝光的中间时刻的位移恰好是40m 。
已知本次摄影的曝光时间是0.2s ,照片中虚影的长度L 相当于实际长度4m ,试计算滑雪板与坡道间的动摩擦因数。
( g =10m/s 2 , sin370=0.6 , cos370=0.8 )13.如图10所示,PQ 为一固定水平放置的光滑细长杆,质量均为m 的两小球A 、B 穿于其上,两小球用长度均为L 的轻线连接,且被穿于杆上的轻弹簧相连.E 为质量不计的光滑定滑轮,被两轻线悬挂,C 、D 球质量分别为m 和2m 用轻绳连接并跨过定滑轮。
当C 、D 球运动时轻弹簧长度也为L ,已知劲度系数为K ,求弹簧的原始长度?(弹簧在弹性限度内,重力加速度为g )14.如图11所示,在倾角θ=37︒的固定斜面上放置一质量M =1kg 、长度L =3m 的薄平板AB 。
平板的上表面光滑,其下端B 与斜面底端C 的距离为7m 。
在平板的上端A 处放一质量m =0.6kg 的滑块,开始时使平板和滑块都静止,之后将它们无初速释放。
设平板与斜面间、滑块与斜面间的动摩擦因数均为μ=0.5,求滑块与平板下端B 到达斜面底端C 的时间差Δt 。
(sin370=0.6,cos370=0.8,g =10m/s 2)图9 A B θ 图11 L L L P A B E C 图10参考答案一、选择题1.B 解析 惯性大小只与质量有关,与其他因素无关。
2.A 解析 他处于超重状态,说明加速度是向上的,因为升降机是封闭的,里面的人无法判断是上升还是下降。
3.BD 解析 只要有相互作用力牛顿第三定律就可以适用,不论力的性质如何、运动状态如何及是否接触.根据力的定义知只施力不受力的物体是不存在的.4.B 解析 绳子断裂后,整体做竖直上抛运动,发生失重,物体对斜面没有力作用。
5.A 解析 据图知向右水平分力变大,向右加速度变大,做非匀变运动,要是向左运动,则是减速。
6.D 解析 三块滑板与圆柱形仓库构成的斜面底边长度均为圆柱形底面半径,则21sin cos 2R gt θθ=,得24sin 2R t g θ=,当θ=45O 时,t 最小;当θ=30O 和60O 时,sin2θ的值相同,故只有D 正确。
7.A 解析 设cd 与水平方向的夹角为θ,则沿cd 运动时,有212sin (sin )2R g t θθ=,t = 8. B 解析 猴子对绳的拉力F=mg+ma ≤Mg a ≤(M -m)g/m =5m/s 2.9.ABD 解析 当0F kv mg ==,加速度为零,A 对;当0F kv mg =<,有kv a g m μ=-,速度变小加速度变大,B 图对;若0F kv mg =>,有kv a g mμ=-,速度变小加速度变小,,当速度减到某值满足时,加速度变为零,此后匀速运动,故C 图错D 图对。
二、填空与实验10.g 332 垂直木板向下 解析 木板对球的支持力N=mg/cos300=mg 332。
当木板AB 突然向下撤离的瞬间,另外两个力重力和弹簧弹力瞬间不变,所以这两个力的合力大小等于原来木板的支持力,方向与原来木板的支持力相反,所以小球的加速度为大小为g 332,方向垂直木板向下。
11.(1)0.16(0.15也算对) (2)如图所示 (3)未计入砝码盘的重力解析 (1)根据纸带求解加速度用公式2x aT ∆=,计算时要弄清公式中各个量的物理意义,x ∆为连续相等时间内的位移差,T 为连续相等的时间间隔,如果每5个点取一个计数点,则连续两计数点间的时间间隔为T=0.1 s ,又x ∆=(3.68—3.52)×10-2m,代入可得加速度a=0.16m/s 2。
也可以使用最后一段和第二段的位移差求解,得加速度a =0.15 m /s 2。
(2)根据题中所给的数据,合理地设计横、纵坐标的刻度值,使图线倾斜程度与水平方向的夹角为45O 左右为宜。
由此确定F 轴的范围从0到1.2 N 较合适,而a 轴则从0到3m/s 2较合适。
设置好刻度,根据数据确定各点的位置,将各点用一条平滑曲线连起来,并延长交坐标轴于某一点。
如图所示。
(3)处理图象问题要注意图线的斜率、交点、拐点、面积等对应的物理意义。
所作图线与纵轴相交而不过原点,该交点说明当不加砝码时,小车仍有加速度,即绳对小车仍有拉力,从此拉力的来源考虑很容易得到答案,是因为砝码盘的重力,而在(2)的图表中只给出了砝码的总重力,没有考虑砝码盘的重力。
三、计算题12..解析 用x 表示题中的位移,θ表示斜面倾角,△t 表示曝光时间,μ表示滑雪板与坡道间的动摩擦因数,m 表示滑雪运动员的质量。
设运动员下滑的加速度为a ,曝光的中间时刻的速度为v 0,则有as v 220= tL v ∆=0 可求得 a =5.0m/s 2又根据牛顿第二定律有 ma mg mg =-θμθcos sinmg F N可求得动摩擦因数为 μ=0.12513.解析 C 、D 球在竖直方向做匀变速运动,g m mg mg a 3132=-=以C 球为研究对象,轻绳拉力T 1 = mg +ma =34 mg 对滑轮,拉线力为T E ,有T E =2T 1=38mg 对轻线,线张力为T ,有2T cos300=T E对A 球,弹簧力为F 弹,有F 弹=T cos600解得F 弹=mg 934 弹簧被压缩,所以弹簧原长L 0=L +x =L + k F 弹=L +mg k934 14.解析 对薄板,由于Mg sin37º<μ(M +m )g cos37º,故滑块在薄板上滑动时,薄板静止不动。
对滑块:在薄板上滑行时加速度a 1=g sin37º=6m/s 2,到达B 点时速度6m/s v =滑块由B 至C 时的加速度a 2=gsin37°-μg cos37º=2m/s 2,设滑块由B 至C 所用时间为t ,则2212BC L vt a t =+,解得t =1s 。
