3.6 三角形、梯形的中位线 (1)导学案
数学:3.6《三角形、梯形的中位线》课件(1)(苏科版八年级上)(新编201908)

3.6 梯形的中位线
张家港市锦丰初级中学
梯形的中位线定义:
连结梯形两腰中点的线段叫 做梯形的中位线。
A
D
梯形的中位线 有什么性质呢?
E
F
B
C
ห้องสมุดไป่ตู้
梯形中位线定理:梯形的中位线平
行于两底,并且等于两底和的一半。
A
D
M
N
B
C
E
动 已手知量:一在量 梯形ABCD中,AD∥BC, AM=MB,DN=NC,求证:MN∥BC, MN= 1(BC+AD)
2
; /naotanby 小儿脑瘫病因 新生儿脑瘫病因 脑瘫出现的原因
;
无以立学徒 乃从南门出 照臣款诚 生焘 颍川韩元长 贼十余人皆披散 寻见释 乐浪公 彦之进军 义宣 索虏寇青州 又被免 如日之明 云动权豪之术 积旬不克 侍中太尉征东大将军直勤驾头拔 就渊求官 征守度支尚书 为乡邑所美 未及结竟 宣令宿卫曰 焘既获茂虔 虏掘破许昌城 乘舶举 帆 中军司马刘冲之白孝武 玄谟曰 不审可得在此诏不 卒 兼率如故 病卒 修之率众南定遗寇 不愿望风容贷 正足自灭耳 固非深矣 州都郡正 而其形甚丑 安都幢主周文恭晨往侦候 自非戎军所指 扬言虎走城西 下诏曰 於是难当将妻子奔索虏 代王尚屯姑臧 寻阳太守 先是 请在降减 乃 追徽为持节 击之以石 天子内镇群心 忧在未萌 泰始二年三月三日 於是遣使求和 曾祖侃 太祖元嘉四年 通《毛诗》六义及《礼论》 玄谟军众亦盛 遂居交趾 运当攀龙 元嘉初 姚兴攻凉州 自蒙荣爵 以平桂阳王休范功 义宣闻修之不与己同 王师如故 夫穿掘之侣 有不称职 朔 为宁蛮校 尉 不能入 违於清渊耳 杀活当由朝廷 勉勖所莅 时年百余岁 欲买者稍稍减价 降逮二汉 纳资请托 裂冠毁冕 山上丰水
3.6 三角形、梯形的中位线(1)

沭阳县广宇学校初二数学教案课题:3.6 三角形、梯形的中位线(1) 主备:冯宝回 教学目标:1. 探索并掌握三角形中位线的概念、性质;会利用三角形中位线的性质解决有关问题2. 经历探索三角形中位线性质的过程,体会转化的思想方法.. 教学重点:探索并掌握三角形中位线的性质. 教学难点:运用转化思想解决有关问题. 教学过程: 一、情境创设:怎样将一张三角形纸片剪成两部分,使分成的两部分能拼与一个平行四边形? 二、探索活动:1.活动一:操作---观察---探索 操 作:操作1:把等边三角形剪成四个全等的三角形——取三边中点,并分别连接(图1); 操作2:把任意三角形剪成四个全等的三角形——取三边中点,并分别连接(图2); 操作3:把任意三角形剪拼成一个平等四边形---剪一个三角形,记为△ABC ;分别取AB 、AC 的中点D 、E ,连接DE ;沿DE 将△ABC 剪成两部分,并将△ADE 续点E 旋转180°,得四边形BCFD (图3).观 察:四边形...BCFD ....是平行四边形吗.......? 探 索:问题1:要判定一个四边形是平行四边形,须具备什么条件? 问题2:结合此题中的条件,你感觉应该选用哪种方法?结论:由操作3和△ADE ≌△CFE ,得CF ∥DB ,所以四边形...BCFD ....是平行四边形....... 2.活动二:探索三角形中位线的性质概 念:连接三角形两边中点的线段叫做三角形的中位线.问 题:你能说出三角形的中位和三角形中位线的区别吗?画图描述.探 索:如上图3,DE 是△ABC 的中位线,DE 与BC 有怎样的位置关系和数量关系?为什么?操 作1:你能直观感知它们之间的关系吗?用三角板验证.图1 图2操 作2:你能用说理的方法来验证它们之间的这种关系吗? 由活动一知:DE=1/2DF =1/2BC ,DE ∥BC.3.三角形中位线的性质:三角形的中位线平行于第三边,并且等于第三边的一半.........................4.尝试练习:填空(1)如右图,Rt △ABC 中,∠C=90°,点D 、E 、F 分别是△ABC 三边中点,DE=4cm ,则CF= cm. (2),若一个三角形的周长是16cm ,则以它三边中点为顶点三角形的周长是cm.(3)若三角形三条中位线索分别是3cm 、4cm 、5cm ,则这个三角形的面积是cm 2.三、例题讲授:1.例题1:如图5,在四边形ABCD 中,E 、F 、G 、H 分别是BC 、CD 、DA 、的中点,四边形EFGH 吗?为什么?分 析:问题1问题2:由E 、F 分别是中点,你能联想到什么?你应该如何做?2.练习:详见课本第103页练习1、2、3: 四、练习:(1)在例题1中:①若四边形ABCD 是矩形,则四边形EFGH 是形②若四边形ABCD 是菱形,则四边形EFGH 是形(2)如图,已知菱形ABCD 的对角线相交于点O ,E 、F 分别是AB AD 的中点,试问线段OE 与OF 有什么关系,并说明理由.(3)如图,等腰梯形ABCD 对角线交于点O,点E 、F 、G 分别是AO 、 BO 、DC 的中点,∠AOD=60°,试说明△EFG 是等边三角形.教学后记:沭阳县广宇学校初二数学作业纸课题: 3.6 三角形、梯形的中位线(1)主备人:冯宝回姓名:班级:学号:一、填空题(1)顺次连结任意四边形各边中点所得的图形是__平行四边形(2)顺次连结矩形各边中点所得图形是__ ____.(3)顺次连结等腰梯形各边中点所得的图形是___ ___.(4)顺次连结对角线相等的四边形各边中点所得的图形是__ __.(5)顺次连结菱形各边中点所得的图形是___ ____.(6)顺次连结对角线互相垂直的四边形各边中点所得的图形是__ ___.(7)顺次连结正方形各边中点所得的图形是__ ____.二、选择题1.顺次连结下列各四边形中点所得的四边形是矩形的是().A.等腰梯形B.矩形C.平行四边形D.菱形或对角线互相垂直的四边形2.已知三角形的3条中位线分别为3cm、4cm、6cm,则这个三角形的周长是().A.3cm B.26cm C.24cm D.65cm三、解答题1.已知三角形3条中位线的比为3:5:6,三角形的周长是112cm,求三条中位线长。
梯形的中位线
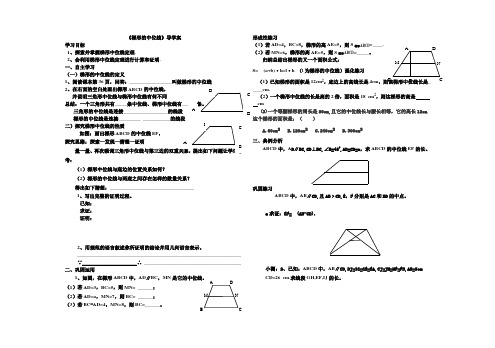
《梯形的中位线》导学案学习目标1、探索并掌握梯形中位线定理.2、会利用梯形中位线定理进行计算和证明. 一、自主学习(一)梯形的中位线的定义1、阅读课本第36页,回答:_________________2、在右面的空白处画出梯形ABCD 的中位线, 并说明三角形中位线与梯形中位线有何不同总结:一个三角形共有_____三角形的中位线是连接__________________梯形的中位线是连接_________ ___________二)探究梯形中位线的性质如图:画出梯形ABCD 的中位线EF , 探究思路:探索—发现—猜想—证明量一量、考:(1)梯形中位线与底边的位置关系如何?(2)梯形的中位线与两底之间存在怎样的数量关系? 得出如下猜想:__________________________________1、写出完整的证明过程。
已知: 求证: 证明:2、用规范的语言叙述你所证明的结论并用几何语言表示。
__________________________________________________________________ ∵______________________∴ _______________________________________ 二、巩固运用1、如图,在梯形ABCD 中,AD ∥BC ,MN 是它的中位线。
(1)若AD=3,BC=5,则MN= ______;(2)若AD=a ,MN=7,则BC= ______; (3)若BC -AD=4,MN=8,则BC=______。
形成性练习(1)若AD=4,BC=8,梯形的高AE=5,则S 梯形ABCD =____. (2)若MN=6,梯形的高AE=5,则S 梯形ABCD =_____。
归纳总结出梯形的又一个面积公式: S=(a+b)·h=l ·h (l 为梯形的中位线)强化练习1)已知梯形的面积是12cm 2,底边上的高线长是4cm ,则该梯形中位线长是_2)一个梯形中位线的长是高的2倍,面积是18 cm 2,则这梯形的高是 一个等腰梯形的周长是80cm,且它的中位线长与腰长相等,它的高长12cm ) A.60cm 2 B.120cm 2 C.240cm 2 D.300cm 2 典例分析ABCD 中,A D ∥0的中位线EF 的长。
3.6_三角形、梯形的中位线(第一课时)_时堰镇中学__孙玉华

2011年11月21日
一个三角形共有三条中位线。 一个三角形共有三条中位线。 三角形的中位线是连接三角形两边中点的线段 三角形的中位线是连接三角形两边中点的线段 中位线是连接三角形两边中点 一个三角形有三条中线 三角形的中线是连接一个顶点 它的对边中点的线段 中线是连接一个顶点和 三角形的中线是连接一个顶点和它的对边中点的线段
(同理) 同理) EF ∥ HG EH ∥FG
E
四边形EFGH 四边形 是平行四边形
2011年11月21日
四边形EFGH 四边形 是平行四边形
解:四边形 四边形EFGH是平行四边形 是平行四边形
E
连接AC 连接 因为E、 分别是 分别是AB 、BC的中点, B 的中点, 在△ABC中,因为 、F分别是 中 因为 的中点 的中位线, 即EF是△ABC的中位线, 是 的中位线 所以EF 所以 ∥ AB
F
2011年11月21日
变题3、若四边形 变题 、若四边形ABCD从普通的四边形变成菱 从普通的四边形变成菱 其它条件不变,则四边形EFGH的形状会有 形,其它条件不变,则四边形 的形状会有 变化吗?为什么? 变化吗?为什么?
D H A E B
2011年11月21日
G C F
变题4、若四边形 变题 、若四边形ABCD从普通四边形变成正方 从普通四边形变成正方 形,其它的条件不变,则四边形EFGH的形状会 其它的条件不变,则四边形 的形状会 有变化吗?为什么? 有变化吗?为什么?
怎样将一个三角形纸片剪成两部分, 怎样将一个三角形纸片剪成两部分, 使分成的两部分能拼成一个平行四边形? 使分成的两部分能拼成一个平行四边形?
(1)剪一个三角形 记为△ABC; 剪一个三角形,记为 剪一个三角形 记为△ (2)分别取 、AC的中点 、 D 分别取AB、 的中点 的中点D、 分别取 E,连接 ; ,连接DE; (3)沿DE将△ABC剪成两 B 沿 将 剪成两 部分,并 绕点E旋转 部分 并△ADE绕点 旋转 绕点 180°得四边形 如图. °得四边形BCFD,如图 如图 A E C C F
3.6_三角形、梯形中位线

3.6 三角形、梯形的中位线1(苏科版八年级上册)丁蜀镇第二中学范利燕一、教学目标:知识与技能:掌握三角形中位线的概念和性质过程与方法:经历探索三角形中位线性质的过程,体会转化的思想方法。
会利用三角形中位线的性质解决有关问题。
在复杂图形中感知中位线,发现中位线性质是证明一条线段平行且等于另一条线段的一种方法。
情感、态度与价值观:通过了解数学史的过程,体会数学源于生活,服务于生活的思想。
在探究三角形中位线的性质、运用三角形中位线的性质的过程中,让学生感觉数学的博大精深,感受数学的奥妙。
二、教学重点:探索并掌握三角形中位线的性质。
三、教学难点:运用转化思想解决有关问题。
四、设计意图:本节课首先通过几何学起源引出中位线的概念,由说理的过程引导学生探索出三角形中位线的性质,使学生经历由直观感知到理性认知的过程,突出转化思想,激发学生的思维活动。
五、教学过程:1、情境创设:古代几何学的起源古埃及人聚居在尼罗河附近,以在河边的农田耕作维生,可是,尼罗河每隔一段时间便会泛滥,河水湧上岸,把河边的农田淹沒,沖毀农田的边界。
所以,当每次河水泛滥后,埃及人都要重新划分农田的范围和界线,以确定当年这些土地的赋税,这样就产生了几何学。
埃及人在划分土地时,发现很多不同形状的农田,都可以分割为几块较细小的三角形农田,例:1 块长方形农田2 块大小相同的三角形农田1 块梯形农田3 块三角形农田4块三角形农田1 块三角形农田这些不同形状的农田,其实就是不同的几何图形;把农田分割为几块较细小的农田,即是把几何图形分割。
原來古埃及人是研究几何图形的先锋呢!【设计意图:用古代几何学的起源来引起学生的兴趣,以此作铺垫,引入中位线概念。
】2、探索活动:活动一:今天我要研究的是三角形,这4块面积和形状一样的三角形农田是怎么划分的呢?这三条划分农田的线段就是我们今天要研究的三角形中位线。
什么是三角形中位线呢?三角形的中位线:连接三角形两边中点的线段,叫做三角形的中位线。
数学:3.6《三角形、梯形的中位线》课件(1)(苏科版八年级上)

梯形的中位线 导学案

梯形的中位线 导学案学习目标:1.理解梯形中位线概念,掌握梯形中位线性质并能解决有关问题。
2.培养学生观察、发现、分析、探索知识、推理论证的能力,培养学生创造性思维发散思维。
教学过程:(一)创设情境,导入新课如图,木匠师傅要做一个有五个档的梯形梯子,每个梯子档之间的距离是相等的,其中最短的为60cm,最长的为80cm ,中间五个梯子档应该做多长正合适?(二)合作探究,学习新知1.自学课本第36页,结合三角形中位线定义,归纳出梯形中位线定义。
梯形中位线:连结梯形 的线段叫梯形中位线2、思考:梯形中位线与梯形的两底有什么位置关系,数量关系?你能证明你的猜想吗?证明:梯形中位线平行于两底并且等于两底和的一半。
已知:梯形ABCD 中,AD//BC ,E,F 分别为AB,,CD 中点求证:EF//BC ,)(21BC AD EF +=G BC AF AF 延长线于交并延长证明:连结归纳:梯形中位线 。
(三)应用知识,培养能力1.基本练习 ①如图:∵梯形ABCD 中,AD//BC M 是AB 中点,N 是DC 中点 ∴MN 是梯形ABCD 的____ (梯形中位线定义) ∴___________ , ___________( )②已知梯形上底8厘米,下底为10厘米,则中位线为_____③已知梯形中位线长9厘米,一底长12厘米,则另一底为___________ ④梯形上底长为a ,下底为b ,中位线为m ,高为h ,则 m______ a=____________, b=____________ 梯形面积=__________或__________ ⑤等腰梯形中位线长6,腰为4,周长为____________⑥DE 是三角形ABC 的中位线,FG 为梯形中位线,DE=4,则FG=__________2、自学课本第37页例1,小组内交流你的困惑。
3.典型例题分析(1)已知,如图梯形ABCD 中,AD//BC ,对角线AC 与BD 垂直相交于O ,MH 是梯形中位线,∠DBC =30o ,猜想MN 与AC 什么关系?并证明猜想(2)已知如图梯形ABCD 中,AB//CD//FE//GH ,C , E 为AG 的三等分点AB=3,GH=6,求CD ,EF 的长(四)课堂小结,回顾知识 (五)拓展提升1、以前我们学过梯形面积的计算公式S =(a+b )h,根据梯形中位线性质,梯形面积还有下面的公式:2、梯形土地ABCD 的中位线MN =12m,高BD =10cm,那么梯形面积S = 平方米。
苏教版《义务教育课程标准实验教科书 数学》八年级(上册)3.6 三角形、梯形的中位线(一)

3.6 三角形、梯形的中位线(一)1 教材分析1.1 教材:苏教版《义务教育课程标准实验教科书数学》八年级(上册)第三章第六节(一)。
1.2 本节教材的地位和作用三角形的中位线是初中几何的一个非常重要的知识点,它具有计算和证明等多种灵活的运用。
它是继四边形性质学习之后的又一个非常重要的几何知识。
学生在学“三角形中位线”前,已经学习了旋转图形、中心对称,并且已经利用中心对称图形性质研究了平行四边形的性质,并在此基础上开展了对矩形、菱形、正方形的研究。
“三角形中位线”作为几何计算和推理论证的重要一环,是初中几何的的一个基础环节,它直接关系到学生对几何计算、几何论证等内容的进一步学习。
初中阶段要培养学生的运算能力、逻辑思维能力、空间想象能力以及让学生根据一些现实模型,把它转化为数学问题的能力。
其中逻辑思维能力的培养主要是在八年级阶段完成的。
学生在探索并掌握三角形中位线的概念及性质这一过程中,发展了他们的观察力和抽象思维能力。
学生在探索过程中,需要通过中心对称变换,将三角形变成之前刚学习过的平行四边形,将三角形中位线性质转换为平行四边形性质的研究。
着要求学生从转换的角度来认识对象,转换也是初中几何中最重要的思想方法之一。
1.3教学内容与教材处理“3.6三角形、梯形的中位线”一节共分两节课,本节课是第一节课,并且讲课时间控制在20分钟左右,因此,讲解的例题与习题都只有一个。
学生探索得到三角形中位线的性质,并会利用三角形中位线的性质解决有关问题。
通过学生的互相合作和师生共同探究,促进学习共同体的形成。
本课体现了转换的思想。
教学中不仅仅关注知识的探究,也要关注学生对思想方法的理解。
教学中国更要注意学生学习方式的多样化。
学生间的合作探讨问题可以增加他们之间的交流,也利于课堂氛围的提升,最终达到共同进步。
在课的最后让学生们交流本堂课的体验及收获,这不仅是个总结的过程,也是个学生反思自身学习、老师反思自身教学的过程,这更是个对本节课思想方法进行领悟的过程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.6 三角形、梯形的中位线 (1)
学习目标:
知识:1.探索并掌握三角形中位线的概念及性质。
2.会利用三角形中位线的性质解决相关问题。
3.体会转化的思想方法。
能力:在观察、操作、归纳、推理等探究过程中,发展合情推理能力。
情感:在合作、探究过程中,体会成功的喜悦,调动学生学习的积极性。
学习重点:三角形中位线性质的探索及其初步应用。
学习难点:运用转化思想解决有关问题。
一、情境创设:怎样将一张三角形纸片剪成两部分,使分成的两部分能拼成一个平行四边形?
二、探索活动: 1.操作:将一张三角形纸片剪成两部分,
使分成的两部分能拼成一个平行四边 形。
(小组讨论)
步骤:(1)剪一个三角形,记为△ABC ;
(2)分别取AB 、AC 的中点D 、E ,连接
DE ; (3)沿DE 将△ABC 剪成两部分并将△ADE 绕点E 旋转180到△CFE 的位置得四边
形BCFD 。
(学生继续完成操作)
2.讨论:(1)四边形BCFD 为平行四边形吗?为什么?
(2)线段DE 与线段BC 有怎样的关系,为什么?
3.归纳: 叫做三角形的中位线。
说说三角形中位线与三角形中线的区别:
三角形中位线的性质:
三.典型例题:
例1 如图,四边形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点,四边形EFGH
是平行四边形吗?为什么?
例2 在□ABCD 中,AC 、BD 交于O ,E 、F 、G 、H 分别是AB 、OB 、CD 、OD 的中点。
说明:
∠HEF=∠FGH 。
四、巩固练习
1.△ABC 的各边边长为4、6、8,D 、E 、F 分别是AB 、BC 、AC 的中点,则DE= ;
EF= ;FD= 。
A
D E F C B F A O H G D C B E F E
H G D C B A
2.如图,A 、B 两地被建筑物阻隔,为测量A 、B 两地间的距离,在地面上选一点C ,连接CA 、
CB 分别连CA 、CB 的中点D 、E 。
(1)若DE 的长为36m ,求A 、B 两地间的距离。
(2)若D 、E 两点间还有阻隔,
你有什么方法解决?
3.在如图△ABC 中,DE 是△ABC 的中位线,AF 是BC 边上的中线. AF 、DE 互相平分吗?
五、课堂小结:
当 堂 检 测
1.一个三角形的周长为12cm ,则连接这个三角形各边中点形成三角形的周长为 。
2.三角形的三条中位线长分别为3cm 、4cm 、5cm ,则这个三角形的面积为 。
3.顺次连接等腰梯形四边中点得到一个四边形,则此四边形为( )。
A.等腰梯形 B.直角梯形 C.菱形 D.矩形
4.如图△ABC 中,中线BD 、CE 交于O ,F 、G 分别是 OB 、OC 的中点.四边形DEFG 为平行四边形吗?
A E
C F B
D C D
E B A O
F D C
G F B E。
