统计学案例
使用统计学方法解决实际问题的案例分析

使用统计学方法解决实际问题的案例分析统计学是一种应用数学,它通过收集、整理、分析和解释数据,来帮助人们理解和解决实际问题。
统计学方法可以应用于各个领域,包括商业、医疗、环境、教育等。
本文将通过案例分析的形式,了解如何使用统计学方法解决实际问题。
案例一:零售业销售数据分析某零售业公司想要了解其销售数据的走势,以便做出更好的营销决策。
他们提供了过去一年的销售数据,包括每月销售额、销售量、促销活动等信息。
首先,利用统计学方法对销售数据进行分析。
通过统计学方法,我们可以计算出销售额和销售量的平均值、中位数和标准差,以了解销售数据的分布情况。
同时,我们可以利用相关系数分析销售额和促销活动之间的关系,以确定促销活动对销售额的影响程度。
接下来,我们可以利用数据可视化工具,如折线图、柱状图等,将销售数据进行可视化展现。
通过可视化分析,我们可以清晰地看到销售额和销售量的变化趋势,以及促销活动对销售额的影响程度。
司提供相关建议,比如哪些产品在不同月份的销售额最高,何时进行促销活动效果最好等。
这些建议将帮助零售业公司改进营销策略,提高销售业绩。
案例二:医疗数据分析某医疗机构想要了解患者的就诊情况,以便改进医疗服务。
他们提供了过去一年的门诊和住院病例数据,包括就诊人数、疾病种类、就诊费用等信息。
首先,利用统计学方法对就诊数据进行分析。
我们可以计算出就诊人数和就诊费用的平均值、中位数和标准差,以了解就诊数据的分布情况。
同时,我们可以利用频数分析疾病种类的分布情况,以确定不同疾病在就诊人群中的比例。
接下来,我们可以利用数据可视化工具,如饼状图、条形图等,将就诊数据进行可视化展现。
通过可视化分析,我们可以清晰地看到不同疾病在就诊人群中的比例,以及不同疾病的就诊费用情况。
提供相关建议,比如哪些疾病在就诊人群中的比例较高,哪些疾病的就诊费用较高等。
这些建议将帮助医疗机构改进医疗服务,提高患者满意度。
综上所述,统计学方法可以帮助人们理解和解决实际问题。
生活中的统计学案例

生活中的统计学案例生活中的统计学案例无处不在,统计学作为一门应用广泛的学科,其实际应用涵盖了生活的方方面面。
从日常生活中的消费数据到医疗领域的疾病统计,从教育领域的学生成绩分析到经济领域的市场调查,统计学都扮演着不可或缺的角色。
下面,我们将通过几个生活中的具体案例,来展示统计学在实际生活中的应用。
首先,我们来看一个关于市场调查的案例。
某公司推出了一款新产品,想要了解消费者对该产品的满意度。
他们进行了一次市场调查,通过问卷调查的方式收集了大量数据。
在统计学的帮助下,他们可以对这些数据进行分析,得出消费者对产品的整体满意度,以及不同年龄、性别、地域等因素对满意度的影响。
通过统计学的分析,公司可以更好地了解消费者的需求,为产品的改进提供依据。
其次,我们来看一个关于医疗领域的案例。
某医院统计了一段时间内的疾病发病率数据,发现某种疾病的发病率呈上升趋势。
统计学的方法可以帮助医院分析这些数据,找出可能的病因和影响因素。
通过统计学的分析,医院可以及时采取相应的预防措施,有效控制疾病的传播。
再次,我们来看一个关于教育领域的案例。
某学校对学生的期末考试成绩进行了统计分析,发现数学成绩普遍较低。
通过统计学的方法,学校可以对学生的学习情况进行分析,找出存在的问题和不足之处。
同时,还可以通过统计学的方法,找出学习成绩较好的学生的学习方法和习惯,为其他学生提供学习的借鉴和指导。
最后,我们来看一个关于日常生活消费数据的案例。
某家庭通过统计每个月的生活消费数据,发现了一些意想不到的情况。
通过统计学的方法,他们可以对不同方面的消费进行分析,找出存在的问题和改进的空间。
通过统计学的分析,他们可以更好地理财,合理安排生活消费,提高生活质量。
通过以上几个生活中的统计学案例,我们可以看到统计学在实际生活中的重要作用。
无论是在市场调查、医疗领域、教育领域,还是在日常生活中的消费数据分析,统计学都可以为我们提供有力的支持和帮助。
因此,学习统计学,掌握统计学的方法和技巧,对我们的生活和工作都是非常有益的。
统计学在决策分析中的实践案例

统计学在决策分析中的实践案例随着社会的发展和竞争的加剧,决策分析在各个领域中的重要性日益凸显。
而统计学作为一种重要的决策工具,在决策分析中也起着关键的作用。
本文通过介绍几个实践案例,来探讨统计学在决策分析中的应用。
案例一:市场营销决策在市场营销中,决策者需要根据市场的需求和竞争情况来进行产品定位和市场推广。
统计学通过市场调研和数据分析,为决策者提供了有力的决策支持。
以某企业的市场推广决策为例,该企业计划推出一款新产品。
为了了解市场的需求,他们进行了一次市场调研,并采集了大量的数据。
通过对这些数据进行统计分析,他们发现目标客户群体更倾向于价格相对较低的产品。
基于这个发现,他们决定以价格优势为主要推广点,制定相应的市场推广策略。
通过引入统计学的分析手段,该企业最终在市场中获得了成功。
案例二:风险管理决策在金融行业中,风险管理是一个重要的问题。
通过统计学的方法,可以对市场风险进行预测和控制。
某投资公司在进行投资决策时,需要考虑不同投资组合的风险和收益。
通过对历史数据进行回归分析和风险评估,他们可以得到不同投资组合的预期风险和收益。
通过权衡各个投资组合的风险和收益,他们可以最大程度地提高投资回报,同时降低投资风险。
案例三:质量管理决策在生产制造领域中,质量管理是确保产品质量的关键环节。
统计学可以帮助企业进行质量控制,提高产品的质量。
某汽车制造公司在生产过程中,发现某批次产品出现了较高的不合格率。
为了解决这个问题,他们通过统计学的方法进行了质量分析。
通过对生产数据进行抽样和假设检验,他们发现问题出现在某个工段的生产过程中。
通过对该工段进行优化和改进,最终将产品的质量问题解决,提高了整体产品的质量水平。
总结统计学作为决策分析的工具之一,在实践中发挥着重要的作用。
通过统计学的方法,可以对市场需求进行分析,帮助企业制定市场推广策略;可以对风险进行预测和控制,帮助金融机构做出更明智的投资决策;可以对质量问题进行分析,帮助企业提高产品质量。
统计学教学案例(精选)

用于研究不同组别间均值差异的显著性,判断因素对结果的影响是 否显著。
回归分析
用于研究变量之间的关系,通过建立回归方程预测因变量的取值。
应用实例
在农业生产中,通过方差分析比较不同施肥方案对作物产量的影响 ,利用回归分析预测未来产量趋势。
04 非参数统计案例
非参数检验方法简介
非参数检验的定义与特点
先验概率
根据以往经验和分析得到的概率。
似然函数
表示在给定参数下,观测数据出现的概率。
后验概率
在得到新的观测数据后,对先验概率进行更新得到的概率。
贝叶斯网络模型构建与评估
贝叶斯网络
一种概率图模型,用于表示变 量间的依赖关系。
网络结构学习
通过数据学习贝叶斯网络的结 构,即变量间的依赖关系。
参数学习
在已知网络结构的情况下,通 过数据学习变量的条件概率分 布。
提高统计软件应用能力
通过实践操作,学生应熟练掌握至少一种统计软 件(如SPSS、R、Python等),提高数据处理 和分析效率。
统计学发展趋势探讨
大数据与人工智能融合
随着大数据和人工智能技术的不 断发展,统计学将更加注重与这 些技术的融合,提高数据处理和 分析的智能化水平。
跨领域应用拓展
统计学将在更多领域发挥重要作 用,如生物医学、环境科学、社 会科学等,为跨学科研究提供有 力支持。
频数分布表
通过分组整理数据,展示 各组数据的频数,直观反 映数据的分布情况。
直方图与条形图
利用图形展示数据的分布 情况,便于观察数据的分 布规律。
概率密度函数
描述连续型随机变量的分 布情况,反映数据在不同 取值范围内的概率大小。
数据集中趋势度量
统计学案例
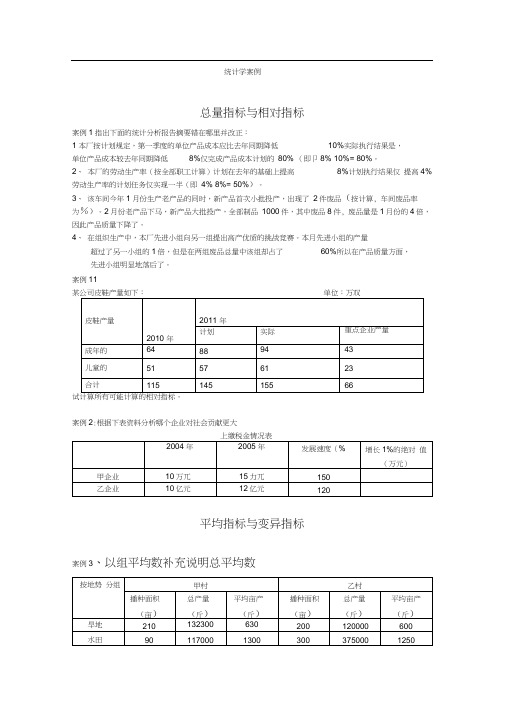
统计学案例总量指标与相对指标案例1指出下面的统计分析报告摘要错在哪里并改正:1 本厂按计划规定,第一季度的单位产品成本应比去年同期降低10%实际执行结果是,单位产品成本较去年同期降低8%仅完成产品成本计划的80% (即卩8% 10%= 80%。
2、本厂的劳动生产率(按全部职工计算)计划在去年的基础上提高8%计划执行结果仅提高4%劳动生产率的计划任务仅实现一半(即4% 8%= 50%)。
3、该车间今年1月份生产老产品的同时,新产品首次小批投产,出现了2件废品(按计算, 车间废品率为%)。
2月份老产品下马,新产品大批投产,全部制品1000件,其中废品8件, 废品量是1月份的4倍,因此产品质量下降了。
4、在组织生产中,本厂先进小组向另一组提出高产优质的挑战竞赛。
本月先进小组的产量超过了另一小组的1倍,但是在两组废品总量中该组却占了60%所以在产品质量方面,先进小组明显地落后了。
案例11案例2:根据下表资料分析哪个企业对社会贡献更大平均指标与变异指标案例3、以组平均数补充说明总平均数根据上表资料分析哪个村成绩更好为什么案例4:某单位有10个人,其中1人月工资为10万元,9人每人月工资为1000元。
该单位职工月平均工资为10900元。
即:100000 1000 910900(兀)10你认为这个平均数有代表性吗如果缺乏代表性应如何改正案例5:以下是各单位统计分析报告的摘录1、本局所属30个工厂,本月完成生产计划的情况是不一致的。
完成计划90%勺有3个,完成96%勺有5个,完成102%勺有10个,完成110%勺有8个,完成120%的有4个。
平均全局生产计划完成程度为%即:90% 3 96% 5 102% 10 110% 8 120% 4 =%30 °2、本厂开展增产节约运动以后,产品成本月月下降,取得显著的成绩,根据财务部门的报告,1月份开支总成本15000元,平均单位产品成本为15元,2月份开支总成本25000 元,平均单位产品成本下降为10元,3月份开支总成本45000元,平均单位产品成本仅8元。
生活中的统计学案例

生活中的统计学案例生活中的统计学案例:在我们的生活中,统计学无处不在。
从市场调查到医疗研究,从人口普查到环境保护,都离不开统计学的应用。
下面我将介绍两个生活中的统计学案例。
案例一:消费者调查假设一家服装公司想了解消费者对他们产品的满意度。
为了收集数据,他们设计了一份问卷调查,并在不同城市的服装店发放给顾客。
调查内容涵盖了产品质量、价格、服务等方面的评价。
回收了一定数量的问卷后,公司利用统计学的方法对数据进行分析。
首先,公司计算了各项评价的平均分数,以了解顾客的总体满意程度。
然后,他们利用统计方法进行分组,比较不同地区、不同性别、不同年龄段的顾客对产品的评价有无差异。
通过这些分析,公司可以了解到不同群体的满意度,并针对不同群体采取不同的改进措施,以提升产品的竞争力。
案例二:医疗研究假设一家医药公司正在研发一种新药,并希望通过临床试验评估其疗效。
为了进行试验,公司首先需要招募一定数量的病人,并将他们分为两组:一组接受新药治疗,另一组接受安慰剂。
在试验开始之前,公司需要确定每组的样本大小,以及评估疗效的指标。
在试验过程中,公司通过记录病人的临床数据,如症状改善程度、不良反应等,以评估新药的疗效和安全性。
为了对结果进行统计学分析,公司利用了一系列统计方法,如方差分析、t检验等。
通过这些分析,公司可以判断新药的疗效是否显著,以决定是否进入下一阶段的研发。
通过上述两个案例,我们可以看到统计学在生活中的应用之广泛。
无论是市场调查还是医疗研究,统计学都为我们提供了强大的工具,帮助我们理解和解释数据,做出科学决策。
因此,对于每个人来说,了解统计学的基本原理和方法,都是非常有益的。
《统计学》案例——时间序列趋势分析

《统计学》案例——时间序列趋势分析囤积粮食可以创高价吗1、问题的提出某贸易公司是经营粮油副食品的批发公司,基于前4年当地的消费物价指数的变化,该公司认为今后两年内消费物价指数将有大幅度上涨,为此该公司计划囤积粮食至下一年(第6年)以创高价。
这个计划是否可行?2、方法的选择根据下表的数据,可采用时间序列的趋势分析方法和季节变动分析方法,进行相应的分析预测,以了解消费物价指数的发展趋势。
表23 122.434 139.373、消费物价指数的预测根据题意需预测出第6年各季的物价指数,若指数升幅较大,那么粮食价格将会提高,否则囤积货物只会增加保管成本而不可能得到高价。
在物价指数预测中,循环变动和不规则变动难以准确预测,故仅考虑长期趋势与季节变动的影响。
本案例分析应用EXCEL软件。
(1)计算移动平均数。
输出结果见下表和图:表3.(2)分离长期趋势T。
对于T×C,按照表8.14中时间顺序,用最小平方法建立长期趋势模型yc=111.498+1.173t ,据以计算各期趋势值T(见上表)。
(3)分离季节变动S。
首先剔除长期趋势的影响y/T×C,即T×C×S×I/T×C=S×I;然后根据S×I序列计算各期季节比率S。
计算结果为:1季度季节比率=0.9773,2季度季节比率=0.9874,3季度季节比率=1.0076,4季度季节比率=1.0277。
(4)预测第6年各季消费物价指数。
首先需要根据时间序列模型计算第6年各季的趋势值,即将t=19、20、21、22分别代入yc=111.498+1.173t计算得第6年各季度趋势值:1季的趋势值为133.792季趋势值为134.963季趋势值为136.144季趋势值为137.31然后分别乘以各自季节比率得到各季预测值,1季物价指数=133.79×0.9773=130.75%2季物价指数=134.96×0.9874=133.26%3季物价指数=136.14×1.0076=137.17%4季物价指数=137.31×1.0277=141.11%。
统计学案例

例6.某食品厂用自动装袋机包装食品,每袋标准 6.某食品厂用自动装袋机包装食品, 某食品厂用自动装袋机包装食品 重量为50 50克 重量为50克,每隔一定时间随机抽取包装袋进行 检验。现随机抽取10袋样本, 10袋样本 检验。现随机抽取10袋样本,测得其平均重量为 50.20克 样本标准差为0.62 0.62克 50.20克,样本标准差为0.62克。若每袋重量服 从正态分布,试以10% 10%的显著水平检验每袋重量 从正态分布,试以10%的显著水平检验每袋重量 是否符合要求。 是否符合要求。(已知 Z 0 . 10 = 1 . 282 , Z 0 . 05 = 1 . 645 ,
) Z 0.025 = 1.96,t0.05 (99) = 1.665,t0.025 (99) = 1.99。
解:首先对以95%的概率总体均值作区间估计。 首先对以95%的概率总体均值作区间估计。 95%的概率总体均值作区间估计 已知 X = 10斤,S 2 = 9斤,n = 100,从而选择 Z 统计量。 统计量。 由此可得: 由 α = 0.05 ,得 Z 0.025 = 1.96 。由此可得:
例4.某制造厂质量管理部门的负责人希望估计移交给 4.某制造厂质量管理部门的负责人希望估计移交给 接收部门的5500包原材料的平均重量。一个由250 5500包原材料的平均重量 250包 接收部门的5500包原材料的平均重量。一个由250包 原材料组成的随机样本所给出的平均值 x = 65千克 。 总体标准差 σ = 15千克。试构造总体平均值 µ 的置 信区间,已知置信概率为95% 总体为正态分布。 95%, 信区间,已知置信概率为95%,总体为正态分布。
S n S n = 791.1 − 2.262 × 17.136 10 17.136 10 = 778.84 (克)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第13章时间序列分析和预测
案例一
新华印刷厂1990—2004年的利润资料如下表所示:
单位:万元
(1
四项移动平均)。
(2)采用最小平方法拟合直线趋势方程,并预测新华印刷厂2005年和2006年的利润。
[参考答案](1)
[参考答案](2)
b n tY t Y n t t a Y bt =
--=⨯-⨯⨯-==-=-⨯=∑∑∑∑∑()()()...
22
2
152424912024591512401201635
2459151635120
15
3313
所以直线趋势方程为:
2005年的利润预测值 = 73.2941635.1613.33=⨯+(万元)
2006年的利润预测值 = 08.3111735.1613.33=⨯+(万元)
案例二
某企业1994—2004年主营销售收入资料如下表所示:
单位:万元
试对该企业的主营销售收入进行动态分析。
要求:(1)计算各种动态分析指标;
(2)测定长期趋势并预测该企业2005年和2006年的主营销售收入。
[参考答案]
(1)计算各种动态分析指标。
1994—2004年主营销售收入的增长量、发展速度及增长速度指标见下表。
1995—2004年主营销售收入年均增长量为 = 25553/10 = 2555.3(万元) 1995—2004年主营销售收入年均发展速度为: %01.1196537
30990
10
==x
1995—2004年主营销售收入年均增长速度为:119.01%—100%=19.01% (2)测定长期趋势,预测该厂2005年和2006年的主营销售收入。
从上图看,主营销售收入呈直线趋势,可以利用最小平方法拟合直线趋势方程:
145.182211
66
673.270711198750673.270766
50611198750
66149034411)())((2
2
2=⨯-=
-==-⨯⨯-⨯=
--=
∑∑∑∑∑t b Y a t t n Y t tY n b
t Y c 637.2707145.1822+=
下图显示了趋势值对实际观测值的拟合情况。
该企业2005年和2002年主营销售收入的预测值为:
(万元)789.3431312637.2707145.1822ˆ2005
=⨯+=Y (万元)426.3702113637.2707145.1822ˆ2006
=⨯+=Y
第14章 指数
案例一
某公司下属三个厂生产某种产品的情况如下:
根据上表资料计算可变组成指数、固定组成指数和结构影响指数,并分析单位成本
水平和产量结构变动对总成本的影响。
参考答案:计算结果如下表:
可变组成指数=%
98.14738.100776
.149010130/1020480076.1490//1
1
01
1
1====
∑
∑∑∑f f x f f x
1490.76—1400.52=486.24 元
固定组成指数=%
41.14852.100476
.14909300/934200010130/15101360//0
111===
∑
∑∑∑f
f x f
f x
1490.76—1007.38=483.38元
结构影响指数=%
28.10052
.100438
.1007//0
00
1
1
0==
∑
∑∑∑f f x
f f x
1007.38—1004.52=2.86元
案例二
某企业工人数及工资资料如下:
要求:(1)计算各组工人工资个体指数;(2)计算总平均工资指数;(3)对总平均工资变动进行因素分析;(4)比较各组工人工资个体指数与总平均工资指数的差异,并分析出现差异的原因;(5)计算由于平均工资水平的变动对企业工资总额支出的影响额。
参考答案:(1)计算各组工人工资的个体指数
技术工:1700
106.25%1600p i =
= 普通工:900
112.50%800
p i ==
(2)总平均工资指数=
1100
1
x f x f f f
÷∑∑∑∑
=
1854000
1120000
=165.54% (3)对总平均工资变动进行因素分析
①可变构成指数=
1100
1
x f x f f f
÷∑∑∑∑=
1236
1120
=110.36% 变动绝对额=
11
1
x f f
∑∑-
00
x f f
∑∑=1854000-1120000=734000
②计算各组工资变动影响指数:
固定构成指数=
1101
1
1
x f x f f f
÷∑∑∑∑=
1236
1136
=108.80% 各组变量水平变动的绝对额=11
1
x f f
∑∑-
01
1
x f f
∑∑=1236-1136=100
③计算结构变动影响指数: 结构影响指数=
01001
x f x f f f
÷∑∑∑∑=
1136
1120
=101.43% 结构影响变动绝对额=
01
1
x f f
∑∑-
000
x f f
∑∑=1136-1120=16
(4)技术工个体工资指数106.25%,普通工个体工资指数112.50%,总工资指数110.36%。
三指数数据大小比较:技术工个体工资指数<总平均工资指数<普通工个体工资指数。
总平均工资指数受各组工人工资水平和工人结构的影响,普通工人数上涨的幅度小于技术工人数上涨的幅度,由于权数的作用,使得总工资指数处于两个个体指数之间。
(5)由于工资水平的变动使得平均工资增加100元,该企业工资总额支出的增加额为: 100×(630+870)=150000(元)。
