有压管道中的恒定流5-1简单管道水力计算的基本定律
有压管道的恒定流

l d
v2 2g
2
i
v2 2g
(
l d
i
)
v 2
2
g
then
:
z0=(
l d
i
v2 )
2g
(
l d
i
v2 )
2g
α0v02 2g
0
1
z v0
α2v 2 2g
vv
2 z0 0 v2≈0v2 Nhomakorabea1 v 2gz0
(
1
2
)
(
l d
i
)
Q vA c A 2gz0 ( c )
1 v02 2g
hwi
v0 1
H1
H10
2 3 pi /γ
23i
4
5
4
5
步骤2:定出管道末端的总水头
1 v02 2g
hwi
v0 1
H1
H10
2 3 pi /γ
23i
4
5
4
5
步骤3:寻求最后一个局部损失处(4)下游
1 v02 2g
hwi
v0 1
H1
H10
2 3 pi /γ
23i
4
5
4
5
步骤4:计算45段的能量损失hf 45
α1v 2 2g
v0
2
H0
0 1
0 2v
1 α0v02
2g
v0
H
0v02 = 2v2 2
2g 2g
hw12
简单管道的水力计算精
hf
k
Q2 K2
l 0.1522 2.464 2
2500 9.5m
H1 2 1 H 2 h f 45 61 25 9.5 18.5m
第六章 孔口、管嘴出流与有压管流
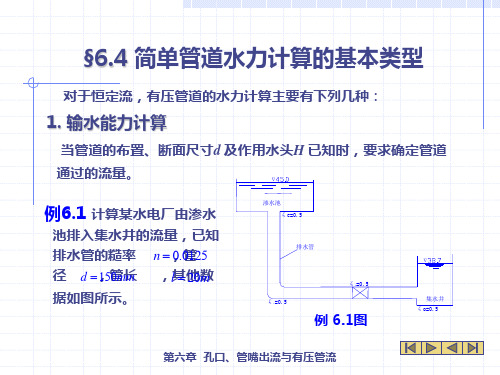
§6.4 简单管道水力计算的基本类型
3. 管道管线布置已定,当要求输送一定的流量时,确定所需 的断面尺寸(圆形管即确定直径)。这时可能出现下列两 种情况:
这种类型的题一般在输流工程中用到的较多,按长管计算:
H
hf
Q2 l, K K2
AC
R,C
1
R
1 6
或者用查表法。
n
供水工程中当 v 1.2时m s
H
hf
k
Q2 K2
l
当 v 1.2时m s
H
hf
k
Q2 K2
l
式中k 查表可得
式中 k 1
第六章 孔口、管嘴出流与有压管流
§6.4 简单管道水力计算的基本类型
2. 管道的输流能力,管长已知,要求选定所需的管径及相应的水头。 这是工程中常见的实际问题。通常是从技术和经济两方面综合考虑,
确定满足技术要求的经济流速。 ①管道的技术要求。流量一定的条件下,所选管径的大小影响着管中的 流速,所选管径应使流速控制在既不会产生过大的压力,降低管道的使 用寿命,又不能过小,使泥沙沉积,阻塞管路。一般情况下,水电站引 水管中流速不应大于(5~6)m/s ,给水管中的流速不应大于(2.5~3) m/s,不应小于0.25m/s 。
例6.2 由水塔向工厂供水,如图所示,采用铸铁管,管长2500m,
管径400mm。水塔处地形标高为 ,工厂1 需61水m 量
,工
厂地Q 形 0标.15高2 m3 s ,管路末端需要的2 自 4由5m水头 ,试设计水塔高
有压管中的恒定流

解:
(1) 扬程 Ht =Z +hw1 +hw2
∴ Ht=18+2.83+3.23=24.06m
(2) 安装高程 hs
根据题意
(3) 绘水头线
Z
例:水泵管路如图所示,铸铁管直径d=150mm,长度
,管路上装有滤水网 与曲率半径之比为 , 流量 试求水泵输出功率 ,水温 。 一个,全开截止阀一个,管半径 的弯头三个,高程 h =100 m
截止阀
得局部阻力的当量管长
, 滤水网
,出口
,于是
管路总阻力长度
将
代入
公式中可得
水泵扬程
最后得水泵输出功率
6、 复杂管道水力计算
1、串联管道
2、并联管道
3、分叉管道
4、沿程泄流管
5、管网
串联管道的水力计算
H H
Q1
q1 Q2
q2 Q3
Q1
q1 Q2
q2 Q3
按短管计 各管段的联接点水流符合连续性方程: 水流满足能量方程:
z 求:管径
解:
采用试算法,可得d=0.53m
例: 离心泵,已知Q=0.02m3/s, 提水高度
z=18m, l吸=8m, l压=20m, d吸=d压
=100mm, λ=0.042, <7mH2O, ζ弯=0.17, ζ进=5。 求:(1) 扬程 H1, Z
pv /ρg
(2) 安装高程 hs
hs
三、已知管线布置和输水流量,求输水管径d 。
对于长管: 按求得的流量模数,即可由4-1确定所需 的管道直径。 对于短管: 上式中μc与管径d有关,所以需要试算。
四、已知流量和管长,求管径d和水头H; 这是工程中常见的实际问题。通常是从技术和经 济两方面综合考虑,确定满足技术要求的经济流速。 有了经济流速就可以求出管径,这样求水头H即转化 为第二类问题。 五、对于一个已知管道尺寸、水头和流量的管道,要求 确定管道各断面压强的大小。 根据能量方程,管路中任意断面处的测压管水头 为:
(完整版)水流量计算公式

水力学教学辅导第五章 有压管道恒定流【教学基本要求】1、了解有压管流的基本特点,掌握管流分为长管流动和短管流动的条件。
2、掌握简单管道的水力计算和测压管水头线、总水头线的绘制,并能确定管道内的压强分布。
3、了解复杂管道的特点和计算方法。
【内容提要和学习指导】前面几章我们讨论了液体运动的基本理论,从这一章开始将进入工程水力学部分,就是运用水力学的基本方程(恒定总流的连续性方程、能量方程和动量方程)和水头损失的计算公式,来解决实际工程中的水力学问题。
本章理论部分内容不多,主要掌握方程的简化和解题的方法,重点掌握简单管道的水力计算。
有压管流水力计算的主要任务是:确定管路中通过的流量Q ;设计管道通过的流量Q 所需的作用水头H 和管径d ;通过绘制沿管线的测压管水头线,确定压强p 沿管线的分布。
5.1 有压管道流动的基本概念(1) 简单管道和复杂管道根据管道的组成情况我们把它分为简单管道和复杂管道。
直径单一没有分支而且糙率不变的管道称为简单管道;复杂管道是指由两根以上管道组成管道系统。
复杂管道又可以分为串联管道、并联管道、分叉管道、沿程泄流管和管网。
(2) 短管和长管在有压管道水力计算中,为了简化计算,常将压力管道分为短管和长管:短管是指管路中水流的流速水头和局部水头损失都不能忽略不计的管道;长管是指流速水头与局部水头损失之和远小于沿程水头损失,在计算中可以忽略的管道为,一般认为( )<(5~10)h f %可以按长管计算。
需要注意的是:长管和长管不是完全按管道的长短来区分的。
将有压管道按长管计算,可以简化计算过程。
但在不能判断流速水头与局部水头损失之和远小于沿程水头损失之前,按短管计算不会产生较大的误差。
5.2简单管道短管的水力计算(1)短管自由出流计算公式(5—1)式中:H 0是作用总水头,当行近流速较小时,可以近似取H 0 = H 。
μ称为短管自由出流的流量系数。
j h g v ∑+2202gH A c Q μ=μ=1(5—2)(2)短管淹没出流计算公式(5—3) 式中:z 为上下游水位差,μc 为短管淹没出流的流量系数(5—4) 请特别注意:短管自由出流和淹没出流的计算关键在于正确计算流量系数。
第五章:有压管道中的恒定流

24
水力长管 如果作用水头的 95%以上用于沿程 水头损失,我们就 可以略去局部损失 及出口速度水头, 认为全部作用水头 消耗在沿程,这样 的管道流动称为水 力长管。否则为水 力短管。
对水力长管,根据连续方程和谢才公 式可知
Q A AC RJ K J K hf l
H hf Q K
第四节 复杂管道的水力计算
Qi 0
q2
B Q 4
Q3
36
n段并联管道的水头损失是相同的,给出n-1个方程
hf i Qi K
2
2 i
li co n st
(i=1,…, n)
流量之和为 总流量,又可 得一个方程
n n
hf AB hf 1=hf 2 =hf 3 H hf CD C
Q1
Q i Ki
1
第五章 有压管道中的恒定流
概
一、概念
有压管流(Penstock) :管道中流体在压力差作用下的流动 称为有压管流。
述
有压恒定管流:管流的所有运动要素均不随时间变化的有压管流。 有压非恒定管流:管流的运动要素随时间变化的有压管流。
二、分类
1、有压管道根据布置的不同,可分为: 简单管路 串联管道 有压管道 复杂管路 并联管道 管 网
2
枝状管网
环状管网 简单管路:是指管径、流速、流量沿程不变,且无分支的单线管道。
复杂管路:是指由两根以上管道所组成的管路系统。
2、按局部水头损失和流速水头之和在总水头损失中所占的比重,管道可分为
有压管道
长管:指管道中以沿程水头损失为主,局部水头损失和流速水头 所占比重小于(5%~10%)的沿程水头损失,可予以忽略 的管道。
H 0 h
水力学主要知识点.

水力学主要知识点(水工专业2008)绪 论(一)液体的主要物理性质 1.惯性与重力特性2.粘滞性:液体的粘滞性是液体在流动中产生能量损失的根本原因. 描述液体内部的粘滞力规律的是牛顿内摩擦定律 :注意牛顿内摩擦定律适用范围:1)牛顿流体, 2)层流运动 3.可压缩性。
在研究水击时需要考虑4.表面张力特性。
进行模型试验时需要考虑水力学的两个基本假设:(二)连续介质和理想液体假设1.连续介质:液体是由液体质点组成的连续体,可以用连续函数描述液体运动的物理量. 2.理想液体:忽略粘滞性的液体 (三)作用在液体上的两类作用力第1章水静力学水静力学包括静水压强和静水总压力两部分内容。
通过静水压强和静水总压力的计算,可以求作用在建筑物上的静水荷载。
(一) 静水压强:主要掌握静水压强特性,等压面,水头的概念,以及静水压强的计算和不同表示方法. 1.静水压强的两个特性:(1)静水压强的方向垂直且指向受压面(2)静水压强的大小仅与该点坐标有关,与受压面方向无关,2.等压面与连通器原理:在只受重力作用,连通的同种液体内, 等压面是水平面.(它是静水压强计算和测量的依据)3.重力作用下静水压强基本公式(水静力学基本公式)p=p 0+g ρh 或其中 z —位置水头,p/g ρ—压强水头 (z+p/g ρ)—测压管水头请注意,“水头”表示单位重量液体含有的能量。
4.压强的三种表示方法:绝对压强p ′,相对压强p , 真空度p v , 它们之间的关系为:p= p ′-p a p v =│p │(当p <0时p v 存在)相对压强:p=g ρh,可以是正值,也可以是负值。
要求掌握绝对压强、相对压强和真空度三者的概念和它们之间的转换关系。
c gpz =+ρd y d u μτ=计算静水总压力包括求力的大小、方向和作用点,受压面可以分为平面和曲面两类。
根据平面的形状:对规则的矩形平面可采用图解法,任意形状的平面都可以用解析法进行计算。
有压管道恒定流例题

称为水泵的总水头或扬程 H t z hw12 hw34
上式表明水泵向单位重量液体所提供的机械能一部分是
用来将水流提高一个几何高度,另一部分是用来克服水头
损失 hw14
3)水泵的配用动力机械功率
要使水泵将一定流量Q的液体提升到高度hp,必须要 克服吸水管和压水管的水头损失。因此水泵需要输入
0.18m
水泵提水高度: z 3 1 105 85 20m
③ 带动水泵的动力机械功率
因
Np
Q(z hw14 ) 1000P
hw14 为吸水管及压力管水头损失之和。已求得吸水
管水头损失为0.18m,当压力管按长管计算时,整个管道
的水头损失为 压力管的流量模数
hw14
0.18
Q K
2 2
2g
l
d
v2 2g
i
v2 2g
H0
2
l d
i
v2 2g
v
1
2
l d
i
2gH 0
令: c
1
1
l d
i
Q vA c A 2gH0
§5.1 简单管道水力计算的基本公式
二、简单管道淹没出流
以0—0为基准面,对1-1断面和2-2 断面建立能量方程
1
淹没出流
1 H1 O
Z
2
H1
1v02
2g
H2
所得直径和第二次假设值非常接近,故设计管径取d=0.95米。
简单管道水力计算实例
3. 水泵装置的水力计算
水泵是通过叶轮的转动作用, 在水泵吸水管端形成真空,使 Z 水流在池面大气压作用下沿吸 水管上升,流经水泵时从水泵 获得新的能量,从而将水流从 低处通过压力管输送到高处的 提水设施。
《水力学》课程教学大纲

《水力学》课程教学大纲课程名称:水力学(Hydraulics)课程类型:专业基础课;范围选修课学时:72学时,4.5学分适用对象:水利水电工程、农业水利工程、给水排水工程本科先修课程:高等数学、大学物理、理论力学一、课程性质、目的与任务以及对先开课程要求水力学是水利类各专业必修的一门主要专业基础课.水力学的任务是研究液体(主要是水)的平衡和机械运动的规律及其实际应用。
通过本课程的学习,使学生掌握水流运动的基本概念、基本理论与分析方法,理解不同水流的特点,学会常见水利工程中的水力计算,并具备初步的试验量测技能,为学习后续课程和专业技术工作打下基础.二、教学重点及难点本课程教学重点:水静力学,水动力学理论基础,流动阻力与水头损失,有压管路,明渠均匀流,明渠非均匀流。
难点:液体的相对平衡,作用在平面、曲面上的力,实际液体的运动微分方程,恒定总流伯诺里方程,恒定总流动量方程,紊流沿程损失的分析与计算,复杂长管的水力计算,管网的水力计算,无压圆管均匀流水力计算,断面单位能量、临界水深,恒定明渠流动的流动型态及判别标准,明渠非均匀渐变流微分方程,棱柱体渠道非均匀渐变流水面曲线的计算.三、与其它课程的关系学习本课程应具备高等数学中有关微分、积分、简单微分方程等高等数学基础;还应具备理论力学、材料力学中有关静力学、动力学、应力与应变、面积矩等方面的工程力学基础。
后续课程为水资源管理、水工建筑物、水利工程施工与水电站。
四、教学内容、学时分配及基本要求第一章绪论(2学时)基本要求:了解液体运动的基本规律及研究液体运动规律的一般方法,掌握液体的主要物理性质.重点:.液体的主要物理性质难点:液体粘性产生原因及作用第一节水力学的任务及其发展概况1、水力学的任务2、水力学发展简史第二节液体的主要物理性质及其作用在液体上的力1、液体的质量和密度2、液体的重量和容重3、液体的粘滞性4、液体的压缩性5、液体的表面张力6、作用于液体上的力第三节液体的基本特征和连续介质1、液体的基本特征2、连续介质假设3、理想液体的概念第四节水力学的研究方法1、科学试验2、理论分析3、数值计算第二章水静力学(8 学时)基本要求:掌握静水压强的特性,压强的表示方法及计量单位,掌握液体平衡微分方程与水静力学的基本方程,掌握液柱式测压仪的基本原理,能熟练计算作用在平面、曲面上的静水总压力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
管道内流速 v Q 0.085 1.21m / s 1.2m / s A 1 3.14 0.32 4
故修正系数k=1
计算水头损失
hf
k
Q2 K2
l
1
0.0852 3500 1.1442
19.3m
所需水塔高度为
H zc Hc h f zb 110.0 25 19.3 130.0 24.3m
lB d
e
b )
v2 2g
hv
即
zs
hv
(a
lB d
e
b
)
(1) 每 根 虹 吸 管 的输水能力;
(2) 当吸虹管中 的最大允许真空 值 hv为7m时,问 虹吸管的最高安 装高程是多少?
解:(1)本题管道出口淹没在水面以下,为淹没出流。 当不计行近流速影响时,可直接计算流量:
上下游水头差为 z 1 2 100 99 1m
先确定λ值,用曼宁公式
C
取符合渐变流条件的
断面1-1和2-2,列能量
方程
z 1v02
2g
2v22
2g
hw12
因 v2 0
则有
z0
z
1v12
2g
hw12
在淹没出流情况下,包括行进流速的上下游水位差 z0 完全 消耗于沿程损失及局部损失。
因为 hw12 h f
hj
(
l d
) v2
2g
整理后可得管内平均流速
4.对一个已知管道尺寸、水头和流量的管道, 要求确定管道各断面压强的大小
先分析沿管道总流测压管水头的变化情况,再计算 并绘制测压管水头线。
因为流量和管径均已知各断面的平均流速即可求出, 入口到任一断面的全部水头损失也可算出。该点压强为
pi
g
H1
zi
ivi 2
2g
hwi
由此可绘出总水头线和测压管水头线。管内压强可 为正值也可为负值。当管内存在有较大负压时,可能产 生空化现象。
1.39m / s
4
流速水头 v2 1.392 0.0989m
2g 19.6
沿程损失
h
f
l d
v2 2g
0.025 800 0.0989 19.79m 0.1
局部损失
hf
v2 (0.5 2 0.3) 0.0989 0.109m
2g
故沿程水头损失占总水头的百分数为
h f 19.79 0.989 98.9% H 20
C
1
(
0.95
)
1 6
1
56.21m 2
/s
0.014 4
8 9.8 0.0248
56.212
c
1
0.0248 50 0.5 0.4 1
0.95
1 0.558 3.20
得 d
43
0.945m
0.5583.14 29.83
因所得直径已和第二次假设值非常接近,故采用管径d 为0.95m。
3.管线布置已定,当要求输送一定流量时, 确定所需的断面尺寸(圆形管道即确定管道直径)
这时可能出现下述两种情况:
1.管道的输水能力、管长l及管道的总水头H均已确定。 若管道为长管 ,流量模数 K Q
H l
由表4-1即可查出所需的管道直径。
若为短管 d
4Q
c 2gH
流量系数 c 与管径有关,需用试算法确定。
例5-1 一简单管道,如图4-3所示。长为800m,管径为 0.1m,水头为20m,管道中间有二个弯头,每个弯头的局
部水头损失系数为0.3,已知沿程阻力系数 =0.025,试
求通过管道的流量。
(一)先将管道作为短管,求通过管道流量。
局部损失共包括进口损失和弯头损失。
进口局部损失系数 Q c A 2gH
v2 2g
H 0
( 2
l d
) v2
2g
取 2 1
则
H0
(1
l d
) v2
2g
管中流速 v
1
1
l d
2gH0
通过管道流量 Q
1
1
l d
A
2gH0
c A
2gH0
式中 c
1
1
l d
称为管道系统的流量系数。
当忽略行近流速时,流量计算公式变为Q c A 2gH
二、简单管道淹没出流
管道出口淹没在水下称为淹没出流。
管道根据其布置情况可分为:简单管道与复杂管道。 复杂管道又可分为:串联管道、并联管道、分叉管道、均
匀泄流管道。
根据hf 与h j 两种水头损失在损失中所占比重的大小,将管 道分为长管及短管两类。
有压管道:管道周界上的各点均受到液体压强的作用。 1 水电站的压力引水隧洞和压力钢管 2 水库的有压泄洪洞或泄水管 3 供给工农业和生活用水水泵装置系统及给水管网 4 虹吸管以及输送石油的管道 特点:有压管道各点的压强一般不等于大气压强。
pa
g
a1v02 2g
zs
pB
g
av2 2g(ຫໍສະໝຸດ lBdeb
)
v2 2g
式中,lB 为从虹吸管进口至B-B断面的长度。
取 a1v02 0; a 1.0 2g
则
pa
g
pB
g
zs
(1
lB d
e
b )
v2 2g
若要求管内真空值不大于某一允许,即
式中 hv为允许真空值,hv =7m。则
zs
(1
例5-2 由水塔沿长度L为3500m,直径d为300mm的新铸铁
管向工厂输水(见图)。设安置水塔处的地面高程 zb 为 130.0m,厂区地面高程 zc 为110.0m,工厂所需水头 Hc 为 25m。若须保证工厂供水量Q为85lm/s,求水塔高度(即地
面至水塔水面的垂直距离)。
解:给水管道常按长管计算。由表4-1查得d=300m的 新铸铁管K=1.144m3/s。
解:倒虹吸管一般作短管计算。
本题管道出口淹没在水下;而且上下游渠道中流
速相同,流速水头消去。
因
Q c A
2gz
c
d 2
4
2gz
所以 d
而 c
4Q
c 2gz
1
l d
因为沿程阻力系数λ或谢才系数C都是d 的复杂函数,
因此需用试算法。
先假设d=0.8m,计算沿程阻力系数:
C
1
1
R6
1
(
0.8
)
1 6
有压管中的恒定流:有压管中液体的运动要素不随时间 而变。
有压管中的非恒定流:运动要素随时间而变。
简单管道:管道直径不变且无分支的管道。
其水力计算分为自由出流和淹没出流。
自由出流
淹没出流
简单管道:管道直径不变且无分支的管道。 实际工程中常见的有虹吸管和水泵。 虹吸管
水泵
1、串联管道:有直径不同的几段管道依次连接而成的管道。
二、简单管道水力计算实例
1.虹吸管的水力计算
虹吸管是 一种压力输水 管道,其顶部 高程高于上游 供水水面。
特点:
顶部真空理论上不能大于10mH2O,一般其真空 值小于(7 8m );虹吸管长度一般不大,应按短管计 算。
例5-4 有一渠道用两根直径d为1.0m的混凝土虹吸管 来跨过山丘(见图),渠道上游水面高程▽1为 100.0m,下游水面高程▽2为99.0m,虹吸管长度l1为 8m,l2为12m,l3为15m,中间有600的折角弯头两个, 每个弯头的局部水头损失系数ξb为0.365,若已知进口 水头损失系数ξc为0.5;出口水头损失系数ξ0为1.0。 试确定:
给水管道中的水流,一般流速不太大,可能属于紊 流的粗糙区或过渡粗糙区。
可近似认为当v<1.2m/s时,管流属于过渡粗糙区,hf 约与流速v的1.8次方成正比。
故当按常用的经验公式计算谢齐系数C求hf 应在右 端乘以修正系数k,即
H
hf
k Q2 l K2
管道的流量模数K,以及修正系数k可根据相关手册 资料得到。
0.01093
由此可见,将上述管道按长管计算,误差很小。
5-2 简单管道、短管水力计算的类型及实例
一、水力计算的任务
对恒定流,有压管道的水力计算主要有下列几种: 1.输水能力计算 已知管道布置、断面尺寸及作用水头时,要求确定管道 通过的流量。 计算如上节例题
2.当已知管道尺寸和输水能力时,计算水头损失 即要求确定通过一定流量时所必须的水头。 计算如下例所示
2gz 0.571 3.1412 4
2 9.81 1.985m3 / s
(1)虹吸管中最大真空一般发生在管子最高位置。本 题中最大真空发生在第二个弯头前,即B-B断面。
具体分析如下:
以上游渠道自由面为基准面,令B-B断面中心至上
游渠道水面高差为,zs 对上游断面0-0及断面B-B列能
量方程
0
1
1
R6
n
计算C,对混凝土管n=0.014
则
C
1
1
R6
1
(
1
)
1 6
1
56.7m 2
/s
n
0.014 4
故
8g C2
8 9.8 56.7 2
0.024
管道系统的流量系数:
c
1
1 d
e
2 b
0
1 0.024 35 0.5 0.73 1
1
1 0.571
3.07
每根虹吸管的输水能力:
Q c A
2.管道的输水量Q,管长l已知,要求选定所需的管径 及相应的水头。 从技术和经济条件综合考虑:
