几何证明—常用辅助线专题版 含答案
【中考数学必备专题】几何辅助线大揭秘 之角平分线问题(含答案)
【中考数学必备专题】几何辅助线大揭秘之角
平分线问题
一、证明题(共3道,每道40分)
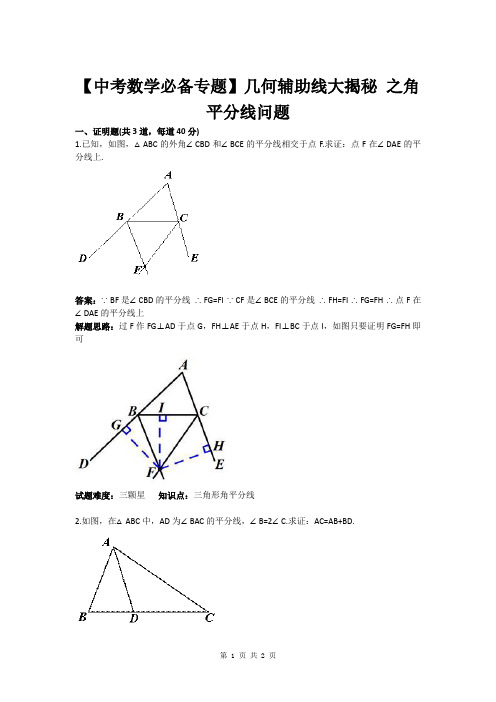
1.已知,如图,△ABC的外角∠CBD和∠BCE的平分线相交于点F.求证:点F在∠DAE的平分线上.
答案:∵BF是∠CBD的平分线∴FG=FI ∵CF是∠BCE的平分线∴FH=FI ∴FG=FH ∴点F在∠DAE的平分线上
解题思路:过F作FG⊥AD于点G,FH⊥AE于点H,FI⊥BC于点I,如图只要证明FG=FH即可
试题难度:三颗星知识点:三角形角平分线
2.如图,在△ABC中,AD为∠BAC的平分线,∠B=2∠C.求证:AC=AB+BD.
答案:∵AD是∠BAC的平分线∴∠BAD=∠EAD 在△ABD和△AED中AB=AE ∠BAD=∠EAD AD=AD ∴△ABD≌△AED(SAS)∴BD=ED,∠B=∠AED ∵∠AED=∠B=2∠C ∴∠CDE=∠AED ﹣∠C=∠C ∴DE=CE ∴BD=CE ∵AC=AE+CE ∴AC=AB+BD
解题思路:在AC上截取AE=AB,连接DE,如图只要证明BD=CE即可
试题难度:三颗星知识点:三角形角平分线
3.已知:如图,在△ABC中,BE平分∠ABC,AD⊥BE,垂足为点D.求证:∠BAD=∠DAE+∠C.
答案:∵BE平分∠ABC,AD⊥BE ∴△ABF为等腰三角形(三线合一)∴∠BAD=∠BFD ∵∠BFD 为△ACF的外角∴∠BFD=∠DAE+∠C ∴∠BAD=∠DAE+∠C
解题思路:延长AD与BC交于点F,如图只要证明∠BFD=∠BAD即可
试题难度:三颗星知识点:三角形角平分线。
八年级数学上册几何添辅助线专题

DCB A全等三角形问题中常见的辅助线的作法(有答案)总论:全等三角形问题最主要的是构造全等三角形,构造二条边之间的相等,构造二个角之间的相等【三角形辅助线做法】图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验。
三角形中两中点,连接那么成中位线。
三角形中有中线,延长中线等中线。
1.等腰三角形“三线合一〞法:遇到等腰三角形,可作底边上的高,利用“三线合一〞的性质解题2.倍长中线:倍长中线,使延长线段与原中线长相等,构造全等三角形3.角平分线在三种添辅助线4.垂直平分线联结线段两端5.用“截长法〞或“补短法〞: 遇到有二条线段长之和等于第三条线段的长,6.图形补全法:有一个角为60度或120度的把该角添线后构成等边三角形7.角度数为30、60度的作垂线法:遇到三角形中的一个角为30度或60度,可以从角一边上一点向角的另一边作垂线,目的是构成30-60-90的特殊直角三角形,然后计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角。
从而为证明全等三角形创造边、角之间的相等条件。
8.计算数值法:遇到等腰直角三角形,正方形时,或30-60-90的特殊直角三角形,或40-60-80的特殊直角三角形,常计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角,从而为证明全等三角形创造边、角之间的相等条件。
常见辅助线的作法有以下几种:最主要的是构造全等三角形,构造二条边之间的相等,二个角之间的相等。
1) 遇到等腰三角形,可作底边上的高,利用“三线合一〞的性质解题,思维模式是全等变换中的“对折〞法构造全等三角形.2) 遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的“旋转〞 法构造全等三角形.3) 遇到角平分线在三种添辅助线的方法,〔1〕可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折〞,所考知识点常常是角平分线的性质定理或逆定理.〔2〕可以在角平分线上的一点作该角平分线的垂线与角的两边相交,形成一对全等三角形。
全等三角形几何证明常用辅助线

几何证明-常用辅助线(一)中线倍长法:例1 、求证:三角形一边上的中线小于其他两边和的一半。
已知:如图,△ABC 中,AD 是BC 边上的中线,求证:AD ﹤21(AB+AC) 分析:要证明AD ﹤21(AB+AC),就是证明AB+AC>2AD ,也就是证明两条线段之和大于第三条线段,而我们只能用“三角形两边之和大于第三边”,但题中的三条线段共点,没有构成一个三角形,不能用三角形三边关系定理,因此应该进行转化。
待证结论AB+AC>2AD 中,出现了2AD ,即中线AD 应该加倍。
证明:延长AD 至E ,使DE=AD ,连CE ,则AE=2AD 。
在△ADB 和△EDC 中,AD =DE ∠ADB =∠EDC BD =DC∴△ADB ≌△EDC(SAS) ∴AB=CE又 在△ACE 中,AC+CE >AE∴AC+AB >2AD ,即AD ﹤21(AB+AC)小结:(1)涉及三角形中线问题时,常采用延长中线一倍的办法,即中线倍长法。
它可以将分居中线两旁的两条边AB 、AC 和两个角∠BAD 和∠CAD 集中于同一个三角形中,以利于问题的获解。
课题练习:ABC ∆中,AD 是BAC ∠的平分线,且BD=CD ,求证AB=AC 例2:中线一倍辅助线作法 △ABC 中方式 AD 是BC 边中线方式2:间接倍长作CF ⊥AD 于F ,延长MD 到N , 作BE ⊥AD 使DN=MD , 连接BE 连接CD 例3:△ABC 中,AB=5,AC=3,求中线例4:已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE 课堂练习:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 交AC 于F ,求证:AF=EF例5:已知:如图,在ABC ∆中,AC AB ≠,D 、E 在BC上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC.求证:AE 平分BAC ∠C 第 1 题图A DBCE图2-1课堂练习:已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAE 作业:1、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
中考数学几何辅助线大全及常考题型解析

中考数学几何辅助线大全及常考题型解析中考数学几何辅助线作法及常考题型解析第一部分常见辅助线做法等腰三角形:1.作底边上的高,构成两个全等的直角三角形2.作一腰上的高; 3.过底边的一个端点作底边的垂线,与另一腰的延长线相交,构成直角三角形。
梯形1.垂直于平行边2.垂直于下底,延长上底作一腰的平行线3.平行于两条斜边4.作两条垂直于下底的垂线5.延长两条斜边做成一个三角形菱形1.连接两对角2.做高平行四边形1.垂直于平行边2.作对角线——把一个平行四边形分成两个三角形3.做高——形内形外都要注意矩形1.对角线2.作垂线很简单。
无论什么题目,第一位应该考虑到题目要求,比如AB=AC+BD....这类的就是想办法作出另一条AB等长的线段,再证全等说明AC+BD=另一条AB,就好了。
还有一些关于平方的考虑勾股,A字形等。
三角形图中有角平分线,可向两边作垂线(垂线段相等)。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验。
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线等中线。
解几何题时如何画辅助线①见中点引中位线,见中线延长一倍在几何题中,如果给出中点或中线,可以考虑过中点作中位线或把中线延长一倍来解决相关问题。
②在比例线段证明中,常作平行线。
③对于梯形问题,常用的添加辅助线的方法有1、过上底的两端点向下底作垂线2、过上底的一个端点作一腰的平行线3、过上底的一个端点作一对角线的平行线4、过一腰的中点作另一腰的平行线5、过上底一端点和一腰中点的直线与下底的延长线相交6、作梯形的中位线7、延长两腰使之相交四边形平行四边形出现,对称中心等分点。
梯形里面作高线,平移一腰试试看。
平行移动对角线,补成三角形常见。
证相似,比线段,添线平行成习惯。
等积式子比例换,寻找线段很关键。
直接证明有困难,等量代换少麻烦。
相似三角形之常用辅助线

相似三角形之常用辅助线在与相似有关的几何证明、计算的过程中,常常需要通过相似三角形,研究两条线段之间的比例关系,或者转移线段或角。
而有些时候,这样的相似三角形在问题中,并不是十分明显。
因此,我们需要通过添加辅助线,构造相似三角形,进而证明所需的结论。
专题一、添加平行线构造“ A ”“X ”型定理:平行于三角形一边的直线和其它两边(或两边延长线)相交,所构成的三角形与原三角形相似.定理的基本图形:例1、平行四边形ABCD中, E为AB中点,AF: FA 1 : 2,求AG GC变式练习:如图,直线交厶ABC的BC,AB两边于D,E,与CA延长线交于F,若—;;=2,求BE:EA的比值.例3、BE^ AD,求证:EF- BO AC- DF变式练习:已知在△ ABC中,AD是/ BAC的平分线.求证:AB BDAC CDBD例2、如图,直线交△ ABC的BC,AB两边于D,E,与CA延长线交于F,若 -DCFC=2,求BE:EA的比值.FA(本题有多种解法,多想想)变式1、如图,△ ABC中,AB<AC,在AB、AC上分别截取BD=CE , DE, BC的延长线相交于点F,证明:AB・DF=AC EF。
例4、已知:如图,在△ ABC中,AD为中线,E在AB上, AE=AQ CE交AD于F,EF: FC=3 : 5,EB=8cm,求AB AC的长.AE 1 AF竺丄,求比。
(试用多种方法解)DE 2 BFA说明:此题充分展示了添加辅助线,构造相似形的方法和技巧•在解题中方法要灵活,思路要开阔. 总结:(1)遇燕尾,作平行,构造.字一般行。
(2)引平行线应注意以下几点:1)选点:一般选已知(或求证)中线段的比的前项或后项,在冋一直线的线段的端点作为引平行线的点。
2)引平行线时尽量使较多已知线段、求证线段成比例。
专题二、作垂线构造相似直角三角形基本图形例1、如图, ABC 中,AB AC, BD AC,那么BC22CA CD吗?试说明理由?(用多种变式练习:平行四边形ABCD中, CEL AE, CF丄AF,求证:AB- A曰AD- AF= AC于G ,求证:FG 2 =CF ?BF2.如图,在△ ABC中,AB=AC D在AB上, E在AC的延长线上,BD=3CE DE交BC于F, 求DF: FE的值。
初中几何辅助线(全面)

三角形辅助线一、 补全图形1. 把残缺图形补全为我们熟悉的图形例1、如图,在四边形ABCD 中,//,45,120,5,10,AB CD A B AB BC ∠=︒∠=︒==则CD 的长为 。
图12. 我们熟悉的图形(1) 等腰三角形性质:等边对等角:两底角相等,两腰的边长相等三线合一:底边的垂线=顶角的角平分线=底边的中线(2) 直角三角形性质:勾股定理:两直角边平方的和等于斜边的平方斜边的中线:斜边的中线等于斜边的一半两个特殊的直角三角形:等腰直角三角形;有一个角为30度的直角三角形; 面积:两直角边的乘积的一半=底边与底边的高的乘积的一半二、 构造全等三角形1. 全等三角形的性质与判定全等三角形的性质:全等三角形的证明:2. 倍长中线/平行(涉及中点)例1、 如图1,AD 是△ABC 的中线,求证:AB +AC >2AD 。
例2、如图,已知在△ABC中,AD是BC边上的中线,E是AD上一点,连接BE并延长交AC于点F,且AF=EF,求证:AC=BE。
3.截长补短(两边之和等于一条边)例1、如图甲,AD∥BC,点E在线段AB上,,∠=∠∠=∠ADE CDE DCE ECB 求证:CD=AD+BC。
例3、如图,△ABC中,∠ACB=2∠B,∠1=∠2。
求证:AB=AC+CD(截长法与补短法)⊥于点G,将△ABG 例3、在正方形ABCD中,点E和F分别在BC和CD上,AE BF∠交BF的延长线于点N,连接CN。
沿AG对称至△AMG,AM平分DAM∆≅∆;(1)求证:ABE BCF(2)求证:AG=NG;(3)试探究线段AG,BN和CN之间的数量关系。
4.折叠(作角平分线,题目中出现二倍角)例1、如图3,在△ABC中,∠1=∠2,∠ABC=2∠C。
求证:AB+BD=AC。
例2、如图,在△ABC中,AD⊥BC于D,∠BAD>∠CAD。
求证:AB>AC。
5.旋转例1、如图11,正方形ABCD中,∠1=∠2,Q在DC上,P在BC上。
初中几何全等三角形常见辅助线作法

全等三角形常见辅助线作法【例1】.已知:如图6, 4BCE、△ACO分别是以8E、为斜边的直角三角形,且= ACDE是等边三角形.求证:△ A3c是等边三角形.【例2】、如图,已知BC>AB, AD=DCo BD 平分NABC。
求证:ZA+ZC=180°.线段的数量关系: 通过添加辅助线构造全等三角形转移线段到一个三角形中证明线段相等。
1、倍长中线法【例.3]如图,己知在△ABC中,ZC = 90°, ZB = 30°, A。
平分NB4C,交BC于点D.求证:BD = 2CD证明:延长DC到E,使得CE=CD,联结AEZC=90°A AC ± CDVCD=CEAD=AEVZB=30° ZC=90°ZBAC=60°YAD 平分NBACJ ZBAD=30°A DB=DA ZADE=60°VDB=DA:.BD=DE/. BD=2DC4B D笫3题•/ ZADE=60° AD=AEA △ ADE为等边三角形,AD=DE【例4.】如图,。
是AABC的边上的点,且CD = AB, ZADB = ZBAD, AE是AARD的中线。
求证:AC = 2AEo 证明:延长AE至IJ点F,使得EF=AE联结DF在4ABE和4FDE中BE=DEZAEB=ZFEDAE=FE/.△ABE 也AFDE (SAS) A AB=FD ZABE=ZFDE VAB=DCJ FD = DCZADC=ZABD+ZBAD ZADB = ZBAD,ZADC=ZABD+ZBDA VZABE=ZFDE・・・NADONADB+NFDE即ZADC= ZADF ffiAADF 和AADC 中AD=AD< ZADF= ZADC、DF =DC・•・△ ADF也ADC(SAS) AAF=ACAC=2AE【变式练习】、如图,AABC中,BD二DOAC, E是DC的中点,求证:AD平分NBAE.【小结】熟悉法一、法三“倍长中线”的辅助线包含的基本图形“八字型”和“倍长中线”两种基本操作方法, 倍长中线,或者倍长过中点的一条线段以后的对于解决含有过中点线段有很好的效果。
几何证明辅助线专题学习(基础)

几何证明专题--辅助线Ⅰ.连结例1:如图,AB=AD,BC=DC,求证:∠B=∠D.ABDC1.连结AC,构造全等三角形;2.连结BD,构造两个等腰三角形例2:如图,AB=AE,BC=ED, ∠B=∠E,AM⊥CD,求证:点M是CD的中点.ABC D EM连结AC、AD构造全等三角形例3:如图,AB=AC,BD=CD, M、N分别是BD、CD的中点,求证:∠AMB=∠AND ABC DM N连结AD构造全等三角形例4:如图,AB与CD交于O, 且AB=CD,AD=BC,OB=5cm,求OD的长.OABDC连结BD构造全等三角形Ⅱ.角平分线上点向两边作垂线段例1:如图,△ABC中, ∠C=90o,BC=10,BD=6,AD平分∠BAC,求点D到AB的距离.B CADE过点D作DE⊥AB.构造了:全等的直角三角形且距离相等例2:如图,△ABC中, ∠C=90o,AC=BC,AD平分∠BAC,求证:AB=AC+DC.BCADE过点D作DE⊥AB.构造了:全等的直角三角形且距离相等思考:若AB=15cm,则△BED的周长是多少?例3:如图,梯形中, ∠A= ∠D =90o,BE、CE均是角平分线,求证:BC=AB+CD.B ADCFE过点E作EF⊥BC.构造了:全等的直角三角形且距离相等B ADC FE例4:如图,OC 平分∠AOB, ∠DOE +∠DPE =180o,求证: PD=PE.ABCOD PEGF过点P作PF⊥OA,PG ⊥OB.构造了:全等的直角三角形且距离相等Ⅲ.垂直平分线上点向两端连线段例1:已知CD是AB的垂直平分线,D、E、F三点共线。
求证FBCFA∠+∠=∠CABFDEⅣ.中线延长一倍例1:AD 是△ABC 的中线,求证:AC)(AB 21+<AD DABCE延长AD 到点E ,使DE=AE ,连结CE.Ⅴ.“周长问题”的转化借助“角平分线性质”例1:如图,△ABC 中,∠C=90o,AC=BC,AD 平分∠CAB,DE ⊥AB.若AB=6cm,则△DBE 的周长是多少?CBADEⅤ.“周长问题”的转化借助“垂直平分线性质”例2:如图,△ABC 中, D 在AB 的垂直平分线上,E 在AC 的垂直平分线上.若BC=6cm,求△ADE 的周长.ABCD E例3:如图,A 、A1关于OM 对称, A 、A2关于ON 对称.,若A1 A2 =6cm,求△ABC 的周长.C MONAA 1A 2B例4:如图, △ABC 中,MN 是AC 的垂直平分线.若AN=3cm, △ABM 周长为13cm ,求△ABC 的周长.MNABCⅤ.“周长问题”的转化借助“等腰三角形性质”例5:如图, △ABC 中,BP 、CP 是△ABC 的角平分线,MN//BC.若BC=6cm, △AMN 周长为13cm ,求△ABC 的周长.ABCPMN。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
+#"$%" ##$& $ ""$( % "%$* ! 大 手 拉 小 手 全 等 问 题 一 两 个 正 方 形 相 关 !!观察图!和图'"若四边形 "#$%$%&') 都是正方形"猜想类似的结论是!!!!!"在图 '中证明你的猜想!
$ #"$%* #%$&" ##$&* #%$& 即 #"$&" #%$# 在""$& 和"%$# 中
*"$"%$ )#"$&" #%$#
+&$"#$
$ ""$&% "%$#&%&
!!
$"&"%# '#$"&" #$%#即 #$"( " #$%* $"%"$"&#$ 均是等边三角形 $"$"%$#"$( " ##$&"3,又点 "$# 在同一条直线上
!!!!!!!!! 证明过点 % 作%& 垂直#" 的延长线于点&作 %'(#$ 于点'如图 ##% 平分#"#$$%&"%' 在 ./""%& 与 ./"$%' 中
!!
'%&"%'
"%"$% $./""%&%./"$%'01$ #%"&" #%$'! 又 ##"%* #%"&"!+,-$ ##"%* #%$'"!+,- 即 ##"%* ##$%"!+,-! '!已知#"$ 平分##"%"$&("#"##*#%"!+,-"求证#"&""%*#&! 证明在 "& 上取'使 &'"&#连接 $' #$&("# $ #$&#" #$&'"2,#&#"&'$&"$& $ "$&#% "$&' $ ##" #$'& # ##* #%"!+,-#$'&* #$'""!+,$ #%" #$'" #"$ 平分##"% $ #%"$" #'"$ #"$""$ $ ""%$% ""'$&%& $"%""' $"&""'*'&""%*#&! (!如图""%$#$"点 & 在 线 段 "# 上"#"%&" #$%&"#%$&" #&$#!求 证#$%""% *#$!
$#% 平分#+#$! )!如图"已知 $ 是线段"# 上任意一点($ 点不与"$# 重合)"分别以 "$$#$ 为边在直线"# 的同侧作等边""$% 和等边"#$&""& 与$% 相交于点 ( "#% 与$& 相交于点 * ! 求 证 #""$( % "%$* ! 解#""$% 和"#$& 是等边三角形 $"$"%$#$"&$#"$%" ##$&"3,- $ #"$%* #%$&" ##$&* #%$& 即 #"$&" #%$#! 在""$& 和"%$# 中 *"$"%$ )#"$&" #%$# +$&"$# $ ""$&% "%$#&%& $ #&"$" ##%$ # #"$%" ##$&"3,- $ #%$&"3,- $ #"$%" #%$&
小聪同学的思路是#延长 %( 交)' 于 - "构造全等三角形"经过推理使问题得到解决!
请 你 参 考 小 聪 同 学 的 思 路 "探 究 并 解 决 下 列 问 题 #
(!)直接写出上面问题中线段 %( 与 () 数量与位置有何关系!!!!!*
(')将图!中的正方形 $&') 绕点$ 顺时 针 旋 转"使 正 方 形 $&') 对 角 线$' 恰 好 与 正 方 形
!!!!!!!!! 证明在 $% 上截取%'""%连接 &' # #"%&" #$%&%'""%%&"%& $""%&%"'%& &%& $ #"" #%'& #"%$#$ $ #"* ##"!+,$ #%'&* ##"!+,# #%'&* #$'&"!+,$ #$'&" ## # #%$&" #&$#$&"$& $"#$&%"'$& %%&
#%'&" #$)&全 等 三 角 形 的 对 应 角 相 等 # "%'&% "$)& $%'"$)%'""$ $$)""$ $ #$)&" #&"$等 边 对 等 角 # #%'&" #$)& $%'$$)内 错 角 相 等 两 直 线 平 行 #%'$$)%'$"# $$)$"# $ #$)&" ##"&两 直 线 平 行 内 错 角 相 等 # #$)&" ##"&#$)&" #&"$ $##"&"#&"$即 "& 平分##"$ )!在四边 形 "#$% 中"#$%$& 为 #$ 边 的 中 点##"&" #&"'"' 与%$ 的延长线 相 交 于 点' 试 探 究 线 段 "# 与 "'$' 之 间 的 数 量 关 系 并 证 明 你 的 结 论 ! 解!延长 "& 交%' 的延长线于点 ( 如图所示 #& 为#$ 的中点 $#&"$& #"#$$% $ ##"&" #( $在""#& 和"($&%&% $"#"($ # ##"&" #&"' $ #&"'" #( $('""' #($"('*$' $"#""'*$'! 截长补短法 !!已知如 图在 四 边 形 "#$% 中#$'"#"% "%$#% 平 分 #"#$!求 证##"% * ##$%"!+,-!
大 手 拉 小 手 全 等 问 题 一 两 个 等 边 三 角 形 相 关
!!如图""%"$$"&#$ 均是等边三角形"点 "$$$# 在同一条直线上"且 "&$#% 分别与$%$ $& 交于点 ( $*!
求证#(!)"&"%#*(')"$(* 为等边三角形!
证明!#"%"$"&#$ 是等边三角形 $"$"%$&$"#$#"$%" ##$&"3,-
解 "&"$)! 证明如图'正方形 "#$% 与正方形%&') 中 #"%"$%%&"%)#"%$" #)%&"2,- 又 #$%)"2,-* #"%)" #"%& $ ""%&% "$%) $"&"$)! '!如图"以锐角""#$ 的边"#$"$ 向外作 正 方 形 "+,# 和 正 方 形 "&'$"连 接 +&"作 "% (#$"垂足为 %"延长 %" 交+& 于点 - !过 + 作+( (%("垂足为 ("过点 & 作&* (%("垂足 为 *! (!)不 再 增 加 线 条 或 字 母 "在 图 中 找 出 一 对 全 等 三 角 形 "并 给 出 证 明 *
