中学初中保送生招生考试数学试卷及参考答案
初三保送生选拔数学试卷及答案
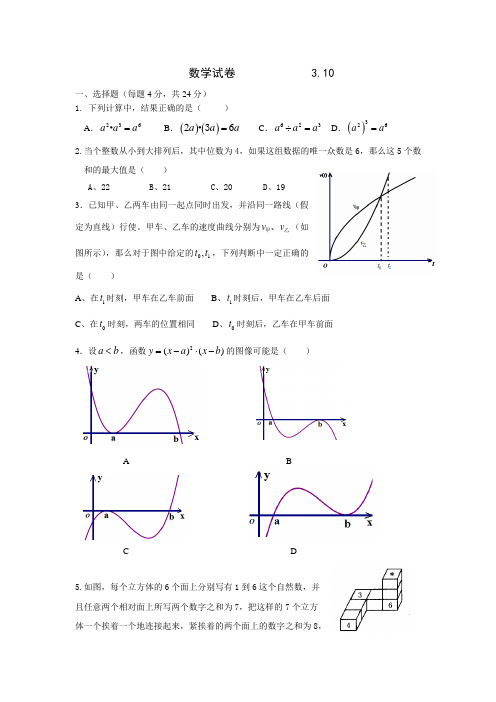
数学试卷 3.10 一、选择题(每题4分,共24分) 1. 下列计算中,结果正确的是( )A .236a a a =· B .()()26a a a =·3 C .623a a a ÷= D .()326aa =2.当个整数从小到大排列后,其中位数为4,如果这组数据的唯一众数是6,那么这5个数和的最大值是( )A 、22B 、21C 、20D 、19 3.已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行使。
甲车、乙车的速度曲线分别为v v 甲乙、(如图所示),那么对于图中给定的01,t t ,下列判断中一定正确的是( )A 、在1t 时刻,甲车在乙车前面B 、1t 时刻后,甲车在乙车后面C 、在0t 时刻,两车的位置相同D 、0t 时刻后,乙车在甲车前面 4.设a b <,函数2()()y x a x b =-⋅-的图像可能是( )A BC D5.如图,每个立方体的6个面上分别写有1到6这个自然数,并 且任意两个相对面上所写两个数字之和为7,把这样的7个立方 体一个挨着一个地连接起来,紧挨着的两个面上的数字之和为8,则图中“*”所在面上的数字是( ) (第6题) A 、4 B 、3 C 、2 D 、1 6. 一个三角形的边长分别为,,a a b ,另一个三角形的边长分别为,,b b a ,其中a b >,若两个三角形的最小内角相等,则ab的值等于( ) AB二、填空题(每题4分,共20分)7、有一个多项式为a 8-a 7b +a 6b 2-a 5b 3+…,按照此规律写下去,这个多项式的第八项是8、有三条绳子穿过一片木板,姊妹两人分别站在木板 的左、右两边,各选该边的一条绳子,若每边每条绳子被选中的机会相等,则两人选到同一条绳子的概率为9.△ABC 中,a ,b ,c 分别是∠A 、∠B 、∠C 的对边.已知a =10,b =23+,c =23-,则b sin B +c sin C 的值等于 。
初中数学保送生数学试卷

一、选择题(每题3分,共30分)1. 已知函数f(x) = x^2 - 4x + 3,其图像的对称轴是:A. x = 1B. x = 2C. x = 3D. x = 42. 在直角三角形ABC中,∠C = 90°,AC = 3,BC = 4,则AB的长度为:A. 5B. 6C. 7D. 83. 已知等差数列{an},a1 = 3,公差d = 2,则a10的值为:A. 21B. 22C. 23D. 244. 已知方程x^2 - 5x + 6 = 0的两个根为a和b,则a^2 + b^2的值为:A. 25B. 30C. 35D. 405. 在等腰三角形ABC中,AB = AC,∠BAC = 40°,则∠B的度数为:A. 40°C. 60°D. 70°6. 已知函数f(x) = |x - 2| + |x + 3|,则f(x)的最小值为:A. 5B. 6C. 7D. 87. 已知方程组:$$\begin{cases}x + 2y = 5 \\3x - y = 7\end{cases}$$的解为:A. x = 1,y = 2B. x = 2,y = 1C. x = 3,y = 0D. x = 4,y = -18. 已知等比数列{an},a1 = 2,公比q = 3,则a6的值为:A. 54B. 162D. 14589. 在等边三角形ABC中,AB = BC = AC,则∠ABC的度数为:A. 30°B. 45°C. 60°D. 90°10. 已知方程x^2 - 6x + 9 = 0的两个根为a和b,则a^3 + b^3的值为:A. 36B. 48C. 60D. 72二、填空题(每题5分,共20分)11. 已知函数f(x) = 2x - 3,若f(x)的值域为[1, 5],则x的取值范围为______。
12. 在等腰三角形ABC中,AB = AC,∠BAC = 50°,则∠ABC的度数为______。
2024年重庆市巴蜀中学初升高保送数学模拟5含参考答案

2023-2024学年重庆市巴蜀中学初升高保送模拟5 姓名:1. 从三边长均为整数且周长为24 的三角形中任取一个,它是直角三角形的概率为 。
2.如图,菱形OABC 的顶点O 在原点,A 坐标为(4,0),反比例函数()0kyk x=≠的图象经过AC 、BO 的交点D ,且与AB 边交于点E ,连接OE 交AD 于点F ,若F 恰为AD 中点,则k = 。
3.如图,点E 是四边形ABCD 内一点,已知BE =EC ,AE =ED ,∠BEC =∠AED =90°,对角线AC 与BD 交于O 点,BD 与EC 交于点F ,AC 与ED 交于点G ,若BE =3,AE =4,AB =6,则CD 的长为 。
4.△ABC是边长为5的等边三角形,△DEC是边长为3的等边三角形,直线BD与直线AE交于点F,如图,若点D在△ABC内,∠DBC=20°,则∠BAF= °;现将△DEC绕点C旋转1周,在这个旋转过程中,线段AF长度的最小值是。
5.中秋鲜果列晶盘,饼样圆分桂魄寒,聚食合家门不出,要同明月作团圆。
沁园的甲、乙两个手工作坊为某公司赶制一批风味独特的月饼,沁园生产部经理调研,把甲、乙两个员工人数不相等的作坊一天生产的手工月饼数量进行对比发现,甲作坊平均每人生产的月饼数量比乙作坊平均每人生产的月饼数量多0.5个,乙作坊的负责人老李说:“我们乙作坊是新手小王影响了平均数,他一天才制作45个月饼,要是不算小王,我们的平均数量会比甲作坊还多一个。
”甲作坊的生产负责人老张说:“我们甲作坊要是不算动作较慢的秦大爷一天生产的20个,我们甲作坊的平均数量也会比乙作坊多1.5个。
”生产经理听了他们的对话,语重心长地说:“时间紧,任务中,让我们一起帮助新手小王和秦大爷,如果他们2人一天生产的数量都提高到正整数x个,那么甲、乙两个作坊一天平均每人生产的月饼数量相同,大家都高兴!”,甲、乙两个作坊的人数之和超过55人,不超过60人,则整数x= 。
九年保送班数学试题(1含答案)

九年级数学试题一、选择题(每小题3分,共24分) 1.代数式2346x x -+的值为9,则2463x x -+的值为( ) A .7B .18C .12D .92.关于x 的方程014)5(2=---x x a 有实数根,则a 应满足的条件为()A .1≥a 且5≠aB .1>a 且5≠aC .1≥aD .5≠a3.如图为做一个试管架,在a cm 长的木条上钻了4个圆孔,每个孔的直径为2 cm ,则x 等于( )A .58+a cm B .516-a cmC .54-a cmD .58-a cm4.下列各图中,可以是一个正方体的平面展开图的是( )A .B .C .D .5. 车轮半径为0。
3 m 的自行车沿着一条直路行驶,车轮绕着轴心转动的转速为100转/分,则自行车的行驶速度为( )A .3.6π km/hB .1。
8π km/hC .30 km/hD .15 km/h6.已知二次函数y=3x 2﹣2x+a ﹣3与x 轴交点的横坐标是x 1,x 2,且x 1≤﹣2,则a 可取的最大值是( )A .﹣13B .﹣5C .D .﹣7. 一个定滑轮起重机装置如图所示,滑轮的半径是10㎝,当重物 上升10㎝时,滑轮的一条半径OA 绕轴心按逆时针方向旋转的角度约为(假设绳索之间没有滑动,结果精确到1°)( ) A .115° B .60° C .29° D .57° 8。
已知是两个连续自然数(m 〈n ),且q=mn,设m q n q p -++=,则p( )A .总是奇数B .总是偶数C .有时是奇数有时是偶数D .有时是有理数有时是无理数 二、填空题(每小题3分,共24分)9. 在实数范围内分解因式:2484m m +-= .10. 把抛物线2x y -=向上平移2个单位,那么所得抛物线与x 轴的两个交点之间的距离是 。
11. 某种商品的进价为800元, 出售时标价为1 200元, 后来由于商品积压, 商店准备打折出售,但只要保持利润率不低于5%,则最多可打 折.12。
初三数学保送生考试试卷

考试时间:120分钟满分:100分一、选择题(每题5分,共50分)1. 下列各数中,无理数是()A. 2.5B. $$ \sqrt {16} $$C. $$ \pi $$D. 0.3333...2. 已知等差数列{an}中,a1=3,d=2,则第10项a10的值为()A. 15B. 17C. 19D. 213. 若方程 $$ x^{2} - 5x + 6 = 0 $$ 的两个根为a和b,则a+b的值为()A. 5B. -5C. 6D. -64. 在直角坐标系中,点P(2,3)关于直线y=x的对称点为()A.(3,2)B.(-2,-3)C.(-3,2)D.(2,-3)5. 下列函数中,是反比例函数的是()A. y=2x+1B. y=$$ \frac {1}{x} $$C. y=x^2D. y=3x^36. 已知二次函数y=ax^2+bx+c(a≠0)的图象开口向上,且顶点坐标为(1,-2),则a的取值范围是()A. a>0B. a<0C. a=0D. a≠07. 在△ABC中,若∠A=60°,∠B=45°,则∠C的度数是()A. 45°B. 60°C. 75°D. 90°8. 下列命题中,正确的是()A. 对顶角相等B. 相邻角互补C. 对顶角互补D. 相邻角相等9. 若等腰三角形底边长为6cm,腰长为8cm,则其周长为()A. 18cmB. 20cmC. 22cmD. 24cm10. 下列各数中,属于有理数的是()A. $$ \sqrt {2} $$B. $$ \pi $$C. 0.1010010001…D. -3二、填空题(每题5分,共50分)1. 已知等差数列{an}中,a1=1,d=2,则第n项an的表达式为______。
2. 若方程 $$ x^{2} - 4x + 3 = 0 $$ 的两个根分别为a和b,则a^2+b^2的值为______。
浙江大学附属中学保送预选生素质测试数学试卷及答案真题版

浙江大学附属中学保送预选生素质测试数学试卷一、选择题(每题6分,共30分)1. 计算aa 1-等于 ( ▲ )A.a -B.aC.a --D.a -2.计算︒-+︒︒30cos 245sin 260tan 的结果是 ( ▲ )A.2B.2C.1D.33.A 地在河的上游,B 地在河的下游,若船从A 地开往B 地速度为v 1,从B 地返回A 地的速度为v 2,则A 、B 两地间往返一次的平均速度为 ( ▲ ) A. 221v v + B.21212v v v v + C.212v v + D.21212v v v v +4.如图,M 是△ABC 的边BC 的中点,AN 平分∠BAC,BN ⊥AN 于点N,且AB=10,BC=15,MN=3.则△ABC 的周长等于 ( ▲ ) A .38B .39C .40D .415.若a,b,c,m,n,p 均为非零实数,则关于x 的方程 m(ax 2+bx +c)+n(ax 2+bx +c )+p=0的所有解的组成不可能是 ( ▲ ) A.{1,2}B.{1,2,3}C.{1,2,3,4}D.{1,2,4,8}二、填空题(每题6分,共36分)6.若n(n ≠0)是关于x 的方程x 2+mx+2n=0的根,则m+n 的值为________________.7.若2)2(45++=++x Bx A x x x ,则常数A=___________ ,B=_____________ .8.若(3x+1)4 =ax 4+bx 3+cx 2+dx+e ,则 a-b+c-d =______________.9.如图,E 、F 分别是▱ABCD 的边AB 、CD 上的点,AF 与DE 相 交于点P ,BF 与 CE 相交于点Q ,若S △APD =10cm 2,S △BQC =20cm 2, 则阴影部分的面积为________.10.若关于x ,y 方程组⎩⎨⎧=+=+222111c y b x a c y b x a 的解为⎩⎨⎧==65y x ,则方程11.如图,在平面直角坐标系xOy 中,多边形OABCDE 的顶点坐标分别是O (0,0),A (0,6),B (4,6),C (4,4),D (6,4),E (6,0).若直线l 经过点M (2,3),且将多边形OABCDE 分割成面积相等的两部分,则直线l 的函数表达式是.三、解答题(第12题16分,第13题18分,共34分)12.如图,AB 为⊙O 的直径,直线CD 与⊙O 相切于点D ,AC ⊥CD ,DE ⊥AB ,C 、E 为垂足,连接AD ,BD .若AC=4,DE=3,求BD 的长.13.某公司计划投资A、B两种金融产品,根据市场调查与预测,A产品的利润W 与投资量x成正比例,其关系如图1,B产品的利润P与投资量x的算术平方根成正比例,其关系如图2,(注:利润与投资量单位:万元)( I )分别将A、B两产品的利润W,P表示为投资量x的函数关系式.(Ⅱ)该公司已有10万元资金,并全部投入A、B两种产品中,公司获得的总利润为y万元,问:怎样分配这10万元投资,才能使公司获得最大利润?其最大利润为多少万?浙江大学附属中学保送预选生素质测试6. -27.A=2,B=38. 15 9. 3010. ⎩⎨⎧==84y x11. 31131+-=x y12.【解答】解:因为CD 与⊙O 相切于点D ,所以∠CDA=∠DBA ,…(2分)又因为AB 为⊙O 的直径,所以∠ADB=90°. 又DE ⊥AB ,所以△EDA ∽△DBA ,所以∠EDA=∠DBA ,所以∠EDA=∠CDA .…(4分) 又∠ACD=∠AED=90°,AD=AD ,所以△ACD ≌△AED . 所以AE=AC=4,所以AD=5,…(6分)13.。
保送生初中数学试卷

一、选择题(每题5分,共50分)1. 下列各数中,不是有理数的是()A. 2.5B. -3C. √4D. 0.101010...2. 已知a、b是实数,且a+b=0,则下列等式中正确的是()A. a^2 = b^2B. a^2 = -b^2C. a^2 = 2b^2D. a^2 = b^2 + 23. 下列各式中,能被3整除的是()A. 15 + 24B. 27 - 18C. 36 + 9D. 48 - 124. 已知一个长方体的长、宽、高分别为a、b、c,则它的体积V=()A. abcB. ab + bc + acC. a^2b + b^2c + c^2aD. a^2b^2c^25. 在直角坐标系中,点P的坐标为(-2,3),则点P关于x轴的对称点坐标是()A. (-2,-3)B. (2,3)C. (2,-3)D. (-2,3)6. 下列各式中,能表示反比例函数的是()A. y = 2x + 1B. y = 3/xC. y = x^2D. y = x^37. 下列各式中,正确的是()A. 3^2 = 9^1B. 4^3 = 64C. 5^2 = 10^1D. 6^3 = 36^18. 已知a、b、c是三角形的三边,且a+b+c=10,若a=3,b=4,则c的取值范围是()A. 3 < c < 7B. 2 < c < 8C. 3 < c < 9D. 2 < c < 109. 下列各图中,能表示y=2x+1的是()A.B.C.D.10. 下列各数中,不是整数的是()A. -1/2B. 3/4C. -2/3D. 5/6二、填空题(每题5分,共50分)11. 计算:-3 + 5 - 2 + 4 = _______12. 若a=2,b=-3,则a^2 - 2ab + b^2 = _______13. 已知长方形的周长为20,长为6,则宽为 _______14. 在直角坐标系中,点A的坐标为(3,4),则点A关于y轴的对称点坐标是_______15. 下列函数中,反比例函数的图象是 _______16. 下列各数中,能被5整除的是 _______17. 若x^2 - 5x + 6 = 0,则x的值为 _______18. 下列各式中,能表示一次函数的是 _______19. 下列各数中,不是有理数的是 _______20. 若a、b、c是等差数列,且a=2,b=5,则c的值为 _______三、解答题(每题20分,共60分)21. 已知一元二次方程x^2 - 4x + 3 = 0,求它的解。
数学推荐生考试试题及答案

数学推荐生考试试题及答案一、选择题(每题2分,共10分)1. 下列哪个数是无理数?A. 3.14159B. 2.71828C. πD. √22. 已知函数f(x) = 2x + 3,求f(-1)的值。
A. -1B. 1C. -5D. 53. 若a > b,且a > 0,b < 0,则下列哪个不等式是正确的?A. a + b > 0B. a - b > 0C. a * b > 0D. a / b > 04. 一个圆的半径为r,圆的面积是πr²,下列哪个选项是圆的面积?A. r²B. πrC. πr²D. 2πr5. 一个等差数列的首项为a,公差为d,第n项的通项公式是什么?A. a + (n-1)dB. a - (n-1)dC. a + ndD. a - nd二、填空题(每空1分,共10分)6. 若一个三角形的三边长分别为3, 4, 5,根据勾股定理,这是一个_________三角形。
7. 函数y = x² + 2x - 3的顶点坐标是_________。
8. 若一个数列{an}的前n项和为S,且S = n² + 1,那么数列的第5项a5 = _______。
9. 一个正弦函数sin(x)的周期是_________。
10. 一个二次方程ax² + bx + c = 0的判别式是_________。
三、解答题(每题15分,共30分)11. 证明:对于任意实数x,等式e^x ≥ x + 1成立。
12. 解不等式:2x² - 5x + 3 > 0,并求其解集。
四、证明题(每题15分,共30分)13. 证明:对于任意正整数n,1² + 2² + 3² + ... + n² = n(n + 1)(2n + 1) / 6。
14. 证明:若函数f(x)在区间[a, b]上连续,且f(a)f(b) < 0,则至少存在一点c ∈ [a, b],使得f(c) = 0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙江省慈溪中学2007年初中保送生招生考试数学试卷(本卷考试时间90分钟,满分130分.)一、选择题(每题6分,共30分)1.将正方形ABCD 折叠,使顶点A 与CD 边上的点M 重合,折痕交AD 于E ,交BC 于F ,边AB 折叠后与BC 边交于点G(如图).如果DM :MC=3:2,则DE :DM :EM=( )(A)7:24:25 (B)3:4:5 (C)5:12:13 (D)8:15:172.假期里王老师有一个紧急通知,要用电话尽快通知给50个同学,假设每通知一个同学 需要1分钟时间,同学接到电话后也可以相互通知,那么要使所有同学都接到通知最快需要的时间为( )(A)8分钟 (B)7分钟 (C)6分钟. (D)5分钟3.已知:二次函数y=2x +2x+a(a 为大于0的常数),当x=m 时的函数值y 1<0;则当x=m+2时的函数值y 1与0的大小关系为( )(A)y 2>0 (B)y 2<0 (C)y 2=O (D)不能确定4.记S=121221121212008200720072007-++++++Λ则S 所在的范围为( )(A)0<S<1 (B)1<S<2 (C)2<S<3 (D)3<S<45.如图,点A 是函数y=x1的图象上的点,点B 、C 的坐标分别为 B(-2,-2)、C(2,2).试利用性质:“函数y=x 1的图象上 任意一点A 都满足|AB-AC|=22”求解下面问题:“作∠BAC 的内角平分线AE ,过B 作AE 的垂线交AE 于F ,已知当点A 在函数 y=x1的图象上运动时,点F 总在一条曲线上运动,则这条曲线为( ) (A)直线 (B)抛物线 (C)圆 (D)反比例函数的曲线二、填空题(每题6分,共36分)6.已知关于x 的不等式(2a-b)x≥a -2b 的解是x>25,则关于x 的不等式 ax+b<0的解为 .7.已知右边方格纸中的每个小方格是边长为1的正方形,A 、B 两点在小方格的顶点上,位置如图所示.在小方格的顶点上确定一点C,连结AB、AC、BC,使△ABC的面积为3个平方单位.则这样的点C共有个.8.直角坐标系中,点A(0,0),B(2,0),C(0,23),若有一三角形与△ABC全等,且有一条边与BC重合,那么这个三角形的另一个顶点坐标是________.9.n个单位小立方体叠放在桌面上,所得几何体的主视图和俯视图均如图所示.那么n的最大值与最小值的和是_______ .10.对大于或等于2的自然数m的n次幂进行如右图方式的“分裂”,仿此,36的“分裂”中最大的数是.11.甲,乙,丙3人用擂台赛形式进行训练,每局2人进行单打比赛,另1人当裁判,每一局的输方去当下一局的裁判,而由原来的裁判向胜者挑战.半天训练结束时发现甲共打了12局,乙共打了21局,而丙共当裁判8局.那么,整个比赛的第10局的输方一定是_____ .三、解答题(每小题16分,共64分)12.△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的顶点E位于边BC的中点上.(1)如图1,设DE与AB交手点M,EF与AC交于点N,求证:△BEM∽△CNE;(2)如图2,将△DEF绕点E旋转,使得DE与BA的延长线交于点M,EF与AC交于点N,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形?并证明你的结论.13.已知函数y=2x +(b-1)x+c(b ,c 为常数),这个函数的图象与x 轴交于两个不同的点A(1x ,0)和B(2x ,0).若x 1,x 2满足12x x >1(1)求证: 2b ≥2(b+2c);(2)若t<1x ,试比较2t +bt+c 与1x 的大小,并加以证明。
14.有A 、B 、C 、D 、E 5位同学依次站在某圆周上,每人手上分别拿有小旗16、8、12、4、15面,现要使每人手中的小旗数相等.要求相邻的同学之间相互调整(不相邻的不作相互调整),设A 给B 有x 1面(x 1>0时即为A 给B 有x 1面;x 1<O 时即为B 给A 有x 1面.以下同),B 给C 有x 2面:C 给D 有x 3面,D 给E 有x 4面,E 给A 有x 5面,问x 1、x 2、x 3、x 4、x 5分别为多少时才能使调动的小旗总数|x 1|+|x 2|+|x 3|+|x 4|+|x 5|最小?如图:已知a 为正常数,F 1(202+-a ,0),F 2(202+a ,0),过F 2作直线l ,点A ,B 在直线l 上,且满足AF 1-AF 2=BF 1-BF 2=2a ,M ,N 分别为△AF 1F 2,△BF 1F 2的内切圆的圆心.(1)设⊙M 与F 1F 2相切于点P 1,⊙N 与F 1F 2切于点P 2,试判断P 1与P 2的位置关系,并加以证明;(2)已知sin ∠BF 2F 1=8/9,且MN=29,试求a 的值[参考答案]一、选择题(每题6分,共30分)1.D 2.C .3.A 4.A 5.C二、填空题(每题6分:共36分)6.x>-8 7.6 8.(2,23)或(3,3)或(-1,3)(全部正确才给分)9.23 10.41 11.甲三、解答题(共64分)12.(16分)证:(1)△ABC 是等腰直角三角形,∴∠MBE=45°.∴∠BME+∠MEB=135°(2分)又∵△DEF 是等腰直角三角形,∴∠DEF=45°∴∠NEC+∠MEB=135°,∴∠BME=∠NEC ,(4分)而∠MBE=∠ECN=45°,∴△BEM ∽△CNE (6分)(2)与(1)同理△BEM ∽△CNE ,BE /CN=EM/NE (10分)又∵BE=EC .(12分)∴EC/CN=EM/NE 则△ECN 与△MEN 中EC/CN =ME/EN ,又∠ECN=∠MEN=45° ∴△ECN ∽△MEN (16分)(如给出答案△MBE ∽△MEN ,同样给相应的分值)13.(16分).证:(1):由已知:x 1,2=24)1()1(2c b b --±--,又x 2-x 1>1,(3分) ∴14)1(2>--c b ,∴b 2-2b+1-4c>1即b 2>2(b+2c)。
(5分)(2)由已知x 2+(b-1)x+c=(x-x 1)(x-x 2) (8分)∴x 2+bx+c=(x-x 1)(x-x 2)+x ,∴t 2+bt+c=(t-x 1)(t-x 2)+t(12分)t 2+bt+c-x 1=(t-x 1)(t-x 2)+t-x 1=(t-x 1)(t-x 2+1) ,∵t<x 1 ∴ t-x 1<0 又x 2-x 1>1∴t<x 1<x 2-1,∴t-x 2+1<0,∴(t-x 1)(t-x 2+1)>0 (15分),即t 2+bt+c>x 1(16分)14.(16分)解:∵共有小旗面数;16+8+12+4+15=55面,要使每人手中的小旗面数相等,每人均为11面.由题意:⎪⎪⎩⎪⎪⎨⎧=+=+=+=+11x -x 1511x -x 4 1 1x -x 121 1x -x 854433221 ∴⎪⎪⎩⎪⎪⎨⎧==+=+=2-x x 6-x x 1x x 3x x 25242321∴|x 1|+|x 2|+|x 3|+x 4|+|x 5|=|x 2+3|+|x 2|+|x 2+1|+|x 2-6|+|x 2-2|=|x 2+3|+|x 2+1|+|x 2|+|x 2-2|+| x 2-6|(6分) 设实数x 2在数轴上的对应点为P实数-3,-1,0,2,6在数轴上的对应点分别为P 1,P 2,P 3,P 4,P 5∴|x 1|+|x 2|+|x 3|+x 4|+|x 5|=|PP 1|+|PP 2|+|PP 3|+|PP 4|+|PP 5|(10分)当且仅当P 在线段P 1P 5上时|PP 1|+|PP 5|有最小值9:当且仅当P 在线段P 2P 4上时|PP 2|+|PP 4|有最小值3:当且仅当P 与点P 3重合时|PP 3|有最小值0(14分)即当且仅当P 与点P 3重合(x 2=0)时x 1+x 2+x 3+x 4+x 5=|PP 1|+|PP 2|+|PP 3|+|PP 4|+|PP 5|有最小值12。
当x 1=3,x 2=0,x 3=1,x 4=-6,x 5=-2时|x 1|+|x 2|+|x 3|+|x 4|+|x 5 |有最小值12(16分)15.(16分)证:(1)由题意:AC=AD ,∵AF 1-AF 2=2a ,∴CF 1-DF 2=2a ,又F 1C=F 1P 1 F 2D=F 2P 1 ∴P 1F 1-P 1F 2=2a (2分),同理P 2F 1-P 2F 2=2a ,∴P 1与P 2重合(3分)(2)由(1)知:MP 1⊥F 1F 2,NP 2⊥F 1F 2,P 1,P 2重合. ∴M ,P 1,N 共线,且MN ⊥F 1F 2(5分). 连接MN ,NE ,MD ,则∠NED=∠MDE=90° 过N 作NH ⊥MD ,H 为垂足,∵∠MP 1F 2=∠MDF 2=90°.∠HMN=∠BF 2F 1(9分) ∴sin ∠HMN=sin ∠BF 2F 1=8/9又MN=9/2∴NH=MNsin ∠HMN=4∴ED=4.(11分).而DF 2=F 2P 1=F 2E∴F 2P 1=2(14分)又由(1)P 1F 1-P 1F 2=2a .∴P 1F 1=2+2a∴P 1F 1+P 1F 2=2+2+2a=2202 a (15分) 解得:a=4……(16分)。
