chap7习题答案
信号与系统奥本海姆英文版课后答案chapter7

137Chapter 7 Answers7.1 From the Nyquist sampling theorem , we know that only if X (j w)=0 for |w| > w s /2 will be signal be recoverable from its samples. Therefore, X(jw)>5000л.7.2 From the Nyquist theorem ,we know that the sampling frequency in this case must be at least w s =2000п.In other words ,the sampling period should be at most T=2п/ (w s )=1*10-3.Clearly ,only (a) and (e) satisfy this condition.7.3 (a) We can easily show that X(j w)=0 for |w| >4000п.Therefore, the Nyquist rate for this signal is w N =2(4000п)=8000п.(b)From the Tables 4.1 and 4.2 we know that X(j w) is a rectangular pulse for which X(j w)=0 for |w| > 4000п.Therefore, the Nyquist rate for this signal is w N =2(4000п)=800п.(c) From the Tables 4.1 and 4.2 we know that X(j w) is the convolution of two rectangular pulses each of which is zero for |w| > 4000п.Therefore ,X(j w)=0 for |w| >8000пand the Nyquist rate for this signal is w N =2(8000п)=16000п.7.4 If the signal x(t) has a Nyquist rate of w o ,then its Fourier transform X (j w)=0 for |w| > w o /2. (a) From chapter 4,y(t) = x (t) + x (t-1) −→←FTY (jw) = X (jw) + e -jwt X (jw).Clearly, we can only guarantee that Y (jw) =0 for |w| > w o /2. Therefore, the Nyquist rate for y(t) is also w o . (b) From chapter 4,y(t) = dtt dx )( −→←FTY (jw)= jw X(jw).Clearly, we can only guarantee that Y (jw) =0 for |w| > w o /2. Therefore, the Nyquist rate for y(t) is also w o . (c) From chapter 4,y(t) =x 2(t) −→←FTY (jw)= (1/2п)[X(jw)*X(jw)]Clearly, we can only guarantee that Y (jw) =0 for |w| > w o . Therefore, the Nyquist rate for y(t) is also 2w o . (d) From chapter 4,y(t)=x(t)cos (w o t) −→←FTY (jw)= (1/2)X(j(w- w o )) +(1/2)X(j(w+ w o )).Clearly, we can guarantee that Y (jw) =0 for |w| > w o + w o /2. Therefore, the Nyquist rate for y(t) is 3w o. 7.5 Using Table 4.2,p(t) −→←FT Tπ2∑∞-∞=-K T K )/2(πωδFrom Table 4.1 p(t-1) −→←FT Tπ2 e -jw T jk k eTk ππωδ2)2(-∞-∞=∑-. Since y(t)=x(t)p(t-1),we haveY (jw)= (1/2п)[X(jw)*FT{P(t-1)}]=(1/T)T jk K e Tk j X ππω2))2((-∞-∞=∑-Therefore, Y(j ω) consists of replicates of X(j ω) shifted by k2π/T and added to earth other (see Figure⎩⎨⎧≤=otherwiseT j H c ,0||,)(ωωωWhere (2/0ω)<c ω<(2π/T) - (2/0ω).7.6 Consider the signal w(t)=x 1(t)x 2(t).The Fourier transform W(j ω) of w(t) is given by W(j ω)=π21[])(*)(21ωωj X j X .Since 0)(1=ωj X for |ω|≥1ωand X 2(j ω)=0 for |ω|≥2ω, we may conclude that W(j ω)=0 for |ω|≥1ω+2ω.Consequently ,the Nyquist rate for w(t) iss ω=2(1ω+2ω).Therefore ,the maximum sampling138period which would still allow w(t) to be recovered is T=2π/(s ω)=π/(1ω+2ω). 7.7 We note thatx 1(t) =h 1(t)*{∑∞-∞=-n nT t nT x )()(δ}Form Figure 7.7 in the book ,we know that the output of the zero-order hold may be written as x 0(t)=h 0(t)* {∑∞-∞=-n nT t nT x )()(δ}where h 0(t) is as shown in Figure S7.7 By taking the Fourier transform of the two above equations, we have X 1(j ω)=H 1( j ω)X p ( j ω)X 0(j ω)=H 0( j ω) X p ( j ω)We now need to determine a frequency response H d ( j ω) for a filter which produces x 1(t) at its output when x 0(t) is its input. Therefore, we needX 0(j ω) H d ( j ω)= X 1(j ω)The triangular function h 1(t) may be obtained by convolving two rectangular pulses as shown in Figure S7.7Therefore,h 1(t)={(1/T ) h 0(t+T/2)}*{( 1/T ) h 0(t+T/2)} Taking the Fourier transform of both sides of the above equation, H 1( j ω)=T1e T j ω H 0( j ω) H 0( j ω) ThereforeX 1(j ω)= H 1( j ω) X p ( j ω)=T 1e T j ω H 0( j ω) H 0( j ω) X p ( j ω) =T1e Tj ω H 0( j ω) X 0(j ω)ThereforeH d ( j ω)=T1eTj ω H 0( j ω)=e2/jwT TT ωω)2/sin(2 7.8 (a) Yes, aliasing does occur in this case .This may be easily shown by considering the sinusoidal term of x(t) for k=5. This term is a signal of the form y(t)=(1/2)5sin(5πt).If x(t) is sampled as T=0.2, then we will always be sampling y(t) at exactly its zero-crossings (This is similar to the idea presented in Figure 7.17 of your textbook). Therefore ,the signal y(t) appears to be identical to the signal (1/2)5sin(0πt) for frequency 5π is a liased into a sinusoid of frequency 0 in the sampled signal.(b) The lowpass filter performs band limited interpolation on the signal ∧x(t).But since aliasing has alreadyresulted in the loss of the sinusoid (1/2)5sin(5πt),the output will be of the formx γ(t)=k k )21(40∑= sin(k πt)The Fourier series representation of this signal is of the form139x γ(t)=∑-=44k k a e )/(t k j π-Where a k =-j(1/2)1+kj(1/2)1+-k7.9 The Fourier transform X(jWe know from the results on impulse-train sampling thatG(jw)=∑∞∞--ωωk j X T ((1s )),Where T=2π/s ω=1/75.therefore,G(jw) is as shown in Figure S7.9 .Clearly, G(jw)=(1/T)X(j ω)=75 X(j ω) for |ω|≤50π.7.10 (a) We know that x(t) is not a band-limited signal. Therefore, it cannot undergo impulse-train sampling without aliasing.(b) Form the given X(j ω) it is clear that the signal x(t) which is bandlimited. That is, X(j ω)=0 for |ω|>0ω.Therefore, it must be possible to perform impulse-train sampling on this signal without experiencing aliasing. The minimum sampling rate required would bes ω=20ω,This implies that thesampling period can at most be T=2π/s ω=π/0ω(c) When x(t) undergoes impulse train sampling with T=2π/0ω,we would obtain the signal g(t) with Fourier transformG(jw)= T1∑∞-∞=-k T k j X ))/2((πωFigure S7.10It is clear from the figure that no aliasing occurs, and that X(jw) can be recovered by using a filter with frequency response T 0≤ωω≤0 H(jw)= 0 otherwiseTherefore, the given statement is true. 7.11 We know from Section 7.4 thatX d (ωj e )= T1∑∞-∞=-k cT k j X ))/2((πω(a) Since X d (ωj e) is just formed by shifting and summing replicas of X(jw),we may argue that ifX d (ωj e ) is real , then X(jw) must also be real(b) X d (ωj e) consists of replicas of X(jw) which are scaled by 1/T,Therefore,if X d (ωj e) has amaximum of 1, then X(jw) must also be real.(c) The region πωπ≤≤||4/3in the discrete-time domain corresponds to the regionT T /||)4/(3πωπ≤≤ in the discrete-time domain. Therefore ,if X d (ωj e )=0 forπωπ≤≤||4/3,then X(jw)=0 for πωπ2000||1500≤≤,But since we already have X(jw)=0 for140πω2000||≥,we have X(jw)=0 for πω1500||≥(d) In this case, sinceπ in discrete-time frequency domain corresponds to 2000π in the continuous-time frequency domain, this condition translates to X(jw)=(j(ω-2000π))7.12 Form Section 7.4 ,we know that the discrete and continuous-time frequencies Ω and ω are related by Ω=ω.Therefore, in this case for Ω=43π,we find the corresponding value of ω toω=43πT1=3000π/4=7500π7.13 For this problem ,we use an approach similar to the one used in Example 7.2 .we assume thatx c (t)=tT t ππ)/sin(The overall output isy c (t)= x c (t-2T)= )2()]2)(/sin[(T t T t T --ππForm x c (t). We obtain the corresponding discrete-time signal x d [n] to be x d [n]= x c (nT)= T1][n δalso, we obtain from y c (t),the corresponding discrete-time signal y d [n] to be y d [n]= y c (nT) =)2()]2(sin[(--n T n ππWe note that the right-hand side of the above equation is always zero when n ≠2.When n=2 ,wemay evaluate the value of ratio using L ,Hospital ,s rule to be 1/T ,Thereforey d [n]= T1]2[-n δWe conclude that the impulse response of the filter is h d [n]= ]2[-n δ7.14 For this problem ,we use an approach similar to the one used in Example 7.2.We assume that x c (t)= tT t ππ)]/sin[(The overall output isy c (t)=)2(T t x dt d c -=)2/()]2/()/[()/(T t T t T COS T ---πππ-2))2/(()]2/)(/sin[(T t T t T --πππForm x c (t) , we obtain the corresponding discrete-time signal x d [n] to be x d [n]= x c (nT)= T1][n δAlso, we obtain from yc(t),the corresponding discrete-time signal y d [n] to beY d [n]=y c (nT)=)2/1()]2/1(cos[)/(--n T n T πππ- )2/1()]2/1(sin[--n T n ππThe first term in rig πht-hang side of the above equation is always zero because cos[π(n-1/2)]=0, therefore, y d [n]= )2/1()]2/1(sin[--n T n ππWe conclude that the impulse response of the filter is h d [n]= )2/1()]2/1(sin[--n T n ππ7.15. in this problem we are interested in the lowest rate which x[n] may be sampled without the possibility of aliasing, we use the approach used in Example 7.4 to solve this problem. To find the lowest rate at which x[n] may be sampled while avoiding the possibility of aliasing, we must find an N such that (22≥Nπ)73πN ≤7/37.16 Although the signal x 1[n]=2sin(πn/2)/( πn) satisfies the first tow conditions, it does not satisfy the thirdcondition . This is because the Flurries transform X 1(e j ω) of this signal is rectangular pulse which is zero for π/2<|ω|<π/2 We also note that the signal x[n]=4[sin(πn/2)/(πn)]2 satisfies the first tow conditions. Fromour numerous encounters with this signal, we know that its Fourier transform X(e j ω) is given by the periodic141convolution of X 1(e j ω) with itself. Therefore, X(e j ω) will be a triangular function in the range 0≤|ω|≤π. This obviously satisfies the third condition as well. T therefore, the desired signal is x[n]=4[sin(πn/2)/(πn)]2.7.17 In this problem .we wish to determine the effect of decimating the impulse response of the given filter by a factor of 2. As explained in Section 7.5.2 ,the process of decimation may be broken up into two steps. In the first step we perform impulse train sampling on h[n] to obtain H p [n]∑∞-∞=k h[2k]δ[n-2k]The decimated sequence is then obtained using h 1[n]=h[2n]=h p [2n]Using eq (7.37), we obtain the Fourier transform H p (e j ω) of h p [n] to beH 1(e j ω)=H p (e jω/2)In other words , H 1(e j ω) is H p (e j ω/2) expanded by a factor of 2. This is as shown in the figure above. Therefore, h 1[n]=h[2n] is the impulse response of an ideal lowpass filter with a passband gain of unity and a cutoff frequency of π/27.18 From Figure 7.37,it is clear interpolation by a factor of 2 results in the frequency response getting compressed by a factor of 2. Interpolation also results in a magnitude sealing by a factor of 2. Therefore, in this problem, the interpolated impulse response will correspond to an ideal lowpass filter with cutoff frequency π/ and a passband gain of 2.7.19 The Fourier transform of x[n] is given by1 |ω|≤ω1X(e j ω)= 0 otherwiseThis is as shown in Figure 7.19.(a) when ω1 ≤3π/5, the Fourier transform X 1(e j ω) of the output of the zero-insertion system is shown inFigure 7.19. The output w(e j ω) of the lowpass filter is as shown in Figure 7.19. The Fourier transform of theoutput of the decimation system Y(e j ω) is an expanded or stretched out version of W(e j ω). This is as shown in Figure 7.19.therefore, y[n]=51nn πω)3/5sin(1(b) When ω1>3π/5, the Fourier’s transform X 1(e j ω) of the output of the zero-insertion system is as shownin Figure 7.19 The output W(e j ω142The Fourier transform of the output of the decimation system Y(e j ω) bis an expanded or stretched outversion of W(e j ω) .This is as shown in Figure S7.19. Therefore,y[n]=][51n δ7.20 Suppose that X(e j ω) is as shown in Figure S7.20, then the Fourier transform X A (e j ω) of the output of theoutput of S A , the Fourier transform X 1(e j ω) of the output of the lowpass filter , and the Fourier transform X B (e j ω) of the output of S B are all shown in the figures below. Clearly this system accomplishes the filtering task .Figure S7.20(b) Suppose that X(e j ω) is as shown in Figure S7.20 ,then the Fourier transform X B (e j ω) of the output ofS B ,the Fourier transform X 1(e j ω)of the output of the first lowpass filter ,the Fourier transfore X A (e j ω) of theoutput of S A ,the Fourier transform X 2(e j ω) of the output of the first lowpass filter are all shown in the figure below .Clearly this system does not accomplish the filtering task. 7.21(a) The Nyquist rate for the given signal is 2×5000π=10000π. Therefore in order to be able to recover x(t)from x p (t) ,the sampling period must at most be T max =2π/10000π=2×10-4 sec .Since the sampling period used is T=10-4<T max ,x(t) can be recovered from x p (t).(b) The Nyquist rate for the given signal is 2×15000π=30000π. Therefore in order to be able to recover x(t)from x p (t) ,the sampling period must at most be T max =2π/30000π=0.66×10-4 sec .Since the sampling period used is T=10-4>T max , x(t) can not be recovered from x p (t).(c) Here,I m {X(j ω)} is not specified. Therefore, the Nyquist rate for the signal x(t) is indeterminate. Thisimplies that one cannot guarantee that x(t) would be recoverable from x p (t).(d) Since x(t) is real,we may conclude that X(j ω)=0 for |ω|>5000. Therefore the answer to this part isidentical to that of part (a)(e) Since x(t) is real, X(j ω)=0 for |ω|>15000π. Therefore the answer to this part is identical to that of part(b)(f) If X(j ω)=0 for |ω|>ω1,then X(j ω)*X(j ω)=0 for |ω|>2ω1,Therefore in this part X(j ω)=0 for |ω|>7500. The Nyquist rate for this signal is 2×7500π=15000π. Therefore in order to be able to recover x(t) from x p (t) ,the sampling period must at most be T max =2π/15000π=1.33×10-4 sec .Since the sampling period used is T=10-4<T max , x(t) can be recovered from x p (t). (g)If |X(j ω)|=0 for ω>5000π,then X(j ω)=0 for |ω|>5000π. Therefore the answer to this part is identical to that of part (a).7.22 Using the properties of the Fourier transform, we obtain Y(j ω)=X 1(j ω)X 2(j ω).Therefore, Y(j ω)=0 for |ω|>1000π.This implies that the Nyquist rate for y(t) is2×1000π=2000π.Therefore, the sampling period T can at most be 2π/(2000π)=10-3sec. Therefore we have to use T<10-3sec in order to be able to recover y(t) from y p (t). 7.23(a) We may express p(t) asP(t)=p 1(t)-p 1(t-△);Where p 1(t)=∑∞-∞=∆-k k t )2(δnow,143P 1(j ω)=∆π∑∞-∞=∆-k )/(πωδTherefore,P(j ω)= P 1(j ω)-e -j ω∆P 1(j )ωIs as shown in figure S7.23. Now,X p (j ω)=)](*)([21ωωπjP j XTherefore, X p (j ω) is as sketched below for △<π/(2ωM ),The corresponding Y(j ω) is also sketched in figure S7.23.(b) The system which can be used to recover x(t) from x p (t) is as shown in FigureS7.23. (c) The system which can be used to recover x(t) from x(t) is as shown in FigureS7.23.(d) We see from the figures sketched in part (a) that aliasing is avoided when ωM ≤π/△.therefore, △max =π/ωM.7.24 we may impress s(t) as s(t)=s(t)-1,where s(t) is as shown in Figure S7.24 we may easily show thats (j )ω= ∑∞-∞=-∆k T k kT k )/2()/2sin(4πωδπFrom this, we obtainS(j =-=)(2)()ωπδωωj S∑∞-∞=-∆k T k k T k )/2()/2sin(4πωδπ-2)(ωπδ Clearly, S(j ω) consists of impulses spaced every 2π/T.(a) If △=T/3, thenS(j =)ω∑∞-∞=-k T k kk )/2()3/2sin(4πωδπ-2)(ωπδNow, since w(t)=s(t)x(t),πω21)(=j W ∑∞-∞=--k X T k j X kk )(2))/2(()3/2sin(4ωππωπTherefore, W(j ω)consists of replicas of X(j ω) which are spaced 2π/T apart. Tn order to avoid aliasing,ωW should be less that π/T. Therefore, T max =2π/ωW. (b) If △=T/3, then(a)(b)()jw Figure S7.24x144S(j =)ω∑∞-∞=-k T k k k )/2()4/2sin(4πωδπ-2)(ωπδ we note that S(j ω)=0 for k=0,±2, ±4,…..This is as sketched in Figure S7.24.Therefore, the replicas of X(j ω)in W(j ω) are now spaced 4π/T apart. Tn order to avoid aliasing,ωW should be less that2π/T. Therefore, T max =2π/ωW. 7.25 Here, x T (kT) can be written asX T (kT)= ∑∞-∞=--k nT x n k n k )()()](sin[ππNote that when n ≠k,0)()](sin[=--n k n k ππAnd when n=k,1)()](sin[=--n k n k ππ Therefore,x τ(kT)=x(kT)7.26. We note thatp(j ω)=Tπ2δ(ω-k2π/T)Also, since x p (t)=x(t)p(t).X p (j ω)=12π{ x(j ω) * P(j ω)}=1Tx(j(ω-k2π/T))Figure S7.26Note that as T increase, Tπ2-ω2 approaches zero. Also, we note that there is aliasingWhen2ω1-ω2<Tπ2-ω2<ω2If 2ω1-ω2≥0(as given) then it is easy to see that aliasing does not occur when 0≤Tπ2-ω2≤2ω1-ω2For maximum T, we must choose the minimum allowable value for Tπ2-ω2 (which is zero).This implies that T max =2π/ω2. We plot x p (j ω) for this case in Figure S7.26. Therefore, A=T, ωb =2π/T, and ωa =ωb -ω11457.27.(a) Let x 1(j ω) denote the Fourier transform of the signal x 1(t) obtained by multiplyingx(t) with e -j ω0t Let x 2(j ω) be the Fourier transform of the signal x 2(t) obtained at the output of the lowpass filter. Then, x 1(j ω), x 2(j ω),and x p (j ω),are as shown in Figure S7.27(b) The Nyquist rate for the signal x 2(t) is 2×(ω2-ω1)/2=ω2-ω1.Therefore, thep 7.28. (a) The fundamental frequency of x(t) is 20π rad/sec.From Chapter 4 we know that the Fourier transform of x(t) is given byX(j ω)=2πk ∞=-∞∑a k δ(ω-20πk).This is as sketched below. The Fourier transform x c (j ω) of the signal x c (t) is also Sketched in Figure S7.28. Note thatP(j ω)=2510π⨯3(2/(510))k k δωπ∞-=-∞-⨯∑Andx p (j ω)=12π[ x c (j ω)* p(j ω)]Therefore, x p (j ω) is as shown in the Figure S7.28.Note that the impulses from adjacentReplicas of x c (j ω) add up at 200π.Now the Fourier transform x(e j Ω) of the sequence x[n] is given byx(e j Ω)= x p (j ω)|ω=ΩT. This is as shown in the Figure S7.28.Since the impulses in x(e j ω) are located at multiples of a 0.1π,the signal x[n] is146(b) The Fourier series coefficients of X[n] aT π2(12)k , k=0,±1,±2,….,±9 a k =4T π(12)10 , k=10 7.29. x p (j ω)=1T((2/))k x j k T ωπ∞=-∞-∑x(jwe ), Y(jwe ), Y p (j ω),and Y c (j ω) are as shown in Figure S7.29. 7.30. (a) Since x c (t)=δ(t),we have()c dy t dt+y c (t)= δ(t) Taking the Fourier transform we obtainj ωY(j ω)+ Y(j ω)=1 Therefore , Y c (j ω)=11j ω+, and y c (t) =e -t u(t). (b) Since y c (t) =e -tu(t) , y[n]= y c (nT)= e -nT u[n].Therefore, j ωH(e j ω)=()()j W e Y e ω=11/(1)T j e e ω---=1-e -T e -j ωTherefore,h[n]= δ[n]-e -T δ[n -1]7.31. In this problem for the sake of clarity we will use the variable Ωto denote discretefrequency. Taking the Fourier transform of both sides of the given difference equation we obtainH(j e Ω)=()()j j Y e X e ΩΩ=1112j e -Ω-Given that the sampling rate is greater than the Nyquist rate, we have147x(j eΩ)=1Tx c (j Ω/T), for -π≤Ω≤π Therefore,Y(j eΩ)=1(/)12c j x j T T e -ΩΩ-For -π≤Ω≤π.From this we getY(j ω)= Y(jw eT)= =1()12c j Tx j T e ωω--For -π/T ≤ω≤π/T. in this range, Y(j ω)= Y c (j ω).Therefore,H c (j ω)=()()c c Y j X j ωω=1/112j TT e ω--7.32. Let p[n]=[14]k n k δ∞=-∞--∑.Then from Chapter 5,p(jwe )= e -j ω24π(2/4)k k δωπ∞=-∞-∑=2π2/4(2/4)j k k k eπδωπ∞--=-∞∑Therefore, G(jw e )=()1()()2j j p e x e d πθωθπθπ--⎰=32/4(2/4)01()4j k j k k e x e πωπ--=∑jwjwFigure S7.32Clearly, in order to isolate just x(jwe ) we need to use an ideal lowpass filter with Cutoff frequency π/4 and passband gain of 4. Therefore, in the range |ω|<π, 4, |ω|<π/4H(e j ω)= 0, π/4≤|ω|≤π7.33. Let y[n]=x[n][3]k n k δ∞=-∞-∑.ThenY(e j ω)=3(2/3)1()3j k k x eωπ-=∑Note that sin(πn/3)/(πn/3) is the impulse response of an ideal lowpass filter with cutoff frequency π/3 and passband gain of 3.Therefore,we now require that y[n] when passed through this filter should yieldx[n].Therefore, the replicas of x(e j ω) contained in Y(e j ω) should not overlap with one another. This ispossible only if x(e j ω) =0 for π/3≤|ω|≤π.7.34. In order to make x(e j ω) occupy the entire region from -πto π,the signal x[n]148must be downsampled by a factor of 14/3.Since it is not possible to directly downsample by a noninteger factor, we first upsample the signal by a factor of 3. Therefore, after the upsampling we will need toreduce the sampling rate by 14/3× 3=14. Therefore, the overall system for performing the sampling rate conversion isy[n][]2nx ,n=0,±3,±6,… y[n]=p[14n] ω[n]= 0, otherwise Figure S7.34)(e xp)(ωj d e x 7.36. (a) Let us decnote the sampled signaled signal by x p (t). We have∑∞-∞=-=n pnT t nT x t x )()()(δSince the Nyquist rate for the signal x(t) is T /2π,we can reconstruct the signal from x p (t). From Section 7.2,we know that)(*)()(t h t x t x p = whereTt T t t h /)/sin()(ππ=Thereforedtt dh t x dtt dx p )(*)()(=Denoting dtt dh )( by g(t),we have∑∞-∞=-==n pnT t g nT x t g t x dtt dx )()()(*)()(Therefore,2)/sin()/cos()()(tT t T tT t dtt dh t g πππ-==(b) No.7.37. We may write p(t) asp(t)=p 1(t)+p 1(t-∆),where∑∞-∞=-=k W k t t p )/2()(1πδTherefore,)()1()(1ωωωj p e j p j ∆-+= where∑∞-∞=-=k kW w j p )()(1ωδω149Let us denote the product p(t)f(t) by g(t).Then,)()()()()()()(11t f t p t f t p t f t p t g ∆-+== This may be written as)()()(11∆-+=t bp t ap t g Therefore,)(()(1)ωωωj p be a j G j ∆-+= with )(1ωj p is specified in eq.(s7.37-1). Therefore [])()(kw be a w j G k w jk -+=∑∞-∞=∆-ωδωWe now have)()()()(1t f t p t x t y = Therefore,[])(*)(21)(1ωωπωj x j G j Y =This give us[]))((2)(1kW j x be a Wj Y wjk -+=∑∆-ωπωIn the range 0<ω<W, we may specify Y 1(j ω) as[]))(()()()(2)(1W j x be a j x b a w j Y w jk -+++=∆-ωωπωsince )()()(112ωωωj H j Y j Y =, in the range 0<ω<W we may specify Y 2(j ω) as []))(()()()(2)(2W j x be a j x b a jW j Y W j -+++=∆-ωωπωSince ),()()(3t p t x t y =in the range 0<ω<W we may specify Y 3(j ω) as []))(()1()(22)(3W j x e j x W j Y W j -++=∆-ωωπωGive that 0<W △<π,we require that )()()(32ωωωj kx j Y j Y =+ for 0<ω<W. That is[][])())(()1(2)()(2ωωπωπj kx W j x e W j x jb ja a Ww j =-++++∆-This implies that01=+++∆-∆-W j Wj jbe ja e Solving this we obtainA=1, b= -1, When W △=π/2. More generally, we also geta=sin(W △)+)tan())cos(1(∆∆+W W and )sin()cos(1∆∆+-=W W bexcept when 2/π=∆W Finally, we also get [])2/(12jb ja Wk ++=π。
特种加工chap7

第七章超声加工一、课内习题及答案1.超声加工时的进给系统有何特点?答:超声加工时的进给系统是靠重锤通过杠杆使工具轻轻压在工件上,靠轻微的压力使工具端面和磨粒与工件表面接触,工件表面去掉多少、进给多少,是悬浮式的柔性进给系统,而不是刚性的进给系统实现的,它与机械加工和电火花加工的进给系统不一样。
2.一共振频率为25kHz的磁致伸缩型超声清洗器,底面中心点的最大振幅为0.01mm,试计算该点最大速度和最大加速度。
它是重力加速度g的多少倍?如果是共振频率为50kHz的压电陶瓷型超声清洗器,底面中心点的最大振幅为0.005mm,则最大速度和加速度又是多少?答:按教材中超声振动时的最大速度υmax和最大加速度a max计算公式υmax= ωA= 2πfA= 2π×25000×0.01= 1570.8 mm/s = 1.57 m/s,a max= ω2A= 4π2×250002×0.01 = 246.74×106 mm/s2= 246740 m/s2,是地心加速度g =9.8 m/s2的25000倍。
如果共振频率增加为一倍f =50kHz,振幅减小成一半A =0.005mm,则υmax= 1.57×2/2 = 1.57 mm/s,a max= 246740×4/2 = 493480 m/s2,是地心加速度g的50000倍。
3.试判断超声加工时:(1)工具整体在作超声振动;(2)只有工具端面在作超声振动;(3)工具各个横截面都在作超声振动,单个截面同一时间的振幅并不一样;(4)工具各个横截面依次都在作“原地踏步”式的振动。
以上各点,哪种说法最确切?有无更确切的说法?答:以上说法中,(3)比较确切,超声波在工具(变幅杆)内传递时,各个横截面都在作超声振动,单个截面在同一时间的振幅不一样,有的截面振幅始终为零(如固定超声系统的驻波点),有的有时振幅最大,如工具端面的加工点。
chapter7习题答案

第七章习题答案7.1 ARM处理器有几种运行模式,处理器如何区别各种不同的运行模式?ARM处理器有7中运行模式:●用户模式(user):ARM处理器正常的程序执行状态●快速中断模式(fiq):处理高速中断,用于高速数据传输或通道处理●外部中断模式(irq):用于普通的中断处理●管理模式(supervisor):操作系统使用的保护模式,系统复位后的默认模式●中止模式(abort):数据或指令预取中止时进入该模式●未定义模式(undefined):处理未定义指令,用于支持硬件协处理器的软件仿真●系统模式(system):运行特权级的操作系统任务处理器使用CPSR寄存器中的M4~M0位来指示不同的运行模式。
7.2 通用寄存器中PC、CPSR和SPSR的作用各是什么?PC:程序计数器,用于保存处理器要取的下一条指令的地址。
CPSR:当前程序状态寄存器,CPSR保存条件标志位、中断禁止位、当前处理器模式标志,以及其他一些相关的控制和状态位。
SPSR:备份程序状态寄存器,当异常发生时,SPSR用于保存CPSR的当前值,当从异常退出时,可用SPSR来恢复CPSR。
7.3 从编程的角度讲,ARM处理器的工作状态有哪两种?这两种状态之间如何转换?从编程角度讲,ARM处理器的两种工作状态为:●ARM状态(复位状态):处理器执行32位的字对齐的ARM指令●Thumb状态:处理器执行16位的半字对齐的Thumb指令ARM指令集和Thumb指令集均有切换处理器状态的指令,并可在两种工作状态之间切换:●进入Thumb状态:当操作数寄存器的状态位(最低位)为1时,执行BX指令就可以进入Thumb状态。
如果处理器在Thumb状态时发生异常(异常处理要在ARM状态下执行),则当异常处理返回时自动切换到Thumb状态●进入ARM状态:当操作数寄存器的状态位(最低位)位0时,执行BX指令就可以进入ARM状态。
处理器进行异常处理时,把PC的值放入异常模式链接寄存器中,从异常向量地址开始执行程序,系统自动进入ARM状态7.5 哪些特征是ARM和其他RISC体系结构所共有的?ARM和其他RISC体系结构共有的三个相同特征:●Load/Store体系结构:也称为寄存器/寄存器体系结构或RR系统结构。
等级考试chap7_等级考试辅导题

等级考试辅导题一.选择题1.在VFP中,若把表单设置为子表单,应设置的属性即属性值为A.设置ShowWindow属性值为2B.设置ShowWindow属性值为0或1,设置Desktop属性值为.F.C.设置ShowWindow属性值为0或1,设置Desktop属性值为.T.D.设置ShowWindow属性值为2,设置Desktop属性值为.T.2.在运行表单时,下列有关表单事件的引发次序正确的是A.Destroy—Init—Load B. Destroy—Load—InitC. Init—Destroy—LoadD. Load—Init—Destroy3.在下列几组VFP基类中,均具有ControlSource属性的是A. ListBox、Label、OptionButtonB. ComboBox、EditBox、GridC. ComboBox、Grid、TimerD. EditBox、CheckBox、OptionButton4.下列表单的哪个属性设置为真时,表单运行时将自动居中A.AutoCenter B.AlwaysOnTop C.ShowCenter D.FormCenter5.下列控件中,在运行时一定不可见。
A.OptionButton B.Page C.OptionGroup D.Timer6.当用鼠标单击正在运行的表单中一个未被禁用的文本框对象时,文本框发生的三个事件的顺序为。
A.GotFocus—When—Click B. When—GotFocus—ClickC. Click—GotFocus—WhenD. Click—When—GotFocus7.如果ComboBox对象的RowSourceType设置为6,以一个表的字段为行数据源,则_____ A)在数据环境中添加此表,运行时用户从下拉列表中选择数据,将移动此表的记录指针B)在数据环境中添加此表,运行时可使用AddItem方法,对列表增加新项C)在数据环境中不必添加此表,ComboBox会找到表文件D)下拉列表不能使用多列方式8.如果ListBox对象的RowSourceType设置为3,则在RowSource属性中写入的SELECT语句,通常包含_____子句A) GROUP BY B)ORDER BY C)INTO TABLE D)INTO CURSOR9.如果要在列表框中一次选择多个项(行),必须设置_____属性为.t.A)MultiSelect B)ListItem C)Controlsv D)Enabled10.确定列表框内的某个条目是否被选定以及确定第几列数据和Value属性进行绑定,应使用的属性是_______A)selected ColumnCount B)selected BoundColumnC)list ColumnCount D)list BoundColumn11.如果表单中有一命令按钮组,命令按纽组包含若干命令按纽,现设定了命令按纽组的Click事件代码,但没有设定命令按纽的Click事件代码。
chap7中级宏观经济学答案 华中科技大学

Microeconomics, 4e (Perloff)Chapter 7 Costs7.1 Measuring Costs1) Economic costs of an input includeA) only implicit costs.B) only explicit costs.C) both implicit and explicit costs.D) whatever management wishes to report to the shareholders.Answer: CTopic: Measuring Costs2) The cost of waiting two months for health care to address a debilitating problem in Canada is most accurately described asA) an explicit cost.B) an accounting cost.C) no real cost.D) an opportunity cost.Answer: DTopic: Measuring Costs3) Sarah earns $40,000 per year working for a large corporation. She is thinking of quitting this job to work full time in her own business. She will invest her savings of $50,000 (which currently has an annual 10% rate of return) into the business. Her annual opportunity cost of this new business isA) $0.B) $40,000.C) $45,000.D) $90,000.Answer: CTopic: Measuring Costs4) The Nifty Gum Co. has purchased a large parcel of land for $1 million. The company recently discovered that the land is contaminated and is worthless to all possible buyers. The opportunity cost of the land isA) $0.B) $1 million.C) some amount greater than $0 but less than $1 million.D) equal to the cost of the factory that was planned to be built there.Answer: ATopic: Measuring Costs5) Johnny has worked as a CPA for five years and wants to open his own public accounting practice. The cost of his college degree in accounting representsA) the opportunity cost of this endeavor.B) a sunk cost.C) an expense.D) a variable cost.Answer: BTopic: Measuring Costs6) Economists proclaim that competitive firms make zero economic profit in the long run. This shows howA) detached economists are from the real world.B) unrealistic economic theory is.C) firms cover all their cost, both monetary and non-monetary.D) firms cover only monetary cost when economic profits are zero.Answer: CTopic: Measuring Costs7) If a firm buys a building so as to have office space for its workers, the monthly opportunity cost of the building is best measured asA) the monthly mortgage payment the firm must pay.B) the price the firm paid divided by twelve.C) zero.D) the rent the firm could earn if it rented the building to another firm.Answer: DTopic: Measuring CostsFor the following, please answer "True" or "False" and explain why.8) When buying a piece of equipment, it is always best for the firm to pay cash instead of borrowing the funds since this renders the equipment less costly.Answer: False. It depends. The opportunity cost of the capital when paying cash is the interest the firm receives on its cash reserves. This is an implicit cost. The opportunity cost of the capital when the funds are borrowed is the interest the firm must pay to the lender. This is an explicit cost. If the rate the firm receives on its cash reserves exceeds the rate at which it borrows, the firm is better off borrowing the funds to buy the equipment.Topic: Measuring Costs9) Four years after graduating from college you must decide if you want to go on as an accountant (your college major) or if you want to make a career change and become a singer. The cost of your education will matter for your decision.Answer: False. At this point the cost of your education represents a sunk cost and therefore should not figure into your decision. You incur it no matter what decision you make.Topic: Measuring Costs10) An accountant may amortize the expense of a durable good by dividing the total amount spent on the good by the number of years the good is expected to last. An economist may amortize the expense of a durable and never fully account for the total expense.Answer: True. The accountant uses a set of predetermined rules to amortize the total expense of the good. The economist amortizes based on the opportunity cost of the good, which may never sum to the total expense of the good.Topic: Measuring Costs11) Your company makes copper pipes. Over the years, you have collected a large inventory of raw copper. The production process involves melting the copper and shaping it into pipes. You also have a large stockpile of pennies. Suppose the price of copper rises so much that the copper in the penny becomes worth more than one cent. Should you melt down your pennies?Answer: This problem appeared as a puzzle in the Journal of Economic Perspectives (Winter, 1988). It is true (in this problem) that the pennies when melted currently have a value greater than one cent. Yet, the price of copper can fluctuate. If the price of copper stays high, it does not matter if you melt pennies or not. However, if the price of copper falls so that the value of the copper in the penny falls below one cent, your unmelted pennies are still worth one cent. Your melted pennies would be worth less than one cent. Thus, as long as you have some other source of copper, you are better off melting that copper and not the pennies.Topic: Measuring Costs12) You have two career options. You can work for someone else for $50,000 a year, or, you can run your own business, with an annual revenue of $100,000, and explicit costs of $40,000 annually. Explain which career option a profit-maximizer would select and why.Answer: In the absence of other implicit costs a profit-maximizer will run their own business. The business owner will receive $100,000 - $40,000 = $60,000. The opportunity cost is only $50,000.Topic: Measuring Costs7.2 Short-Run Costs1) A firm's marginal cost can always be thought of as the change in total cost ifA) the firm produces one more unit of output.B) the firm buys one more unit of capital.C) the firm's average cost increases by $1.D) the firm moves to the next highest isoquant.Answer: ATopic: Short-run Costs2) Fixed costs areA) a production expense that does not vary with output.B) a production expense that changes with the quantity of output produced.C) equal to total cost divided by the units of output produced.D) the amount by which a firm's cost changes if the firm produces one more unit of output.Answer: ATopic: Short-run Costs3) Variable costs areA) a production expense that does not vary with output.B) a production expense that changes with the quantity of output produced.C) equal to total cost divided by the units of output produced.D) the amount by which a firm's cost changes if the firm produces one more unit of output.Answer: BTopic: Short-run Costs4) Which of the following statements is NOT true?A) AC = AFC + AVCB) C = F + VCC) AVC = wage/MP LD) AFC = AC - AVCAnswer: CTopic: Short-run Costs5) Joey's Lawncutting Service rents office space from Joey's dad for $300 per month. Joey's dad is thinking of increasing the rent to $400 per month. As a result Joey's marginal cost of cutting grass willA) increase by $100 divided by the amount of grass cut.B) increase by $100.C) decrease by $100.D) not change.Answer: DTopic: Short-run Costs6) Suppose a firm can only vary the quantity of labor hired in the short run. An increase in the cost of capital willA) increase the firm's marginal cost.B) decrease the firm's marginal cost.C) have no effect on the firm's marginal cost.D) More information is needed to answer the question.Answer: CTopic: Short-run Costs7) Suppose the total cost of producing T-shirts can be represented as TC = 50 + 2q. The marginal cost of the 5th T-shirt isA) 2.B) 10.C) 12.D) 60.Answer: ATopic: Short-run Costs8) Suppose the total cost of producing T-shirts can be represented as TC = 50 + 2q. The average cost of the 5th T-shirt isA) 2.B) 12.C) 52.D) 60.Answer: BTopic: Short-run Costs9) Suppose the total cost of producing T-shirts can be represented as TC = 50 + 2q. Which of the following statements is TRUE at all levels of production?A) MC = AVCB) MC = ACC) MC > AFCD) All of the above.Answer: ATopic: Short-run Costs10) Suppose the short-run production function is q = 10 * L. If the wage rate is $10 per unit of labor, then AVC equalsA) q.B) q/10.C) 10/q.D) 1.Answer: DTopic: Short-run Costs11) Suppose the short-run production function is q = 10 * L. If the wage rate is $10 per unit of labor, then MC equalsA) q.B) q/10.C) 10/q.D) 1.Answer: DTopic: Short-run Costs12) If average cost is decreasingA) Marginal cost equals average cost.B) Marginal cost exceeds average cost.C) Marginal cost is less average cost.D) Not enough informationAnswer: CTopic: Short-run Costs13) If average cost is positiveA) Marginal cost equals average cost.B) Marginal cost exceeds average cost.C) Marginal cost is less average cost.D) Not enough informationAnswer: DTopic: Short-run Costs14) Suppose the short-run production function is q = L0.5. If the marginal cost of producing the tenth unit is $5, what is the wage per unit of labor?A) $1B) $0.5C) $0.25D) It cannot be determined without more information.Answer: CTopic: Short-run Costs15) Suppose the short-run production function is q = 10 * L. If the wage rate is $10 per unit of labor, then AFC equalsA) 0.B) 1.C) 10/q.D) It cannot be determined from the information provided.Answer: DTopic: Short-run Costs16) When a firm produces one unit, the variable cost is $3. When the firm produces two units, the variable cost is $6. What is the marginal cost associated with two units of production?A) $2B) $0.5C) $6D) $3Answer: DTopic: Short-run Costs17) In the short run, the point at which diminishing marginal returns to labor begin is the point at which the marginal cost curveA) peaks.B) bottoms out.C) is upward sloping.D) is downward sloping.Answer: BTopic: Short-run Costs18) If the marginal cost of producing a good is increasing as a firm produces more of the good, then which of the following must be TRUE?A) AFC is rising.B) AVC is rising.C) MC > AVC.D) MPL is falling.Answer: DTopic: Short-run Costs19) If the average cost of producing a good is increasing as a firm produces more of the good, then which of the following must be TRUE?A) AFC is falling.B) AVC is rising.C) MC > AVC.D) All of the above.Answer: DTopic: Short-run Costs20) If a particular production process is subject to diminishing marginal returns to labor at every level of output, then at every level of outputA) AC is upward sloping.B) MC exceeds AVC.C) AFC is constant.D) All of the above.Answer: BTopic: Short-run Costs21) Marginal Cost is equal toA) the increase in total cost from increasing the amount of labor by one unit.B) the increase in average cost from increasing the amount of labor by one unit.C) Both A and B.D) Neither A nor B.Answer: CTopic: Short-run Costs22) Suppose each worker must use only one shovel to dig a trench, and shovels are useless by themselves. In the short run, an increase in the price of shovels will result inA) fewer shovels being purchased.B) more workers being hired.C) a decrease in the firm's output.D) no change in the firm's output.Answer: DTopic: Short-run Costs23) Which of the following will cause the marginal cost curve of making cigarettes to shift?A) A $5 million penalty charged to each cigarette maker.B) A $1 per pack tax on cigarettes.C) A $1 million advertising campaign by the American Cancer Society.D) All of the above.Answer: BTopic: Short-run Costs24) Which of the following will cause the average cost curve of making cigarettes to shift?A) A $5 million penalty charged to each cigarette maker.B) A $1 per pack tax on cigarettes.C) A $1 an hour wage increase paid to all cigarette production workers.D) All of the above.Answer: DTopic: Short-run Costs25) Which of the following will cause the average fixed cost curve of making cigarettes to shift?A) A $5 million penalty charged to each cigarette maker.B) A $1 per pack tax on cigarettes.C) A $3 per hour wage increase.D) An increase in the demand for cigarettes.Answer: ATopic: Short-run Costs26) A specific tax of $1 per unit of output will affect a firm'sA) average total cost, average variable cost, average fixed cost, and marginal cost.B) average total cost, average variable cost, and average fixed cost.C) average total cost, average variable cost, and marginal cost.D) marginal cost only.Answer: CTopic: Short-run CostsFor the following, please answer "True" or "False" and explain why.27) The "Law of Diminishing Marginal Returns" could also be termed the "Law of Increasing Marginal Costs."Answer: True. Since MC = w/MP L in the short run, the fact that MPL eventually declines means that MC must eventually increase.Topic: Short-run Costs28) The marginal cost curve intersects the average fixed cost curve at its minimum.Answer: False. Marginal cost intersects average variable cost (and average cost) at its minimum.Topic: Short-run Costs29) A consumer purchases a book by driving across town to a bookstore, standing in line for five minutes to pay the cashier, and then pays $5. The same book is purchased by another consumer who spends 2 minutes placing the order over the internet for $10. The book necessarily cost the first consumer less.Answer: False. The opportunity cost of driving across town and standing in line may have raised the total cost of the book to the first consumer to more than $10.Topic: Short-run Costs30) A firm's production function for pretzels is shown in the above figure. If the firm's fixed cost equals $100 per time period and the wage rate equals $1 per unit of labor per time period, calculate the firm's MC, AVC, and AC schedules. Do these cost functions follow the general rules concerning the relationships between MC, AVC and AC?Answer:❑✌☞ ✌✞✌ MC > AVC, AVC is rising.MC < AC, AC is falling.Topic: Short-run Costs31) Explain why the marginal cost curve intersects a U-shaped average cost curve at its minimum point. Answer: At low quantities, the average cost curve declines as the quantity increases. The marginal cost is below the average cost. The marginal cost represents the cost of an additional unit of production. Thus, as the marginal cost curve declines, this pulls the average cost down from its previous level. Then, the marginal cost curve will begin to rise. However, the marginal cost is still below the average cost, which will continue to lower the average cost. When the two costs are equal the marginal cost will leave the average cost unchanged. Then, the marginal cost will be above the average cost so it will start to pull up the average cost. Thus, the marginal cost curve will intersect the average cost curve at its minimum point.Topic: Short-run Costs7.3 Long-Run Costs1) In the long run, fixed costs areA) sunk.B) avoidable.C) larger than in the short run.D) not included in production decisions.Answer: BTopic: Long-run Costs2) The slope of the isocost line tells the firm how muchA) capital must be reduced to keep total cost constant when hiring one more unit of labor.B) capital must be increased to keep total cost constant when hiring one more unit of labor.C) more expensive a unit of capital costs relative a unit of labor.D) the isocost curve will shift outward if the firm wishes to produce more.Answer: ATopic: Long-run Costs3) Which of the following does NOT represent a possible shape of the long-run average cost curve?A) downward-slopingB) upward-slopingC) U-shapedD) verticalAnswer: DTopic: Long-run Costs4) The slope of the isoquant tells the firm how muchA) output increases when labor increases by one unit.B) output increases when capital and labor are doubled.C) capital must decrease to keep output constant when labor increases by one unit.D) a unit of capital costs relative to the cost of labor.Answer: CTopic: Long-run Costs5) If an isocost line crosses the isoquant twice, a cost minimizing firm willA) use a different isocost line to select the bundle of inputs.B) use the input bundle associated with the intersection on the higher point of the isoquant.C) use the input bundle associated with the intersection on the lower point of the isoquant.D) Both B and C.Answer: ATopic: Long-run Costs6) When the isocost line is tangent to the isoquant, thenA) MRTS = w/r.B) the firm is producing that level of output at minimum cost.C) the last dollar spent on capital yields as much extra output as the last dollar spent on labor.D) All of the above.Answer: DTopic: Long-run Costs7) A firm can minimize cost byA) picking the bundle of inputs where the lowest isocost line touches the isoquant.B) picking the bundle of inputs where the isoquant is tangent to the isocost line.C) picking the bundle of inputs where the last dollar spent on one input gives as much extra output as the last dollar spent on any other input.D) All of the above.Answer: DTopic: Long-run Costs8) When the isocost line is tangent to the isoquant, thenA) MPL = MPK.B) the firm is producing that level of output at minimum cost.C) the firm has achieved the right economies of scale.D) All of the above.Answer: BTopic: Long-run Costs9) If the wage in increases the isocost line willA) stay the same.B) shift outward in parallel fashion.C) rotate inward around the point where only capital is employed in production.D) shift inward in parallel fashion.Answer: CTopic: Long-run Costs10) If the isoquants are straight lines or L-shaped, then a cost-minimizing firm willA) not be able to minimize costs.B) find the lowest isocost line touching the relevant isoquant.C) find the highest isocost line touching the relevant isoquant.D) choose not to produce any output.Answer: BTopic: Long-run Costs11) If the marginal rate of technical substitution for a cost minimizing firm is 10, and the wage rate for labor is $5, what is the rental rate for capital in dollars?A) .5B) 1C) 2D) 10Answer: ATopic: Long-run Costs12) Suppose MPL = 0.5 * (q/L) and MPK = 0.5 * (q/K). In the long run, the firm will hire equal amounts of capital and laborA) all of the time.B) only when w = r.C) only when w = 0.5 * r.D) at no point in time.Answer: BTopic: Long-run Costs13) Suppose that each worker must use only one shovel to dig a trench, and shovels are useless by themselves. In the long run, an increase in the price of shovels will result inA) fewer shovels being purchased to produce the same number of trenches.B) more workers being hired to produce the same number of trenches.C) the firm wishing to produce more trenches.D) no change in the firm's input mix.Answer: DTopic: Long-run Costs14) Suppose that each worker must use only one shovel to dig a trench, and shovels are useless by themselves. In the long run, the firm will experienceA) increasing returns to scale.B) constant returns to scale.C) decreasing returns to scale.D) The returns to scale cannot be determined from the information provided.Answer: BTopic: Long-run Costs15) Suppose that each worker must use only one shovel to dig a trench, and shovels are useless by themselves. In the long run, the firm's cost function isA) TC = (w/r) * q.B) TC = (w + r)/q.C) TC = (w + r).D) TC = (w + r) * q.Answer: DTopic: Long-run Costs16) At the XYZ Co., a unit of capital costs 3 times as much as a unit of labor. If the isoquants are convex, and the firm does not change its input mix in the long run, we can conclude thatA) MPK = 3 * MP L.B) the firm will not hire any capital.C) the firm will hire 3 times as much labor as capital.D) the firm will hire 3 times as much capital as labor.Answer: ATopic: Long-run Costs17) The production of cigarettes is highly automated; however, a worker is required to monitor each machine. Machines and workers do not interact with one another. Given this information, there are most likelyA) economies of scale.B) economies of scope.C) constant returns to scale.D) increasing returns to scale.Answer: CTopic: Long-run Costs18) Suppose that capital and labor must be kept in a fixed proportion to produce a particular good. For example, digging a trench requires one worker who has one shovel. What does this imply about returns to scale?A) There are constant returns to scale.B) There are increasing returns to scale.C) There are decreasing returns to scale.D) Nothing.Answer: ATopic: Long-run Costs19) A change in relative factor prices will always result inA) a change in the slope of the isoquants.B) a tangency between the new isocost line and a new isoquant.C) a rotation of the isocost lines.D) All of the above.Answer: CTopic: Long-run Costs20) Assuming that w and r are both positive, if the long-run expansion path is horizontal, thenA) MP K = 0.B) MRTS is a function of capital only.C) w = r.D) All of the above.Answer: BTopic: Long-run Costs21) The above figure shows the long-run expansion path. The long-run average cost curve will beA) horizontal.B) downward sloping.C) upward sloping.D) vertical.Answer: BTopic: Long-run Costs22) The long run average cost curve may initially slope downward due toA) decreasing average fixed costs.B) increasing marginal returns.C) economies of scale.D) All of the above.Answer: CTopic: Long-run Costs23) If a production function is represented as q = LαKβ, the long-run average cost curve will be horizontal as long asA) a + b = 0.B) a + b = 1.C) q > 0.D) L = K.Answer: BTopic: Long-run Costs24) If there are diseconomies of scale within a given range of output, which of following is(are) TRUE?A) The short-run average cost curve must be upward sloping within that range of output.B) The long-run average cost curve must be upward sloping within that range of output.C) Long-run average cost must equal short-run average cost.D) All of the above.Answer: BTopic: Long-run Costs25) The total cost of producing one unit is $50. The total cost of producing two units is $75. At a production level of two units, the cost function exhibitsA) economies of scale.B) rising average costs.C) increasing marginal costs.D) constant returns to scale.Answer: ATopic: Long-run CostsFor the following, please answer "True" or "False" and explain why.26) If increasing returns to scale are present, the long-run average cost increases as more output is produced. Answer: False. Increasing returns to scale imply that with a doubling of inputs, output more than doubles. Since average cost is the ratio of total cost divided by output, this increase in inputs will cause the numerator to be just double the old value while the new denominator is more than double the old value. As a result, long-run average cost falls as more output is produced.Topic: Long-run Costs27) Economies of scale and Increasing Returns to Scale are the same thing looked at from either the production or cost perspective.Answer: False. Increasing returns to scale imply economies of scale but the reverse is not true. A firm can experience economies of scale for other reasons (without increasing returns to scale)Topic: Long-run Costs28) Explain the difference between fixed costs in the short run and fixed costs in the long run.Answer: In the short run fixed costs are sunk; in the long run, fixed costs are avoidable.Topic: Long-run Costs29) What are the functions for MC and AC if TC = 100q + 100q2? Are the returns to scale increasing, decreasing, or constant?Answer: MC = 100 + 200qAC = 100 + 100qSince AC increases with an increase in output, there are decreasing returns to scale.Topic: Long-run Costs30) Explain how a firm can have constant returns to scale in production and economies of scale in cost. Answer: A firm can have constant returns to scale in production at every output level. If the firm doubled all inputs the output would double. However, the firm may have a decreasing average cost. As more inputs areused and output increases, the average cost declines, which is known as economies of scale.Topic: Long-run Costs31) Explain why the long-run total cost curve, not the short-run total cost curve, shows the lowest cost of producing any level of output. Is there an exception?Answer: In the long run, all costs are variable so the firm can select the least-cost mix of all inputs to produce any given quantity. The exception would be at minimum long-run cost where min. LR and min. SR costs are equal.Topic: Long-run Costs32) A local non-profit group prints a weekly newsletter. Professional typists earn $10 per hour and can type 2 pages per hour. Unpaid volunteers can type only 1 page per hour. Measuring hours of professional typist services on the vertical axis and hours of unpaid volunteer typist services on the horizontal axis, draw the relevant isoquant and isocost curves if the newsletter is 10 pages long. What input mix is chosen by the non-profit group if they wish to minimize the cost of the newsletter? If the group will reimburse volunteers for expenses (lunch, driving), how much must the reimbursement be for your answer to change? Answer:See the above figure. The isoquant is a straight line with a slope of 1/2. The group can use either 5 pros, 10 volunteers, or some combination of the two. The isocost curves are horizontal since volunteers are free. As a result, the lowest isocost curve is achieved by hiring all volunteers. If the group reimbursed volunteers for expenses (lunch, driving, etc.) then the group will still hire all volunteers as long as they do not cost more than $5 per hour.Topic: Long-run Costs33) A firm pays $5 for each unit of capital. Labor costs $5 per hour for the first 10 hours and $10 per hour for every hour thereafter. Draw the isocost curves for total costs of $50 and $100.Answer:See the above figure.Topic: Long-run Costs34) To dig a trench, each worker needs a shovel. Workers can use only one shovel at a time. Workers without shovels do nothing, and shovels cannot operate on their own. Graphically determine the number of shovels and workers used by a firm to dig 2 trenches when:(a) w = 10 and r = 10(b) w = 10 and r = 5Answer:See the above figure. Because the production process requires fixed proportions of K and L, the firm cannot change input mix when the relative factor costs change.Topic: Long-run Costs35) Suppose the production function is q = 12 L0.25K0.75. Determine the long-run capital-to-labor ratio (K/L) if the cost a unit of capital (r) is three times the cost of a unit of labor (w).Answer: The firm minimizes costs by setting MRTS = w/r. MRTS = MP L/MP K = K/3L = 1/3 = w/r. This firm will set K/L equal to one.Topic: Long-run Costs36) "If the wage rate paid to one form of labor is twice the cost of another form of labor, the first type of labor must be twice as productive." Comment.Answer: This is true. Firms minimize cost by setting the ratio of marginal productivity per unit cost equally across all inputs. If one form of labor is twice as expensive as another, the firm will want the MP of the first type of labor to be twice that of the second.Topic: Long-run Costs。
Principles of Corporate Finance 英文第十版习题解答Chap007

CHAPTER 7Introduction to Risk and ReturnAnswers to Problem Sets1. Expected payoff is $100 and expected return is zero. Variance is 20,000 (%squared) and standard deviation is 141%.2. a. Standard deviation = 19.3%b. Average real return = -2.2%3. Ms. Sauros had a slightly higher average return (14.6% vs. 14.4% for the market).However, the fund also had a higher standard deviation (13.6% vs. 9.4% for themarket).4. a. Falseb. Truec. Falsed. Falsee. Falsef. Trueg. Trueh. False5. d6.7. a. 26% b. zero c. .75d. L ess than 1.0 (the portfolio’s risk is the same as the market, but some ofthis risk is unique risk).8. 1.3 (Diversification does not affect market risk.) 9. A, 1.0; B, 2.0; C, 1.5; D, 0; E, 21.0 10.Recall from Chapter 4 that:(1 + r nominal ) = (1 + r real ) ⨯ (1 + inflation rate)Therefore:r real = [(1 + r nominal )/(1 + inflation rate)] – 1a.The real return on the stock market in each year was: 1929: -14.7% 1930: -23.7% 1931: -38.0% 1932: 0.5% 1933:56.5%b. From the results for Part (a), the average real return was: -3.89%c.The risk premium for each year was: 1929: -19.3% 1930: -30.7% 1931: -45.0% 1932: -10.9% 1933:57.0%d. From the results for Part (c), the average risk premium was: –9.78%e.The standard deviation (σ) of the risk premium is calculated as follows:[22220.0978))0.450(0978))0 0.307(0.0978))0.193(151σ---+---+---⨯⎪⎪⎭⎫ ⎝⎛-=(.((0.1557390.0978))(0.5700.0978))0.109(22=--+---+]((39.46%0.3946370.155739σ===11.a.A long-term United States government bond is always absolutely safe in terms of the dollars received. However, the price of the bond fluctuates as interest rates change and the rate at which coupon payments received can be invested also changes as interest rates change. And, of course, the payments are all in nominal dollars, so inflation risk must also be considered.b.It is true that stocks offer higher long-run rates of return than do bonds, but it is also true that stocks have a higher standard deviation of return. So, which investment is preferable depends on the amount of risk one iswilling to tolerate. This is a complicated issue and depends on numerous factors, one of which is the investment time horizon. If the investor has a short time horizon, then stocks are generally not preferred.c. Unfortunately, 10 years is not generally considered a sufficient amount of time for estimating average rates of return. Thus, using a 10-year average is likely to be misleading.12.The risk to Hippique shareholders depends on the market risk, or beta, of the investment in the black stallion. The information given in the problem suggests that the horse has very high unique risk, but we have no information regarding the horse’s market risk. So, the best estimate is that t his horse has a market risk about equal to that of other racehorses, and thus this investment is not a particularly risky one for Hippique shareholders.13.In the context of a well-diversified portfolio, the only risk characteristic of a single security that matters is the security’s contribution to the overall portfolio risk. This contribution is measured by beta. Lonesome Gulch is the safer investment for a diversified investor because its beta (+0.10) is lower than the beta ofAmalgamated Copper (+0.66). For a diversified investor, the standard deviations are irrelevant. 14.x I = 0.60 σI = 0.10 x J = 0.40 σJ = 0.20a.1ρIJ =)]σσρx 2(x σx σx [σJ I IJ J I 2J 2J 2I 2I 2p ++=b.c. 15.a.Refer to Figure 7.13 in the text. With 100 securities, the box is 100 by 100. The variance terms are the diagonal terms, and thus there are 100variance terms. The rest are the covariance terms. Because the box has (100 times 100) terms altogether, the number of covariance terms is:1002 – 100 = 9,900Half of these terms (i.e., 4,950) are different.b.Once again, it is easiest to think of this in terms of Figure 7.13. With 50 stocks, all with the same standard deviation (0.30), the same weight in the portfolio (0.02), and all pairs having the same correlation coefficient (0.40), the portfolio variance is:σ2 = 50(0.02)2(0.30)2 + [(50)2 – 50](0.02)2(0.40)(0.30)2 =0.03708 σ = 0.193 = 19.3%c.For a fully diversified portfolio, portfolio variance equals the average covariance:σ2 = (0.30)(0.30)(0.40) = 0.036 σ = 0.190 = 19.0%16.a.Refer to Figure 7.13 in the text. For each different portfolio, the relative weight of each share is [one divided by the number of shares (n) in the portfolio], the standard deviation of each share is 0.40, and the correlation between pairs is 0.30. Thus, for each portfolio, the diagonal terms are the same, and the off-diagonal terms are the same. There are n diagonal terms and (n 2 – n) off-diagonal terms. In general, we have:Variance = n(1/n)2(0.4)2 + (n 2 – n)(1/n)2(0.3)(0.4)(0.4)0.0196]0)(0.20)40)(1)(0.12(0.60)(0.(0.20)0.40)((0.10)(0.60)[2222=++=0ρij=0.0148])0.10)(0.2040)(0.50)(2(0.60)(0.(0.20)0.40)((0.10)(0.60)[2222=++=0.50ρIJ =0.0100]0)(0.20)40)(0)(0.12(0.60)(0.(0.20)0.40)((0.10)(0.60)[2222=++=)]σσρx 2(x σx σx [σJ I IJ J I 2J 2J 2I 2I 2p ++=)]σσρx 2(x σx σx [σJ I IJ J I 2J 2J 2I 2I 2p ++=For one share: Variance = 1(1)2(0.4)2 + 0 = 0.160000For two shares:Variance = 2(0.5)2(0.4)2 + 2(0.5)2(0.3)(0.4)(0.4) = 0.104000 The results are summarized in the second and third columns of thetable below.b. (Graphs are on the next page.) The underlying market risk that can not bediversified away is the second term in the formula for variance above:Underlying market risk = (n2 - n)(1/n)2(0.3)(0.4)(0.4)As n increases, [(n2 - n)(1/n)2] = [(n-1)/n] becomes close to 1, so that theunderlying market risk is: [(0.3)(0.4)(0.4)] = 0.048c. This is the same as Part (a), except that all of the off-diagonal terms arenow equal to zero. The results are summarized in the fourth and fifthcolumns of the table below.(Part a) (Part a) (Part c) (Part c)No. of Standard StandardShares Variance Deviation Variance Deviation1 .160000 .400 .160000 .4002 .104000 .322 .080000 .2833 .085333 .292 .053333 .2314 .076000 .276 .040000 .2005 .070400 .265 .032000 .1796 .066667 .258 .026667 .1637 .064000 .253 .022857 .1518 .062000 .249 .020000 .1419 .060444 .246 .017778 .13310 .059200 .243 .016000 .126Graphs for Part (a):Graphs for Part (c):17. The table below uses the format of Figure 7.13 in the text in order to calculate theportfolio variance. The portfolio variance is the sum of all the entries in the matrix. Portfolio variance equals: 0.03664355518.“Safest” means lowest risk; in a portfolio context, thi s means lowest variance of return. Half of the portfolio is invested in Canadian Pacific stock, and half of the portfolio must be invested in one of the other securities listed. Thus, we calculate the portfolio variance for seven different portfolios to see which is the lowest. The safest attainable portfolio is comprised of Canadian Pacific and Nestle.19.⨯ change inchange is +1.25%.b. “Safest” implies lowest risk. Assuming the well-diversified portfolio isinvested in typical securities, the portfolio beta is approximately one. Thelargest reduction in beta is achieved by investing the $20,000 in a stockwith a negative beta. Answer (iii) is correct.20. Expected portfolio return = x A E[R A ] + x B E[R B ] = 12% = 0.12Let x B = (1 – x A )x A (0.10) + (1 – x A) (0.15) = 0.12 ⇒ x A = 0.60 and x B = 1 – x A = 0.40Portfolio variance = x A2σA2 + x B2σB2 +2(x A x B ρAB σA σB )= (0.60 2 ) (20 2 ) + (0.40 2 ) (40 2 ) + 2(0.60)(0.40)(0.50)(20)(40) = 592 Standard deviation = 24.33%592σ==21. a. In general:Portfolio variance = σP2 = x12σ12 + x22σ22 + 2x1x2ρ12σ1σ2Thus:σP2 = (0.52)(30.92)+(0.52)(17.22)+2(0.5)(0.5)(0.31)(30.9)(17.2)σP2 = 395.942Standard deviation = σP = 19.88%b. We can think of this in terms of Figure 7.13 in the text, with threesecurities. One of these securities, T-bills, has zero risk and, hence, zerostandard deviation. Thus:σP2 = (1/3)2(30.92)+(1/3)2(17.22)+2(1/3)(1/3)(0.31)(30.9)(17.2)σP2 = 175.574Standard deviation = σP = 13.25%Another way to think of this portfolio is that it is comprised of one-thirdT-Bills and two-thirds a portfolio which is half Dell and half McDonalds.Because the risk of T-bills is zero, the portfolio standard deviation is two-thirds of the standard deviation computed in Part (a) above:Standard deviation = (2/3)(19.88) = 13.25%c. With 50% margin, the investor invests twice as much money in theportfolio as he had to begin with. Thus, the risk is twice that found in Part(a) when the investor is investing only his own money:Standard deviation = 2 ⨯ 19.88% = 39.76%d. With 100 stocks, the portfolio is well diversified, and hence the portfoliostandard deviation depends almost entirely on the average covariance ofthe securities in the portfolio (measured by beta) and on the standarddeviation of the market portfolio. Thus, for a portfolio made up of 100stocks, each with beta = 1.41, the portfolio standard deviation isapproximately: 1.41 ⨯ 15% = 21.15%For stocks like McDonalds, it is: 0.77 ⨯ 15% = 11.55%22. For a two-security portfolio, the formula for portfolio risk is:Portfolio variance = x12σ12 + x22σ22 + 2x1x2ρρ12σ1σ2If security one is Treasury bills and security two is the market portfolio, then σ1 is zero, σ2 is 20%. Therefore:Portfolio variance = x22σ22 = x22(0.20)2Standard deviation = 0.20x2Portfolio expected return = x1(0.06) + x2(0.06 + 0.85)Portfolio expected return = 0.06x1 + 0.145x2Portfolio X1X2ExpectedReturnStandardDeviation1 1.0 0.0 0.060 0.0002 0.8 0.2 0.077 0.0403 0.6 0.4 0.094 0.0804 0.4 0.6 0.111 0.1205 0.2 0.8 0.128 0.1606 0.0 1.0 0.145 0.20023. The matrix below displays the variance for each of the eight stocks along thediagonal and each of the covariances in the off-diagonal cells:The covariance of BP with the market portfolio (σBP, Market) is the mean of the eight respective covariances between BP and each of the eight stocks in the portfolio. (The covariance of BP with itself is the variance of BP.) Therefore, σBP, Market is equal to the average of the eight covariances in the first row or, equivalently, the average of the eight covariances in the first column. Beta for BP is equal to the covariance divided by the market variance, which we calculated at 0.03664 in problem 17. The covariances and betas are displayed in the table below:。
chap7 矿物的形态

(2) 放射状集合体(radiated aggregate):
由长柱状、针状、片状或板状的许多单体围绕某一中心成放射 状排列而成。 如红柱石。
(3) 晶簇(druse):
指在岩石的空洞或裂隙中、丛生于同一基底、另一端朝向自由 空间发育而具完好晶形的簇状单晶体群。 如石英晶簇、方解石晶簇、辉锑矿晶簇等。 几何淘汰率:晶簇中,晶习具一向延长的单晶体往往最终发育 成与基底近于垂直的、大致平行排列的梳状晶簇(comb)。
三向等长型:
粒状或等轴状。 如:黄铁矿、石榴子石和橄榄石等。 过渡类型:短柱状、板柱状、板条状和厚板状等。
晶体习性
板 状 / 片 状 两 向 延 展
柱 状 / 棒 状 / 针 状
一 向 延 长
三向等长 粒状
晶体形态发育的内因
1)化学成分简单,结构对称程度高的晶体,一般呈等轴状。 如自然金(Au)和石盐(NaCl)等。 2)实际晶体往往沿其内部结构中化学键强的方向发育。 如金红石、辉石和角闪石等链状结构的矿物呈现柱状、 针状晶习,而云母、石墨等层状结构的矿物则呈片状、鳞 片状习性。 3)晶体上发育的晶面都是对应于晶格中面网密度较大的面网。 一般地,面网密度较大的晶面具有较小的比表面能,晶 体的晶面发育总是趋向于使总的表面能最小。
纤维状集合体(直闪石石棉)
放射状集合体(红柱石) 水晶 晶簇
晶簇
晶洞中的石英晶簇
(2) 矿物隐晶集合体和胶体的形态
1、隐晶集合体(cryptocrystalline aggregate):
只有在显微镜的高倍镜下才可分辨矿物单体的集合体称为隐晶集合体。
2、胶态集合体(colloidal aggregate):
本章思考题
1. 实际晶体和理想晶体在外形上有何不同? 2. 结晶习性的含义? 3. 晶面花纹与双晶纹相同吗?晶面条纹在矿物对称性 研究中的意义? 4. 为什么鲕状集合体不能称为粒状集合体? 5. 如何判断集合体中的单体形态? 6. 钟乳石是单体还是集合体?为什么? 7. 几种特殊的胶体/隐晶集合体形态的形成机理?
经济学原理曼昆课后答案chapter7.doc
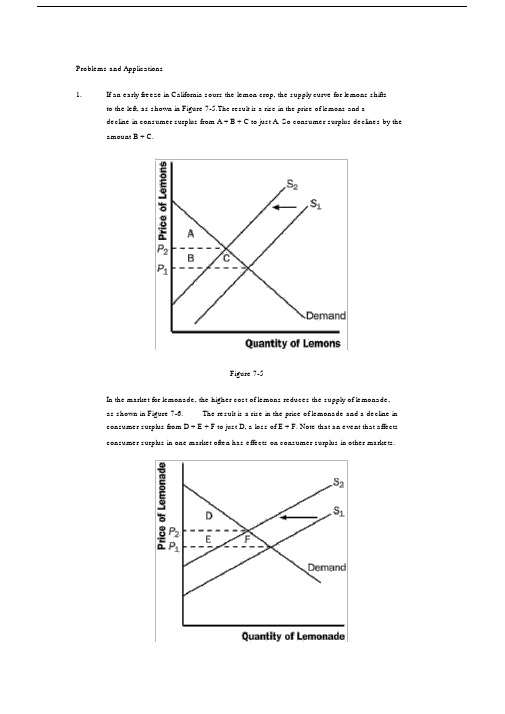
Problems and Applications1.If an early freeze in California sours the lemon crop, the supply curve for lemons shiftsto the left, as shown in Figure 7-5.The result is a rise in the price of lemons and adecline in consumer surplus from A + B + C to just A. So consumer surplus declines by the amount B + C.Figure 7-5In the market for lemonade, the higher cost of lemons reduces the supply of lemonade,as shown in Figure 7-6.The result is a rise in the price of lemonade and a decline inconsumer surplus from D + E + F to just D, a loss of E + F. Note that an event that affectsconsumer surplus in one market often has effects on consumer surplus in other markets.Figure 7-62. A rise in the demand for French bread leads to an increase in producer surplus in themarket for French bread, as shown in Figure 7-7.The shift of the demand curve leads to an increased price, which increases producer surplus from area A to area A + B + C.Figure 7-7The increased quantity of French bread being sold increases the demand for flour, asshown in Figure 7-8.As a result, the price of flour rises, increasing producer surplusfrom area D to D + E + F. Note that an event that affects producer surplus in onemarket leads to effects on producer surplus in related markets.Figure 7-83. a.Bert’ s demand schedule is:Price Quantity DemandedMore than $7 0$5 to $7 1$3 to $5 2$1 to $3 3$1 or less 4Bert’ s demand curve is shown in Figure 7 -9.Figure 7-9b.When the price of a bottle of water is $4, Bert buys two bottles of water.Hisconsumer surplus is shown as area A in the figure.He values his first bottle ofwater at $7, but pays only $4 for it, so has consumer surplus of $3.He valueshis second bottle of water at $5, but pays only $4 for it, so has consumersurplus of $1.Thus Bert’ s total consumer surplus is $3 + $1 = $4, which isthe area of A in the figure.c.When the price of a bottle of water falls from $4 to $2, Bert buys three bottlesof water, an increase of one. His consumer surplus consists of both areas Aand B in the figure, an increase in the amount of area B. He gets consumersurplus of $5 from the first bottle ($7 value minus $2 price), $3 from thesecond bottle ($5 value minus $2 price), and $1 from the third bottle ($3 valueminus $2 price), for a total consumer surplus of $9. Thus consumer surplusrises by $5 (which is the size of area B) when the price of a bottle of water fallsfrom $4 to $2.4. a. Ernie ’ s supply schedule for water is:Price Quantity SuppliedMore than $7 4$5 to $7 3$3 to $5 2$1 to $3 1Less than $1 0Ernie’ s supply curve is shown in Figure 7 -10.Figure 7-10b.When the price of a bottle of water is $4, Ernie sells two bottles of water.Hisproducer surplus is shown as area A in the figure.He receives $4 for his firstbottle of water, but it costs only $1 to produce, so Ernie has producer surplusof $3.He also receives $4 for his second bottle of water, which costs $3 toproduce, so he has producer surplus of$1. Thus Ernie’ s total producersurplus is $3 + $1 = $4, which is the area of A in the figure.c.When the price of a bottle of water rises from $4 to $6, Ernie sells three bottlesof water, an increase of one.His producer surplus consists of both areas Aand B in the figure, an increase by the amount of area B.He gets producersurplus of $5 from the first bottle ($6 price minus $1 cost), $3 from the secondbottle ($6 price minus $3 cost), and $1 from the third bottle ($6 price minus $5price), for a total producer surplus of $9.Thus producer surplus rises by $5(which is the size of area B) when the price of a bottle of water rises from $4to $6.5. a. From Ernie ’ s supply schedule and Bert ’ s demand schedule, the quantitydemanded and supplied are:Price Quantity Supplied Quantity Demanded$ 2 1 34 2 26 3 1Only a price of $4 brings supply and demand into equilibrium, withan equilibrium quantity of 2.b.At a price of $4, consumer surplus is $4 and producer surplus is $4, as shownin problems 3 and 4.Total surplus is $4 + $4 = $8.c.If Ernie produced one fewer bottle, his producer surplus would decline to $3,as shown in problem 4.If Bert consumed one fewer bottle, his consumersurplus would decline to $3, as shown in problem 3. So total surplus would declineto $3 + $3 = $6.d.If Ernie produced one additional bottle of water, his cost would be $5, but theprice is only $4, so his producer surplus would decline by $1.If Bertconsumed one additional bottle of water, his value would be $3, but the priceis $4, so his consumer surplus would decline by $1.So total surplus declinesby $1 + $1 = $2.6. a.The effect of falling production costs in the market for stereos results in a shiftto the right in the supply curve, as shown in Figure 7-11.As a result, theequilibrium price of stereos declines and the equilibrium quantity increases.b.The decline in the price of stereos increases consumer surplus from area A to A+ B + C + D, an increase in the amount B + C + D.Prior to the shift in supply,producer surplus was areas B + E (the area above the supply curve and belowthe price).After the shift in supply, producer surplus is areas E + F + G.Soproducer surplus changes by the amount F + G - B, which may be positive ornegative.The increase in quantity increases producer surplus, while thedecline in the price reduces producer surplus.Since consumer surplus risesby B + C + D and producer surplus rises by F + G - B, total surplus rises by C+ D+F+G.c.If the supply of stereos is very elastic, then the shift of the supply curvebenefits consumers most.To take the most dramatic case, suppose thesupply curve were horizontal, as shown in Figure 7-12.Then there is noproducer surplus at all.Consumers capture all the benefits of fallingproduction costs, with consumer surplus rising from area A to area A + B.Figure 7-11Figure 7-127. Figure 7-13 shows supply and demand curves for haircuts. Supply equals demand ata quantity of three haircuts and a price between $4 and $5. Firms A, C, and D shouldcut the hair of Sally Jessy, Jerry, and Montel. Oprah ’ s willingness to pay is too low and firm B ’ s costs are too high, so they do not participate. The maximum total surplus isthe area between the demand and supply curves, which totals $11 ($8 value minus$2 cost for the first haircut, plus $7 value minus $3 cost for the second, plus $5 valueminus $4 cost for the third).Figure 7-138. a.The effect of falling production costs in the market for computers results in ashift to the right in the supply curve, as shown in Figure 7-14.As a result, theequilibrium price of computers declines and the equilibrium quantity increases.The decline in the price of computers increases consumer surplus from area Ato A + B + C + D, an increase in the amount B + C + D.Figure 7-14Prior to the shift in supply, producer surplus was areas B + E (the area abovethe supply curve and below the price).After the shift in supply, producersurplus is areas E + F + G.So producer surplus changes by the amount F + G- B, which may be positive or negative.The increase in quantity increasesproducer surplus, while the decline in the price reduces producer surplus. Sinceconsumer surplus rises by B + C + D and producer surplus rises by F + G - B,total surplus rises by C + D + F + G.——Figure 7-15b.Since adding machines are substitutes for computers, the decline in the priceof computers means that people substitute computers for adding machines,shifting the demand for adding machines to the left, as shown in Figure 7-15.The result is a decline in both the equilibrium price and equilibrium quantity ofadding machines.Consumer surplus in the adding-machine market changesfrom area A + B to A + C, a net gain of C - B.Producer surplus changes fromarea C + D + E to area E, a net loss of C + D.Adding machine producers aresad about technological advance in computers because their producersurplus declines.c.Since software and computers are complements, the decline in the price andincrease in the quantity of computers means that people’ s demand forsoftware increases, shifting the demand for software to the right, as shown inFigure 7-16. The result is an increase in both the price and quantity of software.Consumer surplus in the software market changes from B + C to A+B, a net increase of A - C. Producer surplus changes from E to C + D + E, anincrease of C + D, so software producers should be happy about the technologicalprogress in computers.d.Yes, this analysis helps explain why Bill Gates is one the world’ s richest msince his company produces a lot of software that’ s a complement withcomputers and there has been tremendous technological advance incomputers.——Figure 7-169. a. Figure 7-17 illustrates the demand for medical care. If each procedure has aprice of $100, quantity demanded will be Q 1 procedures.Figure 7-17b.If consumers pay only $20 per procedure, the quantity demanded will be Q 2procedures.Since the cost to society is $100, the number of proceduresperformed is too large to maximize total surplus.The quantity thatmaximizes total surplus is Q 1 procedures, which is less than Q2.c.The use of medical care is excessive in the sense that consumers getprocedures whose value is less than the cost of producing them.As a result,——the economy’ s total surplus is reduced.d.To prevent this excessive use, the consumer must bear the marginal cost ofthe procedure.But this would require eliminating insurance.Anotherpossibility would be that the insurance company, which pays most of themarginal cost of the procedure ($80, in this case) could decide whether theprocedure should be performed.But the insurance company doesn’ t get thebenefits of the procedure, so its decisions may not reflect the value to theconsumer.10. a. Figure 7-18 illustrates the effect of the drought. The supply curve shifts tothe left, leading to a rise in the equilibrium price from P 1 to P 2 and a decline inthe equilibrium quantity from Q 1 to Q 2 .Figure 7-18b.If the price of water is not allowed to change, there will be an excess demandfor water, with the shortage shown on the figure as the difference between Q 1and Q 3 .c.The system for allocating water is inefficient because it no longer allocateswater to those who value it most highly.Some people who value water atmore than its cost of production will be unable to obtain it, so societysurplus isn’ t maximized.The allocation system seems unfair as well.Water is allocated simply on pastusage, rewarding past wastefulness.If a family’ s demand for water increases,——say because of an increase in family size, the policy doesn ’ t allow them to obtain more water. Poor families, who probably used water mostly fornecessary uses like drinking, would suffer more than wealthier families whowould have to cut back only on luxury uses of water like operating backyardfountains and pools. However, the policy also keeps the price of water lower,which benefits poor families, since otherwise more of their family budgetwould have to go for water.d. If the city allowed the price of water to rise to its equilibrium price P 2 , theallocation would be more efficient. Quantity supplied would equal quantitydemanded and there would be no shortage. Total surplus would bemaximized.Whether the market allocation would be more or less fair than theproportionate reduction in water under the old policy is difficult to say, but it islikely to be more fair. Notice that the quantity supplied would be higher (Q 2)in this case than under the water restrictions (Q 3 ), so there ’ s less reduction inwater usage. To make the market solution even more fair, the governmentcould provide increased tax relief or welfare payments for poor families whosuffer from paying the higher water prices.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章习题答案
7.1 ARM处理器有几种运行模式,处理器如何区别各种不同的运行模式?
ARM处理器有7中运行模式:
●用户模式(user):ARM处理器正常的程序执行状态
●快速中断模式(fiq):处理高速中断,用于高速数据传输或通道处理
●外部中断模式(irq):用于普通的中断处理
●管理模式(supervisor):操作系统使用的保护模式,系统复位后的默认模式
●中止模式(abort):数据或指令预取中止时进入该模式
●未定义模式(undefined):处理未定义指令,用于支持硬件协处理器的软件仿真
●系统模式(system):运行特权级的操作系统任务
处理器使用CPSR寄存器中的M4~M0位来指示不同的运行模式。
7.2 通用寄存器中PC、CPSR和SPSR的作用各是什么?
PC:程序计数器,用于保存处理器要取的下一条指令的地址。
CPSR:当前程序状态寄存器,CPSR保存条件标志位、中断禁止位、当前处理器模式标志,以及其他一些相关的控制和状态位。
SPSR:备份程序状态寄存器,当异常发生时,SPSR用于保存CPSR的当前值,当从异常退出时,可用SPSR来恢复CPSR。
7.3 从编程的角度讲,ARM处理器的工作状态有哪两种?这两种状态之间如何转换?
从编程角度讲,ARM处理器的两种工作状态为:
●ARM状态(复位状态):处理器执行32位的字对齐的ARM指令
●Thumb状态:处理器执行16位的半字对齐的Thumb指令
ARM指令集和Thumb指令集均有切换处理器状态的指令,并可在两种工作状态之间切换:
●进入Thumb状态:当操作数寄存器的状态位(最低位)为1时,执行BX指令就
可以进入Thumb状态。
如果处理器在Thumb状态时发生异常(异常处理要在ARM状态下执行),则当异常处理返回时自动切换到Thumb状态
●进入ARM状态:当操作数寄存器的状态位(最低位)位0时,执行BX指令就可
以进入ARM状态。
处理器进行异常处理时,把PC的值放入异常模式链接寄存器中,从异常向量地址开始执行程序,系统自动进入ARM状态
7.4 作业情况:同学们答的为:ARM支持Thumb和ARM双指令集,内核小,流水线结构;而RISC用寄存器窗口处理异常,延迟转移,单指令周期执行
7.5 哪些特征是ARM和其他RISC体系结构所共有的?
ARM和其他RISC体系结构共有的三个相同特征:
●Load/Store体系结构:也称为寄存器/寄存器体系结构或RR系统结构。
在这类机
器中,操作数和运算结果不能直接从主寄存器中存取,而是必须借用大量的标量或矢量寄存器来进行中转。
采用这一结构的处理器必然要使用更多的通用寄存器存储操作数和运算结果,由于寄存器与运算器之间的数据传输速度远高于主存与运算器之间的数据传输速度,采用这一结构有助于提高计算机整体的运行速度
●采用固定长度精简指令集:这样使得机器译码变得容易,可以通过硬件直接译码
的方式完成对指令的解析。
虽然由于与复杂指令集相比,采用精简指令集需要更多指令来完成相同的任务,但采用硬件直接译码的速度却高于采用微码方式译码。
通过采用高速缓存等提高寄存器存储速度的技术,采用固定长度精简指令集的机器可以获得更高性能
●三地址指令格式:除了除法指令外,ARM的大部分数据处理指令采用三地址指
令。
即在指令中包含了目的操作数、源操作数和第二源操作数。
