《结构力学》作业2答案
结构力学第二次作业答案

结构力学课程——作业二(答案)
1.请叙述引起结构产生位移的因素。
答案:P77
2.请解释何为虚功?
答案:P78
3.请叙述力法的基本概念,并解释力法典型方程中系数的物理意义。
答案:P113,和P119-120
4.请大致叙述力法的计算超静定结构位移的步骤。
答案:P121
5.请大致叙述超静定结构的特性。
答案:P155-157
6.求图1所示简支梁最大挠度,请写明计算的步骤。
q
图1 题6
答案:
答:最大挠度应出现在梁的中心点,在中心点加单位荷载,画出虚拟状态和实际荷载作用下的弯矩图,两图图乘得最大挠度。
注意实际状态和虚拟状态均以梁中心为对称点成正对称关系,故对一侧图乘后加倍即可。
二次曲线的形心位置如图所示,具体可参加教材P104图6-14。
7.请采用力法作出图2所示刚架的M图、F S图和F N图。
图2 题7
答案:
图2 题2
X 2=1
B C
A
B
FL/2
M P
02222112=∆+⋅+⋅P X X δδ。
《结构力学(2)》试题-2012-A-参考答案

M A = 350 × 3+300 × 1 = 1350kN.m (4)综上, M A,max = 1475kN.m ,下侧受拉。
《结构力学(2) 》试卷 A 卷
第 2 页 共 6 页
题 4 解:
EI
1) 自由度 (如图) : (5 分) 2)δ11 计算(5 分)
δ 11 = 1 1 a3 5a 3 2 × × (0.5a ) × a + = EI 3 48 EI 48 EI
M2
1
1
第二振型
题 7 解: 1)2 个自由度如图: (5 分) m1 = 2m 2)建立运动方程: (5 分)
δ 11 = 1 1 1 a 2 3 (a ) 2a + (a ) = 3 EI 3 EI a3 4 EI
3
y1
m2 = m
m
P(t ) = P0 sinθt
A
m
C
y2
3m
专业
3m
M A 影响线
tan α1 = -1 , tan α 2 = 1 , tan α 3 = -1 (2)将各个集中荷载依次移动到 B 点,求解最大负弯矩 ----------(5 分) P4 作用在 B 点时,P P2 不在结构上: 左移, 右移, ∑ Pi tan α i <0 ; ∑ Pi tan α i = -50<0 , 1、 不是临界位置。 P3 作 用 在 B 点 时 , P 1 不 在 结 构 上 : 左 移,
( 32 − λ ) A3 +8 A4 = 0 16 A3 + ( 5 − λ ) A4 = 0
特征方程为 32 − λ 8 =0 16 5−λ 解得: λ1 = 36.11 , λ2 = 0.886 ,即 ω1 = 24 EI EI 24 EI EI = 0.815 , ω2 = = 5.20 。代入振型方 3 3 3 λ1ma ma λ2 ma ma3
结构力学习题及答案(武汉大学)

结构⼒学习题及答案(武汉⼤学)结构⼒学习题第2章平⾯体系的⼏何组成分析2-1~2-6 试确定图⽰体系的计算⾃由度。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图2-7~2-15 试对图⽰体系进⾏⼏何组成分析。
若是具有多余约束的⼏何不变体系,则需指明多余约束的数⽬。
题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图题2-13图题2-14图题2-15图题2-16图题2-17图题2-18图题2-19图题2-20图题2-21图2-1 1W=2-1 9-W=2-3 3-W=2-4 2-=W2-5 1-W=2-6 4-W=2-7、2-8、2-12、2-16、2-17⽆多余约束的⼏何不变体系2-9、2-10、2-15具有⼀个多余约束的⼏何不变体系2-11具有六个多余约束的⼏何不变体系2-13、2-14⼏何可变体系为2-18、2-19 瞬变体系2-20、2-21具有三个多余约束的⼏何不变体系第3章静定梁和静定平⾯刚架的内⼒分析3-1 试作图⽰静定梁的内⼒图。
(a)(b)(c) (d)习题3-1图3-2 试作图⽰多跨静定梁的内⼒图。
(a)(b)(c)习题3-2图3-3~3-9 试作图⽰静定刚架的内⼒图。
习题3-3图习题3-4图习题3-5图习题3-6图习题3-7图习题3-8图习题3-9图3-10 试判断图⽰静定结构的弯矩图是否正确。
(a)(b)(c)(d)部分习题答案3-1 (a )m kN M B ?=80(上侧受拉),kN F RQB 60=,kN F L QB 60-=(b )m kN M A ?=20(上侧受拉),m kN M B ?=40(上侧受拉),kN F RQA 5.32=,kN F L QA 20-=,kN F LQB 5.47-=,kN F R QB 20=(c) 4Fl M C =(下侧受拉),θcos 2F F L QC =3-2 (a) 0=E M ,m kN M F ?-=40(上侧受拉),m kN M B ?-=120(上侧受拉)(b )m kN M RH ?-=15(上侧受拉),m kN M E ?=25.11(下侧受拉)(c )m kN M G ?=29(下侧受拉),m kN M D ?-=5.8(上侧受拉),m kN M H ?=15(下侧受拉) 3-3 m kN M CB ?=10(左侧受拉),m kN M DF ?=8(上侧受拉),m kN M DE ?=20(右侧受拉) 3-4 m kN M BA ?=120(左侧受拉)3-5 m kN M F ?=40(左侧受拉),m kN M DC ?=160(上侧受拉),m kN M EB ?=80(右侧受拉) 3-6 m kN M BA ?=60(右侧受拉),m kN M BD ?=45(上侧受拉),kN F QBD 46.28=3-7 m kN M C ?=70下(左侧受拉),m kN M DE ?=150(上侧受拉),m kN M EB ?=70(右侧受拉) 3-8 m kN M CB ?=36.0(上侧受拉),m kN M BA ?=36.0(右侧受拉) 3-9 m kN M AB ?=10(左侧受拉),m kN M BC ?=10(上侧受拉) 3-10 (a )错误(b )错误(c )错误(d )正确第4章静定平⾯桁架和组合结构的内⼒分析4-1 试判别习题4-1图所⽰桁架中的零杆。
《结构力学》作业2答案

1.求图示体系的计算自由度,并分析其几何构造。
答.W=-4,有多余约束的不变体系。
2.求图示多跨静定梁的弯矩和剪力图。
答.3.试作下图所示结构的弯矩图。
答.4.利用静定结构的一般性质求图示桁架结构的内力。
答.在 F P作用下,只有右柱受了压力,而其它杆件的内力均为零。
5.用静力法求作图示多跨连续梁R A、R D、M E、F QE的影响线。
答.R A影响线R D影响线M E影响线F QE影响线6.图示三铰刚架 A支座往下位移了b,B支座往右位移了a,求C点的竖向位移ΔCV和 C 点的相对转角ϕC。
答. (向下)7. 试利用力法求解图示超静定结构,作出弯矩图,并求C点水平位移。
答. 取BC 杆的轴力为基本未知量X 1,基本方程:01111=∆+P X δ, 求得:EIEI P 64,3128111=∆=δ 则X 1=-3/2最终弯矩:M AB =10KN ·m (左侧受拉)M DC =6KN ·m (左侧受拉)C 点水平位移:)(32→=∆EICH 8. 用位移法求解图示结构。
答.9. 试利用弯矩分配法求图示超静定结构,作出弯矩图。
EI=常数。
答. µBA=4/7,µBC=3/7-m AB =m BA =30KN·mm BC =-20KN·m最终弯矩:M AB=-32.86KN·mM BA=-M BC=24.29KN·m,M CB=- M CD=40KN·m10.写出连续梁单元和桁架单元在局部坐标下的单元刚度矩阵。
答.连续梁单元:桁架单元:或。
奥鹏 东北大学21秋季 《结构力学基础》在线平时作业2 参考答案.doc

1.图示结构,AB杆件B处的轴力为()A.2PB.0C.-PD.P【参考答案】: B2.固定端约束及反力的特点不包括()A.被约束处不能有转角产生B.被约束处不能有线位移产生C.反力通常包括约束反力偶 D.只给被约束物体正交分解的约束反力【参考答案】: D3.下图所示体系的几何组成分析过程中,下面的叙述哪个是错误的()A.可以先除去与大地相连的支座链杆,剩下部分的几何组成性质与原结构相同 B.可以将DE、EB杆作为二元体去除 C.AB、EB、DE整体可以看成一个大刚片 D.体系中没有可以去除的二元体【参考答案】: B4. 下图所示结构( )是中间铰链约束A.A点B.B点C.C点D.E点【参考答案】: C5.根据支座和载荷情况,梁挠曲线的大致形状为()A.(a)B.(b)C.(c)D.(d)【参考答案】: D6.下面物体的整体受力图哪个是正确的()A.B.C.D.【参考答案】: B7.下图所示结构,AB=1m, F1=10 kN,作用于AB 的中点, F2=5 kN ,M=5 kNm,, BC=0.5m,则A处的约束反力()A.向右的约束反力F x=10kN,向上的约束反力F y=5kN,约束反力偶m=12.5kNm,顺时针B.向左的约束反力F x=10kN,向上的约束反力F y=5kN,约束反力偶m=2.5kNm,逆时针C.向左的约束反力F x=10kN,向上的约束反力F y=5kN,约束反力偶m=10kNm,逆时针D.向左的约束反力F x=10kN,向上的约束反力F y=5kN,约束反力偶m=12.5kNm,逆时针【参考答案】: B8.下图所示结构,F1=10 kN,M=5 kNm,AB=1m, BC=0.5m,则A处的约束反力()A.向右的约束反力F x=10kN,约束反力偶m=15kNm,顺时针B.向右的约束反力F x=5kN,约束反力偶m=5kNm,顺时针C.向左的约束反力F x=10kN,约束反力偶m=0D.向左的约束反力F x=10kN,约束反力偶m=5kNm,逆时针【参考答案】: D9.下图所示的复刚结点相当于几个单刚结点()A.1B.2C.3D.4【参考答案】: C10.下图所示结构,F1=10 kN,F2=5 kN,AB=1m, BC=0.5m,则A处的约束反力()A.向右的约束反力Fx=10kN,向上的约束反力Fy=5kN,约束反力偶m=12.5kNm,顺时针B.向右的约束反力Fx=5kN,向上的约束反力Fy=10kN,约束反力偶m=7.5kNm,顺时针 C.向左的约束反力Fx=10kN,向上的约束反力Fy=5kN,约束反力偶m=10kNm,逆时针 D.向左的约束反力Fx=10kN,向上的约束反力Fy=5kN,约束反力偶m=12.5kNm,逆时针【参考答案】: D11.AB=1m,载荷F对A点之矩为()A.10 kNmB.-10 kNmC.-5 kNmD.5 kNm【参考答案】: C12.图示刚架中,AB杆件B处的剪力为()A.80kNB.0C.40kND.-40kN【参考答案】: B13.图示中高宽比h/b=2的矩形截面梁,若将梁的横截面由竖放(图(a))改为平放(图(b)),其他条件不变,则梁的最大挠度和最大正应力分别为原来的()倍。
02-2结构力学第二章 平面体系的几何组成分析-作业答案汇总

38 3 2 29 3 3
3个单铰结点, 3个折算为2个单铰结点的复铰结点
支杆
b3
11/73
(II III) 刚片II
(I II)
刚片III
几何不变且无多余约束
j9 单链杆:12根 复链杆:2根 折算为6根单链杆
W 2 j b 29 12 6 0
5/73
【作业1】分析图示体系的几何构造
图3
【作业1】分析图示体系的几何构造
图4
先考察如图所示结构
∞(II III)
9/73
【作业2】求图示系统的计算自由度
刚片 m 1 单刚结点 g 4 铰结点 h 0 支杆 b 3
内部无多余约束刚片
W 3m 3g 2h b
31 3 4 3 12
10/73
【作业2】求图示系统的计算自由度
刚片 m 8
单刚结点 g 2
W 3m 3g 2h b
铰结点 h 9
刚片 m 14 单铰链结点 h 18
刚片II
刚片III
(I II)
(I III) 刚片I
瞬变体系
其中折算为2个单铰结点的 复铰结点有6个
∞(II III)
其中折算为3个单铰结点的 复铰结点有2个 单刚结点 2个 g 2 和基础相连的支杆 0个 b 0
W 3m 3g 2h b
314 3 2 218 0
∞(II III)
刚片II (I II) (I III) 刚片III
刚片I
几何不变且无多余约束
(I II) 刚片II (I III) 刚片III
刚片I
几何不变且无多余约束
7/73
【作业2】求图示系统的计算自由度
图1 并进行几何构造分析
《结构力学》在线作业二

结构力学在线作业二1. 引言结构力学是土木工程领域中一门重要的学科,它研究物体在外力作用下的力学行为。
本文主要介绍结构力学在线作业二的内容。
2. 问题描述在线作业二主要涉及以下问题:2.1. 悬臂梁的计算有一个悬臂梁,长为L,截面面积为A,弹性模量为E。
求解以下问题:•悬臂梁在端点受到的力、弯曲力和剪力分别是多少?•悬臂梁的最大弯矩是多少?2.2. 杆的轴向变形计算有一个杆长为L,截面积为A,弹性模量为E。
求解以下问题:•杆在两端受到的力是多少?•杆的伸长量是多少?•杆的轴向应变是多少?3. 解决方法为了解决上述问题,我们可以使用结构力学中的公式和理论知识。
具体的解决方法如下:3.1. 悬臂梁的计算方法悬臂梁是一种常见的结构,在计算其受力情况时,可以使用以下公式:•力:根据受力平衡条件,可以得到悬臂梁的端点受力。
•弯曲力:使用弯曲力-剪力曲线的关系,可以得到悬臂梁上任意一点的弯曲力。
•剪力:使用剪力-剪力曲线的关系,可以得到悬臂梁上任意一点的剪力。
•最大弯矩:通过对弯曲力求导数并令导数为零,可以求得弯曲力的最大值,即悬臂梁的最大弯矩。
3.2. 杆的轴向变形计算方法杆的轴向变形计算需要使用以下公式和理论知识:•力:根据受力平衡条件,可以得到杆的两端受力。
•伸长量:使用胡克定律,可以得到杆的伸长量。
•轴向应变:使用应变-应力关系,可以得到杆的轴向应变。
4. 计算实例为了更好地理解解决方法,我们进行以下计算实例:4.1. 悬臂梁计算实例已知悬臂梁的长度L=5m,截面面积A=0.1m^2,弹性模量E=200GPa。
根据悬臂梁的计算方法,我们可以得到以下结果:•端点受力为0N,弯曲力为0N,剪力为0N。
•最大弯矩为0N*m。
4.2. 杆的轴向变形计算实例已知杆的长度L=3m,截面面积A=0.05m^2,弹性模量E=100GPa。
根据杆的轴向变形计算方法,我们可以得到以下结果:•两端受力为0N。
•伸长量为0m。
结构力学第2章习题及参考答案
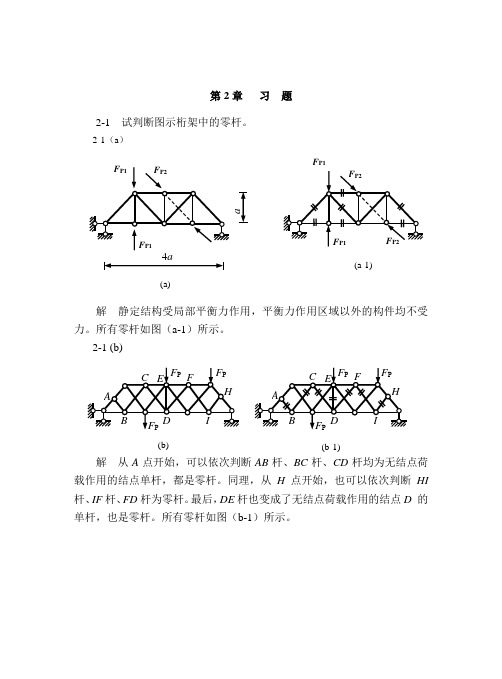
解(1)AB部分(图(a-1)):
, ; ,
(2)BC部分((图(a-2)):
, ; ,
,
(3)CA部分的弯矩图可以从C点开始画。
2-19(b)
解(1)取整体结构为隔离体:
(2)AGE部分:(图(b-1))
: ; :
:
(4)结构的弯矩图(图(b-2))。
2-19(C)
解(1)AB部分(图(c-1)):
解:弯矩图凹向应该与荷载方向相同。改正后的弯矩图如图(e-1)所示。
解铰处无外力偶,弯矩为0。改正后的弯矩图如图(f-1)所示。
2-18试作图示刚架内力图。
2-18(a)
2-18(b)
2-18 (c)
2-18 (d)
2-18 (e)
2-18 (f)
2-18 (g)
2-18(h)
2-19试作图示刚架弯矩图。
解(1)求支座反力。这是一个基——附结构的桁架。先由附属部分开始计算。取D结点以左部分为隔离体
,
取整体为对象
(2)求指定杆轴力。
Ⅰ—Ⅰ截面(图(b)
,
Ⅱ-Ⅱ截面(图(c))
,
:
2-6试判断图示桁架中的零杆并求1、2杆轴力。
解:(1)判断零杆。如图(a)所示。
(2)求支座反力
,
,
,
(3)求指定杆轴力
由I结点的平衡条件,得
:
由比例关系
,
,
: ,
2-10选用较简捷的方法计算图示桁架中指定杆的轴力。
解(1)求支座反力
,
(2)求指定杆轴力
结点C:去掉零杆CD
: ,
结点G
,
Ⅰ—Ⅰ截面(图(a))
:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 求图示体系的计算自由度,并分析其几何构造。
答W=-4,有多余约束的不变体系。
2. 求图示多跨静定梁的弯矩和剪力图。
rm
3.
试作下图所示结构的弯矩图。
lin
2iii
lin I Jin
答.
4
. 答.
L
L
L
L
Bl c
d
L
ni/
L
利用静定结构的一般性质求图示桁架结构的内
力。
在F P作用下,只有右柱受了压力,而其它杆件的内力均为零。
5.用静力法求作图示多跨连续梁甩、RD M、F QE的影响线。
O
D
L h 4
C
A 支座往下位移了 b ,
B 支座往右位移了 a ,求
C 点的竖向位移 A cv 和C
1 , I
b a
—X
b — —
— — (向下)
2 4
2 4
下
7.试利用力法求解图示超静定结构,作出弯矩图,并求
答. R A 影响线 F D 影响线 M E 影响线 F QE 影响线 点的相对转角
2KN/in
6.图示三铰刚架
C 点水平位移。
答.
取BC 杆的轴力为基本未知量 X i ,
则 X i =-3/2
M Dc =6KN- m (左侧受拉)
C 点水平位移:
用位移法求解图示结构。
¥
牛1 J U llll
II 1
zl
t H 确定未制量, (2)尸斓穹範表达式
基本方程: II X
I
IP 0, 求得:
11
128 近T 仃
64
E?
" ■
6x2/ ,也
I 匚片=旳刊 —xA- —
…
12J',空尸
3/
、r M U gH + Al 虻=0
心+討
V F = O
卜g
_打眩—
9/
27/ 、&L
L n
句
—H + - X uA — — Fp =0 h h … la If 2
9.试利用弯矩分配法求图示超静定结构,作出弯矩图。
EI=常数。
-m AB =n BA =30KN-
m c =-20KN ・m
6麻N
JL
BC=3/7
2QKN/D] B J I J J I J
Jc X
2 in lb
4in
20KN
最终弯矩: M A B =10KN- m (左侧受拉)
Xr
0 0 0
最终弯矩:M AB =-32.86KN-m
M B A =-M BC =24.29KN • m M C B =- M c[=40KN-m
写出连续梁单元和桁架单元在局部坐标下的单元刚度矩
阵。
10.
0 0 0
答.
4£?
/ 2E/
连续梁单元: L
2E!
L
4Ef
桁架单元:
EA EA
EA
[叮=
-EA EA。
