三相电压型PWM整流器建模及控制
三相PWM整流器的小信号建模及其双闭环控制

年第期三相PWM整流器的小信号建模及其双闭环控制夏加宽徐纯科黄伟(沈阳工业大学电气工程学院,沈阳110178)摘要采用开关函数描述的三相PWM 整流器的数学模型为非线性模型,控制器的设计比较困难。
利用开关周期平均法建立三相电压型PWM 整流器(VSR)的平均模型,扰动分离后分别得到稳态模型和小信号模型,其小信号模型即为线性时不变模型。
基于小信号模型设计了电压外环和电流内环的PI 控制器。
最后通过Matlab 仿真验证了小信号建模和控制器设计的正确性。
关键词:PWM 整流器;开关周期平均法;小信号模型;双闭环Small-signal Modeling and Double C lose Loop Control ofThree-phase PWM RectifierX ia Jiakuan X u Chunke Huang W ei(School of Electric Engineering,Shenyang University of Technology,Shenyang 110178)Abstr act Due to the mathematical model of traditional 3-phases PWM rectifier which set up by switching function is a non-linear model,it ’s difficult to design the ing the method of average switching period an average model of three-phase PWM rectifier (VSR)is set up;separate the disturbance obtained the steady-state model and small-signal model.This model is a linear time-no varying model.Based on this small-signal model,the PI controller is designed for voltage outer loop and current inner loop.At last,the validity of small-signal model and the controller is verified throng the Matlab simulation.Key words :PWM rectifier ;average switching period ;small-signal model ;double closed loop1引言PWM 整流器因为其网侧功率因数可调性,网侧电流低谐波性,能量的双流动性,实现了电能的“绿色变换”,由于三相PWM 整流器模型的非线性,时变性给控制器的设计带来了很大的不便。
三相电压型PWM整流器建模及控制

三相电压型PWM 整流器建模及控制摘要:本文通过基尔霍夫定律完成了对三相电压型PWM 整流器在三相静止对称坐标系下的数学建模。
并通过MATLAB/SIMULINK 仿真工具对其数学模型进行了仿真验证,可以看出,仿真验证的结果证明了模型的准确性和可靠性。
而后又介绍了一种直接电流控制方法即传统的双闭环PID 控制,并进行了仿真分析。
1 基于基尔霍夫定律对三相VSR 系统建模三相电压型PWM 整流器的电路拓扑结构如图1-1所示。
图中a u 、b u 、c u 为三相交流电源,L 和C 分别为滤波电感和滤波电容,R 是滤波电感的等效电阻,s R 是开关管的等效电阻。
记网侧三相交流电流分别为a i 、b i 、c i ,整流电流为dc i ,流过负载电阻的电流为L i ,负载两端电压为dc v 。
i Le i L图1-1 三相电压型PWM 整流器电路图针对三相VSR 一般数学模型的建立,通常作以下假设: (1) 电网电动势为三相平衡的正弦波电动势(a u ,b u ,c u )。
(2) 网侧滤波电感L 是线性的,且不考虑饱和。
(3) 功率开关管损耗以电阻s R 表示,即实际的功率开关管可由理想开关与损耗电阻s R 串联等效表示。
(4) 为描述VSR 能量的双向传输,三相VSR 其直流侧负载由L R 和直流电动势L e 串联表示。
当直流电动势0L e =时,三相VSR 只能运行于整流模式;当L dce v >时,三相VSR 既可运行于整流模式,又可运行于有源逆变模式;当L dc e v <时,三相VSR 则运行于整流模式。
为分析方便,定义单极性二值逻辑开关函数k s 为10k s ⎧=⎨⎩上桥臂导通,下桥臂关断上桥臂关断,下桥臂导通(,,)k a b c = (1-1)将三相VSR 功率开关管损耗等效电阻s R 和交流滤波电感等效电阻l R 合并,记 s l R R R =+,采用基尔霍夫电压定律建立三相VSR a 相回路方程为()aa a aN NO di LRi u v v dt+=-+ (1-2) 当1S 导通而2S 关断时,1a s =,且aN dc v v =;当1S 关断而2S 导通时,开关函数0a s =,且0aN v =。
【全面版】三相电压型 PWM 整流器原理及控制方法PPT文档

三相电压型 PWM 整流器系统结构图 复位电路采用按键手动复位。
两相电流 传感器
电源 模块
开关器件驱动
直流电压,电流
空基 圆间本,矢 原从量理 而P就 形W是 成M把S(VS三PV相WPWMPWM波)M。控整制流策器略输是入根端据电整压流在器复空平间面电上压转矢换量为切空换间来电控压制矢整与量流保,器护通电的S过V路一P不种W同新M的波的开形控关制状策态略组传。合感构器成8个空间矢量去逼近电压
三相电压型PWM整流
器的拓扑结构如右图所示,
其中在所示的电路中三相电
感L起滤波作用,因此交流 ua ia R
侧电流可近似认为是三相正 弦电流,C为直流侧电容,
ub ib N uc ic
R R
起稳压滤波的作用,当系统
稳定时,可保持直流母线电
压基本不变,故可看作是直
流电压源。R为线路与开关
管的等效电阻,RL为负载。
pW,pV,pU V51+ 的 MPI 接 F F u u 0 0 71C 1 1 0 C1 K 0 01R2 3 C Fu1.0 5 CFu1.0 2 T U O V 5 D 1 N 8 7G 3 N I V F 2 u C 1 1 V51+ F 76 85 u 0 1 3 C3 955PLT 43 21 CCV EGDIRB 0 4 7 R2 7 0 4 7A9U 21 1 J 2NOC MWP
- 直流侧电压
开关管交
流入侧电的压输由此可以看出, PWM整流器的交流回 路的组成有电网电源, 开关管交流侧输入电 压,交流侧电感。
空间矢量PWM(SVPWM)控制策略是根 据整流器空间电压矢量切换来控制整流器的 一种新的控制策略。基本原理就是把三相 PWM整流器输入端电压在复平面上转换为空 间电压矢量,通过不同的开关状态组合构成8 个空间矢量去逼近电压圆,从而形成 SVPWM波。
三相PWM整流电路的建模与仿真
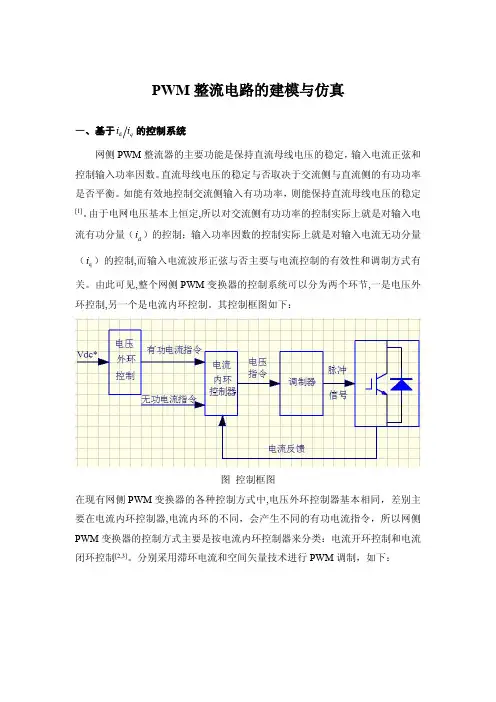
一、基于 id iq 的控制系统 网侧 PWM 整流器的主要功能是保持直流母线电压的稳定, 输入电流正弦和 控制输入功率因数。 直流母线电压的稳定与否取决于交流侧与直流侧的有功功率 是否平衡。 如能有效地控制交流侧输入有功功率,则能保持直流母线电压的稳定
[1]
。 由于电网电压基本上恒定,所以对交流侧有功功率的控制实际上就是对输入电
流有功分量( id )的控制;输入功率因数的控制实际上就是对输入电流无功分量 ( iq )的控制,而输入电流波形正弦与否主要与电流控制的有效性和调制方式有 关。由此可见,整个网侧 PWM 变换器的控制系统可以分为两个环节,一是电压外 环控制,另一个是电流内环控制。其控制框图如下:
图 控制框图 在现有网侧 PWM 变换器的各种控制方式中,电压外环控制器基本相同,差别主 要在电流内环控制器,电流内环的不同,会产生不同的有功电流指令,所以网侧 PWM 变换器的控制方式主要是按电流内环控制器来分类:电流开环控制和电流 闭环控制[2,3]。分别采用滞环电流和空间矢量技术进行 PWM 调制,如下:
化简为:
did 3 L w · L · i R · i · U q d max V d dt 2 Vdq diq Vq L w·L·id R·iq 0 dt
由上述由图可以看出:直接电流控制是一个双闭环控制系统,即电压外环和电流内 环。电压外环用来保持整流器的直流侧电压恒定;电流内环的作用主要是按电压 外环输出的电流指令进行电流控制,实现对单位功率因数的正弦波电流控制。
2、搭建仿真模型 (1)建立仿真模型
图 滞环电流控制PWM仿真模型 (2)系统主要参数
(2)、直流侧电压电流波形
三相电压型PWM整流器的基本原理与建模分析

第三章三相电压型PWM整流器的基本原理与建模分析本文蓄电池充电装置是采用可逆PWM整流器的智能充电装置,PWM整流器既可工作于整流状态又可工作于逆变状态,从而实现能量再生和提高网侧功率因数,降低对电网的谐波污染;并采用馈能放电,将蓄电池电能回馈到电网,节省电能。
三相电压型PWM整流器是本系统研究的基础,担负着为蓄电池充电时提供直流电源及放电时向电网馈电的功能。
本章给出了三相电压型PWM整流器的基本原理及建模仿真。
1.1 PWM整流器基本原理概论PWM整流器是一个可工作在四象限的、交流侧和直流侧全控型的电流变换装置。
首先通过PWM整流器的模型电路来阐述其基本原理。
图3-1图3-1为PWM变流器模型电路。
PWM变流器模型电路由主要由三部分构成:交流网络、桥式功率开关管电路以及直流网络。
其中交流网络可以等效为交流电动势E和网侧电感L的串联;直流网络可以等效为负载电阻RL和负载电动势eL串联;桥式功率开关管电路可以是电压型桥路也可以使电流型桥路。
忽略功率开关管桥路的损耗,根据交流侧和直流侧功率平衡关系可得1.1式(3-1)式中:V , I 一交流侧电压、电流;Vdc, ldc一直流侧电压、电流。
由式(1.1)可知:模型电路的的交,直流两侧相互制约。
下面通过分析模型电路的交流侧电压电流来研究PWM变流器的运行原理。
为简化分析,忽略PWM的谐波分量,只考虑基波,稳态运行时,PWM交流侧电压电流矢量关系如图1.2所示。
以E为参考矢量,控制V,可实现四象限运行。
如不变,则也不变,V的运行轨迹便成了以为半径的圆。
在V分别抵达A, B, C, D四个特殊点时,PWM整流器分别呈现纯电感特性、正电阻特性、纯电容特性和负电阻特性。
A)纯电感特性运行 B)正电阻特性运行 C)纯电容特性运行 D)负电阻特性运行图1.2PWM变流器交流侧稳态矢量关系图E一交流电网电动势矢量 V一交流侧电压矢量VL-交流侧电感电压矢量 I一交流侧电流矢量对PWM整流器在四个特殊点间的运行规律详细分析如下:1.电压矢量v端点在圆轨迹弧AB上运动时,PWM整流器运行于整流状态。
三相电压型PWM整流器设计与仿真(精)

1 绪论随着功率半导体器件技术的进步,电力电子变流装置技术得到了快速发展,出现了以脉宽调制(PWM)控制为基础的各种变流装置,如变频器、逆变电源,高频开关电源以及各类特种变流器等,电力电子装置在国民经济各领域取得了广泛的应用,但是这些装置的使用会对电网造成严重的谐波污染问题。
传统的整流方式会无论是二极管不控整流还是晶闸管相控整流电路能量均不能双向传递,不仅降低能源的利用率还会增加一定的污染,主要缺点是:1)无功功率的增加造成了装置功率因素降低,会导致损耗增加,降低电力装置的利用率等;2)谐波会引起系统内部相关器件的误动作,使得电能的计量出现误差,外部对信号产生严重干扰;3)传统的结构,能量只能单向流动,使得控制系统的能量利用率不高,不能起到节能减排的作用。
电网污染的日益严重引起了各国的高度重视,许多国家都已经制定了限制谐波的国家标准,国际电气电子工程师协会(IEEE),国际电工委员会(IEC)和国际大电网会议(CIGRE)纷纷推出了自己的谐波标准。
国际电工学会于1988年对谐波标准IEC555-2进行了修正,欧洲制定IEC1000-3-2标准。
我国国家技术监督局也于1994年颁布了《电能质量公用电网谐》标准(GB/T 14549-93),传统变流装置大多数已不符合这些新的标准,面临前所未有的挑战。
目前,抑制电力电子装置对电网污染的方法有两种:一是设置补偿装置。
通过对已知频率谐波进行补偿,这种方式适用于所有谐波源,但其缺点是只能对规定频率的谐波进行补偿,应用范围受限。
并且当受到电网阻抗特性或其他外界干扰,容易发生并联谐振,导致某些谐波被放大进而使滤波器过载或烧毁;而是对整流器装置本身性能进行改造,通过优化控制策略和参数设置,使网侧输入的电压和电流呈现接近于同相位的正弦波,实现单位功率因数运行即功率因数为1。
目前治理谐波和无功主要是采用功率因数校正技术(PFC技术),由于PWM调制技术引入整流器中,使得整流器能够获得较好的直流电压并且实现网侧电流正弦化,PWM整流技术已经成为治理电网污染的主要技术手段。
三相电压型PWM整流器控制技术综述
三相电压型PWM整流器控制技术综述一、本文概述随着电力电子技术的不断发展,三相电压型PWM整流器作为一种高效、节能的电能转换装置,在电力系统中得到了广泛应用。
该类整流器采用脉宽调制(PWM)技术,通过控制开关管的通断,实现对输入电流波形的精确控制,从而满足电网对谐波抑制、功率因数校正等要求。
本文旨在对三相电压型PWM整流器控制技术进行综述,分析其基本原理、研究现状和发展趋势,为相关领域的研究和实践提供参考。
本文首先介绍了三相电压型PWM整流器的基本结构和工作原理,包括其主电路拓扑、PWM控制技术以及电流控制策略等。
在此基础上,综述了当前国内外在三相电压型PWM整流器控制技术研究方面的主要成果和进展,包括调制策略优化、电流控制算法改进、系统稳定性分析等方面。
本文还对三相电压型PWM整流器在实际应用中所面临的问题和挑战进行了分析和讨论,如电网电压波动、负载变化等因素对整流器性能的影响。
本文展望了三相电压型PWM整流器控制技术的发展趋势,提出了未来研究的方向和重点,包括高效率、高可靠性、智能化控制等方面。
通过对三相电压型PWM整流器控制技术的综述和分析,本文旨在为相关领域的研究和实践提供有益的参考和借鉴。
二、三相电压型整流器的基本原理三相电压型PWM整流器是一种高效、可控的电力电子设备,它采用脉宽调制(PWM)技术,实现对交流电源的高效整流,将交流电转换为直流电。
整流器主要由三相桥式电路、PWM控制器、滤波电路等部分组成。
三相桥式电路是整流器的核心部分,由六个开关管(通常是IGBT 或MOSFET)组成,每两个开关管连接在一起形成一个桥臂,共三个桥臂。
通过控制开关管的通断,可以实现将三相交流电源整流为直流电源。
PWM控制器是整流器的控制核心,它根据输入电压、电流等信号,生成相应的PWM控制信号,控制开关管的通断时间和顺序,从而实现对输出电压、电流等参数的精确控制。
PWM控制器通常采用数字信号处理器(DSP)或微控制器(MCU)等实现,具有高精度、快速响应等特点。
电力电子系统建模与控制三相PWM整流器动态建模
侧三相线电压与直流侧电压的关系为
xab sa sb sab xbc sb sc vdc sbc vdc xca sc sa sca
第7章 三相PWM整流器动态建模
定义虚拟电流iab、ibc、ica,并满足
这样设计直流侧电压环就变得非常容易,可以将直流 侧对象近似为积分环节,然后将电压环校正成典型II系 统,也可以将电压环PI调节器的零点与直流侧对象的 极点对消,然后将电压环校正成典型I系统。
vref + Kv(τvs+1)/(τvs) idref 1/(Tsvs+1) id RLDd/(RLCs+1) vdc
ia=iab-ica ib=ibc-iab ic=ica-ibc iab+ ibc +ica=0
则有,ia- ib= iab-ica-(ibc-iab)=2 iab-(ica+ ibc)
=3iab, iab=(ia- ib)/3, 同理ibc=(ib- ic)/3,ica=(ic- ia)/3。
第7章 三相PWM整流器动态建模 由表5-1可得
第7章 三相PWM整流器动态建模
将τv设计成与RLC相等,则可将电压环校正成典型I
型系统。因此有 τv =RLC
第7章 三相PWM整流器动态建模
三相PWM整流器仿真系统中,交流侧滤波电感
三相PWM整流器仿真分析
三相电压型PWM整流器的数学模型和主电路设计摘要传统的整流器一般采用二极管整流或相控整流,这种类型的整流器存在着输入电流非正弦,动态性能受到限制和功率因数较低的缺点。
针对以上的问题,本文首先对三相电压型PWM(Pulse Width Modulation)整流器的工作原理进行了分析并得到系统的数学模型,然后推导出PWM整流器双闭环控制系统的传递函数框图并计算电流调节器和电压调节器的参数,最后通过MATLAB对三相电压型PWM整流器系统进行了仿真。
本文采用开关函数法构建了三相VSR(V oltage Source Rectifier)的Simulink 模型,它是依照变换电路的输入与输出的传递函数建立其模型,与电路的拓扑结构无关。
文中详细地论述了电压和电流控制器、整流器、PWM发生单元等各子系统的Simulink建模,并基于所提出的模型研究了PWM整流系统开环控制和双闭环控制下的运行情况和系统特性。
经过仿真发现仿真结果与理论分析相符,验证了模型的正确性。
通过仿真发现滤波电感和直流侧电容参数对系统的稳态运行至关重要。
从仿真的角度验证了三相PWM整流器比传统的相控整流器具备更加良好的性能。
关键词:三相电压型PWM整流器,数学模型,开环控制,双闭环控制MATHEMATICAL MODEL AND MAIN CIRCUIT DESIGN OF THREE-PHASE VOLTAGE-SOURCE PWM RECTIFIERABSTRACTThe traditional rectifier, diode-bridge rectifier or phase-controlled rectifier, cause input current isn't sinusoidal waveform, low power factor, and dynamic performance is limited. In order to solve these problems, first, the mathematical model of 3-phase PWM VSR was created, second, the block diagram of double closed-loop controlled system for three-phase VSR was established. At the same time, the parameters of current regulator and voltage regulator can be calculated, finally, 3-phase PWM VSR was simulated by MATLAB. Based on the above studies, the simulink based model of 3-phase PWM VSR is obtained by using switching function concept which able to model converter circuits according to its input and output transfer functions. The simulink models of the voltage oriented control, voltage controller, current controller, rectifier and PWM generator are developed in detail, and based on these models can analyze the characteristics and system operation of open-loop control and double closed-loop controlled system. The simulation results verify the rectifying state validity of the proposed method. At last, through circuit simulation, we can find filter inductor and DC side capacitance is very important for system. Finally, we can find the PWM rectifier better than traditional rectifier.Key words:three-phase voltage-source PWM rectifier,open-loop control,double closed-loop controlled system,mathematical model目录1 绪论 --------------------------------------------------------------------------------------------------- 11.1 PWM整流技术的发展 --------------------------------------------------------------------- 11.2 PWM整流技术的现状 --------------------------------------------------------------------- 21.3 本文所做的主要工作 ---------------------------------------------------------------------- 42 三相电压型PWM整流电路基本原理和数学模型 ----------------------------------------- 52.1 三相电压型PWM整流电路的拓扑结构和理论分析 ------------------------------- 5三相电压型PWM整流电路的拓扑结构--------------------------------------------- 5三相电压型PWM整流电路的理论分析--------------------------------------------- 62.2 数学模型 ------------------------------------------------------------------------------------- 7整流器开关函数的数学模型------------------------------------------------------------ 8三相静止坐标系下的数学模型--------------------------------------------------------- 9两相静止αβ坐标系模型 --------------------------------------------------------------- 11三相电压型PWM整流器dq模型的建立 ------------------------------------------ 12 3 三相电压型PWM整流器控制系统 ---------------------------------------------------------- 163.1 PWM控制基本原理 ----------------------------------------------------------------------- 163.2 PWM整流器的控制方法 ----------------------------------------------------------------- 173.3 三相电压型PWM整流器双闭环控制 ------------------------------------------------ 19电流内环控制----------------------------------------------------------------------------- 21电压外环控制----------------------------------------------------------------------------- 24 4 主电路交流侧电感和电容设计 ---------------------------------------------------------------- 274.1 三相电压型PWM整流器交流侧电感的计算和选择 ------------------------------ 274.2 三相电压型PWM整流器直流侧电容的参数选择 --------------------------------- 304.3 交流侧电流谐波分析 --------------------------------------------------------------------- 335 三相电压型PWM整流器仿真分析 ---------------------------------------------------------- 365.1 三相电压型PWM整流器系统的开环控制 ------------------------------------------ 365.2 三相电压型PWM整流器双闭环控制仿真 ------------------------------------------ 40各个模块的搭建-------------------------------------------------------------------------- 40仿真参数的设置-------------------------------------------------------------------------- 42仿真结果----------------------------------------------------------------------------------- 43仿真分析----------------------------------------------------------------------------------- 45 结论 ----------------------------------------------------------------------------------------------------- 46 致谢 ----------------------------------------------------------------------------------------------------- 47 参考文献----------------------------------------------------------------------------------------------- 48 附件 ----------------------------------------------------------------------------------------------------- 491.绪论随着电力电子技术的迅猛发展,电力电子器件由早期的不可控二极管、半控型晶闸管,发展到后来的全控型器件POWER-MOSFET、IGBT(Insulated Gate Bipolar Transistor),到目前的IGCT(Integrated Gate Commutated Thyristors)和一体化的IPM (Intelligent Power Module),其开关频率逐步增大,功率等级不断提高,性能更加优异。
三相电压型SVPWM整流器的SIMULINK建模与仿真
No.1
2007.1/2
船电技术 2007 年 第 1 期
三相电压型 SVPWM 整流器的 SIMULINK 建模与仿真
毛文喜 罗隆福
(湖南大学电气与信息工程学院,长沙 410082) 摘 要: 在建立了三相 PWM 整流器数学模型的基础上,将双闭环工程设计方法结合矢量控制策略应用于 SIMULINK 文章编号: 1003-4862( 2007) 01-0023-04
2 三相VSR主电路结构及基本原理
三相 VSR 的主电路结构如 图 1 所示,主要包括 交流侧的电感、电阻、直流电容 以及由全控开关器 件和续流二极管组成的三相整流电路。 ea 、 eb、 ec为电源电压, RL为负载电阻。 开关器件按采用的调制方法动作,由于输入 电感的滤波作用,整流器交流侧的输入可认为是
Vol.27
No.1
2007.1/2
2π 2π ⎤ ⎡ 2 ⎢ cosωt cos(ωt − 3 ) cos(ωt + 3 ) ⎥ T abc→dq = 3 ⎢ 2π 2π ⎥ ⎢− sinωt − sin(ωt − ) − sin(ωt + )⎥ 3 3 ⎦ ⎣
将以上变换作用于 (1)式,则得到整流器在两 相同步旋转 d-q 坐标系下的数学模型为:
PWM 整流器。 通过 MATLAB 的 SIMULINK 工具箱得到系统仿真结果, 验证了该模型和控制方法的可行性。 关键词: PWM 数学模型 空间矢量 中图分类号: TM 461.5 文献标识码: A
The Modeling and Simulation of Three-phase Voltage SVPWM Rectifier
4 空间矢量合成原理
三相 VSR 不同开关组合时的交流侧电压可以 用一个模为 2Udc/3 的空间电压矢量在复平面上表 示出来,由于三相 VSR 开关是双电平控制,其空 间电压矢量只有 23=8种,且 U0(0, 0, 0)、 U7(1, 1, 1)为零矢量 [4]。 空间矢量 PWM控制是通过分配
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三相电压型PWM 整流器建模及控制摘要:本文通过基尔霍夫定律完成了对三相电压型PWM 整流器在三相静止对称坐标系下的数学建模。
并通过MATLAB/SIMULINK 仿真工具对其数学模型进行了仿真验证,可以看出,仿真验证的结果证明了模型的准确性和可靠性。
而后又介绍了一种直接电流控制方法即传统的双闭环PID 控制,并进行了仿真分析。
1 基于基尔霍夫定律对三相VSR 系统建模三相电压型PWM 整流器的电路拓扑结构如图1-1所示。
图中a u 、b u 、c u 为三相交流电源,L 和C 分别为滤波电感和滤波电容,R 是滤波电感的等效电阻,s R 是开关管的等效电阻。
记网侧三相交流电流分别为a i 、b i 、c i ,整流电流为dc i ,流过负载电阻的电流为L i ,负载两端电压为dc v 。
i Le i L图1-1 三相电压型PWM 整流器电路图针对三相VSR 一般数学模型的建立,通常作以下假设: (1) 电网电动势为三相平衡的正弦波电动势(a u ,b u ,c u )。
(2) 网侧滤波电感L 是线性的,且不考虑饱和。
(3) 功率开关管损耗以电阻s R 表示,即实际的功率开关管可由理想开关与损耗电阻s R 串联等效表示。
(4) 为描述VSR 能量的双向传输,三相VSR 其直流侧负载由L R 和直流电动势L e 串联表示。
当直流电动势0L e =时,三相VSR 只能运行于整流模式;当L dce v >时,三相VSR 既可运行于整流模式,又可运行于有源逆变模式;当L dc e v <时,三相VSR 则运行于整流模式。
为分析方便,定义单极性二值逻辑开关函数k s 为10k s ⎧=⎨⎩上桥臂导通,下桥臂关断上桥臂关断,下桥臂导通(,,)k a b c = (1-1)将三相VSR 功率开关管损耗等效电阻s R 和交流滤波电感等效电阻l R 合并,记 s l R R R =+,采用基尔霍夫电压定律建立三相VSR a 相回路方程为()aa a aN NO di LRi u v v dt+=-+ (1-2) 当1S 导通而2S 关断时,1a s =,且aN dc v v =;当1S 关断而2S 导通时,开关函数0a s =,且0aN v =。
由于aN dc a v v s =,上式可写成()aa a dc a NO di LRi u v s v dt+=-+ (1-3) 同理,可得b 相、c 相方程如下:()bb b dc b NO di LRi u v s v dt +=-+ (1-4) ()c c c dc c NO diL Ri u v s v dt+=-+ (1-5) 考虑三相对称系统,则0a b c u u u ++= 0a b c i i i ++= (1-6)故..3dc NO k k a b cv v s ==-∑(1-7)在图1-1中,任何瞬间总有三个开关管导通,其开关模式共有328=种,因此,直流侧电流dc i 可描述为()dc a a b c b b c a c c b a a b a b c i i s s s i s s s i s s s i i s s s =+++++()()()a c a c b b c b c a a b c a b c i i s s s i i s s s i i i s s s ++++++a ab bc c i s i s i s =++ (1-8)另外,对直流侧电容正极节点处应用基尔霍夫电流定律,得dc dc L a a b b c c Ldv v eCi s i s i s dt R -=++- (1-9) 则采用单极性二值逻辑开关函数描述的三相VSR 系统的一般数学模型表达式为:,,,,,,131313a a dc a k ak a b c b b dc b k b k a b c cc dc c k c k a b c dc dc L a a b b c cL d L i Ri v s s u dtd L i Ri v s s u dt d L i Ri v s s u dt dv ve C s i s i s i dt R ===⎧⎛⎫=---+⎪ ⎪⎝⎭⎪⎪⎛⎫⎪=---+ ⎪⎪⎝⎭⎨⎛⎫⎪=---+ ⎪⎪⎝⎭⎪⎪-=++-⎪⎩∑∑∑ (1-10) 2 模型验证在以上的内容中已经对三相VSR 进行了数学建模,在此我们对已经得到的数学模型进行模型验证。
2.1 建立系统仿真模型以u[1],u[2],u[3],u[4],u[5],u[6],u[7],u[8],u[9],u[10],u[11],u[12],u[13],u[14]分别代表a i ,b i ,c i ,a u ,b u ,c u ,a s ,b s ,c s ,dc v ,R ,L ,C ,L R 。
构建出系统的SIMULINK 仿真模型如图2-3所示,故可以根据三相VSR 系统的数学模型可得到函数Fun ,Fun1,Fun2和Fun3的表达式分别为: Fun :(u[4]-u[11]*u[1]-u[10]*u[7]+u[10]*(u[7]+u[8]+u[9])/3)/u[12] Fun1:(u[5]-u[11]*u[2]-u[10]*u[8]+u[10]*(u[7]+u[8]+u[9])/3)/u[12] Fun2:(u[6]-u[11]*u[3]-u[10]*u[9]+u[10]*(u[7]+u[8]+u[9])/3)/u[12] Fun3:(u[1]*u[7]+u[2]*u[8]+u[3]*u[9]-u[10] /u[14])/u[13] Fcn4:(u[1]*u[7]+u[2]*u[8]+u[3]*u[9])系统仿真模型系统模型方程中的常量R ,L ,C ,L R 是可变参数,其可在模型外部进行灵活设置,这里取0.3R =Ω,20mH L =,990μF C =,200L R =Ω。
2.2 系统仿真模型验证针对图1-1所示的三相VSR 主电路结构图, 当采用单极性二值逻辑开关函数描述时:()jN j dc v t s v = (,,)j a b c = (2-1)式中 j s ——单极性二值逻辑开关函数。
当忽略三相VSR 桥路损耗时,其交、直流侧的功率平衡关系为:,,()()()j jN dc dc j a b ci t v t i t v ==∑(2-2)联立上面两式并化简,得:()()()()dc a a b b c c i t i t s i t s i t s =++ (2-3)表2-1给出了不同开关模式调制时的()dc i t 取值:为了检验已搭建完并设置了参数的三相VSR 仿真模型是否与实际系统相符,下面设计了三个实验对模型进行验证,如下表2-2所示:表2-1 三相VSR 不同开关模式调制时()dc i t 取值表2-2 实验设计以下三组实验的实验结果如下图2-1所示:(a) 模型验证实验一曲线(b) 模型验证实验二曲线 (c) 模型验证实验三曲线图2-1 三组模型验证实验数字仿真结果由上面三个实验的结果可以看出,该模型行为与理论分析相符合,因而可以说这个仿真模型是可以很好地代替原系统进行仿真实验的。
3 直接电流控制3.1仿真模型的建立从整流器数学模型式可以看出,直流侧输出电压在稳态时应该达到恒定值,电压控制器作为外环控制,一方面控制输出电压dc v 跟踪电压设定值*dc v ;另一方面,通过控制器得到有功输入电流分量的参考值*d i ,无功电流分量的参考值*0q i 。
此电压外环采用PI 控制策略设计控制系统用来维持直流侧电压dc v 恒定。
控制系统框图如图所示:PWM 整流器的控制系统框图根据三相VSR 的数学模型,及双闭环控制系统的结构图,建立三相VSR 双闭环PID 控制系统的数字仿真模型和三相VSR 被控对象的模型如图3-1和图3-2所示:图3-1 三相VSR 双闭环控制系统数字仿真模型图3-2 三相VSR 模型对于本三相VSR 系统的参数,取78cos a e t ω=,78cos(120)b e t ω=-,78cos(120)c e t ω=+,0.3R =Ω,0.02H L =,负载电阻100L R =Ω,C=990µF 。
对于电流内环PI 控制器理论计算值66.7ip K =,1000iI K =。
仿真实验值100ip K =,++-+-+-+-1212+-i +-i -Ibi +-Ia1000iI K =。
对于电压外环PI 控制器理论计算值13.3up K =,8867up K =,仿真实验值0.1up K =,0.7up K =。
外环电压*0250V u =。
3.2 PID 控制系统仿真实验结果及分析仿真结果如图3-3所示,分别得到了a e ,a i ,d i ,q i ,dc v 以及功率因数的波形。
(a) a e ,a i 的波形(b) d i ,q i 的波形(c) dc v 的波形(d) 功率因数的波形图3-3仿真结果从上述仿真结果可以得到以下结论:(1) 从图3-3中的a e ,a i 的波形和d i ,q i 的波形可以看出电流内环控制系统于0.3t s =时基本趋于稳定,从直流侧输出电压的波形可以看出电压外环控制系统在0.5t s =时基本达到稳态;(2) 从直流侧输出电压的波形可以看出,在系统达到稳态后,稳态时直流输出电压无静差;(3) 从功率因数的波形可以看出,在0t =至0.25t s =之间,由于在开始阶段存在波形畸变,所以功率因数较低。
在达到稳态后,功率因数达到0.999以上,实现了单位功率因数控制。
t/se a /v ,i a /at/si d ,i q /At/su o /Vt/sP F。
