材料力学第八章答案 景荣春
家电公司研发部资料材料力学习题答案(八)

第八章 组合变形及连接部分的计算8-1 矩形截面简支梁其受力如图所示,试求梁截面上的最大正应力,并指出中性轴的位置。
(截面尺寸单位:mm )答:σmax =12MPa解:将F 分解成两个力对杆作用效果之和,133 4.52y M kN m =⨯⨯= , 13462z M kN m =⨯⨯=, 131504.52620015012y y M z MPa I σ⨯===⨯,2320062615020012z zM y MPa I σ⨯===⨯; 则1212MPa σσσ=+=;由3320015012tan tan 0.4515020012y zI I θϕ⨯===⨯,24.23θ=.:8-2 图示圆截面简支梁,直径d =200mm, F 1=F 2=5kN, 试求梁横截面上的最大正应力。
答:σmax =4.74MPa解:由于截面为圆形在可以用和弯矩求解max σ,即求max F ,且max F 最大在截面2-2处,由图可知max3.727F kN =, 则3max23.727100.14.740.264PM MPa I ρσπ⨯⨯===⨯A150题 8 - 1 图FF 2题 8 - 2 图8-3 图示悬臂梁,由试验测得εA =2.1×10-4,εB =3.2×10-4, 已知材料的E =200GPa ,试求P 和β值。
答:F =1.03kN,β='2131ο解:由已知74.210AA E Pa σε==⨯,76.410B B E Pa σε==⨯,又有y A z zF ly My I I σ==得y F =875N ,同理z F =535N 则F =1.03kN,'arctan()3021zyF F β== 8-4图示圆截面轴在弯矩M 和扭矩T 联合作用下,由试验测得A 点沿轴向的线应变为0ε=5×10-4,B 点与轴线成45°方向的线应变为ε45°=4.3×10-4。
《材料力学》第八章课后习题参考答案

解题方法与技巧归纳
受力分析
在解题前首先要对物体进行受力分析, 明确各力的大小和方向,以便后续进 行应力和应变的计算。
图形结合
对于一些复杂的力学问题,可以画出 相应的示意图或变形图,帮助理解和 分析问题。
公式应用
熟练掌握材料力学的相关公式,能够 准确应用公式进行计算和分析。
检查结果
在解题完成后,要对结果进行检查和 验证,确保答案的正确性和合理性。
压杆稳定
探讨细长压杆在压缩载荷作用下的稳定性问题。
解题方法与技巧
准确理解题意
仔细审题,明确题目要求和考查的知识点。
选择合适的公式
根据题目类型和所给条件,选用相应的公式 进行计算。
注意单位换算
在计算过程中,要注意各物理量的单位换算, 确保计算结果的准确性。
检查答案合理性
得出答案后,要检查其是否符合实际情况和 物理规律,避免出现错误。
相关题型拓展与延伸
组合变形问题
超静定问题
涉及多种基本变形的组合,如弯曲与扭转 的组合、拉伸与压缩的组合等,需要综合 运用所学知识进行分析和计算。
超静定结构是指未知力数目多于静力平衡 方程数目的结构,需要通过变形协调条件 或力法、位移法等方法进行求解。
稳定性问题
疲劳强度问题
研究细长压杆在压力作用下的稳定性问题 ,需要考虑压杆的临界力和失稳形式等因 素。
研究材料在交变应力作用下的疲劳破坏行为 ,需要了解疲劳极限、疲劳寿命等概念和计 算方法。
THANKS FOR WATCHING
感谢您的观看
重点知识点回顾
材料的力学性质
包括弹性、塑性、强度、硬度等基本概念和 性质。
杆件的拉伸与压缩
涉及杆件在拉伸和压缩状态下的应力、应变及 变形分析。
材料力学简明教程(景荣春)课后答案4

网
案 b 解
FS
(x)
=
ql 4
−
qx
(0 < x < l)
答 M (x) = ql x − q x2 (0 ≤ x ≤ l)
42
课后 FS
max
=
3 ql 4
,
M = ql2 max 4
( ) c 解
∑MA =0
, − q × 2l × l
+
FB
× 2l
+ ql 2
=
0 , FB
=
ql 2
↑
( ) ∑ Fy
网 FS+C
=
1 ql 2
,
M
+ C
=
− 1 ql 2 ; 8
FSB = 0 , M B = 0
案 4-2 已知各梁如图,求:(1)剪力方程和弯矩方程;(2)剪力图和弯矩图;(3) FS max
和M 。 max
答
后
课
解 设左支座为 A,右支座为 B
( ) ∑ M B = 0 , FA = −F ↓
FS (x) = −F
=
ba a+b
F
FS+C
=
−a a+b
F
,
M
+ C
=
ba a+b
F ; FSB
=
−A a+b
F
,MB
=
0
d解
图(d1), ∑ Fy
=
0,F
=
1 2
ql
,
∑
M
A
= 0,M A
=
− 3 ql 2 8
仿题 a 截面法得
材料力学简明教程(景荣春)课后答案2

7
σ 60o
= 100 cos2 60o
= 100 × (1 )2 2
= 25 MPa
F
τ 60o
= 100 sin 2 × 60o 2
= 100 × 2
3 = 43.3MPa 2
σ 90o
= 0 ,τ 90o
= 100 sin 2 × 90o 2
=0
F
60°
σ 90° = 0 90°
=
l1 − l l
×100% 知,对同
1
种材料, δ 5
> δ10 ,即对
后 δ 5 = 20% 的某材料,其δ10 < 20% ;显然,另 1 种材料δ10 = 20% 塑性性能较好。
课 2-12 由同一材料制成的不同构件,其许用应力是否相同?一般情况下脆性材料的安全
因数为什么要比塑性材料的安全因数选得大些? 答 由同一材料制成的不同构件,其许用应力不一定相同,这取决于工况、环境和重要
(a)
(b)
思考题 2-13 解图
2-14 计算拉压超静定问题时,轴力的指向和变形的伸缩是否可任意假设?为什么?
4
答 计算拉压超静定问题时,轴力的指向假设和变形的伸缩应对应(只有其中 1 个可任 意假设),即轴力设正(负)时,变形应设成拉(缩)。否则,计算结果有问题。
2-15 图示杆件表面有斜直线 AB ,当杆件承受图示轴向拉伸时,问该斜直线是否作平
2-7 某拉伸试验机的结构示意图如图所示。设试验机的杆 CD 与试样 AB 材料同为低 碳钢,其σ p = 200 MPa ,σ s = 240 MPa ,σ b = 400 MPa 。试验机最大拉力为 100 kN。
问:(1)用这一试验机作拉断试验时,试样直径最大可达多大?
材料力学简明教程(景荣春)课后答案

第 3 章扭转思考题3-1何谓扭矩?扭矩的正负号如何规定的?如何计算扭矩?答轴在外力偶矩作用下,由截面法求出的横截面上分布内力向截面形心简化的合力(力偶矩)称为扭矩。
对扭矩T的正负规定为:若按右手螺旋法则把T表示为矢量,当矢量方向与截面的外法线n的方向一致时,T为正;反之为负。
用截面法计算扭矩,注意截面位置应偏离外力偶矩作用面。
3-2薄壁圆筒、圆轴扭转切应力公式分别是如何建立的?假设是什么?公式的应用条件是什么?答等厚薄壁圆筒在两端垂直于轴线的平面内作用大小相等而转向相反的外力偶M e所做试验结果现象表明,当薄壁圆筒扭转时,其横截面和包含轴线的纵向截面上都没有正应力,横截面上只有切应力⎜,因为筒壁的厚度 ™很小,可以假设沿薄壁圆筒筒壁厚度切应力不变。
又因在同一圆周上各点情况完全相同,应力也就相同,从而建立薄壁圆筒扭转切应力计算公式;在圆轴两端施加一对大小相等、方向相反的外力偶。
从实验中观察到的现象,假设轴变形后,横截面仍保持平面,其形状、大小与横截面间的距离均不改变,而且半径仍为直线(圆轴扭转平面假设),连同胡克定律和静力平衡条件推出圆轴扭转切应力计算公式。
公式应用条件为线弹性材料、小变形、等截面(锥度不大的变截面可近似用)。
3-3试述纯剪切和薄壁圆筒扭转变形之间的差异及相互关系。
答单元体 4 个互相垂直的面上只作用切应力的状态称为纯剪切;薄壁圆筒扭转变形时(忽略厚度影响)筒壁各点的应力状态为纯剪切。
3-4试述剪切胡克定律与拉伸(压缩)胡克定律之间的异同点及3 个弹性常量E, G, ⎧之间关系。
答剪切胡克定律⎜ = G©(反映角度的变化)与拉伸(压缩)胡克定律 ⎛ = E∑(反映长度的变化)皆为应力与应变成正比关系。
3 个弹性常量E, G, ⎧之间关系为G =E2(1 + ⎧ )。
3-5圆轴扭转时如何确定危险截面、危险点及强度条件?答等截面圆轴扭转时的危险截面为扭矩最大的横截面,变截面圆轴扭转时的危险截面在其扭矩与扭转截面系数比值最大的横截面;其危险点在该横截面的外边缘。
材料力学刘德华版课后习题问题详解word版
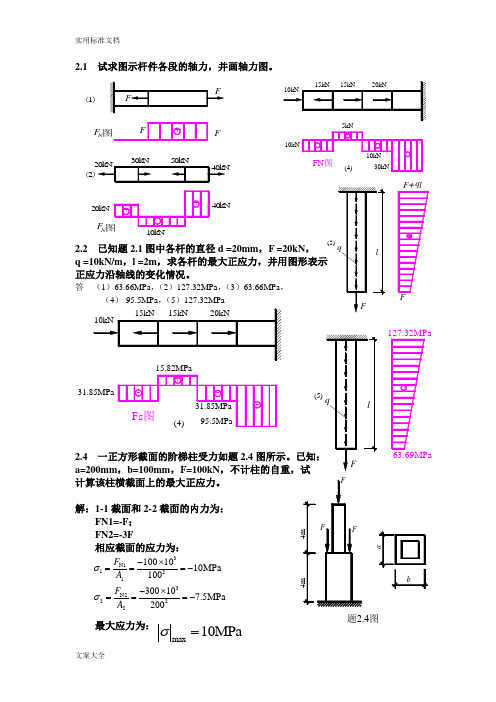
2.1 试求图示杆件各段的轴力,并画轴力图。
2.2 已知题2.1图中各杆的直径d =20mm ,F =20kN ,q =10kN/m ,l =2m ,求各杆的最大正应力,并用图形表示 正应力沿轴线的变化情况。
答 (1)63.66MPa ,(2)127.32MPa ,(3)63.66MPa ,(4)-95.5MPa ,(5)127.32MPa2.4 一正方形截面的阶梯柱受力如题2.4图所示。
已知:a=200mm ,b=100mm ,F=100kN ,不计柱的自重,试 计算该柱横截面上的最大正应力。
解:1-1截面和2-2截面的内力为: FN1=-F ;FN2=-3F相应截面的应力为:最大应力为:15kN15kN20kN10kN(4)10kN5kN10kN 30kN+---FN 图-+++FF FF 20kN 30kN 50kN 40kN40kN10kN 20kN (2)(1)F N 图图N F l(5)q FFF q ll(5)qF+127.32MPa63.69MPa15kN 15kN 20kN 10kN (4)31.85MPa 15.82MPa +---Fs 图31.85MPa95.5MPa 4m4mabF题2.4图FF3N11213N22221001010MPa 100300107.5MPa200F A F A σσ-⨯===--⨯===-max 10MPaσ=2.6 钢杆受轴向外力如图所示,横截面面积为500mm2,试求 ab 斜截面上的应力。
解: FN=20kN2.8 图示钢杆的横截面积 A=1000mm2,材料的弹性模量E=200GPa ,试求:(1)各段的轴向变形;(2)各段的轴向线应变;(3)杆的总伸长。
解:轴力图如图所示2.10 图示结构中,五根杆的抗拉刚度均为EA ,杆AB 长为l ,ABCD 是正方形。
在小变形条件下,试求两种加载情况下,AB 杆的伸长。
解 (a )受力分析如图,由C 点平衡可知:3020kNob aa b a b p αs αατF N o N N 0cos30==F F p A A ααo 2oN 03cos30cos 302010330MPa 5004F p A σ==⨯=⨯=αα3o o o N020103sin30cos30sin3017.32MPa 5004F p A ⨯===⨯=αατ-+20kN20kN 20kN ⅠⅡⅢ20kN20kN1m 1m 2m12320N 0N 20N N N N F k F k F k ===-41119624333962011020010100010020221020010100010N N F l L m EA L m F l L m EA ----⨯∆===⨯⨯⨯∆=⨯∆===-⨯⨯⨯⨯4411122244333101010210102L m l mL l L ml mεεε----∆===∆==∆-⨯===-41243100210L m L m L m--∆=∆=∆=-⨯I II III 0.1mm 00.2mm 0.1mm l l l l ∆=∆+∆+∆=+-=-实用标准文档F ’AC=F ’CB=0;由D 点平衡可知: F ’AD=F ’BD=0; 再由A 点的平衡:因此(b )受力分析如图,由C 点平衡可知:再由A 点的平衡:因此2.12 图示结构中,水平刚杆AB 不变形,杆①为钢杆,直径d1=20mm ,弹性模量E1=200GPa ;杆②为铜杆,直径d2=25mm ,弹性模量E2=100GPa 。
(第八)课后习题答案

Fj
=
FL 8r
=
20 × 300 ×10−3 8 × 75 2 ×10−3
=5
2kN
由图可知,螺栓最大受力
Fmax = Fi2 + Fj 2 + 2Fi Fj cos θ = 2.52 + (5 2)2 + 2 × 2.5 × 5 2 × cos 45° = 9.015kN
∴ τ = Fmax = 9.015 ×103 = 319 > [τ]
+
Ld
− Ld 0 2
= 550 +
2240 − 2214 2
= 563mm
中心距的变化范围为 550 ~ 630mm 。
∴由d0 ≥
4Fmax
π[τ]
可知采用(a)布置形式所用的螺栓直径较小
5-10
第六章 键、花键、无键连接和销连接 习题答案
6-3 在一直径 d = 80mm 的轴端,安装一钢制直齿圆柱齿轮(如下图),轮毂宽度 L = 1.5d ,工作时有轻
微冲击。试确定平键的尺寸,并计算其允许传递的最大扭矩。
[解] 根据轴径 d = 80mm ,查表得所用键的剖面尺寸为 b = 22mm , h = 14mm 根据轮毂长度 L'= 1.5d = 1.5 × 80 = 120mm 取键的公称长度 L = 90mm 键的标记 键 22 × 90GB1096 - 79 键的工作长度为 l = L − b = 90 − 22 = 68mm 键与轮毂键槽接触高度为 k = h = 7mm 2
Θ 5 m s < ν < 30 m s ∴ 带速合适
③计算从动轮的基准直径
dd2
=
d d 1n1 (1 −
材料力学刘德华版课后习题答案word版

材料力学刘德华版课后习题答案word版2.1试求图示杆件各段的轴力,并画轴力图。
f(1)f+fn图30kn50kn20kn(2)+20kn+-fn图10knf10kn15kn15kn20knf10kn5kn-fn图+-10kn30kn-fql40kn(4)40kn(5)q2.2未知题2.1图中各杆的直径d=20mm,f=20kn,q=10kn/m,l=2m,求各杆的最大正应力,并用图形表示正应力沿轴线的变化情况。
l请问(1)63.66mpa,(2)127.32mpa,(3)63.66mpa,(4)-95.5mpa,(5)127.32mpa15kn15kn20kn10kn15.82mpa+-31.85mpa--31.85mpafs图95.5mpa(4)ff127.32mpa+(5)qlfn2?300?103?27.5mpaa220024m2.4一正方形横截面的阶梯柱受力如题2.4图右图。
未知:a=200mm,b=100mm,f=100kn,数等柱的蔡国用,先行排序该柱横截面上的最小正形变。
解:1-1截面和2-2截面的内力为:fn1=-f;ffn2=-3f相应截面的应力为:fn1?100?103?110mpaa110024mff63.69mpafab最大应力为:max10mpa题2.4图2.6钢杆受到轴向外力如图所示,横截面面积为500mm2,试求30aab斜横截面上的形变。
求解:fn=20knbfnfnapα==cos30ofnaaα0fb?α?pαcos30o?ncos230oaa0sαpα20?103330mpaταb50043f20?103ooonτcos30sin3017.32mpaα?pαsin30?a050042.8图示钢杆的横截面内积a=1000mm2,材料的弹性模量e=200gpa,试求:(1)各段的轴向变形;(2)各段的轴向线快速反应;(3)杆的总弯曲。
20kn解:轴力图如图所示20kn20knⅲⅰⅱfn1?20kn1m1m2mfn2?0kn20kn+fn3??20kn-fl20?1?420kn?l1?n11??10m9?6ea200?10?1000?10?l2?0mfn3l320?2?4?l2?10m39?6ea2 00?10?1000?10?l110?4m?4?410?l?10m11l11ml20ml220l2l32104ml32104m3104l32mlliliiliii0.1mm00.2mm0.1mm2.10图示结构中,五根杆的抗拉刚度均为ea,杆ab长为l,abcd是正方形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6 × 1 650 6 × 800 + = 10 × 10 6 4b 3 2b 3
118
b = 90 mm , h = 2b = 180 mm
8-4 夹 器 力 F = 16 kN , 宽度 b
夹
a×b 形,如图 应 力 [σ ] = 160 MPa ,
已
作 厚 a = 20 mm , 偏
夹
器
e = 140 mm
2 F = 0 .2 P 3
y
P × 0.3 = 0.15P 2 TC = M e = 0.15P , TC = M e = 0.15P
M Cy = FBz × 0.3 = 0.06 P , M Cz =
σ r4 =
2 2 M Cy + M Cz + 0.75TC
2
W
≤ [σ ]
32 × 0.062 + 0.152 + 0.75 × 0.152 P ≤ 80 × 106 3 −9 π × 25 × 10
= 8-2 因使 大 力 中 如图(a) ,在 一 应力和 大压应力, 并 影响 ? 一
3 1 ( 2 2 )2 + ( 2 2 )2 0.16 0.12
a , 原 形, 力 F 围内开一 a / 2 宽 口,如图 大 应力 削弱以前 应力值
合
后 应
m−m
几倍
117
(a)
(b)
弱前
σ 1t =
弱后,
度 件
2 2
σ
2
2
2
2F ⎛ 2 F ⎞ ⎛ 16M e ⎞ + ⎜ 2 ⎟ +⎜ ⎟ ≤ [σ ] 2 3 πd ⎝ πd ⎠ ⎝ πd ⎠
8-11 图 度 圆 度 , 已
F1 , 向 F2 力偶 M e 作 , F1 = 500 N , F2 = 15 kN , M e = 1.2 kN ⋅ m ,
, 1 2 圆 别 45 号 制 度 3 度
d 2 = 130 mm 在
2 ,作 向 应
力 Fy′ = 1.473 kN ,向力 Fz′ = 0.536 kN 力 [σ ] = 180 MPa ,
, d = 22 mm ,
(a)
(b)
力如图 b
之
图
T = M e = Fy ⋅
d1 50 = 3.83 × 10 3 × × 10 −3 = 95.75 N ⋅ m 2 2
+ 3τ ≤ [σ ] ;
度
(c)
M 2 +T2 ≤ [σ ] W
出
件,其中
形
况 合 形 ,危 形 中 于何 处于
处于 向弯 向 伸 压 处 应力并建 应 度 件? 处于 向弯 形 , 危 于 形 合 形 ,危 于 形
115
σ max =
M z max Wz
+
M y max Wy
≤ [σ ]
116
出危
8-9 图(a) 制 , 应力 度 件
d,
处
向力 F 单元体 应力
力偶
[σ ] ,
Me 作 ,
4 度
塑 建
图,并
(a)
(b)
σ=
τ max
F 4F = A πd 2 M 16M e = e = Wp πd 3
2 σ eq4 = σ 2 + 3τ max ≤ [σ ]
度
件
⎛ 16 M e ⎞ ⎛ 4F ⎞ ≤ [σ ] ⎜ 2 ⎟ + 3⎜ 3 ⎟ ⎝ πd ⎠ ⎝ πd ⎠
T = 3.2 × 10 3 × 140 × 10 −3 = 448 N⋅ m
它们在 A 别产 应力和 应力,其应力 如图(b),其中
σ =
My Wy
=
32 × 288 = 23.5 × 10 6 Pa = 23.5 MPa −9 3 π × 50 × 10
119
τ=
16 × 448 T = = 18.3 × 106 Pa = 18.3 MPa −9 3 Wp π × 50 × 10
向
122
3 应力
[σ ] = 160 MPa
危
在固定
和
σ=
F2 F1l Me + ,τ = A W Wp
2 2 2 ⎛ Me ⎞ ⎛ F2 F1l ⎞ ⎟ = ⎜ + ⎟ + 4⎜ ⎜W ⎟ ⎝ A W ⎠ ⎝ p ⎠ 2
σ eq3 = σ + 4τ
⎛ 1.2 × 10 3 × 16 ⎛ 15 × 10 3 × 4 500 × 0.9 × 32 ⎞ ⎜ ⎟ + 4 + = ⎜ ⎜ π × 50 3 × 10 −9 ⎜ π × 50 2 × 10 −6 π × 50 3 × 10 −9 ⎟ ⎝ ⎝ ⎠ = 107.4 MPa < [σ ]
8-12 图 (a) 圆 , 带动 在 Ft = 1.9 kN , 向 力 Fr = 740 N , 以 及 平 于 4 度 度
2
⎞ ⎟ ⎟ ⎠
W 即可 A
应力 外力 外力 平 列3个
应力 和 形 各 什么? 作 在 形 合 形 平 平 平 式各
2 2
平 合 况
平
内
其
形后
平
度 件
于什么
( a ) σ 1 − σ 3 ≤ [σ ] ; ( b ) σ
答 它们 式 a 式 b 式 c 8-8 当 形 处?如何 危 答当 形 向 伸 压 度 于任 应力 于平 应力 于圆 弯 合 3
弯
合
形 度
制
,
否仍可
M 2 +T2 ≤ [σ ] W
M 2 + 0.75T 2 ≤ [σ ] W
答 件,
M 2 +T2 ≤ [σ ] W
于塑 , 伸 ,
M 2 + 0.75T 2 ≤ [σ ] W
, 应力 W, 以
3
4
度
出
度
8-5 偏 答 可以 使 8-6 弯 答 弯 形 8-7
否可使 A,弯
应力? 力偏 e, 使e <
=
2 × 20 × 10 −3 × 160 × 10 6 = 0.0673 m = 67.3 mm
d = 50 mm 出
8-5 力如图(a) ,其圆 单元体,并 其 应力及 大 应力
A 处应力
A
τ
σ
(a)
(b)
解
A
在
弯
和
作
,其值
M y = 3.2 × 10 3 × 90 × 10 −3 = 288 N⋅ m
A
应力 如图(a) 4 已 度 d = 25 mm , 大 吊 P=W Q235 ,其 应
力 [σ ] = 80 MPa
(a)
y
400 A 300 300
P/2 z FAz R
D
Me
C
P/2
B x
FBz
P
F
(b)
解
已
∑M ∑M
力图(b),其中 M e = 0.15P ,C 处
危
,其 1
x
= 0 , F × 500 = P × 150 , F = 0.3P = 0 , F × 400 = FBz × 600 , FBz =
F a2 m−m Fa M = 4
a 力如图 b
σ 2t =
F a2 2
σ 2c =
F a2 2
Fa 8F M 2F + = 2 + 4 2 = 2 W a a ⎛a⎞ a⎜ ⎟ ⎝2⎠ 6 Fa M 2F 4F − = 2 − 4 2 =− 2 W a a ⎛a⎞ a⎜ ⎟ ⎝2⎠ 6
, 弱后 大 应力 弱前 应力 8倍
23.5 23.5 2 σ ± ( )2 + τ 2 = ± ( ) + 18.3 2 2 2 2 2 33.5 = 11.8 ± 21.7 = MPa − 9.95 σ2 = 0 σ − σ 3 33.5 + 9.95 τ max = 1 = = 21.7 MPa 2 2
σ 1,3 =
σ
剪力在 8-6 一
件在弯
和
合作
形
弯
合
形
8-2 何 弯 偏 压及弯 答 弯 偏 压及合 形 形在
应力可 叠 原 小 形 件 ,
应力
力
8-3 何弯 合 形 度 件 代 叠 ? 答 弯 形 度 件 单向应力 度 件 度 件, 应力 应力 互垂 , 代
叠
形 只
度 同向
件 剪 应 向 叠
8-4 如
Fy + 2 Fy′
M Cz = FAy × 50 mm = 152.2 N ⋅ m , M Cy = FAz × 50 mm = 37.5 N ⋅ m
σ=
W
圆 ,
32 152.2 2 + 37.5 2 + 95.75 2 = = 176 MPa < [σ ] ,安全 π × 223 × 10 −9
解
力 FN = F ,弯
M = Fe
σ max =
F Fe F 6 Fe + = + ≤ [σ ] A W ab ab 2 F 1 6e b + 6e a[σ ] ( + 2 ) ≤ [σ ] , ≤ F a b b b2 a[σ ] 2 a[σ ] 2 b , b − b − 6e ≥ 0 b + 6e ≤ F F 1 + 1 + 24ea[σ ] / F F (1 + 1 + 24ea[σ ] / F b≥ = 2a[σ ] 2a[σ ] F 16 × 10 3 [1 + 1 + 24 × 140 × 10 −3 × 20 × 10 −3 × 160 × 10 6 /(16 × 10 3 ) ]
