山西省太原市第五中学2017届高三阶段测试(5月模拟)数
【山西省太原第五中学年】2017届高三第二次模拟考试(5月)数学年(理)试题

答案
一、选择题 1~5.CDACB 二、填空题
6~10.BCDCA
11~12.CB
13. 13
14.120 15. 41π 16. 2 017 三、解答题 17.解:(1)在 △BEC 中,据正弦定理,有 BE CE .
sinBCE sin B
2.
5
5
35 2 . 17. 5
4分
1/6
a 16 2 3. 5 9 .
月度市场占有率 y 与月份序号 x 之间的线性回归方程为 y 2x 9 .
5分
当 x 7 时, y 2 7 9 =23 .
故 M 公司 2 017 年 4 月份的市场占有率预计为 2300 .
每辆 B 款车可产生的利润期望值为 2. 7 500 1 200 150 (元).
应该采购 A 款单车.
12 分
19.解:(Ⅰ)取线段 CD 的中点 Q ,连结 KQ ,直线 KQ 即为所求.
如图所示:
10 分
2/6
(Ⅱ)以点 A 为原点, AB 所在直线为 x 轴, AD 所在的直线为 y 轴,建立空间直角坐标系,如图,
B 2π , BE 1,CE 7, sinBCE BE sinB 2 21 .
3
CE
7 14
(2)由平面几何知识,可知 DEA BCE, 在 Rt△AED 中,
A π , AE 5, cosDEA 1 sin2DEA 1 3 5 7 .
当 a 0 时,由 h(x) 0 得, x0 1 a , h(x) 在 ( 1 a , 1 a) 上单调递减,在 ( 1 a , ) 上单调递增.
山西省太原五中2017届高三5月月考试题数学理(含答案)word版
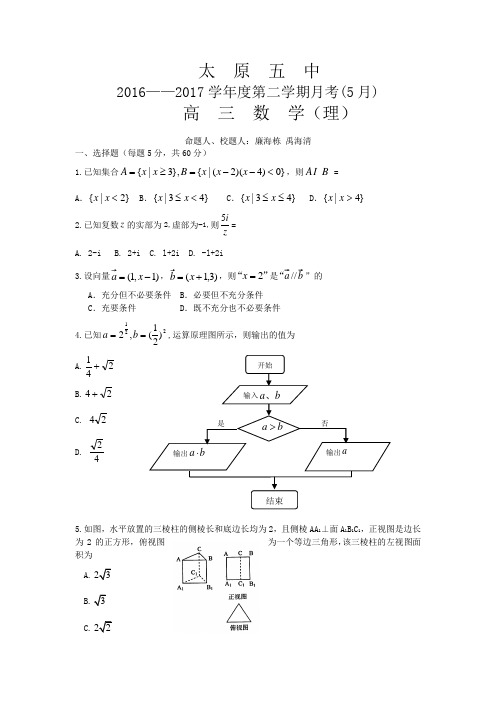
太 原 五 中2016——2017学年度第二学期月考(5月)高 三 数 学(理)命题人、校题人:廉海栋 禹海清一、选择题(每题5分,共60分)1.已知集合}0)4)(2(|{},3|{<--=≥=x x x B x x A ,则A B = A .}2|{<x x B .}43|{<≤x x C .}43|{≤≤x x D .}4|{>x x2.已知复数z 的实部为2,虚部为-1,则5iz= A. 2-i B. 2+i C. l+2i D. -l+2i3.设向量)1,1(-=x a ,)3,1(+=x b ,则”“2=x 是//“”的A .充分但不必要条件B .必要但不充分条件C .充要条件D .既不充分也不必要条件 4.已知221)21(,2==b a ,运算原理图所示,则输出的值为 A.241+ B.24+C. 24D.425.如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱AA 1⊥面A 1B 1C 1,正视图是边长为2的正方形,俯视图为一个等边三角形,该三棱柱的左视图面积为A.C.D.46.等比数列{a n }中,a 3=6,前三项和3304S xdx =⎰,则公比q 的值为( )A.1B.12-C.1或12-D.1-或12-7.设函数1()ln (0)3f x x x x =->,则函数()f x (A) 在区间(0,1)(1,)+∞, 内均有零点 (B) 在区间(0,1)(1,)+∞, 内均无零点(C) 在区间(0,1)内有零点,在区间(1,)+∞内无零点 (D) 在区间(0,1)内无零点,在区间(1,)+∞内有零点8.把函数)||,0)(sin(πφωφω<>+=x y 的图象向左平移6π个单位,再将图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)所得图象解析式为 x sin y =,则(A )62πφω==, (B )32π-=φ=ω,(C )621π=φ=ω, (D )1221π=φ=ω,9.已知函数|lg |)(x x f =,若b a <<0,且)()(b f a f =,则的取值范围是b a +2A. ),22(+∞B. ),22[+∞C. ),3(+∞D. ),3[+∞.10.已知P 为抛物线y=21x 2上的动点,点P 在x 轴上的射影为M ,点A 的坐标是(6,217),则|PA|+|PM|的最小值是 ( ) (A)8 (B)219(C)10(D)221 11.已知球O 是棱长为1的正方体ABCD —A 1B 1C 1D 1的内切球,则平面ACD 1截球O 所得的截面面积为A .36π BC .9π D .6π 12.对于定义域和值域均为[0,1]的函数f(x),定义1()()f x f x =,21()(())f x f f x =,…,1()(())n n f x f f x -=,n=1,2,3,….满足()n f x x =的点x ∈[0,1]称为f 的n 阶周期点.设12,0,2()122,1,2x x f x x x ⎧≤≤⎪⎪=⎨⎪-<≤⎪⎩ 则f 的n 阶周期点的个数是(A) 2n (B) 2(2n-1) (C) 2n(D) 2n 2二、填空题(每小题5分,共20分)13.二项式12)2(xx +的展开式中常数项是第 项。
山西省太原市第五中学2017届高三第二次模拟考试(5月)

太原五中2016-2017学年度第二学期阶段性检测高 三 数 学(理)出题人、校对人:张福兰、王彩凤、李小丽(2017年5月8日)一、选择题(每小题5分,共60分,每小题只有一个正确答案)1.已知全集R U =,}02{2<-=x x x A ,}1{≥=x x B ,则=)(B C A UA .),0(+∞ B. )1,(-∞ C .)2,(-∞ D . (0,1) 2. 如果复数21iz =-+,则 A .的共轭复数为1i + B .的实部为1 C .2z =D .的虚部为1-3.假设有两个分类变量X 和Y 的2×2列联表:对同一样本,以下数据能说明X 与Y 有关系的可能性最大的一组为 A .a=45,c=15 B .a=40,c=20 C .a=35,c=25D .a=30,c=304. 正项等比数列{}n a 中的14033,a a 是函数()3214633f x x x x =-+-的极值点,则62017log a =A.1B.2C.12D. 1- 5.已知错误!未找到引用源。
是坐标原点,点错误!未找到引用源。
,若点错误!未找到引用源。
为平面区域122x y x y ≤⎧⎪≤⎨⎪+≥⎩错误!未找到引用源。
上一个动点,则错误!未找到引用源。
的最大值为A.3B.2C.1D.0 6.我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND 是产生随机数的函数,它能随机产生()01,内的任何一个实数).若输出的结果为521,则由此可估计π的近似值为A .3.119B .3.126C .3.132D .3.1517.过抛物线24y x =的焦点F 的直线交抛物线于,A B 两点,且2AF BF =,则直线AB 的斜率为A ...- D .8.某几何体的三视图如图所示,则该几何体的体积为A .5B .163 C .7 D .1739.小明跟父母、爷爷奶奶一同参加《中国诗词大会》的现场录制,5人坐成一排.若小明的父母至少有一人与他相邻,则不同坐法的总数为 A .60 B .72C .84D .9610.将函数()π2sin 26f x x ⎛⎫=+ ⎪⎝⎭的图像向左平移π12个单位,再向上平移1个单位,得到()g x 的图像.若()()129g x g x =,且[]12,2π,2πx x ∈-,则122x x -的最大值为A .π1249 B.35π6 C.25π6 D.17π411.已知双曲线Γ:)0,0(12222>>=-b a by a x 的焦距为2c ,直线:l y kx kc =-.若k =则l 与Γ的左、右两支各有一个交点;若k =l 与Γ的右支有两个不同的交点,则Γ的离心率的取值范围为 A .(1,2)B .(1,4)C .(2,4)D .(4,16)12.已知函数()()()()221128122x x x f x e x x x -⎧--≤⎪=⎨-+->⎪⎩,如在区间()1 +∞,上存在()2n n ≥个不同的数123 n x x x x ,,,…,,使得比值()()()1212n nf x f x f x x x x ==…=成立,则n 的取值集合是A.{}2 3 4 5,,,B.{}2 3,C.{}2 3 5,,D.{}2 3 4,, 二、填空题(每小题5分,共20分)13.已知12⎛= ⎝⎭a ,()2cos ,2sin αα=b ,a 与b 的夹角为60︒,则2-=a b ___________.14.已知n y x x )2(2-+的展开式中各项系数的和为32,则展开式中25y x 的系数为 .(用数字作答)15.鲁班锁是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙,外观看是严丝合缝的十字立方体,其上下、左右、 前后完全对称.从外表上看,六根等长的正四棱柱体分成三组,经错误!未找到引用源。
山西省太原市第五中学高三第二次模拟考试(5月)——数

山西省太原市第五中学2017届高三第二次模拟考试(5月)数学(理)试题一、选择题(每小题5分,共60分,每小题只有一个正确答案)1.已知全集,,,则A . B. C . D . (0,1) 2. 如果复数,则 A .的共轭复数为B .的实部为1C .D .的虚部为3.假设有两个分类变量X 和Y 的2×2列联表:对同一样本,以下数据能说明X 与Y 有关系的可能性最大的一组为 A .a=45,c=15B .a=40,c=20C .a=35,c=25D .a=30,c=304. 正项等比数列中的是函数()3214633f x x x x =-+-的极值点,则A.1B.2C.D.5.已知是坐标原点,点,若点为平面区域122x y x y ≤⎧⎪≤⎨⎪+≥⎩上一个动点,则的最大值为A.3B.2C.1D.06.我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数是产生随机数的函数,它能随机产生内的任何一个实数).若输出的结果为,则由此可估计π的近似值为 A .3.119B .3.126C .3.132D .3.1517.过抛物线的焦点的直线交抛物线于两点,且,则直线的斜率为 A . B . C .或 D . 8.某几何体的三视图如图所示,则该几何体的体积为 A .5 B . C . D .9.小明跟父母、爷爷奶奶一同参加《中国诗词大会》的现场录制,5人坐成一排.若小明的父母至少有一人与他相邻,则不同坐法的总数为 A .60 B .72C .84D .9610.将函数()π2sin 26f x x ⎛⎫=+ ⎪⎝⎭的图像向左平移个单位,再向上平移1个单位,得到的图像.若,且,则的最大值为A . B. C. D.11.已知双曲线Γ:)0,0(12222>>=-b a by a x 的焦距为2c ,直线.若,则l 与Γ的左、右两支各有一个交点;若,则l 与Γ的右支有两个不同的交点,则Γ的离心率的取值范围为 A .B .C .D .12.已知函数()()()()221128122x x x f x e x x x -⎧--≤⎪=⎨-+->⎪⎩,如在区间上存在个不同的数,使得比值()()()1212n nf x f x f x x x x ==…=成立,则的取值集合是A. B.C.D.4. 填空题(每小题5分,共20分)13.已知12⎛= ⎝⎭a ,,与的夹角为,则___________.14.已知的展开式中各项系数的和为32,则展开式中的系数为 .(用数字作答) 15.鲁班锁是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙,外观看是严丝合缝的十字立方体,其上下、左右、 前后完全对称.从外表上看,六根等长的正四棱柱体分成三组,经榫卯起来,如图,若正四棱柱体的高为,底面正方形的边长为,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积的最小值为__________.(容器壁的厚度忽略不计)16.对于正整数,设是关于的方程的实数根,记()()12n n a n x n =+≥⎡⎤⎣⎦,其中表示不超过实数的最大整数,则()23201511007a a a +++= .三.解答题17.(本小题满分12分)如图,在平面四边形中,已知,,,在边上取点,使得,连接,若,.(1)求的值; (2)求的长.18.(本小题满分12分)随着移动互联网的快速发展,基于互联网的共享单车应运而生.某市场研究人员为了了解共享单车运营公司M 的经营状况,对该公司最近六个月内的市场占有率进行了统计,并绘制了相应的折线图.(Ⅰ)由折线图可以看出,可用线性回归模型拟合月度市场占有率y 与月份代码x 之间的关系.求y 关于x 的线性回归方程,并预测M 公司2017年4月份的市场占有率;(Ⅱ)为进一步扩大市场,公司拟再采购一批单车.现有采购成本分别为1000元/辆和1200元/辆的A 、B 两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致车辆报废年限各不相同.考虑到公司运营的经济效益,该公司决定先对两款车型的单车各100辆进经测算,平均每辆单车每年可以带来收入500元.不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整数年,且以频率作为每辆单车使用寿命的概率.如果你是M 公司的负责人,以每辆单车产生利润的期望值......为决策依据,你会选择采购哪款车型? 参考数据:,61()()35iii x x y y =--=∑, .参考公式:回归直线方程为其中121()()()niii nii x x yy b x x ==--=-∑∑,19.(本小题满分12分)如图,已知多面体的底面是边长为2的正方形,底面,,且.(Ⅰ)记线段的中点为,在平面内过点作一条直线与平面平行,要求保留作图痕迹,但不要求证明. (Ⅱ)求直线与平面所成角的正弦值;20.(本小题满分12分)已知椭圆:22221(0)x y a b a b+=>>的左、右焦点分别为,,点在椭圆上.(Ⅰ)求椭圆的标准方程;(Ⅱ)是否存在斜率为2的直线,使得当直线与椭圆有两个不同交点、时,能在直线上找到一点,在椭圆上找到一点,满足?若存在,求出直线的方程;若不存在,说明理由. 21.(本小题满分12分)已知函数()()()21ln 1,2f x xg x x x =+=-. (Ⅰ)求过点且与曲线相切的直线方程;(Ⅱ)设,其中为非零实数,若有两个极值点,且,求证:.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.作答时请写清题号. 22.(本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系中,曲线的参数方程为(为参数),直线的方程为,以为极点,以轴正半轴为极轴,建立极坐标系,(1)求曲线和直线的极坐标方程; (2)若直线与曲线交于两点,求.23. (本小题满分10分)选修4-5:不等式选讲 (Ⅰ)求不等式2|1||2|0x x -<--+<的解集.(Ⅱ)设a,b,均为正数,}2,,2max {22babb a ah +=,证明:参考答案选择题:CDACB BCDCA CB填空题:13. 14. 120 15.41 16. 2017 17.解:(1)在中,据正弦定理,有.∵,,,∴sinsin14BE BBCECE∙∠===.(2)由平面几何知识,可知,在中,∵,,∴cos14DEA∠===.∴cosEAEDDEA===∠在中,据余弦定理,有22212cos7282()492CD CE DE CE DE CED=+-∙∙∠=+--=∴18.19.解:(Ⅰ)取线段的中点,连结,直线即为所求.如图所示:(Ⅱ)以点为原点,所在直线为轴,所在的直线为轴,建立空间直角坐标系,如图.由已知可得,,,,,∴,,,设平面的法向量为,得取,得平面的一个法向量为,设直线与平面所成的角为,∴sin|cos,|||6n EBθ=<>==.20.解:(Ⅰ)设椭圆的焦距为,则,因为在椭圆上,所以122||||a AF AF=+=因此,,故椭圆的方程为.(Ⅱ)椭圆上不存在这样的点,证明如下:设直线的方程为,设, , , ,的中点为,由222,1,2y x txy=+⎧⎪⎨+=⎪⎩得,所以,且22436(8)0t t∆=-->,故,且由知四边形为平行四边形,而为线段的中点,因此,也是线段的中点,所以45329y ty+==,可得,又,所以,因此点不在椭圆上.21. 解:(Ⅰ)设切点为,则切线的斜率为点在上,,解得切线的斜率为,切线方程为(Ⅱ)()()()()21ln12h x af x g x a x x x=+=++-()()211,111x aah x x xx x+-'=+-=>-++当时,即时,在上单调递增;当时,由得,12x x=当时,由得,在上单调递减,在上单调递增.当时,有两个极值点,即12x x=12120,1x x x x a∴+==-,由得,由()()()2 2122222 20202ln10h x x h x x a x x x->⇔+>⇔++->22211x a x =-∴=-,即证明()()22222221ln 10x x x x -++->即证明()()22221ln 10x x x ++->构造函数()()()()21ln 1,0,1t x x x x x =++-∈,()()()12ln 10,t x x t x '=++>在上单调递增,又,所以在时恒成立,即()()22221ln 10x x x ++->成立 .22.选修4-4:坐标系与参数方程 (1)曲线的普通方程为,则的极坐标方程为24cos 4sin 70ρρθρθ--+=, 由于直线过原点,且倾斜角为,故其极坐标为(或)(2)由24cos 4sin 703ρρθρθπθ⎧--+=⎪⎨=⎪⎩得:22)70ρρ-+=,故,, ∴121211||||2||||||||7OA OB OA OB OA OB ρρρρ+++===. 23. 选修4-5:不等式选讲23.解:(Ⅰ)记3,2,()|1||2|21,21,3, 1.x f x x x x x x ≤-⎧⎪=--+=---<<⎨⎪-≥⎩由,解得,则不等式的解集为.(2) bh abb a h ah 2,,222≥+≥≥824)(4223=⨯≥+≥abab ab b a h。
山西省太原市第五中学2017届高三阶段测试(5月模拟)数学(理)试题

太原五中高三数学一模理答案选择题:CDACB BCDCA CB填空题:13. 错误!未找到引用源。
14. 120 15.41错误!未找到引用源。
16. 201717.解:(1)在BEC ∆中,据正弦定理,有sin sin BE CE BCE B =∠. ∵23B π∠=,1BE =,CE ,∴sin sin BE B BCE CE ∙∠===. (2)由平面几何知识,可知DEA BCE ∠=∠,在Rt AED ∆中,∵2A π∠=,5AE =,∴cos DEA ∠==.∴cos EA ED DEA ===∠在CED ∆中,据余弦定理,有22212cos 7282()492CD CE DE CE DE CED =+-∙∙∠=+--= ∴7CD =18.19.解:(Ⅰ)取线段CD的中点Q,连结KQ,直线KQ即为所求.如图所示:(Ⅱ)以点A为原点,AB所在直线为x轴,AD所在的直线为y轴,建立空间直角坐标系,如图.由已知可得(0,0,0)A ,(0,0,2)E ,(2,0,0)B ,(2,2,0)C ,(0,2,1)F ,∴(2,2,2)EC =- ,(2,0,2)EB =- ,(0,2,1)EF =- ,设平面ECF 的法向量为(,,)n x y z = ,得2220,20,x y z y z +-=⎧⎨-=⎩取1y =,得平面ECF 的一个法向量为(1,1,2)n = ,设直线EB 与平面ECF 所成的角为θ,∴sin |cos ,||n EB θ=<>== . 20.解:(Ⅰ)设椭圆C 的焦距为2c ,则1c =, 因为(1,)2A 在椭圆C上,所以122||||a AF AF =+=因此a = 2221b a c =-=,故椭圆C 的方程为2212x y +=. (Ⅱ)椭圆C 上不存在这样的点Q ,证明如下:设直线l 的方程为2y x t =+,设11(,)M x y ,22(,)N x y ,35(,)3P x ,44(,)Q x y ,MN 的中点为00(,)D x y , 由222,1,2y x t x y =+⎧⎪⎨+=⎪⎩得229280y ty t -+-=, 所以1229t y y +=,且22436(8)0t t ∆=-->, 故12029y y t y +==,且33t -<< 由PM NQ = 知四边形PMQN 为平行四边形, 而D 为线段MN 的中点,因此,D 也是线段PQ 的中点,所以405329y t y +==,可得42159t y -=, 又33t -<<,所以4713y -<<-, 因此点Q 不在椭圆上.21. 解:(Ⅰ)()11f x x '=+ 设切点为()00,x y ,则切线的斜率为011k x =+ 点()00,x y 在()()ln 1f x x =+上,()00ln 1y x ∴=+ ()000ln 1111x x x +∴=++,解得01x e =- ∴切线的斜率为1e,∴切线方程为10x ey -+= (Ⅱ)()()()()21ln 12h x af x g x a x x x =+=++- ()()211,111x a a h x x x x x +-'=+-=>-++ 当10a -≥时,即1a ≥时,()()0,h x h x '≥在()1,-+∞上单调递增; 当01a <<时,由()0h x '=得,12x x ==,故()h x在(1,-上单调递增,在(上单调递减,在)+∞上单调递增; 当0a <时,由()0h x '=得,()0x h x =在(上单调递减,在)+∞上单调递增. 当01a <<时,()h x有两个极值点,即12x x == 12120,1x x x x a ∴+==-,由01a <<得,1210,01x x -<<<< 由()()()2212222220202ln 10h x x h x x a x x x ->⇔+>⇔++->2221x a x =∴=- ,即证明()()22222221ln 10x x x x -++->即证明()()22221ln 10x x x ++->构造函数()()()()21ln 1,0,1t x x x x x =++-∈, ()()()12ln 10,t x x t x '=++>在()0,1上单调递增, 又()00t =,所以()0t x >在()0,1x ∈时恒成立,即()()22221ln 10x x x ++->成立 212ln 0x x ∴->.22.选修4-4:坐标系与参数方程(1)曲线1C 的普通方程为22(2)(2)1x y -+-=, 则1C 的极坐标方程为24cos 4sin 70ρρθρθ--+=, 由于直线2C 过原点,且倾斜角为3π,故其极坐标为()3R πθρ=∈(或tan θ= (2)由24c o s 4s i n 703ρρθρθπθ⎧--+=⎪⎨=⎪⎩得:2(32)70ρρ-+=,故122ρρ+=, 127ρρ=,∴121211||||||||||||OA OB OA OB OA OB ρρρρ+++=== .23. 选修4-5:不等式选讲23.解:(Ⅰ)记3,2,()|1||2|21,21,3, 1.x f x x x x x x ≤-⎧⎪=--+=---<<⎨⎪-≥⎩由2210x -<--<,解得1122x -<<,则不等式的解集为11(,)22-.(2) b h ab b a h a h 2,,222≥+≥≥824)(4223=⨯≥+≥ab abab b a h ∴ 2≥h。
太原市第五中学2017届高三第二次模拟考试(5月)理科综合含答案

太原五中2016—2017学年度第二学期阶段性检测高三理科综合命题人:李杰、李桂荣、易红波校对人:高三理综组(2017。
5)第Ⅰ卷(选择题共126分)本试卷共21小题,每小题6分,共126分。
合题目要求的。
可能用到的相对原子量H 1 C 12 N 14 O 16 Na 23 Mg 24 S 32 Cu 64一、选择题(本大题共13小题,每小题6分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1。
N、P是组成细胞化合物的重要元素,以下关于N、P生理作用的叙述正确的是A. N、P是磷脂等各种脂质共同组成元素B.可用15N和32P分别标记T2噬菌体的蛋白质和DNA,以区分它们在遗传中的作用C。
植物缺乏N和P会使叶子变黄D. N和P位于磷脂分子亲水性头部2.人类成熟的红细胞和心肌细胞结构和功能各不相同。
以下描述中正确的是A.由于两种细胞细胞核的不同,导致其结构和功能的不同B。
心肌细胞含丰富的线粒体,红细胞不含线粒体都体现了细胞结构和功能的适应关系C。
两种细胞中含相同的呼吸酶,都可以进行持续的无氧呼吸D. 红细胞和心肌细胞分别可以通过无丝分裂和有丝分裂补充死亡细胞3。
显微观察生物结构时,都需制作临时装片。
以下操作符合要求的是A.将吸附有口腔上皮细胞牙签的一端,在载玻片中央清水中涂一涂,再滴健那绿,盖盖玻片B.将浸泡过的花生子叶放在载玻片中央的清水中,滴加苏丹Ⅲ,盖上盖玻片C.观察低温诱导后的洋葱根尖细胞的染色体数变化时,需经过解离-漂洗—染色—制片环节D。
调查土壤中小动物类群丰富度时,对肉眼难以识别的小动物,可制成切片,再显微鉴别4.受体是神经—体液—免疫调节网络的结构基础。
关于受体及其生理作用的描述不正确的是A。
胰岛素可作用于肝细胞膜的受体,调节细胞膜上葡萄糖载体蛋白的数量,促进葡萄糖吸收B。
神经递质作用于突触后膜的受体,改变离子通透性,引发突触后膜电位变化C.因为受体是细胞表面接收信息的结构,所以所有的受体分子都在细胞膜上D.淋巴因子作用于B细胞膜上的受体,刺激其增殖分化5.右图是人类某种遗传病的系谱图。
山西省太原市2017届高三数学阶段测试(5月模拟)试题 理(扫描版)
山西省太原市2017届高三数学阶段测试(5月模拟)试题理(扫描版)太原五中高三数学一模理答案选择题:CDACB BCDCA CB填空题:13。
14. 120 15.41 16。
201717.解:(1)在BEC ∆中,据正弦定理,有sin sin BE CE BCE B =∠。
∵23B π∠=,1BE =,7CE =,∴sin 221sin 147BE B BCE CE •∠===.(2)由平面几何知识,可知DEA BCE ∠=∠,在Rt AED ∆中,∵2A π∠=,5AE =,∴2357cos 1sin 12814DEA DEA ∠=-∠=-=。
∴527cos 5714EAED DEA ===∠。
在CED ∆中,据余弦定理,有22212cos 7282727()492CD CE DE CE DE CED =+-••∠=+-⨯⨯⨯-=∴7CD =18。
19。
解:(Ⅰ)取线段CD 的中点Q ,连结KQ ,直线KQ 即为所求. 如图所示:(Ⅱ)以点A 为原点,AB 所在直线为x 轴,AD 所在的直线为y 轴,建立空间直角坐标系,如图.由已知可得(0,0,0)A ,(0,0,2)E ,(2,0,0)B ,(2,2,0)C ,(0,2,1)F ,∴(2,2,2)EC =-,(2,0,2)EB =-,(0,2,1)EF =-,设平面ECF 的法向量为(,,)n x y z =,得2220,20,x y z y z +-=⎧⎨-=⎩取1y =,得平面ECF 的一个法向量为(1,1,2)n =,设直线EB 与平面ECF 所成的角为θ,∴sin |cos ,||n EB θ=<>==.20.解:(Ⅰ)设椭圆C 的焦距为2c ,则1c =,因为A 在椭圆C上,所以122||||a AF AF =+=因此a = 2221b a c =-=,故椭圆C 的方程为2212x y +=.(Ⅱ)椭圆C 上不存在这样的点Q ,证明如下:设直线l 的方程为2y x t =+,设11(,)M x y ,22(,)N x y ,35(,)3P x ,44(,)Q x y ,MN 的中点为00(,)D x y , 由222,1,2y x t x y =+⎧⎪⎨+=⎪⎩得229280y ty t -+-=, 所以1229ty y +=,且22436(8)0t t ∆=-->, 故12029y y ty +==,且33t -<<由PM NQ =知四边形PMQN 为平行四边形,而D 为线段MN 的中点,因此,D 也是线段PQ 的中点, 所以405329y ty +==,可得42159t y -=,又33t -<<,所以4713y -<<-,因此点Q 不在椭圆上.21。
山西省太原市第五中学高三第二次模拟考试(5月)数学(理)Word版含答案
太原五中2017—2018学年度第二学期模拟高三数学(理)出题人、校对人:王文杰、郭舒平、刘锦屏、李廷秀、凌河、闫晓婷(2018.5.25)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1)2()3、是的()必要不充分条件既不充分也不必要条件4)5)66,则判断框中的条件可以是()70~11)8)9、已知某空间几何体的三视图如图所示,其中正视图为等边三角形,则该几何体的最长棱长()10、某人根据自己的爱好,希望从{T,Y,W,Z}中选两个不同的字母,从{0,2,6,8}中选三个不同的数字编拟车牌号,要求前两位是字母,后三位是数字,且数字2不能排在末位,字母Z和数字2不能相邻,那么满足要求的车牌号有()个个个个11),12、已知定义在上的函数满足f x,设与图象的交点坐标为4 6第Ⅱ卷本卷包括必考题和选考题两部分.第13题—第21题为必考题,每个试题考生都必须作答.第22题—第23题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分13、成区域内的概率为________.14、已知正方棱长是底的动点,则的最大值为.15________.16,的取值范围是________.三、解答题:解答应写出文字说明、证明过程或演算步骤.17、(本小题满分12分)(1(2.18、(本小题满分12分).求证:(1(2.19、(本小题满分12分)某高校在2017年自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩共分为五组,得到如下的频率分布表:(1考生的平均成绩;(2)为了能选出最优秀的学生,该高校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取12名考生进入第二轮面试.①求第3、4、5组中每组各抽取多少名考生进入第二轮面试;②从上述进入二轮面试的学生中任意抽取2名学生,记X表示来自第四组的学生人数,求X 的分布列和数学期望;③若该高校有三位面试官各自独立地从这12名考生中随机抽取2名考生进行面试,设其中甲考生被抽到的次数为Y,求Y的数学期望.20、(本小题满分12分)(1(2.21、(本小题满分12分)(1(2.请考生从第22、23 题中任选一题作答,并用2B铅笔将答题卡上所选题目对应的题号右侧方框涂黑,按所选涂题号进行评分;多涂、多答,按所涂的首题进行评分;不涂,按本选考题的首题进行评分.22、(本小题满分10分)【选修4——4:坐标系与参数方程】,以原点为.(1(2)面积的最小值.23、(本小题满分10分)【选修4——5:不等式选讲】(1(2高三二模答案1、2、3、解析:要条件.4、解析()55、解析:,所以6、解析:,7、解:0~1相应平面区域面积为1,两个数能与18、解析:由条件知,,所以,由正弦定理可得,故的面积故选9、解析:10、解析:(1)不含Z不含2(2)含Z不含2(3)不含Z含2(4)含Z也含2所以共有36+36+72+54=19811、解析:设,则由可知:且,所以12、解析:(a,b)对称,又因为,的图象关于(a,b)对称,当且仅当a=b=1时,2.13、 曲线围成区域面积为:14、解析:以原点建立空间直角坐标系,则,设,,其中,则15、解析:2,16、内有两个极值点,,可转换为函数1与g(x)=a(x-1)的图象在内有两个交点.由,,为减函数,上为增函数,当直线g(x)=a(x-1),由导数的几何意义可以得到,可知a=1,17、解析:(1.(218、解(1(2角坐标系。
山西省太原市2017届高三英语阶段测试(5月模拟)试题
山西省太原市2017届高三英语阶段测试(5月模拟)试题(扫描版)听力1-5 BCACA 6-10 BACAB 11-15BCACC 16-20 BCBAAA篇 21—23 CDDB篇24—27 BDABC篇ABDC D篇CACB七选五36-40 GFCEA完型填空41-45 DBCAB 46-50 BCDAA 51-55 DACCD 56-60 BADBC语篇填空61. which 62. travel 63.with 64. other 65.heading 66. and 67.ha ve worked 68.to control 69.Thanks 70.including短文改错71. After I elected ... elected前加was72. ... for us student. student → students73. ... excellently English ...excellently → excellent74. ... cover up what ... 去掉up75. Beside, we took ... Beside → Besides76. ... had been working ... had → have77. ... helps myself a lot ... myself → me78. ... start a school ... start → start ing79. ... an huge responsibility ... an → a80. ... proud of that ... that → what,书面表达Dear Jim,I’m Li Hua, chairman of the Students’ Union. I’m glad to hear that you are coming to teach at our school next te rm. All of our students are expecting your arrival.I feel h onored to be able to recommend a student assistant to you. With regards to your requirements, I shall recommend Wang Ming, a senior three student, to be your assistant. Not only does he do well in all his su bjects, he also has many practical skills. His spoken English is so good that he can communicate with foreigners fluently. W hat’s m ore, he is expert on computer and can operate ma ny kinds of office software skillfully.For more information, please write me. I’m looking forward to your reply.Yours,。
山西省太原市第五中学高三第二次模拟考试(5月)——数
山西省太原市第五中学2017届高三第二次模拟考试(5月)数学(文)试题一、选择题(每小题5分,共60分,每小题只有一个正确答案)1.已知集合-1,0,,则R B)= ( )A. ---2.命题“若x>0,则x 2>0”的否定是( )A. 若x>0 , 则x 2<0B. 若则x 2C. 若x>0 ,则x 2 若x 2则x3.复数41-i - 103+i的共轭复数对应的点所在象限为( ) A.第一象限 B. 第二象限 C. 第三象限 D. 第四象限4.设S n 为等比数列n 的前n 项和,a 2-8a 5=0,则S 8S 4的值为( ) A. 12 B. 1716C. 2D. 17 5.在中,若a 2-b 2 = 3 bc ,且sin(A+B)sinB = 2 3 ,则A= ( ) A.6B. 3C.3 D.66.函数- x 28图象大致为( )7.《九章算术》是我国古代著名数学经典,其中对勾股定理的论述比西方早一千多年,有这样一个问题:“今有圆木材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小.用锯去锯该材料,锯口深 1寸,锯道长1尺.问这块圆柱形木料的直径是多少?长为1丈的圆柱形木料部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦AB=1尺,弓形高CD=1寸,估算该木材镶嵌在墙体中的体积约为( )C(注:1丈=10尺= 100寸,0 513 )A. 600立方寸B. 610立方寸C. 620立方寸D. 633立方寸8. 执行如图(8)所示的程序框图,若输出的k=5,则输入的整数p 的最大值为( )A.7B.15C. 31D. 639.某几何体的三视图如图(9)所示,其正视图的曲线部分为半圆,则该几何体的表面积为( )C. 10 + 62D.13 + 6210.已知实数x,y 满足⎪⎩⎪⎨⎧≥≤-≤+011x y x y x ,且目标函数z=ax+2y 的最大值为2,则实数a 的取值范围为() A. (- -11.已知、、均为单位向量,且满足,则的最大值为( ) A. 2+ 5 B. 2+2 2 C. 3+ 2 D. 1+2 312.已知函数F(x)= (lnx x )2 + (a-1) lnx x +1-a 有三个不同的零点x 1,x 2 ,x 3(x 1<x 2 <x 3),则(1- lnx 1x 1 )2(1- lnx 2x 2 )(1- lnx 3x 3 )的值为( )A. 1-aB. a-1C. – 1D. 1二、填空题(每小题5分,共20分)13.已知某路段最高限速60km/h,电子监控测得连续4辆汽车的速度用用茎叶图表示如图示,若从中任取2辆,则恰好有1辆汽车超速的概率为 .侧视图俯视图 第9题 图第8题图14.已知P是边长为2的正三角形ABC的边BC上的动点,则= .15.已知2),若6)= 35,则- 12)= .16.已知椭圆x2a2+y2b2= 1 (a>b>0)上一点A关于原点的对称点为B,F为其右焦点,若,令且12,4],则该椭圆离心率的取值范围是.三、解答题17.(满分12分)在数列n中,a1=2,a n+1 = 3a n+2.(1)求数列n的通项公式;(2)若b n = a n3(a n+1), 求数列n的前n项和S n.18.(满分12分)某商店计划每天购进某商品若干件,商店每销售1件该商品可获利50元. 若供大于求,剩于商品全部退回,则每件商品亏10元;若供不应求,则从外部调剂,此时每件调剂商品可获利3 0元.(1)若商店一天购进该商品10件,求当天的利润y(单位:元)关于当天需求量n(单位:件,的函数关系式;(216.假设该店在这50天内每天购进10件该商品,求这50天的日利润(单位:元)的平均数;17.若该店一天购进10件该商品,记“当天的利润在区间1400,550]内”为事件A,求19.(满分12分)如图(1)在直角梯形ABCD中,2,AB=BC= AD2= a ,E是AD的中点,O是AC与BE的交点,将沿BE拆起到图(2)中1BE的位置,得到四棱锥A1—BCDE.(2)证明:平面A1OC;(3)当平面A1平面BCDE时,四棱锥A1—BCDE的体积为36 2 ,求a的值.20.(满分12分)已知椭圆C 的方程为 x 2a 2 + y 2b 2 = 1(a>b>0),离心率e=33,点 P(62,1)在椭圆C 上. 1. 求椭圆C 的方程;2. 过C 的右焦点F 作两条弦AB ,CD ,满足=0 ,且=2,=2, 求证:直线MN 过定点,并求出此定点.21.(满分12分)已知函数f(x)= mx x 2+ n在x=1处取得极值2. (1)求f(x)的解析式;(2)设函数g(x)=lnx+ a x,若对任意的x 1-1,1],总存在x 2为自对数的底数), 使得g(x 21)+ 72,求实数a 的取值范围. 请考生在第22、23两题中任选 一题作答,如果多做,则按所做的第一题计分.22.(本题满 分10分)选 修4-4:坐标系与参数方程已知极坐标的极点在平面直角坐标系的原点O 处,极轴与x 轴的非负半轴重合,且长度单 位相同.直线的极坐标方程为- 3 )= 3 ,若点P 为曲线C :,为参数)上的动点.(1)试写直线的直角坐标方程及曲线C 的普通方程;(2)求点P 到直线距离的最大值.23. (本题满 分10分)选修4-5:不等式选讲已知-不等式的解集是- (2)求实数a 的值;(2)若f(x)+f(-x)3存在实数解,求实数k 的取值范围.参考答案19.BCCBA CDBCB AD20.13. 12 ;14. 6 ; 15. 210 ;16. [22 ,63 ].21.17.(1)a n =3n-1 ;(2)S n = 2n-14 ×3n+1- n(n+1)2 + 34 23.(1) y= (nÎN*) ;(2) ① 476 ;② P(A)= 0.724.(1)略 ;(2) a= 625.(1)x 23 + y 22 = 1 ;(2) MN 经过的定点为(35 ,0)26.(1) f(x)= 4x x 2+1 ;(2)a 的取值范围是(- ¥, e ].27.(1):y= 3 x+2 3 ;(2)点P 到直线的最大距离为2+2 3 .28.(1)a = 2 ;(2)k 的取值范围是(- ¥ , - 23 )È(23 ,+ ¥)。
