最优控制课程介绍
最优控制全部PPT课件

J
(x(t f ),t f)
tf t0
F(x(t),u(t),t)dt
为最小。
这就是最优控制问题。
如果问题有解,记为u*(t), t∈ [t0,tf],则u*(t)叫做最优控制(极值控制),相应的轨 线X*(t)称为最优轨线(极值轨线),而性能指标J*=J(u*(·))则称为最优性能指标。
第11页/共184页
目标质心的位置矢量和速度矢量为: xM xM
F(t)为拦截器的推力
x xL xM v xL xM
则拦截器与目标的相对运动方程为:
x v v a(t) F (t)
m(t)
m F (t) c
其中a(t)是除控制加速度外的固有相对加速度,是已知的。
初始条件为: x(t0 ) x0 v(t0 ) v0 m(t0 ) m0 终端条件为: x(t f ) 0 v(t f )任意 m(t f ) me
至于末态时刻,可以事先规定,也可以是未知的。 有时初态也没有完全给定,这时,初态集合可以类似地用初态约束来表示。
第9页/共184页
3:容许控制 在实际控制问题中,大多数控制量受客观条件的限制,只能在一定范围内取 值,这种限制通常可以用如下不等式约束来表示:
0 u(t) umax 或ui i 1,2p
给定一个线性系统,其平衡状态X(0)=0,设计的目的是保持系统处于平衡状态,即 这个系统应能从任何初始状态返回平衡状态。这种系统称为线性调节器。
线性调节器的性能指标为:
J
tf t0
n
xi 2 (t)dt
i 1
加权后的性能指标为:
J
tf t0
n
qi xi 2 (t)dt
i1
对u(t)有约束的性能指标为: J t f 1 [ X T (t)QX (t) uT (t)Ru(t)]dt
《最优控制》课程大纲
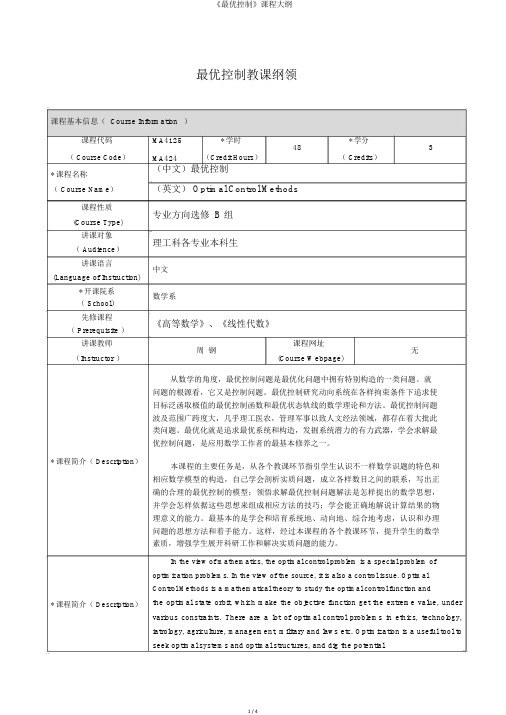
最优控制教课纲领课程基本信息( Course Information )课程代码 MA4125 * 学时 * 学分 3( Course Code ) MA424(Credit Hours )48( Credits )* 课程名称 (中文)最优控制( Course Name )(英文) Optimal Control Methods 课程性质 专业方向选修 B 组(Course Type)讲课对象 理工科各专业本科生( Audience )讲课语言中文(Language of Instruction)* 开课院系 数学系( School )先修课程 《高等数学》、《线性代数》( Prerequisite )讲课教师周 钢课程网址 无(Instructor )(Course Webpage)* 课程简介( Description )* 课程简介( Description )从数学的角度,最优控制问题是最优化问题中拥有特别构造的一类问题。
就问题的根源看,它又是控制问题。
最优控制研究动向系统在各样拘束条件下追求使目标泛函取极值的最优控制函数和最优状态轨线的数学理论和方法。
最优控制问题波及范围广跨度大,几乎理工医农,管理军事以致人文经法领域,都存在着大批此类问题。
最优化就是追求最优系统和构造,发掘系统潜力的有力武器,学会求解最优控制问题,是应用数学工作者的最基本修养之一。
本课程的主要任务是,从各个教课环节指引学生认识不一样数学识题的特色和相应数学模型的构造,自己学会剖析实质问题,成立各样数目之间的联系,写出正确的合理的最优控制的模型;领悟求解最优控制问题解法是怎样提出的数学思想,并学会怎样依据这些思想来组成相应方法的技巧;学会能正确地解说计算结果的物理意义的能力。
最基本的是学会和培育系统地、动向地、综合地考虑,认识和办理问题的思想方法和着手能力。
这样,经过本课程的各个教课环节,提升学生的数学素质,增强学生展开科研工作和解决实质问题的能力。
《最优控制》教学大纲-hyq
第四章极小值原理及其应用(6学时)
4.1连续系统的极小值原理(2学时)
4.2最短时间控制问题(1学时)
4.3最少燃料控制问题(1学时)
4.4离散系统的极小值原理(2学时)
第五章线性系统二次型指标的最优控制——线性二次型问题(6学时)
5.1引言
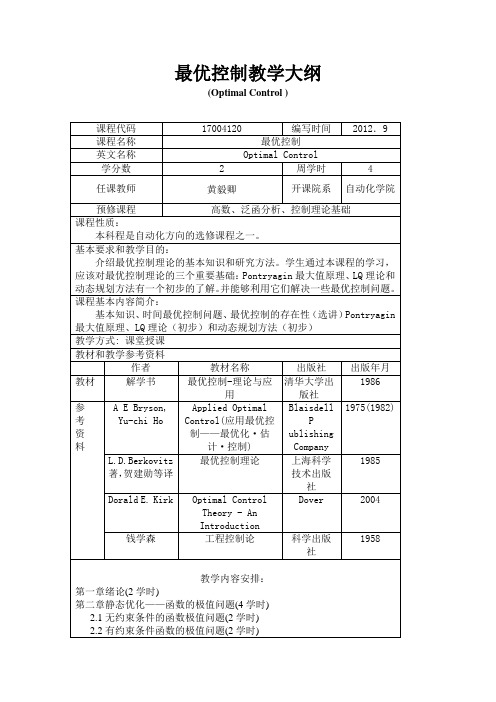
最优控制教学大纲
(Optimal Control
课程代码
17004120
编写时间
2012.9
课程名称
最优控制
英文名称
Optimal Control
学分数
2
周学时
4
任课教师
黄毅卿
开课院系
自动化学院
预修课程
高数、泛函分析、控制理论基础
课程性质:
本科程是自动化方向的选修课程之一。
基本要求和教学目的:
介绍最优控制理论的基本知识和研究方法。学生通过本课程的学习,应该对最优控制理论的三个重要基础:Pontryagin最大值原理、LQ理论和动态规划方法有一个初步的了解。并能够利用它们解决一些最优控制问题。
Applied Optimal Control(应用最优控制——最优化·估计·控制)
Blaisdell P ublishing Company
1975(1982)
L.D.Berkovitz著,贺建勋等译
最优控制理论
上海科学技术出版社
1985
Dorald E. Kirk
Optimal ControlTheory - An Introduction
5.2终端时间有限时连续系统的状态调节器问题(2学时)
5.3稳态时连续系统的状态调节器问题(2学时)
清华大学最优控制--课程概述

1. 2. 3. 4. 5. 6.
因材施教:个别讨论、email答疑等
4/4
1
2/4
教学安排
教学安排
教材:最优控制,清华大学出版社
教学管理:作业30% + 开卷笔试70% (课程论文可代替部分或全部笔试) 提交作业要求: 1周内提交
参考书
解学书:最优控制—理论与应用,清华大学出版社 胡中楫等:最优控制原理及应用,浙大出版社 吴受章等:应用最优控制,西交大出版社 王朝珠等:最优控制原理,科学出版社 B.D.O.Anderson and J.B. Moore: Linear Optimal Control, Prentice-Hall F.L. Lewis and V.L. Syrmos: Optimal Control, John Wiley & Sons, INC.
教 学 安 排
最优控制
授课教师:钟宜生
总ห้องสมุดไป่ตู้时 32学时 主要教学内容
第1章 第2章 第3章 第4章 第5章 第6章 第7章 第8章 第9章 最优控制问题的提出和数学描述 函数极值的基本理论 最优控制中的变分法 极大值原理 动态规划 时间最短和燃料最省控制 线性二次型最优调节系统设计 最优状态调节系统的鲁棒稳定性 最优控制系统的渐近特性和加权矩阵的选择
最优控制介绍课件

状态方程可以表 示为微分方程或 差分方程的形式
03
02
04
状态方程通常包 括系统的状态变 量、输入变量和 输出变量
状态方程在最优 控制问题中用于 描述系统的动态 特性,为控制器 的设计提供依据
控制方程
状态方程: 描述系统 状态的变 化规律
控制方程: 描述控制 输入与系 统状态的 关系
性能指标 方程:描 述系统的 性能指标
02
状态转移方程: 描述状态之间的
递推关系
03
边界条件:定义 初始状态和终止
状态
04
求解过程:从初 始状态开始,逐 步求解子问题, 直至得到最优解
最优控制理论
01
最优控制理论是研究如何找到最优控制策
略,使得系统在特定条件下达到最优性能。
02
最优控制理论包括动态规划、极大值原
理、变分法等方法。
03
最优控制理论广泛应用于工程、经济、
04
间接法:通过求解最优控制问 题的辅助问题来获得最优控制 策略
06
数值解法优缺点:优点是计算 简单、易于实现;缺点是计算 精度较低、收敛速度较慢
机器人控制
1
机器人运动控 制:通过最优 控制算法,实 现机器人的精 确运动控制
2
机器人路径规 划:通过最优 控制算法,规 划机器人的最 优路径
3
机器人抓取控 制:通过最优 控制算法,实 现机器人的精 确抓取控制
交通控制
STEP1
STEP2
STEP3
STEP4
交通信号灯控制: 根据实时交通状况, 自动调整信号灯时 间,提高道路通行 效率
公共交通调度:根 据客流量、车辆位 置等信息,优化公 交线路和发车频率, 降低乘客等待时间
最优控制课程介绍

最优控制先修课程:常微分方程,最优化方法最优控制问题是具有特殊数学结构的一类最优化问题,在科学、工程和管理乃至人文领域都存在大量的最优控制问题。
最优控制研究动态系统在各种约束条件下,寻求目标泛函取极值的最优控制函数与最优状态轨线的数学理论和方法,它是静态最优化在无穷维空间的扩展。
希望学生通过本课程的学习,能够结合实际背景,建立最优控制的模型,理解求解最优控制的三大类基本方法的数学思想,灵活地掌握这些方法的基本过程,并能解释计算结果的意义。
主要内容如下:最优控制问题及其建模;数学基础;变分法及其在最优控制的应用;极小值原理及其应用;动态规划方法及其应用;应用。
最优控制一、课程基本信息 1.先修课程:数学系本科包括到大三的全部课程 2.面向对象:理学院数学系各专业 3.推荐教学参考书:吴沧浦,《最优控制的理论与方法》,国防工业出版社,2000 王朝珠等,《最优控制理论》,科学出版社,2003 邢继祥等,《最优控制应用基础》,科学出版社,2003 W. L. Brogan, Modern C ontrol Theor y, (3th eidition), Prentice-Hall, Englew ood C liffs,1991 二、课程的性质和任务本课程是数学与应用数学专业本科生高年级选修课程之一。
从数学的角度,最优控制问题是最优化问题中具有特殊结构的一类问题。
就问题的来源看,它又是控制问题。
最优控制研究动态系统在各种约束条件下寻求使目标泛函取极值的最优控制函数和最优状态轨线的数学理论和方法。
最优控制问题涉及范围广跨度大,几乎理工医农,管理军事乃至人文经法领域,都存在着大量此类问题。
最优化已是寻求最优系统和结构,挖掘系统潜力的有力武器,学会求解最优控制问题,是应用数学工作者的最基本素养之一。
通过本课程的主要任务是,从各个教学环节引导学生认识不同数学问题的特点和相应数学模型的结构,自己学会分析实际问题,建立各种数量之间的联系,写出正确的合理的最优控制的模型;领会求解最优控制问题解法是如何提出的数学思想,并学会如何根据这些思想来构成相应方法的技巧;学会能正确地解释计算结果的物理意义的能力。
最优控制 李国勇

最优控制一、课程基本情况二、课程内容简介主要内容包括为:最优化问题的基本概念、最优控制中的变分法、极大值原理、动态规划和线性二次型最优控制问题。
为了培养学生现代化的分析与设计能力,在每一部分都涉及利用MATLAB对其实现的方法,让学生在有限的时间内,掌握最优控制的基本原理与应用技术。
三、课程教学大纲第1章绪论(4学时)1. 教学内容及基本要求本章的基本要求是使学生了解最优控制理论的基本知识和基本方法。
主要内容包括:最优控制的发展;最优控制问题;最优控制的提法;最优控制的求解方法。
2. 重点、难点最优控制的提法、最优控制的求解方法等。
第2章最优控制中的变分法(14学时)1. 教学内容及基本要求本章的基本要求是使学生掌握利用变分法求解最优控制的方法。
主要内容包括:静态最优控制的解;变分法;应用变分法求解最优控制问题;角点条件。
2. 重点、难点无约束情况下的角点条件和内点约束情况下的角点条件下最优控制的求解等。
第3章极大值原理(12学时)1. 教学内容及基本要求本章的基本要求是使学生掌握利用极大值原理求解最优控制的方法。
主要内容包括:连续系统的极大值原理;离散系统的极大值原理;极大值原理的应用。
2. 重点、难点极大值原理的应用等。
第4章动态规划(12学时)1. 教学内容及基本要求本章的基本要求是使学生掌握利用动态规划求解最优控制的方法。
主要内容包括:动态规划的基本原理;离散系统的动态规划;连续系统的动态规划;动态规划与变分法和极大值原理的关系。
2. 重点、难点动态规划在微分对策问题中的应用等。
第5章线性二次型最优控制问题(12学时)1. 教学内容及基本要求本章的基本要求是使学生掌握线性二次型最优控制问题的求解方法。
主要内容包括:线性二次型问题;状态调节器;输出调节器;输出跟踪器;离散系统的线性二次型最优控制;利用MATLAB求解二次型最优控制问题。
2. 重点、难点线性二次型的微分对策问题等。
四、课程知识单元与知识点1. 论述●最优控制理论基本概念●最优控制理论常用的求解方法2. 变分法●普通函数的极值问题●变分法的基本概念●变分法在动态最优控制中的应用3. 极大值原理●极大值原理的基本概念●离散系统的动态规划和连续系统的动态规划;●极大值原理的应用4. 动态规划●动态规划的基本概念●基于动态规划的微分对策问题●动态规划与变分法和极大值原理的关系5. 线性二次型最优控制●线性二次型问题●状态调节器●输出调节器●跟踪器各部分都列举了大量的应用实例及利用MATLAB对其实现的方法,便于读者掌握和巩固所学知识。
最优控制 第一章 概述

(1-1)
i = 1,2,…,m
(1-2)
(1-3)
10
那么,最优化任务,是要在式 那么,最优化任务,是要在式(1-2)、式(1-3) 、 的约束条件下,寻求x,使式(1-1)的目标函数取 的约束条件下,寻求 ,使式 的目标函数取 最优(最小或最大 值 最优 最小或最大)值。 最小或最大 上述问题的最优化,由于变量 与时间 与时间t无 上述问题的最优化,由于变量x与时间 无 或在所讨论的时间区间内t为常量 为常量, 关,或在所讨论的时间区间内 为常量,因此属 静态最优化问题。 于静态最优化问题。
第一章 概述 3
有甲、乙两个仓库,分别存有水泥1500包 例:有甲、乙两个仓库,分别存有水泥 包 三个工地, 和1800包。有A、B、C三个工地,分别需要水泥 包 、 、 三个工地 900包、600包和 包 包和1200包。 包和 包 已知从甲库送到A、B、C三个工地,每包水泥 三个工地, 已知从甲库送到 、 、 三个工地 的运费分别为1元 元和4元 从乙库送到A、 、 的运费分别为 元、2元和 元;从乙库送到 、B、C 元和 三个工地的运费分别为4元 元和9元 三个工地的运费分别为 元、5元和 元。 元和 应怎样发送这些水泥,才能使运费最省呢? 应怎样发送这些水泥,才能使运费最省呢?
第一章 概述 6
本例中,目标函数 本例中,目标函数f(x)和约束条件都是自变 和约束条件都是自变 的一次函数, 量x的一次函数,称为线性最优化问题。又因约 的一次函数 称为线性最优化问题。 束条件中存在不等式,故属具有不等式约束条 束条件中存在不等式, 件的线性最优化问题。 件的线性最优化问题。
第一章 概述
古典变分法 极小(大 值原理 极小 大)值原理 动态规划法
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最优控制
先修课程:常微分方程,最优化方法最优控制问题是具有特殊数学结构的一类最优化问题,在科学、工程和管理乃至人文领域都存在大量的最优控制问题。
最优控制研究动态系统在各种约束条件下,寻求目标泛函取极值的最优控制函数与最优状态轨线的数学理论和方法,它是静态最优化在无穷维空间的扩展。
希望学生通过本课程的学习,能够结合实际背景,建立最优控制的模型,理解求解最优控制的三大类基本方法的数学思想,灵活地掌握这些方法的基本过程,并能解释计算结果的意义。
主要内容如下:最优控制问题及其建模;数学基础;变分法及其在最优控制的应用;极小值原理及其应用;动态规划方法及其应用;应用。
最优控制
一、课程基本信息 1.先修课程:数学系本科包括到大三的全部课程 2.面向对象:理学院数学系各专业 3.推荐教学参考书:吴沧浦,《最优控制的理论与方法》,国防工业出版社,2000 王朝珠等,《最优控制理论》,科学出版社,2003 邢继祥等,《最优控制应用基础》,科学出版社,2003 W. L. Brogan, Modern C ontrol Theor y, (3th eidition), Prentice-Hall, Englew ood C liffs,1991 二、课程的性质和任务本课程是数学与应用数学专业本科生高年级选修课程之一。
从数学的角度,最优控制问题是最优化问题中具有特殊结构的一类问题。
就问题的来源看,它又是控制问题。
最优控制研究动态系统在各种约束条件下寻求使目标泛函取极值的最优控制函数和最优状态轨线的数学理论和方法。
最优控制问题涉及范围广跨度大,几乎理工医农,管理军事乃至人文经法领域,都存在着大量此类问题。
最优化已是寻求最优系统和结构,挖掘系统潜力的有力武器,学会求解最优控制问题,是应用数学工作者的最基本素养之一。
通过本课程的主要任务是,从各个教学环节引导学生认识不同数学问题的特点和相应数学模型的结构,自己学会分析实际问题,建立各种数量之间的联系,写出正确的合理的最优控制的模型;领会求解最优控制问题解法是如何提出的数学思想,并学会如何根据这些思想来构成相应方法的技巧;学会能正确地解释计算结果的物理意义的能力。
最根本的是学会和培养系统地、动态地、综合地考虑,认识和处理问题的思想方法和动手能力。
这样,通过本课程的各个教学环节,提高学生的数学素质,加强学生开展科研工作和解决实际问题的能力。
三、教学内容和要求基本要求:期望学生能够结合工程背景认识最优控制问题的数学结构的特点,从而能灵活地建立实际问题的数学模型,深刻领会求解它们的三大类方法的数学思想,熟练地掌握这些方法的运用步骤,能正确地解释求解结果的意义,并学会最优控制问题的数值解法。
第一章最优控制与最优化问题 1.1 最优化问题的源和流 1.2 最优控制问题的例子和数学描述 1.3 最优控制问题求解的基本思想第二章数学基础 2.1 向量与矩阵的求导法则 2.2 函数极值的几个条件 2.3 线性微分方程的解第三章变分法 3.1 泛函的变分与极值 3.2 Euler方程 3.3 等式约束条件下泛函极值问题的必要条件 3.4 几类可用变分方法求解的最优控制问题 3.5 应用实例第四章极小值原理 4.1 极值曲线场与充分条件 4.2 有控制变量不等式约束的极小值原
理 4.3 含有状态变量不等式的极小值原理 *4.4 极小值原理的证明 4.5 极小值原理的应用实例 4.6 离散极小值原理第五章极小值原理的几类应用 5.1 时间最短最优控制问题 5.2 燃料最省最优控制问题 5.3 线性二次型最优控制问题第六章动态规划 6.1 多阶段决策问题与动态规划思想 6.2 用动态规划思想解最优化问题 6.3 离散系统最优控制问题的动态规划解法 6.4 离散线性二次型问题的动态规划解 6.5 连续系统做优控制问题的动态规划解和HJB方程 6.6 连续二次型问题的动态规划解 6.7 Riccatti方程的求解第七章最优控制的新发展 7.1 对策论和微分对策 7.2 随机最优控制四.实验(上机)内容和基本要求本课程无实验和上机的教学安排,但要求学生结合本专业的特点和所研究的课题,选择部分算法自己上机实现。
要求学生熟悉至少一门数学软件平台(Mathematica/ matleb/Maple)和至少一种编程语言。
教学实验就是编程解决实际问题。
至少做有求解
足够规模的问题的大作业3-4次大作业。
五.对学生能力培养的要求本课程采用“引出问题,启发思路,重点分析,课堂讨论,课外探索,自行归纳”的教学方式,使学生在掌握最优控制基本知识的基础上,力求活跃其数学思想,从而培养学生运用较高层次的数学观点和数学知识,能对实际问题进行分析、归纳、提炼和建立数学模型,选择适当的算法,能够编写计算机程序实际求解,并且能对计算结果进行分析和解释。
另一方面,希望在教师引导下,学生逐步学会自己从前人研究的问题、分析问题的过程、演绎推导的结果中,体会和领悟这些人类高级心智文明的成果,使学生自己真正学懂数学,而不是被“教会”数学;同时希望学生通过研究式的钻研、探索乃至犯错误的过程中,培养从错纵复杂的现象事理中和繁杂无序的结果数据中,寻找与总结内在关系和规律的能力,并且体会科学研究的艰辛和乐趣,培养在科学研究和事理处理上百折不挠、持之以恒的毅力和意志。
提高他们的数学素质和数学修养,提高他们开展科技活动和社会实践的能力以及开展科研工作的能力。
尽管本课程的重点放在运用算法解决问题上,但是仍然鼓励和希望学有余力的同学,对于问题建立模型、算法的性态分析和算法实际运行性质的分析,有实质性的研究和提高。
