习题集：第二篇 材料力学
(完整版)材料力学习题集(有答案)汇总,推荐文档
一、 是非题 1. 材料力学主要研究杆件受力后变形与破坏的规律。 （ ） 2. 内力只能是力。 （ ） 3. 若物体各点均无位移，则该物体必定无变形。 （ ） 4. 截面法是分析应力的基本方法。 （ ） 二、选择题
5. 构件的强度是指（ ），刚度是指（ ），稳定性是指（ ）。 A. 在外力作用下构件抵抗变形的能力 B. 在外力作用下构件保持其原有的平衡状态的能力 C. 在外力作用下构件抵抗破坏的能力 1.6 根据均匀性假设，可认为构件的（ ）在各点处相同。 A. 应力 B. 应变 C. 材料的弹性常数 D. 位移 1.7 下列结论中正确的是（ ） A. 内力是应力的代数和 B. 应力是内力的平均值 C. 应力是内力的集度 D. 内力必大于应力 参考答案：1.1 √ 1.2 × 1.3 √ 1.4 × 1.5 C,A,B 1.6 C 1.7 C
5. 杆件某个横截面上，若轴力不为零，则各点的正应力均不为零。 （ ）
6. δ、 y 值越大，说明材料的塑性越大。 （ ）
7. 研究杆件的应力与变形时，力可按力线平移定理进行移动。 （ ）
8. 杆件伸长后，横向会缩短，这是因为杆有横向应力存在。 （ ）
9. 线应变 e 的单位是长度。 （ ）
10. 轴向拉伸时，横截面上正应力与纵向线应变成正比。 （ ）
轴力变化可能有以下四种情况，问哪一种正确？
(A) 两杆轴力均减小；
(B) 两杆轴力均增大； (C) 杆 1 轴力减小，杆 2 轴力增大；
1
2
(D) 杆 1 轴力增大，杆 2 轴力减小。 9. 结构由于温度变化，则：
A aB
a
C
(A) 静定结构中将引起应力，超静定结构中也将引起应力；
F
(B) 静定结构中将引起变形，超静定结构中将引起应力和变形； (C) 无论静定结构或超静定结构，都将引起应力和变形； (D) 静定结构中将引起应力和变形，超静定结构中将引起应力。 10. 单位宽度的薄壁圆环受力如图所示，p 为径向压强，其截
材料力学-习题集(含答案)
《材料力学》课程习题集西南科技大学成人、网络教育学院版权所有习题【说明】：本课程《材料力学》（编号为06001）共有单选题,计算题,判断题,作图题等多种试题类型，其中，本习题集中有[判断题]等试题类型未进入。
一、单选题1.构件的强度、刚度和稳定性________。
(A)只与材料的力学性质有关(B)只与构件的形状尺寸有关(C)与二者都有关(D)与二者都无关2.一直拉杆如图所示，在P力作用下。
(A) 横截面a上的轴力最大(B) 横截面b上的轴力最大(C) 横截面c上的轴力最大(D) 三个截面上的轴力一样大3.在杆件的某一截面上，各点的剪应力。
(A)大小一定相等(B)方向一定平行(C)均作用在同一平面内(D)—定为零4.在下列杆件中，图所示杆是轴向拉伸杆。
(A) (B)(C) (D)P5.图示拉杆承受轴向拉力P的作用，斜截面m-m的面积为A，则σ=P/A为。
(A)横截面上的正应力(B)斜截面上的剪应力(C)斜截面上的正应力(D)斜截面上的应力6.解除外力后，消失的变形和遗留的变形。
(A)分别称为弹性变形、塑性变形(B)通称为塑性变形(C)分别称为塑性变形、弹性变形(D)通称为弹性变形7.一圆截面轴向拉、压杆若其直径增加—倍，则抗拉。
(A)强度和刚度分别是原来的2倍、4倍(B)强度和刚度分别是原来的4倍、2倍(C)强度和刚度均是原来的2倍(D)强度和刚度均是原来的4倍8.图中接头处的挤压面积等于。
P(A)ab (B)cb (C)lb (D)lc9.微单元体的受力状态如下图所示，已知上下两面的剪应力为τ则左右侧面上的剪应力为。
(A)τ/2(B)τ(C)2τ(D)010.下图是矩形截面，则m—m线以上部分和以下部分对形心轴的两个静矩的。
(A)绝对值相等，正负号相同(B)绝对值相等，正负号不同(C)绝对值不等，正负号相同(D)绝对值不等，正负号不同11.平面弯曲变形的特征是。
(A)弯曲时横截面仍保持为平面(B)弯曲载荷均作用在同—平面内；(C)弯曲变形后的轴线是一条平面曲线(D)弯曲变形后的轴线与载荷作用面同在—个平面内12.图示悬臂梁的AC段上，各个截面上的。
材料力学习题
材料力学习题训练22-1.求图示阶梯状直杆横截面1-1﹑2-2和3-3上的轴力，并作轴力图。
如横截面面积，，，求各横截面上的应力。
2-5.图示结构中，已知杆之横截面为的矩形，当杆横截面上的最大正应力为时，求此时的值。
2-6.直杆在两侧面受有沿轴线方向均匀分布的载荷（仅在段），其集度为；在端受集中力作用，。
已知杆横截面面积，，材料的弹性模量。
求：1、画出轴力图； 2、两截面的铅垂位3、过两点与轴线夹角斜截面上的应力。
2-8.图示一手动压力机，在工件上所加的最大压力为150kN。
已知立柱和螺杆所用材料的屈服点MPa，规定的安全系数n=。
（1）试按强度要求选择立柱的直径D；（2）若螺杆的内径d=40mm试校核其强度。
3-1 夹剪如图所示。
销子C的直径d=5mm。
当加力P=，剪直径与销子直径相同的铜丝时，求铜丝与销子横截面的平均剪应力。
已知a=30mm，b=150mm。
3-2 结构受力如图所示，若已知木材的许用切应力，试校核木接头剪切强度是否安全。
3-3 木梁由柱支撑如图所示，今测得柱中的轴向压力为，若已知木梁所能承受的许用挤压应力。
确定柱与木梁之间垫板的尺寸。
3-4 木构件和由两片层合板用胶粘接在一起，承受轴向载荷作用，如图所示。
已知和的空隙为；板宽；胶层的许用切应力。
确定层合板的长度。
3-5 水轮发电机组的卡环尺寸如图所示。
已知轴向荷载P=1450kN，卡环材料的许用剪应力=80MPa，许用挤压应力=150MPa。
试对卡环进行强度校核。
3-6 拉力P=80kN的螺栓连接如图所示。
已知b=80mm，t=10mm，d=22mm，螺栓的许用剪应力=130MPa，钢板的许用挤压应力=300MPa，许用拉应力 =170MPa。
试校核该接头的强度。
3-7 一托架如图所示。
已知外力P=35kN，铆钉的直径d=20mm，铆钉都受单剪。
求最危险的铆钉横截面上剪应力的数值及方向。
3-8 销钉式安全离合器如图所示，允许传递的外力偶矩m=30kN·cm，销钉材料的剪切强度极限=360MPa，轴的直径D=30mm，为保证m>30000N·cm时销钉被剪断，求销钉的直径d。
材力习题集.
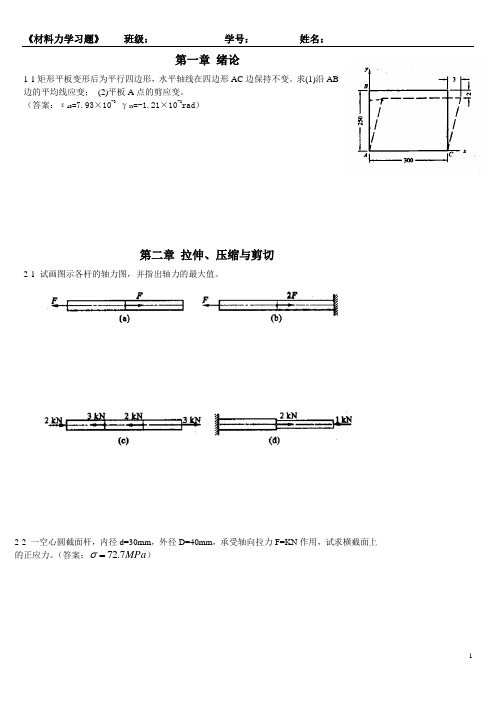
第一章 绪论1-1矩形平板变形后为平行四边形，水平轴线在四边形AC 边保持不变。
求(1)沿AB边的平均线应变； (2)平板A 点的剪应变。
（答案：εAB =7.93×10-3 γXY =-1.21×10-2rad ）第二章 拉伸、压缩与剪切2-1 试画图示各杆的轴力图，并指出轴力的最大值。
2-2 一空心圆截面杆，内径d=30mm ，外径D=40mm ，承受轴向拉力F=KN 作用，试求横截面上的正应力。
（答案：MPa 7.72=σ）2-3 题2－1 c 所示杆，若该杆的横截面面积A=502m m ，试计算杆内的最大拉应力与最大压应力（答案：MPa t 60max ,=σ MPa c 40max ,=σ）2.4图示轴向受拉等截面杆，横截面面积A=5002m m ，载荷F=50KN 。
试求图示截面m-m 上的正应力与切应力，以及杆内的最大正应力与最大切应力。
（答案：MPa MPa MPa MPa 50 ; 100 ; 24.49 ; 32.41max max ==-==τστσαα）2.5如图所示，杆件受轴向载荷F 作用。
该杆由两根木杆粘接而成，若欲使粘接面上的正应力为其切应力的二倍，则粘接面的方位角θ应为何值（答案： 6.26=θ）2.6 等直杆受力如图所示，试求各杆段中截面上的轴力，并绘出轴力图。
2.7某材料的应力－应变曲线如图所示，图中还同时画出了低应变去区的详图，试确定材料的弹性模量E 、屈服极限s σ、强度极限b σ、与伸长率δ，并判断该材料属于何种类型（塑性或脆性材料）。
2.8某材料的应力－应变曲线如图所示，试根据该曲线确定： （1）材料的弹性模量E 、比例极限P σ与屈服极限2.0σ; （2）当应力增加到MPa 350=σ时，材料的正应变ε， 以及相应的弹性应变e ε与塑性应变p ε2.9图示桁架，杆1与杆2的横截面均为圆形，直径分别为d1=30mm 与d2＝20mm ，两杆材料相同，许用应力[]σ＝160MPa ，该桁架在节点A 处承受铅垂方向的载荷F=80KN 作用。
2章习题参考答案材料力学课后习题题解
2.24 图示结构，BC杆为5号槽钢，其许用应力[σ]1=160MPa； AB杆为100×50mm2的矩形截面木杆，许用应力[σ]2=8MPa。试 求：（1）当F=50kN时，校核该结构的强度；（2）许用荷 载[F]。 解：受力分析如图
F F
C
A
y
0: (1)
F
FBC sin 60o FBA sin 30o 0
Fx = 0: FAB = F
因此
LAB
FABl Fl EA EA
（b）受力分析如图， 由C点平衡可知：
F C A D F
(b)
F C F AC B A FAC FAB FAD F AD D F FBD FAB FCB FCB FBD
Fx 0 : F
FBC FAC
B
F
x
0:
FAB 45o 30o C A F 1m 45o 30o FAC A F
FAB cos 45o FAC cos 30o 0 2 FAB 3FAC FAB 3 FAC 2
LAB cos 45o LAC cos 30o LAB LAC cos 30 o cos 45
max 10MPa
2.6 钢杆受轴向外力如图所示，横截面面积为500mm2，试求 ab斜截面上的应力。 解： FN=20kN
a
30
o
20kN
FN FN pα = = cos30o A A0 α
FN α pα cos 30 cos 2 30o A0
o
b a b a b
FN
sα
τ α
B
FAy
1m 1m
F
FDC 4 10 F 40 F 10 [ ] 160 2 2 6 ADC 3 d 3 20 10
材料力学练习册答案
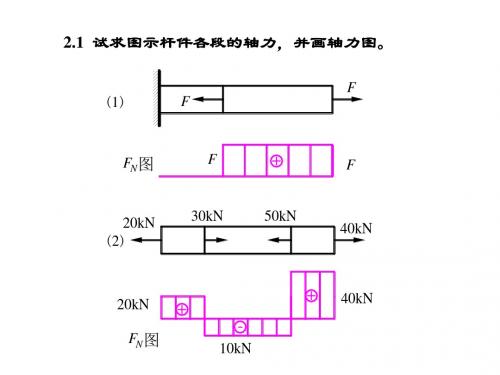
第二章 轴向拉伸和压缩2.1 求图示杆11-、22-、及33-截面上的轴力。
解：11-截面，取右段如)(a 由0=∑x F ，得 01=N F22-截面，取右段如)(b由0=∑x F ，得 P F N -=233-截面，取右段如)(c由0=∑x F ，得 03=N F2.2 图示杆件截面为正方形，边长cm a 20=，杆长m l 4=，kN P 10=，比重3/2m kN =γ。
在考虑杆本身自重时，11-和22-截面上的轴力。
解：11-截面，取右段如)(a 由0=∑xF，得kN la F N 08.04/21==γ22-截面，取右段如)(b由0=∑xF，得kN P la F N 24.104/322=+=γ2.3 横截面为210cm 的钢杆如图所示，已知kN P 20=，kN Q 20=。
试作轴力图并求杆的总伸长及杆下端横截面上的正应力。
GPa E 200=钢。
解：轴力图如图。
杆的总伸长：m EA l F l N59102001.0102001.02000022-⨯-=⨯⨯⨯-⨯==∆ 杆下端横截面上的正应力：MPa A F N 20100020000-=-==σ 2.4 两种材料组成的圆杆如图所示，已知直径mm d 40=，杆的总伸长cm l 21026.1-⨯=∆。
试求荷载P 及在P 作用下杆内的最大正应力。
（GPa E 80=铜，GPa E 200=钢）。
解：由∑=∆EAl F l N ，得)104010806.0410********.04(1026.16296294---⨯⨯⨯⨯⨯+⨯⨯⨯⨯⨯=⨯ππP4/4/4/4/)(a )(b )(c 2N1N )(a kNkN 图NF cm cmcm解得： kN P 7.16= 杆内的最大正应力：MPa A F N 3.13401670042=⨯⨯==πσ 2.5 在作轴向压缩试验时，在试件的某处分别安装两个杆件变形仪，其放大倍数各为1200=A k ，1000=B k ，标距长为cm s 20=，受压后变形仪的读数增量为mm n A 36-=∆，mm n B 10=∆，试求此材料的横向变形系数ν（即泊松比）。
材料力学内部习题集及答案
第二章 轴向拉伸和压缩2-1一圆截面直杆，其直径d ＝20mm,长L =40m ，材料的弹性模量E =200GPa ，容重γ＝80kN/m 3,杆的上端固定，下端作用有拉力F =4KN ，试求此杆的：⑴最大正应力； ⑵最大线应变； ⑶最大切应力；⑷下端处横截面的位移∆。
解：首先作直杆的轴力图⑴最大的轴向拉力为232N,max 80100.024*********.8N 44d F V F L F ππγγ=+=+=⨯⨯⨯⨯+= 故最大正应力为：N,maxN,maxN,maxmax 222445004.8=15.94MPa 3.140.024F F F Addσππ⨯====⨯⑵最大线应变为:64maxmax915.94100.7971020010E σε-⨯===⨯⨯ ⑶当α（α为杆内斜截面与横截面的夹角）为45︒时，maxmax 7.97MPa 2ασττ===⑷取A 点为x 轴起点，2N (25.124000)N 4d F Vx F x F x πγγ=+=+=+故下端处横截面的位移为：240N 0025.1240001d d (12.564000)2.87mm LL F x x x x x EA EA EA+∆===⋅+=⎰⎰2-2试求垂直悬挂且仅受自重作用的等截面直杆的总伸长△L 。
已知杆横截面面积为A ，长度为L ,材料的容重为γ。
解：距离A 为x 处的轴力为 所以总伸长2N 00()L d d 2LL F x Ax L x x EA EA Eγγ∆===⎰⎰ 2-3图示结构，已知两杆的横截面面积均为A =200mm 2,材料的弹性模量E =200GPa 。
在结点A 处受荷载F 作用，今通过试验测得两杆的纵向线应变分别为ε1＝4×10－4，ε2＝2×10－4，试确定荷载P 及其方位角θ的大小。
解:由胡克定律得 相应杆上的轴力为取A 节点为研究对象，由力的平衡方程得解上述方程组得2-4图示杆受轴向荷载F 1、F 2作用，且F 1＝F 2＝F ，已知杆的横截面面积为A ，材料的应力－应变关系为ε＝c σn，其中c 、n 为由试验测定的常数。
《材料力学》课后习题答案(详细)
第二章轴向拉(压)变形[习题2-1]试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。
（a）解：（1）求指定截面上的轴力FN =-11FF F N -=+-=-222（2）作轴力图轴力图如图所示。
（b）解：（1）求指定截面上的轴力FN 211=-02222=+-=-F F N （2）作轴力图FF F F N =+-=-2233轴力图如图所示。
（c）解：（1）求指定截面上的轴力FN 211=-FF F N =+-=-222（2）作轴力图FF F F N 32233=+-=-轴力图如图所示。
（d）解：（1）求指定截面上的轴力FN =-11F F a aFF F qa F N 22222-=+⋅--=+--=-（2）作轴力图中间段的轴力方程为：x aF F x N ⋅-=)(]0,(a x ∈轴力图如图所示。
[习题2-2]试求图示等直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。
若横截面面积2400mm A =，试求各横截面上的应力。
解：（1）求指定截面上的轴力kNN 2011-=-)(10201022kN N -=-=-)(1020102033kN N =-+=-（2）作轴力图轴力图如图所示。
（3）计算各截面上的应力MPa mm N A N 504001020231111-=⨯-==--σMPamm N A N 254001010232222-=⨯-==--σMPa mmN A N 254001010233333=⨯==--σ[习题2-3]试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。
若横截面面积21200mm A =，22300mm A =，23400mm A =，并求各横截面上的应力。
解：（1）求指定截面上的轴力kNN 2011-=-)(10201022kN N -=-=-)(1020102033kN N =-+=-（2）作轴力图轴力图如图所示。
（3）计算各截面上的应力MPa mm N A N 10020010202311111-=⨯-==--σMPa mmN A N 3.3330010102322222-=⨯-==--σMPamm N A N 254001010233333=⨯==--σ[习题2-4]图示一混合屋架结构的计算简图。
材料力学习题集 (有答案)
绪 论一、 是非题1.1 材料力学主要研究杆件受力后变形与破坏的规律。
（ ） 1.2 内力只能是力。
（ ）1.3 若物体各点均无位移，则该物体必定无变形。
（ ） 1.4 截面法是分析应力的基本方法。
（ ） 二、选择题1.5 构件的强度是指（ ），刚度是指（ ），稳定性是指（ ）。
A. 在外力作用下构件抵抗变形的能力B. 在外力作用下构件保持其原有的平衡状态的能力C. 在外力作用下构件抵抗破坏的能力1.6 根据均匀性假设，可认为构件的（ ）在各点处相同。
A. 应力 B. 应变C. 材料的弹性常数D. 位移1.7 下列结论中正确的是（ ） A. 内力是应力的代数和 B. 应力是内力的平均值 C. 应力是内力的集度 D. 内力必大于应力参考答案：1.1 √ 1.2 × 1.3 √ 1.4 × 1.5 C,A,B 1.6 C 1.7 C轴向拉压一、选择题1. 等截面直杆CD 位于两块夹板之间，如图示。
杆件与夹板间的摩擦力与杆件自重保持平衡。
设杆CD 两侧的摩擦力沿轴线方向均匀分布，且两侧摩擦力的集度均为q ，杆CD 的横截面面积为A ，质量密度为ρ，试问下列结论中哪一个是正确的？ (A) q gA ρ=；(B) 杆内最大轴力N max F ql =； (C) 杆内各横截面上的轴力N 2gAlF ρ=；(D) 杆内各横截面上的轴力N 0F =。
2. 低碳钢试样拉伸时，横截面上的应力公式N F A σ=适用于以下哪一种情况? (A) 只适用于σ≤p σ； (B) 只适用于σ≤e σ； (C)3. 在A 和B和点B 的距离保持不变，绳索的许用拉应力为[]σ取何值时，绳索的用料最省？ (A) 0； (B) 30； (C) 45； (D) 60。
4. 桁架如图示，载荷F 可在横梁（刚性杆）DE 为A ，许用应力均为[]σ（拉和压相同）。
求载荷F 的许用值。
以下四种答案中哪一种是正确的？(A)[]2A σ； (B) 2[]3Aσ；(C) []A σ； (D) 2[]A σ。
材料力学习题及答案
材料力学习题一一、计算题1．（12分）图示水平放置圆截面直角钢杆（2ABC π=∠），直径mm 100d =，m l 2=，m N k 1q =，[]MPa 160=σ，试校核该杆的强度。
2．（12分）悬臂梁受力如图，试作出其剪力图与弯矩图。
3．（10分）图示三角架受力P 作用，杆的截面积为A ，弹性模量为E ，试求杆的内力和A 点的铅垂位移Ay δ。
4．（15分）图示结构中CD 为刚性杆，C ，D 处为铰接，AB 与DE 梁的EI 相同，试求E 端约束反力。
5. (15分) 作用于图示矩形截面悬臂木梁上的载荷为：在水平平面内P 1=800N ，在垂直平面内P 2=1650N 。
木材的许用应力[σ]=10MPa 。
若矩形截面h/b=2，试确定其尺寸。
三．填空题 （23分）1．（4分）设单元体的主应力为321σσσ、、，则单元体只有体积改变而无形状改变的条件是＿＿＿＿＿＿＿＿＿＿；单元体只有形状改变而无体积改变的条件是＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。
2．（6分）杆件的基本变形一般有＿＿＿＿＿＿、＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿四种；而应变只有＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿两种。
3．（6分）影响实际构件持久极限的因素通常有＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿，它们分别用＿＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿＿＿＿＿＿来加以修正。
4.（5分）平面弯曲的定义为＿＿＿＿＿＿＿＿＿＿＿＿_＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿_。
5.（2分）低碳钢圆截面试件受扭时，沿 ＿＿＿＿＿＿＿＿＿＿＿＿ 截面破坏；铸铁圆截面试件受扭时，沿 ＿＿＿＿＿＿＿＿＿＿＿＿ 面破坏。
四、选择题（共2题，9分）2．（5分）图示四根压杆的材料与横截面均相同，试判断哪一根最容易失稳。
答案：（ ）材料力学习题二二、选择题：（每小题3分，共24分）1、危险截面是______所在的截面。
习题集第二篇材料力学
习题5-16图
习题5-17图
5-18 图示铆接头受拉力F = 24kN 作用，上下钢板尺寸相同，厚度 t=10mm,宽b =100mm,许用切应力
[τ
[τ
1]=170MPa，铆钉的许用应力
习题9图
习题10图
4-10 三根试件的尺寸相同，但材料不同，其σ-ε曲线如图所 示，其中强度最高的是_______；塑性最好的是 ；刚度 最大的是_______。
4-11 试判断下图中A、B、C、D试件是低碳钢还是铸铁？ A 材料为_________ B 材料为__________ C 材料为__________ D 材料为__________
圆截面钢杆，已知其直径 d = 10mm，
长度L=1m，弹性模量E=2×105MPa 。 试求：（1） BC杆的伸长量ΔL； （2）若BC杆的[]=100MPa，设计BC杆的最小截面积。
4-36 图示三角架，在节点B受铅垂荷载F作 用，其中钢拉杆 AC 截面面积A1=600mm2，许 用应力[σ]=60MPa，木压杆 BC 的截面面积 A2=1000mm2，许用应力[σ]=1.5MPa。试确定 许用荷载[F]。
三、单项选择题（将正确答案选出放在横线或括号内） 4-21 一阶梯杆件受拉力P的作用，其截面1-1，2-2，3-3上的 内力分别为N1，N2和N3，三者的关系为__________。 A、N1≠N2 N2≠N3 B、N1＝N2 N2＝N3 C、N1＝N2 N2＞N3 D、N1＝N2 N2＜N3
4-22 图示阶梯杆，CD段为铝，横截面面积为A；BC 和DE 段为 钢，横截面面积均为2A，设1-1，2-2，3-3截面上的正应力分 别为 ,则其大小次序为_________。 A、σ1>σ2>σ3 B、σ2>σ3 >σ1 C、σ3 >σ1>σ2 D、σ2>σ1 >σ3
《材料力学》第二章课后习题及参考答案
在材料力学中，应力和应变是描述材料受力状态的基本物理量。应力表示单位面积上的 力，而应变则表示材料的变形程度。
简答题3答案
弹性力学和塑性力学是材料力学的重要分支。弹性力学主要研究材料在弹性范围内的应 力、应变和位移，而塑性力学则研究材料在塑性变形阶段的力学行为。
选择题答案
80%
选择题1答案
选择题3解析
这道题考察了学生对材料力学中 弯曲应力的理解，学生需要理解 弯曲应力的概念和计算方法，并 能够根据实际情况进行选择和应 用。
计算题解析
01
计算题1解析
这道题主要考察了学生对材料力学中拉压杆的计算能力，学生需要掌握
拉压杆的应力、应变计算方法，并能够根据实际情况进行选择和应用。
02
计算题2解析
计算题2答案
根据题意，先求出梁的剪力和弯矩，然后根据剪力和弯矩的关系 求出梁的位移分布，最后根据位移和应力的关系求出应力分布。
03
习题解析Biblioteka 简答题解析简答题1解析这道题考查了学生对材料力学 基本概念的理解，需要明确应 力和应变的概念及关系，并能 够解释在材料力学中如何应用 。
简答题2解析
这道题主要考察了学生对材料 力学中弹性模量的理解，以及 如何利用弹性模量进行相关计 算。学生需要理解弹性模量的 物理意义，掌握其计算方法。
C. 材料力学的任务之一是研究材 料的各种力学性能，包括强度、 刚度和稳定性等。
100%
选择题2答案
D. 在材料力学中，应力和应变是 描述材料受力状态的基本物理量 。
80%
选择题3答案
B. 材料力学主要研究材料的力学 性能和内部结构的关系，包括弹 性、塑性和韧性等。
计算题答案
材料力学习题的答案解析
第二章轴向拉伸与压缩2-1 试求图示直杆横截面1-1、2-2、3-3上的轴力，并画出轴力图。
F1=18kN (b)F3=25kN 3力。
解:2-2 图示中部对称开槽直杆，试求横截面1-1和2-2上的正应1 .轴力M1I2- , --------------------------------------------------------- 4kN* -------------- —------------------------------------- r .------------- *—1 2201 F2=3kNF4=10kN2 31518F N F14kN2.应力F N141031 1MPa175MPaA1 1204F N141032 2MPa350A2 22010 4由截面法可求得，杆各横截面上的轴力为2-3 图示桅杆起重机，起重杆 AB 的横截面是外径为 20mm 、 径为18 mm 的圆环，钢丝绳 BC 的横截面面积为 BC 横截面上的应力。
AB 和钢丝绳 o 10mm 2。
试求起重杆解：1 .轴力 取节点 F x 0 :B 为研究对象，受力如图所示， F NBC F NAB cos30 F cos 45 2-4 图示由铜和钢两种材料组成的等直杆，铜和钢的弹性模量分别为 E 1100 GPa 和 E 2210 GPa 。
若杆的总伸长为A l 0.126mm ，试求载荷F 和杆横截面上的应力。
2铜1钢/ /F140 . -400600解:1•横截面上的应力由题意有I 1Fh FI 2 l 2E 1AE 2A由此得到杆横截面上的应力为l h I 2 E 1 E 2 h E 1l 2E 20.126 600 400 100 103 210 103 MPa 15.9MPaF y 0 : 由此解得： 2 .应力 起重杆横截面上的应力为F NABABF NAB sin 30 F sin 45 F NAB 2.83kN ， 2.83 103 A AB ____ 2。
材料力学课后复习习题集
第二章 轴向拉伸与压缩1、试求图示各杆1-1和2-2横截面上的轴力,并做轴力图。
（1） （2）2、图示拉杆承受轴向拉力F =10kN ，杆的横截面面积A =100mm 2。
如以α表示斜截面与横截面的夹角，试求当α=10°,30°,45°,60°,90°时各斜截面上的正应力和切应力,并用图表示其方向。
3、一木桩受力如图所示。
柱的横截面为边长200mm 的正方形,材料可认为符合胡克定律,其弹性模量E =10GPa 。
如不计柱的自重，试求：(1)作轴力图；(2)各段柱横截面上的应力； (3)各段柱的纵向线应变；(4)柱的总变形。
4、(1)试证明受轴向拉伸(压缩)的圆截面杆横截面沿圆周方向的线应变d ε,等于直径方向的线应变d ε。
(2)一根直径为d =10mm 的圆截面杆,在轴向拉力F 作用下,直径减小0.0025mm 。
如材料的弹性摸量E =210GPa ，泊松比ν=0.3,试求轴向拉力F 。
(3)空心圆截面钢杆,外直径D =120mm,内直径d =60mm,材料的泊松比ν=0.3。
当其受轴向拉伸时, 已知纵向线应变ε=0.001,试求其变形后的壁厚δ。
5、图示A和B两点之间原有水平方向的一根直径d=1mm的钢丝,在钢丝的中点C加一竖直荷载F。
已知钢丝产生的线应变为ε=0.0035,其材料的弹性模量E=210GPa，钢丝的自重不计。
试求：(1) 钢丝横截面上的应力(假设钢丝经过冷拉,在断裂前可认为符合胡克定律)；(2) 钢丝在C点下降的距离∆；(3) 荷载F的值。
6、简易起重设备的计算简图如图所示.一直斜杆AB应用两根63mm×40mm×4mm不等边角钢组[σ=170MPa。
试问在提起重量为P=15kN的重物时,斜杆AB是否满足强度成,钢的许用应力]条件?7、一结构受力如图所示,杆件AB,AD均由两根等边角钢组成。
已知材料的许用应力[σ=170MPa，试选择杆AB,AD的角钢型号。
材料力学习题集(超级好,内容全)
2P
3 4 3 4
a
2a
P
P
m Pa
2a
1 1
2 2
(a)
(b )
2 2
a
a/2
1
1
a
4 A 4
R
3 3
P B
R
C
R
45
2 2
c
Page 4
1
D R 1
d
解： 各截面上内力分量的方向从略，仅记大小。
a 2P拉伸，N2 P拉伸；
b Q1
答案： W=U
8.当结构中构件所受未知约束力或内力的数目n多于静 力平衡条件数目m时，单凭平衡条件不能确定全部未知 l nm 0 力，相对静定结构（n=m），称它为（ ）。 称为（ ），这也是“多余”约束力或“多余”约束的 数目。
答案： 静不定结构，静不定次数。
Page 8
二、选择题
1.两端固定的等截面直杆受轴向载荷P作用，则图示AC、 P NCB P。 （ ） N AC 和拉伸 CB段分别受压缩
答案：
C
A
P
B
l l 2.图示结构由两根尺寸完全相同的杆件组成。AC杆为铜 合金，BC杆为低碳钢杆，则此两杆在力P作用下具有相 同的拉应力。 （ ）
A B
A B
C
o
答案： A，B，C，C
Page 10
3.两端固定的阶梯杆如图所示，横截面面积 A2 2 A1 ， 受轴向载荷P后，其轴力图是（ ）。 A2 A1 B P A
x
l
N
P 2
P 2
l
N
x
P 3
材料力学-习题集(含答案)
《材料力学》课程习题集西南科技大学成人、网络教育学院 版权所有习题【说明】：本课程《材料力学》（编号为06001）共有单选题,计算题,判断题,作图题等多种试题类型，其中，本习题集中有[判断题]等试题类型未进入。
一、单选题1. 构件的强度、刚度和稳定性________。
(A)只与材料的力学性质有关(B)只与构件的形状尺寸有关 (C)与二者都有关(D)与二者都无关 2. 一直拉杆如图所示，在P 力作用下 。
(A) 横截面a 上的轴力最大(B) 横截面b 上的轴力最大 (C) 横截面c 上的轴力最大(D) 三个截面上的轴力一样大 3. 在杆件的某一截面上，各点的剪应力 。
(A)大小一定相等(B)方向一定平行 (C)均作用在同一平面内 (D)—定为零 4. 在下列杆件中，图 所示杆是轴向拉伸杆。
(A) (B)(C)(D) 5. 图示拉杆承受轴向拉力P 的作用，斜截面m-m 的面积为A ，则σ=P/A 为 。
(A)横截面上的正应力(B)斜截面上的剪应力 (C)斜截面上的正应力(D)斜截面上的应力 6. 解除外力后，消失的变形和遗留的变形 。
(A)分别称为弹性变形、塑性变形(B)通称为塑性变形 (C)分别称为塑性变形、弹性变形(D)通称为弹性变形 7. 一圆截面轴向拉、压杆若其直径增加—倍，则抗拉 。
(A)强度和刚度分别是原来的2倍、4倍(B)强度和刚度分别是原来的4倍、2倍 (C)强度和刚度均是原来的2倍 (D)强度和刚度均是原来的4倍8. 图中接头处的挤压面积等于 。
P P(A)ab (B)cb (C)lb (D)lc9.微单元体的受力状态如下图所示，已知上下两面的剪应力为τ则左右侧面上的剪应力为。
(A)τ/2(B)τ(C)2τ(D)010.下图是矩形截面，则m—m线以上部分和以下部分对形心轴的两个静矩的。
(A)绝对值相等，正负号相同(B)绝对值相等，正负号不同(C)绝对值不等，正负号相同(D)绝对值不等，正负号不同11.平面弯曲变形的特征是。
材料力学第二章习题
材料力学第二章习题习题2.1试画出图示各杆的轴力图题2.1图2.2图示中段开槽的杆件，两端受轴向载荷P作用，试计算截面1-1和截面2–2上的正应力。
已知：，mmb20=，mmb100=，mmt4=。
题2.2图2.3图示等直杆的横截面直径mmd50=，轴向载荷。
(1)计算互相垂直的截面AB和BC上正应力和切应力；(2)计算杆内的最大正应力和最大切应力。
2.4图示为胶合而成的等截面轴向拉杆，杆的强度由胶缝控制，已知胶的许用切应力[]τ为许用正应力[]σ的1/2。
问α为何值时，胶缝处的切应力和正应力同时达到各自的许用应力。
2．5图示用绳索起吊重物，已知重物,绳索直径。
许用应力,试校核绳索的强度。
绳索的直径应多大更经济。
，2.6冷镦机的曲柄滑块机构如图所示。
镦压工件时连杆接近水平位置，镦压力P=1100KN。
连杆矩形截面的高度h与宽度b之比为：h/b=1.4。
材料为45钢，许用应力【σ】=58MPa,试确定截面尺寸h及b。
2.7图示结构杆1与杆2由同一种材料制成，其许用应力[σ]=100MPa。
杆1横截面面积A1=300mm2,杆2横截面面积A2=200mm2，CE=0.5m,ED=1.5m。
试按杆1，杆2的强度确定许可载荷[F]。
2.8杆长，横截面积均相同的两杆，一为钢杆另一为灰铸铁杆。
欲组装成图示等边三角架。
已知杆长=0.5m，杆的横截面积A=400mm2,钢的许用应力【σ】=160MPa，灰铸铁的许用拉应力=30MPa,许用压应力=90MPa。
试问如何安装较为合理？求这时的最大许可载荷[F]。
2.9图示桁架，由圆截面杆1与杆2组成，并在节点A承受外力F=80kN作用。
杆1，杆2的直径分别为d1=30mm和d2=20mm,两杆的材料相同，屈服极限σ=320MPa，安全系数n=2.0。
试校核桁架的强度。
题2.9图2.10油缸盖与缸体采用6个螺栓连接如图所示。
D=350mm,油压p=1MPa,若螺栓材料的许用应力【σ】=40MPa，试确定螺栓的内径。
《材料力学》习题册附答案
F12312练习 1 绪论及基本概念1-1 是非题（1） 材料力学是研究构件承载能力的一门学科。
（ 是 ）（2）可变形固体的变形必须满足几何相容条件，即变形后的固体既不可以引起“空隙”，也不产生“挤入”现象。
（是）（3） 构件在载荷作用下发生的变形，包括构件尺寸的改变和形状的改变。
（ 是 ） （4） 应力是内力分布集度。
（是 ）（5） 材料力学主要研究构件弹性范围内的小变形问题。
（是 ） （6） 若物体产生位移，则必定同时产生变形。
（非 ） （7） 各向同性假设认为，材料沿各个方向具有相同的变形。
（F ） （8） 均匀性假设认为，材料内部各点的力学性质是相同的。
（是）（9） 根据连续性假设，杆件截面上的内力是连续分布的，分布内力系的合力必定是一个力。
（非） （10）因为构件是变形固体，在研究构件的平衡时，应按变形后的尺寸进行计算。
（非 ）1-2 填空题（1） 根据材料的主要性质对材料作如下三个基本假设：连续性假设、均匀性假设 、各向同性假设 。
（2） 工程中的强度 ，是指构件抵抗破坏的能力； 刚度 ，是指构件抵抗变形的能力。
（3） 保证构件正常或安全工作的基本要求包括 强度 ， 刚度 ，和 稳定性三个方面。
3（4） 图示构件中，杆 1 发生 拉伸 变形，杆 2 发生 压缩 变形，杆 3 发生 弯曲 变形。
（5） 认为固体在其整个几何空间内无间隙地充满了物质，这样的假设称为 连续性假设。
根据这一假设构件的应力，应变和位移就可以用坐标的 连续 函数来表示。
（6） 图示结构中，杆 1 发生 弯曲变形，构件 2发生 剪切 变形，杆件 3 发生 弯曲与轴向压缩组合。
变形。
（7） 解除外力后，能完全消失的变形称为 弹性变形，不能消失而残余的的那部分变形称为 塑性变形 。
（8） 根据 小变形 条件，可以认为构件的变形远 小于 其原始尺寸。
1-3选择题（1）材料力学中对构件的受力和变形等问题可用连续函数来描述；通过试件所测得的材料的力学性能，可用于构件内部的任何部位。
材料力学第二章习题【含答案】
专业班级学姓…………………………………………………………………装订线……………………………………………………………………………………浙江科技学院 2015-2016学年第一学期考试试卷 A 卷 考试科目 材料力学 考试方式 闭 完成时限 2 小时 拟题人 陈梦涛 审核人 批准人 2015 年 9 月17 日 建工 学院 2014 年级 土木工程 专业 一、单项选择题（每小题3分，计30分） 1. 对于塑性材料来说，胡克定律(Hooke's law )使用的范围是 。
A .p σσ<； B. p σσ>； C. s σσ<； D. s σσ> 2．实心圆截面杆直径为D ，受拉伸时的绝对变形为mm l 1=∆。
仅当直径变为2D 时，绝对变形l ∆为 。
A ．1mm B ．1/2 mm C ．1/4 mm D ．2mm 3. 下列有关受压柱截面核心的说法中，正确的是 。
A ．当压力P 作用在截面核心内时，柱中只有拉应力。
B ．当压力P 作用在截面核心内时，柱中只有压应力。
C ．当压力P 作用在截面核心外时，柱中只有压应力。
D ．当压力P 作用在截面核心外时，柱中只有拉应力。
4. 构件的强度、刚度和稳定性 。
A .只与材料的力学性质有关； B.只与构件的形状尺寸关； C.与二者都有关； D.与二者都无关。
5. 如右图所示，设虚线表示为单元体变形后的形状，则该单元体的剪应变为 。
A. α; B.π/2-α; C.π/2-2α; D .2α 6. 图示一杆件的拉压刚度为EA ，在图示外力作用下其应变能U 的下列表达式是 。
7. 应力－应变曲线的纵、横坐标分别为σ＝FN /A ，ε＝△L / L ，其中 。
A.A 和L 均为初始值； B.A 和L 均为瞬时值； C.A 为初始值，L 为瞬时值； D.A 为瞬时值，L 均为初始值。
8. 设一阶梯形杆的轴力沿杆轴是变化的，则发生破坏的截面上 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
5-8 如图所示：电瓶挂钩用插销连
接，已知t、d、P，则插销剪切面上 的剪应力τ =__________；挂钩的 最大挤压应力σbs=____________。
习题5-6图
D h
d
习题5-7图
4-37 某机床工作台进给液压缸如图所示， 已知压力p(MPa)，液压缸内径D(mm)，活 塞杆直径d(mm)，活塞杆材料的许用应力[σ] （MPa）。试校核活塞杆的强度。
4-38 一起重架如图所示，A、B、C 为铰接，在D点处作用一力P =5kN，
2m
C
B
杆AB为方形截面木材制成的，许用 2m
应力[σ]=1.5MPa，求杆AB截面边长。
内力分别为N1，N2和N3，三者的关系为__________。
A、N1≠N2 N2≠N3
B、N1＝N2 N2＝N3
C、N1＝N2 N2＞N3
D、N1＝N2 N2＜N3
4-22 图示阶梯杆，CD段为铝，横截面面积为A；BC 和DE 段为
钢，横截面面积均为2A，设1-1，2-2，3-3截面上的正应力分
别为
C、内力随外力的增大而减小 D、内力沿杆轴是不变的
4-25 一拉伸钢杆, 弹性模量E＝200GPa, 比例极限为200MPa，
今测得其轴向应变ε＝0.0015，则横截面上的正应力___ ___C、200MPa＜σ＜300MPa
D、σ＜200MPa
4-26 脆性材料的危险应力是________ A、比例极限 B、弹性极限 C、屈服极限 D、强度极限
4-16 不经热处理，只是将材料冷拉到强化阶段某一应力值
后就卸载，以提高材料比例极限的方法，称为
。
此方法虽然提高了材料的强度，但降低了材料的
，
增加了脆性。
4-18 现有低碳钢和铸铁两种材料，图示结构
中1选
材料，2选
材料。
4-19 两杆由不同的材料制成，杆1的弹性模量 E1大于杆2的
弹性模量E2。当它们的应变量相等时，
。
5-12 用两块铸铁将两矩形木杆连接如图所示。若两端受载
荷P=60KN，杆宽b=150mm,木杆的许用切应力[τ]=1MPa
许用挤压应力[σbs]=10MPa，则尺寸
a=
，b=
。
若铸铁的许用切应力[τ] = 20MPa，
则铸铁的厚度至少要c=
。
三、单项选择题（将正确答案选出放在横线或括号内）
5-13 如图所示的插销，穿过水平放置的平
思考题
1. 轴向拉压的受力特点和变形特点是什么？什么叫内力？ 2. 什么叫轴力？轴力的正负号是怎样规定的？ 3. 静力学中力的可传性原理，在材料力学中是否适用？为什 么？
4. EA在胡克定律里称为什么？它反映了构件的什么性质？
5. 若两杆的截面积Ａ、长度L载荷P都相同，但所用的材料不 同，问两杆的应力及变形是否相等？ 6. 什么是安全系数？通常安全系数的取值范围是如何确定的？ 7. 两个拉杆轴力相等，截面积及形状相同，但材料不同，它 们的应力是否相等？它们的许用应力是否相等？
一、判断题（对画√，错画×）
5-1 剪切变形的受力特点是：作用在杆件两侧面的外力的合
力大小相等，方向相反，作用线互相平行。
（）
5-2 挤压与压缩是同一个概念，二者没有什么区别。（ ）
5-3 在挤压强度计算中，当挤压接触面为平面时，挤压面积
就是接触面面积；当接触面为曲面时，挤压面积为曲面的正
投影面积。
4-27 拉、压杆的危险截面必为全杆中__________的横截面。
A、面积最小
B、正应力最大
C、轴力最大
4-28 现有钢、铸铁两种杆材，其直径相同。从承载能力与经 济效益两个方面考虑，图示结构中两种合理选择方案是( )。 A、1杆为钢，2杆为铸铁 B、1杆为铸铁，2杆为钢 C、二杆均为钢 D、二杆均为铸铁
变形情况。 4 . 挤压与压缩是否相同?请分析并指出下面（a）、（b）两
图中的构件1哪个需考虑压缩强度?哪个需考虑挤压强度？
思考题4图
5. 图中[σbs]钢> [σbs]铜> [σbs]铝，问应对哪一部分进行挤压
强度计算？
思考题5图
6 . 试确定下图所示连接或接头中的剪切面和挤压面。
思考题6图
练习题
（）
5-4 对于剪切问题，工程上除进行剪切强度校核，以确保构 件正常工作外，有时会遇到相反的问题，即利用剪切破坏。
（） 5-5 构件在发生剪切的同时，总伴随着挤压的产生。（ ）
二、填空题（把正确的答案写在横线上）
5-6 图示铆接钢板用两个铆钉连接，
钢板所受的F=10kN，则每个铆钉横 截面上的剪力Q =__________kN 。
第五章 剪切与挤压
要求:
1. 掌握剪应力和挤压应力的计算 2. 掌握剪切与挤压的强度效核 3. 能根据剪切、挤压强度条件设计 截面尺寸
思考题
1. 以螺栓为例说明，如果剪切强度和挤压强度不足，应分 别采取哪些相应措施?
2 . 如果将剪切中两个平行力的距离加大，变形会有何变化? 3 . 试述机械中连接件承受剪切时，其连接处的受力特点和
习题5-8图
h F
5-9 连接件在受剪时，剪切面与外力方向__________； 挤压面与外力方向__________。
5-10 判断剪切面和挤压面时应注意的是：剪切面是构件的 两部分有发生___ _趋势的平面；挤压面是构件_ _的表面。
5-11 塑性材料被挤压破坏时挤压应力一般要达到
，
而脆性材被挤压破坏时挤压应力一般要达到
已知该结构传递力矩m=3kN·m，键的 尺寸b = 24mm，轴的直径d = 85mm, 键
和带轮材料的许用应力[τ]=40MPa， [σbs]=90MPa。试计算键的长度。
d=17
构件的承载能力习题集
第四章 第五章 第六章 第七章 第八章
轴向拉伸与压缩 剪切挤压 圆轴的扭转 弯曲变形 组合变形
第四章 轴向拉伸与压缩
要求：
1.掌握轴向拉伸和压缩的内力计算 和轴力图的画法 2.掌握轴向拉伸和压缩的应力计算 3.掌握轴向拉伸和压缩的变形及胡 克定律 4.掌握轴向拉伸和压缩的强度校核
,则其大小次序为_________。
A、σ1>σ2>σ3
B、σ2>σ3 >σ1
C、σ3 >σ1>σ2
D、σ2>σ1 >σ3
4-23 材料的塑性指标有__________。 A、σs和δ B、和ψ C、δ和ψ D、δ和ψ
4-24 在下列说法，__________是正确的。
A、内力随外力增大而增大
B、内力与外力无关
求杆的最大及最小应力。
4-34 杆件受力如图所示，己知杆的横截面面积为A= 20mm2， 材料弹性模量E=200GPa，泊松系数μ=0.3。
（1）绘制杆的轴力图； （2）求杆横截面上的最大应力； （3）计算杆的总变形； （4）求杆的线应变。
4-35 图示结构，AB梁上作用着q=10kN/m的均布荷载，BC为
板上的圆孔，在其下端受一拉力Ｐ, 该插
销的剪切面积和挤压面积分别等于_____。
A、πdh，1/4πD ² B、πDh，1/4（D ²-d ²） C、πDh，1/4πD ² D、πdh，1/4π（D ²-d ²） 习题5-13图
5-14 图示铆接件，若板与铆钉为同一
材料，且已知[σjy]＝2[τ], 为提高
杆的内应力大。
如果两杆横截面和长度都相等，当内应力相等时 杆绝对
伸长量大。
4-20 同一棒料下的两杆，杆1是杆2长度的3倍，在相同的载 荷作用下绝对伸长量杆1是杆2的 倍，相对伸长量是 倍。
三、单项选择题（将正确答案选出放在横线或括号内）
4-21 一阶梯杆件受拉力P的作用，其截面1-1，2-2，3-3上的
A
2m D
P
4-39 图示一结构，由刚性杆 AB及两弹性杆EC及FD组成， 在B端受力F作用。两弹性杆 的刚度分别为E1A1和E2A2。试 求杆EC和FD的内力。
4-40 图示结构中AB为刚性杆， DE和BC为弹性杆，两杆的材 料和截面积均相同。己知： F=100kN，E=200GPa，a=1m, l=0.5m, A=400mm2， a=12×10-6 C-1，Δt=－300C。 试求当该结构的温度降低 300C时，两杆的内力。
练习题：
一、判断题：（对画√，错画×）
4-1 构件的强度是指构件抵抗变形的能力。
（）
4-2 脆性材料由于其抗压性能比抗拉性能好，所以适宜于制作
承受压力的构件。
（）
4-3 表示塑性材料的极限应力是材料的强度极限。 （ ）
4-4 轴向拉压杆任意斜截面上只有均匀分布的正应力，而无剪
应力。
（）
4-5 若杆件的总变形为零，则杆内的应力亦必为零。 （ ）
4-32 一中段开槽的直杆，如图所示，
受轴向力F =20kN作用；已知：h=25mm， h0=10mm，b =20mm。试求杆内的最大正
应力。
4-33 图示变截面圆钢杆ABCD，己知 P1=20kN，P2=P3=35kN，l1=l3=300mm, l2=400mm, d1=12mm, d2=16mm,d3=24mm，
习题5-16图 习题5-17图
5-18 图示铆接头受拉力F = 24kN
作用，上下钢板尺寸相同，厚度 F
t=10mm,宽b =100mm,许用切应力
[τ1]=170MPa，铆钉的许用应力 F [τ2]=140MPa，[σbs]=320MPa，
试校核该铆接头强度。
5-19 如图所示带轮和轴用平键连接，