第四章半导体的导电性
半导体物理学第四章
算术平均速度：
8kT 5 7 10 m / s 10 cm / s * m
作为比较： 声速～ 340m / s ，波音767～272m / s
§4.1 载流子的漂移运动，迁移率
无规则运动的原因：载流子（电子）在运动过程中 遭到散射，每次散射后它们的运动方向及速度大小 均发生变化，而且这种变化是随机的，所以速度不 能无限增大。 ②有规则运动（条件：存在电场或载流子浓度梯度）
a) 施加电场，电子（空穴）作 漂移运动，在电场方向上获 得加速度。
设电压为 V ，则电场
q * F qE m a a * E m
V E L
，
图4－1－1 电子在电 场中的运动
§4.1 载流子的漂移运动，迁移率
每次散射经过时间△t，得到附加度 j nqd 。
n型，n p, n N D , n 1 1 N D qn
n
§4.1 载流子的漂移运动，迁移率
1 p型, p n, p N A , p p N A q p
本征，ni pi , i 1
1
i
1 ni q( n p )
n type, 用N D N A 代替N D 存在杂质补偿时 p type, 用N A N D 代替N A
V ( x)
x 0,V (0) V0 示意图 V ( x) V0 Ex V0 x xd ,V ( xd ) 0, E x const d V0 电子电势能 qV ( x) qV0 qEx qV0 q x x0 设 xd 处为电势零点，对应的导带底为 Ec 0 V0 Ec ( x) Ec 0 qV ( x) Ec 0 qV0 qEx Ec 0 qV0 q x 则： xd
半导体的导电性
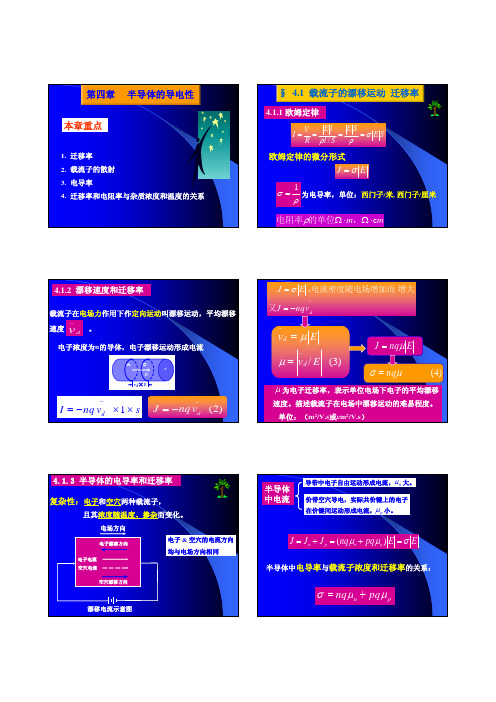
第四章半导体的导电性本章重点1.迁移率2.载流子的散射3.电导率4.迁移率和电阻率与杂质浓度和温度的关系§ 4.1 载流子的漂移运动迁移率4.1.1 欧姆定律S E S E S l l E R V I σρρ====/为电导率，单位：西门子/米, 西门子/厘米ρσ1=mm c ⋅Ω⋅Ω，的单位电阻率ρ欧姆定律的微分形式EJ σ=4.1.2 漂移速度和迁移率载流子在电场力作用下作定向运动叫漂移运动，平均漂移速度。
dv −(2)d J nq v −=−E v d ×1sAO 电子浓度为n 的导体，电子漂移运动形成电流1d I nq v s−=−××−−==dv nq J E J 又增大电流密度随电场增加而，σ/(3)d d v Ev E μμ−−==Enq J μ=)4(μσnq =为电子迁移率，表示单位电场下电子的平均漂移速度。
描述载流子在电场中漂移运动的难易程度。
单位：（m 2/V.s 或cm 2/V.s ）μ漂移电流示意图电场方向4.1.3 半导体的电导率和迁移率复杂性：电子和空穴两种载流子，且其浓度随温度、掺杂而变化。
空穴漂移方向电子电流空穴电流电子漂移方向电子& 空穴的电流方向均与电场方向相同半导体中电流EE pq nq J J J p n p n σμμ=+=+=)(半导体中电导率与载流子浓度和迁移率的关系：pn pq nq μμσ+=导带中电子自由运动形成电流，大。
n μ价带空穴导电，实际共价键上的电子在价键间运动形成电流，小。
p μn nq σμ=对N 型半导体n>>pppq σμ=对P 型半导体p>>n 对本征半导体p ＝n ＝n i()i n p n q σμμ=+电子迁移率大于空穴迁移率，高速开关器件主要依靠电子导电。
电导率主要取决于多子§ 4.2 载流子的散射J E σ=，电场一定，电流密度恒定应不断增加，，载流子受电场力加速J v nq J d −−=矛盾的两方面：原因所在：载流子与晶格原子或电离杂质等发生碰撞而交换能量，从而改变载流子速度的大小和方向4.2.1 载流子散射与漂移运动1、载流子的散射——改变速度的方向和大小处在外电场中的载流子运动：散射+漂移运动。
《半导体物理》第四章
长声学波，声子数最多，作用最大。
电子和声子的碰撞
• 声子的能量为：
1 1 1 a E (n )a a 2 2 exp(a ) 1 k0T
• 电子与声子的碰撞过程：
k 'k q E ' E h
• 具有单一极值、球形等能面的半导体，对导带电子散射 的几率是
k T (m ) Ps v 4 u
2 c 0 * 2 n 2
由形变引起导带底的变化
Ec c
V V0
最后，因电子热运动速度与T1/2成正比，声学波散射几率
Ps T 3 / 2
• 对于硅、锗具有旋转椭球等能面的半导体，切变也会引 起能带极值的变化，即横声学波也参与对电子的散射。 总的散射几率依然如上式，为T3/2关系。
§4.3 迁移率与杂质浓度和温度的关系
1、平均自由时间τ和散射几率P的关系 1 P
当几种散射机构同时存在时
总散射几率： 相应的平均自由时间：
P Pj
j
1
j
1
j
τ-P关系的数学推导 用N(t)表示t时刻未遭到散射的电子数，则在 t ~ t t 被 散射的电子数
• 对于硅、锗及III-V族化合物，其原胞结构均由两套 面心立方原子套构而成，基元有2个原子，三维结构 每个波矢q共有6支格波：3支声学波和3支光学波。 • 3支声学波为2横1纵。声学波是 q = 0时，=0。 • 长声学波代表质心的振动。在长波范围内，波数q越 大，波长越短，能量越大，声子数越少。 同时，其能 量 为量子化的： (n+1/2)h 。
载流子的散射 存在破坏周期性势场的作用因素： 载流子在半导体中运动时，不断与振动 杂质 着的晶格原子或杂质离子发生碰撞，碰撞后 缺陷 载流子速度的大小及方向均发生改变，这种 晶格热振动 现象称为载流子的散射。
华南理工半导体物理—第四章
E=0 2
1 6 3 随机热运动 4
5
当一个小电场E施加于半导体时，每一个电子会从电场上 受到一个-qE的作用力，且在各次碰撞之间，沿着电场的反向 被加速。因此，一个额外的速度成分将再加至热运动的电子上 ，此额外的速度成分称为漂移速度(drift velocity) 一个电子由于随机 的热运动及漂移成分两 者所造成的位移如图所 示。 值得注意的是，电 子的净位移与施加的电 场方向相反。
电离杂质散射 • 半导体中的电离杂质形成正、负电中心， 对载流子有吸引或排斥作用，从而引起载 流子散射。
电离杂质散射几率
Pi N iT
3
2
上式表明，随着温度的降低，散射几率 增大。因此，这种散射过程在低温下是 比较重要的。
Байду номын сангаас
晶格振动散射
半导体晶体中原子的振动是引起载流子 被散射的主要原因之一。
mn n 0.26 0.911030 kg 1000104 m2 / V s c q 1.6 1019 C
1.48 1013 s 0.148 ps.
又
1 3 3kT 2 mn vth kT vth 107 cm / s 2 2 mn
所以，平均自由程则为
漂移运动，迁移率与电导率
• 漂移运动：载流子在电场力作用下的定向运动， 定向运动的速度称为漂移速度
j E
vd n E
j nqvd
jn nqn E
n nqn
J jn j p (nqn nq p ) E
(nqn nq p )
载流子散射
j E
dI dV J E ds dl
半导体中电流的大小还可以从另一个角度 来理解。
第四章 半导体的导电性 布置作业解答
第四章 半导体的导电性1、300K 时，Ge 的本征电阻率为47cm Ω⋅，如电子和空穴迁移率分别为39002cm /(V s)⋅和19002cm /(V s)⋅，试求本征Ge 的载流子浓度。
解：首先，已知Ge 的本征电阻率i ρ＝47cm Ω⋅，可得Ge 的本征电导率i σ＝1i ρ＝1/47S cm 又()i i n p n q σμμ=+本征Ge 的载流子浓度1331921 2.29010/()47/ 1.6010(39001900)/()ii n p n cm q S cm C cm V s σμμ-===⨯+⨯⨯⨯+⋅ 2、试计算本征Si 在室温时的电导率，设电子和空穴迁移率分别为14502cm /(V s)⋅和5002cm /(V s)⋅。
当掺入百万分之一的As 后，设杂质全部电离，试计算其电导率。
比本征Si 的电导率增大了多少倍？解：(1)本征Si 的电导率()i i n p n q σμμ=+已知室温下22103,1450/(),500/(1.51)0n p i u cm V s u c cm m n V s - =⋅ =⨯⋅= ，代入上式得：64.6810/i S cm σ-=⨯(2) 已知Si 的原子密度为223510/cm ⨯，掺入百万分之一的As 后，在Si 中As 的浓度为：22316361510/510/10D N cm cm =⨯⨯=⨯ 因为杂质全电离，所以电离出的电子浓度1630510/D n N cm ==⨯当电离杂质浓度163510/i N cm =⨯时，可查图4-14得电子迁移率为：2850/()n cm V s μ=⋅由于1030(1.510/)i n n cm ⨯ ，又在室温下，则产生载流子以杂质电离为主，可忽略本征激发，即忽略少子空穴对导电的贡献，故此时电导率为： 163192510/ 1.6010850/() 6.8/n nqu cm C cm V s S cm σ-==⨯⨯⨯⨯⋅= 故：666.8// 1.45104.6810/i S cm S cmσσ==⨯⨯ 即电导率增大了145万倍。
第四章-半导体的导电性
单位时间由于散射而失去的能量： 0v l0
单位时间由电场获得的能量： qvd | E|
稳态时两者应相等,即
qd
E
0
v l0
联立解得：v d
80
3
m n
------与电场无关
2、负微分电导
1）负微分电导
负阻效应产生条件：半导体能带结构中存在多能谷， 且能谷的曲率不同；载流子发生能谷间散射。
负微分电导的 产生机理：对GaAS而言，当电场 达到3×103 V/cm后，低能谷1 中的电子可从电 场中获得足够的能量而开始转移到高能谷2中， 发生能谷间的散射，并伴随发射或吸收一个光学 声子．进入能谷2的电子，有效质量大为增加， 迁移率大大降低，平均漂移速度减小，电导率下 降，产生负阻效应．
角频率为ωa的格波，能量是量子化的，只能是
(
n
1 2
)a
声子：晶格振动的能量量子。
根据统计计 算，格波的 平均能量为
1 2
a
exp(
1
a
)-1
a
k0T
包含平均声子 数为
晶格振动对 载流子的散 射可以看成 载流子与声 子的碰撞。
1 nq = exp( ωa )- 1
koT
k'-k q
E'-Ea
声学波散射概率：
d N t liN m t＋ t－ N t＝ P t － N
dt t 0 t
N（ t）N ＝ 0ex（ p p－ ） t
设N0为t＝0时未遭散射的电子数。所以在t到t ＋dt时间内被散射的电子数为：
d＝ NN0Pepd t t
平均自由时间：
＝1 N0
0N0Pte-pdt ＝ t P 1
08-第四章-半导体的导电性
en
vdx1 秒
平均自由时间
弛豫时间
系统从非平衡态恢复到平衡态 所需时间
* 的统计表示 t=0时，撤除电场，有N0个电子作定向运动 N(t)为t时刻还未遭到碰撞的电子数 P为单位时间内电子被碰撞的几率 在tt+dt时间内被碰撞的电子数可表示为：
N (t ) N (t dt) N (t ) Pdt dN (t ) PN (t )
n型半导体载流子浓度随温度的变化曲线ln(n)-1/T n型半导体载流子浓度随掺杂浓度ND的变化曲线 半导体费米能级随掺杂浓度ND - NA的变化曲线
N型半导体中的电子浓度随温度的变化关系
ln(n) 斜率：Eg/2k 斜率：ED/2k
1/T
n型半导体载流子浓度随掺杂浓度ND的变化曲线
p,n
n p
C N * 临界浓度 D 的估算
非简并 弱 简并
简并
强简并
-2kT
0
5kT
Ef-Ec
Ec
ND 3 EC ED KT N D dEf Ef ln 0 ln 2 2 2 N C dT 2NN D3
1 2 1 e t 2 r vd (0)t at * 2 m 2 e
在tt+dt时间内被碰撞的电子数为 PN (t )dt
这些电子定向位移之和为 rPN (t )dt
N0个电子定向位移之总和为 S 0 rPN (t )dt
S
0
1 e 2 e N 0 e 2 t PN exp( Pt ) dt N 0 0 * * * 2 me me P2 me
* 简并的温度范围 简并时的电中性方程：n N D
半导体的导电性
第四章半导体的导电性本章主要内容载流子在外加电场作用下的漂移运动半导体的迁移率、电导率和电阻率随温度和杂质浓度的变化规律迁移率的本质-----散射4.1 载流子的漂移运动迁移率1、欧姆定律对于金属，电流I = V(电压）/R（电阻）V-I关系是直线对于半导体，流过不同截面的电流强度不一定相同，“即电流分布不均匀，而欧姆定律不能说明材料内部各处电流的分布情况。
电流密度：通过垂直于电流方向的单位面积的电流J = ∆I/∆S单位：A/cm2或A/m2欧姆定律微分形式：上式把通过导体中某一点的电流密度和该处的电导率及电场强度直接联系了起来。
S故: 半导体导电= 电子导电J = Jn + Jp = (nqu平均自由程：载流子在连续两次散射间自由运动的平均路程平均自由时间：载流子通过平均自由程所需的平均时间τ电场：载流子加速---定向运动；散射：载流子运动方向改变---杂乱无章，各个方向；半导体的主要散射机构：离化杂质散射晶格散射中性杂质散射位错散射(P为散射几率)起因：常温下，浅施主带正电• 双曲线，电离杂质处于一个焦点 • 速度小，作用时间长，偏离角θ大，τ小 • 弹性散射，不改变入射电子能量，只改变运动方向 τ ∝ T3/2/NI 杂质浓度（2）、晶格散射 晶格原子在其平衡位置附近不断进行热振动，且各个 原子的振动不是孤立的。
分析表明：晶格中原子的振动都 是由若干不同的基本波动按波的叠加原理组合而成，这些 基本波动称为格波。
q代表格波波矢， q 的方向即波的传播方向晶格散射：载流子在运动过程中遭受振动的晶格原子的散射， 失去在电场中获得的能量，失去动量。
在能带具有单一极值的半导体中 起主要散射作用的是长波。
即波 长比原子间距大很多倍的格波。
电子热运动速度~105m/s 电子波波长约10-8m 根据动量守恒要求，声子波长 范围应在同一量级，即10-8m,而 晶体中原子间距为10-10m，因而 起主要散射作用的是长波。
半导体物理学刘恩科第七版第4章导电性
(4)格波的能量和动量
准动量：hq
能 量：有多个可能： （1/2 + n）h1
其中，ha为格波的能量量子，称作声子。当格波能量减 少一个ha，称放出一个声子，当格波能量增加一个ha，称
无外电场时，载流子总是做无规则热运动，宏观上不 能形成定向的运动，故不能形成电流。
外电场作用下，载流子一方面做无规则热运动，一方 面做定向运动(空穴与电场方向一致，电子相反)。 载流子获得漂移速度，宏观上形成定向运动，故形成 电流。
在外电场和散射双重作用下，载流子从电场中获得速 度，散射又不断地将载流子散射到各个方向，使漂移 不能无限地增大。
电子和晶格散射时，将吸收或放出一个声子。
q2 k 2 k' 2 2 k k' cos (k'k)2 2 k k' (1 cos )
若散射前后k=k’, 则
q 2k sin
2
设散射前后电子速度大小为, 声子速度为u， hk=mn* , 对
长声学波，ha =hqu, 散射前后电子能量变化为：
对锗、硅及III-V族化合物半导体，原胞中含有 2个原子，对应一个q有6个不同的格波。6个格 波的频率和振动方式完全不同。
声学波：频率最低的3个格波； 光学波：频率高的3个波。
由N个原胞构成的半导体晶体，有N个不 同波矢q构成的格波 (N为固体内含有的 原子数) 。
每个q有6个不同频率的格波，所以共有6N 个格波，分为6支，3支为声学波,3支为光学 波。
实际半导体中的载流子在外电场作用下，速度不会无限增 大，根本原因: 受散射（碰撞）的缘故。
11-第四章-半导体的导电性
2 2 e v RH p * H h 2 mh v
H
e
2v 2 v
2
v2
2
H
h
2v 2 v
2
v2
2
1 H RH en
e
H RH
2 2 x 1 2 2 H 0 BZ 1 H 2 2 2 2 x x ( BZ 1) H B 1 BZ Z vx J x envx 0 0 en
y方向开路
v y 0 代入(1)式 m* v vx x x
T2 +
+
T1
x
习题：第125页 4，6，11，16，18，19
F
x
f x e x ev y Bz f y e y evx Bz
m *v x
0 0
m *v y
B (0,0, Bz ) (1) ( x , y ,0) (2) v (vx , v y ,0)
y方向短路
vx e 2 v B x Z 从(2)式得 v y m* vx Bz vx Bz 代入(1)式 x
N型半导体
RH
2 2 v2 1 v 2 2 en v
P型半导体
RH
2 v e
2 2 v2 1 v 2 2 ep v
n nee ne
2 v e
m
* e
v
2
m
*
v
2
p pe h pe
2 v e * mh v2
第四章半导体的导电性_半导体物理
第4章 半导体的导电性1. 300K 时，Ge 的本征电阻率为47Ω·cm ，如电子和空穴迁移率分别为3900cm 2/V ·S 和1900cm 2/V ·S ，试求本征Ge 的载流子浓度。
[解]T=300K ，ρ＝47Ω·cm ，μn ＝3900cm 2/V ·S ，μp ＝1900 cm 2/V ·S313191029.2)19003900(10602.1471)(1)(1−−×=+××=+=⇒+=cm q n q n p n i p n i µµρµµρ2. 试计算本征Si 在室温时的电导率，设电子和空穴迁移率分别为1350cm 2/V ·S 和500cm 2/V ·S 。
当掺入百万分之一的As 后，设杂质全部电离，试计算其电导率。
比本征Si 的电导率增大了多少倍？[解] T=300K,，μn ＝1350cm 2/V ·S ，μp ＝500 cm 2/V ·Scm s q n p n i /1045.4)5001350(10602.1105.1)(61910－－×=+××××=+=µµσ 掺入As 浓度为N D ＝5.00×1022×10-6＝5.00×1016cm -3杂质全部电离，2i D n N >>，查P 89页，图4－14可查此时μn ＝900cm 2/V ·Scm nq n /S 2.7900106.110519162＝－××××==µσ6621062.11045.42.7×=×=−σσ 3. 电阻率为10m Ω•的p 型Si 样品，试计算室温时多数载流子和少数载流子浓度。
半导体的导电性
通过升高温度，使半导体材料内部的缺陷和杂质激活，从而改变其导电性能。
退火工艺
将半导体材料加热到一定温度并保持一段时间，然后缓慢冷却。这种方法可以消 除材料内部的应力，并提高其导电性能。
外加电场与磁场的影响
外加电场
通过外加电场，可以改变半导体材料内部的载流子分布和运动状态，从而影响其导电性能。
测量方法
电导率的测量通常采用四 探针法，通过四个接触材 料表面的探针来直接测量 电流和电压。
应用
电导率的测量可用于研究 半导体材料的晶体结构、 缺陷和掺杂等微观性质。
电极化率的测量
概述
电极化率是衡量半导体材 料在电场作用下极化程度 的重要参数，它与材料的 介电常数密切相关。
测量方法
电极化率的测量通常采用 电容法，通过在材料两端 施加交变电场并测量电容 的变化来计算电极化率。
载流子的产生与复合
载流子的产生
半导体材料中的原子或分子受到外部能量的激发，会释放出电子和空穴。
载流子的复合
电子和空穴在运动过程中，可能会重新结合在一起，从而消失。这种过程称为 载流子的复合。
03
半导体材料的导电性测量与表征
电导率的测量
01
02
03
概述
电导率是衡量半导体材料 导电性能的重要参数，它 反映了材料中载流子的迁 移率。
日期:
半导体的导电性
汇报人：
目 录
• 半导体导电性概述 • 半导体材料的导电原理 • 半导体材料的导电性测量与表征 • 半导体材料的导电性调控 • 半导体导电性的应用
01
半导体导电性概述
半导体材料定义
• 半导体材料定义：半导体材料是一种在导电性能上处于绝缘体 和导体之间的材料，具有独特的电子和空穴导电性。它们通常 在一定的温度和光照条件下，能显著提高其导电性。
半导体物理第四章半导体的导电性
=
(−q)nvd S
J
=
I S
=
−nqvdx
欧姆定律的微分形式：
J=σE
Vd：平均漂移速度，和电场强度成正比
v=at=qE/ m* *t
半导体物理
5
迁移率-mobility
vd = μ E
μ = vd
E
迁移率：单位场强下的电子的平均漂移速度， 单位：m2/V·s, cm2/V·s
J = nqvdx = nqμE
半导体物理
37
Si, Ge：
电离杂质散射
μi
=
e m*
T 3/2 BN i
声学波散射
μa
=
e m*
1 AT 3/ 2
∴ μ= e
1
m*
AT
3/2
+
BN i T 3/2
半导体物理
ND>1017 cm-3
38
室温（300 K）下，高纯 Si、Ge、GaAs 的迁移率
Si Ge GaAs
μn (cm2/V⋅s)
P = PI + PII + PIII + ......
μi
=
e m*
T 3/2 BN i
μa
=
e m*
1 AT 3/ 2
e
hν
m=* Ao (e kT − 1)
而 1 = P = 1 + 1 + 1 + ......
τ
τ I τ II τ III
1 = 1 + 1 + 1 + ......
μ μ I μ II μ III
光学波散射几率 Po ∝ [exp(hωo kBT ) − 1]−1 平均声子数
第四章_半导体的导电性
设有N个电子以速度v沿某方向运动，N(t)表示在t时刻尚
未遭到散射的电子数。则 t 到 t＋△t 时间内被散射的电 子数为N(t) P△t，即：
N (t ) N (t t ) N (t ) Pt
当△t很小时，可以写为：
dN t N t＋t －N t lim ＝－ PN t t 0 dt t
30
4.2.2 载流子的散射
3）其他散射机构
a. 中性杂质散射：在温度很低时，未电离的杂质(中性杂质)的数目
比电离杂质的数目大得多，这种中性杂质也对周期性势场有一定 的微扰作用而引起散射．但它只在重掺杂半导体中，当温度很低，
晶格振动散射和电离杂质散射都很微弱的情况下，才起主要的散
射作用． b. 位错散射：位错线上的不饱和键具有受主中心作用，俘获电子后
h l 3 2 1 f h l P0 1 2 nq
k0T
k 0T
n q＝
exph a k0T 1
1
γl为声子频率， nq为平均声子数 ，f h γ k0T 为T的缓缓变函
l
பைடு நூலகம்
其值值0.6变化到1.0
散射几率随温度的变化主要取决于 平均声子数，其随温度按指数上升:
14
4.2.1 漂移运动
迁移率与电导率
总漂移电流密度为：
J nqn ＋pqp E
与欧姆定律微分形式比较得
到半导体电导率表示式为：
nq n ＋pq p
电子和空穴的漂移运动
15
4.2.1 漂移运动
迁移率与电导率
对于n型半导体（n>>p），电导率为
nqn
对于p型半导体（p>>n），电导率为：
半导体物理学——半导体的导电性
半导体物理学黄整载流子输运半导体中载流子的输运有三种形式：¾漂移¾扩散¾产生和复合2沿电场的反方向作定向运动（定向运动的速度称为漂移速度）dv 电流密度Ad I qnv =−dJ qnv =−4d v nq J =E μnq =Eσ=nq σμ=q 5半导体的电导率和迁移率半导体的导电作用为电子导电和空穴导电的总和==n p J J J +当电场强度不大时，满足J =σ E()n p nq pq μμ+En pnq pq σμμ=+N 型半导体n nq σμ=p n >>P 型半导体p pq σμ=n n ===n p >>6本征半导体i p ()i n p n q σμμ+散射概念的提出外加电场的作用下载流子应当作加速运动外加电场的作用下，载流子应当作加速运动−dJ qnv =不断增大但是J σ=E恒定7热运动在无电场作用下，载流子永无停息地做着无规则的、杂乱无章的运动，称为热运动。
晶体中的碰撞和散射引起净速度为零，净电流为零。
平均自由时间为τm~0.1ps8当有外电场作用时，载流子既受电场力的作用，同时不断发生散射。
载流子在外电场的作用下为热运动和漂移运动的叠加，因此电流密度恒定。
9散射的原因根本原因是周载流子在半导体内发生散射的期性势场遭到破坏附加势场ΔV使能带中的电子在不同k状态间跃迁，并使载流子的运动速度及方向发生改变。
10晶格振动对电子的散射格波¾形成原子振动的基本波动¾格波波矢q=2π/λ¾对应于某一q值的格波数目不定，一个晶体中格波的总数取决于原胞中所含的原子数¾Si、Ge半导体的原胞含有两个原子，对应于每一个q就有六个不同的格波，频率低的三个格波称为声学波，频率高的三个为光学波¾长声学波（声波）振动在散射前后电子能量基本不变，为弹性散射；光学波振动在散射前后电子能量有较大的改变，为非弹性散射12长光学波，能谷内部非弹性散射。
半导体物理刘恩科4-3
RH
Ey Ex Bz
称为霍耳系数
• 一种载流子的霍耳效应 • 横向霍耳电场对载流子的作用与洛伦 兹力作用相抵消时，达到稳定状态。 稳定时，霍耳电场应满足：
qEy q x Bz
• x方向的电流：
n型半导体，附加电场Ey沿y轴负方向
J x nq x
RH
1 nq
p 型半导体，附加电场Ey沿y轴正向
− 散射作用：电子在运动过程中不断地遭到散射，波矢产 生突变使分布发生改变。单位时间体积元内因散射电子 数变化为：
Hale Waihona Puke dN2(k '
fk'
vfr'
fs'
)dkdr
体积元dkdr内电子数变化 －非平衡条件
下分布方程：
f t
• r
f
•
k•k
f
f t
s
稳定条件下，分布函数不随时间变化： f 0 t
霍耳效应
概念
把通有电流的半导体放在均匀磁场中， 设电场沿x方向，电场强度为Ex；磁 场方向和电场垂直，沿z方向，磁感 应强度为Bz，则在垂直于电场和磁 场的十y或一y方向将产生一个横向 电场Ey，这个现象称为霍耳效应。
霍耳电场Ey与电流密度Jx和磁感应强度 Ex成正比：
或：
Ey RH Ex Bz
f E
vi
v
j
d
k
对球形等能面
nq2 mn*
v2
v2
所以
n
nq
q mn*
v2
v2
§4.6 强电场下的效应 热载流子（自学）
Effect at Large Field, Hot Carrier
欧姆定律的偏离现象 :
半导体的导电性.ppt
5）载流子与载流子间的散射 ——在强简并下发生
2020/6/15
29
§4.3 迁移率与杂质浓度和温度的关系
Temperature Dependence of Carrier Concentration and Mobility
1. 平均自由时间和散射概率的关系
自由时间: 载流子在电场中作漂移运动时,只有连续两次 散射之间的时间内才作加速运动,这段时间称为自由时间.
载流子在半导体中运动时，不断与晶格原子或杂质离子碰撞，
速度大小和方向发生变化。或者说电子遭到散射。无规则
热运动是不断遭到散射的结果。
2020/6/15
14
自由程：相邻两次散射之间自由 运动的路程。
平均自由程：连续两次散射间自 由运动的平均路程。
平均自由 时间 连续两次散射动间的自平由均运运
2020/6/15
2020/6/15
9
同理，对p型半导体
p p 0 q p 5
这里
空穴迁移率
p
v dp E
v dp 为空穴漂移速度
2020/6/15
10
对一般半导体
n p
nq npq p 6
2020/6/15
11
对本征半导体
因ni np
故 i n qnp qp
n iq n p 7
2020/6/15
温度升高，平均声子数增多，光学波的散射几率迅速增大。
2020/6/15
26
3)其它散射机构
1）等同能谷间散射
半导体中有多个极值能量相同的等能面，载流子在这些 能谷中的分布相同，这些能谷称为等同的能谷。 对这种多能谷半导体，电子可以从一个极值附近散射到另 一个极值附近，这种散射称为谷间散射。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1、
vd at (a 0)
载流子的散射
t , vd J nq vd 出现矛盾
又有J E , E恒定, J恒定;
（1）散射的起因: 周期势场的被破坏,
附加势场对载流子起散射作用.
(理想晶格不起散射作用) （2）散射的结果: • 无外场时,散射作用使载流子作无规则热运动, 载 流子的总动量仍然=0 • 在外场下，载流子的动量不会无限增加.
PS T 2
声学波散射几率随温度的升高而增加
•正离子 负离子 °
平衡时
（3） 纵光学波
1
• • • • • • • • • • ° ° ° °° ° °° ° °
振动方向
2
3
4
5
6
7
8
9
10
←°•→
←•°→ 振动方向
• • • • •• • • • • °° ° ° ° ° ° ° ° － •疏 － •疏 + •密
1、载流子的运动 2、 欧姆定律 3、 迁移率
1.1 载流子的运动
无外场时,半导体中的载流子作无规则的热运动
载流子热运动示意图
•
在外电场下，载流子受到电场力F. 总的效果是,载流子在电场力的作用下作定向运 动—漂移运动： dv/dt=(1/m*)F
金属：
V I R
1.2 欧姆定律 l R :电阻率，单位 m s 1 电导率，单位 S/ m
τ↑，μ↑
空穴的迁移率:
p
q p m* p
m*↑,μ↓
me*< mP*,μn>μP
nq 2 n 电子电导率: n nqn * me
空穴电导率: p pq p
pq p
2
m* p
以Si为例：
b）多极值半导体材料的μ与τ的关系 ky
设电场E沿kx方向 1、2两个能谷 电子的迁移率 3、4、5、6能谷 电子的迁移率
第四章 半导体的导电性（载流子的电输运） §1 载流子的漂移运动 §2 半导体的主要散射机构 §3 迁移率与杂质浓度和温度的关系 §4 电阻率与杂质浓度和温度的关系 §5 §6 强电场效应和多能谷散射 霍尔效应
讨论前提: • 温度是均匀的; • 样品均匀掺杂; • 外场是弱场
§1 载流子的漂移运动
vT—电子的热运动速度
2、
电离杂质库仑场
电离杂质的散射
Z—电离杂质电荷数 r —载流子距电离杂质 距离 v
v
电 离 施 主
+
V’
V’
–
电离杂质散射示意图
电 离 受 主
电离杂质浓度为NI, 载流子速度为v,载流子能 量为E :
T↑，载流子的运动速度↑，散射几率↓； 杂质浓度↑，电离杂质数↑，散射中心↑，散 射几率↑。
°密 °疏 °密
纵光学波的散射
+++ ++++ - +++
--+ ---+ ---
+++ ++++ - +++
--+ ---+ ---
+++ ++++ - +++
+
-
+
-
+
极化场
纵光学波 离子晶体
光学波散射: (非弹性散射)， • 对极性半导体,长纵光学波有重要的散射作用. （与极性光学波形变势相联系） 当温度较高, 有较大的光学波散射几率
no q n mc
2
q n c —电导迁移率 mc
★电导有效质量 有效质量 态密度有效质量 电导有效质量-• 前面得到的迁移率表达式适合于具有单一能 带极值且等能面为球面的半导体 • 对各向异性及多能谷的导带 , 为使各向同性的 迁移率公式形式上仍可应用, 引入电导有效质量
（3）迁移率与杂质浓度,温度的关系 e c
（3）散射几率: P (单位时间内一个载流子受到散射的 次数) • 载流子在连续二次散射之间自由运动的平均时间--平 均自由时间 τ=1/P 设τ1为第一次散射的时间，τ2…,τN为第N次散射的时 间
1 2 3 N
N
• 载流子在连续二次散射之间自由运动的平均路程--平 均自由程 λ= vT∙τ
vdndt
在dt 时间内通过ds的截面电荷量，就是A、B面 间小柱体内的电子电荷量，即
dQ nqvdn dsdt
其中n是电子浓度，q是电子电荷
电子漂移的电流密度Jn为
dQ Jn nqv dn dsdt
在电场不太强时，漂移电流遵守欧姆定律，即
J E
E nqvdn
nqvdn E
Po n e
1
h kT
1
（ 4）
其他因素引起的散射
等同能谷间的散射
--电子与短波声子发生相互作用
中性杂质散射 位错散射 载流子之间的散射
低温时，主要是电离杂质的散射 高温时，主要是晶格散射 原子晶体主要是纵声学波散射 离子晶体主要是纵光学波散射 各个散射机制往往同时存在，在一定的条件下， 某一机制起主要作用
3 / 2
q s As q 3 / 2 s * * T m m
纵光学波
po e
1
h kT
1
o e
h kT h kT
1 1)
h kT
Ao (e
q o qAo o * * (e m m
1)
电离杂质的散射
Pi NiT
1
3 / 2
N (t ) N (t t ) N (t ) P t
△t→0，
解方程得到:
dN (t ) N (t ) dt
t
N (t ) Ae
Noe
t
1 t 时： No 1 N( ) 0.36 N o e
在 dt 内，受到第一次散射的电子数为：
E 2 h nh
• 平均声子数
n e
1
h kT
1
电子和声子的相互作用: 能量守恒,准动量守恒. 对单声子过程(电子与晶格交换一个声子, “ +”—吸收声子, “ -”—发射声子):
hk hk hq E E h a
k,E和k’,E’分别为散射前后电子的波矢,能量
q n 1 ml
kx
6 3 2 1 4
kz
5
q n 2 3 mt
推导电导有效质量示意图
n 每个能谷中分得 电子 6 n n n J x 1qE x 2 qE x 3 qE x 3 3 3 n ( 1qE x 2 qE x 3 qE x ) 3 1 令 ( 1 2 3 ) c 电导迁移率 3 2 q n 1 q 1 1 2 c ( n ) q n ( ) 3 ml mt 3 ml mt q n 1 1 2 1 令 ( ) c 3 ml mt mc mc
i Ni T
Ai N T
Ni是掺入的所有杂质浓度的总和。
对补偿型半导体：
Ni N A N D
平均自由时间：
i Ni T
1
3/ 2
定性图象: • 散射几率大体与电离杂质浓度成正比; • 温度越高,电离杂质散射越弱.
3、
晶格散射
（1）晶格振动理论简要 • 晶格振动—晶体中的原子在其平衡位置附 近作微振动. • 格波—晶格振动可以分解成若干基本振动, 对应的基本波动即为格波. 格波的波矢q, q=1/λ
( N D N A )q n
p型，单一杂质：po=NA， N q A p
补偿型：po=NA－ND，
( N A N D )q p
本征：
n p ni
ni q( n )
p
§2 半导体的主要散射机构
1、载流子的散射 2、电离杂质的散射 3、晶格散射 4、其他因素引起的散射
0
电子平均漂移速度vn
1 qE Pt vn N e P ( ) dt o * No me 0 qE Pt * e Pdt me 0 qE * n me
τ
n 电子的平均自由时间
（2）迁移率和电导率与平均自由时间的关系
a）单极值的半导体材料 vn q n ∵ n ∴ n * E me
vdn E nq
当导体内部电场恒定时，电子应具有一个恒 定不变的平均漂移速度。 电场强度增大时，平均漂移速度也随着E的增 大而增大，反之亦然。所以，平均漂移速度的 大小与电场强度成正比，其比值称为电子迁移 率μ。
因为电子带负电，所以vdn一般应和E 反向，习惯上迁移率只取正值，即
vdn E nq
N (t )dt Noe dt
它们的自由时间总和为：
t
N (t )tdt Noe tdt
1 1 t t N o e tdt e tdt No系 （1） 平均漂移速度 设电子的热运动速度为v0， t=0，E=0，v=v0 t＞0，E≠0，f =－qE
mc
即: μ ∝ τ ∝1/P 1/μ ∝ 1/τ ∝P 当认为半导体中各种散射彼此独立,则有: 总散射几率: P = PI+PS+PO 1/μ =1/μI+1/μS+1/μO 实际迁移率主要取决于最小的分迁移率
a)不同散射机构μ的表达式 纵声学波： 3/ 2
Ps T
s T
As T
3 / 2