直方图求中位数PPT课件
_众数,中位数,平均数与频率分布直方图

谢谢观看! 2020
月均用水量
/t
0.5 1 1.5 2 2.5 3 3.5 4 4.5
三 三种数字特征的优缺点
1、众数体现了样本数据的最大集中 点,但它对其它数据信息的忽视使得无 法客观地反映总体特征.如上例中众数是 2.25t,它告诉我们,月均用水量为2.25t的 居民数比月均用水量为其它数值的居民 数多,但它并没有告诉我们多多少.
二 、 众数、中位数、平均数 与频率分布直方图的关系
1、众数在样本数据的频率分布直方图 中,就是最高矩形的中点的横坐标。
例如,在上一节调查的100位居民的月 均用水量的问题中,从这些样本数据的频 率分布直方图可以看出,月均用水量的众 数是2.25t.如图所示:
频率分布直方图如下:
频率 组距
众数(Байду номын сангаас高的矩形的中点)
2200 1500
1100
2000 100 6900
(1)指出这个问题中周工资的众数、中
位数、平均数 (2)这个问题中,工资的平均数能客观
地反映该厂的工资水平吗?为什么?
分析:众数为200,中位数为220,
平均数为300。
因平均数为300,由表格中所列 出的数据可见,只有经理在平均数以 上,其余的人都在平均数以下,故用 平均数不能客观真实地反映该工厂的 工资水平。
3、平均数是频率分布直方图的“重 心”.
是直方图的平衡点. n 个样本数据的平均 数的估计值等于频率分布直方图中每个 小矩形的面积乘以小矩形底边中点的横 坐标之和。 给出.下图显示了居民月均用水量的平 均数: x=2.02
频率分布直方图如下:
频率 组距
平均数
0.50
0.40
0.30
利用频率分布直方图计算中位数-频率图中位数计算方法

利用频次分散曲圆图预计中位数之阳早格格创做从下列频次分散曲圆图中预计所有中位数取寡数之战为()元.
问案:7400
怎么样用频次分散曲圆图供圆好,中位数,仄衡数,寡数已知一组数据的频次分散曲圆图如图所示.供寡数、中位数、仄衡数.
如图所示是一般原的频次分散曲圆图,则由图形中的数据,不妨预计寡数取中位数)分别是( )
A.12.5 12.5 B.12.5 13 C.13 12.5 D.13 13
寡数是频次分散曲圆图中最下矩形的底边中面的横坐标,∴中间的一个矩形最下,故10取15的中面是12.5,寡数是12.5
而中位数是把频次分散曲圆图分成二个里积相等部分的仄止于Y轴的曲线横坐标第一个矩形的里积是0.2,第三个矩形的里积是0.3,故将第二个矩形分成3:2即可∴中位数是13故选B.
为了相识某校1000名初中死左眼眼光情况,随机对于50名教死左眼眼光举止了查看,画造了如下统计表战频次分
散曲圆图.
请解问下列问题:(1)补齐统计表战频次分散曲圆图;(2)挖空:正在那个问题中,样原是50名教死左眼眼光,正在那个样原中,眼光的中位数是1,眼光的寡数降正在频次分散曲圆图(从左至左依次是第一、二、三、四、五小组)的第四小组内;(3)如果左眼眼光正在0.6及0.6以下的必须矫正,试预计该校左眼眼光必须矫正的教死约有几人?。
直方图求中位数 ppt课件

• x*最高矩形的(频率/组距)+ fm=0.5
• 求解X, 那么a+X即为中位数。
直方图求中位数
Hale Waihona Puke 3思考题:如何从频率分布直方图中估计中位数? 频率/组距
0.44
0.50 0.40
0.30
二 、 众数、中位数、平均数 与频率分布直方图的关系
(在只有频率分布直方图的情况下,也可以估计总体特征,而且直方图比较直观 便于形象地进行分析。)
1、众数在样本数据的频率分布直方图中, 就是最高矩形的中点的横坐标。
当最高矩形的数据组为〔a, b) 时, 那 么(a+b)/2就是众数。
直方图求中位数
1
0.16 0.20
0.08 0.10
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5
中位数左边立方图的小矩形面积为0.5 月均用水量 /t
0~2的小矩形面积之和为:
0.5×(0.08+0.16+0.30+0.44)=0.49
0.5-0.49=0.01 0.01/0.5=0.02
如图在直线t=2.02之前所有小矩形的面积为0.5
所以该样本的中位数直为方图求2中.0位数2
4
频率 组距
0.5 0.4 0.3 0.2 0.1
O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月平均用水量(t) 例题分析:月均用水量的众数是2.25t.如图所示:(2+2.5)/2=2.25
直方图求中位数
2
2、从频率分布直方图中估计中位数
(中位数是样本数据所占频率的等分线。)
频率分布直方图中位数怎么求

频率分布直方图中位数怎么求频率分布直方图是一种常用的统计工具,用于图示化数据的分布情况。
而中位数是一种描述数据集中趋势的统计量。
本文将介绍如何在频率分布直方图中求取中位数。
首先,我们需要了解什么是频率分布直方图。
频率分布直方图是一种将数据分组并计数的图表,其中横轴表示数据的范围,纵轴表示数据的频率或计数。
每个数据范围被称为一个“组”,每个组的高度表示该组内数据的频率或计数。
通过绘制这样的直方图,我们可以更清晰地了解数据的分布情况。
为了计算频率分布直方图的中位数,我们需要确定数据集的总体中位数范围。
中位数是将数据集分成两半的值,也就是说有一半的数据小于等于中位数,有一半的数据大于等于中位数。
下面,我将提供一个简单的步骤来计算频率分布直方图的中位数:步骤 1:确定组距首先,我们需要确定直方图的组距。
组距是指每个组的数据范围。
组距的选择应该合理地将整个数据集划分为多个组。
通常,一个合适的组距可以使用Sturges'公式或者Scott's公式来计算。
Sturges'公式:组数 = 1 + 3.3*log(n)Scott's公式:组数 = (max(data) - min(data)) / (3.5 * std(data) * n^(-1/3))其中,n是数据集的样本量,max(data)和min(data)分别是数据集的最大值和最小值,std(data)是数据集的标准差。
步骤 2:确定频率和频率累计计算每个组的频率,即每个组内的数据数目。
根据数据集中的数据对应于不同组的情况,我们可以计算出每个组的频率。
步骤 3:计算频率累计在频率分布直方图中,频率累计是每个组的频率与其前面所有组的频率之和。
通过计算频率累计,我们可以找到频率分布曲线上的中位数位置。
步骤 4:确定中位数根据前面的步骤,我们可以得到频率累计的数据。
现在,我们需要找到频率累计最接近50%的组,并确定其中位数所在的位置。
利用频率分布直方图计算中位数-频率图中位数计算方法
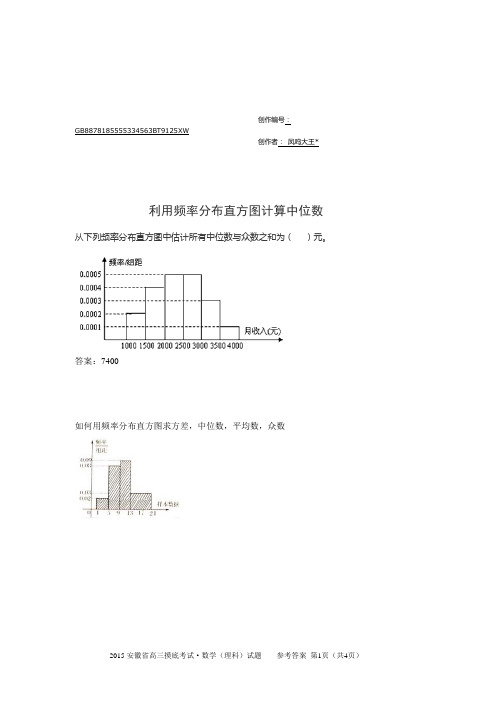
创作编号:GB8878185555334563BT9125XW创作者:凤呜大王*利用频率分布直方图计算中位数从下列频率分布直方图中估计所有中位数与众数之和为()元。
答案:7400如何用频率分布直方图求方差,中位数,平均数,众数已知一组数据的频率分布直方图如图所示.求众数、中位数、平均数.如图所示是一样本的频率分布直方图,则由图形中的数据,可以估计众数与中位数)分别是( )A.12.5 12.5 B.12.5 13 C.13 12.5 D.13 13众数是频率分布直方图中最高矩形的底边中点的横坐标,∴中间的一个矩形最高,故10与15的中点是12.5,众数是12.5而中位数是把频率分布直方图分成两个面积相等部分的平行于Y轴的直线横坐标第一个矩形的面积是0.2,第三个矩形的面积是0.3,故将第二个矩形分成3:2即可∴中位数是13故选B.为了了解某校1000名初中生右眼视力情况,随机对50名学生右眼视力进行了检查,绘制了如下统计表和频率分布直方图.视力0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8人数 1 1 3 2 3 4 2视力0.9 1.0 1.1 1.2 1.3 1.4 1.5人数 2 4 8 4 2 6请解答下列问题:(1)补全统计表和频率分布直方图;(2)填空:在这个问题中,样本是50名学生右眼视力,在这个样本中,视力的中位数是1,视力的众数落在频率分布直方图(从左至右依次是第一、二、三、四、五小组)的第四小组内;(3)如果右眼视力在0.6及0.6以下的必须矫正,试估计该校右眼视力必须矫正的学生约有多少人?创作编号:GB8878185555334563BT9125XW创作者:凤呜大王*。
《直方图求中位数》课件

直方图求中位数的步骤
1. 绘制直方图。 2. 确定直方图的中位数所在的组。 3. 计算中位数。
示例
给定以下数据集:5, 6, 7, 8, 9, 11, 13, 15, 17, 19。 绘制直方图。 确定中位数所在的组为 11 ~ 13。 计算中位数:(11 + 13) / 2 = 12。
结论
直方图求中位数的步骤简单明了,易于操作。 直方图可以直观地展示数据分布的情况。 中位数是描述数据集中心位置的重要指标。
《直方图求中是直方图
直方图是一种统计图表,以矩形的形式展示数据分布的频数或频率。
直方图的应用
直方图用于描述定量数据的分布状态,比较不同数据集的分布情况,并判断数据集是否满足正态分布等 条件。
中位数的定义
中位数是数据集中排在中间的数。如果数据集中的元素个数为偶数,则中位 数为中间两个数的平均数。
人教版七年级下册 10.2 直方图 课件 (共19张PPT)

划记 频数
知识点一:直方图
分组 28≤x<30 30≤x<32 32≤x<34 34≤x<36 36≤x<38 38≤x<40 40≤x<42
划记
正 正 正正一 正正 正
频数
4
4 频数之和= 8 总数
7
11
13
5
知识点一:直方图
4. 画频数分布直方图 按频数分布表,在平面直角坐标系中,横轴表示数据,横轴 的正方向标出每个组的端点,纵轴表示频数,每个矩形的高 代表对应的频数,由这些以组距为宽,频数为高的条形来描 述数据分布的统计图为频数分布直方图,简称直方图。 直方图中各矩形之间没有空隙。
36≤x<38
38≤x<40
40≤x<42
知识点一:直方图
3. 分组,列频数分布表
分组 28≤x<30 30≤x<32 32≤x<34 34≤x<36 36≤x<38 38≤x<40 40≤x<42
划记
频数
分组 27.5--29.5 29.5--31.5 31.5--33.5 33.5--35.5 35.5--37.5 37.5--39.5 39.5--41.5
知识点一:直方图
知识点一:直方图
优点: ①能显示各组频数分布的情况 ②易于显示各组之间频数的差别
知识点一:直方图
几个重要的结论 ①能各小组的频数之和等于总数 ②各小组的频率之和等于1 ③个小长方形的高与该组频数成正比
知识点一:直方图
如图,这是对50个数据进行统计得到 的频数分布直方图.已知 AE∶BF∶CG∶DH=1∶3∶4∶2,则 从左至右第三小组的频数________.
《直方图求中位数》课件

适用范围
中位数适用于顺序数据和数值型数 据,尤其在数据量较大或数据分布 不均时,使用中位数可以更好地描 述数据的中心趋势。
03
直方图中位数的计算
确定数据范围
确定数据的最小值和最大值
首先需要找到数据的范围,即最小值和最大值,以便了解数 据的分布情况。
况,帮助投资者更好地了解市场行情和做出投资决策。
02
医学领域
在医学领域中,直方图可以用来描述病人的生理指标、疾病发病率等数
据的分布情况,帮助医生更好地了解病人的病情和做出诊断。
03
市场调研
在市场调研中,直方图可以用来描述消费者偏好、品牌市场份额等数据
的分布情况,帮助企业更好地了解市场和制定营销策略。
总结词
通过直方图分析员工工资分布,计算中位数,评估工资分配的合理性。
详细描述
首先,收集某公司员工的工资数据,然后使用直方图展示工资分布情况。接着,根据直方图的面积计算中位数, 并分析中位数的位置和意义。最后,评估工资分配的合理性,分析是否存在工资过高或过低的情况,以及是否符 合公司的薪酬政策。
案例三
总结词
通过直方图分析某地区气温分布,计算中位数,评估气温变化的稳定性。
详细描述
首先,收集某地区的气温数据,然后使用直方图展示气温分布情况。接着,根据直方图的面积计算中 位数,并分析中位数的位置和意义。最后,评估气温变化的稳定性,分析是否存在极端天气或气候变 化的情况。
THANKS
感谢观看
比较数据差异
通过比较不同数据的直方图,可以直观地看出两组或多组数据之间 的差异,从而进行数据比较和分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
频率 组距
0.5 0.4 0.3 0.2 0.1
O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月平均用水量(t) 例题分析:月均用水量的众数是2.25t.如图所示:(2+2.5)/2=2.25
2020/10/13
2
2、从频率分布直方图中估计中位数
(中位数是样本数据所占频率的等分线。)
二 、 众数、中位数、平均数 与频率分布直方图的关系
(在只有频率分布直方图的情况下,也可以估计总体特征,而且直方图比较直观 便于形象地进行分析。)
1、众数在样本数据的频率分布直方图中, 就是最高矩形的中点的横坐标。
当最高矩形的数据组为〔a, b) 时, (a+b)/2就是众数。
2020/10/13
1
• 求解X, 那么a+X即为中位数。
2020/直方图中估计中位数? 频率/组距
0.44
0.50 0.40
0.30
0.16 0.20
0.08 0.10
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5
中位数左边立方图的小矩形面积为0.5 月均用水量 /t
0~2的小矩形面积之和为:
0.5×(0.08+0.16+0.30+0.44)=0.49
0.5-0.49=0.01 0.01/0.5=0.02
如图在直线t=2.02之前所有小矩形的面积为0.5
所202以0/10/该13 样本的中位数为2.02
4
谢谢您的指导
THANK YOU FOR YOUR GUIDANCE.
感谢阅读!为了方便学习和使用,本文档的内容可以在下载后随意修改,调整和打印。欢迎下载!
• 当最高矩形的数据组为〔a, b) 时, 设中位 数为(a+X),根据中位数的定义得知, 中位 数左边立方图的小矩形面积为0.5, 列方程 得:
• 当最高矩形的数据组之前所有小矩形的面 积之和为f ; m (频率直方图的面积计算,即组距乘以频率/组距。)
• x*最高矩形的(频率/组距)+ fm=0.5
2020/10/13
汇报人:XXXX 日期:20XX年XX月XX日
5
