初三数学第24章圆导学案范文整理
人教版九年级数学上册教材《圆》导学案

CB第二十四章圆导学案(五)24.1.4 圆周角(2)一.学习目标:1、掌握直径(或半圆)所对的圆周角是直角及90°的圆周角所对的弦是直径的性质, 并能运用此性质解决问题.2、经历圆周角性质的过程,培养学生分析问题和解决问题的能力3、激发学生探索新知的兴趣,培养刻苦学习的精神,进一步体会数学源于生活并用于生活二.学习重点、难点:重点:圆周角的推论学习 难点:圆周角推论的应用 三.学习活动 (一)导学驱动1、圆周角定义:_________________________________。
2、圆周角定理:_________________________________。
3、如图,点A 、B 、C 、D 在⊙O 上,若∠BAC=40°,则(1)∠BOC= °,理由是 ; (2)∠BDC= °,理由是 。
(二)探究交流1、如图,点A 、B 、C 在⊙O 上,若BC 是⊙O 的直径,它所对的圆周角∠BAC 是多少?为什么? 若∠BAC=90°,弦BC 经过圆心吗?为什么?由此,你能得出的结论是:_____________________________________。
2、如图,四边形ABCD 的四个顶点都在⊙O 上, 求证:∠A+∠C=180°ODCBAEODCBA(三)释疑内化已知:如图,⊙O 的直径AB 为10cm ,弦AC 为6cm ,∠ACB 的平分线交⊙O 于D 点, 求BC 、AD 、BD 的长。
(四)巩固迁移 课堂检测1、如图,AB 是⊙O 的直径,∠A=10°,则∠ABC=________.2、如图,AB 是⊙O 的直径,CD 是弦,∠ACD=40°,则∠BCD=_______,∠BOD=_______.3、如图,AB 是⊙O 的直径,D 是⊙O 上的任意一点(不与点A 、B 重合),延长BD 到点C ,使DC=BD ,判断△ABC 的形状:__________。
人教九年级上册:第24章圆的全章导学案

24.1.1 圆学习目标:1.理解圆的有关概念,了解等圆、等弧等基本概念,能够从图形中识别;2.理解“直径与弦”、“半圆与弧”、“等弧与长度相等的弧”等模糊概念;一、自主学习、课前诊断(一)温故知新1.自己回忆一下,小学学习过圆的哪些知识?2.结合教材图24.1-1(教材P78-79),说说生活中有哪些物体是圆形的?为什么生活中将车轮做成圆形的?(二)设问导读认真阅读教材P78-79的内容自己动手画圆并完成下列问题1.理解圆的定义(1)描述性定义:________________________________。
从圆的定义中归纳:①圆上各点到定点(圆心O)的距离都等于______;②到定点的距离等于定长的点都在_____. (2)集合性定义:___________________________________。
(3)圆的表示方法:以O点为圆心的圆记作______,读作______.(4)要确定一个圆,需要两个基本条件,一个是______,另一个是_____,其中_____确定圆的位置,______确定圆的大小. 2.圆的相关概念:(1)弦、直径;(2)弧及其表示方法;(3)等圆、等弧、半圆。
如图1,弦有线段,直径是,最长的弦是,优弧有;劣弧有。
若⊙O1和⊙O2的半径相等则称⊙O1和⊙O2是。
若弧AB和弧CD是两段能够完全重合的弧,则称弧AB和弧CD是。
3.阅读课本P80例1后完成教材P81练习3二、学用结合、提高能力(一)巩固训练★1.判断下列说法是否正确,为什么?(1)直径是弦.()(2)弦是直径.()(3)半圆是弧.( ) (4)弧是半圆.( )(5) 等弧的长度相等.( )(6) 长度相等的两条弧是等弧.( )★★2.教材P81练习2题★★★3.⊙O的半径为2㎝,弦AB所对的劣弧为圆周长的61,则∠AOB=,AB=★★★★4.已知:如图2,OA OB、为⊙O的半径,C D、分别为OA OB、的中点,求证:(1);A B∠=∠ (2)AE BE=★★★★★5.如图,AB为⊙O的直径,CD是⊙O中不过圆心的任意一条弦。
人教版九年级数学上册导学案 第二十四章 圆 24.2.1 点和圆的位置关系

人教版九年级数学上册导学案第二十四章圆24.2.1 点和圆的位置关系【学习目标】1.理解并掌握点与圆的三种位置关系并会熟练运用.2.理解并掌握不在同一直线上的三个点确定一个圆并会熟练运用.3.了解三角形的外接圆和三角形外心的概念。
4.了解反证法,进一步体会解决数学问题的策略.【课前预习】1.已知点P在半径为5cm的圆内,则点P到圆心的距离可以是()A.4cm B.5cm C.6cm D.7cm2.已知⊙O的半径为5,若PO=4,则点P与⊙O的位置关系是()A.点P在⊙O内B.点P在⊙O上C.点P在⊙O外D.无法判断3.已知⊙O的半径r=3,PO=,则点P与⊙O的位置关系是( )A.点P在⊙O内;B.点P在⊙O上;C.点P在⊙O外;D.不能确定4.有下列结论:(1)三点确定一个圆;(2)垂直于弦的直径平分弦;(3)三角形的外心到三角形各边的距离相等。
其中正确的个数有()A.3个B.2个C.1个D.0个5.下列说法:①三点确定一个圆;②相等的圆周角所对的弧相等;③同圆或等圆中,等弦所对的弧相等;④等边三角形的内心与外心重合;⑤三角形的外心到三角形各顶点距离相等其中,正确的个数共有()A.1B.2C.3D.46.已知⊙O的直径为3cm,点P到圆心O的距离为3cm,则点P在⊙O()A.外部B.内部C.上D.不能确定7.若一个点到圆上的点的最小距离为4cm,最大距离为10cm,则该圆的半径是()A.7cm B.3cm C.3cm或7cm D.6cm或14cm8.在Rt△ABC中,∠C=90°,AC=3cm,AB=5cm,若以C为圆心,4cm为半径画一个圆,则下列结论中,正确的是()A.点A在圆C内,点B在圆C外B.点A在圆C外,点B在圆C内C.点A在圆C上,点B在圆C外D.点A在圆C内,点B在圆C上9.已知⊙O的半径是5 cm,P是⊙O外一点,则OP的长可能是()A.3 cm B.4 cm C.5 cm D.6 cm10.下列说法:①三点确定一个圆;②圆中最长弦是直径;③长度相等的弧是等弧;④三角形只有一个外接圆.其中真命题有()A.4个B.3个C.2个D.1个【学习探究】自主学习阅读课本,完成下列问题1.点与圆的位置关系通过上面第3题的作图总结归纳点与圆的三种位置关系:(圆的半径r,点P与圆心的距离为d )点P在圆外⇔;点P在圆上⇔;点P在圆内⇔;2.确定作圆的条件(1)作经过已知点A的圆,这样的圆你能作出多少个?(2)做经过已知点A,B的圆,这样的圆有多少个?它们的圆心分布有什么特点?(3)作经过A,B,C,三点的圆,三点应符合什么条件才能作圆?这样的圆有多少个?如何确定它的圆心?通过以上作圆可知过几个点作圆实质是确定圆心和半径,因此过一点的圆有个,圆心是,半径是 .过两点的圆有个,圆心是,半径是。
人教版九年级数学第24章圆导学案

本课课时安排数:总课时数:第二十四章圆24. 1. 1 圆(1)学习目标1.了解圆的基本概念,并能准确地表示出来.2. 理解并掌握与圆有关的概念:弦、直径、圆弧、等圆、同心圆等.学习重难点重点:与圆有关的概念.难点:圆的有关概念的理解.学习过程一、激趣定标1、阅读课本第二十四章圆的引言2、板书课题,展示目标二、自学互动(适时点拨)互动1自学:研读课本P79~80内容,理解记忆与圆有关的概念,并完成下列问题.探究:①在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做____,固定的端点O叫做圆心,线段OA叫做____.②用集合的观点叙述以O为圆心,r为半径的圆,可以说成是到定点O的距离为____的所有的点的集合.③连接圆上任意两点的____叫做弦,经过圆心的弦叫做____;圆上任意两点间的部分叫做____;圆上任意一条直径的两个端点把圆分成两条弧,每条弧都叫做半____,大于半圆的弧叫做____,小于半圆的弧叫做____.互动21.以点A为圆心,可以画____个圆;以已知线段AB的长为半径可以画____个圆;以点A为圆心,AB的长为半径,可以画____个圆.师点拨:确定圆的两个要素:圆心(定点)和半径(定长).圆心确定圆的位置,半径确定圆的大小.2.到定点O的距离为5的点的集合是以___为圆心,____为半径的圆.三、测评训练1.⊙O的半径为3 cm,则它的弦长d的取值范围是____.2.⊙O中若弦AB等于⊙O的半径,则△AOB的形状是____.3.一点和⊙O上的最近点距离为4 cm,最远点距离为10 cm,则这个圆的半径是___cm或___ cm.4.如图,图中有____条直径,____条非直径的弦,圆中以A为一个端点的优弧有____条,劣弧有____条.5、同步练习册对应的练习题四、小结学生总结本堂课的收获与困惑.1.圆的定义、圆的表示方法及确定一个圆的两个基本条件.2.圆的相关概念:(1)弦、直径;(2)弧及其表示方法;(3)等圆、等弧.本课课时安排数:总课时数:24.1.1圆(2)学习目标:1、初步了解圆的意义,初步理解并掌握圆的相关概念、圆的记法以及弦、弧、圆心角等概念;2会用圆规画图,并进一步感知圆是由圆心和半径确定的──圆心确定了圆的位置,半径确定了圆的大小.学习重、难点重点:圆的意义,弦和弧的概念、弧的表示方法;难点:对弧及优弧、劣弧的概念的感知与理解。
中学人教版九年级上册数学24章圆的专题复习 导学案
学习目标:1、系统熟悉圆的有关概念。
2、巩固有关圆的一些性质和定理。
3、进一步掌握用圆的有关知识解决某些数学问题。
教学重点:有关圆的计算;教学难点:应用圆的有关知识分析问题。
教学方法:采取学生小组合作为主的教学方法,激发学生思维的积极性,充分展现学生的主体作用。
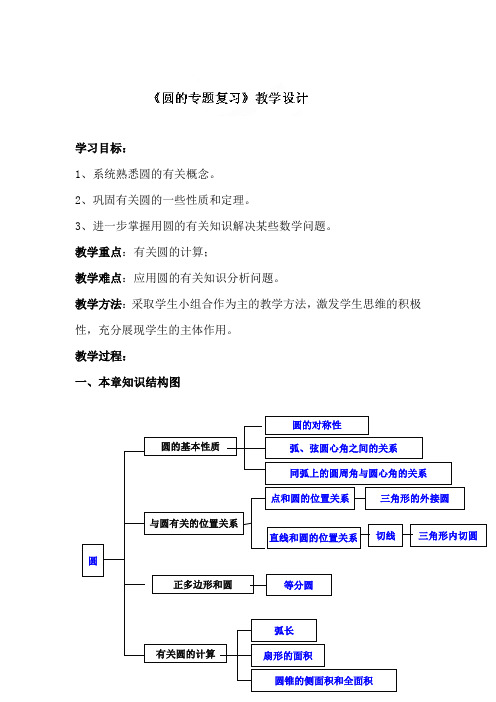
教学过程:一、本章知识结构图二、新课讲解以4人小组为单位,完成以下练习题的讲解:1.⊙O的半径为10cm,弦AB∥CD,AB=12cm,CD=16cm,则AB和CD的距离为( )A.2cm B.14cmC.2cm或14cm D.10cm或20cm2.如图23-14,⊙O的直径为10,弦AB=8,P是弦AB上一个动点,那么OP的长的取值范围是_________.3.如图23-15,AB为⊙O的直径,弦CD⊥AB,垂足为E,那么下列结论不正确的是( )A.CE=DE B. C.∠BAC=∠BAD D.AC>AD4.如图23-10,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么AE的长为( )A. 2 B.3 C.4 D.55.在直径为52cm的圆柱形油桶内装入一些油后,截面如图23-16所示,如果油的最大深度为16cm,那么油面宽度为_________cm.6.如图23-17,点A是半圆上一个三等分点,B点是的中点,P为直径AMN上一动点,⊙O的半径为1,则AP+BP的最小值为( )A.1 B. C.D.7.如图23-11,CA为⊙O的切线,切点为A,点B在⊙O上,如果∠CAB=55°,那么∠AOB等于( )A.35° B.90° C.110°D.120°8.如图23-19,在△ABC中,∠C=90°,AC=3,BC=4,若以C为圆心,R为半径的圆与斜边AB有两个公共点,则R的取值范围是________.9.如图23-20,C是⊙O的直径AB延长线上一点,过C作⊙O的切线CD,D为切点,连结AD、OD、BD.请根据图中所给出的已知条件(不再标注或使用其他字母,不再添加任何辅助线),写出两个你认为正确的结论_________________.10.圆内接四边形ABCD中,∠A︰∠C=1︰3,则∠C=_________.11.如图23-22,⊙O、⊙B、⊙C、⊙D、⊙E相互外离,它们的半径都是1,顺次连结5个圆心得到五边形ABCDE,则图中五个扇形(阴影部分)的面积之和为( )A.1πB.1.5πC.2πD.2.5π12.如图23-23,施工工地的水平地面上,有三根外径都是1米的水泥管,两两相切地堆放地一起,则其最高点到地面的距离是___________.13.如果圆柱的底面半径为4cm,母线长为5cm,那么侧面积等于( )A. B. C. D.14.一个扇形的弧长为20πcm,面积为,则该扇形的圆心角为__________.15.已知圆锥的底面直径为4,母线长为6,则它的侧面积为_________.二、课堂小结三、教学反思今天的这节圆的复习课我的预设目标是让学生在月考前,对圆的知识有了一个系统的认识和巩固练习,通过小组合作交流学习,让较好的学生带动中差的学生完成习题的讲解,让中差的学生在这节课上有所收获。
九年级数学第24章《圆》24.1.1《圆》导学案

2、以点 O 为圆心作圆,可以作( A、1 个 B、 2 个 C、3 个 )
3、确定一个圆的条件为( A、圆心 B、半径
C、圆心和半径
D、以上都不对
4、如图,以坐标原点 O 为圆心的圆与 Y 轴交于点 A、B,且 OA=1,则点 B 的坐标是 ( ) B、 (0,-1) C、 (1,0) D、 (-1,0)
E、半径相等的两个半圆是等弧 等
F、长度相等的两条弧是等弧
(2)如图,点 A、B、C 在
OO 上,∠ABO=38 ,∠ACO=32 ,则∠BOC=
。
(3)⊿ABC 中,∠C 是直角,求证:A、B、C 三点在同一个圆上。
A、 (0,1)
5、如图:⊿ABC 的边 AB,BC 的垂直平分线交于点 O。求证:A、B、C 三个点在以 点 O 为圆心的同一个圆上。
三、合作交流:
(1)下列命题:1、直径相等的圆是等圆
3、过圆心的直线是直径 其中正确的有( ) A、0 个 B、 1 个
2、圆中最长的弦是直径 4、长度相等的两条弧是等弧。
(4)如图,已知两个同心圆的圆心为 O,大圆的半径 OC,OD 分别交小圆于 A、B
两点,判断 AB 与 CD 的位置关系并说明理由。
四、质疑探究: 五、小结与检测: 1、课堂小结: 2、课堂检测: ( 1 )下列说法正确的有 A、直径是弦 B、弦是直径 。 C、半径是弦 D、半圆是弧,但弧不一定是半圆 G、等弧的长度一定相
课 题
24.1.1 圆
知识和能力
授课教师:陕县菜园乡中
孙群念
一、定向 导学:
探索圆的两种定义,理解并掌握弧、弦、优弧、劣弧、半圆等 基本概念,能够从图形中识别. 体会圆的不同定义方法,感受圆和实际生活的联系. 在解决问题过程中使学生体会数学知识在生活中的普遍性.
九年级数学导学案第24章 圆13 第二十四章小结与复习

第二十四章小结与复习【学习目标】1.正确理解圆的定义、弧、弦、圆心角、圆周角概念、三角形的外接圆和三角形外心的概念、切线、切线长的概念、三角形的内切圆和三角形的内心的概念,圆内接多边形、多边形的外接圆等概念、正多边形的中心、半径、中心角、边心距的概念及有关计算.2.通过对圆的有关性质定理与判定定理的复习,熟练掌握圆的有关性质定理与判定定理的综合运用.【学习重点】垂径定理、圆周角定理、切线的判定及性质的有关运用.【学习难点】圆的有关性质与判定的综合运用.教学建议:建议本课时分成2个课时,第一课时复习情景导入(一)~(三)内容,自学互研并交流展示知识模块一~三,当堂演练中相应的题目;第2课时复习情景导入(四)~(七)内容,自学互研并交流展示知识模块三~四,当堂演练中相应的题目.【导学流程】一、情景导入感受新知本节课对全章的知识作一回顾,梳理其知识脉络,熟悉其知识构架,进一步澄清那些易混点,易错点,同时对本章中的一些常用辅助线和常见分类作一整理.二、自学互研生成新知【自主探究】①结合下面的知识结构框图复习整理本章知识要点.圆⎩⎪⎪⎪⎨⎪⎪⎪⎧圆的基本性质⎩⎪⎨⎪⎧轴对称性→垂径定理任意旋转不变性→弧、弦、圆心角的关系定理圆周角定理→圆内接四边形的性质与圆有关的位置关系⎩⎨⎧点和圆→圆的确定定理(三角形外心)直线和圆→切线⎩⎨⎧判定性质三角形内切圆(三角形内心)与圆有关的计算⎩⎪⎨⎪⎧正多边形与圆弧长扇形面积圆锥的侧面积和全面积②常规辅助线.a .与弦有关:垂直于弦的直径.b .已知直径:垂直于直径的弦.c .证切线:有明确公共点,连接圆心与公共点;无明确公共点, 过圆心作切线的垂线段.d .已知切线:垂直于切线且过切点的半径.③圆中的分类讨论(各举一例和同桌交流).a .点和圆的位置关系:点到圆的最近距离和最远距离问题.b .圆的轴对称性:求圆的两平行弦的距离;求有公共端点的两弦夹角.c .弦所对的圆周角.d .与三角形的外心有关的计算.师生活动:①明了学情:关注学生提纲中三个方面的整理情况.②差异指导:根据学情进行分类指导.③生助生:小组内相互交流、研讨、改正.三、典例剖析 运用新知【合作探究】典例1:①如图,⊙O 的直径CD =10 cm ,AB 是⊙O 的弦,AB ⊥CD ,垂足为M ,OM ∶OC =3∶5,则AB 的长为( A )A .8cmB .91cmC .6cmD .2cm②如图,AB 与⊙O 相切于点C ,OA =OB ,⊙O 的直径为8 cm ,AB =10 cm ,求OA 的长.解:连接OC.∵AB 与⊙O 相切于点C ,∴∠ACO =90°.又∵OA =OB ,∴AC =CB =12AB =5 cm.在Rt △AOC 中,OA =OC 2+AC 2=16+25=41(cm).③如图,在足球比赛中,甲带球向对方球门PQ 进攻,当他带球冲到A 点时,同伴乙已经助攻冲到B 点,此时甲是直接射门好,还是将球传给乙,让乙射门好?(仅从射门角度考虑)解:∵A 在圆外,B 在圆上,∴∠PAQ <∠PBQ.∴让乙射门好.典例2:已知,如图,扇形AOB 的圆心角为120°,半径OA 为6 cm .(1)求扇形AOB 的弧长和扇形面积;(2)若把扇形纸片AOB 卷成一个圆锥无底纸盒,求这个纸盒的高OH.解:(1)扇形AOB 的弧长=4π(cm),扇形AOB 的扇形面积=12π(cm 2).(2)设圆锥底面圆的半径为r ,所以2πr =4π,解得r =2.在Rt △OHC 中,HC =2,OC =6,所以OH =OC 2-HC 2=42(cm).四、课堂小结 回顾新知(1)总结本节课的收获.(2)再次回顾全章知识要点.五、检测反馈 落实新知1.如图,在⊙O 中,弦AB ,CD 相交于点P ,∠A =40°,∠APD =75°,则∠B 等于( D )A .15°B .40°C .75°D .35°,(第1题图)),(第2题图))2.如图,PA,PB分别切⊙O于点A,B,∠P=70°,则∠C=(B)A.70°B.55°C.110°D.140°3.如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,求证:AC平分∠DAB.证明:连接OC.∵OA=OC,∴∠OAC=∠OCA.又∵DC是⊙O的切线,∴OC⊥CD.又AD⊥CD,∴AD∥CO.∴∠DAC=∠OCA,∴∠DAC=∠OAC.∴AC平分∠DAB.六、课后作业巩固新知(见学生用书)。
第二十四章《圆》导学案(全章)

AQP24.1.1圆(第1课时)【自主学习】 (一) 新知导学1.圆的运动定义:把线段OP 的一个端点O ,使线段OP 绕着点O 在 旋转 ,另一端点P 运动所形成的图形叫做圆,其中点O 叫做 ,线段OP 叫做 .以O 为圆心的圆记作 .2.圆的集合定义:圆是到 的点的集合. 3.点与圆的位置关系:如果⊙O 的半径为r ,点P 到圆心的距离为d ,那么 点P 在圆内⇔ ;点P 在圆上⇔ ; 点P 在圆外⇔ .【合作探究】1.如图,已知:点P 、Q ,且PQ=4cm.(1)画出下列图形: ①到点P 的距离等于2cm 的点的集合; ②到点Q 的距离等于3cm 的点的集合;(2)在所画图中,到点P 的距离等于2cm ;且到点Q 的距离等于3cm 的点有几个?请在图中将它们画出来.(3)在所画图中,到点P 的距离小于或等于2cm ;且到点Q 的距离大于或等于3cm 的点的集合是怎样的图形?把它画出来. 【自我检测】为圆心, 为半径的圆.为圆心,以 为半径的圆上. 3.矩形ABCD 边AB=6cm,AD=8cm ,(1)若以A 为圆心,6cm 长为半径作⊙A ,则点B 在⊙A______,点C 在⊙A_______,点D 在⊙A________,AC 与BD 的交点O 在⊙A_________;(2)若作⊙A ,使B 、C 、D 三点至少有一个点在⊙A 内,至少有一点在⊙A 外,则⊙A 的半径r 的取值范围是_______.4.一个点与定圆最近点的距离为4cm, 与最远点的距离是9cm ,则圆的半径是5.如图,已知在⊿ABC 中,∠ACB=900,AC=12,AB=13,CD ⊥AB,以C 为圆心,5为半径作⊙C ,试判断A,D,B 三点与⊙C 的位置关系左下图,一根长4米的绳子,一端拴在树上,另一端拴着 .7.已知:如右上图,△ABC ,试用直尺和圆规画出过A ,B ,C 三点的⊙O .8.△ABC 中,∠A=90°,AD⊥BC 于D ,AC=5cm ,AB=12cm ,以D 为圆心,AD 为半径作圆,则三个顶点与圆的位置关系是什么?画图说明理由.9.如右图,(1)若点O 为⊙O 的圆心,则线段__________是圆O 的半径; 线段________是圆O 的弦,其中最长的弦是______; ______是劣弧;______是半圆.(2)若∠A =40°,则∠ABO =______,∠C =______,∠ABC =______.10.已知:如图,AB 是⊙O 的直径,CD 是⊙O 的弦,AB ,CD 的延长线交于E ,若AB =2DE ,∠E =18°,求∠C 及∠AOC 的度数.树S小狗4m24.1.1圆(第2课时)【自主学习】 (一)复习巩固: 1.圆的集合定义.2.点与圆的三种位置关系.⊙O 的半径为5cm ,点P 是⊙O 外一点,则OP 的长可能是( )(二)新知导学 1.与圆有关的概念①弦:连结圆上任意两点的 叫做弦. ②直径:经过 的弦叫做直径.③弧: ,弧分为:半圆( 所对的弧叫做半圆)、劣弧(小于 的弧)和优弧(大于 的弧).④同心圆: 相同, 不相等的两个圆叫做同心圆. ⑤等圆:能够互相 的两个圆叫做等圆.⑥等弧:在 或 中,能够互相 的弧叫做等弧. 2.同圆或等圆的性质:在同圆或等圆中,它们的 相等. 【合作探究】1.圆心都为O 的甲、乙两圆,半径分别为r 1和r 2,且r 1<OA <r 2,那么点A 在( ) A. 甲圆内 B.乙圆外 C. 甲圆外、乙圆内 D. 甲圆内、乙圆外2.下列判断:①直径是弦;②两个半圆是等弧;③优弧比劣弧长,其中正确的是( ) A. ① B.②③ C. ①②③ D.①③ 【自我检测】1.已知⊙O 中最长的弦为16cm ,则⊙O 的半径为________cm . 2.过圆内一点可以作出圆的最长弦_____条. 3.下列语句中,不正确的个数是( )①直径是弦; ②弧是半圆; ③长度相等的弧是等弧; •④经过圆内任一定点可以作无数条直径. A .1个 B .2个 C .3个 D .4个 4.下列语句中,不正确的是( )A .圆既是中心对称图形,又是旋转对称图形B .圆既是轴对称图形,又是中心对称图形C .当圆绕它的圆心旋转89°57′时,不会与原来的圆重合D .圆的对称轴有无数条,对称中心只有一个第6题ABA CD31圆周的弧叫做( ) A .劣弧 B .半圆 C .优弧 D .圆6.如图,⊙O 中,点A 、O 、D 以及点B 、O 、C 分别在一条直线上,图中弦的条数有(• ) A .2条 B .3条 C .4条 D .5条7.以已知点O 为圆心,已知线段a 为半径作圆,可以作( ) A .1个 B .2个 C .3个 D .无数个8.如图,CD 是⊙O 的直径,∠EOD=84°,AE 交⊙O 于点B ,且AB=OC ,求∠A 的度数.9.如图,在△ABC 中,∠ACB=90°,∠A=40°;以C 为圆心、CB 为半径的圆交AB•于点D ,求∠ACD 的度数.10.如图,CD 是⊙O 的弦,CE=DF ,半径OA 、OB 分别过E 、F 点. 求证:△OEF 是等腰三角形.BACEDOO BAC FE11.如图,在⊙O中,半径OC与直径AB垂直,OE=OF,则BE与CF的大小关系如何?并说明理由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三数学第24章圆导学案
数学课题24.1.2垂直于弦的直径
课型新授班级九年级姓名
学习
目标1.理解圆的轴对称性;
2.了解拱高、弦心距等概念;
3.使学生掌握垂径定理,并能应用它解决有关弦的计算和证明问题。
;
沉默是金难买课堂一分,跃跃欲试不如亲身尝试!
学法指导合作交流、讨论、
一、自主先学————相信自己,你最棒!
⒈叙述:请同学叙述圆的集合定义?
⒉连结圆上任意两点的线段叫圆的________,圆上两点间的部分叫做_____________,
在同圆或等圆中,能够互相重合的弧叫做______________。
课本P80页有关“赵州桥”问题。
二、展示时刻——集体的智慧是无穷的,携手解决下面的问题吧!
)、动手实践,发现新知
⒈同学们能不能找到下面这个圆的圆心?动手试一试,
有方
法的同学请举手。
⒉问题:①在找圆心的过程中,把圆纸片折叠时,两个半圆_______
②刚才的实验说明圆是____________,对称轴是经过圆心的每
一条_________。
)、创设情境,探索垂径定理
⒈在找圆心的过程中,折叠的两条相交直径可以是哪样一些位置关系呢?
垂直是特殊情况,你能得出哪些等量关系?
⒉若把AB向下平移到任意位置,变成非直径的弦,观察
一下,还有与刚才相类似的结论吗?
⒊要求学生在圆纸片上画出图形,并沿cD折叠,实验后提出猜想。
⒋猜想结论是否正确,要加以理论证明引导学生写出已知,求证。
然后让学生阅读课本P81证明,并回答下列问题:
①书中证明利用了圆的什么性质?
②若只证AE=BE,还有什么方法?
⒌垂径定理:
分析:给出定理的推理格式
.辨析题:下列各图,能否得到AE=BE的结论?为什么?
三、学生展示——面对困难别退缩,相信自己一定行!!!
.如图1,如果AB为⊙o的直径,弦cD⊥AB,垂足为E,那么下列结论中,?错误的是.
A.cE=DEB.c.∠BAc=∠BADD.Ac>AD
.如图2,⊙o的直径为10,圆心o到弦AB的距离o的长为3,则弦AB的长是
A.4B.6c.7D.8
.如图3,已知⊙o的半径为5,弦AB=8,则圆心o到AB 的距离是
A.1B.2c.3D.4
.P为⊙o内一点,oP=3c,⊙o半径为5c,则经过P点的最短弦长为________;?
最长弦长为_______.
.如图4,oE⊥AB、oF⊥cD,如果oE=oF,那么_______ 已知,如图所示,点o是∠EPF的平分线上的一点,以o 为圆心的圆和角的两边分别
交于点A、B和c、D。
求证:AB=CD
五、当堂训练
一、定理的应用
已知:在圆o中,⑴弦AB=8,o到AB的距离等于3,求圆o的半径。
⑵若oA=10,oE=6,求弦AB的长。
练习P82页练习2
四、自我反思:
本节课我的收获:。
1.2垂直于弦的直径作业纸
设计:韩伟班级姓名
一、必做题
⊙o的半径是5,P是圆内一点,且oP=3,过点P最短弦、最长弦的长为.
如右图2所示,已知AB为⊙o的直径,且AB⊥cD,垂足为,cD=8,A=2,
则o=.
⊙o的半径为5,弦AB的长为6,则AB的弦心距长为.
已知一段弧AB,请作出弧AB所在圆的圆心。
问题1:如图1,AB是两个以o为圆心的同心圆中大圆的直径,AB交小圆交于c、D两点,求证:Ac=BD 问题2:把圆中直径AB向下平移,变成非直径的弦AB,如图2,是否仍有Ac=BD呢?问题3:在圆2中连结oc,oD,将小圆隐去,得图4,设oc=oD,求证:Ac=BD 问题4:在图2中,连结oA、oB,将大圆隐去,得图5,设Ao=Bo,求证:Ac=BD
,AB=10若上一点,AB是P的弦,o是⊙AB已知如图,.PB=4,oP=5,
求⊙o的半径的长。
