八年级数学经典压轴题：一次函数与几何问题综合.doc

合集下载

专题08 一次函数与几何综合的五种考法(解析版)-2024年常考压轴题攻略(8年级上册北师大版)

专题08一次函数与几何综合的五种考法类型一、等腰三角形存在性问题(1)求直线CB的解析式；(2)点E在x轴上，【答案】(1)12y x =+(2)(4,0)、(16,0)-、当10BE AB ==时，1E 点的坐标为(4,0)，2E 点的坐标为当AB AE =时，点B 与点E 是关于y 轴对称，E 当EA EB =时，设点E 坐标为(,0)x ，则2228(6)x x +=+，解得：73x =4E 点的坐标为7(,0)3，(1)当点P 在线段BO 上时，①求证：AOP BOQ ≌△△；②若点P 为BO 的中点，求△(2)在点P 的运动过程中，是否存在某一位置，的坐标；若不存在，请说明理由．当点P 在线段OB 上时，若OC OQ =，由于OP OQ =，则有在OCP △中，OPC AOP ∠=∠+OC OP ∴>，即OC OQ =不可能；若CQ OQ =，由于OP OQ =，则有过点C 作CH x ⊥轴于点H ，显然即CQ OQ =不可能，∴当COQ 是等腰三角形时，只有当点P在BO的延长线上时，同理可得：(0,424)P--，综上所述：(0,424)P-或P【点睛】本题考查了一次函数与几何图形综合，图形是解题的关键．【变式训练2】如图，在平面直角坐标系中，一次函数分别交于点B、A，点P为y(1)求点A、B的坐标；(2)当点P在y轴负半轴上，且ABP的面积为6时，求点(3)是否存在点P使得ABP为等腰三角形?若存在，求出点设()()0,0P n n <，则2PA =-所以()22224PA n n n =-=-+所以224416n n n -+=+解得3n =-，所以此时点P 的坐标为(0,3-综上所述，存在点P 使得ABP 例．如图，直线24y x =+与x 轴交于点A ，与y 轴交于点B ，点C 是OB 的中点．(1)求点C 的坐标：(2)在x 轴上找一点D ，使得ACD ABC S S = ，求点D 的坐标；(3)在x 轴上是否存在一点P ，使得ABP 是直角三角形？若存在，请写出点P 的坐标；若不存在，请说明理由．【答案】(1)()0,2C (2)点D 的坐标为()4,0-或()0,0(3)存在，满足条件的P 点的坐标为()0,0或()8,0(1)填空：b =，m =，k =；(2)如图2，点D 为线段BC 上一动点，将ACD 沿直线AD 翻折得到AED △，线段AE 交轴于点F ．①求线段AE 的长度；②当点E 落在y 轴上时，求点E 的坐标；③若DEF 为直角三角形，请直接写出满足条件的点D 的坐标．【答案】(1)8，2-，12-(2)①45；②点E 的坐标为()0,4219-；③点D 的坐标为()20，或()254,0-【分析】（1）根据待定系数法求解即可；（2）①过点A 作AH y ⊥轴于点H ，作AG x ⊥轴于点G ，根据勾股定理得到()222262480AE AC ==++=，于是得到结论；②利用勾股定理求出219HE =，可得2194OE =-，即可得答案；③分两种情况讨论，当90EDF ∠=︒时，求出135ADC ∠=︒，得45ADO ∠=︒，得DG AD ==得点D 坐标；当90DFE ∠=︒时，设DF x =，则8DE DC x ==-，由勾股定理得：()()2228454x x -=+-，求出DF ，得点D 坐标．【详解】（1）解：把()40B -，代入2y x b =+，∵()024b =⨯-+，∴8b =，∴直线AB ：28y x =+，把()4A m ，代入28y x =+，∴2m =-，∵ACD 翻折得到AED△∴()222262480AE AC ==++=，∴45AE =②当E 点落在y 轴上时，在Rt AHE △中，∵222AE AH HE -=∴222802HE AE AH =-=-=∴2194OE HE OH =-=-，∴点E 的坐标为()04219-，；③如下图，当90EDF ∠=︒时，由翻折得ADC ∠∴1359045ADO ∠︒︒=-=︒，∵4AG =，∴4DG AG ==，∴422OD DG OG =-=-=，∴点D 的坐标为()20，；如下图，当90DFE ∠=︒时，80AE AC ==设DF x =，则8DE DC x ==-，在Rt DEF △中，由勾股定理得：(解得：252x =-，∴254OD DF OF =-=-，∴点D 的坐标为()254,0-，综上，点D 的坐标为()20，或(2【点睛】本题考查了一次函数的综合题，勾股定理，角平分线的性质，直角三角形的性质和判定，翻折的性质，解题的关键是作辅助线．(1)如图1，求出AOP 的面积；(2)如图2，已知点C 是直线85y x =上一点，若APC △是以AP 为直角边的等腰直角三角形，求点C 的坐标．【答案】(1)AOP 的面积为40(2)点C 的坐标为()1016，或162,⎛⎫⎪∵直线l x ∥轴，点B ∴8PH OB ==，∴12AOP S OA PH == 故答案为：40；（2）设点(),8P n (n ≠过点P 作直线FE ，交APC 为等腰直角三角形，则90APE FPC ∴∠+∠=︒，APE FCP ∴∠=∠，90PEA CFP ∠=∠=︒ ，(AAS)PEA CFP ∴ ≌，同理可得：(AAS)AMP ANC ≌AM AM ∴=且MP NC =，8|10|m ∴=-或8105n m -=解得：2565m n =⎧⎪⎨=⎪⎩或181945m n =⎧⎪⎨=⎪⎩(1)求直线l 的解析式；(2)求证：ABC 是等腰直角三角形；(3)将直线l 沿y 轴负方向平移，当平移恰当的距离时，直线与在直线CD 上存在点P ，使得A △的坐标．【答案】(1)142y x =-+∴90DPE A PB ''∠=∠=︒，∴A PD B PE ''∠=∠，∵90A FP CEB ''∠=∠=︒，∴A FP CEB '' ≌，∴4,PE PF A F B E ''===，此时点P 的坐标为()44--，；如图，若以点P 为直角顶点时，过点同理此时点P 的坐标为()44-，；如图，若以点B '为直角顶点时，过点P 作同理A OB B GP ''' ≌，∴44OB PG OF t '====+，B '∴8t =-或0（舍去），∴8B G OA ''==，∴12OG =，∴此时点P 的坐标为()412--，；如图，若以点B '为直角顶点时，过点B '作B M CD '⊥轴于点M ，则4B M OF '==，OB MF '=，同理PB M A B O ''' ≌，∴44B M B O t ''===+，82PM OA t '==+，∴0=t （舍去）；如图，若以点A '为直角顶点时，同理A PF B A O ''' ≌，∴,PF A O B O A F '''==，∴4482t t --=---，解得：8t =-，∴8PF =，此时点P 的坐标为()48-，；如图，若以点A '为直角顶点时，同理A PF B A O ''' ≌，∴,PF A O B O A F '''==，∴4824t t --=++，解得：163t =-，∴83PF =，∴此时点P 的坐标为84⎛⎫--，；(1)①A 的坐标是_____________②求直线AB 的表达式；(2)点P 是直线y =(3)当ABP 为等腰直角三角形时，请直接写出【答案】(1)①(0,3【分析】（1）把x（3）解：如图1，当点P 为顶点时，过点P 作PE x ⊥轴，过点A 作AF 垂直于PE 的延长线于点F ，∵ABP 是等腰直角三角形，AP PB ∴=，APB ∠=90︒，=90FAP APF +∠︒ ，=90APF BPE ∠+∠︒，=FAP BPE ∴∠∠，在AFP 和PEB △中，F E FAP EPB AP PB ∠=∠⎧⎪∠=∠⎨⎪=⎩，()AFP PEB AAS ∴≅ ，AF PE ∴=，BE PF =，===90O F E ∠∠∠︒ ，∴四边形AOEF 是矩形，==AF PE OB BE ∴+，===AO FE FP PE BE PE ++，==2AO BE OB BE BE OB +++，()0,3A 、()1,0B ，=3AO ∴，1OB =，21=3BE ∴+，=1BE ∴，==31=2PE AO BE --，==11=2OE OB BE ∴++，∴点P 的坐标为()2,2；如图2，当点B 为顶点时，过点P 作PG x ⊥轴，ABP 是等腰直角三角形，AB BP ∴=，=90ABO OAB ∠+∠︒ ，=90ABO PBG ∠+∠︒，=OAB PBG ∴∠∠，在AOB 和BGP 中，O PGB OAB PBG AB BP ∠=∠⎧⎪∠=∠⎨⎪=⎩，()AOB BGP AAS ∴≅ ，=PG OB ∴，BG AO =，()0,3A 、()1,0B ，=3AO ∴，1OB =，==13=4OG OB BE ∴++，=1PG ，∴点P 的坐标为()4,1；如图3，当点A 为顶点时，过点P 作PM y ⊥轴，PAB △是等腰直角三角形，PA AB ∴=，=90PAB ∠︒，90MAP OAB ∠+∠=︒ ，90MAP MPA ∠+∠=︒，=MPA OAB ∴∠∠，在PMA △和AOB 中，M O MPA OAB AP AB ∠=∠⎧⎪∠=∠⎨⎪=⎩()PMA AOB AAS ∴≅ ，=MP AO ∴，=MA OB ，()0,3A 、()1,0B ，=3AO ∴，1OB =，3MP ∴=，==13=4OM MA AO ++，∴点P 的坐标为()3,4，故答案为：()2,2；()4,1；()3,4．【点睛】本题考查了一次函数的综合运用，等腰直角三角形的性质和矩形的性质及全等三角形的性质的判定，熟练求一次函数的解析式和构造全等三角形是解题的关键．类型四、全等问题(1)点A坐标为________，点B坐标为(2)当BOP△的面积是4时，求点(3)在y轴上是否存在点Q，使得以接写出所有符合条件的点P的坐标，否则请说明理由．【答案】(1)(3,0)，(0,4)，12 5(2)4(2,)20(2,)125OM OQ ==，12(0,)5Q 或12(0,)5-，6(5P ，12)5或24(5，12)5-；②如图3，图4，当OMP PQO ≌△△时，125PQ OM ∴==，12(5P ∴-，36)5或12(5，4)5；综上所述：P 点坐标为(65，12)5或24(5，12)5-或12(5-，36)5或12(5，4)5．【点睛】本题考查一次函数的图象及性质，判定及性质，分类讨论，数形结合是解题的关键．【变式训练1】如图，一次函数364y x =+的图象与于点C ，点P 在直线AB 上运动，点Q 在(1)求点A ，B 的坐标；(2)求OC 的长；(3)若以O ，P ，Q 为顶点的三角形与【答案】(1)()8,0A -，(B (3)Q 的坐标为120,5⎛⎫ ⎪⎝⎭或0,⎛ ⎝则OC PQ=，∴245PQ =，∴245m=-，∴33241266 4455m⎛⎫+=⨯-+=⎪⎝⎭，∵PQ OC=，∴245 PQ=．∴245=m，∴33244866 4455m+=⨯+=，∴48 0,5Q⎛⎫ ⎪⎝⎭；则245 OQ OC==，∴240,5Q⎛⎫ ⎪⎝⎭；综上所述，Q的坐标为12 0,5⎛⎫ ⎪⎝⎭或(1)求点B 的坐标及直线BC 的函数表达式；(2)在坐标系平面内，存在点D ，使以点A ，B ，D 为顶点的三角形与ABC 全等，画出ABD ，并求出点D 的坐标．【答案】(1)点B 的坐标为(0，3)，33y x =-+；(2)图见解析，点D 的坐标为(4-，3)或(3-，4)或(0，1)-．【分析】（1）将点点(3A -，0)代入解析式得出3b =，继而得出点B 的坐标为(0，3)，根据:3:1OB OC =得出1OC =，即点C 的坐标为(1，0)，然后待定系数法求解析式即可求解；（2）分在x 轴上方：BAD ABC ≌和(ABD ABC ≌如图1)和点D 在y 轴上(如图②)两种情况，根据全等三角形的性质即可求解．【详解】（1）解：∵直线AB ：y x b =+过点(3A -，0)，03b ∴=-+，3b ∴=．当0x =时，3y x b b =+==，∴点B 的坐标为(0，3)，即3OB =．OB ：3OC =：1，1OC ∴=．点C 在x 轴正半轴，∴点C 的坐标为(1，0)．设直线BC 的解析式为()0y kx c k =+≠，将(0B ，3)、(1C ，0)代入y kx c =+，得：30c k c =⎧⎨+=⎩，解得：33k c =-⎧⎨=⎩，∴直线BC 的函数表达式为33y x =-+．（2）分在x 轴上方：BAD ABC ≌和(ABD ABC ≌如图1)和点D 在y 轴上(如图②)两种情况考虑：如图①：①当BAD ABC ≌时，3OA OB == ，45BAC ∴∠=︒．BAD ABC ≌，45ABD BAC ∴∠=∠=︒，4BD AC ==，BD ∴∥AC ，∴点D 的坐标为(4-，3)；②当ABD ABC ≌时，45BAD BAC ∠=∠=︒，4AD AC ==，90DAC ∴∠=︒，∴点D 的坐标为(3-，4)．如图②当ABD BCA ≌时，4BD AC ==，1OD ∴=，∴点D 的坐标为(0，1)-．综上所述，点D 的坐标为(4-，3)或(3-，4)或(0，1)-．【点睛】本题考查了一次函数与几何图形，坐标与图形，全等三角形的性质与判定，数形结合是解题的关键．【变式训练3】如图①，已知直线24y x =-+与x 轴、y 轴分别交于点A 、C ，以OA OC ，为边在第一象限内作长方形OABC ．类型五、角度之间关系过点P 作EF y ⊥轴于点E ，过点H 作∴45POG ∠=︒，∵()3,1P ，∴1,3EP OE ==∵OA OB =，45AOB ∠=︒∴AOB 是等腰直角三角形，∵45APO EOP ∠+∠=︒，PQO APO∠=∠∴45PQO EOP ∠+∠=︒又∵9045EOP GOQ POG ∠+∠=︒-∠=∴GOQ GQO∠=∠∴GQ GO =，即点G 在OG 的垂直平分线上，∵90OEP PFH OPH ∠=∠=∠=︒，∴90OPE FPH PHF ∠=︒-∠=∠，(1)求直线AB的关系式；(2)连接PD，当线段PD AB⊥时，直线AD上有一点动M∴1284,2525S ⎛⎫-- ⎪⎝⎭，∵45,DKR DAO KT RK ∠=∠=︒⊥∴45DKR DKT ∠=︒=∠，∴KT KP =，∴P ，T 关于直线AD 对称，连接TS 交AD 于M ，交x 轴于N 4y x =-+12x =-得y =∵3,4OB OA ==，∴34PH PH AH HW==，设3PH t =，则4AH HW t ==∴5PW t OW ==，∵4OW HW AH OA ++==，∵12POA BAO ∠=∠，∴2POA APO POA ∠+∠=∠∴APO POA ∠=∠，∴4AO AP ==，∵34PF OB AF AF ==，∴165AF =36(1)求直线BC 的函数解析式；(2)设点M 是x 轴上的一个动点，过点M 作y 轴的平行线，交直线于点Q ．①若PQB △的面积为83，求点M 的坐标．②连接BM ，如图2，在点M 的运动过程中是否存在点P ，使∠求出点P 坐标，若不存在，请说明理由．则113(3)22PQ m m m =-+-+=，则PQB ∆的面积21122PQ BD m =⋅=故点M 的坐标为43(3，0)或4(-②如图，当点M 在y 轴的左侧时，点C 与点A 关于y 轴对称，AB BC ∴=，BAC BCA ∴∠=∠，BMP BAC ∠=∠ ，BMP BCA ∴∠=∠，90BMP BMC ∠+∠=︒ ，90BMC BCA ∴∠+∠=︒(1)求点A，B的坐标；(2)若直线AC⊥AB交y轴负半轴于点(3)在y轴上是否存在点P，使以求出点P的坐标；若不存在，请说明理由．【答案】(1)A(−1，0)；B(0，2)(2)1.25；(3)y轴上存在点P，使以A，当BA＝BP时，BP＝∴点P1的坐标为(0，当PB＝PA时，设OP ∴(2−x)2=1+x2，解得：∴点P3的坐标为(0，当AB＝AP时，OP＝∴点P4的坐标为(0，综上所述：y轴上存在点标为(0，2+5）或(0(1)填空：=a ______，b =______；(2)在射线CD 上有一动点E ，过点E 作EF 平行于y 轴交直线AB 时，求点E 的坐标；(3)点M 为直线AB 上一点，且45CDM ∠=︒，求点M 的坐标．【答案】(1)1，2-1112132⎛⎫∴90QCP QPC ∠+∠=︒，∵CP CD ⊥，∴90QCP DCL ∠+∠=︒∴QPC DCL ∠=∠，∴QPC LCP ≌△△，∵()1,1C -，()0,2D -，∴CG HK =，GH KD =，∵()1,1C -，()0,2D -，设(,H c d ∴2c =-，1d =-，∴()2,1H --，可得直线DH 的解析式为联立12213y x ⎧=--⎪⎪⎨，解得721x ⎧=-⎪⎪⎨(1)求点C的坐标；∥轴交AB于点(2)如图2，过点C作直线CD x①求线段CD的长；②在坐标平面内，是否存在点M（除点B外），全等？若存在，请直接写出所有符合条件的点M DC≌△BDC时，当△1M和点B关于直线则点1M的坐标为：（-1∴点1M CD≌△BDC时，当△2。

八年级一次函数几何综合

一次函数几何综合【例题精讲一】1、如图①所示，直线L：y=mx+5m与x轴负半轴，y轴正半轴分别交于A、B两点．（1）当OA=OB时，求点A坐标及直线L的解析式；（2）在（1）的条件下，如图②所示，设Q为AB延长线上一点，作直线OQ，过A、B两点分别作AM⊥OQ于M，BN⊥OQ于N，若AM=，求BN的长；（3）当m取不同的值时，点B在y轴正半轴上运动，分别以OB、AB为边，点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE，连EF交y轴于P点，如图③．问：当点B在y轴正半轴上运动时，试猜想PB的长是否为定值？若是，请求出其值；若不是，说明理由．例2．如图1，已知一次函数y=﹣x+6分别与x、y轴交于A、B两点，过点B的直线BC交x轴负半轴与点C，且OC=OB．（1）求直线BC的函数表达式；（2）如图2，若△ABC中，∠ACB的平分线CF与∠BAE的平分线AF相交于点F，求证：∠AFC=∠ABC；（3）在x轴上是否存在点P，使△ABP为等腰三角形？若存在，请直接写出P点的坐标；若不存在，请说明理由．【课堂练习】1．已知：如图1，一次函数y=mx+5m的图象与x轴、y轴分别交于点A、B，与函数y=﹣x的图象交于点C，点C的横坐标为﹣3．（1）求点B的坐标；（2）若点Q为直线OC上一点，且S△QAC=3S△AOC，求点Q的坐标；（3）如图2，点D为线段OA上一点，△ACD=△AOC．点P为x轴负半轴上一点，且点P到直线CD和直线CO的距离相等．△在图2中，只利用圆规作图找到点P的位置；（保留作图痕迹，不得在图2中作无关元素．）△求点P的坐标．2．如图，直线l：y=x+6交x、y轴分别为A、B两点，C点与A点关于y轴对称．动点P、Q分别在线段AC、AB上（点P不与点A、C重合），满足△BPQ=△BAO．（1）点A坐标是，BC=．（2）当点P在什么位置时，△APQ△△CBP，说明理由．（3）当△PQB为等腰三角形时，求点P的坐标．【例题精讲2】例题1、在平面直角坐标系中，△AOC中，△ACO=90°．把AO绕O点顺时针旋转90°得OB，连接AB，作BD△直线CO于D，点A的坐标为（﹣3，1）．（1）求直线AB的解析式；（2）若AB中点为M，连接CM，动点P、Q分别从C点出发，点P沿射线CM以每秒个单位长度的速度运动，点Q沿线段CD以每秒1个长度的速度向终点D运动，当Q点运动到D点时，P、Q同时停止，设△PQO的面积为S（S≠0），运动时间为T秒，求S与T的函数关系式，并直接写出自变量T的取值范围；（3）在（2）的条件下，动点P在运动过程中，是否存在P点，使四边形以P、O、B、N（N为平面上一点）为顶点的矩形？若存在，求出T的值．例题2、若直线y=mx+8和y=nx+3都经过x轴上一点B，与y轴分别交于A、C（1）填空：写出A、C两点的坐标，A_________，C_________；（2）若△ABO=2△CBO，求直线AB和CB的解析式；（3）在（2）的条件下若另一条直线过点B，且交y轴于E，若△ABE为等腰三角形，写出直线BE的解析式（只写结果）．例题3、如图，在平面直角坐标系中，O是坐标原点，点A的坐标为（﹣4，0），点B的坐标为（0，b）（b＞0）． P是直线AB上的一个动点，作PC△x轴，垂足为C．记点P关于y轴的对称点为P'（点 P'不在y轴上），连接P P'，P'A，P'C．设点P的横坐标为a．（1）当b=3时，求直线AB的解析式；（2）在（1）的条件下，若点P'的坐标是（﹣1，m），求m的值；（3）若点P在第一像限，是否存在a，使△P'CA为等腰直角三角形？若存在，请求出所有满足要求的a的值；若不存在，请说明理由．【课堂练习】1、已知如图，直线y=﹣x+4与x轴相交于点A，与直线y=x相交于点P．（1）求点P的坐标；（2）求S△OPA的值；（3）动点E从原点O出发，沿着O→P→A的路线向点A匀速运动（E不与点O、A重合），过点E分别作EF△x 轴于F，EB△y轴于B．设运动t秒时，F的坐标为（a，0），矩形EBOF与△OPA重叠部分的面积为S．求：S与a 之间的函数关系式．2、如图，直线y=x+6与x轴、y轴分别相交于点E、F，点A的坐标为（﹣6，0），P（x，y）是直线y=x+6上一个动点．（1）在点P运动过程中，试写出△OPA的面积s与x的函数关系式；（2）当P运动到什么位置，△OPA的面积为，求出此时点P的坐标；（3）过P作EF的垂线分别交x轴、y轴于C、D．是否存在这样的点P，使△COD△△FOE？若存在，直接写出此时点P的坐标（不要求写解答过程）；若不存在，请说明理由．【例题精讲3】1、如图，在平面直角坐标系xoy中，直线AP交x轴于点P（p，0），交y轴于点A（0，a），且a、b满足．（1）求直线AP的解析式；（2）如图1，点P关于y轴的对称点为Q，R（0，2），点S在直线AQ上，且SR=SA，求直线RS的解析式和点S的坐标；（3）如图2，点B（﹣2，b）为直线AP上一点，以AB为斜边作等腰直角三角形ABC，点C在第一象限，D为线段OP上一动点，连接DC，以DC为直角边，点D为直角顶点作等腰三角形DCE，EF△x轴，F为垂足，下列结论：△2DP+EF的值不变；△的值不变；其中只有一个结论正确，请你选择出正确的结论，并求出其定值．2、如图，直线L：y=﹣x+2与x轴、y轴分别交于A、B两点，在y轴上有一点C（0，4），动点M从A点以每秒1个单位的速度沿x轴向左移动．（1）求A、B两点的坐标；（2）当M在x轴正半轴移动并靠近0点时，求△COM的面积S与M的移动时间t之间的函数关系式；当M在O 点时，△COM的面积如何？当M在x轴负半轴上移动时，求△COM的面积S与M的移动时间t之间的函数关系式；请写出每个关系式中t的取值范围；（3）当t为何值时△COM△△AOB，并求此时M点的坐标．【课堂练习】1. 已知，如图直线y=2x+3与直线y=﹣2x﹣1相交于C点，并且与两坐标轴分别交于A、B两点．（1）求两直线与y轴交点A，B的坐标及交点C的坐标；（2）求△ABC的面积．2．如图△，直线y=﹣x+1分别与坐标轴交于A，B两点，在y轴的负半轴上截取OC=OB（1）求直线AC的解析式；（2）如图△，在x轴上取一点D（1，0），过D作DE△AB交y轴于E，求E点坐标．课后作业A B C O y 2y 1xy P5、如图，在平面直角坐标系xOy 中，一次函数1223y x =-+与x 轴、y 轴分别相交于点A 和点B ，直线2 (0)y kx b k =+≠经过点C （1，0）且与线段AB 交于点P ，并把△ABO 分成两部分．（1）求△ABO 的面积；（2）若△ABO 被直线CP 分成的两部分的面积相等，求点P 的坐标及直线CP 的函数表达式。

部编数学八年级下册专题09一次函数与几何图形综合的七种考法(解析版)含答案

专题09 一次函数与几何图形综合的七种考法类型一、面积问题例．如图，直线AB 的表达式为364y x =-+，交x 轴，y 轴分别与B ，A 两点，点D 坐标为()4,0-点C 在线段AB 上，CD 交y 轴于点E ．(1)求点A ，B 的坐标．(2)若CD CB =，求点C 的坐标．(3)若ACE △与DOE V 的面积相等，在直线AB 上有点P ，满足DOC △与DPC △的面积相等，求点P 坐标．∵CD CB =，∴DF BF =，∵点D 坐标为()4,0-，点B 的坐标为(∴12BD =，8OB =，∴6BF =，∴2OF =，∵DOC △与DPC △的面积相等，∴点O 和点P 到距离相等，此时OP ∥∴直线OP 的解析式为35y x =，联立得：36435y x y xì=-+ïïíï=ïî，解得：x y ì=ïïíï=ïî【变式训练1】如图，直线1:1l y kx =+与x 轴交于点D ，直线2:l y x b =-+与x 轴交于点A ，且经过定点(1,5)B -，直线1l 与2l 交于点(2,)C m ．(1)填空：k =________；b =________；m =________；(2)在x 轴上是否存在一点E ，使BCE V 的周长最短？若存在，请求出点E 的坐标；若不存在，请说明理由；(3)若动点P 在射线DC 上从点D 开始以每秒1个单位的速度运动，连接AP ，设点P 的运动时间为t 秒．是否存在t 的值，使ACP △和ADP △的面积比为1:2？若存在，直接写出t 的值；若不存在，请说明理由．（3）∵点P 在射线DC 上从点∴(2,0)D -，∵(2,2)C ，∴22(22)225CD =++=，∵点P 的运动时间为t 秒．②点P 在线段DC 的延长线上，∵ACP △和ADP △的面积比为1:∴12CP DP =，∴22545DP =´=，综上：存在t 的值，使ACP △和【变式训练2】在平面直角坐标系中，O 为原点，点()4,0A ，()2,0B -，()3,2C -，点D 是y 轴正半轴上的动点，连接CD 交x 轴于点E ．(1)如图①，若点D 的坐标为()0,2，求ACD V 的面积；(2)如图②，若12ABD ABC S S =V V ，求点D 的坐标．(3)如图③，若BDE ACE S S =△△，请直接写出点D 的坐标．【变式训练3】如图，平面直角坐标系中，直线AB ：13y x b =-+交y 轴于点()0,1A ，交x 轴于点B ．过点()1,0E 且垂直于x 轴的直线DE 交AB 于点D ，P 是直线DE 上一动点，且在点D 的上方，设()1,P n ．(1)求直线AB 的解析式和点B 的坐标；(2)求ABP V 的面积（用含n 的代数式表示）；(3)当ABP V 的面积为2时，以PB 为边在第一象限作等腰直角三角形BPC ，求出点C 的坐标．，则90PEB BP CGB Ð=Ð=Ð=°，PB BC =，∴90PBE BPE Ð+Ð=°，90BPE CPG Ð+Ð=°，∴BPE CPG Ð=Ð，∴()AAS BEP PGC ≌V V ，∴2BE PG ==，2PE CG ==，∴点()3,4C ；②以PB 为底时，如图，过点C 作CG PE ^于点G ，作CH x ^轴于点H ，则90PGC CGE CHB PEB PCB Ð=Ð=Ð=°=Ð=Ð，CP CB =，∴90GCH PCB Ð=°=Ð，∴PCG BCH Ð=Ð，∴∴()AAS BCH PCG ≌V V ，∴BH PG =，CH CG =，∴BE BH PE PG +=-，即22BH BH +=-，∴0BH PG ==，∴点()3,2C ；综上，符合题意的点C 坐标为()5,2或()3,4或()3,2．类型二、最值问题例．如图，在平面直角坐标系xOy 中，一次函数()0y kx b k =+¹的图像经过()4,0A 、()0,4B 两点．(1)k =______，b =______．(2)已知()1,0M -、()3,0N ，①在直线AB 上找一点P ，使PM PN =．用无刻度直尺和圆规作出点P （不写画法，保留作图痕迹）；②点P 的坐标为______；③点Q 在y 轴上，那么PQ NQ +的最小值为______．【答案】(1)1-，4；(2)①见解析；②()1,3；③5【详解】（1）解：将()4,0A 、()0,4B 代入()0y kx b k =+¹中，得：044k b b =+ìí=î，解得；14k b =-ìí=î，故答案为：1-，4；（2）①如图，点P 即为所求；【变式训练1】在平面直角坐标系中，已知直线l经过1,32Aæöç÷èø和()3,2B-两点，且与x轴，y轴分别相交于C，D两点．(1)求直线l的表达式；V的面积等于2时，求点E的坐标；(2)若点E在直线AB上，当ODE-的值最小，则点P的坐标为______；(3)①在x轴上找一点P，使得PA PB-的值最大，则点Q的坐标为______．②在x轴上找一点Q，使得QA QB【变式训练2】如图，一次函数2y x =+的图象分别与x 轴和y 轴交于C ，A 两点，且与正比例函数y kx=的图象交于点()1,B m -．(1)求正比例函数的表达式；(2)点D 是一次函数图象上的一点，且OCD V 的面积是4，求点D 的坐标；(3)点P 是y 轴上一点，当BP CP +的值最小时，若存在，点P 的坐标是______．取点C 关于y 轴的对称点C ¢，则PC PC =CP BP C P BP C B ¢¢\+=+³，即点P 位于C B ¢与x 轴的交点时，BP +∵点(2,0)C - ，【变式训练3】如图，在平面直角坐标系内，()3,4A -，()3,2B ，点C 在x 轴上，AD x ^轴，垂足为D ，BE x ⊥轴，垂足为E ，线段AB 交y 轴于点F ．若AC BC =，ACD CBE Ð=Ð．(1)求点C 的坐标；(2)如果经过点C 的直线y kx b =+与线段BF 相交，求k 的取值范围；(3)若点P 是y 轴上的一个动点，当PA PC -取得最大值时，求BP 的长．类型三、等腰三角形存在性问题例．如图，在平面直角坐标系中，一次函数21y x =--的图像分别交x 轴、y 轴于点A 和B ．已知点C 的标为()3,0-，若点P 是x 轴上的一个动点．(1)A 的坐标是______，B 的坐标是______；(2)过点P 作y 轴的平行线交AB 于点M ，交BC 于点N ，当点P 恰好是MN 的中点时，求出P 点坐标．(3)若以点B 、P 、C 为顶点的BPC △为等腰三角形时、请求出所有符合条件的P 点坐标．【变式训练1】直线8y kx =-与x 轴、y 轴分别交于B C 、两点，且43OC OB =．(1)求OB 的长和k 的值：(2)若点A 是第一象限内直线8y kx =-上的一个动点，当它运动到什么位置时，AOB V 的面积是12？(3)在（2）成立的情况下，y 轴上是否存在点P ，使POA V 是等腰三角形？若存在，求出点P 的坐标；若不存在，请说明理由．（写过程）由题意得，12OB AD ´´=6OB =Q ，\解得，AD当21294OA OP =+==当397OA OP ==时，3P 当22AP OP =时，作2P H ^22AP OP =Q Q 2P 为线段OA 垂直平分线与【变式训练2】在平面直角坐标系中，直线MN 交x 轴正半轴于点M ，交y 轴负半轴于点()0,3N -，30Ð=°ONM ，作线段MN 的垂直平分线交x 轴于点A ，交y 轴于点B ．(1)如图1，求直线MN 的解析式和A 点坐标；(2)如图2，过点M 作y 轴的平行线l ，P 是l 上一点，若ANP S =△P 坐标；(3)如图3，点Q 是y 轴的一个动点，连接QM 、AQ ，将MAQ V 沿AQ 翻折得到1M AQ △，当1M MN △是等腰三角形时，求点Q 的坐标．过T 作TS AM ^于S ，则AT ∴22333322AS æö=-=ç÷èø，同理2315Q P y x =--：，综上：()3,6P ，(3,P -（3）①如图，当MN MM =由轴对称的性质可得：AM ∵()223323AN =+=，∴()0,1Q ．②当1NM NM =时，如图，由23AN NM AM ===，∴ANM V 为等边三角形，此时Q ，N 重合，∴()0,3Q -；③当11M M M N =时，1M 在直线∵30OAB Ð=°，【变式训练3】如图，一次函数()0y kx b k =+¹的图象与x 轴交于点C ，与y 轴交于点()0,5A ，与正比例函数12y x =的图象交于点B ，且点B 的横坐标为2，点P 为y 轴上的一个动点．(1)求B 点的坐标和k 、b 的值；(2)连接CP ，当ACP △与AOB V 的面积相等时，求点P 的坐标；(3)连接BP ，是否存在点P 使得PAB V 为等腰三角形?若存在，请求出点P 的坐标；若不存在，请说明理由．③当PA PB =时，如图2，设(0,P m 22(5)PA m =-，1PH m =-，所以PB 所以222(5)(1)2m m -=-+，解得m类型四、直角三角形存在性问题例．如图1，在平面直角坐标系xOy 中，点O 为坐标原点，直线AB :3y 4x b =+与直线AC ：9y kx =+交于点(2,)A n ，与x 轴分别交于点0()6,B -和点C ．点D 为线段BC 上一动点，将ABD △沿直线AD 翻折得到ADE V ，线段AE 交x 轴于点F ．(1)直线AC 的函数表达式．(2)当点D 在线段BO 上，点E 落在y 轴上时，求点E 的坐标．(3)若DEF V 为直角三角形，求点D 的坐标．【变式训练1】综合与探究：如图，在平面直角坐标系中，直线2y x =+与x 轴，y 轴分别交于点A ，B ，与直线11433y x =-+交于点C ．直线11433y x =-+与x 轴交于点D ，若点P 是线段AD 上的一个动点，点P 从点D 出发沿DA 方向，以每秒2个单位长度匀速运动到点A （到 A 停止运动）．设点P 的运动时间为s t ．(1)求点A 和点B 的坐标；△的面积为12时，求t的值；(2)当ACP△为直角三角形？若存在，请直接写出t的值；(3)试探究，在点P运动过程中，是否存在t的值，使ACP若不存在，请说明理由．【变式训练2】如图，平面直角坐标系中，直线AB 与x 轴交于点()30A -，与y 轴交于点()06B ，，点C 是直线AB 上的一点，它的坐标为()4m ，，经过点C 作直线CD x ∥轴交y 轴于点D ．(1)求点C 的坐标；(2)已知点P 是直线CD 上的动点，①若POC △的面积为4，求点P 的坐标；②若POC △为直角三角形，请求出所有满足条件的点P 的坐标．②Q OCP Ð一定不是直角，当90OPC Ð=°时，点P 恰好在点D ，\()04P ，，当90POC Ð=°时，，由题可得221417OC =+=，2222416OP DP DP =+=+，()221CP DP =+，Q 222CP OC OP =+，\()2211716DP DP +=++，\16DP =，\()164P ，，综上所述，所有满足条件的点P 的坐标为()04，或()164P ，．【变式训练3】如图，已知函数1y x =+的图象与y 轴交于点A ，一次函数y kx b =+的图象经过点()0,1B -，与x 轴以及1y x =+的图象分别交于点C ，D ，且点D 的坐标为()1,n ．(1)则k =______，b =______，n =______；(2)关于x ，y 的二元一次方程组y =x +1,y =kx +b的解为______；(3)求四边形AOCD 的面积；(4)在x 轴上是否存在点P ，使得以点P ，C ，D 为顶点的三角形是直角三角形，请求出点P 的坐标．①当P D DC ¢^时，22P C P D ¢¢=类型五、等腰直角三角形存在性问题例．模型建立：如图1，等腰直角三角形ABC 中，90ACB Ð=°，CB CA =，直线ED 经过点C ，过A 作AD ED ^于D ，过B 作BE ED ^于E ．(1)求证：BEC CDA V V ≌．(2)模型应用：已知直线14:43l y x =+与y 轴交与A 点，将直线1l 绕着A 点顺时针旋转45°至2l ，如图2，求2l 的函数解析式．(3)如图3，矩形ABCO ，O 为坐标原点，B 的坐标为()8,6，A 、C 分别在坐标轴上，P 是线段BC 上动点，设PC m =，已知点D 在第一象限，且是直线26y x =-上的一点，若APD △是不以A 为直角顶点的等腰直角三角形，请直接写出点D 的坐标．∵45BAC Ð=°，∴ABC V 为等腰直角三角形，由（1）得：CBD BAO V V ≌∴BD AO =，CD OB =，∵直线4:4l y x =+，∴()626122AE x =--=-由（1）得：ADE DPF △△≌∴DF AE =，即1228x x -=-，解得：4x =；∴()4,2D ；∴266212BF x x =--=-；同（1）得，APB PDF △≌△∴8AB PF ==，PB DF ==∴()88BF PF PB x =-=--=∴21216x x -=-，解得：283x =；∴2838,33D æöç÷èø；【变式训练1】综合与探究：如图1，平面直角坐标系中，一次函数334y x =-+的图像分别与x 轴、y 轴交于点A ，B ，点C 是线段OA 的中点，点D 与点C 关于y 轴对称，作直线BD ．(1)求A ，B 两点的坐标；(2)求直线BD 的函数表达式；(3)若点P 是直线BD 上的一个动点．请从A ，B 两题中任选一题作答．我选择______题．A ．如图2，连接AP ，CP ．直接写出ACP △为直角三角形时点P 的坐标．B ．如图3，连接CP ，过点P 作PQ x ^轴于点Q ．直接写出CPQ V 为等腰直角三角形时点P 的坐标．【变式训练2】如图，平面直角坐标系中，直线1:3AB y x b =-+交y 轴于点()0,1A ，交x 轴于点B ．直线1x =交AB 于点D ，交x 轴于点E ，P 是直线1x =上一动点，且在点D 的上方，设()1,P n ．(1)求直线AB 的解析式；(2)当2ABP S =△时，在第一象限内找一点C ，使BCP V 为等腰直角三角形，求点C 的坐标．∵1x =时，12133y x =-+=，P 在点∴23PD n =-，∴12PAB APD BPD S S S PD AM =+=×+V V V ∵2ABP S =△，3∵90,45CPB EPB Ð=°Ð=°，∴45NPC EPB Ð=Ð=°．又∵90,CNP PEB BP PC Ð=Ð=°=，∴CNP BEP ≌V V ，∴2PN =NC =EB =PE =，∴224NE NP+PE ==+=，∴()3,4C ；若90,PBC BP BC Ð=°=，如图，过点C 作CF x ^轴于点F ．∵90,45PBC EBP Ð=°Ð=°，∴45CBF PBE Ð=Ð=°．又∵90,CFB PEB BC BP Ð=Ð=°=，∴CBF PBE ≌V V ．∴2BF CF PE EB ====，∴325OF OB BF =+=+=，∴()5,2C ；若90,PCB CP EB Ð=°=，如图，∴45CPB EBP Ð=Ð=°，∵,,CP EB CPB EBP BP BP =Ð=Ð=，∴PCB PEB ≌V V ，∴2PC CB PE EB ====，∴()3,2C ；∴点C 的坐标是()3,4或()5,2或()3,2．【变式训练3】如图，在平面直角坐标系xOy 中，直线AP 交x 轴于点(),0P p ，与y 轴交于点()0,A a ，且a ，p ()230a +=．(1)求直线AP 的解析式；(2)如图1，直线2x =-与x 轴交于点N ，点M 在x 轴上方且在直线2x =-上，若MAP △的面积等于6，请求出点M 的坐标；(3)如图2，已知点()2,4C -，若点B 为射线AP 上一动点，连接BC ，在坐标轴上是否存在点Q ，使BCQ △是以BC 为底边，点Q 为直角顶点的等腰直角三角形，若存在，请直接写出点Q 坐标；若不存在，请说明理由．∵MD AP P ，MAP △的面积等于∴DAP V 的面积等于6，∴162A DP y ××=，即12DP ×∴4DP =，∴()3,0D -，y∴,33OE t BE t ==-，∵BCQ △是以BC 为底边的等腰直角三角形，∴BQ CQ =，90BQC Ð=∴90BQE NQC Ð=°-Ð=又∵BEQ QNC Ð=Ð，∴()AAS BEQ QNC V V ≌，∴BG t =，33OG t =-，∴BT t =，33OT t =-，同②可证CFQ QTB V V ≌∴QF BT t ==，QT CF =∴OQ OT QT OF =+=+∴52t =，∴513422OQ =+=，类型六、平行四边形存在性问题例．在平面直角坐标系xOy 中，直线36y x =+分别与x 、y 轴相交于A 、B 两点，将线段AB 绕点A 顺时针旋转90°得到线段AC ．连接BC 交x 轴于点D ．(1)求点C 的坐标；(2)P 为x 轴上的动点，连接PB ，PC ，当PB PC -的值最大时，求此时点P 的坐标．(3)点E 在直线AC 上，点F 在x 轴上，若以B 、D 、E 、F 为顶点的四边形是平行四边形，请直接写出点F 的坐标；【答案】(1)点C 的坐标为()4,2-(2)()6,0P (3)点F 的坐标为()17,0-或()13,0或()23,0【详解】（1）解：令0y =，则2x =-，()2,0A \-，令0x =，则6y =，()0,6B \，26OA BO \==，，过点C 作CH x ^轴于H ，9090CAD BAO BAO ABO ÐÐÐÐ+=°+=°Q ，，CAD ABO ÐÐ\=，90AHC BOA ÐÐ\==°，由旋转得AB AC =，()AAS ABO CAH \V V ≌，26CH OA AH BO \====，，4OH AH OA \=-=，\点C 的坐标为()4,2-；（2）作点C 关于x 轴的对称点C ¢，连接BC ¢延长交x 轴于点P ，则点P 就是所求的最大值点，\()4,2C ¢设直线BC ¢的解析式为y kx b =+，\642b k b =ìí+=î，解得16k b =-ìí=î，6y x \=-+，()6,0P \；（3）()()()2,04,20,6A C B --Q ，，，设直线AC 的解析式为y mx n =+，则2042m n m n -+=ìí+=-î【变式训练1】如图1，在平面直角坐标系中，直线AB 与x 轴交于点(),0A m ，与y 轴交于点()0,B n ，且m n ，满足：()260m n n ++-=．(1)求：AOB S V 的值；(2)D 为OA 延长线上一动点，以BD 为直角边作等腰直角BDE V ，连接EA ，求直线EA 与y 轴交点F 的坐标；(3)在（2）的条件下，当2AD =时，在坐标平面内是否存在一点P ，使以B E F Р、、、为顶点的四边形是平行四边形，如果存在，直接写出点Р的坐标，若不存在，说明理由．∵EDB △为等腰直角三角形，∴,90DE DB EDB =Ð=°，∴18090EDG ODB Ð+Ð=°-。

(完整版)一次函数压轴题经典.docx

一次函数压轴题训练典型例题题型一、 A 卷压轴题一、 A 卷中涉及到的面积问题例 1、如图，在平面直角坐标系xOy 中，一次函数 y 12x 2 与 x 轴、 y 轴分别相交于点3A 和点B ，直线 y 2 kx b (k0) 经过点 C （ 1，0）且与线段 AB 交于点 P ，并把△ ABO 分成两部分．（ 1）求△ ABO 的面积；（ 2）若△ ABO 被直线 CP 分成的两部分的面积相等，求点 P 的坐标及直线CP 的函数表达式。

yy 1B PO CAxy 2练习 1、如图，直线 l 1 过点 A （ 0， 4），点 D （ 4， 0），直线 l 2 ： y1x 1与 x 轴交于点 C ，2两直线 l 1 ， l 2 相交于点 B 。

l 1y（1）、求直线 l 1 的解析式和点 AB 的坐标；l 2（2）、求△ ABC 的面积。

BCODx二、 A 卷中涉及到的平移问题例 2、正方形 ABCD的边长为4，将此正方形置于平面直角坐标系中，使AB边落在X轴的正半轴上，且 A 点的坐标是（1， 0）。

4 8①直线 y=3x- 3经过点 C，且与 x 轴交与点E，求四边形AECD的面积；②若直线 l 经过点E且将正方形ABCD分成面积相等的两部分求直线l 的解析式，③若直线 l1经过点F3 .0 且与直线y=3x平行,将②中直线l沿着y轴向上平移2个单位23交 x 轴于点M , 交直线l1于点N , 求NMF 的面积.练习 1、如图，在平面直角坐标系中，直线l1： y4x 与直线 l2： y kx b 相交于3点 A，点 A 的横坐标为 3，直线l2交y轴于点 B，且OA 1OB 。

2（1）试求直线l 2函数表达式。

（6分）（2）若将直线l 1沿着x轴向左平移3个单位，交y 轴y 于点 C，交直线l2于点 D；试求△ BCD的面积。

（4分）。

L 2l 1A1x题型二、 B 卷压轴题一、一次函数与特殊四边形例 1、如图，在平面直角坐标系中，点A、B 分别在 x 轴、y 轴上，线段OA、 OB的长 (0A<OB)2x y2x 与直线是方程组的解，点 C是直线y3x y6AB的交点，点 D 在线段 OC上， OD=25(1)求点 C 的坐标；(2)求直线 AD的解析式；(3)P是直线AD上的点，在平面内是否存在点Q，使以 0、A、P、Q为顶点的四边形是菱形?若存在，请直接写出点Q的坐标；若不存在，请说明理由．练习 1、. 如图 , 在平面直角坐标系xOy 中,已知直线PA是一次函数y=x+m( m>0)的图象,直线 PB是一次函数y3x n(n > m )的图象,点P是两直线的交点, 点 A、B、C、Q分别是两条直线与坐标轴的交点。

一次函数与几何综合一

一次函数与几何综合(一)标模块一一次函数与线段长例1(2017江岸区八下期末)如图，直线l: y=2x+4.(1)①直接写出直线l关于y轴对称的直线l i的解析式：；②直接写出直线l向右平移2个单位得到的直线12的解析式： ;(2)在(1)的基础上，点M是x轴上一点，过点M作x轴的垂线交直线l i于点Q、交直线l2于点P,若PM = 2PQ,求M 点的坐标.例2(2017斫口区八下期末)图1中两条经过原点O的射线组成的图形E表示y关于x的函数关系式.(1)直接写出图形E表示的函数解析式；(2)如图2,过直线y=3上一点P(m, 3)作x轴的垂线交图形E于点C,交直线y=- x- 1于点D.①若m>0,试比较PC与PD的大小，并证明你的结论；②若CD <3,求m的取值范围.图图2挑战压轴题(2017黄陂区八下期末第24题)如图，直线l i经过点P(2, 2),分别交x轴、y轴于点A(4, 0)、B.(1)求直线l i的解析式；(2)点C为x轴负半轴上一点，过点C的直线l2：y=mx+ n交线段AB于点D.①如图1,当点D恰与点P重合时，点Q(t, 0)为x轴上一动点，过点Q作QM，x轴，分别交直线11、12于点M、N,若m= - , MN = 2MQ,求t 的值；2②如图2,若BC=CD,试判断m、n之间的数量关系并说明理由.模块二一次函数与特殊三角形知识导航1.等腰直角三角形一三垂直全等如图，△ ABC中，AB = AC, / BAC=90°,可构造如图所示的三垂直全等模型，“△ ACD^A BAE"，从而可以转化为水平线段长度与点坐标的基本计算.若已知等腰直角三角形三个顶点坐标中的两个便可通过此方法求第三顶点坐标.2.等腰三角形的存在性一两圆一中垂已知A、B为定点，C为动点，△ ABC为等腰三角形，则分下列情况：(1)若CA = CB,则点C在AB中垂线上(不与AB共线).(2)若AC = AB,则点C在以A为圆心，AB为半径的圆上(不与点B重合).(3)若BA=BC,则点C在以B为圆心，AB为半径的圆上(不与点A重合).3.直角三角形的存在性一两垂一圆已知A、B为定点，C为动点，△ ABC为直角三角形，则分下列情况：(1)若/ CAB = 90°,则点C在过点A且垂直AB的直线上(不与点A重合).(2)若/ CBA = 90°,则点C在过点B且垂直AB的直线上(不与点B重合).(3)若/ ACB = 90°,则点C在以AB为直径的圆上(不与点A、B重合).八下会把特殊三角形的顶点放在一次函数背景下讨论、计算.例3如图，在直角坐标系中，矩形OABC的两边在坐标轴上，其中点B的坐标为(4, 3),过点A的直线AD 的解析式为y=2x+3,点P是直线AD上一动点，点Q是线段BC(包才B, C两点)上一动点.若AP = AQ 且AP^AQ,求点P的坐标及直线AQ的解析式；练习如图1,在平面直角坐标系中，A(a, 0), B(0, b),且b= "a -4+”5 +16a 2(1)求直线AB的解析式；(2)如图2,若点M为直线y=mx在第一象限上一点，且^ ABM是等腰直角三角形，求m.图1 图2例4在平面直角坐标系中，直线y=kx— k经过一定点P.(1)直接写出P点坐标；(2)在y轴上有一点A(0, 2),当k = 2时，将直线y=kx—k向上平移2个单位得到直线1,在直线l上找点C,使得△ ACO为等腰三角形，求点C的坐标.练习3 ........................................... 如图，在平面直角坐标中，一次函数y= — x+ 2的图象与x轴交于A点，与y轴交于B点，在x轴上是3否存在点P,使^ PAB为等腰三角形？若存在，求出符合条件的P点的坐标；若不存在，请说明理由.3 ............... ............................ 例5如图，在平面直角坐标系中，直线y=- ^r-x+ 6与x轴、y轴分别交于B、A点，已知点C从点A出3发沿AO以每秒1cm的速度向点O运动，同时点D从点B出发沿BA以每秒2cm的速度向点A运动，运动时间为t秒(0<t<6),过点D作DELOB于点E.连接DC,当t为何值时，△ DEC为直角三角形？模块三一次函数与特殊四边形例61如图，已知函数y=- -x+ b的图象与x轴、y轴分别交于点A, B,与函数y=x的图象交于点E,点E的3横坐标为3.⑴求点A的坐标.1(2)在x轴上有一点F(a, 0),过点F作x轴的垂线，分别交函数y=—-x+b和y=x的图象于点C、D.若3以点B, O, C, D为顶点的四边形为平行四边形，求a的值.练习如图，在平面直角坐标系xOy中，直线y=kx+b交x轴于点A,交y轴于点B,线段AB的中点E的坐标为(2, 1).⑴求k、b的值；(2)P为直线AB上一点，PC^x轴于点C, PD^y轴于点D,若四边形PCOD为正方形，求点P的坐标.例7(2017东湖高新区八下期末)平面直角坐标系中，直线y=ax+b与x轴分别交于点B、C,且a、b满足a= *6-b + J b — 6 +3,不论k为何值，直线l: y=kx—2k都经过x轴上一定点A.(1)a =, b =, 点A 的坐标为;(2)如图1,当k= 1时，将线段BC沿某个方向平移，使点B、C对应的点M、N恰好在直线l和直线y= 2x—4上.请你判断四边形BMNC的形状，并说明理由；(3)如图2,当k的取值发生变化时，直线l: y=kx—2k绕着点A旋转，当它与直线y=ax+b相交的夹角为450时，求出相应的k的值.图1 图2拓展1平面直角坐标系中，直线li： y= —/x+3与x轴交于点A,与y轴交于点B,直线12：y=kx+2k与x轴父于点C,与直线l i交于点P.(1)当k=1时，求点P的坐标；(2)如图1,点D为PA的中点，过点D作DE^x轴于点巳交直线12于点F,若DF=2DE,求k的值.(3)如图2,点P在第二象限内，PM^x轴于M,以PM为边向左作正方形PMNQ, NQ的延长线交直线11 于点R,若PR= PC,求点P的坐标.课后作业A基础巩固1.已知点A的坐标是(2, 2),若点P在x轴上，且^ APO是等腰三角形，则点P的坐标为 .1 2.如图，P是y轴上一动点，是否存在平行于y轴的直线x=t(t>0),使它与直线y=x和直线y=-2x+2分别交于点D、E(E在D的上方)，且4 PDE为等腰直角三角形.若存在，求t的值及点P的坐标；若不存在，请说明理由.3.如图，直线y=kx+b与坐标轴分别交于点A, B,且A(—4, 0), &AOB =4.(1)求直线y= kx+ b的解析式；(2)若点P为直线y=kx+b上一点，PC^x轴于C, PD^y轴于D,若四边形PCOD为正方形，求点P坐标.4 .如图，在平面直角坐标系中，直线 y=- — x+ 6与x 轴、y 轴分别交于A 、B 点，已知点C 从点A 出 3发沿AO 以每秒1cm 的速度向点O 运动，同时点D 从点B 出发沿BA 以每秒2cm 的速度向点A 运动，运动时间为t 秒(0<t<6),过点D 作DELOB 于点E.(1)①直接写出/ ABO 的度数为②证明在C 、D 运动过程中，四边形 ACED 是平行四边形; 5 . (2017洪山区八下期末)3y=— —x+b 分别与x 轴、y 轴父于点 A 、B,且点A 坐标为(8, 0),点 4C 为AB 的中点.⑴写出点B 的坐标(2)如图1,点P 为直线AB 上的一个动点，过点 P 作x 轴的垂线，与直线 OC 交于点Q,设点P 的横坐标为m,线段PQ 的长度为d,求d 与m 的函数解析式(请直接写出自变量 m 的取值范围)；数学故事为什么2187是个幸运的数字尽管不符合常规理解的“幸运”含义，2187这个数字仍有一系列让人吃惊的特征.在纪念马丁加德纳 100周年诞辰之际，我们来回顾他在 1997年为《数学信使》(MathematicalIntelligencer)写的一篇文章.在这篇文章中，他问他想象中的好友欧文约书亚矩阵博士(Dr. Irving JoshuaMatrix)关于数字2187的问题.欧文约书亚矩阵博士是“世界最著名的数字命理学家”，也是在《科学美国人》(Scientific American )"数学游戏”(Mathematical Games)专栏中经常出现的角色；而 2187,则是加德纳儿时在美国俄克拉荷马州(Okla)塔尔萨(Tulsa)老家的门牌号码.矩阵博士立刻列举了一系列关于 2187的事实，这让加德纳感到非常兴奋： 2187,是3的7次方，它的.三进制写法是 10000000; 9999减去2187等于7812,恰好与其顺序相反；21乘以87等于1827, 27乘以81又刚好等于2187.“每个数字都有数不尽的独特的特征，”矩阵博士点评说，同时补充道， 2187也是一个幸运数.幸运数是素数的远亲，素数是只能被1和它本身整除的正整数.尽管这两者在很多方面都不同，但它们都可以利用被称为“筛法”的方法得到.希腊数学家埃拉托斯特尼 (Eratosthenes)设计了一种在正整数序列中寻找素数的方法一一著名的埃拉托斯特尼筛法：首先删除所有除2以外2的倍数，然后删除3的倍数，然后是5, 7, 11等等.这样不断删除到无穷大，就可以得到所有素数.波兰裔美国数学家斯塔尼斯拉夫乌拉姆(Stanislaw Ulam)在20世纪50年代中期开发出了另一种筛法：同样是从正整数序列开始，先将数列中的第 2n 个数（偶数）删除，只留下奇数；这样剩下的数列中第二项是 3，因此将新数列的第 3n 个数删除；(2)当 t = 时，四边形ACED 是菱形.如图，在平面直角坐标系中，直线(3)如图2,当点P 在线段 AB 上，在第一象限内有一点 N,使得四边形 OBNP 为菱形，求出N 点坐标.B 综合训练再剩下的新数列中的第三项为7，因此将新数列的第7n 个数删除；再剩下的新数列中的第四项为9，因此将新数列的第9n 个数删除；这样继续下去，最终有一些数永远地逃离了被删除的命运而留下来，这就是为什么乌拉姆把它们称作“幸运数”．幸运数和素数有一些由奇妙的筛法得到的数字的共同特征．比如说，在小于100 的数中，有25 个素数和23 个幸运数，其中有八对孪生素数（之差为 2 的两个素数）以及七对孪生幸运数．关于素数，尚未解决的最有名的问题之一就是哥德巴赫猜想——任一大于2 的偶数，都可表示成两个素数之和．同样另一个未解决的问题是一个相似的命题——任一大于2 的偶数，都可表示成两个幸运数之和．关于2187，还有另一个有趣的事实——如下所示，等号右边的数字之和等于左边与2187 相加的排列不同的数字之和．2187 + 1234=34212187+12345= 145322187 + 123456= 1256432187 + 1234567= 12367542187+ 12345678=123478652187+ 123456789= 123458976。

一次函数综合题(解析版)--2024年中考数学压轴题专项训练

一次函数综合题通用的解题思路：(1)一次函数与几何图形的面积问题首先要根据题意画出草图，结合图形分析其中的几何图形，再求出面积．(2)一次函数的优化问题通常一次函数的最值问题首先由不等式找到x 的取值范围，进而利用一次函数的增减性在前面范围内的前提下求出最值．(3)用函数图象解决实际问题从已知函数图象中获取信息，求出函数值、函数表达式，并解答相应的问题．1(2024•鼓楼区一模)如图，直线y =-3x +6与⊙O 相切，切点为P ，与x 轴y 轴分别交于A 、B 两点．⊙O 与x 轴负半轴交于点C ．(1)求⊙O 的半径；(2)求图中阴影部分的面积．【分析】(1)由OP =OA ⋅sin60°，即可求解；(2)由图中阴影部分的面积=S 扇形COP -S ΔPOC ，即可求解．【解答】解：(1)对于直线y =-3x +6，令y =-3x +6=0，则x =23，即OA =23，由一次函数的表达式知，OB =6，则tan ∠BAC =OB AO =623=3，则∠BAC =60°连接OP ，则OP ⊥AB ，则OP =OA ⋅sin60°=23×32=3；(2)过点P 作PH ⊥AC 于点H ，∵∠POH =30°，则∠POC =150°，PH =12OP =32，则图中阴影部分的面积=S 扇形COP -S ΔPOC =150°360°×π×32-12×3×32=15π-94．【点评】本题考查了一次函数和圆的综合运用，涉及到圆切线的和一次函数的性质，解直角三角形，面积的计算等，综合性强，难度适中．2(2023•宿豫区三模)如图①，在平面直角坐标系中，直线l 1:y =x +1与直线l 2:x =-2相交于点D ，点A 是直线l 2上的动点，过点A 作AB ⊥l 1于点B ，点C 的坐标为(0,3)，连接AC ，BC ．设点A 的纵坐标为t ，ΔABC 的面积为s ．(1)当t =2时，求点B 的坐标；(2)s 关于t 的函数解析式为s =14t 2+bt -54t -1或t 5 a t +1 t -5 (-1<t <5)，其图象如图②所示，结合图①、②的信息，求出a 与b 的值；(3)在直线l 2上是否存在点A ，使得∠ACB =90°，若存在，请求出此时点A 的坐标；若不存在，请说明理由．【分析】(1)解法一：先根据t =2可得点A (-2,2)，因为B 在直线l 1上，所以设B (x ,x +1)，利用y =0代入y =x +1可得G 点的坐标，在Rt ΔABG 中，利用勾股定理列方程可得点B 的坐标；解法二：根据可以使用y =x +1与x 轴正半轴夹角为45度来解答；(2)先把(7,4)代入s =14t 2+bt -54中计算得b 的值，计算在-1<t <5范围内图象上一个点的坐标值：当t =2时，根据(1)中的数据可计算此时s =94，可得坐标2,94，代入s =a (t +1)(t -5)中可得a 的值；(3)存在，设B (x ,x +1)，如图5和图6，分别根据两点的距离公式和勾股定理列方程可解答．【解答】解：(1)解法一：如图1，连接AG ，当t =2时，A (-2,2)，设B (x ,x +1)，在y =x +1中，当x =0时，y =1，∴G (0,1)，∵AB ⊥l 1，∴∠ABG =90°，∴AB 2+BG 2=AG 2，即(x +2)2+(x +1-2)2+x 2+(x +1-1)2=(-2)2+(2-1)2，解得：x 1=0(舍)，x 2=-12，∴B -12，12；解法二：如图1-1，过点B 作BE ⊥x 轴于E ，过点A 作AH ⊥BE 于H ，当x =0时，y =1，当y =0时，x +1=0，则x =-1，∴OF =OG =1，∵∠GOF =90°，∴∠OGF =∠OFG =45°，∴BE =EF ，∵∠ABD =90°，∴∠ABH =∠BAH =45°，∴ΔABH 是等腰直角三角形，∴AH =BH ，当t =2时，A (-2,2)，设B (x ,x +1)，∴x +2=2-(x +1)，∴x =-12，∴B -12，12 ；(2)如图2可知：当t =7时，s =4，把(7,4)代入s =14t 2+bt -54中得：494+7b -54=4，解得：b =-1，如图3，过B 作BH ⎳y 轴，交AC 于H ，由(1)知：当t =2时，A (-2,2)，B -12，12 ，∵C (0,3)，设AC 的解析式为：y =kx +n ，则-2k +n =2n =3 ，解得k =12n =3 ，∴AC 的解析式为：y =12x +3，∴H -12，114，∴BH =114-12=94，∴s=12BH⋅|x C-x A|=12×94×2=94，把2,9 4代入s=a(t+1)(t-5)得：a(2+1)(2-5)=94，解得：a=-1 4；(3)存在，设B(x,x+1)，当∠ACB=90°时，如图5，∵∠ABD=90°，∠ADB=45°，∴ΔABD是等腰直角三角形，∴AB=BD，∵A(-2,t)，D(-2,-1)，∴(x+2)2+(x+1-t)2=(x+2)2+(x+1+1)2，(x+1-t)2=(x+2)2，x+1-t=x+2或x+1-t=-x-2，解得：t=-1(舍)或t=2x+3，RtΔACB中，AC2+BC2=AB2，即(-2)2+(t-3)2+x2+(x+1-3)2=(x+2)2+(x+1-t)2，把t=2x+3代入得：x2-3x=0，解得：x=0或3，当x=3时，如图5，则t=2×3+3=9，∴A(-2,9)；当x=0时，如图6，此时，A(-2,3)，综上，点A的坐标为：(-2,9)或(-2,3)．【点评】本题考查二次函数综合题、一次函数的性质、等腰直角三角形的判定和性质、三角形的面积、两点间距离公式等知识，解题的关键是灵活运用所学知识解决问题．3(2023•溧阳市一模)如图1，将矩形AOBC放在平面直角坐标系中，点O是原点，点A坐标为(0,4)，点B坐标为(5,0)，点P是x轴正半轴上的动点，连接AP，ΔAQP是由ΔAOP沿AP翻折所得到的图形．(1)当点Q落在对角线OC上时，OP=　165　；(2)当直线PQ经过点C时，求PQ所在的直线函数表达式；(3)如图2，点M是BC的中点，连接MP、MQ．①MQ的最小值为；②当ΔPMQ是以PM为腰的等腰三角形时，请直接写出点P的坐标．【分析】(1)通过Q 点在OC 上，可以通过∠BOC 的三角函数和∠OAP 的三角函数来导出对应的边的关系，求得结果；(2)通过直角ΔAQC 中，得到QC 的长度，然后通过OP =PQ =x ，可以在Rt ΔBCP 中，得到对应的x 值然后求出结果；(3)通过QA =OA =4，可得出Q 点的运动轨迹，是以A 点为圆心，4为半径长度的圆弧，从而可知，MA 的连线上的Q 点为最短的MQ 长度，通过分类讨论，PM =PQ ，PM =QM ，PQ =QM 来求得对应的P 的坐标．【解答】解：(1)如图1，∵∠OAP +∠AOE =90°，∠BOC +∠AOE =90°，∴∠OAP =∠BOC ，又∵∠AOP =∠OBC =90°，∴ΔOAP ∽ΔBOC ，∴OP BC =OA OB ，即OP 4=45，∴OP =165，故答案为：165；(2)如图，∵AQ ⊥PQ ，∴∠AQC =90°，∴QC =AC 2-AQ 2=52-42=3，∵AQ =AO =4，设OP =PQ =x ，则CP =3+x ，PB =5-x ，∴CP 2=BP 2+BC 2，(3+x )2=(5-x )2+42，x =2，∴P 点的坐标为(2,0)，将P (2,0)和C (5,4)代入y =kx +b 中，0=2k +b 4=5k +b ，解得：k =43b =-83，∴PQ 所在直线的表达式为：y =43x -83；(3)如图，①∵AQ =AO =4，∴Q 点的运动轨迹，是以A 为圆心，4为半径的圆弧，∴MQ 的最小值在AM 的连线上，如图，MQ ′即为所求，∵M 是BC 中点，CM =12BC =2，∴AM =52+22=29，MQ ′=MA -AQ ′=29-4，故答案为：29-4；②如图，设OP =PQ =x ，BP =5-x ，∴PM 2=(5-x )2+22=x 2-10x +29，当PM =PQ 时，PM 2=PQ 2，∴x 2-10x +29=x 2，x =2910，∴P 2910，0，当MP =MQ 时，如图，若点Q 在AC 上，则AQ =OA =4，∵MP =MQ ，MB =MC ，∠PBM =∠QCM ，∴ΔPMB ≅ΔQMC (HL )，∴PB =QC ，QC =AC -AQ =5-4=1，∴PB =1，∴OP =BO -PB =5-1=4，∴P (4,0)；若点Q 在AC 上方时，由对称性可知OM =MQ ，∵MQ =MQ ，∴MO =MP ，∴P (10,0)；当MQ =PQ 时，不符合题意，不成立，故P 点坐标为P 2910，0或P (4,0)或(10,0)．【点评】本题考查一次函数的图象及应用，通过一次函数坐标图象的性质，三角函数的性质，全等三角形的性质和勾股定理，来求得对应的解．4(2022•启东市模拟)我们知道一次函数y =mx +n 与y =-mx +n (m ≠0)的图象关于y 轴对称，所以我们定义：函数y =mx +n 与y =-mx +n (m ≠0)互为“M ”函数．(1)请直接写出函数y =2x +5的“M ”函数；(2)如果一对“M ”函数y =mx +n 与y =-mx +n (m ≠0)的图象交于点A ，且与x 轴交于B ，C 两点，如图所示，若∠BAC =90°，且ΔABC 的面积是8，求这对“M ”函数的解析式；(3)在(2)的条件下，若点D 是y 轴上的一个动点，当ΔABD 为等腰三角形时，请求出点D 的坐标．【分析】(1)根据互为“M ”函数的定义，直接写出函数y =2x +5的“M ”函数；(2)现根据已知条件判断ΔABC 为等腰直角三角形，再根据互为“M ”函数的图象关于y 轴对称，得出OA =OB =OC ，再根据函数解析式求出点A 、B 、C 的坐标，再根据ΔABC 的面积是8求出m 、n 的值，从而求出函数解析式；(3)ΔABD 为等腰三角形，分以A 为顶点，以B 为顶点，以D 为顶点三种情况讨论即可．【解答】(1)解：根据互为“M ”函数的定义，∴函数y =2x +5的“M ”函数为y =-2x +5；(2)解：根据题意，y =mx +n 和y =-mx +n 为一对“M 函数”．∴AB =AC ，又∵∠BAC =90°，∴ΔABC 为等腰直角三角形，∴∠ABC =∠ACB =45°，∵OB =OC ，∴∠BAO =∠CAO =45°，∴OA =OB =OC ，又∵S ΔABC =12×BC ×AO =8且BC =2AO ，∴AO =22，∵A 、B 、C 是一次函数y =mx +n 与y =-mx +n (m ≠0)的图象于坐标轴的交点，∴A (0,n )，B -n m ，0 ，C n m ，0，∵OA =OB =n ，∴n m=22，∴m =1，∴y =x +22和y =-x +22；(3)解：根据等腰三角形的性质，分情况，∵AO =BO =22，∴AB =4，由(2)知，A (0，22)，B (-22，0)，C (22，0)，∴①以A 为顶点，则AB =AD ，当点D 在点A 上方时，AD =22+4，当点D 在点A 下方时，AD =22-4，∴D 1(0，22+4)，D 2(0，22-4)，②以B 为顶点，则BA =BD ，此时点D 在y 轴负半轴，∴D 3(0,-22)，③以D 为顶点，则DA =DB ，此时D 为坐标原点，∴D 4(0,0)．∴D 点坐标为D 1(0，22+4)，D 2(0，22-4)，D 3(0,-22)，∴D 4(0,0)．【点评】本题考查一次函数的综合应用，以及新定义、等腰三角形的性质等知识，关键是理解新定义，用新定义解题．5(2024•新北区校级模拟)如图①，动点P 从矩形ABCD 的顶点A 出发，以v 1的速度沿折线A -B -C 向终点C 运动；同时，一动点Q 从点D 出发，以v 2的速度沿DC 向终点C 运动，当一个点到达终点时，另一个点也停止运动．点E 为CD 的中点，连接PE ，PQ ，记ΔEPQ 的面积为S ，点P 运动的时间为t ，其函数图象为折线MN -NF 和曲线FG (图②)，已知，ON =4，NH =1，点G 的坐标为(8,0)．(1)点P 与点Q 的速度之比v 1v 2的值为　85　；AB AD的值为；(2)如果OM =15．①求线段NF 所在直线的函数表达式；②求FG 所在曲线的函数表达式；③是否存在某个时刻t ，使得S ≥154？若存在，求出t 的取值范围：若不存在，请说明理由．【分析】(1)由函数图象可知t =3时，Q 与E 重合，t =4时，P 与B 重合，t =6时，P 与C 重合，则Q 的速度v 2=DE 4，P 的速度v 1=AB 4，从而得出答案；(2)①当t =0时，P 与A 重合，Q 与D 重合，此时S ΔADE =2，可得AD =BC =DE =15，AB =CD =53AD =10，从而得出点P 与Q 的速度，即可得出点F 的坐标，利用待定系数法可得答案；②设FG 所在的曲线的数解析式为S =a (t -6)2+k (a ≠0)，把F 5,154，G (8,0)代入解析式求得a ，k 值即可求解答；③利用待定系数法求出直线MN 的函数解析式，当S =154时，可得t 的值，根据图象可得答案．【解答】解：(1)∵ON =4，NH =1，G (8,0)，∴N (4,0)，H (5,0)，由图象可知：t =4时，Q 与E 重合，t =5时，P 与B 重合，t =8时，P 与C 重合，∴Q 的速度v 2=DE 4，P 的速度v 1=AB 5，∵四边形ABCD 是矩形，∴AB =CD ，AD =BC ，∵E 为CD 的中点，∴DE =12CD =12AB ，∴v 1v 2=AB5DE 4=AB 5⋅4DE =85，∵P 从A 到B 用了5秒，从B 到C 用了3秒，∴AB =5v 1，BC =3v 1，∴AB =53BC ，∴AB :AD 的值为53，故答案为：85，53；(2)①∵OM =15，∴M (0,15)，由题知，t =0时，P 与A 重合，Q 与D 重合，∴S ΔEPQ =12AD ⋅DE =15，∵AB :AD =53，DE =12AB ，∴DE =56AD ，∴12AD ⋅56AD =15，∴AD =BC =6(舍去负值)，∴AB =CD =53AD =10，∴v 2=DE 4=54，当t =5时，DQ =v 2t =54×5=254，∴QE =DQ -DE =254-5=54，此时P 与B重合，∴S ΔEPQ =12EQ ⋅BC =12×54×6=154，∴F 5,154 ，设直线NF 的解析式为S =kt +b (k ≠0)，将N (4,0)与F 5,154 代入得：4k +b =05k +b =154，∴k =154b =-15 ，∴线段NF 所在直线的函数表达式为S =154t -15(4<t ≤5)；②设FG所在的曲线的数解析式为S=1254t-5(16-2t)=-54t2+15t-40，∴FG所在的曲线的函数解析式为S=-54t2+15t-40(5≤t≤8)；③存在，分情况讨论如下：当Q在DE上，P在AB上时，∵直线MN经过点M(0,15)，N(4,0)，可求得直线MN的解析式为S=-54t+15(0≤t≤4)，当s=154时，-154t+15=154，∴x=3，∵s随x的增大而减小，∴当0≤x≤3时，S≥154，当Q在CE上，P在BC上时，直线NF的解析式为S=154t-15(4<t≤5)；由F5,15 4知：当t=5时，S=154，当S=154时，-54t2+15t-40=154，∴t=7或5，由图象知：当5≤x≤7，x的取值范围为0≤t≤3或5≤t≤7．【点评】本题是一次函数综合题，主要考查了待定系数法求函数解析式，三角形的面积，矩形的性质等知识，理解函数图象中每一个拐点的意义是解题的关键．6(2024•梁溪区校级模拟)在平面直角坐标系xOy 中，二次函数y =-ax 2+3ax +4a 的图象与x 轴交于A 、B 两点(点A 在点B 的左侧)，与y 轴正半轴交于点C ，直线y =12x 交于第一象限内的D 点，且ΔABC 的面积为10．(1)求二次函数的表达式；(2)点E 为x 轴上一点，过点E 作y 轴的平行线交线段OD 于点F ，交抛物线于点G ，当GF =5OF 时，求点G 的坐标；(3)已知点P (n ,0)是x 轴上的点，若点P 关于直线OD 的对称点Q 恰好落在二次函数的图象上，求n 的值．【分析】(1)在y =-ax 2+3ax +4a 中，令y =0得A (-1,0)，B (4,0)，根据ΔABC 的面积为10，即得OC =4，C (0,4)，用待定系数法即得二次函数的表达式为y =-x 2+3x +4；(2)设E (m ,0)，则F m ,12m ，G (m ,-m 2+3m +4)，由GF =5OF ，可得-m 2+52m +4=5×52m ，即可解得G (2,6)；(3)连接PQ 交直线OD 于K ，过Q 作QT ⊥x 轴于T ，设Q (r ,s )，可得K n +r 2，s 2 ，即得s 2=12×n +r 2，n +r =2s ①，又r 2+s 2=n 2，(n +r )(n -r )=s 2②，可解得r =35n ，s =45n ，故Q 35n ，45n ，代入y =-x 2+3x +4得45n =-35n 2+3×35n +4，解得n =5或n =-209．【解答】解：(1)如图：在y =-ax 2+3ax +4a 中，令y =0得-ax 2+3ax +4a =0，解得x =4或x =-1，∴A (-1,0)，B (4,0)，∴AB =5，∵ΔABC 的面积为10，∴12AB ⋅OC =10，即12×5⋅OC =10，∴OC =4，∴C (0,4)，把C (0,4)代入y =-ax 2+3ax +4a 得：4a =4，∴a =1，∴二次函数的表达式为y =-x 2+3x +4；(2)如图：设E (m ,0)，则F m ,12m ，G (m ,-m 2+3m +4)，∴OF =m 2+12m 2=52m ，GF =-m 2+3m +4-12m =-m 2+52m +4，∵GF =5OF ，∴-m 2+52m +4=5×52m ，解得m =2或m =-2(舍去)，∴G (2,6)；(3)连接PQ 交直线OD 于K ，过Q 作QT ⊥x 轴于T ，如图：∵P (n ,0)关于直线对称点为Q ，∴OQ =OP =|n |，K 是PQ 中点，设Q (r ,s )，∴K n +r 2，s 2，∵K 在直线y =12x 上，∴s 2=12×n +r 2，整理得：n +r =2s ①，∵OT 2+QT 2=OQ 2，∴r 2+s 2=n 2，变形得：(n +r )(n -r )=s 2②，把①代入②得：2s (n -r )=s 2，∵s ≠0，∴n -r =s2③，由①③可得r =35n ，s =45n ，∴Q 35n ，45n ，∵Q 在抛物线y =-x 2+3x +4上，∴45n =-35n 2+3×35n +4，解得n =5或n =-209，答：n 的值为5或-209．【点评】本题考查一次函数、二次函数综合应用，涉及待定系数法，三角形面积，对称变换等知识，解题的关键是用含n 的代数式表示Q 的坐标．7(2023•邗江区校级一模)如图1，在平面直角坐标系中，直线l :y =-33x +43分别与x 轴、y 轴交于点A 点和B 点，过O 点作OD ⊥AB 于D 点，以OD 为边构造等边ΔEDF (F 点在x 轴的正半轴上)．(1)求A 、B 点的坐标，以及OD 的长；(2)将等边ΔEDF ，从图1的位置沿x 轴的正方向以每秒1个单位的长度平移，移动的时间为t (s )，同时点P 从E 出发，以每秒2个单位的速度沿着折线ED -DF 运动(如图2所示)，当P 点到F 点停止，ΔDEF 也随之停止．①t =3或6(s )时，直线l 恰好经过等边ΔEDF 其中一条边的中点；②当点P 在线段DE 上运动，若DM =2PM ，求t 的值；③当点P 在线段DF 上运动时，若ΔPMN 的面积为3，求出t 的值．【分析】(1)把x =0，y =0分别代入y =-33x +43，即可求出点A 、B 的坐标，求出∠BAO =30°，根据直角三角形的性质，即可得出OD =12OA =6；(2)①当直线l 分别过DE 、DF 、EF 的中点，分三种情况进行讨论，得出t 的值，并注意点P 运动的最长时间；②分点P 在直线l 的下方和直线l 上方两种情况进行讨论，求出t 的值即可；③分点P 在DN 之间和点P 在NF 之间两种情况进行讨论，求出t 的值即可．【解答】解：(1)令x =0，则y =43，∴点B 的坐标为(0,43)，令y =0，则-33x +43=0，解得x =12，∴点A 的坐标为(12,0)，∵tan ∠BAO =OB OA=4312=33，∴∠BAO =30°，∵OD ⊥AB ，∴∠ODA =90°，∴ΔODA 为直角三角形，∴OD =12OA =6；(2)①当直线l 过DF 的中点G 时，∵ΔDEF 为等边三角形，∴∠DFE =60°，∵∠BAO =30°，∴∠FGA =60°-30°=30°，∴∠FGA =∠BAO ，∴FA =FG =12DF =3，∴OF =OA -FA =9，∴OE =OF -EF =9-6=3，∴t =3；当l 过DE 的中点时，∵DE ⊥l ，DG =EG ，∴直线l 为DE 的垂直平分线，∵ΔDEF 为等边三角形，∴此时点F 与点A 重合，∴t =12-61=6；当直线l 过EF 的中点时，运动时间为t =12-31=9；∵点P 从运动到停止用的时间为：6+62=6，∴此时不符合题意；综上所述，当t =3s 或6s 时，直线l 恰好经过等边ΔEDF 其中一条边的中点，故答案为：3或6；②∵OE =t ，AE =12-t ，∠BAO =30°，∴ME =6-t2，∴DM =DE -EM =t2，∵EP =2t ，∴PD =6-2t ，当P 在直线l 的下方时，∵DM =23DP ，∴t 2=23(6-2t )，解得：t =2411；当P 在直线l 的上方时，∵DM =2DP ，∴t2=2(6-2t )，解得t =83；综上所述：t 的值为2411或83；③当3<t ≤6时，∵∠D =60°，∠DMN =90°，DM =t2，∴∠DNM =90°-60°=30°，∴MN =DM ×tan60°=32t ，DN =2DM =2×t2=t ，∵DP =2t -6，∴PN =DN -DP =t -(2t -6)=6-t ，∵∠DNM =30°，∴边MN 的高h =12PN =3-12t ，∵ΔPMN 的面积为3，∴12×32t 3-12t =3，整理得：t 2-6t +8=0，解得t =2(舍)或t =4当点P 在NF 之间时，∵∠D =60°，∠DMN =90°，DM =t2，∴∠DNM =90°-60°=30°，∴MN =DM ×tan60°=32t ，DN =2DM =2×t2=t ，∵DP =2t -6，∴PN =DP -DN =2t -6-t =t -6，∵∠DNM =30°，∴∠FNA =∠DNM =30°，∴边MN 的高h =12PN =12t -3，∵ΔPMN 的面积为3，∴12×32t 12t -3 =3，解得t =3+17(舍)或t =3-17(舍)，综上所述，t 的值为4s ．【点评】本题主要考查了一次函数的性质、等边三角形的性质、直角三角形的性质、利用三角函数解直角三角形，熟练掌握含30°的直角三角形的性质并注意进行分类讨论是解题的关键．8(2023•武进区校级模拟)在平面直角坐标系xOy 中，对于任意两点P 1(x 1，y 1)与P 2(x 2，y 2)的“非常距离”，给出如下定义：若|x 1-x 2|≥|y 1-y 2|，则点P 1与点P 2的“非常距离”为|x 1-x 2|；若|x 1-x 2|<|y 1-y 2|，则点P 1与点P 2的“非常距离”为|y 1-y 2|．例如：点P 1(1,2)，点P 2(3,5)，因为|1-3|<|2-5|，所以点P 1与点P 2的“非常距离”为|2-5|=3，也就是图1中线段P 1Q 与线段P 2Q 长度的较大值(点Q 为垂直于y 轴的直线P 1Q 与垂直于x 轴的直线P 2Q 交点)．(1)已知点A -12，0，B 为y 轴上的一个动点，①若点A 与点B 的“非常距离”为2，写出一个满足条件的点B 的坐标；②直接写出点A 与点B 的“非常距离”的最小值；(2)已知C 是直线y =34x +3上的一个动点，①如图2，点D 的坐标是(0,1)，求点C 与点D 的“非常距离”的最小值及相应的点C 的坐标；②如图3，E 是以原点O 为圆心，1为半径的圆上的一个动点，求点C 与点E 的“非常距离”的最小值及相应的点E 与点C 的坐标．【分析】(1)①根据点B 位于y 轴上，可以设点B 的坐标为(0,y )．由“非常距离”的定义可以确定|0-y |=2，据此可以求得y 的值；②设点B 的坐标为(0,y )．因为-12-0 ≥|0-y |，所以点A 与点B 的“非常距离”最小值为-12-0 =12；(2)①设点C 的坐标为x 0，34x 0+3 ．根据材料“若|x 1-x 2|≥|y 1-y 2|，则点P 1与点P 2的“非常距离”为|x 1-x 2|”知，C 、D 两点的“非常距离”的最小值为-x 0=34x 0+2，据此可以求得点C 的坐标；②根据“非常距离”的定义，点E 在过原点且与直线y =34x +3垂直的直线上，且C 与E 的横纵坐标差相等时，点C 与点E 的“非常距离”取最小值，据此求出C 与E 的坐标及“非常距离”的最小值．【解答】解：(1)①∵B 为y 轴上的一个动点，∴设点B 的坐标为(0,y )．∵-12-0 =12≠2，∴|0-y |=2，解得，y =2或y =-2；∴点B 的坐标是(0,2)或(0,-2)；②点A 与点B 的“非常距离”的最小值为12．(2)①如图2，当点C 与点D 的“非常距离”取最小值时，需要根据运算定义“若|x 1-x 2|≥|y 1-y 2|，则点P 1与点P 2的“非常距离”为|x 1-x 2|”解答，此时|x 1-x 2|=|y 1-y 2|．即AC =AD ，∵C 是直线y =34x +3上的一个动点，点D 的坐标是(0,1)，∴设点C 的坐标为x 0，34x 0+3 ，∴-x 0=34x 0+2，此时，x 0=-87，∴点C 与点D 的“非常距离”的最小值为：|x 0|=87，此时C -87，157；②如图3，当点E 在过原点且与直线y =34x +3垂直的直线上，且CF =EF 时，点C 与点E 的“非常距离”最小，设E (x ,y )(点E 位于第二象限)．则y x=-43x 2+y 2=1 ，解得x =-35y =45，故E -35，45．设点C 的坐标为x 0，34x 0+3 ，-35-x 0=34x 0+3-45，解得x0=-8 5，则点C的坐标为-8 5，95，点C与点E的“非常距离”的最小值为1．【点评】本题考查了一次函数综合题．对于信息给予题，一定要弄清楚题干中的已知条件．本题中的“非常距离”的定义是正确解题的关键．9(2023•海安市一模)对于平面直角坐标系xOy中的图形W和点P，给出如下定义：F为图形W上任意一点，将P，F两点间距离的最小值记为m，最大值记为M，称M与m的差为点P到图形W的“差距离”，记作d(P,W)，即d(P,W)=M-m，已知点A(2,1)，B(-2,1)(1)求d(O,AB)；(2)点C为直线y=-1上的一个动点，当d(C,AB)=1时，点C的横坐标是　(2-5)或(5-2，)　；(3)点D为函数y=x+b(-2≤x≤2)图象上的任意一点，当d(D,AB)≤2时，直接写出b的取值范围．【分析】(1)画出图形，根据点P到图形W的“差距离”的定义即可解决问题．(2)如图2中，设C(m,-1)．由此构建方程即可解决问题．(3)如图3中，取特殊位置当b=6时，当b=-4时，分别求解即可解决问题．【解答】解：(1)如图1中，∵A(2,1)，B(-2,1)，∴AB⎳x轴，∴点O到线段AB的最小距离为1，最大距离为5，∴d(O,AB)=5-1．(2)如图2中，设C(m,-1)．当点C在y轴的左侧时，由题意AC-2=1，∴AC=3，∴(2-m)2+22=9，∴m=2-5或2+5(舍弃)，∴C(2-5，-1)，当点C在y轴的右侧时，同法可得C(5-2，-1)，综上所述，满足条件的点C的坐标为(2-5，-1)或(5-2，-1)．故答案为：(2-5，-1)或(5-2，-1)．(3)如图3中，当b=6时，线段EF:y=x+6(-2≤x≤2)上任意一点D，满足d(D,AB)≤2，当b=-4时，线段E′F′:y=x-4(-2≤x≤2)上任意一点D′，满足d(D′,AB)≤2，观察图象可知：当b≥6或b≤-4时，函数y=x+b(-2≤x≤2)图象上的任意一点，满足d(D,AB)≤2．【点评】本题属于一次函数综合题，考查了一次函数的性质，点P到图形W的“差距离”的定义等知识，解题的关键是理解题意，学会利用参数解决问题，学会寻找特殊位置解决问题，属于中考创新题型．10(2022•姑苏区校级模拟)平面直角坐标系xOy中，对于任意的三个点A、B、C，给出如下定义：若矩形的任何一条边均与某条坐标轴平行，且A，B，C三点都在矩形的内部或边界上，则称该矩形为点A，B，C的“三点矩形”．在点A，B，C的所有“三点矩形”中，若存在面积最小的矩形，则称该矩形为点A，B，C的“最佳三点矩形”．如图1，矩形DEFG，矩形IJCH都是点A，B，C的“三点矩形”，矩形IJCH是点A，B，C的“最佳三点矩形”．如图2，已知M(4,1)，N(-2,3)，点P(m,n)．(1)①若m=2，n=4，则点M，N，P的“最佳三点矩形”的周长为18，面积为；②若m=2，点M，N，P的“最佳三点矩形”的面积为24，求n的值；(2)若点P在直线y=-2x+5上．①求点M，N，P的“最佳三点矩形”面积的最小值及此时m的取值范围；②当点M，N，P的“最佳三点矩形”为正方形时，求点P的坐标；(3)若点P(m,n)在抛物线y=ax2+bx+c上，当且仅当点M，N，P的“最佳三点矩形”面积为12时，-2≤m≤-1或1≤m≤3，直接写出抛物线的解析式．【分析】(1)①利用“最佳三点矩形”的定义求解即可，②利用“最佳三点矩形”的定义求解即可；(2)①利用“最佳三点矩形”的定义求得面积的最小值为12，②由“最佳三点矩形”的定义求得正方形的边长为6，分别将y=7，y=-3代入y=-2x+5，可得x分别为-1，5，点P的坐标为(-1,7)或(4,-3)；(3)利用“最佳三点矩形”的定义画出图形，可分别求得解析式．【解答】解：(1)①如图，画出点M，N，P的“最佳三点矩形”，可知矩形的周长为6+6+3+3=18，面积为3×6=18；故答案为：18，18．②∵M(4,1)，N(-2,3)，∴|x M-x N|=6，|y M-y N|=2．又∵m=2，点M，N，P的“最佳三点矩形”的面积为24．∴此矩形的邻边长分别为6，4．∴n=-1或5．(2)如图，①由图象可得，点M，N，P的“最佳三点矩形”面积的最小值为12；分别将y=3，y=1代入y=-2x+5，可得x分别为1，2；结合图象可知：1≤m≤2；②当点M，N，P的“最佳三点矩形”为正方形时，边长为6，分别将y=7，y=-3代入y=-2x+5，可得x分别为-1，4；∴点P的坐标为(-1,7)或(4,-3)；(3)设抛物线的解析式为y=ax2+bx+c，经过点(-1,1)，(1,1)，(3,3)，∴a -b +c =1a +b +c =19a +3b +c =3，a =14b =0c =34，∴y =14x 2+34，同理抛物线经过点(-1,3)，(1,3)，(3,1)，可求得抛物线的解析式为y =-14x 2+134，∴抛物线的解析式y =14x 2+34或y =-14x 2+134．【点评】本题主要考查了一次函数的综合题，涉及点的坐标，正方形及矩形的面积及待定系数法求函数解析式等知识，解题的关键是理解运用好“最佳三点矩形”的定义．11(2022•太仓市模拟)如图①，动点P 从矩形ABCD 的顶点A 出发，以v 1的速度沿折线A -B -C 向终点C 运动；同时，一动点Q 从点D 出发，以v 2的速度沿DC 向终点C 运动，当一个点到达终点时，另一个点也停止运动．点E 为CD 的中点，连接PE ，PQ ，记ΔEPQ 的面积为S ，点P 运动的时间为t ，其函数图象为折线MN -NF 和曲线FG (图②)，已知，ON =3，NH =1，点G 的坐标为(6,0)．(1)点P 与点Q 的速度之比v 1v 2的值为　32　；AB :AD 的值为；(2)如果OM =2．①求线段NF 所在直线的函数表达式；②是否存在某个时刻t ，使得S ≥23？若存在，求出t 的取值范围；若不存在，请说明理由．【分析】(1)由函数图象可知t =3时，Q 与E 重合，t =4时，P 与B 重合，t =6时，P 与C 重合，则Q 的速度v 2=DE 3，P 的速度v 1=AB4，从而得出答案；(2)①当t =0时，P 与A 重合，Q 与D 重合，此时S ΔADE =2，可得AD =BC =DE =2，AB =CD =2AD =4，从而得出点P 与Q 的速度，即可得出点F 的坐标，利用待定系数法可得答案；②利用待定系数法求出直线MN 的函数解析式，当S =23时，可得t 的值，根据图象可得答案．【解答】解：(1)∵ON =3，NH =1，G (6,0)，∴N (3,0)，H (4,0)，由图象可知：t =3时，Q 与E 重合，t =4时，P 与B 重合，t =6时，P 与C 重合，∴Q 的速度v 2=DE 3，P 的速度v 1=AB4，∵四边形ABCD 是矩形，∴AB =CD ，AD =BC ，∵E 为CD 的中点，∴DE =12CD =12AB ，∴v 1v 2=AB4DE 3=AB 4⋅3DE =AB 4⋅312AB =32，∵P 从A 到B 用了4秒，从B 到C 用了2秒，∴AB =4v 1，BC =2v 1，∴AB =2BC ，∴AB :AD 的值为2，故答案为：32,2；(2)①∵OM =2，∴M (0,2)，由题知，t =0时，P 与A 重合，Q 与D 重合，∴S ΔEPQ =12AD ⋅DE =2，∵AB :AD =2，∴AD =DE =12AB ，∴12AD 2=2，∴AD =BC =DE =2，AB =CD =2AD =4，∴v 2=DE 3=23，当t =4时，DQ =v 2t =23×4=83，∴QE =DQ -DE =83-2=23，此时P 与B 重合，∴S ΔEPQ =12EQ ⋅BC =12×23×2=33，∴F 4,23，设直线NF 的解析式为S =kx +b (k ≠0)，将N (3,0)与F 4,23 代入得：3k +b =04k +b =23 ，∴k =23b =-2，∴线段NF 所在直线的函数表达式为S =23x -2(3<x ≤4)；②存在，分情况讨论如下：当Q 在DE 上，P 在AB 上时，∵直线MN 经过点M (0,2)，N (3,0)，同理求得直线MN 的解析式为S =-23x +2(0≤x ≤3)，当s =23时，-23x +2=2，∴x =2，∵s随x的增大而减小，∴当0≤x≤2时，S≥23，当Q在CE上，P在AB上时，直线NF的解析式为S=23x-2(3<x≤4)，由F4,2 3知：当x=4时，S=23，当Q在CE上，P在BC上时，SΔEPQ=12EQ⋅CP，∵DQ=v2t=23t，∴EQ=DQ-DE=23t-2，∵v1=AB4=44=1，∴AB+BP=v1t=t，∵AB+BC=4+2=6，∴CP=6-t，∴S=1223t-2(6-t)=-13t2+3t-6(4<x≤6)，当S=23时，-13t2+3t-6=23，∴t=4或5，由图象知：当4<x≤5时，S≥2 3，综上，S≥23时，x的取值范围为0≤x≤2或4≤x≤5．【点评】本题是一次函数综合题，主要考查了待定系数法求函数解析式，三角形的面积，矩形的性质等知识，理解函数图象中每一个拐点的意义是解题的关键．12(2022•邗江区校级一模)在平面直角坐标系xOy中，对于点P和线段ST，我们定义点P关于线段ST的线段比k=PSST(PS<PT)PTST(PS≥PT) ．(1)已知点A(0,1)，B(1,0)．①点Q(2,0)关于线段AB的线段比k=　22　；②点C(0,c)关于线段AB的线段比k=2，求c的值．(2)已知点M(m,0)，点N(m+2,0)，直线y=x+2与坐标轴分别交于E，F两点，若线段EF上存在点使得这一点关于线段MN的线段比k≤14，直接写出m的取值范围．【分析】(1)①求出QA、QB、AB，根据线段比定义即可得到答案；②方法同①，分c>0和c≤0讨论；(2)分两种情况，画出图象，根据线段比定义，分别在M(N)为“临界点”时列出不等式，即可得到答案．【解答】解：(1)①∵A(0,1)，B(1,0)，Q(2,0)，∴AB=2，QA=5，QB=1，根据线段比定义点Q(2,0)关于线段AB的线段比k=QBAB=22；故答案为：22；②∵A (0,1)，B (1,0)，C (0,c )，∴AB =2，AC =|1-c |，BC =1+c 2，AC 2=1+c 2-2c ，BC 2=1+c 2，当c >0时，AC 2<BC 2，即AC <BC ，由C (0,c )关于线段AB 的线段比k =2可得：|1-c |2=2，解得c =3或c =-1(舍去)，∴c =3，当c ≤0时，AC 2≥BC 2，即AC ≥BC ，由C (0,c )关于线段AB 的线段比k =2可得：1+c 22=2，解得c =3(舍去)或c =-3，∴c =-3，综上所述，点C (0,c )关于线段AB 的线段比k =2，c =3或c =-3；(2)∵直线y =x +2与坐标轴分别交于E ，F 两点，∴E (-2,0)，F (0,2)，∵点M (m ,0)，点N (m +2,0)，∴MN =2，N 在M 右边2个单位，当线段EF 上的点到N 距离较小时，分两种情况：①当M 、N 在点E 左侧时，如图：线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14，∴NE MN≤14，即-2-(m +2)2≤14，解得：m ≥-92，②当N 在E 右侧，M 在E 左侧时，过M 作MG ⊥EF 于G ，如图：线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14，∴GM MN ≤14，即GM 2≤14，∴GM ≤12，而E (-2,0)，F (0,2)，∴∠FEO =45°，∴ΔHEM 时等腰直角三角形，∴GM =22EM ，∴22EM ≤12，即22[(m +2)-(-2)]≤12，解得m ≤-4+22，∴线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14，线段EF 上的点到N 距离较小时，-92≤m ≤-4+22，当线段EF 上的点到M 距离较小时，也分两种情况：①当N 在E 右侧，M 在E 左侧时，如图：线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14，∴ME MN≤14，即-2-m 2≤14，解得m ≥-52，②当M 、N 在点E 右侧时，过M 作MH ⊥EF 于H ，如图：线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14，∴HM MN ≤14，即HM 2≤14，∴HM ≤12，而E (-2,0)，F (0,2)，∴∠FEO =45°，∴ΔHEM 时等腰直角三角形，∴HM =22EM ，∴22EM ≤12，即22[m -(-2)]≤12，解得：m ≤-2+22，∴线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14，线段EF 上的点到M 距离较小时，-52≤m ≤-2+22，综上所述，线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14，则-92≤m ≤-4+22或-52≤m ≤-2+22．【点评】本题考查一次函数应用，解题的关键是读懂线段比的定义，找出“临界点”列不等式．13(2022•泰州)定义：对于一次函数y 1=ax +b 、y 2=cx +d ，我们称函数y =m (ax +b )+n (cx +d )(ma +nc ≠0)为函数y 1、y 2的“组合函数”．(1)若m =3，n =1，试判断函数y =5x +2是否为函数y 1=x +1、y 2=2x -1的“组合函数”，并说明理由；(2)设函数y 1=x -p -2与y 2=-x +3p 的图像相交于点P ．①若m +n >1，点P 在函数y 1、y 2的“组合函数”图像的上方，求p 的取值范围；②若p ≠1，函数y 1、y 2的“组合函数”图像经过点P ．是否存在大小确定的m 值，对于不等于1的任意实数p ，都有“组合函数”图像与x 轴交点Q 的位置不变？若存在，请求出m 的值及此时点Q 的坐标；若不存在，请说明理由．【分析】(1)由y =5x +2=3(x +1)+(2x -1)，可知函数y =5x +2是函数y 1=x +1、y 2=2x -1的“组合函数”；(2)①由y =x -p -2y =-x +3p得P (2p +1,p -1)，当x =2p +1时，y =m (2p +1-p -2)+n (-2p -1+3p )=(p-1)(m +n )，根据点P 在函数y 1、y 2的“组合函数”图象的上方，有p -1>(p -1)(m +n )，而m +n >1，可得p <1；②由函数y 1、y 2的“组合函数” y =m (x -p -2)+n (-x +3p )图象经过点P ，知p -1=m (2p +1-p -2)+n (-2p -1+3p )，即(p -1)(1-m -n )=0，而p ≠1，即得n =1-m ，可得y =(2m -1)x +3p -(4p +2)m ，令y =0得(2m -1)x +3p -(4p +2)m =0，即(3-4m )p +(2m -1)x -2m =0，即可得m =34时，“组合函数”图象与x 轴交点Q 的位置不变，Q (3,0)．【解答】解：(1)函数y =5x +2是函数y 1=x +1、y 2=2x -1的“组合函数”，理由如下：∵3(x +1)+(2x -1)=3x +3+2x -1=5x +2，∴y =5x +2=3(x +1)+(2x -1)，∴函数y =5x +2是函数y 1=x +1、y 2=2x -1的“组合函数”；(2)①由y =x -p -2y =-x +3p得x =2p +1y =p -1 ，∴P (2p +1,p -1)，∵y 1、y 2的“组合函数”为y =m (x -p -2)+n (-x +3p )，∴x =2p +1时，y =m (2p +1-p -2)+n (-2p -1+3p )=(p -1)(m +n )，∵点P 在函数y 1、y 2的“组合函数”图象的上方，∴p -1>(p -1)(m +n )，∴(p -1)(1-m -n )>0，∵m +n >1，∴1-m -n <0，∴p -1<0，∴p <1；②存在m =34时，对于不等于1的任意实数p ，都有“组合函数”图象与x 轴交点Q 的位置不变，Q (3,0)，理由如下：由①知，P (2p +1,p -1)，∵函数y 1、y 2的“组合函数”y =m (x -p -2)+n (-x +3p )图象经过点P ，∴p -1=m (2p +1-p -2)+n (-2p -1+3p )，∴(p -1)(1-m -n )=0，∵p ≠1，∴1-m -n =0，有n =1-m ，∴y =m (x -p -2)+n (-x +3p )=m (x -p -2)+(1-m )(-x +3p )=(2m -1)x +3p -(4p +2)m ，令y =0得(2m -1)x +3p -(4p +2)m =0，变形整理得：(3-4m )p +(2m -1)x -2m =0，∴当3-4m =0，即m =34时，12x -32=0，∴x =3，∴m =34时，“组合函数”图象与x 轴交点Q 的位置不变，Q (3,0)．【点评】本题考查一次函数综合应用，涉及新定义，函数图象上点坐标的特征，一次函数与一次方程的关系等，解题的关键是读懂“组合函数“的定义．14(2024•钟楼区校级模拟)在同一平面内，具有一条公共边且不完全重合的两个全等三角形，我们称这两个三角形叫做“共边全等”．(1)下列图形中两个三角形不是“共边全等”是③；AB，点E、F分别在AC、BC边(2)如图1，在边长为6的等边三角形ABC中，点D在AB边上，且AD=13上，满足ΔBDF和ΔEDF为“共边全等”，求CF的长；(3)如图2，在平面直角坐标系中，直线y=-3x+12分别与直线y=x、x轴相交于A、B两点，点C是OB 的中点，P、Q在ΔAOB的边上，当以P、B、Q为顶点的三角形与ΔPCB“共边全等”时，请直接写出点Q 的坐标．【分析】(1)由于第③个图不符合共边要求，所以图③即为答案；(2)DF为两个全等三角形的公共边，由于F点在BC边上，E在AC边上，两个三角形的位置可以如图②，在公共边异侧，构成一个轴对称图形，也可以构成一个平行四边形(将图③的两条最长边重合形成)，分两类讨论，画出图形，按照图②构图，会得到一个一线三等角模型，利用相似，列出方程来解决，按照平行四边形构图，直接得到ΔADE为等边三角形，计算边长即可求得；(3)由题目要求，可以知道两个全等三角形的公共边为PB边，由于要构成ΔPCB，所以P点只能在OA和OB边上，当P在OA边上，两个三角形可以在PB同侧，也可以在PB异侧，当在PB异侧构图时，可以得到图3和图4，在图3中，当在PB同侧构图时，可以得到图6，当P在OB边上时，Q只能落在OA上，得到图7，利用已知条件，解三角形，即可求出Q点坐标．【解答】解：(1)①②均符合共边全等的特点，只有③，没有公共边，所以③不符合条件，∴答案是③；(2)①如图1，当ΔBDF≅ΔEFD，且是共边全等时，∠BFD=∠EDF，∴DE⎳BC，∵ΔABC是等边三角形，∴ΔADE是等边三角形，AB=2，∵AD=13∴DE=AE=BF=2，∴CF=BC-BF=4，②如图2，当ΔBDF≅ΔEDF，且是共边全等时，BD=DE=6-AD=4，∠DEF=∠B=60°，EF=BF，∴∠AED+∠FEC=120°，又∠AED+∠EDA=120°，。

一次函数与几何及动点综合题(含解析)

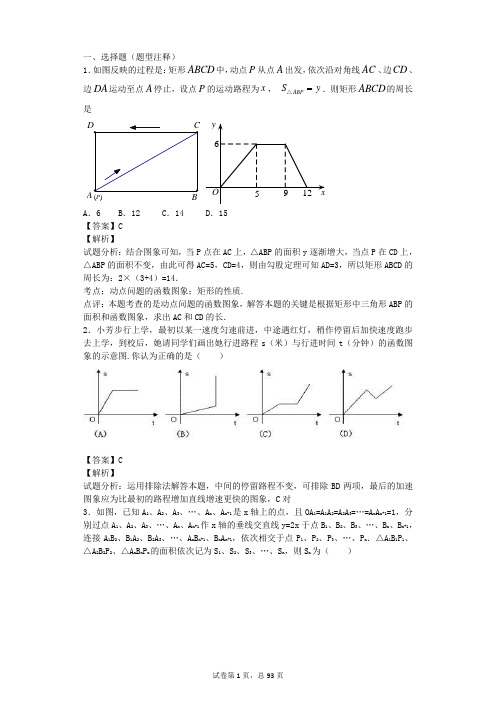
一、选择题（题型注释）1．如图反映的过程是：矩形ABCD 中，动点P 从点A 出发，依次沿对角线AC 、边CD 、边DA 运动至点A 停止，设点P 的运动路程为x ， ABP S y △．则矩形ABCD 的周长是(P )D A BC61295Oy xA ．6B ．12C ．14D ．15 【答案】C 【解析】试题分析：结合图象可知，当P 点在AC 上，△ABP 的面积y 逐渐增大，当点P 在CD 上，△ABP 的面积不变，由此可得AC=5，CD=4，则由勾股定理可知AD=3，所以矩形ABCD 的周长为：2×（3+4）=14．考点：动点问题的函数图象；矩形的性质.点评：本题考查的是动点问题的函数图象，解答本题的关键是根据矩形中三角形ABP 的面积和函数图象，求出AC 和CD 的长．2．小芳步行上学，最初以某一速度匀速前进，中途遇红灯，稍作停留后加快速度跑步去上学，到校后，她请同学们画出她行进路程s （米）与行进时间t （分钟）的函数图象的示意图.你认为正确的是（）【答案】C 【解析】试题分析：运用排除法解答本题，中间的停留路程不变，可排除BD 两项，最后的加速图象应为比最初的路程增加直线增速更快的图象，C 对3．如图，已知A 1、A 2、A 3、…、A n 、A n+1是x 轴上的点，且OA 1=A 1A 2=A 2A 3=…=A n A n+1=1，分别过点A 1、A 2、A 3、…、A n 、A n+1作x 轴的垂线交直线y=2x 于点B 1、B 2、B 3、…、B n 、B n+1，连接A 1B 2、B 1A 2、B 2A 3、…、A n B n+1、B n A n+1，依次相交于点P 1、P 2、P 3、…、P n ．△A 1B 1P 1、△A 2B 2P 2、△A n B n P n 的面积依次记为S 1、S 2、S 3、…、S n ，则S n 为（）A．121nn++B．31nn-C．221nn-D．221nn+【答案】D．【解析】试题分析：∵A1、A2、A3、…、A n、A n+1是x轴上的点，且OA1=A1A2=A2A3=…=A n A n+1=1，∴A1（1，0），A2（2，0），A3（3，0），…A n（n，0），A n+1（n+1，0），∵分别过点A1、A2、A3、…、A n、A n+1，作x轴的垂线交直线y=2x于点B1、B2、B3、…、B n、B n+1，∴B1的横坐标为：1，纵坐标为：2，则B1（1，2），同理可得：B2的横坐标为：2，纵坐标为：4，则B2（2，4），B3（2，6），…B n（n，2n），B n+1（n+1，2n+2），根据题意知：P n是A n B n+1与 B n A n+1的交点，设：直线A n B n+1的解析式为：y=k1x+b1，直线B n A n+1的解析式为：y=k2x+b2，∵A n（n，0），A n+1（n+1，0），B n（n，2n），B n+1（n+1，2n+2），∴直线A n B n+1的解析式为：y=（2n+2）x﹣2n2﹣2n，直线B n A n+1的解析式为：y=﹣2n x+2n2+2n，∴P n（22221n nn++，24421n nn++）∴△A n B n P n的A n B n边上的高为：22221n nnn+-+=21nn+,△A n B n P n的面积S n为:21222121n nnn n⨯⋅=++．故选D ．考点：一次函数图象上点的坐标特征． 4．如图，已知直线l ：x y 33，过点A （0，1）作y 轴的垂线交直线l 于点B ，过点B 作直线l 的垂线交y 轴于点A 1；过点A 1作y 轴的垂线交直线l 于点B 1，过点B 1作直线l 的垂线交y 轴于点A 2；…；按此作法继续下去，则点A 4的坐标为 A.（0，64） B.（0，128） C.（0，256） D.（0，512）【答案】C. 【解析】试题分析：∵直线l 的解析式为；3， ∴l 与x 轴的夹角为30°， ∵AB ∥x 轴， ∴∠ABO=30°， ∵OA=1， ∴OB=2， ∴3，∵A 1B ⊥l ，∴∠ABA 1=60°， ∴A 1O=4， ∴A 1（0，4），同理可得A 2（0，16）， …∴A 4纵坐标为44=256， ∴A 4（0，256）．故选C ．考点：一次函数综合题．5．如图，在矩形ABCD 中，O 是对角线AC 的中点，动点P ，Q 分别从点C ，D 出发，沿线段CB ，DC 方向匀速运动，已知P ，Q 两点同时出发，并同时到达终点B ，C ．连接OP ，OQ ．设运动时间为t ，四边形OPCQ 的面积为S ，那么下列图象能大致刻画S 与t 之间的关系的是【答案】A ．【解析】试题分析：作OE ⊥BC 于E 点，OF ⊥CD 于F 点，如图，设BC=a ，AB=b ，点P 的速度为x ，点F 的速度为y ，则CP=xt ，DQ=yt ，所以CQ=b-yt ， ∵O 是对角线AC 的中点，∴OE 、OF 分别是△ACB 、△ACD 的中位线， ∴OE=12b ，OF=12a ， ∵P ，Q 两点同时出发，并同时到达终点， ∴a bx y=，即ay=bx ， ∴S=S △OCQ +S △OCP =12•12a•（b-yt ）+12•12b•xt=14ab-14ayt+14bxt=14ab （0＜t ＜a x）， ∴S 与t 的函数图象为常函数，且自变量的范围为0＜t ＜ax）．故选A ．考点：动点问题的函数图象．6．函数321+=x y 的图象与x 、y 轴分别交于点A 、B ，点P )(y x ，为直线AB 上的一动点（0>x ）过P 作PC ⊥y 轴于点C ，若使PBC ∆的面积大于AOB ∆的面积，则P的横坐标x 的取值范围是（）A 、30<<xB 、3>xC 、63<<xD 、6>x【解析】试题分析：由题意知：PC=x ，OC=132x + ∴BC=12x ∵PBC ∆的面积大于AOB ∆的面积∴x ＞6. 故选D.考点: 一次函数综合题.7．如图1，在直角梯形ABCD 中，动点P 从点B 出发，沿BC ，CD 运动至点D 停止．设点P 运动的路程为，△ABP 的面积为y ，如果y 关于x 的函数图象如图2所示，则△BCD 的面积是（）A ．3B ．4C ．5D ．6 【答案】A 【解析】试题分析：动点P 从直角梯形ABCD 的直角顶点B 出发，沿BC ，CD 的顺序运动，则△ABP 面积y 在BC 段随x 的增大而增大；在CD 段，△ABP 的底边不变，高不变，因而面积y 不变化．由图2可以得到：BC=2，CD=3，△BCD 的面积是12×2×3=3．故选A ．考点：动点问题的函数图象．8．如图，正方形ABCD 的边长为4，P 为正方形边上一动点，沿A →D →C →B →A 的路径匀速移动，设P 点经过的路径长为x ，△APD 的面积是y ，则下列图象能大致反映y 与x 的函数关系的是A ．B ．C ．D ．【解析】当点P 由点A 向点D 运动时，y 的值为0；当点p 在DC 上运动时，y 随着x 的增大而增大；当点p 在CB 上运动时，y 不变；当点P 在BA 上运动时，y 随x 的增大而减小。

八上数学复习专题之压轴题(一次函数)(含答案)

八上数学复习专题之压轴题（一次函数）一、二条直线的交点问题：1．如图，平面直角坐标系中，函数3y x b =-+的图象与y 轴相交于点B ，与函数43y x =-的图象相交于点A ，且OB =5．（1）求点A 的坐标；（2）求函数3y x b =-+、43y x =-的图象与x 轴所围成的三角形的面积．2．如图，已知直线l 1经过点A （0，﹣1）与点P （2，3），另一条直线l 2经过点P ，且与y 轴交于点B （0，m ）．（1）求直线l 1的解析式；（2）若△APB 的面积为3，求m 的值．3. 已知：如图，平面直角坐标系xOy 中，B （0，1），OB =OC =OA ，A 、C 分别在x 轴的正负半轴上．过点C的直线绕点C旋转，交y轴于点D，交线段AB于点E．（1）求∠OAB的度数及直线AB的解析式；（2）若△OCD与△BDE的面积相等，求点D的坐标．4. 如图，直线l1的解析式为443y x=+，与x轴，y轴分别交于A，B；直线l2与x轴交于点C（2，0）与y轴交于点D3(0,)2，两直线交于点P．（1）求点A，B的坐标及直线l2的解析式；（2）求证：△AOB≌△APC；（3）若将直线l2向右平移m个单位，与x轴，y轴分别交于点C'、D'，使得以点A、B、C'、D'为顶点的图形是轴对称图形，求m的值？二、与等腰三角形结合的问题1．如图，在平面直角坐标系中，过点A（0，6）的直线AB与直线OC相交于点C（2，4）动点P沿路线O →C →B 运动．（1）求直线AB 的解析式；（2）当△OPB 的面积是△OBC 的面积的14时，求出这时点P 的坐标；（3）是否存在点P ，使△OBP 是直角三角形？若存在，直接写出点P 的坐标，若不存在，请说明理由．2．如图，在平面直角坐标系中，直线l 1的解析式为y =﹣x ，直线l 2与l 1交于点A （a ，﹣a ），与y轴交于点B （0，b ），其中a ，b 满足2(2)0a ++=．（1）求直线l 2的解析式；（2）在平面直角坐标系中第二象限有一点P （m ，5），使得S △AOP =S △AOB ，请求出点P 的坐标；（3）已知平行于y 轴且位于y 轴左侧有一动直线，分别与l 1，l 2交于点M 、N ，且点M 在点N 的下方，点Q 为y 轴上一动点，且△MNQ 为等腰直角三角形，请直接写出满足条件的点Q 的坐标．3. 在平面直角坐标系中，直线l 1的函数关系式为2y x b =+，直线l 2过原点且与直线l 1交于点P （﹣1，﹣5）．（1）试问（﹣1，﹣5）可以看作是怎样的二元一次方程组的解？（2）设直线l1与直线y x=交于点A，求△APO的面积；（3）在x轴上是否存在点Q，使得△AOQ是等腰三角形？若存在，求出点Q的坐标；若不存在，请说明理由．4. 如图，直线l：122y x=-+与x轴，y轴分別交于点A，B，在y轴上有一点C（0，4），动点M从点A出发以毎秒1个単位长度的速度沿x轴向左运动，设运动的时间为t秒．（1）求点A的坐标；（2）请从A，B两题中任选一题作答．A．求△COM的面积S与时间t之间的函数表达式；B．当△ABM为等腰三角形时，求t的值．5．在平面直角坐标系中，直线y=x+6与x轴、y轴分别交于B、A两点，点C在x轴的正半轴，且OB=OC，点D为AC的中点．（1）求直线AC的解析式；（2）点P 从点B 出发，沿射线BD t 秒，△APD 的面积为S ，求S 与t 的函数关系，并直接写出自变量的取值范围；（3）在（2）的条件下，连接AP 、CP ，当△ACP 是以PC 为腰的等腰三角形时，求点P 的坐标．三、面积问题：1. 如图，在平面直角坐标系中，直线l 1：y =﹣x ﹣1分别与x 轴，y 轴交于点A ，B ，将直线l 1向上平移3个单位长度，得直线l 2．经过点A 的直线l 3与直线l 2交于第一象限的点C ，过点C 作x 轴的垂线，垂足为点D ，且AD =2CD （1）求直线l 3的解析式．（2）连接BC ，求△ABC 的面积．2. 如图，直线l 1：3y x =+分别与直线2:(0)l y kx b k =+≠、直线3111:(0)l y k x b k =+≠交于A 、B 两点，直线l 1交y 轴于点E ，直线l 2与x 轴和y 轴分别交于C 、D 两点，已知点A 的纵坐标为32，B 的横坐标为1，l 2∥l 3，OD =1，连BD ．（1）求直线l 3的解析式；（2）求△ABD 的面积．3. 当m ，n 是正实数，且满足m n mn +=时，就称点(,)mP m n为“完美点”．（1）若点E 为完美点，且横坐标为2，则点E 的纵坐标为；若点F 为完美点，且横坐标为3，则点F 的纵坐标为；（2）完美点P 在直线（填直线解析式）上；（3）如图，已知点A （0，5）与点M 都在直线5y x =-+上，点B ，C 是“完美点”，且点B 在直线AM 上．若MC =AM = △MBC 的面积．4. 如图（含备用图），在直角坐标系中，已知直线y =kx +3与x 轴相交于点A （2，0），与y 轴交于点B ．（1）求k 的值及△AOB 的面积；（2）点C 在x 轴上，若△ABC 是以AB 为腰的等腰三角形，直接写出点C 的坐标；（3）点M（3，0）在x轴上，若点P是直线AB上的一个动点，当△PBM的面积与△AOB的面积相等时，求点P的坐标．5. 图（1），在平面直角坐标系中，直线y=﹣x+4交坐标轴于A、B两点，过点C（﹣4，0）作CD⊥AB于D，交y轴于点E．（1）求证：△COE≌△BOA；（2）如图2，点M是线段CE上一动点（不与点C、E重合），ON⊥OM交AB于点N，连接MN．①判断△OMN的形状．并证明；②当△OCM和△OAN面积相等时，求点N的坐标．6．在直角坐标系中，点P（a，b）的“变换点”的坐标定义如下：当a≥b时，点P1的坐标为（a，﹣b）；当a＜b时，点P1的坐标为（b，﹣a）．（1）直接写出点A（5，6）、B（3，2）、C（4，4）的变换点A1、B1、C1的坐标；（2）P（a，b）为直线y=﹣2x+6上的任一点，当a＜b时，点P（a，b）的变换点在一条直线M上，求点M的函数解析式并写出自变量的取值范围；（3）直线y =﹣2x +6上所有点的变换点组成一个新的图形L ，直线y =kx +1与图形L 有两个公共点，求k 的取值范围．答案：一、两直线交点问题：1. 解：（1）由OB =5可得B （0，﹣5），把（0，﹣5）代入3y x b =-+，可得b =﹣5， ∴函数关系式为y =﹣3x ﹣5，求两直线的交点坐标得：点A 的坐标为（﹣3，4）；（2）设直线AB 与y 轴交于点C ，则点C 的坐标为5(,0)3-，CO =53，所围成的三角形即为△ACO ，过A 作AE ⊥x 轴于E ，由A （﹣3，4）可得AE =4，∴S △ACO =103． 2. 解：（1）设直线l 1的表达式为y =kx +b ，2,1k b ==-∴直线l 1的函数关系式为：y =2x ﹣1．（2）过P 作PH ⊥y 轴于H ，则PH =2，∵S △APB =3，∴AB =3，∵A （0，﹣1），∴B （0，2）或（0，﹣4），∴m =2或﹣4．3. 解：（1）∵OB =OC =OA ，∠AOB =90°，∴∠OAB =45°；∵B （0，1），∴A （1，0），设直线AB 的解析式为y =kx +b ． ∴直线AB 的解析式为y =﹣x +1；（2）∵S △COD =S △BDE ，1,1k b =-=∴S △COD +S 四边形AODE =S △BDE +S 四边形AODE ，即S △ACE =S △AOB ， ∵点E 在线段AB 上，∴点E 在第一象限，且y E ＞0，点E 的纵坐标是12∴直线AB 的解析式得：=﹣x +1，设直线CE 的解析式是：y =mx +n ，∵C （﹣1，0），11(,)22E 代入得：解得：11,33m n ==， ∴直线CE 的解析式为1133y x =+，∴D 的坐标为1(0,)3．5. （1）解：当0x =时，4y =，∴点B 的坐标为（0，4）；当y =0时，解得：x =﹣3，∴点A 的坐标为（﹣3，0）．设直线l 2的解析式为y kx b =+，将C （2，0）、D （0，）代入y kx b =+，得：33,42k b =-= ∴直线l 2的解析式为3342y x =-+．（2）证明：连接两直线解析式成方程组，解得点P 的坐标为612(,)55-． ∵A （﹣3，0），C （2，0），B （0，4）， ∴AO =3，AC =5，AB =5，AP =3， ∴AO =AP ，AB =AC ．在△AOB 和△APC 中，,,AO AP BAO CAP AB AC =∠=∠=， ∴△AOB ≌△APC （S A S ）．（3）解：连接BC ′，如图所示．∵平移后直线C ′D ′的解析式为333442y x m =-++， ∴点C ′的坐标为（m +2，0），点D ′的坐标为33(0,)42m +．∵以点A 、B 、C '、D '为顶点的图形是轴对称图形，∴△ABC′≌△D′BC′，∴AB=D′B，AC′=D′C′．∵A（﹣3，0），B（0，4），∴D′B=3542m-，AC′=m+5，D′C′=5(2)4m+，∴3554255(2)4mm m⎧-=⎪⎪⎨⎪+=+⎪⎩解得：m=10．∴当以点A、B、C'、D'为顶点的图形是轴对称图形时，m的值为10．二、与等腰三角形结合问题1. 解：（1）∵点A的坐标为（0，6），∴设直线AB的解析式为y=kx+6，∵点C（2，4）在直线AB上，∴2k+6=4，∴k=﹣1，∴直线AB的解析式为y=﹣x+6；（2）由（1）知，直线AB的解析式为y=﹣x+6，令y=0，∴﹣x+6=0，∴x=6，∴B（6，0），∴S△OBC=12，∵△OPB的面积是△OBC的面积的14，∴S△OPB=3，设P的纵坐标为m，∴S△OPB=3m=3，∴m=1，∵C（2，4），∴直线OC的解析式为y=2x，当点P在OC上时，12x=，∴1(,1)2P，当点P在BC上时，x=6﹣1=5，∴P（5，1），即：点1(,1)2P或（5，1）；（3）∵△OBP是直角三角形，∴∠OPB=90°，当点P在OC上时，由（2）知，直线OC的解析式为y=2x①，∴直线BP的解析式的比例系数为12 -，∵B（6，0），∴直线BP的解析式为132y x=-+②，联立①②，可求得612 (,) 55 P，当点P在BC上时，由（1）知，直线AB的解析式为y=﹣x+6③，∴直线OP的解析式为y=x④，联立③④解得，可求得P（3，3），即：点P的坐标为612(,)55P或（3，3）．2. 解：（1）由条件得a+2=0，b﹣3=0，∴a=﹣2，b=3，∴点A的坐标为（﹣2，2），点B的坐标为（0，3）．设直线l2的解析式为y=kx+c（k≠0），将A（﹣2，2）、B（0，3）代入y=kx+c，得：1,32k c==∴直线l2的解析式为132y x=+．（2）∵S△AOP=S△AOB，∴点P到AO的距离与点B到AO的距离相等，且点P位于l1两侧．①当点P在l1的右侧时，设点P为P1，则P1B∥l1，∴直线P1B的解析式为：y=﹣x+3，当y=5时，有﹣x+3=5，解得：x=﹣2，∴点P1的坐标为（﹣2，5）；②当点P在l1的左侧时，设点P为P2，点P2的坐标为（﹣8，5）．综上所述：点P的坐标为（﹣2，5）或（﹣8，5）．（3）设动直线为x=t，由题可得﹣2＜t＜0，则点M的坐标为（t，﹣t），点N的坐标为1(,3)2t t+，∴332MN t=+．①当∠NMQ=90°时，有MN=MQ，65t=-，∴点M的坐标为66(,)55-．∵MQ∥x轴，∴点Q的坐标为6 (0,)5；②当∠MNQ=90°时，有MN=NQ，即t+3=﹣t，t=﹣，∴点Q的坐标为12 (0,)5；③当∠MQN=90°时，点Q的坐标为12 (0,)7．综上所述：点Q的坐标为6(0,)5或12(0,)5或12(0,)7．3. 解：（1）∵点P（﹣1，﹣5）在直线l1上，∴﹣2+b=﹣5，∴b=﹣3∴直线l1的解析式为y=2x﹣3，设直线l2的解析式为y=kx，则有﹣k=﹣5，∴k=5，∴直线l2的解析式为y=5x，∴（﹣1，﹣5）可以看成二元一次方程组235y xy x=-⎧⎨=⎩的解．（2）A（3，3），∵点P（﹣1，5）在直线y=2x﹣3上，直线P A交y轴于C（0，﹣3），∴S△AOP=S△POC+S△AOC=6．（3）∵A（3，3），∴OA=①当OA=OQ时，可得Q1（﹣0），Q2（，0）；②当QA =QO 时，Q 3（3，0）；② 当AO =AQ 时，Q 4（6，0），综上所述，满足条件的点Q 坐标为（﹣0）或（3，0）或（，0）或（6，0）．4. 解：（1）对于直线AB ：122y x =-+，当x =0时，y =2；当y =0时，x =4，则A 、B 两点的坐标分别为A （4，0）、B （0，2）；（2）A 、∵C （0，4），A （4，0）∴OC =OA =4，当0≤t≤4时，OM =OA ﹣AM =4﹣t ，S △OCM =×4×（4﹣t ）=8﹣2t ；当t ＞4时，OM =AM ﹣OA =t ﹣4，S △OCM =×4×（t ﹣4）=2t ﹣8；B 、△ABM 是等腰三角形，有三种情形：①当BM =AM 时，设BM =AM =x ，则OM =4﹣x ，在Rt △OBM 中，∵OB 2+OM 2=BM 2，∴2222(4)x x +-=，∴ 2.5x =，∴AM =2.5，∴t=2.5时，△ABM 是等腰三角形．③ 当AM ′=AB =t =△ABM 是等腰三角形．③当BM ″=BA 时，∵OB ⊥AM ″，∴OM ″=OA =4，∴AM ″=8，∴t=8时，△ABM 是等腰三角形．综上所述，满足条件的t 的值为52或8s ．5. 解：（1）令y =x +6中x =0，则y =6，∴A （0，6）；令y =x +6中y =0，则x =﹣6，∴B （﹣6，0）．∵点C 在x 轴的正半轴，且OB =OC ，∴C （6，0）．设直线AC 的解析式为y =kx +b ，将A （0，6）、C （6，0）代入y =kx +b 中，得1,6k b =-=∴直线AC 的解析式为6y x =-+；（2）∵点D 为AC 的中点，∴点D 的坐标为（3，3），设BD 的直线解析式为：y =mx +n ，把B （﹣6，0），D （3，3）代入解析式可得：1,23m n ==，所以直线BD 的解析式为：123y x =+①， ∴G （0，2），∵A （0，6），∴AG =4．∵直线AC 的解析式为6y x =-+②，联立①②解得，x =3，y =3，∴D （3，3），设BP 时，P 点坐标为（﹣6+3t ，t ），当点P 在线段BD 上时，△APD 的面积S=12AG ×（x D ﹣x P ）=18﹣6t （0＜t ＜3）；当点P 在BD 的延长线上时， △APD 的面积S=12×4×（﹣6+3t ﹣3）=6t ﹣18（t ＞3）（3）要使△APC 是等腰三角形，且以PC 为腰，如备用图1，有两种情况：①AP =PC ，∴点P 是线段AC 的垂直平分线上，∵点D 是AC 的中点，∴点P 和点D 重合，不符合题意，②AC =PC =，可得：222(63t 6)t +-++=，可得：126,65t t ==，所以点P 的坐标为126(,)55-，（12，6）．三、面积问题1. 解：（1）由直线l 1：y =﹣x ﹣1可知：A （﹣1，0），B （0，﹣1），将直线l 1向上平移3个单位长度，得直线l 2：y =﹣x +2，设C （m ，n ），∵AD =2CD ，∴1+m =2n ，∵点C 在直线l 2：y =﹣x +2上，∴n =﹣m +2，∴C （1，1），设直线l 3的解析式为y =kx +b ，把A （﹣1，0）和C （1，1）代入得12k b ==， ∴直线l 3的解析式为1122y x =+．（2）令x =0，则y =12，S △ABC =12． 2. 解：（1）在y =x +3中，令32y =，则32x =-，∴33(,)22A -， ∵OD =1，∴D （0，﹣1），把点A ，D 的坐标代入l 2：y =kx +b ，可得5,13k b =-=-∴25:13l y x =--，在y =x +3中，令x =1，则y =4，∴B （1，4），∵l 2∥l 3，∴153k =-，∴直线l 3的解析式为51733y x =-+；（2）在y =x +3中，令x =0，则y =3，∴E （0，3），∴DE =3+1=4，∴S △ABD =DE （|x A |+|x B |）=5．3.解：（1）把m =2代入m +n =mn 得：2+n =2n ，解得：n =2，即1m n =，所以E 的纵坐标为1；把m =3代入m +n =mn 得：3+n =3n ，解得32n =，即2m n=，所以F 的纵坐标为2；（2）设直线AB 的解析式为y =kx +b ，从图象可知：与x 轴的交点坐标为（1，0）A （0，5），得：k =﹣1，b =5，即直线AB 的解析式是y =﹣x +5，设直线BC 的解析式为y =ax +c ，从图象可知：与y 轴的交点坐标为（0，﹣1），与x 轴的交点坐标为（1，0），得：a =1，c =﹣1，即直线BC 的解析式是y =x ﹣1，∵P (,)m m n，m +n =mn 且m ，n 是正实数， ∴除以n 得：1m m n +=∴P （m ，m ﹣1）即“完美点”P 在直线y =x ﹣1上；故答案为：y =x ﹣1；（3）∵直线AB 的解析式为：y =﹣x +5，直线BC 的解析式为y =x ﹣1，∴B （3，2），∵一、三象限的角平分线y =x 垂直于二、四象限的角平分线y =﹣x ，而直线y =x ﹣1与直线y =x 平行，直线y =﹣x +5与直线y =﹣x 平行，∴直线AM 与直线y =x ﹣1垂直，∵点B 是直线y =x ﹣1与直线AM 的交点，∴垂足是点B ，∵点C 是“完美点”，∴点C 在直线y =x ﹣1上，∴△MBC 是直角三角形，∵B （3，2），A （0，5），∴AB =AM =MB =∴BC =1，∴S △MBC =12BC ×BM ．4. 解：（1）将点A（2，0）代入直线y=kx+3，得0=2k+3，解得32k=-，∴332y x=-+．当x=0时，y=3．∴B（0，3），OB=3．∴A（2，0），OA=2，∴S△AOB=12OA•OB=3．（2）如图2，①当AB=BC时，点C与点A（2，0）关于y轴对称，故C（﹣2，0）符合题意；②当AB=AC时，由A（2，0），B（0，3）得到AB AC=AC C′，0）、C″2，0）．综上所述，符合条件的点C的坐标是（﹣2，0，02，0）；（3）∵M（3，0），∴OM=3，∴AM=3﹣2=1．由（1）知，S△AOB=3，∴S△PBM=S△AOB=3；①当点P在x轴下方时，S△PBM=S△PBM+S△APM=3，∴|y P|=3，∵点P在x轴下方，∴y P=﹣3．当y=﹣3时，代入332y x=-+得x=4．∴P（4，﹣3）；②当点P在x轴上方时，S△PBM=S△PBM﹣S△APM=3，∴|y P|=9，∵点P在x轴上方，∴y P=3．当y=9时，代入y=﹣x+3得，9=﹣x+3，解得x=﹣4．∴P（﹣4，9）．5. 解：（1）把x=0代入443y x=-+，解得：y=4，∴OB=4，把y=0代入443y x=-+，解得：x=3，∴OA=3，∵C（﹣4，0），∴OC=4，∴OB=OC，∵CD⊥AB，∴∠ACD+∠CAD=90°，∵∠ACD+∠OEC=90°，∴∠CAD=∠OEC，∴△COE≌△BOA（AA S）；（2）①∵ON⊥OM，∴∠MON=90°，∴∠COM+∠AON=90°，∵∠AON+∠BON=90°，∴∠COM=∠BON，∵△COE≌△BOA，∴∠OCM=∠OBN，∴△COM≌△BON（A S A），∴OM=ON，∠COM=∠BON，∵∠COM+∠MOE=90°，∴∠BON+∠MOE=90°，即∠MON=90°，∴△MON是等腰直角三角形；②∵△COM≌△BON，△OCM与△OAN面积相等，∴△BON与△OAN面积相等，即△OAN面积是△AOB面积的一半，得y N=2，解得：x=1.5，∴点N的坐标为（1.5，2）6. 解：（1）A（5，6）的变换点坐标是（6，﹣5），B（3，2）的变换点坐标是（3，﹣2），C（4，4）的变换点坐标是（4，﹣4）；（2）当a=b时，a=b=2，∵（2，2）的变换点为（2，﹣2），∵当a＜b时，点P（a，b）的变换点坐标为（b，﹣a），∴x＜2，∵（0，6）的变换点为（6，0），∴点P（a，b）的变换点经过（2，﹣2）和（6，0），设点M的函数解析式为y=kx+m，1,32k b==-∴13(2)2y x x=-<．（3）由题意，新的图形L的函数解析式为13(2)226(2)x xyx x⎧-<⎪=⎨⎪-≥⎩新图形L的拐点坐标为（2，﹣2），画出图形如图所示．当y=kx+1过点（2，﹣2）时，有﹣2=2k+1，解得：32k=-；当y=kx+1与y=2x﹣6平行时，k=2；当y=kx+1与132y x=-平行时，12k=．结合图形可知：直线y=kx+1与图形L有且只有两个公共点时，322k-<<且12k≠．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第14讲：一次函数与几何问题综合
22. （2012・无锡〉如图197T8所示，对于平面直角坐标系中的任意两点P ）（Q 』）、巳（七，力），我们把 &】
一文2丨+ ®—如叫做B 、P2两点间的直角距离，记作£（戸，几）・
（1）已知O 为坐标原点，动点PQ ，W 满足d （O ・P ） = l,请写岀工与y 之间满足的关
系式，并在所给的直角坐标系中画出所有符合条件的点P 所组成的图形；
⑵设Po （x o ,y o ）是一定点,Q&Q ）是直线y=ax+b±的动点，我们把”（P°,Q ）的最小值叫
做P 。

到直线了 =处十5的直角距离.试求点M （2,l 〉到直线罗=工+2的直角距离.
23. （2012・鞍山）如图1齐4-19所示，正方形ABCO 的边OA 、OC 在坐标轴上，点B 坐标（3,3）,将正方形
ABCO 绕点A 顺时针旋转角度«（0°<a<90°）,得到正方形ADEEMED 交线段OC 于点G,ED 的延长
线交线段BC 于点P ,连AP 、AG ・
（1〉求证:△ AOG 空△ADG ；
（2）求ZPAG 的度数;并判断线段OG 、PG 、B F 之间的数量关系，说明理由;
（3〉当Z 1 = Z2时，求直线PE 的解析式.
24. 如图19・4・20所示,ZXAOB 为正三角形，点B 的坐标为（2,0）,过点C （一2,0）
作直线Z 交A0于点D,交AB 于点E,且AADE 与△DCO 的面积相等，求直线I 的
解析式.1 ■ y ■ 」 0 1 X
图 19-4-18
图 19-4-20
25. 已知，直线I 、：y=kx+k-l 与直线l t
冷=4 + 1&+上Q 是正整数)及x 轴围成的三角形的面积为S*. (1) 求证:无论”取何值，直线与仏的交点均为定点；
(2) 求 S1+S2+S3 ------- $20)9 的值.
26 •如图(3)所示，在矩形ABCD 中，AB=2,动点P 在长方形的边BC.CD.DA 上沿B-C^D-A 的方. 向运动，且点P
与点B 、A 都不重合.图(b)是此运动过程中的面积y 与点P 经过的路程x 之间的函数图像的一部分.
濟结合以上信息回答下列问题：
(1) 长方形ABCD 中，边BC 的长为 _____________ ；
(2) 若长方形ABCD 中，M 为CD 边的中点，当点P 运动
到与点M 重合时，工= ___________ *= _____________ ;
(3〉当6<x<10时力与x 之间的函数关系式是 __________ ；〈4)利用第(3)问求得的结论，在图(b)所示中将相应的，与工的函数图像补充完整.
27.如右图所示.直线人的解析式为丿=一3乂+3,且厶与工轴交于点D,直线2经过点A,乩直线厶仏交于
点C.
(1) 求点D 的坐标；
(2) 求直线12的解析式；
(3〉求厶ADC 的面积；
(4) 在直线12上存在异于点C 的另一点P,使得△ ADP 与厶ADC 的面积相等, 请專琴写
出点P 的坐标.
(5) 在；廟上求作一点使得BM+CM 的和最小，直接写出点M 的坐标. B
p。