湖北省孝感市八校联谊2014-2015学年八年级数学上学期12月联考试题新人教版
2014届湖北八第一次校联考数学卷及答案(理)

鄂南高中 华师一附中 黄冈中学 黄石二中 荆州中学 襄阳四中 襄阳五中 孝感高中湖北省八校2014届高三第一次联考数学试题(理科)命题学校:黄冈中学 命题人:尚厚家 审题人:张卫兵考试时间:2013年12月13日下午 15︰00—17︰00 试卷满分150分 考试用时120分钟本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页。
全卷满分150分,考试时间120分钟.★ 祝考试顺利 ★注意事项:1.考生在答题前,请务必将自己的姓名、准考证号等信息填在答题卡上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号,答在试卷上无效.3.填空题和解答题用0.5毫米黑色墨水签字笔答在答题卡上每题对应的答题区域内. 答在试题卷上无效.第Ⅰ卷(选择题,共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.方程2250x x -+=的一个根是( ) A .12i +B .12i -+C .2i +D .2i -2.集合2{3,log }P a =,{,}Q a b =,若{0}P Q = ,则P Q = () A .{3,0}B .{3,0,2}C .{3,0,1}D .{3,0,1,2}3.下列命题,正确的是()A .命题:x ∃∈R ,使得210x -<的否定是:x ∀∈R ,均有210x -<.B .命题:若3x =,则2230x x --=的否命题是:若3x ≠,则2230x x --≠. C .命题:存在四边相等的四边形不是正方形,该命题是假命题. D .命题:cos cos x y =,则x y =的逆否命题是真命题.4.已知,x y 满足220240330x y x y x y +-⎧⎪-+⎨⎪--⎩≥≥≤,则关于22x y +的说法,正确的是( )A .有最小值1B .有最小值45C .有最大值13D .有最小值2555.函数32()(0,)f x ax bx cx d a x =+++≠∈R 有极值点,则() A .23b ac ≤ B. 23b ac ≥ C .23b ac < D . 23b ac >6.一个几何体的三视图如图,则该几何体的体积为()A .13 B.23C .2D .1 7.△ABC 中,角,,A B C 成等差数列是sin (3cos sin )cos C A A B =+成立的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件8.在弹性限度内,弹簧所受的压缩力F 与缩短的距离l 按胡克定律F kl =计算.今有一弹簧原长80cm ,每压缩1cm 需0.049N 的压缩力,若把这根弹簧从70cm 压缩至50cm (在弹性限度内),外力克服弹簧的弹力做了( )功(单位:J ) A .0.196B .0.294C .0.686D .0.989.在正方体1111ABCD A B C D -中,E 是棱1CC 的中点,F 是侧面11BCC B内的动点,且1A F ∥平面1D AE ,记1A F 与平面11BCC B 所成的角为θ, 下列说法错误的是()A .点F 的轨迹是一条线段B .1A F 与1D E 不可能平行C .1A F 与BE 是异面直线D .tan 22θ≤10.若直线1y kx =+与曲线11||||y x x x x=+--有四个公共点,则k 的取值 集合是( )A .11{0,,}88-B .11[,]88-C .11(,)88-D .11{,}88-二、填空题:本大题共5小题,每小题5分,共25分. (一)必考题(11—14题)11.平面向量,a b 满足||1,||2==a b ,且()(2)7+⋅-=-a b a b ,则向量,a b 的夹角为______.12.已知正三角形内切圆的半径r 与它的高h 的关系是:13r h =,把这个结论推广到空间正四面体,则正四面体内切球的半径r 与正四面体高h 的关系是_________.11111正(主)视图 侧(左)视图俯视图第6题图A1D 1C D C1B B1A E F第9题图13.将函数sin(2)y x ϕ=+的图象向左平移4π个单位后得到的函数图象关于点4(,0)3π成中心对称,那么||ϕ的最小值为________.14.无穷数列{}n a 中,12,,,m a a a 是首项为10,公差为2-的等差数列;122,,,m m m a a a ++ 是首项为12,公比为12的等比数列(其中*3,m m ∈N ≥),并且对于任意的*n ∈N ,都有2n m n a a +=成立.若51164a =,则m 的取值集合为____________.记数列{}n a 的前n 项和为n S ,则使得12852013m S +≥ *3,)m m ∈(N ≥的m 的取值集合为____________.(二)选考题(请考生在15、16两题中任选一题作答.如果全选,则按第15题作答结果计分) 15.(选修4—1:几何证明选讲)已知⊙O 1和⊙O 2交于点C 和D ,⊙O 1上的点P 处 的切线交⊙O 2于A 、B 点,交直线CD 于点E ,M 是⊙O 2上的一点,若PE =2,EA =1,45AMB ∠= ,那么⊙O 2的半径为.16.(选修4—4:坐标系与参数方程)在极坐标系中,曲线1:4C ρ=上有3个不同的点到曲线2:sin()4C m πρθ+=的距离等于2,则______m =.三、解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)已知向量2(2sin(),2)3x πω=+a ,(2cos ,0)x ω=b (0)ω>,函数()f x =⋅a b 的图象与直线23y =-+的相邻两个交点之间的距离为π. (Ⅰ)求ω的值;(Ⅱ)求函数()f x 在[0,2]π上的单调递增区间.18.(本小题满分12分)设等差数列{}n a 的前n 项和为n S ,满足:2418,a a +=791S =.递增的等比数列{}n b 前n 项和为n T ,满足:12166,128,126k k k b b b b T -+===. (Ⅰ)求数列{}n a ,{}n b 的通项公式; (Ⅱ)设数列{}n c 对*n ∀∈N ,均有12112n n nc c c a b b b ++++= 成立,求122013c c c +++ .19.(本小题满分12分)如图,在直三棱柱111ABC A B C -中,底面△ABC 为等腰直角三角形,90ABC ∠= ,D 为棱1BB 上一点,且平面1DA C ⊥平面11AAC C .(Ⅰ)求证:D 为棱1BB 的中点;(Ⅱ)ABAA 1为何值时,二面角1A A D C --的平面角为60 .20.(本小题满分12分)如图,山顶有一座石塔BC ,已知石塔的高度为a .(Ⅰ)若以,B C 为观测点,在塔顶B 处测得地面上一点A 的俯角为α,在塔底C 处测得A 处的俯角为β,用,,a αβ表示山的高度h ;(Ⅱ)若将观测点选在地面的直线AD 上,其中D 是塔顶B 在地面上的射影.已知石塔高度20a =,当观测点E 在AD 上满足6010DE =时看BC 的视角(即BEC ∠)最大,求山的高度h .21.(本小题满分13分)已知n a 是关于x 的方程1210n n n x x x x --++++-= (0,2)x n n >∈N 且≥的根,证明:(Ⅰ)1112n n a a +<<<;(Ⅱ)11()22n n a <+.22.(本小题满分14分)已知函数()e 1x f x ax =--(e 为自然对数的底数). (Ⅰ)求函数()f x 的单调区间;(Ⅱ)当0a >时,若()0f x ≥对任意的x ∈R 恒成立,求实数a 的值;(Ⅲ)求证:22222232323ln 1ln 1ln 12(31)(31)(31)n n ⎡⎤⎡⎤⎡⎤⨯⨯⨯++++++<⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦.ABC DP M EO 1O 2 ABCA 1B 1C 1D 第19题图第20题湖北省八校2014届高三第一次联考 理科数学参考答案及评分细则一、选择题(每小题5分,共10小题)1—5A C B B D6—10 B A A B A 10. 答案:110,,88⎧⎫-⎨⎬⎩⎭注意到11()f x x x x x=+--是偶函数, 考察0x >的情形,2(01)2(1)x x y x x<≤⎧⎪=⎨>⎪⎩,作图0k =时,直线1y kx =+与曲线有四个交点,满足题意0k ≠时,若直线1y kx =+与2y x =相切,由21kx x +=得220kx x +-=,△=0, 18k =-直线绕(0,1)逆时针旋转,开始出现5个交点 顺时针旋转,3个交点18k =-符合题意.根据对称性,18k =也满足题意.二.填空题(每小题5分,共5小题)11.2π 12. 14r h = 13. 6π14. {}45,15,9;{}6第一个空2分,第二个空3分15.32216. 2m =±14. 答案:{}45,15,9;{}665111()642a ==,等比数列部分最少6项,即6m ≥ 由6251m m k ++⋅=,得(21)45k m += 0,1,2k ∴=时,45,15,9m =;1285212564m m S S a a a +=++++ 26430m S =+2211112m m S m m =-++-()g m =,(1)()g m g m +- =111022m m +-+,35m ∴≤≤时,(1)()g m g m +>即6m =时,2m S 最大,128564(6)302013m S g +∴≤+= 故12852013m S +=,则6m = 三、解答题(共5小题,共75分) 17. (Ⅰ)2()4sin()cos 3f x x x πωω=+1分134sin ()cos cos 22x x x ωωω⎡⎤=⋅-+⋅⎢⎥⎣⎦223cos 2sin cos x x x ωωω=-3(1cos 2)sin 2x x ωω=+-2cos(2)36x πω=++5分 由题意,T π=,2,12ππωω∴== 6分(Ⅱ)()2cos(2)36f x x π=++,[]0,2x π∈时,2,4666x ππππ⎡⎤+∈+⎢⎥⎣⎦故[]2,26x πππ+∈或[]23,46x πππ+∈时,()f x 单调递增9分即()f x 的单调增区间为511,1212ππ⎡⎤⎢⎥⎣⎦和1723,1212ππ⎡⎤⎢⎥⎣⎦12分 18. (Ⅰ)由题意24317742187()7912a a a a a S a +==⎧⎪⎨+===⎪⎩得349,13a a ==,则43n a n =- 2分 211k k b b b b -= ,1,k b b ∴方程2661280x x -+=的两根,得12,64k b b == 4分111(1)12611k k k b b qb q S q q---===-- ,12,64k b b ==代入求得2q =,2n n b ∴=6分(Ⅱ)由12112n n nc c ca b b b ++++=x0 y112121(2)n n n c c c a n b b b --+++=≥ 相减有1n n n nc a a b +=-4=22,42n n n n c b +∴≥==,9分又121ca b =,得110c = 210(1)2(2)n n n c n +=⎧=⎨≥⎩122013c c c ∴+++= 45201520161022226++++=-12分19.解:(Ⅰ)过点D 作DE ⊥A 1 C 于E 点,取AC 的中点F ,连BF ﹑EF∵面DA 1 C ⊥面AA 1C 1C 且相交于A 1 C ,面DA 1 C 内的直线DE ⊥A 1 C 故直线DE ⊥面11ACC A3分又∵面BA C ⊥面AA 1C 1C 且相交于AC ,易知BF ⊥AC ,∴BF ⊥面AA 1C 1C 由此知:DE ∥BF ,从而有D ,E ,F ,B 共面,又易知BB 1∥面AA 1C 1C ,故有DB ∥EF ,从而有EF ∥AA 1,又点F 是AC 的中点,所以DB =EF =21 AA 1=21BB 1,即D 为1BB 的中点 6分(Ⅱ)解法1:建立如图所示的直角坐标系, 设AA 1= 2b ,AB =BC =a ,则D (0,0,b ), A 1 (a ,0,2b ), C (0,a ,0)所以,),,0(),,0,(1b a DC b a DA -==设面DA 1C 的法向量为),,(z y x n =则0,00=-+⋅=+⋅+bz ay x bz y ax可取),,(a b b n --= 8分 又可取平面AA 1DB 的法向量 )0,,0(a BC m ==cos ,m n u r r222222200ab b aa b a ba b mn m n +-=⋅+⋅--⋅=⋅⋅=据题意有:21222=+a b b解得:ABAA 1=22=a b12分 (Ⅱ)解法2:延长A 1 D 与直线AB 相交于G ,易知CB ⊥面AA 1B 1B ,过B 作BH ⊥A 1 G 于点H ,连CH ,由三垂线定理知:A 1 G ⊥CH , 由此知∠CHB 为二面角A -A 1D - C 的平面角; 9分设AA 1= 2b ,AB =BC =a ;在直角三角形A 1A G 中,易知AB = BG .在∆Rt DBG 中,BH =DG BGBD ⋅=22ba ab +⋅,在∆Rt CHB 中,tan ∠CHB =BHBC=b b a 22+,据题意有:bb a 22+=tan 600 =3,解得:22=a b 所以ABAA1= 2.12分20. 解:(1)在△ABC 中,BAC αβ∠=-,90BCA β∠=+,由正弦定理得:sin sin BC ABBAC BCA=∠∠sin(90)cos sin()sin()a a AB ββαβαβ+∴==--则cos sin sin sin()a h AB a a βαααβ=⋅-=--=cos sin sin()a αβαβ⋅- 4分(2)设DE x =,20tan h BED x +∠=,tan hCED x∠= A 1C 1B 1B DOZ A 1C 1 B 1 A C BD HE FGtan tan tan 1tan tan BED CEDBEC BED CED ∠-∠∴∠=+∠⋅∠ 6分22020(20)(20)1x h h h h x x x==++++10(20)h h ≤+ 当且仅当(20)h hx x+=即(20)x h h =+时,tan BEC ∠最大,从而BEC ∠最大 由题意,(20)6010h h +=,解得180h = 12分21. (Ⅰ)设12()1nn n f x x xx x --=++++- ,则'12()(1)21n n f x nx n x x --=+-+++显然'()0f x >,()f x ∴在R +上是增函数(1)10(2)f n n =->≥11(1())122()11212n f -=--1()02n =-< ()f x ∴在1(,1)2上有唯一实根,即112n a << 4分假设1n n a a +≥,*1()k k n n a a k N +∴≥∈则1()n f a +=111111111n n n n n n n n n n n n a a a a a a a ++-+++++++-≥++++-11n n n n n a a a ->+++- ()n f a =1()()0n n f a f a +== ,矛盾,故1n n a a +<8分(Ⅱ)111111()()1()()()12222n n n n n n nn f a f a a a --⎡⎤-=+++--+++-⎢⎥⎣⎦11111(())(())()222n n n n n n n a a a ---+-++- 12n a >-(12n a > )()0n f a = ,11()()22n f =-11()22n n a ∴<+13分方法二:121nn n n nn a a a a --=+++由(Ⅰ)1n a -=12n n n n n a a a -+++ 12111()()()222nn ->+++ =11()22n -11()22n n a ∴<+22 (Ⅰ)'()xf x e a =-1分 0a ∴≤时,'()0f x >,()f x 在R 上单调递增。
新人教版数学2014-2015学年八上第一次月考试卷[1][含答案]
![新人教版数学2014-2015学年八上第一次月考试卷[1][含答案]](https://img.taocdn.com/s3/m/527af913c281e53a5802ff3f.png)
2014-2015学年【R】数学八(上)第一次月考卷(1)大海数学培训命题一.选择题(共10小题)1.如图,在△ABC中,BE是中线,AD是角平分线,AD与BE相交于点O,连接DE.其中正确的有()①AO是△ABE的中线②BO是△ABD的角平分线③DE是△ADC的中线(第1题)(第3题)(第6题)2.线段BC上有3个点P1、P2、P3,线段BC外有一点A,把A和B、P1、P2、P3、C连5.(2014•泰山区模拟)已知三角形的三边长分别为3、8、x,若x的值为偶数,则x的(第7题)(笫8题)(第10题)10.(2014•遂宁)如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,11.(2014•抚州)如图,a∥b,∠1+∠2=75°,则∠3+∠4=_________.12.(2014•抚顺)将正三角形、正四边形、正五边形按如图所示的位置摆放.如果∠3=32°,那么∠1+∠2=_________度.(第12)(第13题)(第14题)13.(2013•建邺区一模)如图,∠1+∠2+∠3+∠4+∠5=_________°.14.(2010•贵港)如图所示,已知O是四边形ABCD内一点,OB=OC=OD,∠BCD=∠BAD=75°,则∠ADO+∠ABO=_________度.15.(2014•老河口市模拟)如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为_________.(第15题)(第16题)(第17题)16.(2013•长沙)如图,BD是∠ABC的平分线,P为BD上的一点,PE⊥BA于点E,PE=4cm,则点P到边BC的距离为_________cm.17.(2013•海门市二模)如图,在△ABC中,AD为BC边上的中线.已知AC=5,AD=4,则AB的取值范围是_________.18.如图,已知点P为△ABC三条内角平分线AD、BE、CF的交点,作DG⊥PC于G,则(第18题)(第19题)19.(2012•香坊区三模)如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为8,则BE=_________.20.(2005•荆门)如图,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3=_________度.三.解答题(共9小题)21.(2009•嘉兴)在四边形ABCD中,∠D=60°,∠B比∠A大20°,∠C是∠A的2倍,求∠A,∠B,∠C的大小.22.小明在计算一个多边形的内角和,求得的内角和为2220°,经过检查发现少加了一个内角,请问这个内角为多少度?这个多边形是几边形?23.一个多边形除一个内角∠A外,其余所有角之和为2190°,你能求出这个多边形的边数及∠A度数吗?24.(2014•吉林)如图,△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE,求证:△ABD≌△AEC.25.(2014•宜昌)如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.(1)求∠CAD的度数;(2)延长AC至E,使CE=AC,求证:DA=DE.26.(2014•陕西)如图,在Rt△ABC中,∠ABC=90°,点D在边AB上,使DB=BC,过点D作EF⊥AC,分别交AC于点E,CB的延长线于点F.求证:AB=BF.27.(2014•沙坪坝区一模)已知:如图,在梯形ABCD中,AB∥CD,AD=BC,AB=10,CD=18,∠ADC=60°,过BC上一点E作直线EH,交CD于点F,交AD的延长线于点H,且EF=FH.(1)求梯形ABCD的面积;(2)求证:AD=DH+BE.28.(2013•河北一模)已知,在△ABC中,AB=AC,在射线CA上截取线段CE,在射线AB上截取线段BD,连接DE,DE所在直线交直线BC于点M.(1)如图1,当点E在线段AC上时,点D在AB的延长线上时,若BD=CE,请判断线段MD和线段ME的数量关系,并证明你的结论.(2)如图2,当点E在CA的延长线上,点D在AB的延长线上时,若BD=CE,则(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由.(3)如图3,当点E在CA的延长线上,点D在线段AB上(点D不与A、B重合),DE 所在直线与直线BC交于点M,若CE=mBD,(m>1),请直接写出线段MD与线段ME 的数量关系.2014-2015学年【R】数学八(上)第一次月考卷参考答案与试题解析一.选择题(共10小题)1.如图,在△ABC中,BE是中线,AD是角平分线,AD与BE相交于点O,连接DE.其中正确的有()①AO是△ABE的中线②BO是△ABD的角平分线③DE是△ADC的中线④ED是△EBC的中线.2.线段BC上有3个点P1、P2、P3,线段BC外有一点A,把A和B、P1、P2、P3、C连周长之差为()4.(2013•莘县模拟)在直角坐标系中A(2,0),B(﹣3,﹣4),O(0,0),则△AOB的=DE∥AB,交AC于E,则∠ADE的大小是()BAD=∠×7.(2014•临沂)如图,已知l1∥l2,∠A=40°,∠1=60°,则∠2的度数为()8.(2014•泰安)如图,把一直尺放置在一个三角形纸片上,则下列结论正确的是()10.(2014•遂宁)如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是()××二.填空题(共10小题)11.(2014•抚州)如图,a∥b,∠1+∠2=75°,则∠3+∠4=105°.那么∠1+∠2=70度.5=540°BAD=75°,则∠ADO+∠ABO=135度.的一个动点,若PA=2,则PQ的最小值为2.则点P到边BC的距离为4cm.则AB的取值范围是3<AB<13.,则∠PDG等于(A)AD于点E,且四边形ABCD的面积为8,则BE=.BE==223=135度.21.(2009•嘉兴)在四边形ABCD中,∠D=60°,∠B比∠A大20°,∠C是∠A的2倍,24.(2014•吉林)如图,△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE,求证:△ABD≌△AEC.(1)求∠CAD的度数;(2)延长AC至E,使CE=AC,求证:DA=DE.CAD=∠26.(2014•陕西)如图,在Rt△ABC中,∠ABC=90°,点D在边AB上,使DB=BC,过点D作EF⊥AC,分别交AC于点E,CB的延长线于点F.求证:AB=BF.CD=18,∠ADC=60°,过BC上一点E作直线EH,交CD于点F,交AD的延长线于点H,且EF=FH.(1)求梯形ABCD的面积;(2)求证:AD=DH+BE.,=×=56AB上截取线段BD,连接DE,DE所在直线交直线BC于点M.(1)如图1,当点E在线段AC上时,点D在AB的延长线上时,若BD=CE,请判断线段MD和线段ME的数量关系,并证明你的结论.(2)如图2,当点E在CA的延长线上,点D在AB的延长线上时,若BD=CE,则(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由.(3)如图3,当点E在CA的延长线上,点D在线段AB上(点D不与A、B重合),DE 所在直线与直线BC交于点M,若CE=mBD,(m>1),请直接写出线段MD与线段ME 的数量关系.。
2014-2015年湖北省孝感市孝南区八年级上学期数学期中试卷与答案
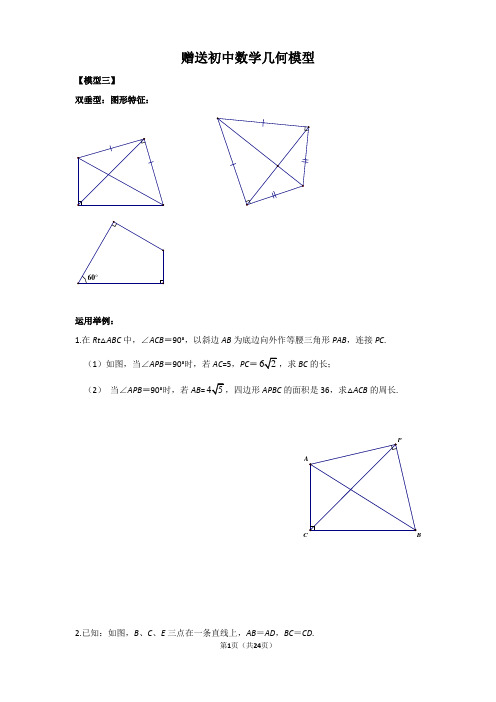
赠送初中数学几何模型【模型三】双垂型:图形特征:60°运用举例:1.在Rt△ABC中,∠ACB=90°,以斜边AB为底边向外作等腰三角形PAB,连接PC. (1)如图,当∠APB=90°时,若AC=5,PC=62,求BC的长;(2)当∠APB=90°时,若AB=45APBC的面积是36,求△ACB的周长.P 2.已知:如图,B、C、E三点在一条直线上,AB=AD,BC=CD.(1)若∠B=90°,AB=6,BC=23,求∠A的值;(2)若∠BAD+∠BCD=180°,cos∠DCE=35,求ABBC的值.3.如图,在四边形ABCD中,AB=AD,∠DAB=∠BCD=90°,(1)若AB=3,BC+CD=5,求四边形ABCD的面积(2)若p= BC+CD,四边形ABCD的面积为S,试探究S与p之间的关系。
DBC2014-2015学年湖北省孝感市孝南区八年级(上)期中数学试卷一.选择题1.(3分)以下是回收,绿色包装,节水,低碳四个标志,其中是轴对称图形的是()A.B. C.D.2.(3分)在平面直角坐标系中,点(3,﹣2)关于y轴对称的点的坐标是()A.(3,2) B.(3,﹣2)C.(﹣3,2)D.(﹣3,﹣2)3.(3分)下列长度的三条线段,不能组成三角形的是()A.3,8,4 B.4,9,6 C.15,20,8 D.9,15,84.(3分)画△ABC的BC边上的高,正确的是()A. B. C.D.5.(3分)如图,△ABC中,点D在AB边上,∠A=∠1,∠B=∠2,则△ABC的形状是()A.锐角三角形B.直角三角形C.钝角三角形D.无法确定6.(3分)若一个正多边形的一个外角是36°,则这个正多边形的边数是()A.7 B.8 C.9 D.107.(3分)如图,在下列条件中,不能直接证明△ABD≌△ACD的是()A.BD=DC,AB=AC B.∠ADB=∠ADC,BD=DCC.∠B=∠C,∠BAD=∠CAD D.∠B=∠C,BD=DC8.(3分)等腰三角形中有一个内角等于40゜,其余两个角的度数为()A.40゜,100゜B.70゜,70゜C.40゜,100゜或70゜,70゜D.60゜,80゜9.(3分)已知△ABC中,AB=AC,下列结论:①若AB=BC,则△ABC是等边三角形;②若∠A=60゜,则△ABC是等边三角形;③若∠B=60゜,则△ABC是等边三角形,其中正确的有()A.0个 B.1个 C.2个 D.3个10.(3分)如图,在△ABC中,BC⊥AC,点M,N分别在AB,AC上,MN是AC的垂直平分线,则下列判断:①AM=CM,②∠2=∠B,③AM=BM,其中错误个数是()A.0个 B.1个 C.2个 D.3个11.(3分)如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB,BD=2CD,DE=3,则BC的长为()A.7 B.8 C.9 D.1012.(3分)如图,△ABC中,AB=AC,BD平分∠ABC交AC于G,DM∥BC交∠ABC的外角平分线于M,交AB,AC于F,E,以下结论:①MB⊥BD,②FD=EC,③EC=EF+DG,④CE=,其中一定正确的有()A.1个 B.2个 C.3个 D.4个二.填空题13.(3分)如图,AB=AC,要使△ABE≌△ACD,应添加的条件是(添加一个条件即可).14.(3分)已知点P(a+1,2a﹣5)关于x轴对称点在第一象限,则符合条件a 的整数值为.15.(3分)如图,AD,CE是△ABC的高,已知AD=10,CE=9,AB=12,则BC=.16.(3分)如图,∠A=∠1=36°,∠C=72°,则图中共有个等腰三角形.17.(3分)如图,△ABC中,∠ACB=90゜,将△ABC的边BC沿∠ACB的平分线CD折叠到B′C,B′在AC上.若∠B′DA=20゜,则∠B=.18.(3分)如图,这是由边长为1的等边三角形摆出的一系列图形,按这种方式摆下去,则第n个图形的周长是.三.解答题19.(6分)如图,某校准备在校内一块四边形ABCD草坪内栽上一颗银杏树,要求银杏树的位置点P到边AB,BC的距离相等,并且点P到点A,D的距离也相等,请用尺规作图作出银杏树的位置点P(不写作法,保留作图痕迹)20.(8分)如图,△ABC中,点D是AC边上一点,若AB=BD=AC,∠DBC=30°,求∠BDC的度数.21.(10分)如图,六边形ABCDEF的内角都相等,∠1=60°.(1)求证:ED∥AB;(2)若去掉“∠1=60°”这个条件,其余不变,上述结论是否仍成立,请说明理由.22.(10分)在平面直角坐标系中,△ABC的三个顶点的位置如图所示(顶点在格点上).现将△ABC沿某直线翻折,使点A变换为点A′,A点坐标为(﹣2,3),A′的坐标为(4,3).(1)指出其对称轴,画出翻折后的△A′B′C′,直接写出点B′,C′的坐标.对称轴是:,B′(,)C′(,)(2)若△ABC内部一点P的坐标(a,b),则点P的对称点P′的坐标是(,)(3)求△A′B′C′的面积.23.(10分)如图,在△ABC中,D,E分别是AB,AC上的一点,BE与CD交于点O,给出下列四个条件:①∠DBO=∠ECO;②∠BDO=∠CEO;③BD=CE;④OB=OC.(1)上述四个条件中,哪两个可以判定△ABC是等腰三角形?(2)选择第(1)题中的一种情形为条件,试说明△ABC是等腰三角形.24.(11分)已知△ABC与△ADE均为等边三角形,点A,E在BC的同侧.(1)如图甲,点D在BC上,求证:CE+CD=AC;(2)如图乙,若点D在BC的延长线上,其它条件不变,上述结论是否成立?若成立,请予以证明,若不成立,请说明理由.25.(11分)如图,已知点A(a,0),B(0,b),且(a+2)2+|b﹣4|=0,以B 点为直角顶点在第二象限作等腰直角△ABC.(1)填空:a=,b=;(2)求C点的坐标;(3)在坐标平面内是否存在点P(不与点C重合),使△PAB与△ABC全等?若存在,请直接写出满足条件的所有P点的坐标(不需要过程);若不存在,请说明理由.2014-2015学年湖北省孝感市孝南区八年级(上)期中数学试卷参考答案与试题解析一.选择题1.(3分)以下是回收,绿色包装,节水,低碳四个标志,其中是轴对称图形的是()A.B. C.D.【解答】解:A、不是轴对称图形,故本选项错误;B、不是轴对称图形,故本选项错误;C、是轴对称图形,故本选项正确;D、不是轴对称图形,故本选项错误.故选:C.2.(3分)在平面直角坐标系中,点(3,﹣2)关于y轴对称的点的坐标是()A.(3,2) B.(3,﹣2)C.(﹣3,2)D.(﹣3,﹣2)【解答】解:点(3,﹣2)关于y轴对称的点的坐标是(﹣3,﹣2),故选:D.3.(3分)下列长度的三条线段,不能组成三角形的是()A.3,8,4 B.4,9,6 C.15,20,8 D.9,15,8【解答】解:A,∵3+4<8∴不能构成三角形;B,∵4+6>9∴能构成三角形;C,∵8+15>20∴能构成三角形;D,∵8+9>15∴能构成三角形.故选:A.4.(3分)画△ABC的BC边上的高,正确的是()A. B. C.D.【解答】解:画△ABC的BC边上的高,即过点A作BC边的垂线.故选:C.5.(3分)如图,△ABC中,点D在AB边上,∠A=∠1,∠B=∠2,则△ABC的形状是()A.锐角三角形B.直角三角形C.钝角三角形D.无法确定【解答】解:由三角形的内角和定理得,∠A+∠B+∠1+∠2=180°,∵∠A=∠1,∠B=∠2,∴2(∠1+∠2)=180°,∴∠1+∠2=90°,即∠ACB=90°,∴△ABC是直角三角形.故选:B.6.(3分)若一个正多边形的一个外角是36°,则这个正多边形的边数是()A.7 B.8 C.9 D.10【解答】解:360°÷36°=10,所以这个正多边形是正十边形.故选:D.7.(3分)如图,在下列条件中,不能直接证明△ABD≌△ACD的是()A.BD=DC,AB=AC B.∠ADB=∠ADC,BD=DCC.∠B=∠C,∠BAD=∠CAD D.∠B=∠C,BD=DC【解答】解:∵AD=AD,A、当BD=DC,AB=AC时,利用SSS证明△ABD≌△ACD,故正确;B、当∠ADB=∠ADC,BD=DC时,利用SAS证明△ABD≌△ACD,故正确;C、当∠B=∠C,∠BAD=∠CAD时,利用AAS证明△ABD≌△ACD,故正确;D、当∠B=∠C,BD=DC时,符合SSA的位置关系,不能证明△ABD≌△ACD,故错误.故选:D.8.(3分)等腰三角形中有一个内角等于40゜,其余两个角的度数为()A.40゜,100゜B.70゜,70゜C.40゜,100゜或70゜,70゜D.60゜,80゜【解答】解:分情况讨论:(1)若等腰三角形的顶角为40°时,另外两个内角=(180°﹣40°)÷2=70°;(2)若等腰三角形的底角为40°时,它的另外一个底角为40°,顶角为180°﹣40°﹣40°=100°.故另外两个内角的度数分别为:40°、100°或70°、70°.故选:C.9.(3分)已知△ABC中,AB=AC,下列结论:①若AB=BC,则△ABC是等边三角形;②若∠A=60゜,则△ABC是等边三角形;③若∠B=60゜,则△ABC是等边三角形,其中正确的有()A.0个 B.1个 C.2个 D.3个【解答】解:∵AB=AC,AB=BC,∴AB=AC=BC,∴△ABC是等边三角形,∴①正确;∵AB=AC,∠A=60°,∴△ABC是等边三角形,∴②正确;∵AB=AC,∠B=60°,∴△ABC是等边三角形,∴③正确;正确的有3个,故选:D.10.(3分)如图,在△ABC中,BC⊥AC,点M,N分别在AB,AC上,MN是AC的垂直平分线,则下列判断:①AM=CM,②∠2=∠B,③AM=BM,其中错误个数是()A.0个 B.1个 C.2个 D.3个【解答】解:∵NM是AC的垂直平分线,∴AM=CM,∴①正确;且∠1=∠A,∵BC⊥AC,∴∠1+∠2=∠A+∠B=90°,∴∠2=∠B,∴②正确;∴BM=CM,∴AM=BM,∴③正确;所以没有错误的结论,故选:A.11.(3分)如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB,BD=2CD,DE=3,则BC的长为()A.7 B.8 C.9 D.10【解答】解:∵∠ACB=90°,AD平分∠BAC,DE⊥AB,∴CD=DE=3,∵BD=2CD,∴BD=2×3=6,∴BC=BD+CD=6+3=9.故选:C.12.(3分)如图,△ABC中,AB=AC,BD平分∠ABC交AC于G,DM∥BC交∠ABC的外角平分线于M,交AB,AC于F,E,以下结论:①MB⊥BD,②FD=EC,③EC=EF+DG,④CE=,其中一定正确的有()A.1个 B.2个 C.3个 D.4个【解答】解:如图,∵BD分别是∠ABC及其外角的平分线,∴∠MBD=180°=90°,故MB⊥BD,①成立;∵DM∥BC,∴,而AB=AC,∴BF=CE;∵DF∥BC,∴∠FDB=∠DBC;∵∠FBD=∠DBC,∴∠FBD=∠FDB,∴FD=BF,FD=EC,②成立;∵∠DBM=90°,MF=DF,∴BF=DM,而CE=BF,∴CE=DM,④成立.故选:C.二.填空题13.(3分)如图,AB=AC,要使△ABE≌△ACD,应添加的条件是∠B=∠C或AE=AD(添加一个条件即可).【解答】解:添加∠B=∠C或AE=AD后可分别根据ASA、SAS判定△ABE≌△ACD.故答案为:∠B=∠C或AE=AD.14.(3分)已知点P(a+1,2a﹣5)关于x轴对称点在第一象限,则符合条件a 的整数值为0、1、2.【解答】解:∵点P(a+1,2a﹣5)关于x轴对称点在第一象限,∴点P在第四象限,∴,解不等式①得,a>﹣1,解不等式②得,a<,所以,a的取值范围是﹣1<a<,∵a是整数,∴a=0、1、2.故答案为:0、1、2.15.(3分)如图,AD,CE是△ABC的高,已知AD=10,CE=9,AB=12,则BC=.【解答】解:∴△ABC的面积=AB•CE=BC•AD,∴AB•CE=BC•AD,∵AD=10,CE=9,AB=12,∴BC===.故答案为.16.(3分)如图,∠A=∠1=36°,∠C=72°,则图中共有3个等腰三角形.【解答】解:∵∠1=36°,∠C=72°,∴∠BDC=180°﹣∠1﹣∠C=72°,∴BD=BC,∴△BDC为等腰三角形;∵∠A=36°,且∠A+∠ABD=∠BDC,∴∠ABD=∠BDC﹣∠A=72°﹣36°=36°,∴DA=DC,∴△ABD为等腰三角形;∵∠1=36°,∴∠ABC=∠ABD+∠1=72°=∠C,∴AB=AC,∴△ABC为等腰三角形,故答案为:3.17.(3分)如图,△ABC中,∠ACB=90゜,将△ABC的边BC沿∠ACB的平分线CD折叠到B′C,B′在AC上.若∠B′DA=20゜,则∠B=55゜.【解答】解:∵将△ABC的边BC沿∠ACB的平分线CD折叠到B′C,B′在AC上,∴∠ACD=∠BCD,∠BDC=∠B′DC,∵∠ACB=90°,∠B′DA=20°,∠BCD=45°∴∠CDB=×(180°﹣20°)=80°,∠BCD=45°∴∠B=180°﹣45°﹣80°=55°,故答案为:55°.18.(3分)如图,这是由边长为1的等边三角形摆出的一系列图形,按这种方式摆下去,则第n个图形的周长是2+n.【解答】解:由已知一系列图形观察图形依次的周长分别是:(1)2+1=3,(2)2+2=4,(3)2+3=5,(4)2+4=6,(5)2+5=7,…,所以第n个图形的周长为:2+n.故答案为:2+n.三.解答题19.(6分)如图,某校准备在校内一块四边形ABCD草坪内栽上一颗银杏树,要求银杏树的位置点P到边AB,BC的距离相等,并且点P到点A,D的距离也相等,请用尺规作图作出银杏树的位置点P(不写作法,保留作图痕迹)【解答】解:如图所示:P点即为所求.20.(8分)如图,△ABC中,点D是AC边上一点,若AB=BD=AC,∠DBC=30°,求∠BDC的度数.【解答】解:∵AB=BD=AC,∴∠ABC=∠DCB,∠A=∠ADB,设∠BDC=x°,则∠C=180°﹣∠BDC﹣∠DBC=180°﹣x°﹣30°=150°﹣x°,∴∠ABC=150°﹣x°,∴∠ABD=∠ABC﹣∠DBC=150°﹣x°﹣30°=120°﹣x°,在△ABD中,∠A=∠ADB=180°﹣∠BDC=180°﹣x°,∴∠ABD=180°﹣2(180°﹣x°)=2x°﹣180°,∴120﹣x=2x﹣180,解得x=100,即∠BDC=100°.21.(10分)如图,六边形ABCDEF的内角都相等,∠1=60°.(1)求证:ED∥AB;(2)若去掉“∠1=60°”这个条件,其余不变,上述结论是否仍成立,请说明理由.【解答】(1)证明:六边形的内角和为:(6﹣2)×180°=720°.∵六边形ABCDEF的内角都相等,∴每个内角的度数为:720°÷6=120°.又∵∠1=60°,四边形ABCD的内角和为360°,∴∠CDA=360°﹣∠DAB﹣∠B﹣∠C=360°﹣60°﹣120°﹣120°=60°,∴∠EDA=120°﹣∠CDA=120°﹣60°=60°,∴∠EDA=∠DAB=60°,∴AB∥DE(内错角相等,两直线平行).(2)成立;∵六边形ABCDEF的内角都相等,∴每个内角的度数为:720°÷6=120°.又∵四边形ABCD的内角和为360°,∴∠CDA+∠1=360°﹣120°﹣120°=120°,∵∠2+∠CDA=120°,∴∠1=∠2,∴AB∥DE(内错角相等,两直线平行).22.(10分)在平面直角坐标系中,△ABC的三个顶点的位置如图所示(顶点在格点上).现将△ABC沿某直线翻折,使点A变换为点A′,A点坐标为(﹣2,3),A′的坐标为(4,3).(1)指出其对称轴,画出翻折后的△A′B′C′,直接写出点B′,C′的坐标.对称轴是:直线x=1,B′(3,﹣1)C′(0,2)(2)若△ABC内部一点P的坐标(a,b),则点P的对称点P′的坐标是(2﹣a,2﹣b)(3)求△A′B′C′的面积.【解答】解:(1)如图所示,对称轴是直线x=1,B′(3,﹣1)C′(0,2).故答案为:直线x=1;3,﹣1;0,2;(2)∵P的坐标(a,b),对称轴是直线x=1,∴P′的横坐标=2﹣a,纵坐标=2﹣b,∴P′(2﹣a,2﹣b).故答案为:2﹣a,2﹣b;(3)S=4×4﹣×1×4﹣×1×4﹣×3×3=16﹣2﹣2﹣=.△A′B′C′23.(10分)如图,在△ABC中,D,E分别是AB,AC上的一点,BE与CD交于点O,给出下列四个条件:①∠DBO=∠ECO;②∠BDO=∠CEO;③BD=CE;④OB=OC.(1)上述四个条件中,哪两个可以判定△ABC是等腰三角形?(2)选择第(1)题中的一种情形为条件,试说明△ABC是等腰三角形.【解答】解:(1)①③,①④,②③和②④;(2)以①④为条件,理由:∵OB=OC,∴∠OBC=∠OCB.又∵∠DBO=∠ECO,∴∠DBO+∠OBC=∠ECO+∠OCB,即∠ABC=∠ACB,∴AB=AC,∴△ABC是等腰三角形.24.(11分)已知△ABC与△ADE均为等边三角形,点A,E在BC的同侧.(1)如图甲,点D在BC上,求证:CE+CD=AC;(2)如图乙,若点D在BC的延长线上,其它条件不变,上述结论是否成立?若成立,请予以证明,若不成立,请说明理由.【解答】解:(1)证明:∵△ABC和△ADE均为等边三角形,∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°,∴∠BAD=∠CAE,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴BD=CE,∴CE+CD=BD+CD=BC=AC;(2)上述结论不成立,CE﹣CD=AC;∵△ABC和△ADE均为等边三角形,∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°,∴∠BAD=∠CAE,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴BD=CE,∴CE﹣CD=BD﹣CD=BC=AC.25.(11分)如图,已知点A(a,0),B(0,b),且(a+2)2+|b﹣4|=0,以B 点为直角顶点在第二象限作等腰直角△ABC.(1)填空:a=2,b=4;(2)求C点的坐标;(3)在坐标平面内是否存在点P(不与点C重合),使△PAB与△ABC全等?若存在,请直接写出满足条件的所有P点的坐标(不需要过程);若不存在,请说明理由.【解答】解:(1)∵(a+2)2+|b﹣4|=0,∴a+2=0,b﹣4=0,解得:a=﹣2,b=4;故答案为:﹣2,4;(2)如图1,过点C作CE⊥y轴于点E,∵∠ABC=90°,∴∠CBE+∠ABO=90°,∵∠ECB+∠CBE=90°,∴∠ECB=∠ABO,在△CBE和△BAO中,,∴△CBE≌△BAO(AAS),∴AO=BE,BO=EC,∵a=2,b=4,∴BO=CE=4,AO=BE=2,∴C(﹣4,6);(3)如图2,当P1A⊥AB,且AB=P1A,则△P1AB≌△ABC,故P1(﹣6,2),当P2B⊥AB,且AB=P2B,则△P2BA≌△ABC,故P2(4,2),当P3A⊥AB,且AB=P3A,则△P3AB≌△ABC,故P3(2,﹣2).。
湖北省孝感市八校联谊2014-2015学年七年级数学上学期12月联考试题新人教版

湖北省孝感市八校联谊2014-2015学年七年级数学上学期12月联考试题(本试卷满分120分,考试时间120分钟)一、精心选一选,相信自己的判断!(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中只有一项是符合题目要求的)1.a,b,c 三个数在数轴上的位置如图所示,则下列结论中错误的是 ( ) (A)a+b<0 (B)a+c<0(C)a -b>0 (D)b -2.若两个有理数的和是正数,那么一定有结论( )(A )两个加数都是正数; (B )两个加数有一个是正数;(C )一个加数正数,另一个加数为零; (D )两个加数不能同为负数 3.两个非零有理数的和是0,则它们的商为: ( )A 、0B 、-1C 、+1D 、不能确定 4.据科学家估计,地球的年龄大约是4600 000 000年,这个数用科学记数法表示为( )A.4. 6×108 ;B. 46×108 ;C. 4.6×109 ;D. 0.46×1010. 5.已知数轴上的三点A 、B 、C 分别表示有理数a ,1,1-,那么1+a 表示( ). A .A 、B 两点的距离 B .A 、C 两点的距离C .A 、B 两点到原点的距离之和D . A 、C 两点到原点的距离之和 6.下列各式中,去括号或添括号正确的是( )A 、c b a a c b a a +--=+--2)2(22 B 、)123(123-+-+=-+-y x a y x a C 、1253)]12(5[3+--=---x x x x x x D 、-)1()2(12-+--=+--a y x a y x 7.已知yxxn m n m 2652与-是同类项,则( ) A 、1,2==y x B 、0,3==y x C 、1,23==y x D 、1,3==y x 8.若23(2)0m n -++=,则2m n +的值为( ) A .4-B .0C . 1-D .49.下列两个方程的解相同的是( )A .方程635=+x 与方程42=xB .方程13+=x x 与方程142-=x xC .方程021=+x 与方程021=+x D .方程5)25(36=--x x 与3156=-x x 10.有两支同样长的蜡烛,一支能点燃4小时,另一支能点燃3小时,一次遇到停电,同时点燃这两支蜡烛,来电后同时吹灭,发现其中的一支是另一支的一半,停电时间为( )小时。
2014-2015学年八年级上学期期中联考数学试题(含答案)
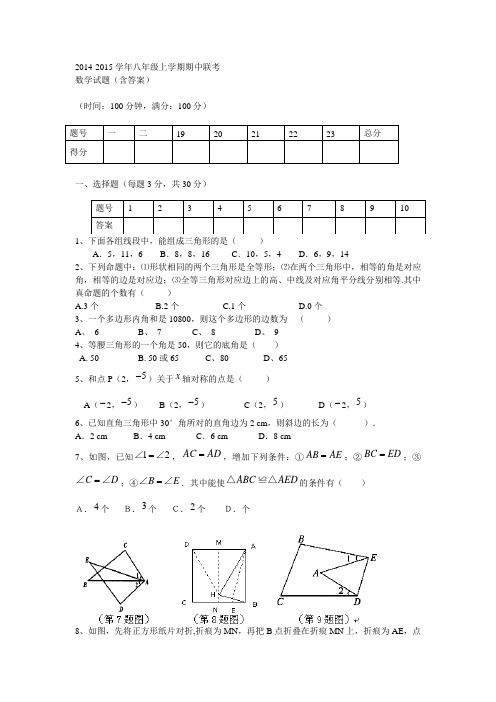
2014-2015学年八年级上学期期中联考 数学试题(含答案)(时间:100分钟,满分:100分)一、选择题(每题3分,共30分)1、下面各组线段中,能组成三角形的是( )A .5,11,6B .8,8,16C .10,5,4D .6,9,142、下列命题中:⑴形状相同的两个三角形是全等形;⑵在两个三角形中,相等的角是对应角,相等的边是对应边;⑶全等三角形对应边上的高、中线及对应角平分线分别相等.其中真命题的个数有( )A.3个B.2个C.1个D.0个 3、一个多边形内角和是10800,则这个多边形的边数为 ( ) A 、 6 B 、 7 C 、 8 D 、 9 4、等腰三角形的一个角是50,则它的底角是( ) A. 50 B. 50或65 C 、80 D 、65 5、和点P (2,5-)关于x 轴对称的点是( )A (-2,5-)B (2,5-)C (2,5)D (-2,5) 6、已知直角三角形中30°角所对的直角边为2 cm ,则斜边的长为( ). A .2 cm B .4 cm C .6 cm D .8 cm7、如图,已知12=∠∠,AC AD =,增加下列条件:①AB AE =;②BC ED =;③C D =∠∠;④B E =∠∠.其中能使ABC AED △≌△的条件有( )A.4个 B.3个 C.2个 D.个8、如图,先将正方形纸片对折,折痕为MN ,再把B 点折叠在折痕MN 上,折痕为AE ,点B 在MN 上的对应点为H ,沿AH 和DH 剪下,这样剪得的三角形中 ( ) A .AD DH AH ≠= B .AD DH AH ==C .DH AD AH ≠= D .AD DH AH ≠≠9、如图,把△ABC 纸片沿DE 折叠,当点A 落在四边形BCDE 内部时,∠A 与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( ) A .∠A =∠1+∠2 B .2∠A =∠1+∠2 C .3∠A =2∠1+∠2 D .3∠A =2(∠1+∠2)10、把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换.在自然界和日常生活中,大量地存在这种图形变换(如图1).结合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,两个对应三角形(如图2)的对应点所具有的性质是( ) A .对应点连线与对称轴垂直 B .对应点连线被对称轴平分C .对应点连线被对称轴垂直平分D .对应点连线互相平行二、填空题(每题3分,共24分)11、为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根 木条这样做的道理是_______________。
2014—2015学年度八年级数学第一次考试试卷分析 (1)

2014——2015学年度人教版第一学期八年级数学第一次考试试卷分析一、试题简析本次数学试题覆盖面全,难易程度适中,突出重点,灵活性较强。
多数试题都属于平时训练的重点内容。
试题主要特点如下:1、注重对基础知识和基本技能应用的考查。
如一题的1——11题,二题的1、2、3、6题,四题都注重对基本概念的应用的考查,三题是对最基本的运算技能的考查。
2、注重对基本数学能力的考查。
一题的3、11题,二题的8题考查学生的空间想象能力,七题注重考查学生的观察猜想和说理的能力,八题注重对学生的识图能力的考查,。
3、注重对数学思想方法的考查。
如一题12、13题,二题5、6、8题,四题2题,八题注重对数形结合思想的考查;一题12题,二题7题,四题,五、六题及八题注重渗透方程思想解决问题;二题4题是对整体思想的渗透。
4、注重对用数学意识和能力的引导和培养。
如一题12,二题7题,四、五、六、八题都注重学生解决实际问题能力的考查。
5、题目设计灵活,解决问题的方法开放。
能够起到对学生思维灵活性的引导和考查。
如一题7、12题,六、七、八题等题目灵活,方法多样,使得不同层次的学生有不同的解决问题的方法。
二、试卷分析全校共参考645人,其中数学单科最高分120分,最低分15分,120分24人。
全县及格率为70.2%,全校均分为75.6分。
三、教学建议与措施1.在新授课的教学中,注重对基础知识和基本技能强化和落实,最课标中的最基本要求,要做到个个过关,人人落实。
不能做夹生饭。
注意技能的形成必须有适量的习题训练做保障,不可以眼高手低。
2.在八(上)学期中,要注意对“实数”一章教材的深度处理,将二次根式的基本计算技能训练形成。
在教材的基础上,选择和增添一定量的相关计算加以训练和巩固.3.加强数形结合思想方法的培养。
八(上)学期的教材中集中体现了数形结合思想方法(如三角形全等和方位角),教学中要注意培养学生的观察能力和识图能力,使学生养成数与形很好的结合的习惯。
【真卷】2014-2015年湖北省孝感市孝南区八年级上学期数学期末试卷及答案

2014-2015学年湖北省孝感市孝南区八年级(上)期末数学试卷一、选择题(共10小题,每小题3分,满分30分)1.(3分)如果分式有意义,则x的取值范围是()A.2B.﹣3C.x≠2D.x≠﹣32.(3分)某红外线遥控器发出的红外线波长为0.000 000 94m,用科学记数法表示这个数是()A.9.4×10﹣7m B.9.4×107m C.9.4×10﹣8m D.9.4×108m 3.(3分)下列运算正确的是()A.a2+a3=a5B.a2•a3=a5C.(a2)3=a5D.a10÷a2=a5 4.(3分)如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠B=40゜,∠CAD=60゜,则∠BCD=()A.160゜B.120゜C.80゜D.100゜5.(3分)下列等式从左到右变形,属于因式分解的是()A.a(x﹣y)=ax﹣ay B.x2+2x﹣1=x(x+2)﹣1C.a2﹣a=a(a﹣1)D.a2﹣1=a(a﹣)6.(3分)如图,已知正六边形ABCDEF和正方形AGHF,则∠ABG的度数为()A.75°B.70°C.65°D.60°7.(3分)仔细观察图形,依据图形面积间的关系,不添加辅助线,便可得到一个熟悉的公式,这个公式是()A.(x﹣y)2=x2﹣xy+y2B.(x﹣y)2=x2﹣2xy+y2C.(x+y)2=x2+2xy+y2D.(x+y)2=x2+y28.(3分)如图,线段AC与BD相交于点O,且OA=OC,请添加一个条件,使△OAB≌△OCD,这个条件可以是()A.∠A=∠D B.OB=OD C.∠B=∠C D.AB=DC9.(3分)如图,直线L是一条河,P,Q是两个村庄.欲在L上的某处修建一个水泵站,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是()A.B.C.D.10.(3分)如图,A,B是3×3的正方形网格中的两个格点,C也是网格中的一个格点,连接AC、BC,当△ABC为等腰三角形时,格点C的不同位置有()A.5个B.6个C.7个D.8个二、填空题(共6小题,每小题3分,满分18分)11.(3分)分解因式:x3﹣4x=.12.(3分)ab=2,a+b=3,则(a﹣b)2=.13.(3分)如图,已知△ABC是等边三角形,点D、E在BC的延长线上,G是AC上一点,且CG=CD,F是GD上一点,且DF=DE,则∠E=度.14.(3分)等腰三角形一边的长是4,另一边的长是8,则它的周长是.15.(3分)如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,已知AF=1,DF=DC=2,则BD=.16.(3分)如图为杨辉三角表,它可以帮助我们按规律写出(a+b)n(其中n 为正整数)展开式的系数,请仔细观察表中规律,填出(a+b)4的展开式中所缺的系数.(a+b)1=a+b;(a+b)2=a2+2ab+b2;(a+b)3=a3+3a2b+3ab2+b3;(a+b)4=a4+ a3b+ a2b2+ ab3+b4.三、解答题(共8小题,满分72分)17.(10分)计算和求值:①(﹣1)2014﹣(﹣)0+()﹣1②先化简,再求值:,其中x=.18.(6分)解方程:.19.(8分)如图,在△ABC中,∠C=90度.(1)用圆规和直尺在AC上作点P,使点P到A、B的距离相等;(保留作图痕迹,不写作法和证明)(2)当满足(1)的点P到AB、BC的距离相等时,求∠A的度数.20.(8分)△ABC在方格中的位置如图所示(图中每个小方格的边长均为1).(1)请你在方格上建立适当的平面直角坐标系使得A、B两点的坐标分别为A (4,3),B(3,1),求此时C点的坐标.(2)作出△ABC关于y轴对称的△A1B1C1,并写出A1、B1、C1的坐标.21.(8分)如图,在等腰直角三角形ABC中,AB=AC,点D在BC上,且∠ADB=60°,将△ADC沿AD翻折后点C后落在C′.(1)求∠CAD的度数;(2)连BC′,试判断△ABC′的形状,并说明理由.22.(10分)如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.(1)求证:AD=AE;(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.23.(10分)一项工程,甲,乙两公司合作,12天可以完成,共需付施工费102000元;如果甲,乙两公司单独完成此项工程,乙公司所用时间是甲公司的 1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元.(1)甲,乙两公司单独完成此项工程,各需多少天?(2)若让一个公司单独完成这项工程,哪个公司的施工费较少?24.(12分)(1)如图(1)在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:DE=BD+CE;(2)如图(2)将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请给出证明;若不成立,请说明理由.2014-2015学年湖北省孝感市孝南区八年级(上)期末数学试卷参考答案与试题解析一、选择题(共10小题,每小题3分,满分30分)1.(3分)如果分式有意义,则x的取值范围是()A.2B.﹣3C.x≠2D.x≠﹣3【分析】根据分式有意义,分母不等于0列式计算即可得解.【解答】解:由题意得,x﹣2≠0,解得x≠2.故选:C.2.(3分)某红外线遥控器发出的红外线波长为0.000 000 94m,用科学记数法表示这个数是()A.9.4×10﹣7m B.9.4×107m C.9.4×10﹣8m D.9.4×108m【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【解答】解:0.000 000 94=9.4×10﹣7.故选:A.3.(3分)下列运算正确的是()A.a2+a3=a5B.a2•a3=a5C.(a2)3=a5D.a10÷a2=a5【分析】根据同底数幂相乘,底数不变指数相加;幂的乘方,底数不变指数相乘;同底数幂相除,底数不变指数相减,对各选项计算后利用排除法求解.【解答】解:A、a2与a3不是同类项,不能合并,故本选项错误;B、a2•a3=a5,正确;C、应为(a2)3=a2×3=a6,故本选项错误;D、应为a10÷a2=a10﹣2=a8,故本选项错误.故选:B.4.(3分)如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠B=40゜,∠CAD=60゜,则∠BCD=()A.160゜B.120゜C.80゜D.100゜【分析】根据轴对称的性质可得∠D=∠∠B=60°,∠BCA=∠DCA,再根据∠DCA 的度数,进而得到答案.【解答】解:根据轴对称的性质可得∠D=∠∠B=60°,∵∠CAD=60゜,∴∠DCA=180°﹣60°﹣40°=80°,根据轴对称的性质可得∠BCA=∠DCA=80°,∴∠BCD=160°,故选:A.5.(3分)下列等式从左到右变形,属于因式分解的是()A.a(x﹣y)=ax﹣ay B.x2+2x﹣1=x(x+2)﹣1C.a2﹣a=a(a﹣1)D.a2﹣1=a(a﹣)【分析】根据因式分解是把一个多项式转化成几个整式积的形式,可得答案.【解答】解:A、是整式的乘法,故A错误;B、没把一个多项式转化成几个整式积的形式,故B错误;C、把一个多项式转化成几个整式积的形式,故C正确;D、没把一个多项式转化成几个整式积的形式,故D错误;故选:C.6.(3分)如图,已知正六边形ABCDEF和正方形AGHF,则∠ABG的度数为()A.75°B.70°C.65°D.60°【分析】正六边形的每个内角为120°,即可求∠BAF,正方形每个内角为90°,即可求∠GAF,进而求∠BAG的大小,根据AB=AG即可求∠ABG的度数.【解答】解:∵正六边形的每个内角为120°,正方形每个内角为90°,∴∠BAF=120°,∠GAF=90°,∴∠BAG=30°,又∵AB=AG,∴∠ABG==75°.故选:A.7.(3分)仔细观察图形,依据图形面积间的关系,不添加辅助线,便可得到一个熟悉的公式,这个公式是()A.(x﹣y)2=x2﹣xy+y2B.(x﹣y)2=x2﹣2xy+y2C.(x+y)2=x2+2xy+y2D.(x+y)2=x2+y2【分析】大正方形分成四部分:两个边长分别为x、y的正方形和两个长为x,宽为y的长方形,算出四部分的面积和就是大正方形的面积;由此算出面积联立等式即可.【解答】解:大正方形面积为:(x+y)2,大正方形面积=4个小图形的面积和=x2+y2+xy+xy,∴可以得到公式:(x+y)2=x2+2xy+y2.故选:C.8.(3分)如图,线段AC与BD相交于点O,且OA=OC,请添加一个条件,使△OAB≌△OCD,这个条件可以是()A.∠A=∠D B.OB=OD C.∠B=∠C D.AB=DC【分析】首先根据图形,可知∠AOB=∠COD,又由已知OA=OC,可知当OB=OD,根据SAS即可判定△OAB≌△OCD;又由∠A=∠D与∠B=∠C都不是全等三角形的对应角,即可判定A与C错误,又由SSA不能判定三角形全等,即可判定D错误.【解答】解:∵∠AOB=∠COD,OA=OC,A、∵∠A与∠D不是对应角,∴无法判定△OAB≌△OCD,故本选项错误;B、在△OAB和△OCD中,,∴△OAB≌△OCD(SAS),故本选项正确;C、∵∠B与∠C不是对应角,∴无法判定△OAB≌△OCD,故本选项错误;D、∵AB=DC与OA=OC,它们的夹角是∠A与∠C,而不是∠AOB=∠COD,∴无法判定△OAB≌△OCD,故本选项错误.故选:B.9.(3分)如图,直线L是一条河,P,Q是两个村庄.欲在L上的某处修建一个水泵站,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是()A.B.C.D.【分析】利用对称的性质,通过等线段代换,将所求路线长转化为两定点之间的距离.【解答】解:作点P关于直线L的对称点P′,连接QP′交直线L于M.根据两点之间,线段最短,可知选项D铺设的管道,则所需管道最短.故选:D.10.(3分)如图,A,B是3×3的正方形网格中的两个格点,C也是网格中的一个格点,连接AC、BC,当△ABC为等腰三角形时,格点C的不同位置有()A.5个B.6个C.7个D.8个【分析】分AB是腰长时,根据网格结构,找出一个小正方形与A、B顶点相对的顶点,连接即可得到等腰三角形,AB是底边时,根据线段垂直平分线上的点到线段两端点的距离相等,AB垂直平分线上的格点都可以作为点C,然后相加即可得解.【解答】解:如图,AB是腰长时,红色的4个点可以作为点C,AB是底边时,黑色的4个点都可以作为点C,所以,满足条件的点C的个数是4+4=8.故选:D.二、填空题(共6小题,每小题3分,满分18分)11.(3分)分解因式:x3﹣4x=x(x+2)(x﹣2).【分析】应先提取公因式x,再对余下的多项式利用平方差公式继续分解.【解答】解:x3﹣4x,=x(x2﹣4),=x(x+2)(x﹣2).故答案为:x(x+2)(x﹣2).12.(3分)ab=2,a+b=3,则(a﹣b)2=1.【分析】将a+b=3两边平方,利用完全平方公式化简,将ab的值代入计算求出a2+b2的值,所求式子利用完全平方公式展开,将各自的值代入计算即可求出值.【解答】解:将a+b=3平方得:(a+b)2=a2+2ab+b2=9,把ab=2代入得:a2+b2=5,则(a﹣b)2=a2﹣2ab+b2=5﹣4=1.故答案为:1.13.(3分)如图,已知△ABC是等边三角形,点D、E在BC的延长线上,G是AC上一点,且CG=CD,F是GD上一点,且DF=DE,则∠E=15度.【分析】由DF=DE,CG=CD,得出∠E=∠DFE,∠CDG=∠CGD,再由三角形的外角的意义得出∠GDC=∠E+∠DFE=2∠E,∠ACB=∠CDG+∠CGD=2∠CDG,从而得出∠ACB=4∠E,进一步求得答案即可.【解答】解:∵DF=DE,CG=CD,∴∠E=∠DFE,∠CDG=∠CGD,∵GDC=∠E+∠DFE,∠ACB=∠CDG+∠CGD,∴GDC=2∠E,∠ACB=2∠CDG,∴∠ACB=4∠E,∵△ABC是等边三角形,∴∠ACB=60°,∴∠E=60°÷4=15°.故答案为:15.14.(3分)等腰三角形一边的长是4,另一边的长是8,则它的周长是20.【分析】因为等腰三角形的两边分别为4和8,但没有明确哪是底边,哪是腰,所以有两种情况,需要分类讨论【解答】解:当4为底时,其它两边都为8,4、8、8可以构成三角形,周长为20;当4为腰时,其它两边为4和8,因为4+4=8,所以不能构成三角形,故舍去.所以答案只有20.故填20.15.(3分)如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,已知AF=1,DF=DC=2,则BD=3.【分析】首先证明∠FBD=∠CAD,证出△BDF≌△ADC,得出BD=AD=AF+DF=3【解答】解:∵AD⊥BC,BE⊥AC,∴∠BDF=∠ADC=∠BEC=90°,∴∠FBD+∠C=90°,∠CAD+∠C=90°,∴∠FBD=∠CAD,在△BDF和△ADC中,,∴△BDF≌△ADC(AAS),∴BD=AD,∵AD=AF+DF=1+2=3,∴BD=3.16.(3分)如图为杨辉三角表,它可以帮助我们按规律写出(a+b)n(其中n 为正整数)展开式的系数,请仔细观察表中规律,填出(a+b)4的展开式中所缺的系数.(a+b)1=a+b;(a+b)2=a2+2ab+b2;(a+b)3=a3+3a2b+3ab2+b3;(a+b)4=a4+ 4a3b+ 6a2b2+ 4ab3+b4.【分析】观察本题的规律,下一行的数据是上一行相邻两个数的和,根据规律填入即可.【解答】解:(a+b)4=a4+4a3b+6a2b2+4ab3+b4.三、解答题(共8小题,满分72分)17.(10分)计算和求值:①(﹣1)2014﹣(﹣)0+()﹣1②先化简,再求值:,其中x=.【分析】①原式第一项利用乘方的意义化简,第二项利用零指数幂法则计算,第三项利用负指数幂法则计算即可得到结果;②原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.【解答】解:①原式=1﹣1+2=2;②原式=÷=•=﹣x+1,当x=时,原式=.18.(6分)解方程:.【分析】观察两个分母可知,公分母为x﹣2,去分母,转化为整式方程求解,结果要检验.【解答】解:去分母,得5+(x﹣2)=﹣(x﹣1),去括号,得5+x﹣2=﹣x+1,移项,得x+x=1+2﹣5,合并,得2x=﹣2,化系数为1,得x=﹣1,检验:当x=﹣1时,x﹣2≠0,∴原方程的解为x=﹣1.19.(8分)如图,在△ABC中,∠C=90度.(1)用圆规和直尺在AC上作点P,使点P到A、B的距离相等;(保留作图痕迹,不写作法和证明)(2)当满足(1)的点P到AB、BC的距离相等时,求∠A的度数.【分析】(1)作线段AB的垂直平分线即可;(2)到一个角的两边距离相等的点在这个角的平分线上.那么点P是∠B的平分线和线段AB的垂直平分线的交点.【解答】解:(1)(2)连接BP.∵点P到AB、BC的距离相等,∴BP是∠ABC的平分线,∴∠ABP=∠PBC.又∵点P在线段AB的垂直平分线上,∴PA=PB,∴∠A=∠ABP.∴.20.(8分)△ABC在方格中的位置如图所示(图中每个小方格的边长均为1).(1)请你在方格上建立适当的平面直角坐标系使得A、B两点的坐标分别为A (4,3),B(3,1),求此时C点的坐标.(2)作出△ABC关于y轴对称的△A1B1C1,并写出A1、B1、C1的坐标.【分析】(1)根据题意画出坐标系,根据点C在坐标系中的位置即可得出C点坐标;(2)根据关于y轴对称的点的坐标特点画△A1B1C1出即可.【解答】解:(1)如图所示,由图可知,C(1,2);(2)如图所示,△ABC与△A1B1C1关于y轴对称,∵A(4,3),B(3,1),C(1,2),∴A1(﹣4,3),B1(﹣3,1),C1(﹣1,2)21.(8分)如图,在等腰直角三角形ABC中,AB=AC,点D在BC上,且∠ADB=60°,将△ADC沿AD翻折后点C后落在C′.(1)求∠CAD的度数;(2)连BC′,试判断△ABC′的形状,并说明理由.【分析】(1)证明∠C=45°;运用三角形外角的性质,即可解决问题.(2)借助翻折变换,求出∠BAC′=60°;证明AB=AC′,即可解决问题.【解答】解:(1)∵△ABC为等腰直角三角形,∴∠C=45°;∵∠ADB=60°,∴∠CAD=60°﹣45°=15°.(2)△ABC′是等边三角形;理由如下:由题意得:∠C′AD=∠CAD=15°,∴∠CAC′=30°,∴∠C′AB=90°﹣30°=60°;∵AB=AC,AC′=AC,∴AB=AC′,∴△ABC′为等边三角形.22.(10分)如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.(1)求证:AD=AE;(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.【分析】(1)根据全等三角形的判定方法,证明△ACD≌△ABE,即可得出AD=AE,(2)根据已知条件得出△ADO≌△AEO,得出∠DAO=∠EAO,即可判断出OA是∠BAC的平分线,即OA⊥BC.【解答】(1)证明:在△ACD与△ABE中,∵,∴△ACD≌△ABE,∴AD=AE.(2)答:直线OA垂直平分BC.理由如下:连接BC,AO并延长交BC于F,在Rt△ADO与Rt△AEO中,∴Rt△ADO≌Rt△AEO(HL),∴∠DAO=∠EAO,即OA是∠BAC的平分线,又∵AB=AC,∴OA⊥BC且平分BC.23.(10分)一项工程,甲,乙两公司合作,12天可以完成,共需付施工费102000元;如果甲,乙两公司单独完成此项工程,乙公司所用时间是甲公司的 1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元.(1)甲,乙两公司单独完成此项工程,各需多少天?(2)若让一个公司单独完成这项工程,哪个公司的施工费较少?【分析】(1)设甲公司单独完成此项工程需x天,则乙工程公司单独完成需1.5x 天,根据合作12天完成列出方程求解即可.(2)分别求得两个公司施工所需费用后比较即可得到结论.【解答】解:(1)设甲公司单独完成此项工程需x天,则乙公司单独完成此项工程需1.5x天.根据题意,得+=,解得x=20,经检验知x=20是方程的解且符合题意.1.5x=30故甲公司单独完成此项工程,需20天,乙公司单独完成此项工程,需30天;(2)设甲公司每天的施工费为y元,则乙公司每天的施工费为(y﹣1500)元,根据题意得12(y+y﹣1500)=102000,解得y=5000,甲公司单独完成此项工程所需的施工费:20×5000=100000(元);乙公司单独完成此项工程所需的施工费:30×(5000﹣1500)=105000(元);故甲公司的施工费较少.24.(12分)(1)如图(1)在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:DE=BD+CE;(2)如图(2)将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请给出证明;若不成立,请说明理由.【分析】(1)根据BD⊥直线m,CE⊥直线m得∠BDA=∠CEA=90°,而∠BAC=90°,根据等角的余角相等得∠CAE=∠ABD,然后根据“AAS”可判断△ADB≌△CEA,则AE=BD,AD=CE,于是DE=AE+AD=BD+CE;(2)利用∠BDA=∠BAC=α,则∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,得出∠CAE=∠ABD,进而得出△ADB≌△CEA即可得出答案.【解答】证明:(1)∵BD⊥直线m,CE⊥直线m,∴∠BDA=∠CEA=90°,∵∠BAC=90°,∴∠BAD+∠CAE=90°,∵∠BAD+∠ABD=90°,∴∠CAE=∠ABD,∵在△ADB和△CEA中,,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE;(2)∵∠BDA=∠BAC=α,∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,∴∠CAE=∠ABD,∵在△ADB和△CEA中,,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE.附赠:初中数学易错题填空专题一、填空题1、如果一个数的绝对值等于它的相反数,那么这个数一定是____ _____。
湖北省孝感市孝南区三校14—15学年八年级12月月考数学试题(附答案)
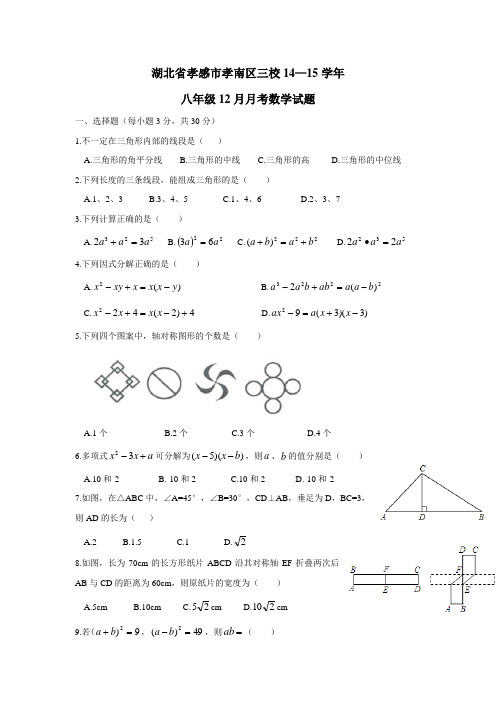
湖北省孝感市孝南区三校14—15学年八年级12月月考数学试题一、选择题(每小题3分,共30分) 1.不一定在三角形内部的线段是( )A.三角形的角平分线B.三角形的中线C.三角形的高D.三角形的中位线 2.下列长度的三条线段,能组成三角形的是( )A.1、2、3B.3、4、5C.1、4、6D.2、3、7 3.下列计算正确的是( )A.52332a a a =+ B.()2263a a = C.222)(b a b a +=+ D.53222a a a =∙4.下列因式分解正确的是( )A.)(2y x x x xy x -=+-B.2223)(2b a a ab b a a -=+-C.4)2(422+-=+-x x x xD.)3)(3(92-+=-x x a ax 5.下列四个图案中,轴对称图形的个数是( )A.1个B.2个C.3个D.4个6.多项式a x x +-32可分解为))(5(b x x --,则a 、b 的值分别是( )A.10和-2B.-10和2C.10和2D.-10和-27.如图,在△ABC 中,∠A=45°,∠B=30°,CD ⊥AB ,垂足为D ,BC=3, 则AD 的长为( )A.2B.1.5C.1D.28.如图,长为70cm 的长方形纸片ABCD 沿其对称轴EF 折叠两次后AB 与CD 的距离为60cm ,则原纸片的宽度为( ) A.5cm B.10cm C.25cm D.210cm 9.若9)2=+b a (,49)(2=-b a ,则=ab ( )A.-10B.-40C.10D.4010.已知实数x 、y 满足4=+y x ,1=xy ,则22y x +的值是( )A.6B.10C.14D.16二、填空(每小题3分,共18分)11.将一副三角板ABC 和DEF 按如图放置(其中∠A=60°,∠F=45°),使点E 落在AC 上,且ED ∥BC ,则∠CEF 的度数为___________. 12.分解因式=-a a 3____________________________ 13.计算:()=∙232a a ___________________________14.如图,等边三角形网格中,已有两个小等边三角形被涂黑,再将图中其余小等边三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有__________种.15.等腰三角形一腰上的高与另一腰的夹角为36°,则该等腰三角形的底角的度数为____________________.16.当白色小正方形个数n 等于1,2,3,……时,由白色小正方形和黑色小正方形组成的图形分别如图所示,则第n 个图形中白色小正方形的个数是___________和黑色小正方形的个数是____________(用n 表示,n 是正整数). 三、解答题(共72分) 17.(10分)分解因式:(1)1442+-a a (2))1)1(2+++a a a a (19.(9分)如图,在平面直角坐标系xOy 中,△ABC 的顶点坐标分别为A (-2,5),B (-4,3),C (-1,-1).(1)请画出△ABC 关于x 轴对称的△A 1B 1C 1,并写出点A 1的坐标; (2)请画出△ABC 关于y 轴对称的△A 2B 2C 2,并写出A 2的坐标;(3)在边AC 上有一点P (a 、b ),直接写出以上两次图形变换后的对称点P 1、P 2的坐标.20.(8分)已知02122=-+++b a a ,求3422-+-b a 的值.21.(10分)如图,在△ABC 中,点D 、E 分别在边AC 、AB 上,BD 与CE 交于点O.给出下列三个条件:①∠EBO=∠DCO ;②BE=CD ;③OB=OC.(1)(5分)上述三个条件中,由哪两个条件可以判定△ABC 是等腰三角形?(用序号写出所有成立的情形)(2)(5分)请选择(1)中的一种情形,写出证明过程.22.(8分)观察下列各式:1)1)(1(2-=+-x x x1)1)(1(32-=++-x x x x 1)1)(1(423-=+++-x x x x x……(1)(3分)根据以上规律,可得=++++++-)1)(1(23456x x x x x x x _____________. (2)(5分)计算:122222222222345678910++++++++++.23.(9分)大学生小李毕业后回乡自主创业投资办养猪场,分成猪和仔猪两个互不相邻的正方形猪场,已知成猪场的面积比仔猪场的面积大40m2,两个猪场围墙总长80m,求猪仔场的面积.解:设成猪场的边长为x m,仔猪场的边长为y m,则24.(10分)如图,在△ABC中,D是BC的中点,过点D的直线GF交AC于点F,交AC 的平行线BG于点G.(1)(5分)求证:BG=CF;(2)(5分)DE⊥GF交AB于点E,连接EF,试判断BE+CF与EF的大小,并证明你的结论.答题卷一、选择题(每小题3分,共30分)二、填空(每小题3分,共18分)11._______________________ 12.__________________________ 13._______________________ 14.__________________________15._______________________ 16.__ __________ ____________三、解答题(共72分)17.(10分)(1)(2)18.(8分)19.(9分)(1)(2)(3)20.(8分)21.(10分)(1)(2)22.(8分)(1)_________________________ (2)23.(9分)24.(10分)(1)(2)参考答案19.(1))5,2(1--A (2) )5,2(2A (3)),(1b a P - ),(2b a P -21.(1)①②;①③ (2)例:选①③ ∵OB=OC ∴∠OBC=∠OCB 又∠EBO=∠DCO∴∠OBC+∠EBO=∠OCB+∠DCO 即∠ABC=∠ACB∴AB=AC 即△ABC 是等腰三角形.22.(1)17-x (2)原式=)12222()12(2910+++++∙- =20471211=- 23.②①⎩⎨⎧=+=-80444022y x y x由①得40))((=-+y x y x 由②得20=+y x ∴2=-y x∴⎩⎨⎧==911y x∴121112=,8192=∴成猪场的面积为121m 2,仔猪场的面积为81m 2.24.(1)证明:∵AC∥BG(2)解:BE+CF>EF理由如下:连接EG∵△DCF≌△DBG∴GD=DF又DE⊥GF∴DE是GF的垂直平分线∴EG=EF在△BGE中BE+BG>EG即BE+CF>EF。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
湖北省孝感市八校联谊2014-2015学年八年级数学上学期12月联考试题本试卷满分120分,考试时间120分钟.一、精心选一选,相信自己的判断!(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中只有一项是符合题目要求的.)1.下列图案是我国几家银行的标志,其中是轴对称图形的有( )A .4个B .3个C .2个D .1个2.一个长方体的长、宽、高分别是34a -、2a 、a ,它的体积等于( ). A .3234a a - B .3268a a - C .2a D .268a a - 3.2()a b --等于( ).A .22a b +B .22a b -C .222a ab b ++D .222a ab b -+ 4.若多项式ax 2+bx +c 因式分解的结果为(x —2)(x +4),则abc 的值为A .— 16B .16C .8D .— 85.( 2,—6)关于x 轴对称点的坐标为( )A. (—2,6)B. (2,6) C . (2,—6) D. (—2,—6)6.如图, 在△ABC 中, AD 是它的角平分线, AB = 8 cm, AC = 6 cm, 则 S △ABD : S △ACD = ( ) A. 4 : 3 B. 3 : 4C. 9 : 16D. 16 : 9B CD第6题图DAEC ′7.如图,△BDC ′是将长方形纸片ABCD 沿BD 折叠得到的,图中(包括实线和虚线在内)共有全等三角形( )对.A .5B .4C .3D .28. 如图,正方形ABCD 的边长为4,将一个足够大的直角三角板的直角顶点放于点A 处,该三角板的两条直角边与CD 交于点F ,与CB 延长线交于点E .四边形AECF 的面积是( ).A. 4 B.8 C.12 D.169.等腰三角形一腰上的高与另一腰的夹角为50°,则该三角形的顶角的度数为A .40°B .50°C .40°或140°D .50°或140°10. 在直角坐标系中,已知A (3,3),在x 轴、y 轴上确定一点P ,使△AOP 为等腰三角形,则符合条件的点P 共有( ) A .10个 B .8个 C .6个D .4个11.如图,P 是△ABC 的BC 边上的一点,且BP=PA=AC=PC, 则∠B 的度数为( )A.50OB.40OC.30OD.20O12.如图,点M 为∠COD 的角平分线上一点,过点M 作MC ⊥OC 于点C ,MD ⊥OD 于点D ,连接CD 交OM 于点N,则下列结论:①MC=MD,②∠CMO=∠DMO,③OM ⊥CD,且NC=ND,④若∠1=300,则OD=2MD,正确的有( )AC B P 第11题图 O DNMC 1 第12题图A.①②③B.①②④C.③④D.①③④ 二、细心填一填,试试自己的身手!(本大题共6小题,每小题3分,共18分.) 13.计算=23)2(y x .14.若1a b -=,则代数式222a b b --的值为 15.等腰三角形的底角是70°,那么它的顶角的度数是.16.已知:如图, 三角形纸片ABC 中,∠A =80º,∠B =60º,将纸片的角折叠,使点C 落在△ABC 内,若∠α=30º,则∠β=17.如图,ABCD 是正方形,中间有两个正方形,则图中有对全等三角形.18.如图,在△ABC 中,∠ABC 和∠ACB 的外角平分线相交于点O ,若∠A =50°,则∠BOC =度.三、用心做一做,显显自己的能力!(本大题共7小题,满分66分.) 19.(本题满分8分) 分解因式:(1) (2a +1)2-(2a +1)(-1+2a) (2) 4(x+y)2-(x-y)2 20.(本题满分8分)先化简,再求值:y (x +y ) +(x +y )(x -y )-x 2,其中x =-2, y =21. 21、(本题满分8分)如图,△ABC 中,∠C=90º,AD 是∠CAB 的角平分线,∠ADC=60º,求∠B 的度数。
22、 (本题满分8分)第21题图第22题图如图,已知∠1=20º,∠2=30º,∠A=50º,求∠BDC 的度数。
23. 如图,有一池塘,要测池塘两端A 、B 的距离,可先在平地上取一个可以直接到达A 和B 的点C,连结AC 并延长到D,使CD=CA.连结BC 并延长到E,使EC=CB,连结DE,量出DE 的长,就是A 、B 的距离.写出你的证明..24.如图, 已知:AB ⊥BC 于B , EF ⊥AC 于G , DF ⊥BC 于D , BC=DF .求证:AC=EF . 25.(本题满分10分)如图,在平面直角坐标系xoy 中,A (1-,5),B (1-,0),C (4-,3).(1)求出△ABC 的面积;(2)在图中作出△ABC 关于y 轴的对称图形111A B C △; (3)写出点111A B C ,,26. (本题满分8分)如图,已知AD ∥BC ,∠PAB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .FGE DCBAPEDCBA 第23题图第24题图一.(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中只有一项是符合题目要求的.)1B 2B 3C 4A 5B 6A 7B 8A 9C 10C 11B 12A 二.(本大题共6小题,每小题3分,共18分.)15. 40°. 16. 50º 17.7 .18.65 度.三、用心做一做,显显自己的能力!(本大题共7小题,满分66分.) 19. (本题满分8分)(2) 4(x+y)2-(x-y)2解:4(x+y)2-(x-y)2=(2x+2y+x-y )(2x+2y-x+y )=(3x+y )(x+3y )―――――――――――――――4分20. (本题满分8分)先化简,再求值)1a 2)(1a 2()1a (a 4-+-+,其中43-=a解:)1a 2)(1a 2()1a (a 4-+-+=4a2+4a -(4a2-1)=4a+1 ―――――――――――――――4分当43a -=时,4a+1=4(43-) + 1=-2 ――――――――――――821、(本题满分8分)B如图,△ABC中,∠C=90度,AD是∠CAB的角平分线,∠ADC=60度,求∠解:∵△ADC中,∠C=90度∴∠CAD+∠ADC=90°∵∠ADC=60°∴∠CAD=30°∵AD是∠CAB的角平分线∴∠BAC=60°,∵∠BAC+∠B=90°∴∠B=30°22. (本题满分8分)如图,已知∠1=20度,∠2=25度,∠A=35度,求∠BDC的度数。
解:∠BDC=∠1+∠DEC=∠1+∠A+∠2=20°+25°+35°=80°E23. (本题满分8分)解:在△CAB和△CDE中,CA=CD ∠ACB=∠DCE CB=CE ∴△CAB≌△CDE∴DE=AB24. (本题满分8分)如图, 已知:AB ⊥BC 于B , EF ⊥AC 于G , DF ⊥BC 于D , BC=DF .求证:AC=EF . 证明:△DEF中∠1+∠F=90度 △EGC 中∠1+∠C=90度 ∴∠F=∠C在△CAB和△FDE中, CB=FD ∠B=∠FDE CB=CE ∴△CAB≌△FED∴AC=EF 25.(本题满分10分) 解:(1)AB=5 △ABC 的面积为2155=321⨯⨯ ―――――――――――――――4分 (2)―――――――――――――――7分(3)点111A B C ,,的坐标分别为A (1,5),B (1,0),C (4,3).―――――――――――――――10分 26. (本题满分8分)如图,已知AD ∥BC ,∠PAB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .证明:在AB上取点F使BF=BC在△EFB和△CBE中, EB=EB ∠EBF=∠FBE FB=BCCBPEDCBA F∴△BEF≌△BEC∴∠BEF=∠BEC∵AD∥BC,∴∠DAB+∠ABC=180 º∵∠PAB的平分线与∠CBA的平分线相交于E ∴∠EAB+∠ABE=90 º∴∠BEA=90 º∴∠DEA+∠CEB=90 º∴∠FEA+∠FEB=∠DEA+∠CEB=90 º∵∠BEF=∠BEC∴∠FEA=∠DEA在△EFA和△ADE中,∵FB=BC∴AD+BC=AF+FB=AB∴AD+BC=AB。
