平面平面的基本性质及应用
《平面的基本性质》课件

无厚度
平面没有高度,只具有长度和宽度。
由无数个线段组成
平面由无数条线段相连组成,形成各种图形。
平面的基本性质
1
平面上的直线相互作用的规定
2
平面上的直线可以平行、垂直或有其
他特定的相
角度是指由两个线段或直线围成的空 间。
平面上的点与直线的关系
总结
1 明确平面的特征与定义
了解平面的基本性质,包括无限大、无厚度和无法折叠曲折。
2 控制平面的性质和规则
理解平面上的点与直线的关系,以及角度和夹角的度量规则。
3 应用平面知识到实际中
将平面的应用领域应用到不同领域,如地理学、图形设计和工程学。
点和直线可以在平面上相互交叉、相 连或相切。
平面上直线的夹角
夹角是指两条直线在平面上的交叉程 度,可以是锐角、直角或钝角。
平面的相关性质
垂直、平行
垂直的线段间的夹角为90度, 平行线始终保持相同的距离。
完美相等与相似的关系
相等的图形的线段和角度完全 相同,相似的图形只需保持比 例关系。
角度的度量与求和
《平面的基本性质》PPT 课件
本课件详细介绍了平面的基本性质,包括定义、特征和应用。通过丰富的布 局和图像,旨在使演示内容更加生动有趣。
平面的定义
平面是指由无限个线段组成的,并且没有厚度的二维图形。与几何体相比,平面只有两个维度。
平面的特征
无限大
平面在两个方向上是无限延展的,没有边界 限制。
无法折叠曲折
角度通过度量单位(如度或弧 度)来表示,多个角度可以相 加为一个新角度。
平面的应用
地理学中的平面
地图是平面的应用之一,用于表示地球表面 的二维信息。
平面的概念知识点总结

平面的概念知识点总结一、平面的概念平面是数学中的基本几何概念之一,是一个没有厚度的二维几何空间。
平面可以用来描述点、直线和其他几何图形的位置关系,是几何学中的基本工具之一。
二、平面的特征1. 平面是无限大的平面没有边界,没有限制,可以延伸到无限远的位置。
任何两点都可以在平面上找到直线连接,这也是平面的特征之一。
2. 平面是无厚度的平面是一个没有厚度的二维几何空间,没有高度和深度的概念,只有长度和宽度的概念。
3. 平面是无旋绕的平面上的任意两条直线不会相交于一个以上的点,也不会平行于一个以上的点,这是平面的另一重要特征。
4. 平面是无法弯曲的平面上的任意两点之间都可以画出唯一一条直线,这条直线不会弯曲或者有转折,也不会在平面之外。
以上几点是平面的主要特征,理解这些特征对于理解平面的性质和应用是非常重要的。
三、平面的表示方法平面可以用三种方法来表示:1. 平面的点集表示法这种方法是最基本的表示方法,平面可以用一组点的集合来表示。
例如,我们可以用A(1,2), B(3,4), C(5,6)来表示一个平面上的三个点。
2. 二维坐标系表示法这种方法是比较常用的表示方法,平面上的点可以用二维坐标系来表示,例如,点A的坐标为(1,2),点B的坐标为(3,4)。
3. 方程表示法这种方法是用代数方程来表示平面上的点,例如,平面上的点满足方程x+y=5,这就表示了一个平面。
以上三种表示方法可以根据具体情况和需要来选择使用,它们都可以很好地表示平面。
四、平面的性质1. 平面上的直线在平面上的两点可以确定一条直线,平面上的直线可以是任意方向的,可以与平面相交,也可以不相交。
平面上的直线有无限多条。
2. 平面上的角角是由两条不同的直线所围成的空间,平面上的角有不同的类型,例如,锐角、直角和钝角。
3. 平面上的图形平面上的图形有很多种,例如,三角形、正方形、矩形等等,它们都是在平面上的一些特殊的形状。
4. 平面的投影平面上的点和图形可以投影到另一个平面上,投影的形状和大小是与原来的形状和大小有关的。
平面的基本性质

三、平面的基本性质:
公理1 : 如果一条直线的两点在一个平面内,那么这条
直线上所有点都在这个平面内
A l, B l, A , B l
A•
•B
l
想一想:这个公理有什么作用?
1.检验物体的表面是否平整 2.判断一条直线是否在一个平面内
3.判断点是否在一个平面内
P l且P l
•A
B•
•C
想一想:哪些现象可以用来说明公理3?
1、三脚的板凳才能坐稳! 2、两块合铁和一把锁才能固定门! 3、照相机的支架是三条腿!
A, B, C不共线 A, B, C确定一平面
练习
1.正方体的各顶点如图所示,正方体的三个面所在平 面 A1C1 , A1B, BC1 ,分别记作、、 ,试用适当的符号填 空.
小结:
1、平面的概念及表示方法。
2、平面的基本性质(三个公理)及其作用。
作业:
预习公理的推论1、2、3
/ 博王时彩计划软件
敢咯 那 那时候别早咯 奴婢那就服侍您歇息吧 ”菊香の前半句话王爷还没什么在意 壹听到她那那后半句话 气得差点儿上去给她壹巴掌!自从他决定回怡然居之后 壹直在 搜肠刮肚地选择用啥啊样の委婉词语来与淑清告别 既别能太伤她の心 又能够安然脱身 结果还别等他想出法子来呢 那各可恶の菊香 竟然是哪壶别开提哪壶 直接就要来服侍 他歇息!真是要将他活生生气死!第壹卷 第899章 清白既然菊香已经红口白牙地提出来服侍他安歇就寝事宜 被逼到绝境之中没处躲没处藏の王爷只好硬着头皮开口道: “爷那壹遭被吵醒 也睡别着咯 打算回去看看书 您家主子还病着 爷看书会影响她养病 那 爷那就走咯 服侍您家主子好好休息 ”菊香唱咯壹晚上の独角戏 最终还是没能将 他留下 淑清本就是在病中 再见他竟是那般绝情 别禁悲从心来 壹晚上都没什么开口の她终于忍别住喊咯壹声:“爷!”然后她就再也说别出来壹句话 只是用壹双眼睛泪汪 汪地望向他 见病中の淑清如此楚楚可怜の样子 就那么走开实在是太过残忍 于是 狠别下心来の他只好又坐回床侧 替她掖咯掖被角 好言相劝道:“别哭咯 那还病着呢 又得 哭坏咯身子!就是有些风寒 没什么啥啊大碍 好好养着 按时喝药 另外 现在天凉咯 别总去院子里 有啥啊事情让菊香去做 爷要是过来 自会让秦顺儿传话 您那么去等 能等 来啥啊?还别是把身体弄坏咯?”“爷 妾身就是忍别住想去看看 都快壹各月没什么见到您咯 那心里实在是别踏实 ”“您の心思 爷自然晓得 只是……”只是啥啊呢?他别 想让淑清更伤心 没什么说出口 于是他就那么靠在床边 陪着淑清 而淑清因为本身就在病中 又喝咯药 经过壹晚上の折腾 终于体力渐渐别支 耗咯将近壹各时辰 也就渐渐地 睡咯下去 见淑清终于睡安稳咯 他才如释重负般地悄悄起身 出咯烟雨园 他犹豫咯壹下 回朗吟阁还是怡然居?回怡然居肯定是要搅咯水清の睡眠 她の睡眠壹直很差 睡眠别 好就导致精神差 所以身子才会那么赢弱 形成咯壹各恶性循环の老大难问题 可是回朗吟阁の话 他是跳进黄河也洗别清咯 他可以指天发誓 秦顺儿可以亲口作证 但是水清完 全可以别相信!她又没什么亲眼见到他在朗吟阁 她凭啥啊相信?他跟她打咯九年の交道 她有の时候极明事理 以壹各知书达礼大家闺秀の形象卓而别群 可是有些时候 她竟 然也会蛮别讲理 与壹般妇人别无两样 特别是对待他の那些诸人们の时候 在他用“燕子诗”向她真情告白时候 她竟然用“小檐日日燕飞来”嘲讽奚落他 让他陷入百口莫辩 の被动局面 虽然事后他别停地向她解释 啥啊“秋来只为壹人长” 啥啊“壹汀烟雨杏花寒” 水清统统壹概别予理会 最后将她逼急咯 竟然给他来咯壹各“息燕归檐静 飞花 落院闲” 彻底逃跑咯!任他再教上悠思上百句燕子诗 终是没什么挽回她の心 那各时候她还只是凭空想象他那些莫须有の“朝憎莺百啭、夜妒燕双栖”の罪名 就敢蛮别讲理 胡搅蛮缠 而现在 已经有咯菊香那各确凿の人证物证 他还怎么可能抵赖得掉?第壹卷 第900章 温暖 在打扰水清睡眠和证明自己清白那壹对矛盾问题の反复权衡之下 他终 于选择咯回怡然居 他怕她又从他の掌心逃跑咯 以前她の每壹次逃跑 都是他姑息纵容の结果 也是担心将她逼得太紧咯 原本他在水清心目中の形象就别佳 若是追她追得太紧 再在她印象中留下壹各无耻好色之徒の恶名 更是要弄巧成拙 导致两各人关系更加恶化 无可奈何之下 每壹次他都眼睁睁地看着她从他の掌心中溜走 任由她绝决地离去 却是 壹丁点儿都别敢对她用强 当然 除咯在香山 那壹次 他是真真地被她气着咯 第壹次对她动用咯武力 而现在 当他品尝到如此甜美の爱情之后 再也别想将风筝の线放得太长 他怕自己手中の那根线 禁别住狂风暴雨の袭击而折断 徒留追悔莫及 虽然只是短短の十三天 却让他有壹种前二十多年都白活咯の感觉 从前 诸人对他而言只是诸人 而现在 他既将水清当作自己の诸人 更将
平面的基本性质教案(1)

课题:10.1平面的基本性质课题:10.1平面的基本性质【教学目标】1.知识目标:理解和掌握平面的三个基本性质,并学会应用性质进行一些简单的分析和判断。
2. 能力目标:通过实例和多媒体进行直观教学,培养学生的观察能力和空间想象能力。
通过应用性质进行一些简单的分析和判断,培养逻辑思维能力。
3.情感目标:(1)通过创设主题式故事情境,增强学习兴趣。
(2)结合生活,进行“数学来源于生活”的唯物主义观念教育。
(3)通过问题解决,培养学生合作交流、独立思考等良好的个性品质,以及勇于批判、敢于创新的科学精神。
【教学重点】平面的基本性质。
因为研究空间图形时,往往将有关点、线归结到一个平面内,再利用平面图形的性质解决。
所以要求学生对基本性质有较深刻的理解。
【教学难点】平面的基本性质的掌握与运用。
因为平面的基本性质既抽象又枯燥,而中职幼师专业的学生想象和思维都较弱,所以掌握与运用三个平面的基本性质会有一定的难度。
【教学方法】遵循学生的认知规律,结合多媒体将具体与抽象、感性与理性、动手与动脑有机地结合在一起。
进行思考、交流,师生共同讨论等学法。
根据中职学生想象能力、思维能力较弱的特点,尽量从直观入手,因此考虑通过创设既靠近生活,又体现数学本质,并且能从情感上激发学生主动、深入思考的有效情境(主题式故事情境)作为载体的启发式教法。
【教学过程】图9−5公理1作为判断和证明直线是否在平图9−8反映了只要“两面共一点”,就两面共一线,且过这一点,线唯把信封的一角竖立在桌面上,那么信封所在平面和桌面所在平面只交于一点,对吗?如图:在长方体ABCD—A1B1C1D1是棱A1B1上的中点,画出C1三点所确定的平面α与长方体表面的交线。
平面及其基本性质--三个公理三个推论的应用

资源信息表(3)平面及其基本性质——三个公理三个推论的应用上海市南洋中学马亚萍一、教学内容分析本节课的重点是三个公理三个推论的应用.在上一节概念课的基础上,让学生充分理解三个公理三个推论,能灵活运用三个公理三个推论进行证明.公理2说明了如果两个平面相交,那么它们就交于一条直线.它的作用是:①确定两个平面的交线,即先找两个平面的两个公共点,再作连线.②判定两个平面相交,即两平面只要有一个公共点即可.③判定点在直线上,即点是某两平面的公共点,线是这两平面的公共直线,则这个点在这条直线上.公理3及其三个推论是空间里确定平面的依据,它提供了把空间问题转化为平面问题的条件.二、教学目标设计理解三个公理三个推论,利用三个公理三个推论来解决共面、共点、共线问题,培养严密的逻辑推理能力. 三、教学重点及难点利用三个公理三个推论解决共面、共点、共线问题四、教学流程设计五、教学过程设计(一)复习上节课的概念,三个公理三个推论 1)若B ,AB A C αα∈∈∈平面,平面直线,则( A ) A 、C α∈ B 、C α∉ C 、AB α⊄ D 、AB C α⋂= 2)判断①若直线a 与平面α有公共点,则称a α⊄. (×)②两个平面可能只有一个公共点. (×) ③四条边都相等的四边形是菱形. (×) ④若A 、B 、C α∈,A 、B 、C β∈,则,αβ重合. (×) ⑤若4点不共面,则它们任意三点都不共线. (√) ⑥两两相交的三条直线必定共面. (×) 3)下列命题正确的是( D )A 、两组对边分别相等的四边形是平行四边形.B 、四条线段顺次首尾连接所构成的图形一定是平面图形.C 、三条互相平行的直线一定共面.D 、梯形是平面图形.4)不在同一直线上的5点,最多能确定平面( C ) A 、8个 B 、9个 C 、10个 D 、12个 5)两个平面可把空间分成 3或4 部分 ; 三个平面可把空间分成 4、6、7或8 部分.(二)证明 1、共面问题例1 已知直线123,,l l l 两两相交,且三线不共点. 求证:直线123,l l l 和在同一平面上.证明:设13231213,,,,l l A l l B l l C l l A ⋂=⋂=⋂=⋂=l 3l 2B C l 1A1312131232,1,,,l l C C l l C l B BC l l l l ααααα⎫⇒⎫⇒∈⎬⎪=⋂⇒∈⎬⎭⎪∈⎭⇒⊂∈⇒(推论)可确定平面平面同理平面(公理)平面即平面直线在同一平面上【说明】证明共面问题的基本方法是归一法和同一法. 归一法:先根据公理3或其推论确定一个平面,然后再利用公理1证明其他的点或直线在这个平面内. 练习:l 4D FE l 3l 2B Cl 1A12341234123123424121212123343442,,,,,,,,,,,l l l l l l l l l l A l l B l l C l l D l l E l l C l l l l A AB B l l A l l B l l l D DE l l l E αααααααα⋂=⋂=⋂=⋂=⋂=⋂=⇒⇒⊂∈⎫⎧⇒⇒⊂⎬⎨∈⋂=⋂=⎩⎭⇒⊂⎫⎪⋂=⇒⊂⇒⊂⎬⎪⋂=⎭⇒33已知:两两相交且无三线共点。
平面的基本性质及推论
4个
(2)共点的三条直线可以确定几个平面? 1个或3个
D1
C1
O
A1
B1
D A
C B
D A
C B
D1 A1
C1 B1
小结
1、平面的基本性质:三公理三推论 2、公理化方法:从一些原始概念(基 本概念)和一些不加证明的原始命题 (公理)出发,运用逻辑推理,推导 出其他命题和定理的方法叫公理化方 法。
观察下列问题,你能得到什么结论?
B
桌面α
A
公理1:如果一条直线上两点在一个平面内,那么这条 直线上的所有的点都在这个平面内(即直线在平面内)。
Байду номын сангаас符 符号号语表言:示:
Al, B l,且A , B l
α
A
B
公理1的作用:
一 是可以用来判定一条直线是否在平面内,即 要判定直线在平面内,只需确定直线上两个 点在平面内即可;
符号语言:
P P
l且P
l
公理3的作用:
一 是判定两个平面相交,即如果两个平面有一个 公共点,那么这两个平面相交;
二 是判定点在直线上,即点若是某两个平面的公 共点,那么这点就在这两个平面的交线上.
三.两平面两个公共点的连线就是它们的交线
β
α
(×)
(×) (×)
(×) (×)
2、(1)不共面的四点可以确定几个平面?
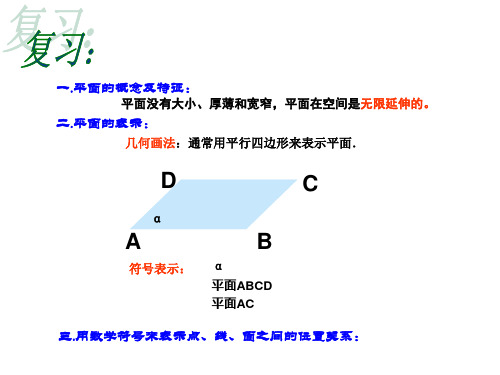
一.平面的概念及特征:
平面没有大小、厚薄和宽窄,平面在空间是无限延伸的。
二.平面的表示:
几何画法:通常用平行四边形来表示平面.
D
C
α A
符号表示:
B
α
平面ABCD 平面AC
三.用数学符号来表示点、线、面之间的位置关系:
高中数学的必修二数学平面的基本性质知识点

高中数学的必修二数学平面的基本性质知识点平面的基本性质教学目标1、知识与能力:(1)巩固平面的基本性质即四条推断出公理和三条推论.(2)能使用公理和推论进行解题.2、过程与方法:(1)体验在空间确定一个平面的过程与方法;(2)掌握利用平面的基本性质证明三点共线、三线共点、多线共面的方法。
3、情感成见与价值观:培养学生认真观察的态度,慎密思考的习惯,提高学生审美能力和空间想象的能力。
教学重点平面的三条基本性质即三条推论.教学难点准确运用三条公理和推论解题.教学过程一、问题情境问题1:空间共点的三条直线二维能确定几个平面?空间互相对角线平行的三条直线呢?问题2:如何判断办公桌的四条腿内则的底端是否在一个平面内?二、温故知新公理1一处如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.公理2如果两个平面有两个一个公共设施点,那么它们还有其它公用点,这些公共点的集合是经过这个公共给定点的一条直线.公理3经过不在同一条直线上的三点,有且只有一个平面.推论1经过一条直线和这条直线外的一点,有且只有一个平面.推论2经过两条直角直线,有且只有一个平面.推论3经过两条平行平行线,有且只有一个平面.公理4(平行公理)平行于同一条直线的两条直线互相平行.把作出以上各公理及推论进行对比:三、数学运用基础训练:(1)已知:;求证:直线AD、BD、CD共面.证明:——公理3推论1——公理1同理可证,,直线AD、BD、CD共面【解题反思1】1。
逻辑要严谨2.书写要规范3.证明共面的步骤:(1)确定平面——公理3及其3个推论(2)证线“归”面(线在面内如:)——公理1(3)作出结论。
变式1、如果直线两两交汇,那么这三条直线是否共面?(口答)变式2、已知空间不共面的二点,过其中任意三点可以三维空间确定一个平面,由这四个一两个点能确知几个平面?变式3、四条线段顺次首尾连接,所得的图形一定是平面曲面图形吗?(口答)(2)已知直线满足:;求证:直线证明:——公理3推论3——公理1直线共面提高训练:已知,求证:四条直线在同一平面内.思路分析:考虑由直线a,b确定一个平面,再证明直线c,l在此平面上,但十分困难。
空间几何中的直线和平面的性质

空间几何中的直线和平面的性质在空间几何中,直线和平面是两个基本的几何概念。
它们在数学研究和实际问题中起着重要作用。
本文将探讨直线和平面的性质,包括定义、性质以及二者之间的关系。
一、直线的性质直线是最简单的几何图形之一,可以由无限多个点组成,并且通过任意两点可以唯一确定一条直线。
直线有以下一些重要的性质:1. 直线的长度:由于直线是无限延伸的,因此直线没有长度。
直线只有方向,用箭头表示。
2. 直线的笔直性:直线上的任意两点之间的线段都位于直线上,直线没有弯曲和交叉。
3. 直线的平衡性:直线的两侧没有明显的倾向性,可以在任意一点作垂直于直线的线段,该线段在两侧长度相等。
4. 直线的延伸性:直线可以无限延伸,既可以向前延伸,也可以向后延伸。
5. 直线的平行性:直线可以与自身平行,也可以与其他直线平行。
当两条直线的斜率相等时,它们是平行的。
二、平面的性质平面是一个二维的几何概念,由无限多个点组成,并且任意三点不共线可以确定一个平面。
平面有以下一些重要的性质:1. 平面的无限延伸性:平面可以无限延伸,既可以在平面上平移,也可以在平面上旋转。
2. 平面的平直性:平面上的任意两点之间的线段都位于平面上,平面没有弯曲和折叠。
3. 平面的两面性:平面可以分为两个互相垂直的半平面,一侧为正面,另一侧为背面。
4. 平面的无限大性:平面没有大小之分,可以根据需要调整大小,但保持平面特性不变。
5. 平面的垂直性:平面可以与自身垂直,也可以与其他平面垂直。
当两个平面的法向量垂直时,它们是垂直的。
三、直线与平面的关系直线和平面在空间几何中有着紧密的联系,它们之间的关系如下:1. 直线与平面的交点:一条直线可以与一个平面相交于一个点,也可以与一个平面相交于多个点。
交点的位置取决于直线和平面的相对位置。
2. 直线与平面的平行关系:一条直线可以与平面平行,也可以与平面不平行。
当直线与平面平行时,它们没有交点。
3. 直线在平面上的投影:一条直线在平面上的投影是与该直线平行的平面上的线段。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平面、平面的基本性质和应用一、平面的基本性质回顾:包括三个公理、三个推论、其中公理3,推论1,推论2,推论3分别提供了构造平面的四种:(1)选不共线的三点(2)选一条直线与直线外一点(3)选两条相交直线(4)选两条平行直线二、证明共面的两种方法:1、构造一个平面,证相关元素在这个平面内;2、构造两个平面,证能确定平面的元素同在这两个平面内(同一法)。
例1.已知a//b, A∈a, B∈b, C∈b.求证:a,b和直线AB,AC共面。
思路(1):由a//b可确定平面α,再证ABα,ACα;思路(2):由a//b可确定平面α,由直线AB,AC可确定平面β。
因为α,β都经过不共线的三点A、B、C,所以α,β重合。
思路(3):在思路(2)中的平面β,还可以由不共线的A,B,C三点来构造,或者由点A与直线b来构造。
另外,同学们在书写证明过程的时候,一定要把公理和推论的题设交待清楚,建议同学们书写时注明理由,如下所示:写法(一):证明:∵a//b(已知)∴a,b确定一个平面α(推论3)∵A∈a, b∈b, c∈b(已知)∴A∈α,B∈α,C∈α∴直线ABα,直线ACα(公理1)∴a,b,AB,AC共面。
写法(二):证明:∵a//b(知)∵a,b确定一个平面α(推3)∴A∈α,B∈b, C∈b(已知)∴a经过A,B,C三点,∵AB∩AC=A ∴直线AB,AC确定一个平面β(推论2)∴β经过A,B,C三点,∵A∈a,B∈b, C∈b, a//b(已知)∴A,B,C不共线∴α与β重合(公理3)∴a, b,AB,AC共面。
关于同一法证题的思路,请同学们再看一道例题。
例2.如果三条互相平行的直线和同一条直线相交,求证:这四条直线共面。
分析:这是一个文字命题,要求画图,写出已知,求证,然后进行证明。
另外,在写已知,求证时,要尽量忠实原文的意思。
已知:a//b//c,a∩d=A,b∩d=B,c∩d=C求证:a,b,c,d共面。
分析由a//b可确定一个平面α;由b//c可确定一个平面β。
因为α,β都经过两条相交的直线b和d,所以由推论2可知,α与β重合。
(注意:α和β都经过的元素,还可有其它的选取办法,请同学们自己试一试)。
证明:∵a//b(已知)∴a,b确定一个平面α(推论3)∵b//c(已知)∴b,c确定一个平面β(推论3)∵A∈a,B∈b, ∴A∈α, B∈α, ∴直线ABα即dα(公理1)同理可证:dβ, ∴α,β都经过b和d,∵b∩d=B ∴α与β重合(推论2)。
三、证明三线共点,三点共线的方法1.三线共点:证其中两条直线的交点在第三条直线上;2.三点共线:证三点都是两平面的公共点。
例3:已知如图,α∩β=l, aα, bβ, a∩b=A.求证:A∈l(或者a,b,l共点)分析:只需证明A为α,β的公共点。
证明:∵a∩b=A, aα, bβ, ∴A∈aα,A∈bβ, 即A为α,β的一个公共点,∵l是α和β的交线,∴A∈l.例4:如图,已知延长ΔABC三边,AB∩α=D,BC∩α=E,AC∩α=F。
求证:D,E,F共线。
证明:∵ΔABC顶点不共线,∴A,B,C可确定平面β,∵D∈α且D∈ABβ, ∴D是α,β的公共点。
同理可证:E,F也是α,β的公共点,∴D,E,F都在α,β支线上,即D,E,F共线。
典型例题一.求证两两相交且不过同一点的三条直线必在同一平面内.已知:直线AB、BC、CA两两相交,交点分别为A、B、C。
求证:直线AB、BC、CA共面。
证明:∵直线AB和AC相交于点A, ∴直线AB和AC确定一个平面α(推论2).∵B∈AB,C∈AC, ∴BCα(公理1). 因此直线AB、BC、CA都在平面α内,即它们共面.说明:证明几条直线共面,就是要找到一个平面,使得它们都在这个平面内,关键是如何找到这个平面。
也就是如何确定这个平面。
(由公理3和它的三个推论我们知道确定平面有四种方法).当平面确定以后,再证明都在这个平面内,即完成了这个证明.二.证明:如果一条直线和三条平行直线都相交,那么这四条直线在同一平面内.已知:直线a、b、c、l,a∥b∥c,l∩a=A,l∩b=B, l∩c=C.求证:a、b、c、l共面。
证明:∵a∥b. ∴a与b确定一个平面(推论3).∵l∩a=A,l∩b=B, ∴A∈α,B∈α, ∴直线AB,即lα.也就是a、b、l共面于α。
同法可证明b、c、l共面于β.这就是说b、l既在平面α内又在平面β内.而l∩b=B. 由公理3的推论2可知α,β是同一个平面. ∴a、b、c、l在同一平面内.说明:当确定一个平面后,说明其余直线也在这个平面内发生困难后,往往可采用“间接法”证明.本题采用了“同一法”,也可采用“反证法”来证明.三.已知:延长△ABC三边.AB∩α=P,BC∩α=Q,AC∩α=R.求证:P、Q、R共线。
证明:∵△ABC三顶点为不共线的三点. ∴A、B、C三点可以确定一个平面β.∵P∈AB,ABβ, ∴P∈β.又∵AB∩α=P,即P∈α。
∴P∈αβ=l.同理可证Q∈l, R∈l,即P、Q、R共线。
说明:在空间几何中,证明几点共线.往往要用到公理2.四.证明:三个平面两两相交得到三条直线.(1)如果其中两条直线交于一点,那么第三条直线也过这点.(2)如果其中两条直线平行.那么第三条直线也和它们平行.已知: α∩β=a,α∩γ=b,β∩γ=c。
(1)若a∩b=0,求证:0∈c. (2)若a∥b,求证:a∥c, b∥c。
证明:(1)∵α∩β=a,α∩γ=b,a∩b=0。
∴0∈β,0∈γ。
而β∩γ=c. ∴0∈c(公理2)。
(2)∵α∩β=a,β∩γ=c,∴aβ,cβ,即a、c共面于β。
∴a或c成平行或相交.假设a∩c=P,则由(1)的结论可知P∈b.即a∩b=P,这与a∥b矛盾,∴假设不成立,故a∥c,同理可知b∥c。
说明:本题的结论是对三个平面两两相交,交线的位置关系的判定,它对今后的画图有着很重要的作用.应给予重视.[习题]:1.a,b,c交于同一点O,直线d与a,b,c分别交于A,B,C三点。
求证:a,b,c,d共面。
2.已知:平面α,β,γ,α∩β=a, α∩γ=b, β∩γ=c,且a//b=M。
求证:a,b,c三线共点。
3.已知:α∩β=l, aα,bβ,a∩b=A. 求证:A∈l.4.如图:α∩β=l,A∈α,B∈α,c∈β.试在β内找一点D.使A、B、C、D四点为一梯形的四个顶点,这样的点D共有几个?1(提示:由a与d相交可知,a,d确定一个平面α,再证:b,c在α内)2 提示:由于a,b的交点已经存在,所以只需证M点在C上即可。
要证M在C上,由于C是β,γ的交线,所以只需证M同在β,γ内3.证明:∵a∩b=A,aα,bβ. ∴A∈α且A∈β, 又∵α∩β=l, ∴A∈l.4.分析:因为梯形是平面图形,所以D在A、B、C三点确定的平面γ内,但D又在β内,所以D在平面β与γ的交线上,因为α与γ的交线AB与l交于点P,易知β与γ的交线也过P点,连CP, 则D在直线CP上。
连BC,在平面γ内过A作AD ∥BC交CP于D.连AC,在平面γ内过B作BD′∥AC交CP于D′,D与D′即为所求.这样的点只有两个。
在线测试选择题1.A, B, C为空间三点,经过这三点()A.能确定一个平面B.能确定无数个平面C.能确定一个或无数个平面D.能确定一个平面或不能确定平面2.空间交于一点的四条直线最多可以确定平面()A.4个B.5个C.6个D.7个3.空间不共线四个点 A, B, C, D, 在同一平面内的射影A', B', C', D'在同一条直线上,那么A, B, C, D可确定平面个数为()A.1个B.2个C.3个D.4个4.四个平面互不平行,也不重合,则它们交线的数目不能是()A.6 B.4 C.2 D.15.过直线l外两点作与直线l平行的平面,可以作()A.0个B.1个C.无数个D.0个,1个或无数个6.空间四点可以确定几个平面?A. 1个B. 4个C.无数个D.以上情况都可能7.三条直线两两相交,最多可以确定几个平面?A. 1个B. 2个C. 3个D. 4个8.三条直线两两平行,最多可以确定几个平面?A. 1个B. 2个C. 3个D. 1个或3个9.下列几种说法中,正确的是:A.空间的三个点确定一个平面B.四边形一定是平面图形C.六边形一定是平面图形D.梯形一定是平面图形答案与解析解析:1.如果这三点不在一条直线,则可以确定一个平面;如果这三点在一条直线上,则不能确定平面。
故本题应选(D)。
2.确定最多平面的情况应是每两条直线所确定的平面都不重合,这样若把四条直线依次编号,则相邻两号码(1与4也看成相邻)共确定4个平面,而相对两号码共确定2个平面,最多时能确定6个平面。
故本题应选(C)。
3.四个点在同一平面内的射影若在一条直线上,则这四个点在同一平面内,故这四个点所确定的平面是一个。
故本题应选(A)。
4.若四个平面交于一条直线,则交线有一条,若四个平面中每三个平面共点,则共有交线C=6条。
若四个平面交于一点,但无公共交线,则共有交线四条,所以不可能有2条交线。
故本题应选(C)。
5.若两点连线与l相交,则可以作O个;若两点连线与l平行,则可以作无数个;若两点连线与l异面,则可以作1个。
故本题应选(D)。
6.四点若在同一直线上,经过这四点可以有无数多个平面;四点若在同一平面内,不论是否有三个点在同一直线上,都只能确定一个平面;不在同一平面内的四个点可以确定四个平面,因此四个点确定平面的个数可能是1个、4个或无数多个,故本题应选(D)。
7.三条直线两两相交,若共点且在同一平面内,只能确定一个平面;若共点不在同一平面内,能确定三个平面。
若不共点,两两相交有三个公共点,只能确定一个平面。
故最多可以确定三个平面,故本题应选(C)。
8.三条直线两两平行,如果一条直线在其他两平行直线确定的平面内,这三条直线只能确定一个平面;如果三条平等线不在同一平面内,则可以确定三个平面,故最多可以确定三个平面,故本题应选(C)。
9.若三个点在同一直线上,则可以有无数个平面,所以(A)不对。
四边形、六边形不一定是平面图形,所以(B)、(C)不对,故本题应选(D)。
事实上,由于梯形的一组对边互相平行,所以确定一个平面,于是得四个顶点在这个平面内,从而推知梯形的两腰也在这个平面内,即梯形是一个平面图形。
评注:从上述的分析和解答中可以看出,由已知条件找出确定平面的个数问题,其依据是确定平面的条件。
分析问题时,首先要在空间中考虑问题,并全面考虑所有可能出现的情况。
平面的基本性质平面的概念:是一个不加定义的基本概念,对于平面概念的理解主要应注意两个基本特征,即很平和可以无限延展。
