西工大《阵列信号处理》考点整理
阵列信号处理
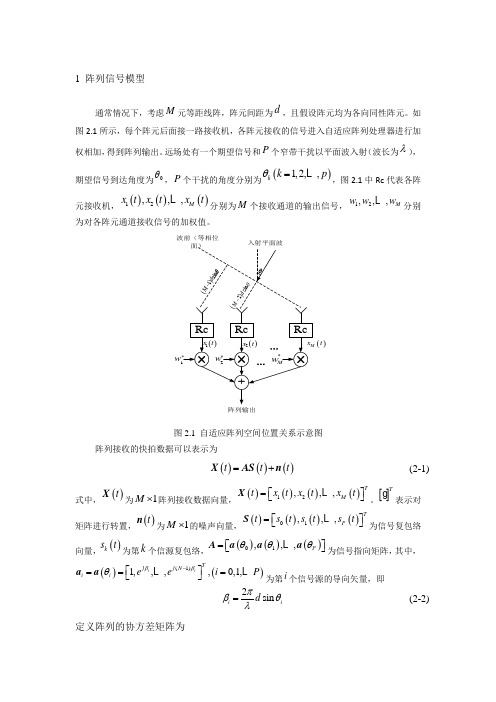
1 阵列信号模型通常情况下,考虑M 元等距线阵,阵元间距为d ,且假设阵元均为各向同性阵元。
如图2.1所示,每个阵元后面接一路接收机,各阵元接收的信号进入自适应阵列处理器进行加权相加,得到阵列输出。
远场处有一个期望信号和P 个窄带干扰以平面波入射(波长为λ),期望信号到达角度为0θ,P 个干扰的角度分别为()1,2,,k k p θ= ,图2.1中Rc 代表各阵元接收机,()()()12,,,M x t x t x t 分别为M 个接收通道的输出信号,12,,,M w w w 分别为对各阵元通道接收信号的加权值。
()t w 阵列输出波前(等相位图2.1 自适应阵列空间位置关系示意图阵列接收的快拍数据可以表示为()()()t t t =+X AS n(2-1)式中,()t X 为1M ⨯阵列接收数据向量,()()()()12,,,TM t x t x t x t =⎡⎤⎣⎦X 。
[]T表示对矩阵进行转置,()t n 为1M ⨯的噪声向量,()()()()01,,,TP t s t s t s t =⎡⎤⎣⎦S 为信号复包络向量,()k s t 为第k 个信源复包络,()()()01,,,P θθθ=⎡⎤⎣⎦A a a a 为信号指向矩阵,其中,()()(1)1,,,,0,1,i iTj j N i i e e i P ββθ-⎡⎤===⎣⎦a a 为第i 个信号源的导向矢量,即2sin i i d πβθλ=(2-2)定义阵列的协方差矩阵为()()2H H x s n E t t σ⎡⎤==+⎣⎦R X X AR A I (2-3)式中,()()H s E t t ⎡⎤=⎣⎦R S S 为信号的协方差矩阵,I 为M 维单位矩阵,2n σ为阵元的噪声功率,本文中约定,[]T表示转置,[]*表示共轭,[]H表示共轭转置。
式(2-3)常由接收数据采样协方差矩阵ˆx R 代替,即()()11ˆNH xiii t t N==∑R x x(2-4)如图2.1所示的自适应阵列模型,阵列的M 个通道接收信号经加权处理后,最后的输出信号为()()()1MH i i i y t w x t t *===∑w x(2-5)阵列的方向图()p θ定义为()()H p θθ=w a(2-6)调整自适应阵列的权矢量w ,可以改变阵列的方向图,即改变各个方向上入射信号增益。
阵列信号处理

B
B
1 有 zB t 2
B
2
z e jt d z B t
因此
s r , t z B t e j0t e j0 s 0, t e j0
2
小结: 信号带宽足够小使得波到达 r 处时的复包络基本 不变。 T r 表示了波传播的空间信息(方向、位置), 它仅含于载波项中,而与信号复包络无关。
s exp[ j t r ]d
T
这里函数 s 是任意的,只要其Fourier变换存在即 可。该式表达了沿同一方向 传播的任意波形(信 号),其频率分量任意。
B. 波动方程球坐标系中的解
球坐标系 r , , ,但是,当波动方程的解具有球形 对称时,函数s r , , , t 并不依赖于 和 ,使解简化, 这时波动方程可简化为:
T
波动方程的任意解可以分解为无穷多个“单频” 解的迭加(传播方向和频率分量均任意)。
波动方程的单频解可以写成单变量的函数:
s r , t A exp[ j (t k r ) A exp[ j t r ]
T T
k ,其大小等于传播速度的倒数,其方向与 式中
时间频率 空间频率
b) 任意解:由四维Fourier变换表示: j t k r 1 s r, t s u , e d kd 4 2 j t k r s k , s t , r e d rdt 其中
T
a t 带宽越宽,信号起伏越快。窄带条件即要求a t cos 变化比 0t t 变化慢。
阵列信号处理(知识点)

信号子空间:设N 元阵接收p 个信源,则其信号模型为:()()()()1piiii x t s t a N t θ==+∑在无噪声条件下,()()()()()12,,,P x t span a a a θθθ∈称()()()()12,,,P span a a a θθθ为信号子空间,是N 维线性空间中的P 维子空间,记为P N S 。
P N S 的正交补空间称为噪声子空间,记为N P N N -。
正交投影设子空间m S R ∈,如果线性变换P 满足,()1),,,2),,,0m mx R Px S x S Px x x R y S x Px y ∀∈∈∀∈=∀∈∀∈-=且则称线性变换P 为正交投影。
导向矢量、阵列流形设N 元阵接收p 个信源,则其信号模型为:()()()()1piiii x t s t a N t θ==+∑,其中矢量()i ia θ称为导向矢量,当改变空间角θ,使其在空间扫描,所形成的矩阵称为阵列流形,用符号A 表示,即(){|(0,2)}a A θθπ=∈波束形成波束形成(空域滤波)技术与时间滤波相类似,是对采样数据作加权求和,以增强特定方向信号的功率,即()()()()HHy t W X t s t W a θ==,通过加权系数W 实现对θ的选择。
最大似然已知一组服从某概率模型()f X θ的样本集12,,,N X X X ,其中θ为参数集合,使条件概率()12,,,N f X X X θ最大的参数θ估计称为最大似然估计。
不同几何形态的阵列的阵列流形矢量计算问题假设有P 个信源,N 元阵列,则先建立阵列的几何模型求第i 个信源的导向矢量()i i a θ 选择阵元中的一个作为第一阵元,其导向矢量()1[1]i a θ=然后根据阵列的几何模型求得其他各阵元与第一阵元之间的波程差n ∆,则确定其导向矢量()2jn i a eπλθ∆=最后形成N 元阵的阵列流形矢量()11221N j j N Pe A e πλπλθ-∆∆⨯⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦ 例如各向同性的NxM 元矩形阵,阵元间隔为半个波长,当信源与阵列共面时:首先建立阵列几何模型:对于第m 行、第n 列的阵元,其与第1行、第1列阵元之间的波程差为(1)sin()(1)cos()mn i i n d m d θθ∆=---故:()1122(sin()cos())22((1)sin()(1)cos())11N j j d j j d N M NM P NM Pe e A e e ππθθλλππθθλλθ-∆-∆---⨯⨯⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦而当信源与阵列不共面时: 首先将信源投影到阵列平面然后建立阵列模型对于第m 行、第n 列的阵元,其与第1行、第1列阵元之间的波程差为[(1)sin()(1)cos()]sin()mn i i i n d m d θθϕ∆=-+-故:()1122(sin()cos())cos()22((1)sin()(1)cos())cos()11N j j d j j d N M NM P NM Pe e A e e ππθθϕλλππθθϕλλθ-∆-∆---⨯⨯⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦线性约束最小方差准则(LCMV )的自适应波束形成算法: 对于信号模型:()()()0X t s t a J N θ=++, 波束形成输出:()()()()0()H H H yt W X t s t W a W J N θ==++LCMV 准则实际上是使()0HW a θ为一个固定值的条件下,求取使得()HWJ N +方差最小的W 作为最有权值,即:()0min .H X W HW R Ws t W a Fθ⎧⎪⎨⎪=⎩,其中F 为常数利用拉格朗日乘子法可解得:()10X opt W R a μθ-=当取1F =时,则()()11H X a R a μθθ-=,μ的取值不影响SNR 和方向图。
阵列信号处理第一讲04_03_10

•
离散的空间阵列(Array)
5
阵列处理问题的示意图
6
阵列信号处理的研究内容
• 阵列的配置(configuration)
• 信号的空时特征(Spatial and Temporal Characteristics) • 干扰的空时特征
• 阵列信号处理的目的
7
一、阵列的配置
(1) 每个天线阵元的方向性
频域形式为:
46
我们定义上式右端为频率—波数响应函数:
波束方向图(Beam Pattern):
我们假设信号是一个带通信号:
对于(2.13)中的平面波信号,我们有:
47
在很多情况下,信号的复包络的带宽很小,满足:
我们定义: 为了满足(2.46)式的条件,我们需要:
我们称满足上述条件的信号为:窄带信号
均匀加权权值: 频率-波数函数为:
或者:
56
也可以写成:
可视区域内的波束方向图几种表示方法:
57
58
其中:
59
60
61
波束方向图的主要参数:
(1)3-dB波束宽度(半功率波束宽度,HPBW) (2)第一个零点之间的距离(BWNN)
(3)到第一旁瓣的距离
(4)第一旁瓣的高度
(5)其余零点的位置
N为奇数时,可以写成:
该共扼对称性质可以用于简化运算量和改进性能。例 如,当权值也是共扼对称时,波束方向图为:
54
如何构造一个特定波束方向图
由于: 我们可以选择特定的N个点,使满足 : 则定义: 和: 则: 注意: (1)我们是在N个点上满足要求; (2)上述推导过程适合于任意阵列。
55
2.4 均匀加权线性阵列
阵列信号处理的基本知识分析

diag{g ej1 ,, g e } jM
1
M
阵元之间的互藕 有关因素:阵元之间的间距大小,系统工作 频段,采用的传感器类型等。 设所有阵元之间的藕合系数矩阵为C,则考 虑到阵元间互藕的阵列输出信号模型为:
x(t) CAs(t) n(t)
阵元位置 阵元测向的关键信息是空间信号入射到各阵 元的相对延迟相位,而这一相位依赖于阵元 之间的空间位置,阵元位置误差直接导致延 迟相位估计误差,从而影响信号参数估计。
信号参数估计(DOA,频率,极化参数,距离, 时延等): 谱估计方法(子空间方法,波束形成 方法),参数化方法(最大似然,基于子空间逼 近方法)。
Ref[1] H.krim and M.Viberg, Two decdees of array processing research: the parametric approach, IEEE signal processing Magazine, Vol.13, Vol.4, 1996. Ref.[2] D.H.Johnson, D.E.Dudgeon, Array signal processing, Prentice-Hall,1993. Ref.[3] IEE Proc. 1991. Ref.[4] Vaccaro, R.J, The past, present, and the future of underwater acoustic signal processing, IEEE Signal Processing Magazine, Vol.15 , No.4 , 1998.
-25
-30
-35
-40
-45
-50
-80 -60 -40 -20
0
20
第七章 阵列信号处理

阵列信号处理在通信中应用
阵列处理是改善蜂窝和个人通信服务系统质量、 覆盖范围和容量的一种强有力的工具.
实际感兴趣的阵列处理是将接收天线阵列用于反 向连接(客户到基站)。多个接收天线能够收集更 多的信号能量,若天线在空间足够分离或极化各 异,则多个天线能够提供很好的分集接收,并抑 制多径传输引起的衰落。这些好处可以扩大基站 的覆盖范围,改善通信质量.
雷达信号处理国防科技重点实验室
阵列信号处理的最重要应用
信(号)源定位——确定阵列到信源的仰角和 方位角,甚至距离(若信源位于近场); 信源分离——确定各个信源发射的信号波 形.各个信源从不同方向到达阵列,这一 事实使得这些信号波形得以分离,即使它 们在时域和频域是叠加的; 信道估计——确定信源与阵列之间的传输 信道的参数(多径参数).
j 1 J
N个快拍的波束形成器输出的平均功率
1 P( w) N 1 | y ( t ) | N t 1
2 N N H 2 | w x ( t ) | t 1 J N
1 | w H a( d ) |2 N
1 2 | d ( t ) | [ t 1 j 1 N
1 2 H 2 | i ( t ) | | w a ( ) | || w ||2 j ij N t 1
1
与MMSE多用户检测器具有类似的形式
R s1 c1 T 1 s1 R s1
西安电子科技大学 雷达信号处理国防科技重点实验室
1
7.3
空间谱估计
R a( d ) H 1 a ( )R a( d )
1
最佳波束形成器设计
wopt
阵列信号处理某高校课程

医学成像中的阵列信号处理
总结词
医学成像中的阵列信号处理主要用于提高成像质量和诊断准确率。
详细描述
医学成像技术如超声成像、核磁共振成像等,利用不同频率的声波或电磁波获取人体内部结构的信息 。阵列信号处理技术可以对接收到的信号进行处理,实现图像增强、去噪和分辨率提升。阵列信号处 理在医学成像中能够提高成像质量和诊断准确率,对于医疗诊断和治疗具有重要意义。
阵列信号处理将进一步与其他 领域的技术融合,如机器学习 、人工智能等。通过跨域协同 ,可以实现更高效、更精准的 信号处理和分析。
随着传感器技术的发展,阵列 的构成和排列方式也将不断创 新。未来的阵列信号处理系统 将更加灵活、多样化和智能化 。
阵列信号处理技术的应用领域 将继续拓展,如智能感知、无 人系统、物联网等新兴领域。 通过与这些领域的交叉融合, 阵列信号处理将发挥更大的作 用和价值。
信号的波束形成
通过调整阵列天线接收信号的相位和幅度,实现信号的 波束形成,增强特定方向的信号强度。
阵列信号的传播特性
信号的空间传播
阵列信号在空间中传播时,会受到环境因素的影 响,如多径效应、阴影衰落等。
信号的方向特性
阵列信号的方向特性包括方向图、波束宽度、副 瓣电平等,这些特性决定了阵列对信号的接收和 定向发射能力。
05
课程总结与展望
课程总结
阵列信号处理的基本原理
阵列信号处理是一门研究如何通过多个传感器接收信号,并通过对这些信号的处理和分析,实现对信号源的定位、跟 踪和识别的学科。其基本原理包括信号的传播、阵列的几何排列、信号的波束形成等。
课程内容与学习目标
本课程介绍了阵列信号处理的基本概念、原理和方法,包括信号模型、阵列模型、信号参数估计、波束形成等。通过 学习,学生应能掌握阵列信号处理的基本理论和方法,并能够运用所学知识解决实际问题。
阵列信号处理答案

1.(1)关于接收天线阵列的假设。
接收阵列由位于空间已知坐标处的无源阵元按一定的形式排列而成。
假设阵元的接收特性仅与其位置有关而与其尺寸无关(认为其是一个点),并且阵元都是全向阵元,增益均相等,相互之间的互耦忽略不计。
阵元接收信号时将产生噪声,假设其为加性高斯白噪声,各阵元上的噪声相互统计独立,且噪声与信号是统计独立的。
(2)关于空间源信号的假设。
假设空间信号的传播介质是均匀且各向同性的,这时空间信号在介质中按直线传播,同时又假设阵列处在空间信号辐射的远场中,所以空间源信号到达阵列时可以看做是一束平行的平面波,空间源信号到达阵列各阵元在时间上的不同延时,可由阵列的几何结构和空间波的来向所决定。
空间波的来向在三维空间中常用仰角和方位角来表征。
其次,在建立阵列信号模型时,还常常要区分空间源信号是窄带信号还是宽带信号。
所谓窄带信号是指相对于信号(复信号)的载频而言,信号包络的带宽很窄(包络是慢变的),因此在同一时刻,该类信号对阵列各阵元的不同影响仅在于因其到达各阵元的波程不同而导致的相位差异。
2.自适应波束形成亦称空域滤波,是阵列处理的一个主要方面,逐步成为阵列信号处理的标志之一,其实质是通过对各阵元加权进行空域滤波,来达到增强期望信号、抑制干扰的目的;而且可以根据信号环境的变化自适应嘚改变各阵元的加权因子。
虽然阵列天线的方向图是全方向的,但阵列的输出经过加权求和后,可以被调整到阵列接收的方向增益聚集在一个方向,相当于形成了一个波束,这就是波束形成的物理意义所在。
波束形成技术的基本思想是:通过将各阵元输出进行加权求和,将天线阵列波束导向到一个方向上,对期望信号得到最大输出功率的导向位置即给出波达方向估计。
3. ULA :()1exp(2sin )exp(2(1)sin )Tk k k d dj j M θπθπθλλ⎡⎤=---⎢⎥⎣⎦αL 阵:(,)[(,),(,)]T x y a a a θφθφθφ=,其中2sin cos 2(1)sin cos (,)[1,...],,T j d j M x a e e πθφπθφθφ---=2s i n s i n 22s i ns i n 2(1...(,)[,,,]j d jd jM T y a ee e πθφπθφπθφθφ----=面阵: 12()()()M D D D ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦x y x y x y A A A A A A A ,其中112211222cos sin /2cos sin /2cos sin /2(1)cos sin /2(1)cos sin /2(1)cos sin /111K K K K j d j d j d x j d M j d M j d M e e e e e e πθφλπθφλπθφλπθφλπθφλπθφλ---------⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦A112211222sin sin /2sin sin /2sin sin /2(1)sin sin /2(1)sin sin /2(1)sin sin /111K K K K j d j d j d y j d M j d M j d M e ee ee e πθφλπθφλπθφλπθφλπθφλπθφλ---------⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦A4. 输公式烦死了,详见张老师写的书《阵列信号处理的理论和应用》38页和45页(应该是,挑一个写,这玩意我也不懂)5. MUSIC: 利用信号子空间和噪声子空间的正交性,通过谱峰搜索得到DOA 估计,适用任意阵列结构。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
西工大《阵列信号处理》复习考点整理
考试形式:
一、8道问答题,每道题5分;
二、六道大题,包括PPT 上老师给出的那一道。
一
1. 均匀线列阵在波束扫描时,波束图怎么变化?
当波束指向法线方向时,波束图具有最窄的主瓣宽度;随着阵元指向逐渐远离法线方向,主瓣一直指向所调方向并且展宽;除了指向法线方向外,主瓣都关于波束倾角轴不对称;当达到某一临界角时不能形成波束,但是在端射方向又可以形成波束。
且在端射方向形成一个较宽的主瓣。
2.DI 是什么?
DI 表示指向性指数,其表达式为
D 为方向性,是阵列和孔径的一个常用性能度量。
⎰⎰⋅=ππ
φθθφθπφθ200
),(sin 41)
,(P d d P D T T 3. DC 加权的特点
(1)旁瓣级给定时,主瓣宽度最小; (2)主瓣宽度给定时,旁瓣级最低; (3)等旁瓣级。
4. 频域快拍模型是什么,步骤是什么,常用的频域快拍取的时间有什么关系? (1)记住《最优阵列处理技术》245页图
5.1 (2)步骤:
①把总的观测时间T 分为K 个不重叠的时间区域,区域长度为△T ; ②对时域快拍进行FT ;
③对频域向量(频域快拍)进行窄带波束形成; ④对上述频域信号进行IFT 。
(3)△T 的选择准则
①△T 必须远大于平面波通过阵列的传播时间;
②△T 依赖于输入信号的带宽和信号的时域谱,16≥∆⋅T B (B*△T 足够大,选用频域快拍模型)。
5. 什么是均匀阵的瑞利限?
常规波束形成分辨率的极限。
表达式为
6. 空间白噪声的阵增益的相关计算。
阵列增益ωA 的定义为阵列的输出SNR 和一个阵元上的输入SNR 的比值。
下标“ω”表示空域不相关的噪声输入。
表达式如下:
2
2
10
1
)
()
(--===
=
∑
n
N n n
in o SNR SNR A ωωωωω
对于一个标准线阵(阵元间距为d=λ/2),白噪声阵列增益等于阵列的方向性D ; 对于一个均匀加权阵列,
有ωn =1/N(n=0,…,N-1),N A =ω(或单位为dB 时,为N log 10) 7. N 元ULA 可以分辨有多少来波?
可以分辨N-1个来波个数(N 元阵有1个参考元,所以自由度为N-1).
二
1. 对于阵元数N =5和N =6两种情况,推导并绘制标准均匀线列阵指向阵列法线方向,均匀加权得到的波束图)(u B ,注意旁瓣个数以及端射方向的波束形状。
已知ULA 的指向性函数为
)
sin()
sin(
)(u d N u d
N u B λπλπ⋅=
,
11≤≤-u (1)当N=5,d=λ/2时,
)
2
sin(5)25sin(
)(u u u B ππ
=
令
ππm u ±=25,即m u 5
2
±=(m=1,2) πm u ±≠,零点有52±,5
4
±。
令)2(25πππ+±=m u ,即)5152(+±=m u (m=1,2),极点有5
3±,1±。
当5
3
±=u 时,247.0)(=u B ,1=u 时,2.0)(=u B 。
波束图见PPT
(2)当N=6,d=λ/2时,
)
2
sin(6)
3sin()(u u u B ππ=
令ππm u ±=3,ππm u ±≠2(m=1,2,3),1,32
,31±±±=u
令)2(3πππ+±=m u ,)6131(+±=m u (m=1,2),6
5
,21±±=u 。
当21±=u 时,236.0)(=u B ,6
5
±=u 时,173.0)(=u B 。
波束图见PPT
2. 波束扫描(扫描害怕栅瓣)避免出现栅瓣的条件(一维,二维都推导过) 已知ULA 的指向性函数为
)
sin sin()
sin sin()(θλ
πθλπθd
N d N B ⋅=
当分子,分母均为零,即
πθλ
πm d
±=sin 时,出现栅瓣。
所以,第一栅瓣的位置为d
u u T λ
±=,则 ①0>T u ,1-≤-
d
u T λ
;②0<T u ,1
≥+
d
u T λ
解得 m a x s i n 1111θλ
+=+≤
T u d
(max
θ是扫描角度,和法线
方向夹角)
二维:
φθcos sin ⋅=x u ,
φ
θsin sin ⋅=y u ,栅瓣:
x
x d m u λ
⋅
±=,
y
y d m u λ
⋅±=
Tx
x
u d +≤
11
λ
,
Ty
y
u d +≤
11λ
3. 计算DI,WNG.
DI 表示方向性指数,其表达式为
D 为方向性,是阵列和孔径的一个常用性能度量。
WNG 是白噪声增益。
4. MVDR
(关键点:约束条件,信号无失真通过,旁瓣最低,输出噪声最小) 影响MVDR 性质
(公式中的量,测量的信号不对,阵列流形)
方向向量()s K W V ,和噪声谱矩阵()W S n 对MVDR 均有影响。
(1)使用了不准确的信号频率,传播速度和入射角度,以及阵列扰动均会造成方向向量的失配;
(2)使用有限数目的数据会造成噪声谱矩阵估计不准。
5. MUSIC 的流程
(思路:做一个数值器分析,找前多少个,把噪声空间取出来,把信号取出来,
拿噪声空间一比,噪声分辨率分之一可得出结果)
MUSIC算法介绍
MUSIC算法叫做多信号分类算法(Multiple Signal classification),MUSIC算法的基本思想则为将任意阵列输出数据的协方差矩阵进行特征分解,从而得到与信号分量相对应的信号子空间和信号分量相正交的噪声子空间,然后利用这两个子空间的正交性来估计信号的参数(入射方向、极化信息和信号强度)。
MUSIC算法具有普遍的适用性,只要已知n天线阵的布阵形式,无论是直线阵列还是圆阵列,不管阵元是否是等间距分布,都可以得到高分辨率的结果。
原理
()()()()t N t S V t X +⋅=0θ
[]
nn H
ss H R V R V X X E R +⋅⋅=⋅=00
步骤:
(1)计算基阵接收数据的协方差矩阵R ,并对R 进行特征值分解;
(2)将R 的特征值按从小到大排列,较大的特征值对应的特征向量组成信号子空间U S ,其余特征向量构成噪声子空间U N ; (3)计算方位谱
()()
θθV u u V P H
n n H ⋅⋅=
1。
影响因素
(与MVDR 相差一个目标个数)。
方向向量()0θV ,协方差矩阵R ,同时需要已知目标的个数。
