计量经济学案例分析汇总
最新计量经济学案例分析一元回归模型实例分析

案例分析1— 一元回归模型实例分析依据1996-2005年《中国统计年鉴》提供的资料,经过整理,获得以下农村居民人均消费支出和人均纯收入的数据如表2-5:表2-5 农村居民1995-2004人均消费支出和人均纯收入数据资料 单位:元 年度 1995199619971998199920002001200220032004人均纯收入1577.7 1926.1 2090.1 2161.1 2210.3 2253.4 2366.4 2475.6 2622.2 2936.4人均消费支出1310.4 1572.1 1617.2 1590.3 1577.4 1670.1 1741.1 1834.3 1943.3 2184.7一、建立模型以农村居民人均纯收入为解释变量X ,农村居民人均消费支出为被解释变量Y ,分析Y 随X 的变化而变化的因果关系。
考察样本数据的分布并结合有关经济理论,建立一元线性回归模型如下:Y i =β0+β1X i +μi根据表2-5编制计算各参数的基础数据计算表。
求得:082.1704035.2262==Y X∑∑∑∑====3752432495.1986.788859011.516634423.1264471222ii i i iX y x y x 根据以上基础数据求得:623865.0423.126447986.788859ˆ21===∑∑iii xyx β8775.292035.2262623865.0082.1704ˆˆ10=⨯-=-=X Y ββ 样本回归函数为:ii X Y 623865.08775.292ˆ+= 上式表明,中国农村居民家庭人均可支配收入若是增加100元,居民们将会拿出其中的62.39元用于消费。
二、模型检验1.拟合优度检验952594.0011.516634423.1264471986.788859))(()(22222=⨯==∑∑∑iii i yx y x r2.t 检验525164.3061 210423.12644710.623865011.166345 2ˆˆ222122=-⨯-=--=∑∑n x y iiβσ049206.0423.1264471525164.3061ˆ)ˆ()ˆ(2211====∑ie xVar S σββ6717.112525164.3061423.126447110137.52432495ˆ)ˆ()ˆ(22200=⨯===∑∑σββii e xn X Var S 在显著性水平α=0.05,n-2=8时,查t 分布表,得到:306.2)2(2=-n t α提出假设,原假设H 0:β1=0,备择假设H 1:β1≠067864.12049206.0623865.0)ˆ(ˆ)ˆ(111==-=ββββe S t)2(67864.12)ˆ(21->=n t t αβ,差异显著,拒绝β1=0的假设。
计量经济学 案例分析
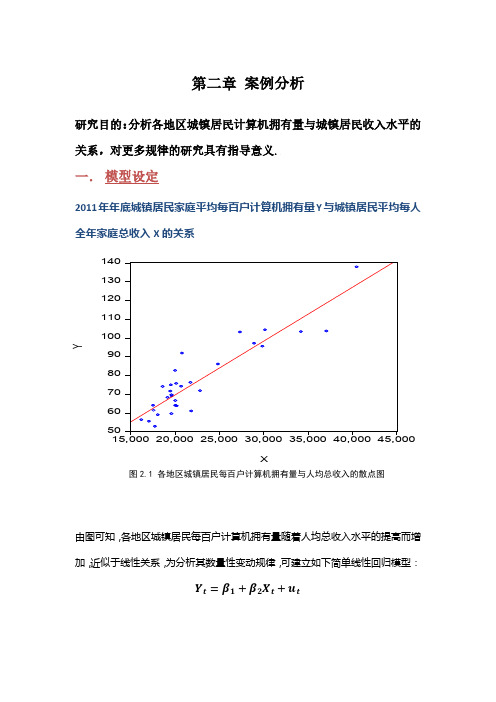
第二章 案例分析研究目的:分析各地区城镇居民计算机拥有量与城镇居民收入水平的关系,对更多规律的研究具有指导意义.一. 模型设定2011年年底城镇居民家庭平均每百户计算机拥有量Y 与城镇居民平均每人全年家庭总收入X 的关系图2.1 各地区城镇居民每百户计算机拥有量与人均总收入的散点图由图可知,各地区城镇居民每百户计算机拥有量随着人均总收入水平的提高而增加,近似于线性关系,为分析其数量性变动规律,可建立如下简单线性回归模型:Y t =β1+β2X t +u t5060708090100110120130140XY二.估计参数假定所建模型及其随机扰动项u i满足各项古典假设,用普通最小二乘法(OLSE)估计模型参数.其结果如下:表2.1 回归结果Dependent Variable: YMethod: Least SquaresDate: 11/13/17 Time: 12:50Sample: 1 31Included observations: 31Variable Coefficient Std. Error t-Statistic Prob.C 11.95802 5.622841 2.126686 0.0421X 0.002873 0.000240 11.98264 0.0000R-squared 0.831966 Mean dependent var 77.08161 Adjusted R-squared 0.826171 S.D. dependent var 19.25503 S.E. of regression 8.027957 Akaike info criterion 7.066078 Sum squared resid 1868.995 Schwarz criterion 7.158593 Log likelihood -107.5242 Hannan-Quinn criter. 7.096236 F-statistic 143.5836 Durbin-Watson stat 1.656123 Prob(F-statistic) 0.000000由表2.1可得,β1=11.9580,β2=0.0029故简单线性回归模型可写为:^ YX tt=11.9580+0.0029其中:SE(β1)=5.6228, SE(β2)=0.0002R-squared=0.8320,F=143.5836,n=31三.模型检验1.经济意义参数β1=11.9580 ,β2=0.0029,说明城镇居民家庭人均总收入每增加1元,城镇居民每百户拥有量平均增加0.0029台,与预期经济意义相符.2.拟合优度和统计检验拟合优度的度量:因为R-squared=0.8320,说明所建模型在整体上对样本数据拟合较好,解释变量对被解释变量的解释程度较高.回归系数的t检验:原假设H0:β1=0及H0:β2=0.回归系数β1的标准误差和t值分别为:SE(β1)= 5.6228,t(β1)=2.1267;回归系数β2的标准误差和t值分别为:SE(β2)= 0.0002,t(β2)= 11.9826.取α=0.05,故临界值t0.025(29)= 2.045,因为t(β1)= 2.1267>t0.025(29)= 2.045,故拒绝H0:β1=0;t(β2)= 11.9826.>t0.025(29)= 2.045,故拒绝H0:β2=0.对斜率系数的显著性检验表明:城镇居民人均总收入对城镇居民每百户计算机拥有量有显著影响. 四.回归预测若西部地区某省城镇居民家庭人均收入能达到25000元/人,利用所估计模型预测城镇居民每百户计算机拥有量。
计量经济学案例分析报告

《计量经济学》实验报告实验课题:各章节案列分析姓名:茆汉成班级:会计学12-2班学号:指导老师:蒋翠侠报告日期:目录第二章简单线性回归模型案例 (1)1 问题引入 (1)2 模型设定 (1)3 估计参数 (3)4 模型检验 (3)第三章多元线性回归模型案例 (5)1 问题引入 (5)2 模型设定 (5)3 估计参数 (6)4 模型检验 (6)第四章多重线性案例 (8)1 问题引入 (8)2 模型设定 (8)3 参数估计 (8)4 对多重共线性的处理 (9)第五章异方差性案例 (10)1 问题引入 (11)2 模型设定 (11)3 参数估计 (11)4 异方差检验 (11)5 异方差性的修正 (14)第六章自相关案例 (14)1 问题引入 (15)2 模型设定 (15)3 用OLS估计 (15)4 自相关其他检验 (15)5 消除自相关 (16)第七章分布滞后模型与自回归模型案例 (18)7.2案例1 (19)1 问题引入 (19)2 模型设定 (19)3 参数估计 (19)7.3案例2 (20)1 问题引入 (21)2 模型设定 (21)3、回归分析 (21)4 模型检验 (23)第八章虚拟变量回归案例 (23)1 问题引入 (24)2 模型设定 (24)3 参数估计 (26)4 模型检验 (27)第二章简单线性回归模型案例1、问题引入居民消费在社会经济的持续发展中有着重要的作用。
适度的居民消费规模和合理的消费模型是人民生活水平的具体体现,有利于经济持续健康的增长。
随着社会信息化程度和居民的收入水平的提高,计算机的运用越来越普及,作为居民耐用消费品重要代表的计算机已经为众多的城镇居民家庭所拥有。
研究中国各地区城镇居民计算机拥有量与居民收入水平的数量关系。
影响居民计算机拥有量的因素有多种,但从理论和经验分析,最主要的影响因素应是居民收入水平。
从理论上说居民收入水平越高,居民计算机拥有量越多。
所以我们设定“城镇居民家庭平均每百户计算机拥有量(台)”为被解释变量,“城镇居民平均每人全年家庭总收入(元)”为解释变量。
计量经济学实际案例

二、均值分析1、分性别对身高进行的比较假设男女身高相等,否定假设可认为男生身高明显高于女生。
2、分南北地区进行比较(1)身高假设两者均值相等,检验结果不能否定原假设,因而不能认为南北方身高有显著差异。
(2)体重通过假设两者均值相等,检验结果无法否定原假设,因而认为南北方体重没有明显差异。
3、分出生年份月份进行比较年份性别身高体重84 男均值172.00 56.00N 1 1总计均值172.00 56.00N 1 185 男均值180.33 70.67N 3 3女均值161.00 51.00N 2 2总计均值172.60 62.80N 5 586 男均值174.20 65.40N 20 20女均值162.11 52.28N 18 18总计均值168.47 59.1887 男均值178.50 66.58N 6 6女均值164.83 52.83N 18 18总计均值168.25 56.27N 24 2488 男均值170.50 65.00N 2 2女均值167.00 53.50N 2 2总计均值168.75 59.25N 4 489 女均值165.00 50.00N 1 1总计均值165.00 50.00N 1 1总计男均值175.28 65.80N 32 32女均值163.56 52.46N 41 41总计均值168.70 58.31N 73 73ANOVA 表由表可看出,各年份出生的人身高体重无显著性差异。
总计均值171.00 64.00N 6 6 3 男均值174.50 69.50N 4 4 女均值160.25 50.75N 4 4 总计均值167.38 60.13N 8 8 4 男均值181.25 68.50N 4 4 女均值162.25 52.00N 4 4 总计均值171.75 60.25N 8 8 5 男均值169.50 65.25N 2 2 女均值156.00 43.00N 1 1 总计均值165.00 57.83N 3 3 6 男均值175.00 63.00N 1 1 女均值171.50 57.50N 4 4 总计均值172.20 58.60N 5 5 7 男均值171.00 64.33N 3 3 女均值167.00 50.50N 2 2 总计均值169.40 58.80N 5 5 8 男均值179.20 64.90N 5 5 女均值161.50 52.50N 2 2 总计均值174.14 61.36N 7 7 9 男均值171.67 58.00N 3 3 女均值163.33 54.33N 3 3 总计均值167.50 56.1710 男均值174.67 61.83N 3 3总计均值174.67 61.83N 3 311 女均值162.50 51.67N 12 12总计均值162.50 51.67N 12 1212 男均值171.00 66.50N 2 2女均值167.00 57.00N 1 1总计均值169.67 63.33N 3 3总计男均值175.28 65.80N 32 32女均值163.56 52.46N 41 41总计均值168.70 58.31N 73 73ANOVA 表由表同样可得出,各月出生的人身高体重无显著性差异。
金融计量分析(完整版)

⾦融计量分析(完整版)案例⼀:中国居民总量消费函数(序列相关性)⼀、研究⽬地居民消费在社会经济地持续发展中有着重要地作⽤.居民合理地消费模式和居民适度地消费规模有利于经济持续健康地增长.建⽴总量消费函数是进⾏宏观经济管理地重要⼿段.为了研究全国居民总量消费⽔平及其变动地原因,从总量上考察居民总消费与居民收⼊间地关系,需要作具体地分析.为此,可以建⽴相应地计量经济模型去研究.⼆、模型设定研究对象:中国居民实际消费总⽀出与居民实际可⽀配收⼊之间地关系.模型变量:影响中国居民消费总⽀出有多种不同地因素,但从理论和经验分析,最主要地影响因素应是居民实际可⽀配收⼊,其他因素虽然对居民消费也有影响,但有地不易取得数据;有地与居民收⼊可能⾼度相关.因此这些其他因素可以不列⼊模型,可归⼊随即扰动项中.考虑到数据地可得性,我们将“实际可⽀配收⼊”作为解释变量X,“居民实际消费总⽀出”作为被解释变量.关于变量地符号与涵义如表1所⽰.表1 变量定义内⽣产总值GDP、名义居民总消费CONS以及表⽰宏观税收税收总额TAX、表⽰价格变化地居民消费价格指数CPI(1990=100),并由这些数据整理出实际⽀出法国内⽣产总值GDPC =GDP/CPI、居民实际消费总⽀出Y=CONS/CPI,以及实际可⽀配收⼊X=(GDP-TAX)/CPI.这些数据观测值是连续不同中地数据.表2 中国居民总量消费⽀出与收⼊数据资料中国居民总量消费⽀出与收⼊资料单位:亿元图2:X与Y地散点图从散点图可以看出居民实际消费总⽀出(Y)和实际可⽀配收⼊(X)⼤体呈现为线性关系,所以建⽴地计量经济模型为如下线性模型:三、估计参数假定所建模型及随机扰动项满⾜古典假定,可以⽤OLS法估计其参数.回归结果下:表3得: Y=2091.295+0.437527X剩余项(Residual)、实际值(Actual)、拟合值(Fitted)地图形,如图2所⽰.图2四、模型检验(⼀)经济意义检验所估计地参数(斜率项)为0.438,符合经济理论中边际消费倾向在0与1之间地假说,经济意义为在1978-2006年间,以1990年价计地中国居民可⽀配收⼊每增加1亿元,居民总量消费⽀出⽔平平均增加0.438亿元.(⼆)拟合优度和统计检验拟合优度检验:可决系数为0.987955,说明所建模型整体上对样本数据拟合较好,即解释变量“居民实际可⽀配收⼊”对被解释变量“居民实际消费总⽀出”地绝⼤部分差异作出了解释.对回归系数地t检验:截距项与斜率项t值都通过变量地显著性检验,这表明,居民实际可⽀配收⼊对居民实际消费总⽀出有显著影响.F统计量检验:F值较⼤,附带地概率也通过了检验,说明模型总体线性较显著.(三)计量经济学检验1、模型设定偏误检验:RESET检验表4在5%地显著性⽔平下,从F统计值地伴随概率看,拒绝原模型没有设定偏误地假设,表明原模型存在设定偏误.因为Y与X都是时间序列,⽽且它们表现出共同地变动趋势,因此怀疑较⾼地R2部分地由于这⼀共同变动趋势带来地.为排除时间趋势项地影响,在模型中引⼊时间趋势项,将这种影响分离出来.从趋势图看,X与Y呈现⾮线性变化趋势,故引⼊T地平⽅地形式,结果为:表5再次进⾏RESET检验:表6可以看出,引⼊时间趋势项地模型已经不存在设定偏误问题.2、异⽅差检验(对引⼊时间趋势项地模型进⾏White检验)从nR2统计量对应值地伴随概率可以看出,在5%在显著性⽔平下,因此拒绝原模型同⽅差地假设,即含有时间趋势项地模型存在异⽅差性.3.异⽅差地修正(WLS估计法)以resid^2为权数进⾏来进⾏加权最⼩⼆乘法如下修正后地回归⽅程为:Y = 6229.342 + 0.362278*X4、序列相关性检验(对引⼊时间趋势项地模型进⾏LM检验)表8从nR2统计量对应值地伴随概率可以看出,在5%在显著性⽔平下,拒绝原模型不存在序列相关性地假设,即含有时间趋势项地模型存在⼀阶序列相关性.从下部分Test Equation 中可以看出,RESID(-1)显著不为0,这进⼀步说明原模型存在⼀阶序列相关性.进⼀步检验滞后2阶情况,结果如下:表9可以看出,RESID(-2)地系数没有通过t显著性检验,即不存在2阶序列相关性.5、⼀阶序列相关性地修正(⼴义差分法)表10估计结果为:= 3505.7 + 0.1996X + 19.24T^2 +0.748AR(1)对上式进⾏LM检验:表11从nR2统计量对应值地伴随概率可以看出,在1%在显著性⽔平下,不拒绝原模型不存在序列相关性地假设,即模型已经不存在⼀阶序列相关性.从下部分Test Equation中可以看出,RESID(-1)前系数显著地为0,这进⼀步说明模型已经不存在⼀阶序列相关性.故现在地模型变为:= 3505.7 + 0.1996X + 19.24T+0.748AR(1) (1) 6、⼀阶序列相关性地修正(序列相关稳健估计法)序列相关稳健估计法估计结果为:= 3328.2 + 0.1762X + 21.66 T (2)(14.62)(7.53)(9.79)R=0.9976 F=5380.8 D.W.=0.442表126、序列相关性检验由于模型地R2与F值都较⼤,⽽且各参数估计值地t检验值都显著地不为零,说明各解释变量对Y地联合线性作⽤显著,⽽且各解释变量独⾃对Y地独⽴作⽤也⽐较显著,故各解释变量间不存在序列相关性五、回归预测2007年,以当年价计地中国GDP为263242. 5亿元,税收总额45621.9亿元,居民消费价格指数为409.1,由此可得出以1990年价计地可⽀配总收⼊X约为95407.4亿元,由上述回归⽅程可得2007年居民总量消费预测地点估计值:⽤式(1)进⾏估计:Y= 3505.7 + 0.1996*95407.4 + 19.24*30+0.748*0.7479=39860.5⽤式(2)进⾏估计:Y= =3328.2 + 0.1762*95407.4 + 21.66 *30=39624.62007年,中国名义居民消费总量为93317.2亿元,以1990年为基准地居民消费价格指数为228.1,由此可推出当年中国实际居民消费总量为40910.7亿元,可见相对误差为2.57%(⽤式(1)结果进⾏计算),可以说还是相对⽐较准确地结果.案例⼆;农作物产值模型(异⽅差地检验和修正)⼀、模型设定⼀取1986年中国29个省市⾃治区农作物种植业产值y t(亿元)和农作物播种⾯积x t (万亩)数据(见表1)研究⼆者之间地关系.建⽴如下模型:⼆、数据搜集根据表中数据进⾏OLS回归,得估计地线性模型如下,yt = -5.6610 + 0.0123 xt (-0.95) (12.4)R2=0.85 =0.846 F =155.0四、异⽅差检验图2 残差图从模型地残差图(见图2)可以发现数据中存在异⽅差.(1)⽤White⽅法检验是否存在异⽅差.在上式回归地基础上,做White检验得:图3输出结果中地概率是指χ2 (2)统计量取值⼤于8.02地概率为0.018. 因为TR2 = 8.02 > χ2α (2) = 6,所以存在异⽅差.五、异⽅差地修正下⾯使⽤三种⽅法来修正异⽅差.(1)改变模型设定形式法.对yt和xt同取对数,得两个新变量Lnyt 和Lnxt(见图3).⽤Lnyt 对Lnxt 回归,得:Lnyt = - 4.1801 + 0.9625 Lnxt .(-8.54) (16.9)R2 = 0.91, F = 285.6,因为TR2 = 2.58 < 20.05 (2) = 6.0,所以经White检验不存在异⽅差.图4(2)WLS估计法为了找到适当地权w,作ln(e^2)关于x地回归结果如下:图5结果显⽰,前参数地5%显著性⽔平下不为零,同时F检验也表明⽅程地线性关系在5%地显著性⽔平下成⽴,于是,可⽣成权序列W命令为Genr w=1/@sqrt(exp(3.56405028673 + 0.000209806008672*X))进⾏加权修正后地回归结果如下:图6我们可以再次对经过加权处理地模型进⾏异⽅差检验,如图:图7显然,nR^2值所附带地概率表明,不拒绝同⽅差地原假设,也就是模型已经不存在异⽅差了.修正后地回归结果为:Y=0.256182+0.01115*X(4.545095) (0.000917)R2=0.845671 =0.839956 F =147.9514(3)异⽅差地稳健标准误法修正原模型中地OLS标准差.图8可见系数了原模型基本⼀致,但X对应系数地标准差⽐OLS估计地有所增⼤,这表明原模型OLS估计结果低估了X地标准差.案例三:(多重共线性)⼀、研究⽬地与背景经济理论指出,居民消费⽀出(Y)不仅取决于可⽀配收⼊(X1)和利率(X2)还取决于个⼈财富(X3)地影响.可⽀配收⼊和个⼈财富对于居民消费⽀出地作⽤是正⽅向地;按照古典经济学地观点,利率对于储蓄地作⽤是也是正⽅向地,即利率地提⾼可以刺激储蓄、抑制消费;利率地降低则抑制储蓄,刺激消费.所以综上所述设定如下形式地计量经济模型:Yt = C + β1X1t - β1X2t + β2X3t + µt其中Y=家庭消费⽀出,X1=可⽀配收⼊,X2=利率,X3=个⼈财富⼆、模型估计与检验为估计模型参数,收集旅游事业发展最快地2001-2010年地统计数据,如表1所⽰:表1果如图1:输⼊统计资料: DATA Y X1 X2 X3建⽴回归模型: LS Y C X1 X2 X3因此,X1、X2、X3对居民地消费⽀出函数为:= (2.427712) (0.874457) (-0.503673) (-0.222169)R^2= 0.963636 ^2= 0.945455由此可见,该模型可决系数很⾼,F检验值52.99996, 给定α=5%,查表得临界值(3,6)=4.76 判断:F值>临界值,拒绝参数整体不显著地原假设,模型整体线性显著.给定显著性⽔平α=0.05,可得到临界值tα/2(n-k-1)=2.447,由样本求出统计量|t|=0.874457 |t|= 0.503673 |t|=0.222169,计算得所有变量地t值都⼩于该临界值,所以接受原假设H0,即是说包括常数项地3个解释变量都在95%地置信⽔平下不显著.⽽且X3系数地符号与预期地相反,这表明很可能存在严重地多重共线性.计算各解释变量地相关系数,选择X1、X2、X3数据,点“view/correlations”得相关系数矩阵,或在命令窗⼝中键⼊:cor X1、X2 x3.如表2所⽰:表2由相关系数矩阵可以看出:各解释变量相互之间地相关系数较⾼,证实确实存在严重多重共线性.三、模型地修正采⽤逐步回归地办法,去检验和解决多重共线性问题.分别作Y 对X1、X2、X3地⼀元回归,结果如图2、3、4所⽰:图2图3图4表3以X1为基础,加⼊X2变量回归,回归结果为:图5Y=285.0087 + 0.523886X1 – 25.56223X2 t=(2.682801) (10.90078) (-0.493513)第⼀步,在初始模型中引⼊X2,模型拟合优度提⾼,参数符号合理,当取时,,但X2参数地t 检验不显著.第⼆步,去掉X2,引⼊X3,如图6:图6Y = 245.52 + 0.568*X1 - 0.0058*X3306. 2 ) 2 10 ( ) ( 025 . 0 2 = - = - t k n t αt=(3.53) (0.793781) (-0.082975)拟合优度略有下降,但是X3符号不合理,且未通过t检验.所以X2、X3都应该剔除.综上所述,最终地居民消费函数应该以Y=f(X1)为最优,拟合结果如下:= 244.5455 + 0.509091X1结论本次作业考虑到每组数据同时出现三种问题地可能性不⼤,故由每⼈负责⼀种情况地检验与修正.鉴于数据地可得性,对于有些样本数据空间地数量还远远达不到模型本⾝所要求地数量,这样去估计模型是没有实际预测意义地.同样,囿于所学⽔平有限,变量地选取还是按照书上地例⼦来选取,这种模型本⾝设定形式是否正确,还有待进⼀步验证.我们相信,随着所学知识地进⼀步深⼊,对于实证分析地⼀般过程和具体⽅法都会逐步完善.参考⽂献:[1]李⼦奈,陈绍业.计量经济学(第三版)[M].⾼等教育出版社,2010.[2]张晓峒.EViews使⽤指南与案例[M].机械⼯业出版社,2007.[3]程振源.计量经济学:理论与实验[M].上海财经⼤学出版社,2009.[4]于俊年.计量经济学软件-EViews地使⽤[M].对外经济贸易⼤学出版社,2006.版权申明本⽂部分内容,包括⽂字、图⽚、以及设计等在⽹上搜集整理。
计量经济学案例分析

0.714371 0.600119 6386.730 6.12E+08 -219.7672 1.975920
Mean dependent var S.D. dependent var Akaike info criterion Schwarz criterion F-statistic Prob(F-statistic)
-1.74E-11 10099.81 20.61520 20.96235 6.252598 0.001875
可以看出,n=22*0.714371=15.716162, 相伴概率为p=0.000387,因此在显著水 平α=0.05的条件下,拒绝无自相关的原
假设,即随机干扰项存在自相关。又 因为的回归系数显著不为0(P值为 0.0062),表明存在一阶自相关。又的 回归系数不为0,但是对应的P值 =0.1363>0.05,所以表明不存在二阶自
首先,一国进出贸易的发展程度很 大程度上依赖于这个国家的经济发展 水平,衡量一个国家经济发展水平的 最有效的指标就是GDP。国民经济越发 达,与国外的联系也会越紧密,从而 推动国家进出口贸易的发展。
其次,进出口额是指一国出口商品 所得收入和进口 商品的外汇支出的总 额。它直接产生的关税就是财政收入 。所以财政收入越多,进出口额也同 步增长。另一方面,财政支出若是增 多,我国则会减少多进出口贸易的投 资支出,所以财政支出与进出口额也 密切相关。
95539.1
159878.3
2005
116921.8
184937.4
2006
140974
216314.4
2007
166863.7
265810.3
2008
179921.4702
2019年南开大学《计量经济学》案例分析.doc

南开大学《计量经济学》案例分析案例一:用回归模型预测木材剩余物(file:b1c3)伊春林区位于黑龙江省东北部。
全区有森林面积218.9732万公顷,木材蓄积量为2.324602亿m3。
森林覆盖率为62.5%,是我国主要的木材工业基地之一。
1999年伊春林区木材采伐量为532万m3。
按此速度44年之后,1999年的蓄积量将被采伐一空。
所以目前亟待调整木材采伐规划与方式,保护森林生态环境。
为缓解森林资源危机,并解决部分职工就业问题,除了做好木材的深加工外,还要充分利用木材剩余物生产林业产品,如纸浆、纸袋、纸板等。
因此预测林区的年木材剩余物是安排木材剩余物加工生产的一个关键环节。
下面,利用一元线性回归模型预测林区每年的木材剩余物。
显然引起木材剩余物变化的关键因素是年木材采伐量。
给出伊春林区16个林业局1999年木材剩余物和年木材采伐量数据如表1.1。
散点图见图1.1。
观测点近似服从线性关系。
建立一元线性回归模型如下:y t = β0 + β1 x t + u t表1.1 年剩余物y t和年木材采伐量x t数据林业局名年木材剩余物y t(万m3)年木材采伐量x t(万m3)乌伊岭26.13 61.4 东风23.49 48.3 新青21.97 51.8 红星11.53 35.9 五营7.18 17.8 上甘岭 6.80 17.0 友好18.43 55.0 翠峦11.69 32.7 乌马河 6.80 17.0 美溪9.69 27.3 大丰7.99 21.5 南岔12.15 35.5 带岭 6.80 17.0 朗乡17.20 50.0 桃山9.50 30.0 双丰 5.52 13.8合计202.87 532.00图1.1 年剩余物y t和年木材采伐量x t散点图图1.2 EViews输出结果EViews估计结果见图1.2。
在已建立Eviews数据文件的基础上,进行OLS估计的操作步骤如下:打开工作文件,从主菜单上点击Quick键,选Estimate Equation 功能。
计量经济学案例分析汇总

计量经济学案例分析1一、研究的目的要求居民消费在社会经济的持续发展中有着重要的作用。
居民合理的消费模式和居民适度的消费规模有利于经济持续健康的增长, 而且这也是人民生活水平的具体体现。
改革开放以来随着中国经济的快速发展, 人民生活水平不断提高, 居民的消费水平也不断增长。
但是在看到这个整体趋势的同时, 还应看到全国各地区经济发展速度不同, 居民消费水平也有明显差异。
例如, 2002年全国城市居民家庭平均每人每年消费支出为6029.88元, 最低的黑龙江省仅为人均4462.08元, 最高的上海市达人均10464元, 上海是黑龙江的2.35倍。
为了研究全国居民消费水平及其变动的原因, 需要作具体的分析。
影响各地区居民消费支出有明显差异的因素可能很多, 例如, 居民的收入水平、就业状况、零售物价指数、利率、居民财产、购物环境等等都可能对居民消费有影响。
为了分析什么是影响各地区居民消费支出有明显差异的最主要因素, 并分析影响因素与消费水平的数量关系, 可以建立相应的计量经济模型去研究。
二、模型设定我们研究的对象是各地区居民消费的差异。
居民消费可分为城市居民消费和农村居民消费, 由于各地区的城市与农村人口比例及经济结构有较大差异, 最具有直接对比可比性的是城市居民消费。
而且, 由于各地区人口和经济总量不同, 只能用“城市居民每人每年的平均消费支出”来比较, 而这正是可从统计年鉴中获得数据的变量。
所以模型的被解释变量Y选定为“城市居民每人每年的平均消费支出”。
因为研究的目的是各地区城市居民消费的差异, 并不是城市居民消费在不同时间的变动, 所以应选择同一时期各地区城市居民的消费支出来建立模型。
因此建立的是2002年截面数据模型。
影响各地区城市居民人均消费支出有明显差异的因素有多种, 但从理论和经验分析, 最主要的影响因素应是居民收入, 其他因素虽然对居民消费也有影响, 但有的不易取得数据, 如“居民财产”和“购物环境”;有的与居民收入可能高度相关, 如“就业状况”、“居民财产”;还有的因素在运用截面数据时在地区间的差异并不大, 如“零售物价指数”、“利率”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计量经济学案例分析1一、研究的目的要求居民消费在社会经济的持续发展中有着重要的作用。
居民合理的消费模式和居民适度的消费规模有利于经济持续健康的增长,而且这也是人民生活水平的具体体现。
改革开放以来随着中国经济的快速发展,人民生活水平不断提高,居民的消费水平也不断增长。
但是在看到这个整体趋势的同时,还应看到全国各地区经济发展速度不同,居民消费水平也有明显差异。
例如,2002年全国城市居民家庭平均每人每年消费支出为元, 最低的黑龙江省仅为人均元,最高的上海市达人均10464元,上海是黑龙江的倍。
为了研究全国居民消费水平及其变动的原因,需要作具体的分析。
影响各地区居民消费支出有明显差异的因素可能很多,例如,居民的收入水平、就业状况、零售物价指数、利率、居民财产、购物环境等等都可能对居民消费有影响。
为了分析什么是影响各地区居民消费支出有明显差异的最主要因素,并分析影响因素与消费水平的数量关系,可以建立相应的计量经济模型去研究。
二、模型设定我们研究的对象是各地区居民消费的差异。
居民消费可分为城市居民消费和农村居民消费,由于各地区的城市与农村人口比例及经济结构有较大差异,最具有直接对比可比性的是城市居民消费。
而且,由于各地区人口和经济总量不同,只能用“城市居民每人每年的平均消费支出”来比较,而这正是可从统计年鉴中获得数据的变量。
所以模型的被解释变量Y选定为“城市居民每人每年的平均消费支出”。
因为研究的目的是各地区城市居民消费的差异,并不是城市居民消费在不同时间的变动,所以应选择同一时期各地区城市居民的消费支出来建立模型。
因此建立的是2002年截面数据模型。
影响各地区城市居民人均消费支出有明显差异的因素有多种,但从理论和经验分析,最主要的影响因素应是居民收入,其他因素虽然对居民消费也有影响,但有的不易取得数据,如“居民财产”和“购物环境”;有的与居民收入可能高度相关,如“就业状况”、“居民财产”;还有的因素在运用截面数据时在地区间的差异并不大,如“零售物价指数”、“利率”。
因此这些其他因素可以不列入模型,即便它们对居民消费有某些影响也可归入随即扰动项中。
为了与“城市居民人均消费支出”相对应,选择在统计年鉴中可以获得的“城市居民每人每年可支配收入”作为解释变量X。
从2002年《中国统计年鉴》中得到表的数据:表 2002年中国各地区城市居民人均年消费支出和可支配收入如图:图从散点图可以看出居民家庭平均每人每年消费支出(Y)和城市居民人均年可支配收入(X)大体呈现为线性关系,所以建立的计量经济模型为如下线性模型:12i i i Y X u ββ=++三、估计参数假定所建模型及随机扰动项i u 满足古典假定,可以用OLS 法估计其参数。
运用计算机软件EViews 作计量经济分析十分方便。
利用EViews 作简单线性回归分析的步骤如下: 1、建立工作文件首先,双击EViews 图标,进入EViews 主页。
在菜单一次点击File\New\Workfile ,出现对话框“Workfile Range ”。
在“Workfile frequency ”中选择数据频率:Annual (年度) Weekly ( 周数据 )Quartrly (季度) Daily (5 day week ) ( 每周5天日数据 ) Semi Annual (半年) Daily (7 day week ) ( 每周7天日数据 ) Monthly (月度) Undated or irreqular (未注明日期或不规则的)在本例中是截面数据,选择“Undated or irreqular ”。
并在“Start date ”中输入开始时间或顺序号,如“1”在“end date ”中输入最后时间或顺序号,如“31”点击“ok ”出现“Workfile UNTITLED ”工作框。
其中已有变量:“c ”—截距项 “resid ”—剩余项。
在“Objects ”菜单中点击“New Objec ts”,在“New Objects”对话框中选“Group”,并在“Name for Objects”上定义文件名,点击“OK ”出现数据编辑窗口。
若要将工作文件存盘,点击窗口上方“Save ”,在“SaveAs ”对话框中给定路径和文件4000600080001000012000400060008000100001200014000XY名,再点击“ok ”,文件即被保存。
2、输入数据在数据编辑窗口中,首先按上行键“↑”,这时对应的“obs”字样的空格会自动上跳,在对应列的第二个“obs”有边框的空格键入变量名,如“Y ”,再按下行键“↓”,对因变量名下的列出现“NA ”字样,即可依顺序输入响应的数据。
其他变量的数据也可用类似方法输入。
也可以在EViews 命令框直接键入“data X Y ”(一元时) 或 “data Y 1X2X … ”(多元时),回车出现“Group”窗口数据编辑框,在对应的Y 、X 下输入数据。
若要对数据存盘,点击 “fire/Save As”,出现“Save As ”对话框,在“Drives ”点所要存的盘,在“Directories ”点存入的路径(文件名),在“Fire Name ”对所存文件命名,或点已存的文件名,再点“ok ”。
若要读取已存盘数据,点击“fire/Open”,在对话框的“Drives”点所存的磁盘名,在“Directories”点文件路径,在“Fire Name”点文件名,点击“ok”即可。
3、估计参数方法一:在EViews 主页界面点击“Quick ”菜单,点击“Estimate Equation ”,出现“Equation specification ”对话框,选OLS 估计,即选击“Least Squares”,键入“Y C X ”,点“ok ”或按回车,即出现如表那样的回归结果。
表在本例中,参数估计的结果为: ^282.24340.758511i i Y X =+() t=20.935685r = F= df=29方法二:在EViews 命令框中直接键入“LS Y C X ”,按回车,即出现回归结果。
若要显示回归结果的图形,在“Equation ”框中,点击“Resids ”,即出现剩余项(Residual )、实际值(Actual )、拟合值(Fitted )的图形,如图所示。
图 四、模型检验 1、经济意义检验所估计的参数^20.758511β=,说明城市居民人均年可支配收入每相差1元,可导致居民消费支出相差元。
这与经济学中边际消费倾向的意义相符。
2、拟合优度和统计检验用EViews 得出回归模型参数估计结果的同时,已经给出了用于模型检验的相关数据。
拟合优度的度量:由表中可以看出,本例中可决系数为,说明所建模型整体上对样本数据拟合较好,即解释变量“城市居民人均年可支配收入”对被解释变量“城市居民人均年消费支出”的绝大部分差异作出了解释。
对回归系数的t 检验:针对01:0H β=和02:0H β=,由表中还可以看出,估计的回归系数^1β的标准误差和t 值分别为:^1()287.2649SE β=,^1()0.982520t β=;^2β的标准误差和t 值分别为:^2()0.036928SE β=,^2()20.54026t β=。
取0.05α=,查t 分布表得自由度为231229n -=-=的临界值0.025(29) 2.045t =。
因为^10.025()0.982520(29) 2.045t t β=<=,所以不能拒绝01:0H β=;因为^20.025()20.54026(29) 2.045t t β=>=,所以应拒绝02:0H β=。
这表明,城市人均年可支配收入对人均年消费支出有显著影响。
五、回归预测由表中可看出,2002年中国西部地区城市居民人均年可支配收入除了西藏外均在8000以下,人均消费支出也都在7000元以下。
在西部大开发的推动下,如果西部地区的城市居民人均年可支配收入第一步争取达到1000美元(按现有汇率即人民币8270元),第二步再争取达到1500美元(即人民币12405元),利用所估计的模型可预测这时城市居民可能达到的人均年消费支出水平。
可以注意到,这里的预测是利用截面数据模型对被解释变量在不同空间状况的空间预测。
用EViews 作回归预测,首先在“Workfile ”窗口点击“Range ”,出现“Change Workfile Range ”窗口,将“End data”由“31”改为“33”,点“OK ”,将“Workfile ”中的“Range ”扩展为1—33。
在“Workfile ”窗口点击“sampl”,将“sampl”窗口中的“1 31”改为“1 33”,点“OK ”,将样本区也改为1—33。
为了输入18270f X =,212405f X =在EViews 命令框键入data x /回车, 在X数据表中的“32”位置输入“8270”,在“33”的位置输入“12405”,将数据表最小化。
然后在“E quation ”框中,点击“Forecast ”,得对话框。
在对话框中的“Forecast name ”(预测值序列名)键入“fY ”, 回车即得到模型估计值及标准误差的图形。
双击“Workfile ”窗口中出现的“Yf ”,在“Yf ”数据表中的“32”位置出现预测值16555.132f Y =,在“33”位置出现29691.577f Y =。
这是当18270f X =和212405f X =时人均消费支出的点预测值。
为了作区间预测,在X 和Y 的数据表中,点击“View”选“Descriptive Stats\Cmmon Sample”,则得到X 和Y 的描述统计结果,见表:表根据表的数据可计算:222(1)2042.682(311)125176492.59ix xn σ=-=⨯-=∑221()(82707515.026)569985.74f X X -=-=222()(124057515.026)23911845.72f X X -=-= 取0.05α=,f Y平均值置信度95%的预测区间为:^^21f Y t n ασ18270f X =时6555.13 2.045413.1593⨯6555.13162.10=212405f X =时9691.58 2.045413.1593⨯ 9691.58499.25=即是说,当18270f X =元时,1f Y 平均值置信度95%的预测区间为(,)元。
当212405f X =元时,2f Y 平均值置信度95%的预测区间为(,)元。
fY 个别值置信度95%的预测区间为:^^21fY tασ+18270f X =时6555.13 2.045413.1593⨯6555.13860.32=212405f X =时9691.58 2.045413.1593⨯9691.58934.49=即是说,当第一步18270f X =时,1f Y 个别值置信度95%的预测区间为(,)元。
