北师大版数学七年级上册求解一元一次方程
北师大版七年级数学上册第5章第2节求解一元一次方程课件

学习新课
问题1: ①什么是去括号法则 ? ②什么是乘法分配律 ?
问题1: ①什么是去括号法则 ? 1)括号前面是“+”号,把括号和它前面的 “+”号去掉,括号里各项都不变符号. 2)括号前面是“-”号,把括号和它前面的 “-”号去掉,括号里各项都改变符号. ②什么是乘法分配律 ? 两个数的和同一个数相乘,等于把两个加数 分别同这个数相乘,再把两个积加起来,结果 不变。
议一议:视察上述两种解方 程的方法,说出它们的区分, 与同伴进行交流.
解方程
(1) 2(x-1)+3=3(x-1)
(2) 4( y 1) y 2( y 1) 2
归纳总结
问题5:解一元一次方程的一般步骤?
解一元一次方程,一般要通过 ①去分母, ②去括号, ③移项, ④合并同类项, ⑤未知数的系数化为1等 步骤; 1)去分母时注意不要漏乘,再者分母去掉了,分 数线变成了括号; 2)去括号要注意不要漏乘,再者注意符号变化问题; 3)移项注意变号; 4)合并同类项注意每一项都包括它前面的符号; 5)未知数的系数化为1注意未知数的系数做分母, 而不是做分子.
你来试试
5. 如果方程3x+2a=12和方程3x-4=2的解相
同,那么a=_3__.
6. 若m+2与2m-2不相等,则m不能为__4__.
7. 若x=0是方程2006x-a=2007x+3的解,那
么代数式-a+2的值是__5_.
8.如果方程6x+3a=21与方程3x+5=11的解
相同,那么a= (B )
a (b+c) =ab+ac
去、添括号法则(口诀) 去括号、添括号,关键看符号; 括号前面是正号,去、添括号不 变号;
七年级数学上册第五章一元一次方程2求解一元一次方程课件(新版)北师大版

知识点三 解一元一次方程——去分母 5.(2017江西赣州期末联考)解方程 -1= 时,去分母正确的是 ( A.3x-1=2(x-1) C.3x-6=2(x-1)
x 2 x 2 x 1 3
)
B.3x-3=2(x-1) D.3x-6=2x-1
x 1 3
x 2
答案 C 方程 -1= 两边同乘6,得6 1 =6× ,即3x-6=2(x-1).
解一元一次方程的一般步骤
步骤 去分母 去括号 具体做法 在方程两边都乘各分数的分母的最小公倍数 一般先去小括号,再去中括号,最后去大括号 依据 等式的基本性质2 注意事项 不要漏乘不含分母的项;分数线的括号作用
乘法对加法的分配 不要漏乘括号里的任何一项 律、去括号法则
续表
步骤 移项 合并同类项 系数化为1 具体做法 把含有未知数的项移到方程的一边,其他项移到另一边 把方程中的同类项分别合并,化成“ax=b(a≠0)”的形式
2 3
知识点三 解一元一次方程——去分母
定义 去分母 依据 做法 方程两边同时乘所有分母的 最小公倍数 一元一次方程中如果有分母,在方程的两边同 等式的基本性质2 时乘所有分母的最小公倍数,将分母去掉.这 一变形过程叫做去分母 重要 提示 (1)由于分数线相当于除号,其又有括号的作用,去分母时,如果分子是一个多项式,应该用括号把这个分子 作为一个整体用括号括起来; (2)去分母是在方程两边同时乘所有分母的最小公倍数,不能漏乘没有分母的项
温馨 提示 (1)如果括号前是“-”号,去括号后各项的符号应与原括号内相应各项的符号相反;(2)去括号时,括号前的 系数要乘括号内的每一项,不要漏乘任何一项
例2 解方程3-(x-2)=5x+1. 分析 去括号时,要注意括号前面的符号是负号时去掉括号后要改变括
北师大版七年级上册数学《求解一元一次方程》一元一次方程说课教学复习课件

知2-练
1 已知关于x的方程3a-x= x +3的解为2,则式子a2 2
-2a+1的值是_____1___.
2 方程3x-4=3-2x的解答过程的正确顺序是( C )
①合并同类项,得5x=7;②移项,得3x+2x=3+4;
③系数化为1,得x= 7 . 5
A.①②③
B.③②①
C.②①③
总结
知1-讲
移项与交换律的根本区别是移项时移动的 项要跨越等号,并且一定要记住移项要变号.
(来自《点拨》)
知1-练
1 把方程3y-6=y+8变形为3y-y=8+6,这种变形 叫做___移__项___,依据是__等__式__的__性__质__1__.
2 解方程时,移项法则的依据是( C )
A.加法交换律
数的系数.
解:(1)系数化为1,得x=-3.
(2)系数化为1,得x=-2.
(3)系数化为1,得x=-6.
(来自《点拨》)
总结
知1-讲
将系数化为1是解一元一次方程的最后一步, 解答时注意两点:一是未知数的系数是1而不是 “-1”;二是未知数的系数是分数时,可以将方 程两边同时乘以未知数系数的倒数.
(来自《点拨》)
C)
A.x=20
B.x=40
C.x=60
D.x=80
知3-练
(来自《典中点》)
2 下面解方程的结果正确的是( D )
A.方程4=3x-4x的解为x=4
B.方程 3 x= 1 的解为x=2 23
CD..方方程程312-=48=x的1解x的为x解=为x14=-9 3
知3-练
(来自《典中点》)
知3-讲
第五章 一元一次方程
5.2 求解一元一次方程
北师大版七年级数学上册《求解一元一次方程》评课稿

北师大版七年级数学上册《求解一元一次方程》评课稿一、课程背景和目标1.1 课程背景《求解一元一次方程》是北师大版七年级数学上册的一节重要课程,涉及到一元一次方程的基本概念、解法和应用。
通过学习本课程,学生将能够掌握一元一次方程的解法,培养逻辑思维和问题解决能力。
1.2 课程目标本节课的主要目标是:•理解一元一次方程的定义和基本概念;•掌握一元一次方程的解法,包括等式的加减法和乘除法消元法;•能够运用所学知识解决实际问题。
二、课程内容和流程2.1 课程内容本节课的主要内容包括:•一元一次方程的定义和基本概念;•等式的加减法消元法;•等式的乘除法消元法;•运用解一元一次方程解决实际问题。
2.2 课程流程本节课的教学流程如下:第一步:引入•引入一元一次方程的概念和定义,与学生共同探讨一元一次方程的特点和解法的重要性。
第二步:讲解•讲解等式的加减法消元法,引导学生理解这一解法的原理并进行相关练习;•讲解等式的乘除法消元法,通过示例演示该解法的应用,并带领学生练习。
第三步:实践•设计一些实际问题,要求学生运用所学知识解决;•学生个别或小组合作,通过讨论和解答问题,巩固所学知识。
第四步:总结•小结一元一次方程的解法,重点强调加减法消元法和乘除法消元法;•鼓励学生互相分享解题思路和心得体会。
第五步:作业布置•布置相关习题作业,要求学生独立完成;•鼓励学生提出问题,并承诺在下节课共同解答。
2.3 教学方法和手段•提问法:通过提问学生,激发学生的思考和参与,引导学生主动探索解题方法;•讲解演示法:通过讲解和示范解题过程,帮助学生理解一元一次方程的解法;•合作学习法:鼓励学生个别或小组合作,通过合作讨论和解答问题,促进学生的互相学习和交流。
三、教学评价和反思3.1 教学评价通过对本节课的评价,可以对学生的学习效果和掌握程度进行评估。
主要评价指标包括:•学生对一元一次方程的理解程度;•学生对等式加减法消元法和乘除法消元法的掌握能力;•学生能否熟练运用所学知识解决实际问题。
北师大版七年级数学上册《求解一元一次方程(第1课时)》教学教案
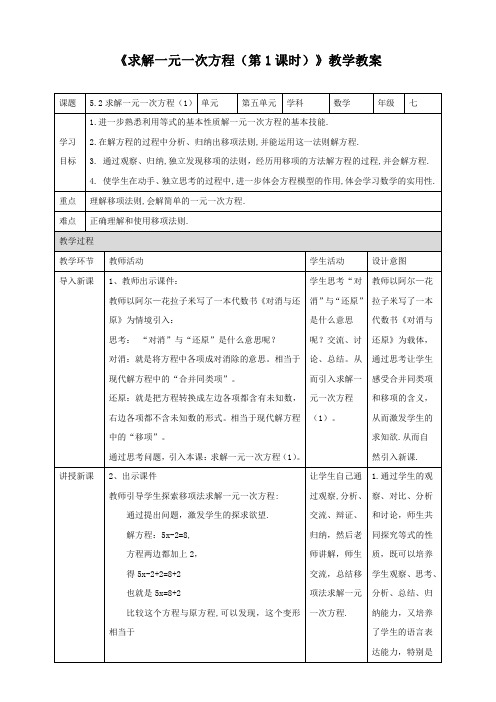
《求解一元一次方程(第1课时)》教学教案教师引导学生思考:(1)与原方程相比,哪些项的位置发生了改变?哪些没变?(2)改变位置的项的符号是否发生了变化?没改变位置的项的符号是否发生了变化?与原方程相比常数项-2的位置发生了改变,一次项5x 和常数项8没变常数项-2的位置由等号的左边移动到了右边,符号由“-”变成了“+”,一次项5x 和常数项8的位置没变,符号也没变.师生总结出移项:移项:把方程中的某一项改变符号后,从方程的一边移到另一边,这种变形叫移项。
做一做:例1下列计算,其中属于移项变形的是(C)A.由5+3x-2,得3x-2+5B.由-10x-5=-2x,得-10x-2x=5C.由5x+3=-4x+1,得5x+4x=1-3D.由5x=15,得x=3易错提醒:1.移项时必须是从等号的一边到另一边,并且不要忘记对移动的项变号,如从3+6x=7得到6x=7+3是不对的.鼓励学生积极思考,主动解决问题,小组交流,总结发言,教师及时纠正.培养了学生用符号语言表示等式的两个基本性质.加深学生对方程概念的理解,同时还可以锻炼学生思维的主动性.2.没移项时不要误认为移项,如从-2=x得到x=2,犯这样的错误,其原因在于对等式的基本性质(对称性)与移项的区别没有分清.3、出示课件做一做:教师引导学生利用移项求解一元一次方程例1解下列方程:(1)2x+6=1;(2)3x+3=2x+7;解:(1)移项,得2x=1-6.合并同类项,得2x=-5.方程两边同除以2,得x=-5 2 .(2)移项,得3x-2x=7-3.合并同类项,得x=4.例2解方程:14x=-12x+3.解:移项,得14x+12x=3.合并同类项,得34x=3.方程两边同除以34(或同乘以43),得x=4.师生共同总结:利用移项解方程的步骤:(1)移项;(2)合并同类项;(3)系数化为1.做一做:1.用移项法解方程:7-2x=3-4x;解:(1)移项,得4x-2x=3-7.合并同类项,得2x=-4.方程两边同除以2,得x=-2.2.x为何值时,代数式4x+3与15-2x的值相等?解:4x+3=15-2x 鼓励学生积极思考,自主解决问题,小组交流,总结发言,大胆提出自己的观点,教师及时鼓励和纠错。
第五章第4课时 求解一元一次方程-北师大版七年级数学上册课件

购买4套A型课桌凳需_____元, 则购买了乙种人参(_______)棵, 列得方程为______________=1 820. 解:设王叔叔购买了甲种人参x棵, 了解解一元一次方程的一般步骤,并能灵活应用. 这个工厂去年上半年每月平均用电是多少? 购买4套A型和5套B型课桌凳共1 820元, 购买4套A型课桌凳需_____元, 由题意得_______+70(_______)=1 200, 下半年共用电____________千瓦时, 掌握解一元一次方程的基本方法:移项、去括号. 第4课时 求解一元一次方程(2)
6x+6x=150 000+12 000 12x=162 000 x=13 500
【例3】一个两位数,个位上的数是2,十位上的数是x,把2和x对调,新两位数的2倍还比原两位数小18,求x的值. 购买4套A型和5套B型课桌凳共1 820元, 列得方程为______________=1 820. 列得方程为______________=1 820. (2)解含有括号的方程,运算过程中,特别防止符号的错误. 能熟练求解数字系数的一元一次方程,并能根据实际问题判别解的合理性. 答:王叔叔购买甲种人参_____棵. 购买一套A型课桌凳和一套B型课桌凳各需多少元? 由题意得_______+70(_______)=1 200, 甲种人参每棵100元,乙种人参每棵70元,王叔叔花1 200元在此特产商店购买这两种人参共15棵. (2)解含有括号的方程,运算过程中,特别防止符号的错误. 解:设王叔叔购买了甲种人参x棵, 分析:设A型课桌凳每套x元, 根据全年用电15万千瓦时,列得方程为________________________. 能熟练求解数字系数的一元一次方程,并能根据实际问题判别解的合理性. 甲种人参每棵100元,乙种人参每棵70元,王叔叔花1 200元在此特产商店购买这两种人参共15棵. 购买4套A型课桌凳需_____元,
北师大版七年级上册数学教案:5.2求解一元一次方程优秀教学案例
为了实现上述目标,我设计了以下教学过程:首先,通过引入生活实例,激发学生的学习兴趣,引导学生发现实际问题中的一元一次方程;其次,通过自主学习、合作探究的方式,引导学生掌握一元一次方程的解法;最后,通过巩固练习和拓展延伸,检验学生的学习效果,提高学生运用数学知识解决实际问题的能力。
(二)问题导向
1.自主学习:引导学生自主探究一元一次方程的解法,培养学生独立思考和解决问题的能力。
2.合作探究:组织学生进行小组讨论,共同解决问题,培养学生的团队合作意识和交流能力。
3.教师引导:在学生探究过程中,教师进行有效引导,启发学生思考,帮助学生论,分享各自的学习心得和解题方法,培养学生之间的交流与合作能力。
在整个教学过程中,我注重关注每一个学生,充分调动学生的积极性,鼓励学生积极参与课堂讨论,培养学生的主体意识。同时,我运用多种教学方法,如讲解、示范、引导、激励等,使学生在轻松愉快的氛围中掌握知识,提高能力。
二、教学目标
(一)知识与技能
1.理解一元一次方程的概念,掌握一元一次方程的解法。
2.学会运用一元一次方程解决实际问题,提高运用数学知识解决实际问题的能力。
3.教师评价:教师对学生的学习过程和结果进行全面、客观的评价,给予肯定和鼓励,激发学生的学习积极性。
在整个教学过程中,我注重关注每一个学生,充分调动学生的积极性,鼓励学生积极参与课堂讨论,培养学生的主体意识。同时,我运用多种教学方法,如讲解、示范、引导、激励等,使学生在轻松愉快的氛围中掌握知识,提高能力。
北师大版七年级上册数学教案:5.2求解一元一次方程优秀教学案例
北师大版七年级数学上册《一元一次方程——求解一元一次方程》教学PPT课件(3篇)
新课探究
解方程:5 x – 2 = 8. 方程两边都加上 2,得
5x – 2 + 2 = 8 + 2, 也就是 5x = 8 + 2.
观察比较
比较这个方程与原方程,可以发现,这个
变形相当于
5 x – 2 = 8.
注意
5x = 8 + 2
移项要变号
即把原方程中的 –2 改变符号后,从方程 的一边移到另一边,这种变形叫移项.
解:(3)移项,得
16
3 2
x
x
.
合并同类项,得
1 2
x
16 .
方程两边同除以 1 ,得 x = –32. 2
(4) 1 3 x 3x 5 ;
2
2
解:(4)移项,得
3 2
x
3x
5 2
1.
合并同类项,得
9x 2
3 2
.
方程两边同除以 9 ,得 x = 1 .
2
3
2. 解下列方程:
(1)2.5x + 318 = 1 068
2.求解一元一次方程
第1课时
北师大版·七年级上册
新课导入
用合并同类项进行化简: 1. 20x – 12x = ____8_x___ 2. x + 7x – 5x = ___3_x____ 3. 1 y 2 y 2 y = ___-_y____
33 4. 3y – 4 y –(–2y)=___y_____
因此,方程 5x – 2 = 8 也可以这样解:
移项,得
5x = 8 + 2.
化简,得
5x = 10.
方程两边同除以 5,得 x = 2.
例 1 解下列方程: (1)2x + 6 = 1; (2)3x + 3 = 2x + 7.
北师大数学七年级上册第五章解一元一次方程总结
第02讲_解一元一次方程知识图谱解一元一次方程知识精讲步骤 具体做法依据注意事项去分母 在方程两边同乘以各分母的最小公倍数等式性质2①不含分母的项不要漏乘 ②注意分数线有括号作用,去掉分母后,如果分子是多项式,要加括号去括号由内向外去括号,即先去小括号,再去中括号,最后去大括号 分配律,去括号法则①运用分配律去括号时,不要漏乘括号内的项②如果括号前是“-”号,去括号时,括号内各项要变号 移项 把含未知数的项都移到方程的一边(通常是左边),不含未知数的项都移到方程的另一边 等式性质1①移项必须变号②一般把含未知数的项移到左边,其他项移到右边 合并同类项把方程两边同类项分别合并,把方程化为()0ax b a =≠的形式合并同类项法则合并同类项是同类项的系数相加,字母及其指数不变未知数系数化1在方程两边同除以未知数系数a ,得到方程的解b x a =看不清楚解,不会调整等式性质2 应注意系数a 不能等于0注意:这五个步骤在解一元一次方程中,有时可能用不到,有时可能需重复用,使用时不一定严格按从(1)到(5)的顺序进行,要根据方程的特点灵活运用.例:解方程121123x x +--= 去分母:3(1)2(21)6x x +--=去括号:33426x x +-+= 移项:34632x x -=-- 合并同类项:1x -= 未知数系数化1:1x =-三点剖析一.考点:解一元一次方程.二.重难点:解一元一次方程三.易错点:1.在解方程的过程中,移项不变号;2.去括号时容易漏乘括号内的项或弄错符号.一元一次方程的解法例题1、 在解方程123123x x -+-=时,去分母正确的是( ) A.134)1(3=+--x x B.63413=+--x xC.13413=+--x xD.6)32(2)1(3=+--x x 【答案】 D【解析】 暂无解析 例题2、 解下列方程:(1)76163x x +=-; (2)1111122x ⎛⎫--= ⎪⎝⎭(3)()()5310679x x x x --=-- (4)x 1x 3100.20.1++-=-【答案】 (1)1x =;(2)10x =;(3)335x =;(4)-3x =【解析】 去括号时,要注意考虑两个因素:一是系数,二是符号. 例题3、 解下列方程: (1)4﹣3(2﹣x )=5x ;(2)2x 0.250.1x=0.10.030.02-+ . 【答案】 (1)﹣1 (2)﹣186925【解析】 (1)去括号得:4﹣6+3x=5x , 移项合并得:2x=﹣2, 解得:x=﹣1; (2)方程变形得:200x 3+2510x2-=0.1, 去分母得:400x+75﹣30x=0.6,移项合并得:370x=﹣74.4, 解得:x=﹣186925. 例题4、 仔细观察下面的解法,请回答为问题.解方程:52x 421x 3+=-﹣1 解:15x ﹣5=8x+4﹣1,15x ﹣8x=4﹣1+5, 7x=8, x=87. (1)上面的解法错误有_______处.(2)若关于x 的方程52x 421x 3+=-+a ,按上面的解法和正确的解法的得到的解分别为x 1,x 2,且x 21x 1-为非零整数,求|a|的最小值. 【答案】 (1)2(2)97【解析】 (1)上面的解法错误有2处; (2)52x 421x 3+=-+a , 错误解法为:15x ﹣5=8x+4+a ,移项合并得:7x=9+a , 解得:x=a 97+,即x 1=a97+; 正确解法为:去分母得:15x ﹣5=8x+4+10a , 移项合并得:7x=9+10a ,解得:x=7a 109+,即x 2=7a109+, 根据题意得:x 2﹣1x 1=7a 109+﹣7a 9+=7a9,由7a 9为非零整数,得到|a|最小值为97.随练1、 将方程212134x x -+=-去分母,得( ) A.4(2x ﹣1)=1﹣3(x+2) B.4(2x ﹣1)=12﹣(x+2) C.(2x ﹣1)=6﹣3(x+2) D.4(2x ﹣1)=12﹣3(x+2) 【答案】 D【解析】 去分母得:4(2x ﹣1)=12﹣3(x+2)随练2、 已知x=3是关于x 的方程x+m=2x ﹣1的解,求(m+1)2的值为__________. 【答案】 9【解析】 将x=3代入方程求出m 的值,即可求出所求式子的值. 解:将x=3代入方程得:3+m=6﹣1, 解得:m=2, 则(m+1)2=32=9 随练3、 解方程(1)4﹣x=2﹣3(2﹣x )(2)2x 13-﹣10x 16+=2x 14+﹣1. 【答案】 (1)x=2 (2)x=16【解析】 (1)4﹣x=2﹣3(2﹣x ) 4﹣x=2﹣6+3x ,﹣x ﹣3x=2﹣6﹣4, ﹣4x=﹣8, x=2;(2)去分母得:4(2x ﹣1)﹣2(10x+1)=3(2x+1)﹣12, 8x ﹣4﹣20x ﹣2=6x+3﹣12, 8x ﹣20x ﹣6x=3﹣12+4+2, ﹣18x=﹣3, x=16. 随练4、 解方程:(1)31223x x --=+;(2)321123x x x --+=-.【答案】 (1)1118-(2)5【解析】 (1)去分母,得-12x -9=6x +2 移项,得-12x -6x =2+9 合并同类项,得-18x =11系数化为1,得1118x =-;(2)去分母,得3(x -3)+2(2x -1)=6(x -1), 去括号,得3x -9+4x -2=6x -6, 移项,得3x +4x -6x =-6+2+9 合并同类项,得x =5.拓展1、 解方程(1)()9316x x --=(2)131125x x +--=. 【答案】 (1)12;(2)3-. 【解析】 (1)()9316x x --= 9336x x -+= 63x = 12x =. (2)131125x x +--=,()()5110231x x +-=-,551062x x +-=-,3x =-. 2、 ()212511254326x x x +-⎛⎫--=- ⎪⎝⎭.【答案】 23x =-【解析】 ()212511254326x x x +-⎛⎫--=- ⎪⎝⎭去分母(两边同乘以12):()()2532412252x x x -⎛⎫+--=- ⎪⎝⎭,去括号:364410410x x x +-+-=-,移项:344461010x x x +-=-+-,合并同类项:32x =-,系数化为1:23x =-,∴23x =-是原方程的解.3、 解下列方程:(1)0.040.090.30.250.050.32x x x ++--=; (2)0.210.010.0310.30.04x x ---=;(3)21101211364x x x -++-=-.【答案】 (1)10921x =;(2)435x =;(3)16x =【解析】 (1)原方程等价于49325532x x x ++--=; ()()()6491032155x x x +-+=-;245430201575x x x +--=-;243015755420x x x --=--+;21109x -=-,10921x =. (2)原方程等价于2103134x x ---=.去分母,得()()42103312x x ---= 去括号,得8403912x x --+=,移项,得8312409x x -=+-,合并同类项,得543x =系数化为1,得435x =.(3)21101211364x x x -++-=-,()842026312x x x --+=+-82066312x x x --=+-,183x -=-,16x =.4、 解下列方程:(1)111246819753x ⎧⎫⎡+⎤⎛⎫+++=⎨⎬ ⎪⎢⎥⎝⎭⎣⎦⎩⎭(2)111233234324x x x x ⎧⎫⎡⎤⎛⎫----=+⎨⎬ ⎪⎢⎥⎝⎭⎣⎦⎩⎭【答案】 (1)1x =,(2)229x =-【解析】 根据一元一次方程的解题步骤即可解得.。
北师大版数学七年级上册5.2.1求解一元一次方程教学设计
(一)导入新课
1.教学活动设计
在课堂开始时,教师通过一个与学生生活息息相关的问题情境引入新课:“小明的年龄比小红大3岁,三年后,小明的年龄将是小红的两倍。请问现在小明和小红各是多少岁?”这个问题能够激发学生的好奇心,引导学生用数学知识解决实际问题。
2.教学过程
(1)让学生独立思考,尝试解决这个问题。
4.设计不同难度的练习题,使学生在巩固基础知识的同时,逐步提高解题能力。
(三)情感态度与价值观
1.培养学生对待数学学科的积极态度,激发学生学习数学的兴趣和自信心。
2.通过一元一次方程的学习,让学生认识到数学在解决实际问题中的重要作用,增强学生的数学应用意识。
3.培养学生勇于挑战、克服困难的精神,使学生在面对问题时,能够主动寻找解决方案。
(2)运用探究式教学法,引导学生自主探究一元一次方程的解法,培养学生的自主学习能力和思维能力。
(3)利用数形结合法,借助图形帮助学生理解一元一次方程的解法,提高学生的几何直观。
(4)设计小组合作活动,让学生在合作交流中互相学习、互相启发,共同克服学习难点。
2.教学策略:
(1)注重分层教学,针对学生的认知水平和学习风格,设计不同难度的教学任务,使每位学生都能在课堂上获得成就感。
4.预习作业:
(6)预习下一节内容,提前了解一元一次不等式的概念和解法,为接下来的学习打下基础。
作业布置注意事项:
1.作业量适中,确保学生能够在课后合理安排时间,既巩固了所学知识,又不会过度负担。
2.鼓励学生独立完成作业,培养他们的自主学习能力和解决问题的能力。
3.教师应及时批改作业,给予学生反馈,帮助学生发现和纠正错误,提高学习效果。
(2)引导学生通过讨论,发现解决这个问题需要列出一个方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在前面的解方程中,移项后的“化简”只用到了对常数
项的合并.试试看下述的解方程.
【例1】解下列方程:
(1) 3x+3=2x+7
(2) 1 x 1 x 3
42
解:移项,得 3x-2x=7-3解:移项,得 1 x 1 x 3
42
合并同类项,得 x=4;
合并,得 3 x 3
4
系数化为1,得 x=4.
2
Hale Waihona Puke (2) 5x-2=7x+8
(4) 1- x=233x+
5 2
2.某航空公司规定:乘坐飞机普通舱旅客一人最多可免费 托运20kg行李,超过部分每千克按飞机票价的1.5%购买 行李票,一名旅客托运了35kg行李,机票连同行李费共付 1323元,求该旅客的机票票价.
课堂小结 移项:把方程中的某一项改变符号后,从方程的一边移到 另一边,这种变形叫做移项.
①含未知数的项往左移,常数项往右移. ②左边对含未知数的项合并,右边对常数项合并.
想一想:
1听果奶多少钱? 如果设1听果奶x元,可列出方程: 4(x+0.5)+x=20
-3.
例题
【例2】 解方程:4(x+0.5)+x=17
【解析】去括号,得 4x+2+x=17, 移项,得 4x+x=17-2, 合并同类项,得 5x=15, 方程两边同除以5,得 x=3.
(1)等式两边同时加上(或减去)同一个代数式,所得结果 仍是等式.
①若a=b,则a+c=b+c ②若a=b,则a(2)c等=式b-两c 边同时乘同一个数(或除以同一个不为0的数), 所得结果仍是等式.
③若a=b,则ac=bc ④若a=b,且c≠0时,则 a= b cc
例题
1.利用等式性质解下列方程:
2.(柳州·中考)一个物体现在的速度是5米/秒, 其速度每秒增加2米,则再过 秒,它的速度为 15米/秒. 【解析】设再过x秒它的速度为15米/秒,根据题 意列方程为5+2x=15,解得x=5. 答案:5
3.(乐山·中考)解方程:5(x-5)+2x=-4.
【解析】去括号,得5x-25+2x=-4, 移项,得5x+2x=-4+25,
合并同类项,得7x=21, 方程的两边同除以7,得x=3.
通过本课时的学习,需要我们掌握: 1. 从方程的一边移到另一边的变形叫做移项. 2.解一元一次方程的一般步骤: 去分母;去括号;移项;合并同类项;系数化1.
伟人之所以伟大,是因为他与别人共处逆 境时,别人失去了信心,他却下决心实现 自己的目标.
2.求解一元一次方程
第1课时
1.判断下列方程是不是一元一次方程,是的打“√”,
不是的打“×”.
(1) -2t+5=3 ( √ ) (3) 2m=0 ( √)
(2) 2x2+3=1 ( ) ×
(4) χ﹥ 3 ( )
×
(5) χ+y=8 ( ×) (6) 3-x=7x ( ) √
2.等式的基本性质是什么?用字母表示.
跟踪训练
解方程:-2(x-1)=4
解法一:
去括号,得 -2x+2=4
移项,得 -2x=4-2
化简,得 -2x=2
方程两边同除以-2,
得
x= -1.
解法二: 方程两边同除以-2,
得 x-1=-2 移项,得 x=-2+1
即 x= -1.
1.(安顺·中考)已知关于x的方程4x-3m=2的 解是x=m,则m的值是______________. 【解析】把x=m代入原方程,得4m-3m=2, 合并同类项,得m=2. 答案:2
备用练习: P134 习题5.2
利用等式的性质解方程:
5x-2=8 方程两边同时加上2, 得:5x-2+2=8+2, 也就是:5x=8+2,
通过与原方程比较可以 发现,这个变形相当于:
5 x -2 =8
5x = 8 +2
把原方程中的-2改变符号后,从方程的一边移到另 一边,这种变形叫移项.
例题
①含未知数的项往左移,常数项往右移.
②左边对含未知数的项合并,右边对常数项合并.
议一议:
(1) 移项实际上是对方程两边进行 同加减 , 使用的是等式的性质 一 ;
(2) 系数化为1实际上是对方程两边进行 同乘除,
使用的是等式的性质
二.
跟踪训练
1.解下列方程: (1) 10x-3=9 (3) x= 3x+16
(1) x+2=5
(2) 3=x-5
(3) -3x=15
(4) - -2=1n0
3
解:(1)方程两边都减去2, 解:(2)方程两边都加5,
得 x+2-2=5-2
得 3+5=x-5+5
合并同类项, 得 x=3
合并同类项, 得 8 =x
即 x=8
例题
1.利用等式性质解下列方程:
(1) x+2=5
(2) 3=x-5
演示结束!
感谢聆听!
THANK YOU FOR WATCHING!
(3) -3x=15
(4) - -2=10n3
解:(3)方程两边都除以-3, 解:(4)方程两边都加2,
得 x=-5
得 - =n312
方程两边都乘以-3,得
n=-36
1.利用等式性质解下列方程: (1) x-9=8 (2) 5-y=-16 (3) 3x+4=-13 (4) -123x=5
2.小红编了一道题:我是4月出生的,我的年龄的2倍加上8, 正好是我出生那一个月的总天数,你猜我有几岁?请你求出 小红的年龄.
