【精选】截交线练习题题解
全等三角形证明题辅助线专题--截长补短和倍长中线
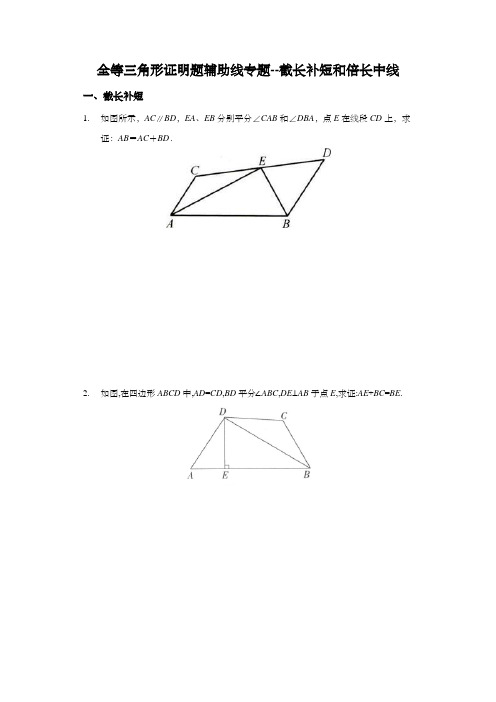
全等三角形证明题辅助线专题--截长补短和倍长中线一、截长补短1.如图所示,AC∥BD,EA、EB分别平分∠CAB和∠DBA,点E在线段CD上,求证:AB=AC+BD.2.如图,在四边形ABCD中,AD=CD,BD平分∠ABC,DE⊥AB于点E,求证:AE+BC=BE.3.如图,△ABC中,∠CAB=∠CBA=45∘,点E为BC的中点,CN⊥AE交AB于点N,连接EN.求证AE=CN+EN.4.如图,△ABC的∠B和∠C的平分线BD,CE相交于点F,∠A=60°,(1)求∠BFC的度数.(2)求证:BC=BE+CD.5.如图,在△ABC中,∠A=100°,∠ABC=40°,BD是∠ABC的平分线,延长BD至E,使DE=AD.求证:第2页,共28页BC=AB+CE.6.(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E,F分别是边BC,CD上的点,且∠EAF=1∠BAD,求证:EF=BE+DF;2(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF=1∠BAD,(1)中的结论是否仍然成立?2(3)如图3,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E,F分别是边BC,CD延长线上的点,且∠EAF=1∠BAD,(1)中的结论是否仍然成立?若成立,请证明;2若不成立,请写出它们之间的数量关系,并证明.7.如图,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点,且∠EAF = 60°.探究图中线段BE,EF,FD之间的数量关系.8.如图,在△ABC中,∠B=60°,△ABC的角平分线AD、CE相交于点O,(1)求∠AOC的度数;(2)求证:OE=OD;(3)猜测AE,CD,AC三者的数量关系,并证明.第4页,共28页9.如图在△ABC中,∠ABC=60°,AC=2AB,AD平分∠BAC交BC于点D,延长DB点F,使BF=BD,连接AF.(1)求证:AF=CD;(2)若CE平分∠ACB交AB于点E,试猜想AC、AF、AE三条线段之间的数量关系,并证明你猜想的结论.二、倍长中线10.如图,在△ABC和△DEF中,AB=DE,AC=DF,AM和DN分别是中线,且AM=DN.求证:△ABC≌△DEF.11.(1)【问题情境】课外兴趣小组活动时,老师提出了如下问题:如图①,△ABC中,若AB=13,AC=9,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:Ⅰ.由已知和作图能得到△ADC≌△EDB,依据是______.A.SSS B.SAS C.AAS D.HLⅡ.由“三角形的三边关系”可求得AD的取值范围是______.解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.(2)【初步运用】如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且∠FAE=∠AFE.若AE=4,EC=3,求线段BF的长.12.已知:在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BC交AC于F,求证:AF=EF.第6页,共28页13.如图,在△ABC中,AD是中线,∠BAC=∠BCA,点E在BC的延长线上,CE=AB,连接AE.求证:AE=2AD.14.如图,Rt△ABC中,∠ABC=90°(1)如图1,若BD为高线,AB=4,BC=3,AC=5,求BD的长(2)如图2,若BD为中线,求证:BD=1AC215.如图,在五边形ABCDE中,∠E=90O,BC=DE,,连接AC,AD,且AB=AD,AC⊥BC.(1)求证:AC=AE(2)如图,若∠ABC=∠CAD,AF为BE边上的中线,求证:AF⊥CD;(3)如图,在(2)的条件下,AE=8,DE=5,则五边形ABCDE的面积为_______。
截交线习题

截交线习题截交线习题1. 完成平面立体被平面截切后的侧面投影2. 完成五棱柱被二平面截切后的侧面投影3 完成四棱锥被平面截切后的三面投影4. 完成四棱锥被平面截切后的三面投影5. 求平面立体的截交线6. 画出穿孔六棱柱被截切后的水平投影,并补全其侧面投影截交线习题7.完成圆柱被平面截切后的侧面投影8. 完成圆柱被平面截切后的水平投影9. 完成立体被平面截切后的水平投影10.补画出立体的侧面投影11. 补画立体的侧面投影12. 补画立体的侧面投影13. 补画立体的侧面投影14. 求作回转体第三视图15. 求截交线16. 补画侧面投影17. 已知圆柱开一个正方形的孔,补画左视图18. 补画圆柱开槽后的正面投影19. 补全左视图中所缺的线条20. 完成圆锥被平面截切后的水平投影和侧面投影21. 求圆锥的截交线22.补画带缺口圆锥的侧面投影,并补全其水平投影。
23. 补全圆锥截断体的三面投影24. 补全俯视图,并完成左视图。
25. 补全圆球穿方孔的三面投影26. 完成半球被平面截切后的水平投影和侧面投影27. 完成半球被平面截切后的水平投影和侧面投影28. 求圆球的截交线29. 作出半球开槽后的H面及W面投影30. 完成左视图,画出俯视图31. 完成立体被平面截切后的水平投影32. 完成立体被平面截切后的水平投影33. 完成立体被平面截切后的水平投影34. 求组合体的截交线35. 作立体切割后的水平投影和侧面投影36. 求作截切后立体的侧面投影37. 补画圆球和圆柱组合体开槽后的水平和侧面投影38. 补画水平投影及侧面投影漏线39. 完成穿孔圆柱被截切后的水平投影40. 完成立体的水平投影。
第四章截交和相贯习题答案

4—3 3
1、求作主视图。 求作主视图。
1' 6' 3'(4') 5' 2'
相贯立体的投影
1" 6" 4" 2" 3" 5"
两圆柱轴线垂直相 交,其轴线分别为 铅垂线和侧垂线。 相贯线的侧面投影 积聚在圆周上,水 平投影积聚在部分 圆周上。 相贯线左右对称。
4 1 (2) 6(5) 3
2、求作左视图。
2 4
1 5
3
7、完成相贯体的三视图。 完成相贯体的三视图。
圆球上截去两个等 直径的圆柱孔,两 孔与球为同轴线相 贯。两孔的轴线垂 直相交。其相贯线 均为平面曲线。
8、完成相贯体的三视图。 完成相贯体的三视图。
1' 5'(6') 3'(4') 7'(8')
1" 6" 4" 8" 5" 3" 7"
2'
2"
圆柱和圆锥台轴线 垂直相交。圆柱的 轴线为侧垂线,圆 柱的侧面投影是有 积聚性的圆。圆锥 台的轴线为铅垂线, 作图采用辅助水平 面求出相贯线的水 平和正面投影。 判断相贯线的可见 性:主视图中相贯 线前后重影。俯视 图中下半个圆柱面 上的相贯线为不可 见,3、4为可见与 不可见的分界点。
(2)
圆柱体被两个水 平面和一个正垂 面截切。正垂面 截切处需找一般 点。
(4) 在圆筒的左端,上 下对称截切,在圆 筒的右端前后对称 切槽。 左、右两端对称截 切的截交线,水平 面为矩形,侧面为 圆弧。 注意:圆筒的内外 都产生截交线。
(3) 圆柱的轴线为铅垂线, 被两个左右对称的正 垂面截切,截交线为 部分椭圆;水平面截 切的截交线为部分圆 弧。三个截平面间产 生三条交线,在俯左 视图均为不可见。
三角形全等之辅助线——截长补短类经典习题讲解

三角形全等之截长补短一、知识点睛截长补短:题目中出现线段间的和差倍分时,考虑截长补短;截长补短的目的是把几条线段间的数量关系转为两条线段的等量关系.二、精讲精练例题1、已知:如图,在△ABC 中,∠1=∠2,∠B =2∠C .求证:AC =AB +BD .提示:方法一:在AC 上截取AE =AB ,连接DE ,证明△ABD ≌△AED ,然后再证明CE =BD ;方法二:延长AB 到E ,使BE =BD ,证明△ADE ≌△ADC练习1、如图,在梯形ABCD 中,AD ∥BC ,CE ⊥AB 于E ,△BDC 为等腰直角三角形,∠BDC =90°,BD CD ,CE 与BD 交于F ,连接AF .求证:CF =AB +AF .方法一:延长BA 交CD 的延长线交于点H ,证明 △BDH ≌△CDF ,得DH =DF ,BH =CF ,再证明 △ADH ≌△ADF ,得AH =AF ;方法二:在CF 上截取CH =AB ,连接DH ,证明△DHC ≌△DAB ,得DH =DA ,CH =BA ,∠HDF =∠ADF =45°,再证明△ADF ≌△HDF ,得AF =HF )21DCBA 21DCBAB F CE DA B F C E D A练习2、已知:如图,在正方形ABCD 中,AD =AB ,∠D =∠ABC =∠BAD =90°,E ,F 分别为DC ,BC 边上的点,且∠EAF =45°,连接EF .求证:EF =BF +DE .提示:延长FB 到G ,使BG =DE ,连接AG ,证明 △ABG ≌△ADE ,再证明△AFG ≌△AFE )练习3、已知:如图,在△ABC 中,∠A =90º,AB =AC ,BD 平分∠ABC ,CE ⊥BD 交BD 的延长线于点E .求证:CE =21BD .练习4、 如图,ABC ∆中,100=∠=A AC AB ,,BD 平分ABC ∠。
截交线与相贯线习题

第五节截交线与相贯线截交线和相贯线是立体表面常见的两种表面交线,立体被平面截切,表面就会产生截交线,两立体相交,表面就产生相贯线,二者有共同点,也有不同点。
一、截交线的特性及画法【考纲要求】1、掌握特殊位置平面截断棱柱和棱锥的截交线画法;2、掌握特殊位置平面截断圆柱、圆锥、圆球的截交线画法;3、掌握简单的同轴回转体的截交线画法;【要点精讲】(一)截交线的定义:由平面截断基本体所形成的表面交线称为截交线。
(二)截交线的特性:1、任何基本体的截交线都是一个封闭的平面图形(平面体是平面多边形,曲面体是平面曲线或由平面曲线与直线共同组成的图形);2、截交线是截平面与基本体表面的共有线,截交线上的每一点都是截平面与基本体表面的共有点(共有点的集合)。
(三)求截交线的方法:①积聚性求点法;②辅助(素)线法;③辅助平面法。
(四)求截交线的步骤:1、确定被截断的基本体的几何形状;2、判断截平面的截断基本体的位置(回转体判别截平面与轴线的相对位置3、想象截交线的空间形状;4、分析截平面与投影面的相对位置,弄清截交线的投影特性;5、判别截交线的可见性,确定求截交线的方法;6、将求得的各点连接,画出其三面投影。
(五)平面体的特殊截交线及画法:1、特性:平面体的截交线都是由直线所组成的封闭的平面多边形。
多边形的各个顶点是棱线与截平面的交点,多边形的每一条边是棱面与截平面的交线。
2、画法:求平面体截交线的方法主要是用积聚性求点法和辅助线法。
画平面体的截交线就是求出截平面与平面体上各被截棱线的交点(即平面多边形的各个顶点),然后依次连接即得截交线。
根据截交线是截平面与基本体表面的共有线,截交线上的点也是截平面与基本体表面的共有点,我们所要求掌握的是特殊位置平面截切平面立体的截交线,我们可以利用积聚性求点法或辅助平面法,求出截平面与平面立体的各棱线的交点,然后依次连接,也就求出了截交线。
例如图5-1所示,先根据截交线具有积聚性投影的正面投影和具有收缩性的水平投影确定出截平面与六棱柱棱线的六个交点(截交线平面多边形的六个顶点),再利用积聚性求点法求出其侧面投影。
浙教新版九年级上册《4.2 由平行线截得比例线段》2024年同步练习卷(4)+答案解析

浙教新版九年级上册《4.2由平行线截得比例线段》2024年同步练习卷(4)一、选择题:本题共5小题,每小题3分,共15分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.如图,在中,点D,E分别在AB,AC边上,若AD::1,则AE:EC等于()A.3:1B.3:4C.3:5D.2:32.如图,已知直线,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若,则()A.B.C.D.13.如图,已知,那么下列结论正确的是()A. B. C. D.4.如图,已知在中,点D、E、F分别是边AB、AC、BC上的点,,,且AD::5,那么CF:()A.5:8B.3:8C.3:5D.5:35.平行四边形ABCD中,E是AB上的点,DE交对角线AC于F,过点F作交DC于G,若DF::1,则DG:GC:()A.2:3:5B.2:3:4C.1:2:3D.2:4:5二、填空题:本题共4小题,每小题3分,共12分。
6.如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A,B,C都在横格线上.若线段,则线段______7.如图,已知,AD与BC相交于点E,,,,则AE的长等于______.8.如图,中,,AD:DF::2:3,若,则______.9.如图,点E是AC中点,且BC::2,交AB于点G,则AF:______,BG:______,BF:______.三、解答题:本题共5小题,共40分。
解答应写出文字说明,证明过程或演算步骤。
10.本小题8分已知线段AB,在AB上求作一点C,使AC::保留作图痕迹,不要求写作法11.本小题8分如图,已知在中,点D,E,F分别是边AB,AC,BC上的点,且,,AD::3,,求BF的长.12.本小题8分如图,,,若,,求AE的长.13.本小题8分已知:如图,在中,的平分线CD交AB于D,过B作交AC的延长线于点求证:;求证:14.本小题8分已知:如图,在中,,,点D、E分别是边AB、AC的中点,交DE的延长线于点求证:四边形ADCF是菱形;联结BE,如果,求证:答案和解析1.【答案】A【解析】解:,:故选:根据平行线分线段成比例定理列出比例式,计算即可.本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.2.【答案】B【解析】解:,故选:直接根据平行线分线段成比例定理求解.本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.3.【答案】A【解析】【分析】本题主要考查平行线段成比例定理,确定出对应线段是解题的关键.根据平行线分线段成比例确定出对应线段,进行判断即可.【解答】解:由平行线分线段成比例可知是被平行线所截的线段才有可能是对应线段,、EF不是对应线段,故C、D不正确;和AD对应,CE和DF对应,,故A正确;故选:4.【答案】D【解析】解:::5,::8,,:::8,,:::::3,故选:先由AD::5,求得BD:AB的比,再由,根据平行线分线段成比例定理,可得CE::AB,然后由,根据平行线分线段成比例定理,可得CF::AC,则可求得答案.此题考查了平行线分线段成比例定理.此题比较简单,注意掌握比例线段的对应关系是解此题的关键.5.【答案】C【解析】解:平行四边形ABCD中,,∽,,,即E为AB的中点,,,,,,,:GC::GC::2:故选:先由平行四边形ABCD得∽,从而,,再由得,从而,,即可得DG:GC::GC::2:本题考查的是相似三角形的判定和性质、平行四边形的性质,掌握相似三角形的判定定理的和性质定理是解题的关键,6.【答案】9【解析】解:练习本中的横格线都平行,且相邻两条横格线间的距离都相等,,,故答案为:根据平行线分线段成比例定理列出比例式,代入计算解答即可.本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.7.【答案】3【解析】解:,∽,,即;又,由于,可证得∽,根据相似三角形所得比例线段,即可求得AE的长.此题主要考查了相似三角形的判定和性质,难度不大.8.【答案】12【解析】【分析】本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.根据平行线分线段成比例定理列出比例式,代入已知数据计算即可.【解答】解:,:EG::DF::2:3,又,,,,,,故答案为9.【答案】1:13:25:2【解析】解:,,点E是AC的中点,,::1,,:::2,::故答案为:1:1,3:2,5:根据平行线分线段成比例定理得以及BG::CD,进行解答即可.本题主要考查了平行线分线段成比例定理,解决此题的关键是清楚三条平行线截两条直线,所得的对应线段成比例.推论:平行于三角形一边的直线截其他两边或两边的延长线,所得的对应线段成比例.10.【答案】解:如图所示:点C即为所求.【解析】先作出射线AZ,在射线AZ上依次截取线段,连结BH,作交AB于C,点C即为所求.此题主要考查了复杂作图,以及比例线段,关键是正确画出图形.11.【答案】解:,,四边形BFED为平行四边形,,∽,,,【解析】由、可得出四边形BFED为平行四边形,根据平行四边形的性质可得出,根据可得出∽,根据相似三角形的性质结合AD::3、可求出DE的长度,再由可得出BF的长.本题考查了平行四边形的判定与性质以及相似三角形的判定与性质,根据相似三角形的性质求出DE的长度是解题的关键.12.【答案】解:,,,,,,【解析】根据平行线分线段成比例定理得到,再利用等线段代换即可得到,然后根据比例性质计算即可.本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.也考查了比例的性质.13.【答案】证明:平分,又,,,,,又,【解析】本题主要考查了等腰三角形的判定及性质和角平分线定理、平行线分线段成比例定理,关键是熟练掌握平行线分线段成比例定理和平行线的性质.根据CD平分,可知;由,可求出是等腰三角形,故;根据平行线的性质,及可得出结论.14.【答案】证明:点D、E分别是边AB、AC的中点,是的中位线,,,,,,,,四边形DBCF为平行四边形,,,,,四边形ADCF是平行四边形,,四边形ADCF是菱形;如图,设,,则,,,,,,∽,,即,,由勾股定理得:,,,,【解析】先根据三角形的中位线定理可得:,,证明四边形DBCF为平行四边形,可得,再证明,根据对角线互相平分且垂直的四边形是菱形可得结论;如图,设,,则,证明∽,得,并结合勾股定理可得结论.本题考查了平行四边形的判定与性质,菱形的性质和判定,三角形的中位线的性质,直角三角形的性质,第有难度,证明∽是解题的关键.第11页,共11页。
截交线例题

33.求圆球截交线
34.求作四棱锥被截切后的水平投影和侧面投影。
(4') 3' 2' 1'
3" 4"
2"
1"
分析:截平面为正垂面 截交线的正面投影积聚 为直线。截平面与四条 棱线相交,从正面可直 接找出交点。
4• 1
3 2•
作出各对应点的投影, 依次连接各点。
补全棱锥体的外形投影。
被截切后的投影图:
线——正平线,椭圆的短轴是垂 直与(长42)轴补再的全作正侧一垂面般线转点。向。轮廓线。
Ⅳ Ⅰ
正垂线
Ⅱ Ⅲ
正平线
2’ 5’6’ 3’4’
7’8’
1’
8 46
1
2
7 35
2”
6”
5”
4”
3”
8”
7”
1”
30 已知立体的正面投影,试完成H、W两面投影。
1’ (4)’
(2)’
3’
(8)’ (12)’ 5’ 7’ 11’ (6)’
q′ e′
f′ f″(g″) q″
d′
e″(d″) P″
a′
c′
a″(c″)
P′ b′
b″
e q a
b
d
P c
A,B,C在棱线上
24. 求斜截圆柱体的投影
分析:截交线正面投影积聚为直线,水平投影在 圆周上。可利用V面和H面投影求截交线侧面投影。 作图步骤:(1)求特殊点;(2)求一般点;
(3)光滑连接各点并完善图形。
请点击鼠标左键显示左视图形
请点击鼠标左键显示后视图形
请点击鼠标左键显示俯视图形
请点击鼠标左键显示右视图形
平行四边形全等之辅助线——截长缩短类经典习题讲解

平行四边形全等之辅助线——截长缩短类
经典习题讲解
本文将介绍平行四边形全等中的辅助线截长缩短类经典题解析。
1. 问题描述
设ABCD是一个平行四边形,点E是AB延长线上的一个点,连接EC,交AD于点F,使得AF=DC。
证明:EF=BF。
2. 解题思路
首先,根据题目中给出的条件,我们可以发现ABCD是一个平行四边形且AF=DC。
我们要证明EF=BF。
接下来,我们将使用辅助线来辅助证明。
我们在平行四边形ABCD中引入一条辅助线BG,使其与AE平行,并交CD于点G。
由于AE和BG互相平行,根据平行线截取等比例定理,我们可以得到AF/FC = BG/GC。
由于AF=DC,我们可以将等式重写为DC/FC = BG/GC。
同样地,由于平行四边形ABCD的性质,我们有DC/FC = AB/BF。
将上述两个等式结合起来,我们可以得到AB/BF = BG/GC。
由于AE和BG是平行的,所以三角形AEB与三角形BGC是全等的,从而可以推导出AB/EA = BG/GC。
由于AB/EA = BG/GC,根据等比例定理,我们可以得到
EF=BF。
综上所述,我们通过引入辅助线BG,证明了EF=BF。
3. 总结
在本文中,我们通过使用辅助线截长缩短的方法,证明了平行四边形全等中的一个经典题。
通过引入辅助线并运用平行线截取等比例定理,能够简化问题并得出结论。
希望本文对你理解平行四边形全等中的辅助线截长缩短类经典习题有所帮助!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4-2 求作俯视图并用彩色笔勾画出平面Q的投影。
4-3-1 补画俯视图
4-4 求三棱锥被截切后的俯视图和左视图。
4´ 3´
6´ 1´ 2´≡5 ´
4″
5″≡6″ 2″
3″ 1″
5 6
4 2
3
1
*4-7 补全俯视图和左视图上所缺的线。
4-8 求作左视图。
4-28 求作左视图。
4-29 求作左视图。
4-30 求圆球被截切后的俯视图和左视图。
4-31 求圆球被截切后的俯视图和左视图。
5-39 已知主视图和俯视图,选择正确的左视图。
⑴
⑵
⑶
⑷
正确的左视图是 ⑶
5-40 已知主视图和俯视图,选择正确的左视图。
⑴
⑵
⑶
⑷
正确的左视图是 ⑷
4-10 求作俯视图并标出平面P的其余两投影。
*4-11 求作左视图。
*4-13 补全主视图和俯视图上所缺的线。
*4-14 补全主视图和俯视图上所缺的线。
*4-15 补全主视图和左视图上所缺的线并标 出P、Q面的投影。
4-16 求作俯视图。
4-17 求作俯视图。
4-18 求作俯视图。
54
4-23 补全主视图上所缺的接交线,并作左试图。
4-24 补全俯视图并求左视图。
4-20 补全左视图
4-21 补全左视图4-2 Nhomakorabea 补全左视图并求俯视图。
4-26 求作俯视图。
4-27 求作俯视图。 4.画出顶尖的水平投影。
1′ 4′(5′)
2′(3′)
6′(7′)
5 37 1
26 4
4-19 求作俯视图。
第三节 立体与立体相交 二、平面立体与曲面立体相交
【例】空心圆柱开矩形孔
分析:本例为圆柱与四棱柱 外-内相贯、内内相贯。
交线在水平投影和侧面投 影有重影性,已确定。需要 求其正面投影 过程: (1)先求内棱柱表面与外圆 柱面的交线 (2)再求内棱柱表面与内圆 柱面的交线 注意:由于切割,相交处的 内、外转向轮廓线都不存在 (3)可见性判别,不可见轮廓 线画虚线
