扭转理解练习知识题目解析
材料力学第3 章 扭 转习题及答案

第 三 章 扭 转一、判断题1.杆件受扭时,横截面上的最大切应力发生在距截面形心最远处。
( × ) 2.薄壁圆管和空心圆管的扭转切应力公式完全一样。
( × ) 3.圆杆扭转变形实质上是剪切变形。
( √ ) 4.非圆截面杆不能应用圆截面杆扭转切应力公式,是因为非圆截面杆扭转时“平截面假设”不能成立。
( √ )5.材料相同的圆杆,它们的剪切强度条件和扭转强度条件中,许用应力的意义相同,数值相等。
( × ) 6.切应力互等定理,仅适用于纯剪切情况。
( × ) 7.受扭杆件的扭矩,仅与杆件受到的转矩(外力偶矩)有关,而与杆件的材料及其横截面的大小、形状无关。
( √ ) 8.受扭圆轴在横截面上和包含轴的纵向截面上均无正应力。
( √ ) 9.受扭圆轴的最大切应力只出现在横截面上。
( × ) 10. 因木材沿纤维方向的抗剪能力差,故若受扭木质圆杆的轴线与木材纤维方向平行,当扭矩达到某一极限值时,圆杆将沿轴线方向出现裂纹。
( √ )二、填空题1.一级减速箱中的齿轮直径大小不等,在满足相同的强度条件下,高速齿轮轴的直径要比低速齿轮轴的直径( 小 )。
2. 当实心圆轴的直径增加1培时,其抗扭强度增加到原来的( 8 )倍,抗扭刚度增加到原来的( 16 )倍。
3. 直径D=50mm 的圆轴,受扭矩T=2.15kn.m ,该圆轴横截面上距离圆心10mm 处的剪应力τ=(35.0 MPa ),最大剪应力τmax=(87.6 MPa )。
4. 一根空心轴的内外径分别为d ,D ,当D=2d 时,其抗扭截面模量为(33256153215D d ππ或)。
5. 直径和长度均相等的两根轴,在相同的扭矩作用下,而材料不同,它们的τmax 是( 相 )同的,扭转角φ是( 不 )同的。
6. 等截面圆轴扭转时的单位长度相对扭转角为θ,若圆轴直径增大一倍,则单位长度扭转角将变为(16θ)。
(仅供参考)第3章扭转作业参考解答
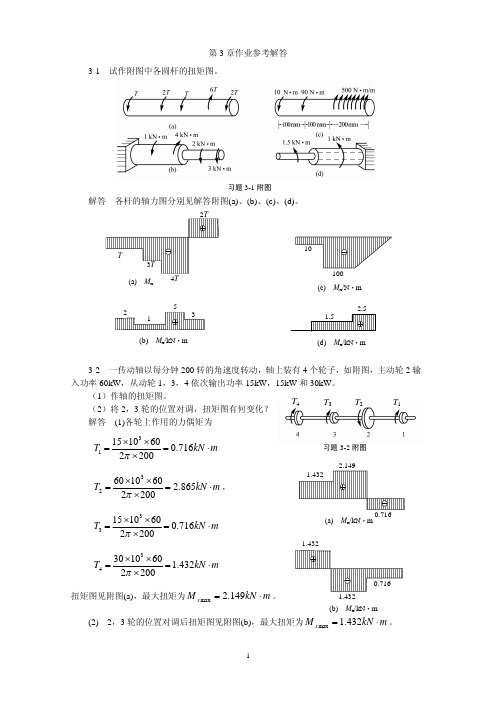
第3章作业参考解答3-1 试作附图中各圆杆的扭矩图。
习题3-1附图解答 各杆的轴力图分别见解答附图(a)、(b)、(c)、(d)。
3-2 一传动轴以每分钟200转的角速度转动,轴上装有4个轮子,如附图,主动轮2输入功率60kW ,从动轮1,3,4依次输出功率15kW ,15kW 和30kW 。
(1)作轴的扭矩图。
(2)将2,3轮的位置对调,扭矩图有何变化? 解答 (1)各轮上作用的力偶矩为m kN T ×=´´´=716.0200260101531pm kN T ×=´´´=865.2200260106032p ,m kN T ×=´´´=716.0200260101533pm kN T ×=´´´=432.1200260103034p扭矩图见附图(a),最大扭矩为m kN M x ×=149.2max 。
(2) 2,3轮的位置对调后扭矩图见附图(b),最大扭矩为m kN M x ×=432.1max 。
(a) M x(c) M x /N ·m(b)M x /kN ·m(d) M x /kN ·m习题3-2附图T 1T 2 T 3 T 4 (a)M x /kN ·m1.432(b) M x /kN ·m3-3 一直径d =60mm 的圆杆,其两端受T =2kN·m 的外力偶矩作用而发生扭转,如附图示。
设轴的切变模量G =80GPa 。
试求横截面上1,2,3点处的切应力和最大切应变,并在此三点处画出切应力的方向。
解答 1,2,3点处的切应力分别为MPaMPa W T p 4.313/22.4716/06.014.320000.031332===´===t t t t 切应力方向见附图(1)。
扭转典型习题解析

扭转典型习题解析1 一内径d =100mm 的空心圆轴如图示,已知圆轴受扭矩m kN 5⋅=T ,许用切应力][τ=80MPa ,试确定空心圆轴的壁厚。
解题分析:因为不知道壁厚,所以不能确定是不是薄壁圆管。
分别按薄壁圆管和空心圆轴设计。
解: 1、按薄壁圆管设计薄壁圆管扭转时,假设切应力沿壁厚均匀分布,设壁厚为δ,平均半径为2/0)(δ+=d R ,则扭转切应力为 δτ20π2R T=强度条件为][ττ≤,于是得][π22τδδTd =+)( ][π22223τδδδTd d =++ ()Pa1080πm N 1052m 10100m 1010026323233××⋅××=×+××+−−δδδ解得 mm 70.3m 1070.33=×=−δ 2、按空心圆轴设计强度条件为 ][pmax ττ≤=W T将δ216π44p +=−=d D d D DW );(代入得][π16][π][π164444=−−≤−τττd TD D d D DT,)(0Pa)108(m 1.0πm N 10516Pa 1080π64346=××−×⋅××−×××)(D D解得mm 107.7m 10107.73=×=−Dmm 85.32mm100mm 7.1072=−=−=d D δ 比较可知,两种设计的结果非常接近。
讨论: 当10/0R ≤δ时,即认为是薄壁圆管,可以直接使用薄壁管扭转公式。
2 图示受扭圆杆,沿平面ABCD 截取下半部分为研究对象,如图b 所示。
试问截面ABCD 上的切向内力所形成的力偶矩将由哪个力偶矩来平衡?解题分析:由切应力互等定理可知截面ABCD 上的切向内力分布及其大小。
该截面上切向内力形成一个垂直向上的力偶矩。
在图b 中,左右两个横截面上的水平切向内力分量形成垂直于截面ABCD 的竖直向下的力偶矩,正好与截面ABCD 上切向内力的合力偶矩平衡。
材料力学 扭转2 习题及参考答案

扭转 第二次 作业1. 已知图示实心圆轴的直径d = 100mm 。
材料的剪切弹性模量G = 80GPa 。
(1)求1-1横截面上A 、B 、C 三点的切应力;(2)求1-1横截面上A 点的切应变;(3)整个圆轴上最大的切应力。
2kN·m6kN·m10kN·m2kN·m1-1截面2kN·m4kN·m10kN·m解:由圆轴的扭矩图可知,1-1截面的扭矩T 1 = 4kN·m ,最大扭矩T max = 10kN·m圆截面的极惯性矩 4464π 3.140.19.8110m 3232P d I -⨯===⨯扭矩截面系数 3343π 3.140.1 1.9610m 1616P d W -⨯===⨯(1) 3714410 2.0410Pa 20.4MPa 1.9610A B P T W ττ-⨯====⨯=⨯ 1110.2MPa 2C A P T I ρττ=== (2)由剪切胡克定律 Gτγ=得63920.4100.255108010AA G τγ-⨯===⨯⨯ (3)对于等截面圆轴,最大切应力出现在扭矩最大截面的最外缘37max max41010 5.1010Pa 51.0MPa 1.9610P T W τ-⨯===⨯=⨯ 2. 阶梯状圆轴如图所示,AE 段为空心,外直径D = 140mm ,内直径d = 100mm ;BC 段为实心,直径d = 100mm 。
外力偶矩M A = 18kN·m ,M B = 32kN·m ,M C = 14kN·m 。
已知许用切应力[τ ] = 80MPa 。
试校核该轴的强度。
18kN·m14kN·m解:由扭矩图可知T AB = 18kN·m , |T BC | =14kN·mAE 段()4334431π 3.140.1410011 3.9810m 1616140P D W α-⎛⎫⨯⎛⎫=-=-=⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭[]36max41181045.210Pa 45.2MPa<3.9810AB P T W ττ-⨯===⨯=⨯ BC 段33432π 3.140.1 1.9610m 1616P d W -⨯===⨯ []36max 42141071.410Pa 71.4MPa<1.9610BC P T W ττ-⨯===⨯=⨯ 故,该轴安全。
材料力学 扭转答案

3—1 一传动轴作匀速转动,转速,轴上装有五个轮子,主动轮Ⅱ输入的功率为60kW,从动轮,Ⅰ,Ⅲ,Ⅳ,Ⅴ依次输出18kW,12kW,22kW和8kW。
试作轴的扭矩图。
解:kNkNkNkN返回3—2(3-3)圆轴的直径,转速为。
若该轴横截面上的最大切应力等于,试问所传递的功率为多大?解:故即又故返回3—3(3—5)实心圆轴的直径mm,长m,其两端所受外力偶矩,材料的切变模量。
试求:(1)最大切应力及两端截面间的相对扭转角;(2)图示截面上A,B,C三点处切应力的数值及方向;(3)C点处的切应变。
解:=返回3-4(3—6)图示一等直圆杆,已知,,,。
试求:(1)最大切应力;(2)截面A相对于截面C的扭转角。
解:(1)由已知得扭矩图(a)(2)返回3-5(3—12)长度相等的两根受扭圆轴,一为空心圆轴,一为实心圆轴,两者材料相同,受力情况也一样。
实心轴直径为d;空心轴外径为D,内径为,且。
试求当空心轴与实心轴的最大切应力均达到材料的许用切应力),扭矩T相等时的重量比和刚度比。
解:重量比=因为即故故刚度比==返回3—6(3-15)图示等直圆杆,已知外力偶矩,,许用切应力,许可单位长度扭转角,切变模量。
试确定该轴的直径d。
解:扭矩图如图(a)(1)考虑强度,最大扭矩在BC段,且(1)(2)考虑变形(2)比较式(1)、(2),取返回3-7(3—16) 阶梯形圆杆,AE段为空心,外径D=140mm,内径d=100mm;BC段为实心,直径d=100mm。
外力偶矩,,。
已知:,,。
试校核该轴的强度和刚度。
解:扭矩图如图(a)(1)强度=,BC段强度基本满足=故强度满足。
(2)刚度BC段:BC段刚度基本满足.AE段:AE段刚度满足,显然EB段刚度也满足.返回3—8(3-17)习题3—1中所示的轴,材料为钢,其许用切应力,切变模量,许可单位长度扭转角。
试按强度及刚度条件选择圆轴的直径。
解:由3—1题得:故选用.返回3-9(3-18)一直径为d的实心圆杆如图,在承受扭转力偶矩后,测得圆杆表面与纵向线成方向上的线应变为。
材料力学复习题第三章 扭 转

第三章 扭 转一、判断题1.圆杆受扭时,杆内各点均处于纯剪切状态。
( ) 2.非圆截面杆不能应用圆杆扭转切应力公式,是因为非圆截面杆扭转时“平面假设”不能成立。
( ) 3.当剪应力超过材料的剪切比例极限时,剪应力互等定律亦成立。
( ) 4.一点处两个相交面上的剪应力大小相等,方向指向(或背离)该两个面的交线。
( ) 5.直径和长度相同,材料不同的两根轴,受相同的扭转力偶矩作用,它们的最大剪应力和最大扭转角都相同。
6. 杆件受扭时,横截面上最大切应力发生在距截面形心最远处。
( )7. 薄壁圆管和空心圆管的扭转切应力公式完全一样。
( )8. 圆杆扭转变形实质上是剪切变形。
( )9. 横截面的角点处的切应力必为零。
( ) 1.√ 2.√ 3.√ 4.× 5.× 6.×(非圆截面) 7.× 8.√ 9.× 二、单项选择题1. 图示圆轴曲面C 左、右两侧的扭矩MC+和M C-的( )。
A .大小相等,正负号相同;B .大小不等,正负号相同; C .大小不等,正负号不同;D .大小相等,正负号不同。
2. 直径为D 的实心圆轴,两端受扭转力矩作用。
轴内最大剪应力τ,若轴的直径改为D/2,则轴内的最大剪应力变为( )。
A .2τ; B .τ; C . 8τ; D .16τ。
3. 阶梯圆轴的最大切应力发生在( )。
A .扭矩最大的截面;B .直径最小的截面;C .单位长度扭转角最大的截面;D .不能确定。
4.空心圆轴的外径为D ,内径为d,α=d/D 。
其抗扭截面系数为( )。
A .()απ-=1163D W P ;B 。
()23116απ-=D W P ;C 。
()33116απ-=D W PD .()43116απ-=D WP5.扭转的切应力公式ρτρPPI M =适用于( )杆件。
A .任意截面; B .任意实心截面;C .任意材料的圆截面; D .线弹性材料的圆面。
材料力学扭转详细讲解和题目,非常好
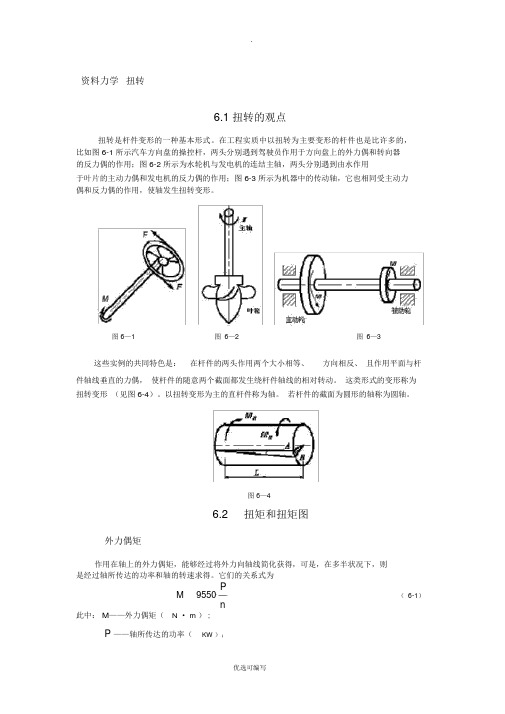
.资料力学扭转6.1扭转的观点扭转是杆件变形的一种基本形式。
在工程实质中以扭转为主要变形的杆件也是比许多的,比如图 6-1 所示汽车方向盘的操控杆,两头分别遇到驾驶员作用于方向盘上的外力偶和转向器的反力偶的作用;图 6-2 所示为水轮机与发电机的连结主轴,两头分别遇到由水作用于叶片的主动力偶和发电机的反力偶的作用;图 6-3 所示为机器中的传动轴,它也相同受主动力偶和反力偶的作用,使轴发生扭转变形。
图 6—1图6—2图6—3这些实例的共同特色是:在杆件的两头作用两个大小相等、方向相反、且作用平面与杆件轴线垂直的力偶,使杆件的随意两个截面都发生绕杆件轴线的相对转动。
这类形式的变形称为扭转变形(见图 6-4)。
以扭转变形为主的直杆件称为轴。
若杆件的截面为圆形的轴称为圆轴。
图 6—46.2扭矩和扭矩图外力偶矩作用在轴上的外力偶矩,能够经过将外力向轴线简化获得,可是,在多半状况下,则是经过轴所传达的功率和轴的转速求得。
它们的关系式为PM 9550(6-1)n此中: M——外力偶矩(N · m ) ;P ——轴所传达的功率(KW );n ——轴的转速(r/ min )。
外力偶的方向可依据以下原则确立:输入的力偶矩若为主动力矩则与轴的转动方向相同;输入的力偶矩若为被动力矩则与轴的转动方向相反。
扭矩圆轴在外力偶的作用下,其横截面大将产生连续散布内力。
依据截面法,这一散布内力应构成一作用在横截面内的协力偶,进而与作用在垂直于轴线平面内的外力偶相均衡。
由分布内力构成的协力偶的力偶矩,称为扭矩,用 M n表示。
扭矩的量纲和外力偶矩的量纲相同,均为 N·m或 kN· m。
看作用在轴上的外力偶矩确立以后,应用截面法能够很方便地求得轴上的各横截面内的扭矩。
如图6-5( a)所示的杆,在其两头有一对大小相等、转向相反,其矩为M 的外力偶作用。
为求杆任一截面 m-m 的扭矩,可设想地将杆沿截面 m-m 切开分红两段,观察此中任一部分的均衡,比如图 6-5( b)中所示的左端。
(修订)第7章 圆轴的扭转-习题解答

第7章 圆轴的扭转 习题解答题7-1 (a) 解: 题7-1 (b) 解:题7-2 (a) 解:4.5kN ·m 1.5kN ·m 2kN ·kN 125.15.41⋅-=++-=T 1.5kN ·m 2kN ·mT 2m kN 5.325.12⋅=+=T2kN ·mT m kN 23⋅=T 3题7-3 解:(1)计算各轮的转矩:(2)计算各段轴的扭矩:AB 段 m N 59.114e ⋅-=-=A AB M TBC 段 m 152.78N m N 37.267m N 59.114e e ⋅=⋅+⋅-=+-=B A BC M M T CD 段 m N 29.57e ⋅==D CD M T (3)绘制扭矩图题7-4 解:(1)计算各段轴的扭矩AB 段 BC 段CD 段(2)计算各截面上的最大切应力1-1截面 ()53M P a Pa 103.5mm kN 3.11616733P max 1=⨯=10⨯50π⋅⨯=π==3-AB AB AB D T W T A B τ 2-2截面 ()20.5M P a Pa 1005.2mmkN 7.11616733P max 2=⨯=10⨯75π⋅⨯=π==3-BC BC BC D T W T B C τm57.29N m N 2505.195499549m 95.49N m N 2505.295499549m 114.59N m N 250395499549e e e ⋅=⋅==⋅=⋅==⋅=⋅==n P M n P M n P M D D C CA A m267.37N m N 250795499549e ⋅=⋅==n P M B B m kN 7.0m1.7kN m 3kN m kN 3.1m kN 3.1e e e e ⋅==⋅=⋅+⋅-=+-=⋅-=-=D CD B A BC A AB M T M M T M T3-3截面 ()28.5M P a Pa 1085.2m1050m kN 7.016167333P max 3=⨯=⨯π⋅⨯=π==-CD CD CD D T W T CD τ (3)绘制扭矩图题7-5 解:(1)计算轴上扭矩m 716.18N m N 1005.795499549⋅=⋅==n P T (2)计算实心轴D 1[]45m m m 104.5m 18.71616162-331=⨯=10⨯40⨯π⨯=π≥6τT D (3)计算空心轴D 2[]46m m m 106.4m )18.71616)1(162342=⨯=0.5-(1⨯10⨯40⨯π⨯=-π≥-463ατT D题7-6 解:(1)校核轴的强度()51M P aPa 10519025.2901m mN 105.116)1(16643343P max=⨯=⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⨯--⨯10⨯90⨯π⋅⨯⨯=-π==3-ατD T W T []M P a60MPa 51max =<=ττ (2)计算实心轴D 153m m m 105.3m 1051105.116162-63max 1=⨯=⨯⨯π⨯⨯=π≥33τT D (3)比较空心轴与实心轴的重量之比()()()()31.0mm 26.5mm 42.5452D 5.22D 2D 222222122=-=⎪⎭⎫ ⎝⎛π--π==实心轴空心轴实心轴空心轴A A W W题7-7 解:(1)计算最大起重载荷W(2)计算轴的直径由于轴上各段的扭矩绝对值相等,故只需计算一段轴的直径即可。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Me1 0.4F (0.4 200)N m 80N m
由平衡方程
Me2 2Me1 160N m
max
T Wt
Me1 Wt
80
d3
[ ]
16
d
3
16 80 40 106
m
21.7mm
80N m
d 22mm
80N m
设齿轮间的切向力为F,则由平衡条件
0.2F Me2 F 800N
➢ 解:
T 9549 P 9549 7.5 N m 716N m
n
100
由实心轴的强度条件
max
T Wt
16T
d3
[ ]
d1
3
16T
[ ]
3
16 716 40 106
m
45mm
由空心轴的强度条件
max
T Wt
16T
D23(1 4 )
[ ]
D2
3
16T
[ ](1 4 )
0.25W 0.35F Wmax 1120N
➢ 3.7 机床变速箱第II轴如图所示,轴所传递的功率 为P=5.5kW,转速n=200r/min,材料为45钢, [τ]=40MPa。试按扭转的强度条件初步设计轴的 直径。
➢ 解:
II轴所传递的扭矩
T 9549 P (9549 5.5 )N m
0 GIp
GI p
0.091 rad
➢ 一刚性杆,被固定在直径 20 mm 的铝轴末端,若 加载前刚性杆与支座D的间隙为10 mm,求加载 后铝轴内的最大剪应力。已知:G=28 GPa。
➢ 解:
由原图,在力偶的作用下
EF
Tl1 GI p
100 0.5
28 109 d4
0.1137(rad)
第三章 扭转
CHAPTER 3 TORSION Thursday, August 06, 2020
➢ 3.1 作图示各杆的扭矩图。
T
x
O
M 2M
2M
O
x
M
15kN m
T
5kN m
x
O
10kN m 30kN m
➢ 3.2 直径D=50 mm的圆轴,某横截面上的扭矩 T=2.15 kN·m。试求该横截面上距轴心20mm 处 的切应力及最大切应力。
Pa
53.2MPa [ ] 60 MPa
DB
TDB WtDB
1433 16
0.073
Pa
21.3MPa [ ] 60 MPa
668N m
1432N m
刚度条件
AC
TAC GI PAC
668
80 109 0.044
180
1.9(0 ) /m [ '] 2(0 ) /m
TII
9549
P2 nII
(9549
22.1)N m 300
703kN m
II
TII Wt
703 16
0.063
Pa 16.6MPa [ ] 20 MPa
各轴均满足强度要求
➢ 3d由P料.215==轮 的阶713剪04梯输km切Wm形入许。,圆的用轴轴轴功应作上的率力匀装直为[速有τ径P]3=转三=分63动个0别0Mk,带为WP转轮ad,,1速,=轮G4n如01==m输图8200m出所G0,rP的/示ma功,。in率许已。为用知材 扭转角[φ’]=2(0)/m 。试校核轴的强度和刚度。
➢ 解:
Me1
9549
P1 n
(9549
14 )N m 200
668N m
Me2
9549
P1 n
(9549
30 14 )N m 200
764N m
Me1 668N m Me2 764N m Me3 1432N m
强度条件
AC
TAC WtAC
668 16
0.043
3
40
16 106
716 (1
0.5
4
)
m
46mm
d1 45mm D2 46mm
17
➢ 3.11 图示传动轴的转速为n=500 r/min,主动轮I 输P[φ2=入’]1=功417率(k0WP)/1m,=,36PG83=k=2W8201,GkP从Wa。动。轮已2知和[τ3]分=7别0M输P出a,功率
Me1 72N m Me3 28N m
max
Tmax Wt
T1 d3
16
45.8MPa
➢ 解:
水轮机主轴的强度
T横9截549面上152最0500大0 N切应m 力 5为73kN m
max
T Wp
D3
T (1
4)
16
573000 0.553 [1 (
d
)4
]
Pa
19.2
MPa
16
D
主轴满足强度要求。
➢ 3.4 图示AB轴的转速n=120r/min,从B轮输入功 率P=44.13 kW,功率的一半通过锥形齿轮传给垂 直Dd32=轴=62I04Im0,mm另m,一,[半τd]=有1=201水M00平Pm轴am。I,输试d出对2=。各8已0轴m知进mD行,1强=6度00校mm核,。
➢ 解: Tmax Me
x
max
Me Wt
[ ]
Me
[
]Wt
70 106
(22 103 )3
16
146N m
Me
T
m Me 0.1 146 0.1 N m /m 1460N m /m
l1 T1dx l2 T2dx
0 GIp l1 GIp
0.1 mxdx 0.2Me
32
DB
TDB GI PDB
1432
80 109 0.074
32
180 0.435(0 ) /m [ '] 2(0 ) /m
各段均满足强度、刚度 要求
668N m
1432N m
➢ 3.6 图示绞车同时由两人操作,若每人加在手柄上 的力都是F=200N,已知轴的许用切应力 [τ]=40MPa,试按扭转条件初步估算AB轴的直径, 并确定最大起重量W。
[ ]
d2 3
16TBC
[ ]
3
16 4220
70 106
m
67.5mm
' BC
TBC GIP
180
32TBC
G d4
180
[ ']
d2
4
180TBC 32
G 2[ ']
4
180 80
4220
109 2
32 1
m
74.5mm
d2 75mm
(2)若取同一直径, 则轴的直径取
32
铝轴所允许的转过的自由角度为
0.01 0.05(rad)
0.2
FC
由平衡方程 Me1 Me2 Me3 0
T1 Me1 T2 Me3
EF EC
EF
T1l1 GI p
0.5Me1 GI p
EC
T2l1 GI p
0.5Me3 GI p
M e1
M e2
M e3
F
E
C
➢ 解:
T
IP
2.15 103 0.02 32
0.054
70(MPa)
T Wt
2.15 103 16
0.053
87.6(MPa)
➢ 3.3 发电量为15000kW的水轮机轴如图所示。 D=560mm, d=300mm,正常转速n=250 r/min。 材料的许用应力[τ]=50MPa。试校核该轴的强度。
(1)试确定AB段的直径 和BC段的直径 (2)若AB和BC两段选用同一直径,试确定直径d (3)主动轮和从动轮如何安排才合理?
➢ 解:
M e1
M e2
M e3
Me3
9549
P3 n
9549
221 N m 500
4220N m
Me2
9549 P2 n
9549 147 N m 500
[ ]
d1
3
16TAB
[ ]
3
16 7030
70 106
m
80mm
由刚度条件
' AB
TAB GIP
180
32TAB
G d4
180
[ ']
d1
4
180TAB 32G 源自[ ']4180 80
7030
109 2
32 1
m
84.6mm
d1 85mm
BC
T BC
Wt
TBC d23 16
n
200
263 N m
max
T Wt
16T
d3
[ ]
d
3
16T
[ ]
3
16 263
40 106
m
32.2mm
d 33mm
➢ 3.8 图示实心轴和空心轴通过牙嵌离合器连接在一 起。已知轴的转速n=100 r/min,传递的功率为 P=7.5kW,材料的许用切应力为[τ]=40 Mpa。试 选轴择 外实 径D心2圆。 轴的直径D1和内外径比值为0.5的空心
2810N m
Me1 Me2 Me3 (2810 4220)N m 7030N m
Me1 7030N m Me2 2810N m Me3 4220N m
A
M e1 T
B M e2
C M e3
O
x
4220N m
7030N m
由强度条件
