结构动力学期末复习题_2014
结构动力学试题1

2013-2014学年第 1 学期《结构动力学》试卷专业: 姓名: 学号:一、单项选择题1.图示体系作动力计算时,内力和位移动力系数相同的体系是:AB :C D :3.图示体系(EI= 常数)的自振频率 为: A :)2/(33mL EI B: )4/(33mL EI LC :)/(33mL EID :)/(3mL EI二、填空题1. 在结构控制中,AMD (active mass damper ) 系统如图所示。
其中,质量块的作用是:弹簧的作用是:阻尼器的作用是: ;设作动器作用于质量块的力为F P (t ),质量块的质量为m T ,弹簧刚度为K T ,阻尼器粘阻系数为C T ,受控结构受到的AMD 系统的控制力为F U (t )。
则,质量块的动平衡方程2.图示体系不计阻尼的稳态最大动位移 y max =4P l 3/9EI,其最大动弯矩为:( )A.7P l/3B.4P l/3C.PD. P l/3 Psin θt m为: ;受控结构在AMD 处受到的控制力F U (t )= 。
2.如图所示体系质点1的质量为m 1,质点m 2由弹簧与质点1相连,梁的刚度为EI ,梁长为L ,动荷载为Psin θt ,式中θ已知。
为消除m 1在动荷载作用下引起的振动,则弹簧的刚度K= 。
L/2 L/2三、阐明下述概念,必要时绘图描述。
(1)振型阻尼比;(2)主振型、振型正交性;(3)瞬态响应、稳态响应;(4)频响函数;(5)临界阻尼;(6)简谐振动;(7)单元质量矩阵;(8)对数衰减率;(9)材料阻尼。
四、(a )试求图示单自由度体系的自振频率。
(b )试求图示刚架的自振频率和振型。
l lI l /2 l /22m。
《结构动力学》考试复习题

《结构动力学》考试复习题一、(概念题)(1) (填空题)某等效单自由度振动系统具有下列参数:17.5m kg =,70/k N cm =,阻尼比0.2ξ=,则系统的固有频率ω为 rad/s ,等效阻尼系数c 为 N. s/m 。
(2) (填空题)某振动系统具有下列参数:17.5m kg =,70/k N cm =,0.7/c N s cm =⋅,则系统的固有频率ω为 ,阻尼比ξ为 ,对数衰减率n 为 。
(3) (简单计算题)一弹簧悬挂某质量块,弹簧产生了静变形mm 4=∆st ,试确定系统作自由振动的固有频率 (重力加速度取2s m /10=g )。
(10分)(4) (填空题)当系统受简谐力作用发生共振时,系统所受的外力是由 来平衡。
(5) (问答题)某单自由度系统具有非线性的弹簧,其运动方程为:()()mx cx f x F t ++=,能否用杜哈美积分计算该系统的受迫振动响应?并说明理由。
(6) (填空题)同种材料的弦承受相同的张力,如果长度增加到原来的4倍,截面积减小到原来的4倍,则作该弦横向振动的各阶固有频率将 。
(7) (填空题)图示两个系统,已知各质点的质量 i m ,刚架的质量不计,忽略杆的轴向变形,试分别确定两系统的动力自由度: (1) n = ; (2) n = 。
(8) (作图题) 0.1ξ=时单自由度系统受迫振动的相频曲线如图所示,其中ω为系统的固有频率,p 为激振力的频率,ϕ为位移响应滞后于激振力的相位角。
试大致绘出0.05ξ=和0.2ξ=时相频曲线的形状。
(9) (问答题)模态分析法能否求解多自由度系统的弹塑性地震响应?并说明理由。
(10) (选择题) 对于一个单自由度系统而言,其临界阻尼与系统的固有特性参数 ,与系统所受的阻尼力 。
(a) 有关,有关;(b) 无关,无关;(c) 有关,无关;(d) 无关,有关2ωpππ二、(计算题)(1) 图示两个系统,已知EI 和M ,弹簧刚度316k EI l =,不计梁的质量,试确定:(1) 简支梁的等效刚度L k ;(2)两个系统的等效刚度a k 和b k ;(3) 两个系统的固有频率a ω和b ω。
结构动力学例题复习题
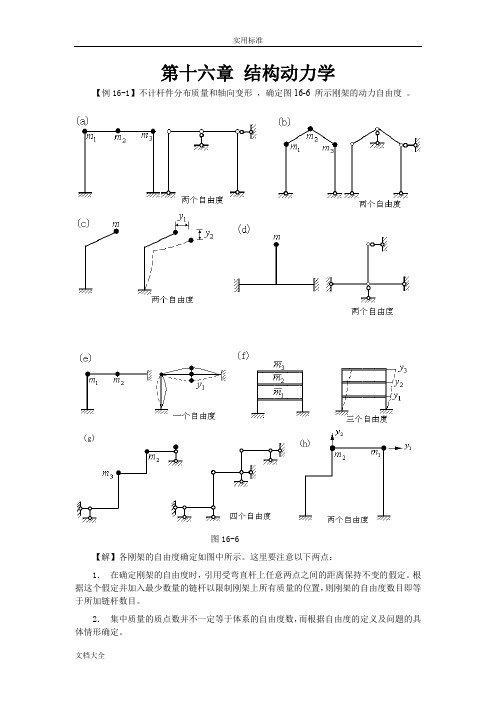
第十六章结构动力学【例16-1】不计杆件分布质量和轴向变形,确定图16-6 所示刚架的动力自由度。
图16-6【解】各刚架的自由度确定如图中所示。
这里要注意以下两点:1.在确定刚架的自由度时,引用受弯直杆上任意两点之间的距离保持不变的假定。
根据这个假定并加入最少数量的链杆以限制刚架上所有质量的位置,则刚架的自由度数目即等于所加链杆数目。
2.集中质量的质点数并不一定等于体系的自由度数,而根据自由度的定义及问题的具体情形确定。
【例16-2】 试用柔度法建立图16-7a 所示单自由度体系,受均布动荷载)t (q 作用的运动方程。
【解】本题特点是,动荷载不是作用在质量上的集中荷载。
对于非质量处的集中动荷载的情况,在建立运动方程时,一般采用柔度法较为方便。
设图a 质量任一时刻沿自由度方向的位移为y (向下为正)。
把惯性力I 、阻尼力R 及动荷载)(t P ,均看作是一个静荷载,则在其作用下体系在质量处的位移y ,由叠加原理(见图b 、c 、d 及e ),则)(R I y P D I P +δ+∆=∆+∆+∆=式中,)t (q EI38454P =∆,EI 483 =δ。
将它们代入上式,并注意到ym I -=,y c R -=,得)(48)(384534y c y m EIt q EI y --+=图16-7经整理后可得)(t P ky y c y m E =++式中,3EI 481k =δ=,)(85)(t q k t P P E =∆= )(t P E 称为等效动荷载或等效干扰力。
其含义为:)(t P E 直接作用于质量上所产生的位移和实际动荷载引起的位移相等。
图a 的相当体系如图f 所示。
【例16-3】 图16-8a 为刚性外伸梁,C 处为弹性支座,其刚度系数为k ,梁端点A 、D 处分别有m 和3m质量,端点D 处装有阻尼器c ,同时梁BD 段受有均布动荷载)t (q 作用,试建立刚性梁的运动方程。
【解】 因为梁是刚性的,这个体系仅有一个自由度,故它的动力响应可由一个运动方程来表达,方程可以用直接平衡法来建立。
结构动力学复习题

结构力学下复习题一. 判断题1. 对于单自由度体系有如下关系k =δ-1对于多自由度体系也同样成立。
( )2. 仅在恢复力作用下的振动称为自由振动。
( )3. 如果使单自由度体系的阻尼增大,其结果是周期变短。
( )4、 体系在θϖ>时,)(t y 与)(t p 方向相同。
ϖ为自振频率,EI 为常数。
( )5. 在无限自由度体系的弹性稳定分析中,用静力法和能量法(瑞利-里兹法)得到的临界荷载是相同的。
( )6. 只要两个杆件的截面面积相同、所用材料相同,它们的极限弯矩就是相同的。
( )二. 单项选择题1.对图示结构,若要使其自振频率增大,可以( )。
A. 增大F P ; C. 增大m ;B. 增大 EI ; D. 增大l 。
2 . 单自由度简谐受迫振动中,若算得位移放大系数μ 为负值,则表示( )。
A. 体系不可能振动; C. 动位移小于静位移;B. 干扰力频率与自振频率不同步; D. 干扰力方向与位移方向相反。
3.单自由度体系在简谐荷载作用下如果频率比大于1,则要减小振动幅值需采取措施A 增加刚度,减少质量;B 增加刚度,增加质量;C 减少刚度,减少质量;D 减少刚度,增加质量;4.图示两组压杆的临界荷载分析为Pcr 1 F 和Pcr 2 F ,则两者的关系是A 21cr cr F F =B 212cr cr F F =C 212cr cr F F =D 215.1cr cr F F =题4三 . 填充题1.图示体系不计杆件质量和轴向变形,各杆抗弯刚度为常数,其动力自由度为 。
2.图示体系的自振频率为 。
3、对于矩形截面,极限弯矩为屈服弯矩的 倍。
4、已知质点m 的最大竖向位移st y y 5max = ,且初始时质点竖向位移为st y (st y 为静位移),则质点的初始速度为 。
四. 计算分析题1.)已知θ = 0.4ω ,试求图示体系的振幅和最大动弯矩。
2.试求图示体系质点的振幅和A 截面动弯矩幅值,已知ϖθ6.0=3.试求图示基础的振幅 A及地基所受的动压力N。
结构动力学试题及答案

结构动力学试题及答案(本文按试题和答案格式进行编写)试题一:1. 请问什么是结构动力学?2. 简述结构动力学的研究对象和主要内容。
3. 结构动力学分析常用的方法有哪些?4. 结构动力学分析中常用的数学模型有哪些?5. 结构动力学的应用领域有哪些?答案一:1. 结构动力学是研究结构在外力作用下的动态响应及其稳定性的学科。
2. 结构动力学的研究对象是各种工程结构,主要内容包括结构的振动、冲击响应、瞬态响应和稳态响应等。
3. 结构动力学分析常用的方法有模态分析法、频率响应分析法、时程分析法等。
4. 结构动力学分析中常用的数学模型有单自由度体系、多自由度体系、连续体系等。
5. 结构动力学的应用领域广泛,包括建筑结构工程、桥梁工程、风力发电机组、地震工程等。
试题二:1. 结构动力学分析中,模态分析的基本原理是什么?2. 简述模态分析的步骤和计算方法。
3. 常用的模态分析软件有哪些?4. 请问什么是结构的固有频率和阻尼比?5. 结构的模态振型对结构动力响应有什么影响?答案二:1. 模态分析是基于结构的振动特性,通过求解结构的固有频率、模态振型和阻尼比等参数,来研究结构的动力响应。
2. 模态分析的步骤包括建立结构有限元模型、求解结构的固有频率和模态振型、计算结构的阻尼比等。
常用的计算方法有有限元法、拉普拉斯变换法等。
3. 常用的模态分析软件有ANSYS、ABAQUS、MSC.NASTRAN等。
4. 结构的固有频率是结构在无外力作用下自由振动的频率,阻尼比是结构振动过程中能量耗散的程度。
5. 结构的模态振型对结构动力响应有很大影响,不同的模态振型会导致不同的振动特性和反应。
试题三:1. 结构动力学分析中,频率响应分析的基本原理是什么?2. 简述频率响应分析的步骤和计算方法。
3. 频率响应分析和模态分析有什么区别?4. 结构的频率响应函数和传递函数有什么区别?5. 频率响应分析在结构设计中的应用有哪些?答案三:1. 频率响应分析是研究结构在单频激励下的响应特性,通过求解结构的频率响应函数,来获得结构的响应。
结构动力学试卷及答案

考生请注意:1.本试题共6 题,共2 页,考生请认真检查;2.答题时,直接将答题内容写在我校提供的答题纸上;答在试卷上一律无效;3.本试题不得拆开,拆开后遗失后果自负。
一、简述题(本题共20分,每小题5分)1.自由振动、强迫振动自由振动:系统受到初始激励作用后,仅靠其本身的弹性恢复力“自由地”振动,其振动特性仅取决于系统本身的物理特性(质量和刚度)。
强迫振动:系统受到外界持续的激励作用而“被动地”进行振动,其振动特性除取决于系统本身的特性外,还取决于激励的特性。
2.广义坐标、振型函数广义坐标:是一种坐标形式,它是有几组互相正交的模态组成,任何变量都可由这几组模态的唯一线性组合而成。
振型函数:是一种函数形式,描述振型在几维空间中的振幅值的表现。
3.稳态响应、瞬态响应稳态响应:当系统在外力作用下,经过一段时间后,系统振动趋于稳定时的响应。
瞬态响应:当系统在外力作用下,在系统振动趋于稳定之前的响应。
瞬态响应发生在稳态响应之前,他们组合构成完整的外力作用时的振动响应。
4.哈密顿原理具有完整约束的动力学系统,在满足协调性条件、约束条件或边界条件,同时满足起始t1时刻与结束t2时刻条件的可能的位移随时间变化的形式中,真实解对应的那种变化形式使Lagrange泛函L取最小值,即2 1(T V W)0t t dt式中:T为系统的动能,V为系统的势能,W为外力所作虚功。
二.质量均为m 的两个球,系于具有很大张力T 的弦上,如图所示,求系统的固有频率。
(本题10分)解:由于弦的张力T 很大,两个球只能在竖向发生微幅振动。
(1分)如下图所示,两个球在外力1()F t 和2()F t 作用下发生竖向微幅振动,位移分别为1x 和2x 。
对两个球,分别作受力分析:外荷载;惯性力; 张力分力。
(3分)运用达朗贝尔原理,分别列出 两个球的竖向运动方程:12111()x x x mx T T F t L L-+⋅-⋅=22122()x x xmx T T F t L L-+⋅+⋅= (5分)写成矩阵形式:1112222()002()TT x x F t m L L m x T T x F t L L ⎡⎤-⎢⎥⎧⎫⎧⎫⎧⎫⎡⎤+=⎢⎥⎨⎬⎨⎬⎨⎬⎢⎥⎣⎦⎩⎭⎩⎭⎩⎭⎢⎥-⎢⎥⎣⎦得频率方程:[][]222202T Tm LLK M T T m L Lωωω---==-- (7分) 解得: 1ω=2ω= (10分)ll l F 2(t)三.图示简支梁,梁长为4l ,在四等分处有3个质量m 1=m 2=m 3=m ,梁的抗弯刚度为EI ,忽略梁自身的质量,要求:(1)写出系统振动方程;(2)求系统的各阶固有频率; (3)画出相应的主振型。
(完整word版)结构动力学历年试题

(完整word版)结构动力学历年试题结构动力学历年试题(简答题)1.根据荷载随时间的变化规律,动力荷载可以划分为哪几类?每一类荷载包括哪几种,请简述每一种荷载的特点。
P22.通过与静力问题的对比,试说明结构动力计算的特点。
P33.动力自由度数目计算类4.什么叫有势力?它有何种性质。
P145.广义力是标量还是矢量?它与广义坐标的乘积是哪个物理量的量纲?P166.什么是振型的正交性?它的成立条件是什么?P1057.在研究结构的动力反应时,重力的影响如何考虑?这样处理的前提条件是什么?P328.对于一种逐步积分计算方法,其优劣性应从哪些方面加以判断?P1329.在对结构动力反应进行计算的思路上,数值积分方法与精确积分方法的差异主要表现在哪里?第五章课件10.利用Rayleigh法求解得到的振型体系的基本振型和频率及高阶振型和频率与各自的精确解相比有何特点?造成这种现象的原因何在?P20911.根据荷载是否预先确定,动荷载可以分为哪两类?它们各自具有怎样的特点?P112.坐标耦联的产生与什么有关,与什么无关?P9613.动力反应的数值分析方法是一种近似的计算分析方法,这种近似性表现在哪些方面?P132及其课件14.请给出度哈姆积分的物理意义?P8115.结构地震反应分析的反应谱方法的基本原理是什么?P84总结16.某人用逐步积分计算方法计算的结构位移,得到如下的位移时程的计算结果:。
17.按照是否需要联立求解耦联方程组,逐步积分法可以分为哪两类?这两类的优劣性应该如何进行判断?P13218.根据荷载随时间的变化规律,动力荷载可以划分为哪几类?每一类荷载又包括哪些类型,每种类型请给出一种实例。
P219.请分别给出自振频率与振型的物理意义?P10320.振型叠加法的基本思想是什么?该方法的理论基础是什么?P111参考25题21.在振型叠加法的求解过程中,只需要取有限项的低阶振型进行分析,即高阶振型的影响可以不考虑,这样处理的物理基础是什么?P11522.我们需要用数值积分方法求解一座大型的高坝结构的地震反应时程,动力自由度的总数为25000个,我们如何缩短计算所耗费的机时?P10323.什么是结构的动力自由度?动力自由度与静力自由度的区别何在?P11及卷子上答案24.一台转动机械从启动到工作转速正好要经过系统的固有频率(又称为转子的临界转速),为减小共振,便于转子顺利通过临界转速,通常采用什么措施比较直接有效?简要说明理由。
结构动力学试题

结构动力学试题一、选择题1. 结构动力学中的“动力响应”是指:A. 结构在静态载荷下的变形B. 结构在动态载荷下的变形C. 结构的自然频率D. 结构的阻尼比2. 单自由度系统的周期公式为:A. T = 2π√(m/k)B. T = 2π√(k/m)C. T = 2π/mD. T = π√(m/k)3. 多自由度系统的振型分解法是基于以下哪个原理?A. 结构的对称性B. 结构的不确定性C. 结构的线性叠加原理D. 结构的能量守恒原理4. 在地震分析中,反应谱方法的主要优点是:A. 考虑了地震动作用的非线性B. 可以处理任意形状的地震波形C. 能够直接给出结构的响应结果D. 适用于快速评估结构的地震安全性5. 结构阻尼比的增大通常会导致:A. 自然频率的提高B. 振幅的减小C. 周期的延长D. 响应的不稳定二、填空题1. 在结构动力学中,________是用来描述结构在动态载荷作用下的运动状态。
2. 动态载荷下,结构的响应可以通过________方法进行求解,该方法基于结构振动的线性叠加原理。
3. 地震波的________特性对结构的响应有显著影响,因此在进行地震分析时需要特别考虑。
4. 结构的阻尼比可以通过________方法进行实验测定,以评估结构的能量耗散能力。
5. 在进行结构动力分析时,通常需要将结构简化为________自由度系统,以便于计算和分析。
三、简答题1. 请简述单自由度系统与多自由度系统的区别及其各自的适用场景。
2. 描述地震波的基本特性,并解释为什么需要对其进行频谱分析。
3. 说明结构阻尼对动力响应的影响,并讨论如何通过设计来提高结构的阻尼性能。
四、计算题1. 一个单自由度系统的质量为500 kg,刚度为2000 N/m。
请计算该系统的自然频率和阻尼比为0.05时的周期。
2. 假设一个结构在地震作用下的最大加速度为0.3g,其中g为重力加速度(9.81 m/s²),请使用反应谱方法计算该结构在自然频率为2Hz时的响应加速度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结构动力学期末复习题
1.试用哈密顿原理推证第二类拉格朗日方程。
日方程求出图示系统在指定的广义坐标
下的运动微分方程。
若仅考虑小变形振
动,写出其运动微分方程。
图中弹簧1
l,弹簧2未变形时的
未变形时的原长为
1
原长为a。
5. 试讨论对于多自由度体系如何形成一致质量矩阵、一致刚度(包括几何刚度)矩阵、一致荷载列阵并分析与集中质量矩阵的区别。
6. 一栋多层楼房,在地震地面运动作用下运动,若结构在运动中保持为弹性,
试述求解该结构弹性动力反应的振型叠加法的原理以及求解步骤。
7. 一栋多层楼房,在地震地面运动作用下运动,结构产生非线性变形,试讨论如果将结构简化为集中质量的串模型,如何采用逐步积分法分析该结构在地震地面运动作用下结构的非线性反应时程,写出线性加速度法、Wilson-θ法、Newmark-β法、中央差分法等几种方法中的一种方法分析求解非线性多自由度体系的动力反应的步骤,并就你所知,讨论用于结构非线性时程反应分析的这些逐步积分方法在稳定性和求解精度方面的优缺点,提出你的改进意见和方法。
8.
9. ()(l A x o =ρ)1()(l
x
EI x EI o +=试采用
10. kg
m 10001=,kg m 5002=m KN k /350=波形,可表示为l
z
a x s π2sin
=,其中,m l 5=。
求拖车在满载和空载时的振幅比。
11. 试推导粘性阻尼力在一周内消耗的能量的表达式。
12. 试求振动系统02=++kx x x m n
ζω在图示方波激励下的稳态受迫振动。
13. 图示结构,受到如图所示周期性荷载,可表示如下的正弦级数:
t b t p n n n ωsin )(1∑∞
==,其中,n n n p b )1(20
--
=π
,不考虑阻尼,且荷载频率与结构自振频率之比为:
4
3
1=ωω,试求出结构在此荷载作用下的稳态反应。
14. 长为L ,质量为m 的两个相同的单摆用刚度系数为k 的弹簧相连如图,当两摆在铅垂位置时,弹簧没有变形。
试求系统在同一铅垂平面内作微幅振动的固有频率和振型,并由求得的振型向量证明振型矩阵对于质量矩阵和刚度矩阵的正交性。
15. 实际结构在振动中的能量损失机理很复杂,建立结构的振动微分方程时阻尼项中的阻尼系数必须要采用实验方法求得,试就你所知,例举3种以上求结构阻尼的实验方法,并说明其原理。
16.一台精密仪器设备重w=500kN ,用四个弹簧刚度各为33kN/cm 的弹簧竖向隔振,若地基运动为初相位相同的两个垂直正弦波的合成,振幅均为1μm ,振动频率分别为f 1=3Hz ,f 2=15Hz 。
设精密设备的允许振动速度为[v]=0.05mm/s 。
试求该设备振动时铅垂方向的最大速度,并问是否满足允许振动速度的要求。
(设为零阻尼)
17.
的相角θ为10%,⎢⎢⎢⎣⎡=.0.000
.1φ⎪⎩⎪⎨⎧=.45.27.11ω18
19.
20. 试就目前科技水平的发展,分析结构动力学今后的发展趋势(每人应有不同的见解)。
