智能控制指导作业
智能控制作业_模糊自适应PID控制

模糊自适应PID 控制的Matlab 仿真设计研究姓名:陈明学号:201208070103班级:智能1201一、 模糊控制思想、PID 控制理论简介:在工业生产过程中,许多被控对象受负荷变化或干扰因素很多基于模糊自适应控制理论, 设计了一种模糊自适应PID 控制器, 具体介绍了这种PID 控制器的控制特点及参数设计规则, 实现PID 控制器的在线自整定和自调整。
通过matlab 软件进行实例,仿真表明, , 提高控制系统实时性和抗干扰能力,易于实现.便于工程应用。
1.1 模糊控制的思想:应用模糊数学的基本理论和方法, 控制规则的条件、操作用模糊集来表示、并把这些模糊控制规则以及有关信息, 诸如PID 控制参数等作为知识存入计算机知识库, 然后计算机根据控制系统的实际情况(系统的输入, 输出) , 运用模糊推理。
1.2 PID 算法:u(t)=k p * e(t)+k i * ∫e(t)t 0dt +k d *de(t)dt= k p *e(t)+ k i *∑e i (t) + k d * e c (t)其中, u (t) 为控制器输出量, e(t) 为误差信号, e c (t)为误差变化率, k p , k i , k d 分别为比例系数、积分系数、微分数。
然而,课本中,为了简化实验难度,只是考虑了kp ,ki 参数的整定。
1.3 模糊PID 控制器的原理图:二、基于Matlab的模糊控制逻辑模块的设计关于模糊逻辑的设计,主要有隶属函数的编辑,参数的选型,模糊规则导入,生成三维图等观察。
2.1 模糊函数的编辑器的设定:打开matlab后,在命令窗口输入“fuzzy”,回车即可出现模糊函数编辑器,基本设置等。
基于课本的实验要求,我选的是二输入(e, e c)二输出(k p ,k i)。
需要注意的是,在命名输入输出函数的时候,下标字母需要借助下划线的编辑,即e_c 能够显示为e c。
2.2四个隶属函数的N, Z, P 函数设定:在隶属函数的设定中,N 选用的是基于trimf(三角形隶属函数) , Z是基于zmf(Z型隶属函数),P是基于smf(S型隶属函数)。
智能控制技术第二章作业

求:
(1)误差为零和误差为正小的隶属度函数
(2)误差为零或误差为正小的隶属度函数
解
定义2-4并:并 的隶属函数 对所有 被逐点定义为取大运算,即 ,式中,符号“∨”为取极大值运算。
定义2-5交:交 的隶属函数 对所有 被逐点4已知模糊矩阵P、Q、R、S为
求:
(1)
(2)
(3)
解
定义2-14模糊关系合成:如果R和S分别为笛卡尔空间 和 上的模糊关系,则R和S的合成是定义在笛卡尔空间 上的模糊关系,并记作 ,其隶属度函数的计算方法
上确界(Sup)算子
(1)
(2)
2-6设有论域 , ,并定义
试确定模糊条件语言“如果x轻,则y重,否则y不非常重”所决定的模糊关系矩阵R,并计算出当x为非常轻,重条件下所对应的模糊集合y。
(不做)
解:B′=非常重=
B″=不非常重=B =
关系矩阵R=(A×B)U
A×B=
(完整版)智能控制题目及解答

智能控制题目及解答第一章绪论作业作业内容1.什么是智能、智能系统、智能控制?2.智能控制系统有哪几种类型,各自的特点是什么?3.比较智能控制与传统控制的特点.4.把智能控制看作是AI(人工智能)、OR(运筹学)、AC(自动控制)和IT(信息论)的交集,其根据和内涵是什么?5.智能控制有哪些应用领域?试举出一个应用实例,并说明其工作原理和控制性能.1 答:智能:能够自主的或者交互的执行通常与人类智能有关的智能行为,如判断、推理、证明、识别、感知、理解、通信、设计、思考、规划、学习等一系列活动的能力,即像人类那样工作和思维。
智能系统:是指具有一定智能行为的系统,对于一定的输入,它能产生合适的问题求解相应。
智能控制:智能控制是控制理论、计算机科学、心理学、生物学和运筹学等多方面综合而成的交叉学科,它具有模仿人进行诸如规划、学习、逻辑推理和自适应的能力。
是将传统的控制理论与神经网络、模糊逻辑、人工智能和遗传算法等实现手段融合而成的一种新的控制方法。
2 答:(1)人作为控制器的控制系统:人作为控制器的控制系统具有自学习、自适应和自组织的功能。
(2)人—机结合作为作为控制器的控制系统:机器完成需要连续进行的并需快速计算的常规控制任务,人则完成任务分配、决策、监控等任务。
(3)无人参与的自组控制系统:为多层的智能控制系统,需要完成问题求解和规划、环境建模、传感器信息分析和低层的反馈控制任务.3 答:在应用领域方面,传统控制着重解决不太复杂的过程控制和大系统的控制问题;而智能控制主要解决高度非线性、不确定性和复杂系统控制问题。
在理论方法上,传统控制理论通常采用定量方法进行处理,而智能控制系统大多采用符号加工的方法;传统控制通常捕获精确知识来满足控制指标,而智能控制通常是学习积累非精确知识;传统控制通常是用数学模型来描述系统,而智能控制系统则是通过经验、规则用符号来描述系统。
在性能指标方面,传统控制有着严格的性能指标要求,智能控制没有统一的性能指标,而主要关注其目的和行为是否达到。
智能控制作业

1、已知某一炉温控制系统,要求温度保持在600度恒定。
针对该控制系统有以下控制经验:(1)若炉温低于600度,则升压;低的越多升压越高。
(2)若炉温高于600度,则降压;高的越多降压越低。
(3)若炉温等于600度,则保持电压不变。
设模糊控制器为一维控制器,输入语言变量为误差,输出为控制电压。
输入、输出变量的量化等级为7级,取5个模糊集。
试设计隶属度函数误差变化划分表、控制电压变化划分表和模糊控制规则表。
解:1)确定变量定义理想温度为600℃,实际温度为T,则温度误差为E=600-T。
将温度误差E作为输入变量2)输入量和输出量的模糊化将偏差E分为5个模糊集:NB、NS、ZO、PS、PB,分别为负小、负大、零、正小、正大。
将偏差E的变化分为7个等级:-3 -2 -1 0 1 2 3,从而得到温度模糊表如表1所示。
表1 温度变化E划分表控制电压u也分为5个模糊集:NB、NS、ZO、PS、PB,分别为负小、负大、零、正小、正大。
将电压u的变化分为7个等级:-3 -2 -1 0 1 2 3,从而得到电压变化模糊表如表2所示。
表2 电压变化u划分表表3 模糊控制规则表E PB PS ZO NS NB u PB PS ZO NS NB2、利用MATLAB,为下列两个系统设计模糊控制器使其稳态误差为零,超调量不大于1%,输出上升时间≤0.3s 。
假定被控对象的传递函数分别为:255.01)1()(+=-s e s G s)456.864.1)(5.0(228.4)(22+++=s s s s G解:在matlab 窗口命令中键入fuzzy ,得到如下键面:设e 的论域范围为[-1 1],de 的论域范围为[-0.1 0.1],u 的论域范围为[0 2]。
将e 分为8个模糊集,分别为NB ,NM, NS, NZ, PZ, PS, PM, PB; de 分为7个模糊集,分别为NB ,NM ,NS, Z ,PS ,PM ,PB;u分为7个模糊集,分别为NB ,NM ,NS, Z ,PS ,PM ,PB; MATLAB中的设置界面如下:模糊规则的确定:模糊控制器的输出量在simulink中调用模糊控制器,观察输出结果运行结果为ScopeScope1 Scope23、利用去模糊化策略,分别求出模糊集A 的值。
智能控制(神经网络)-作业

智能控制作业学生姓名: 学号: 专业班级:(一)7-2 采用BP网路、RBF网路、DRNN网路逼近线性对象, 分别进行matlab 仿真。
(二)采用BP网络仿真网络结构为2-6-1。
采样时间1ms, 输入信号, 权值的初值随机取值, 。
仿真m文件程序为:%BP simulationclear all;clear all;xite=0.5;alfa=0.5;w1=rands(2,6); % value of w1,initially by randomw1_1=w1;w1_2=w1;w2=rands(6,1); % value of w2,initially by randomw2_1=w2;w2_2=w2_1;dw1=0*w1;x=[0,0]';u_1=0;y_1=0;I=[0,0,0,0,0,0]'; % input of yinhanceng cellIout=[0,0,0,0,0,0]'; % output of yinhanceng cellFI=[0,0,0,0,0,0]';ts=0.001;for k=1:1:1000time(k)=k*ts;u(k)=0.5*sin(3*2*pi*k*ts);y(k)=(u_1-0.9*y_1)/(1+y_1^2);for j=1:1:6I(j)=x'*w1(:,j);Iout(j)=1/(1+exp(-I(j)));endyn(k)=w2'*Iout; %output of networke(k)=y(k)-yn(k); % error calculationw2=w2_1+(xite*e(k))*Iout+alfa*(w2_1-w2_2); % rectify of w2for j=1:1:6FI(j)=exp(-I(j))/(1+exp(-I(j))^2);endfor i=1:1:2for j=1:1:6dw1(i,j)=e(k)*xite*FI(j)*w2(j)*x(i); % dw1 calculation endendw1=w1_1+dw1+alfa*(w1_1-w1_2); % rectify of w1% jacobian informationyu=0;for j=1:1:6yu=yu+w2(j)*w1(1,j)*FI(j);enddyu(k)=yu;x(1)=u(k);x(2)=y(k);w1_2=w1_1;w1_1=w1;w2_2=w2_1;w2_1=w2;u_1=u(k);y_1=y(k);endfigure(1);plot(time,y,'r',time,yn,'b');xlabel('times');ylabel('y and yn');figure(2);plot(time,y-yn,'r');xlabel('times');ylabel('error');figure(3);plot(time,dyu);xlabel('times');ylabel('dyu');运行结果为:(三)采用RBF网络仿真网路结构为2-4-1, 采样时间1ms, 输入信号, 权值的初值随机取值, , 高斯基函数初值, 。
智能控制技术作业1
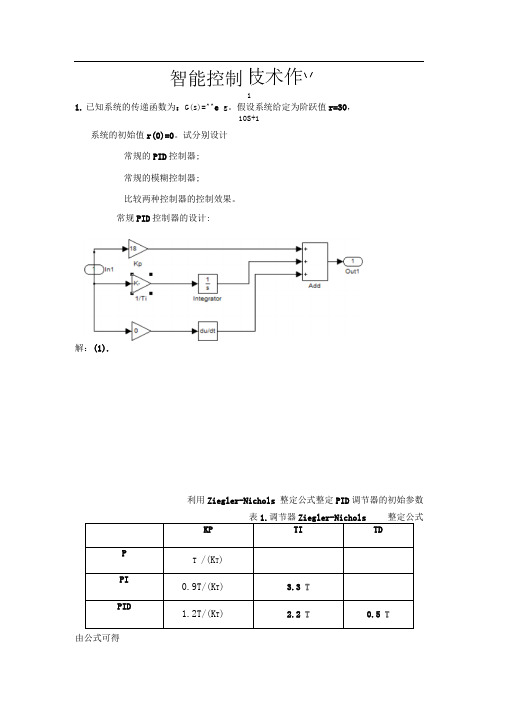
智能控制11.已知系统的传递函数为:G(s)=^^e g。
假设系统给定为阶跃值r=30,10S+1系统的初始值r(0)=0。
试分别设计常规的PID控制器;常规的模糊控制器;比较两种控制器的控制效果。
解:(1).利用Ziegler-Nichols 整定公式整定PID调节器的初始参数表1.调节器Ziegler-Nichols 整定公式KP TI TDPT /(K T)PI0.9T/(K T) 3.3 TPID1.2T/(K T)2.2 T0.5 T由公式可得\ /常规PID控制器的设计:P=18Ti=1.65Td=O SIMULINK仿真图^Bl*ck FardBCtcrsL Step]—S-tn 口tiJM:F:n且!valae.|35Saocrle tiae:pP iRt^Tpret vect{}r pEiTKHteri AB 1-D1*7 二「二匕二匸匚rzzrinb c -二:"〔二r.QBl*ck rarutt«rs: Tr^nsstrl Dclarp Tf Dfrlaj丄口sir <PE匚LT;td do:口T tp the qrpvt ;iEnJl- n;匚ur*cr i;au订:<hiTi tm delay i i lariE^r t郎an tJifr iinlat^on it»口i;£«上冒itlA* Ln^tLBl iTlDUt'I偌斗设定仿真时间为10s仿真结果CdX1C«l M*lp ApplyU2SJ 厂Direct r*fr;throi;ch at input liiXiiu liJieaxisttian.Pndfl prdflh tfo-T ;incari;ftt iQTL;:A也Q何丹ASS S昌嘩ffl 也| ** C? ® e附币■(2).模糊控制器的设计:1.在matlab命令窗口输入“ fuzzy ”确定模糊控制器结构:即根据具体的系统确定输入、输出量。
智能控制题目及解答

智能控制题目及解答 Document number:WTWYT-WYWY-BTGTT-YTTYU-2018GT智能控制题目及解答第一章绪论作业作业内容1.什么是智能、智能系统、智能控制2.智能控制系统有哪几种类型,各自的特点是什么3.比较智能控制与传统控制的特点。
4.把智能控制看作是AI(人工智能)、OR(运筹学)、AC(自动控制)和IT(信息论)的交集,其根据和内涵是什么5.智能控制有哪些应用领域试举出一个应用实例,并说明其工作原理和控制性能。
1 答:智能:能够自主的或者交互的执行通常与人类智能有关的智能行为,如判断、推理、证明、识别、感知、理解、通信、设计、思考、规划、学习等一系列活动的能力,即像人类那样工作和思维。
智能系统:是指具有一定智能行为的系统,对于一定的输入,它能产生合适的问题求解相应。
智能控制:智能控制是控制理论、计算机科学、心理学、生物学和运筹学等多方面综合而成的交叉学科,它具有模仿人进行诸如规划、学习、逻辑推理和自适应的能力。
是将传统的控制理论与神经网络、模糊逻辑、人工智能和遗传算法等实现手段融合而成的一种新的控制方法。
2 答:(1)人作为控制器的控制系统:人作为控制器的控制系统具有自学习、自适应和自组织的功能。
(2)人-机结合作为作为控制器的控制系统:机器完成需要连续进行的并需快速计算的常规控制任务,人则完成任务分配、决策、监控等任务。
(3)无人参与的自组控制系统:为多层的智能控制系统,需要完成问题求解和规划、环境建模、传感器信息分析和低层的反馈控制任务。
3 答:在应用领域方面,传统控制着重解决不太复杂的过程控制和大系统的控制问题;而智能控制主要解决高度非线性、不确定性和复杂系统控制问题。
在理论方法上,传统控制理论通常采用定量方法进行处理,而智能控制系统大多采用符号加工的方法;传统控制通常捕获精确知识来满足控制指标,而智能控制通常是学习积累非精确知识;传统控制通常是用数学模型来描述系统,而智能控制系统则是通过经验、规则用符号来描述系统。
智能控制作业

题目1:求取模糊控制表(课本62-67页,matlab编程求解)解:MATLAB编程如下:%实现功能:计算模糊控制表clcclear%x的隶属度表,其中x代表的是误差eX=[1.0 0.8 0.7 0.4 0.1 zeros(1,8);0.2 0.7 1.0 0.7 0.3 zeros(1,8);0 0.1 0.3 0.7 1.0 0.7 0.2 zeros(1,6);zeros(1,4) 0.1 0.6 1.0 zeros(1,6);zeros(1,6) 1.0 0.6 0.1 zeros(1,4);zeros(1,6) 0.2 0.7 1.0 0.7 0.3 0.1 0;zeros(1,8) 0.2 0.7 1.0 0.7 0.3;zeros(1,8) 0.1 0.4 0.7 0.8 1.0];%y的隶属度表,其中y表示的是误差的导数Y=[1.0 0.7 0.3 zeros(1,10);0.3 0.7 1.0 0.7 0.3 zeros(1,8);0 0 0.3 0.7 1.0 0.7 0.3 zeros(1,6);zeros(1,4) 0.3 0.7 1.0 0.7 0.3 zeros(1,4);zeros(1,6) 0.3 0.7 1.0 0.7 0.3 0 0;zeros(1,8) 0.3 0.7 1.0 0.7 0.3;zeros(1,10) 0.3 0.7 1];%z的隶属度表,其中z表示的是控制量uZ=Y;%模糊控制规则表%其中: 1代表NB,2代表NM,3代表NS% 4代表ZE,5代表PS,6代表PM,7代表PBrule=[1 1 1 1 2 4 4;1 1 1 12 4 4;2 2 2 2 4 5 5;2 23456 6;2 23456 6;3 34 6 6 6 6;4 4 6 7 7 7 7;4 4 6 7 7 7 7];Set=[-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6]; %模糊集合control_data=[]; %control_data待求的模糊控制表for i=1:13 %控制模糊表的行变量control=[];for j=1:13 %控制模糊表的列变量x0=Set(i);y0=Set(j);CCC=[]; %存放Ci;CCC矩阵将来存放的是56*13维的矩阵for m=1:8 %模糊控制规则表的行变量Ai=X(m,:); %Ai为列向量for n=1:7 %模糊控制规则表的列变量Bi=Y(n,:); %Bi为列向量Ci=Z(rule(m,n),:); %模糊控制规则表的控制变量%得到RiA矩阵RiA=zeros(13,13);for p=1:13for q=1:13RiA(p,q)=min(Ai(p),Ci(q));endend%AA表示A' 矩阵AA=zeros(1,13);[a1,b1]=find(x0==Set);AA(a1,b1)=1;%最小最大原则求取CiACIA_temp=zeros(13,13);for ii=1:13CIA_temp(:,ii)=min(AA',RiA(:,ii));%先取小endCIA=max(CIA_temp);%再取大%%%%%%%%%%%%%%%%%%%%%%%%%得到RiB矩阵RiB=zeros(13,13);for p=1:13for q=1:13RiB(p,q)=min(Bi(p),Ci(q));endend%BB表示B' 矩阵BB=zeros(1,13);[a2,b2]=find(y0==Set);BB(a2,b2)=1;%最小最大原则求取CiBCIB_temp=zeros(13,13);for ii=1:13CIB_temp(:,ii)=min(BB',RiB(:,ii));endCIB=max(CIB_temp);%求CIA和CIB的交C=min(CIA,CIB);CCC=[CCC;C];endend%求出56个Ci的并C_max=max(CCC);%利用重心法解模糊temp=C_max.*Set;control_temp=sum(temp)/sum(C_max);control=[control,control_temp];endcontrol_data=[control_data;control];enddisp('模糊控制表如下:');control_data=roundn(control_data,-2) %保留2位小数且四舍五入fid=fopen('kongzhi.txt','w');count=fprintf(fid,'%d\n',control);fclose(fid);运行结果如下:题目二:被控对象)14)(12(20)(++=s s s G 给定为100,设计一个模糊控制器实现对象系统的控制。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
语言变量X ,Y ,Z 的隶属度函数.设计带有纯延迟的一阶惯性环节(假设T=6,=0.02):G(s)=se s6102.0+的模糊控制器,观察仿真结果。
编程如下:%被控系统建模 num=1; den=[6,1];[a1,b,c,d]=tf2ss(num,den);%传递函数转换到状态空间 x=[0];%系统参数T=0.01;h=T;td=0.02;N=1000; nd=td/T;%系统纯延迟 R=ones(1,N);%参考输入%定义输入和输出变量及隶属度函数a=newfis('Simple');a=addvar(a,'input','e',[-4 4]);a=addmf(a,'input',1,'NB','trimf',[-4,-4,-2]); a=addmf(a,'input',1,'NS','trimf',[-4,-2,0]); a=addmf(a,'input',1,'ZO','trimf',[-2,0,2]);a=addmf(a,'input',1,'PS','trimf',[0,2,4]);a=addmf(a,'input',1,'PB','trimf',[2,4,4]);a=addvar(a,'input','de',[-4 4]);a=addmf(a,'input',2,'NB','trimf',[-4,-4,-2]); a=addmf(a,'input',2,'NS','trimf',[-4,-2,0]); a=addmf(a,'input',2,'ZO','trimf',[-2,0,2]);a=addmf(a,'input',2,'PS','trimf',[0,2,4]);a=addmf(a,'input',2,'PB','trimf',[2,4,4]);a=addvar(a,'output','u',[-4 4]);a=addmf(a,'output',1,'NB','trimf',[-4,-4,-2]); a=addmf(a,'output',1,'NS','trimf',[-4,-2,0]); a=addmf(a,'output',1,'ZO','trimf',[-2,0,2]); a=addmf(a,'output',1,'PS','trimf',[0,2,4]);a=addmf(a,'output',1,'PB','trimf',[2,4,4]); %模糊规则矩阵rr=[5 5 4 4 35 4 4 3 34 4 3 3 24 3 3 2 23 3 2 2 1];r1=zeros(prod(size(rr)),3);k=1;for i=1:size(rr,1)for j=1:size(rr,2)r1(k,:)=[i,j,rr(i,j)];k=k+1;endend[r,s]=size(r1);r2=ones(r,2);rulelist=[r1,r2];a=addrule(a,rulelist);%采用模糊控制器的二阶系统仿真e=0;de=0;ke=30;kd=5;ku=1;for k=1:N%输入变量变换至论域e1=ke*e;de1=kd*de;if e1>=4e1=4;elseif e1<=-4e1=-4;endif de1>=4de1=4;elseif de1<=-4de1=-4;end%模糊推理,计算出被控对象的控制输入in=[e1 de1];u=ku*evalfis(in,a);uu(1,k)=u;if k<=ndu=0;elseu=uu(1,k-nd);end%控制作用于被控系统,计算系统输出;利用龙格—库塔法进行系统仿真k0=a1*x+b*u;k1=a1*(x+h*k0/2)+b*u;k2=a1*(x+h*k1/2)+b*u;k3=a1*(x+h*k2)+b*u;x=x+(k0+2*k1+2*k2+k3)*h/6;y=c*x+d*u;yy(1,k)=y;%计算系统输出误差及误差导数e1=e;e=y-R(1,k);de=(e-e1)/T;end%典型二阶环节的模糊控制输出曲线kk=[1:N]*T;figure(1);plot(kk,R,'k',kk,yy,'r');grid onxlabel('时间(秒)');ylabel('输出');智能控制大作业姓名: 何成东 学号: S0703234 专业: 导航、制导与控制模糊控制器部分大作业已知()()0.525123s G e s s s -=+++,分别设计PID 控制与模糊控制,使系统达到较好性能,并比较两种方法的结果。
具体要求:1、分别采用fuzzy 工具箱和编程实现模糊控制器。
2、分析量化因子和比例因子对模糊控制器控制性能的影响。
3、分析系统在模糊控制和PID 控制作用下的抗干扰能力(加噪声干扰)、抗非线性能力(加死区和饱和特性)以及抗时滞的能力(对时滞大小加以改变)。
4、讨论系统在模糊控制和PID 控制作用下的时间参数和结构变化下的抗干扰能力。
模糊控制部分大作业旨在利用模糊控制器和PID 控制器实现对已知系统的控制,分别得到较好的控制效果。
然后改变系统的参数、结构或者加入非线性环节,以验证模糊控制器的鲁棒性能。
以下是作业过程:1、PID 控制考虑到系统中存在纯延迟环节,使得系统的稳定性大大降低。
如果系统的反馈信号没有延迟,系统的响应特性将会得到很好的改善。
因此,对于存在纯滞后环节的系统,特别是大延迟过程,一般采用Smith 预估控制,即将纯滞后补偿模型与PID 控制器并接。
本题中,延迟环节的时间常数不是很大,仅为0.2,因此基本上不会影响系统的稳定,采用常规PID 控制也基本可以达到很好的控制效果。
常规PID 控制框图如图1-1(相应文件:PID.mdl )图1-1 常规PID 控制框图PID 参数选取:38.0=p K ,285.0=i K ,1.0=d K 常规PID 控制的单位阶跃响应曲线:图1-2 常规PID控制响应曲线2.模糊控制模糊控制规则(相应文件:zdh.fis)各变量论域输入变量:E:[-6 6];EC:[-6 6];输出变量:U:[0 7]语言变量E:NB、NM、NS、NZ、PZ、PS、PM、PB(8个)EC:NB、NM、NS、ZE、PS、PM、PB(7个)U:NB、NM、NS、ZE、PS、PM、PB(7个)各变量隶属度函数:三角形函数(trimf)模糊推理:Mamdani推理法去模糊化:中位数法(bisector)模糊控制框图(相应文件:mohu.mdl)图1-3 模糊控制框图选取量化因子:7.1=e K ,5.0=ec K 选取比例因子:171.0=u K 模糊控制响应曲线图1.4 模糊控制响应曲线在模糊控制器的设计过程中,选择合适的论域和量化因子、比例因子是至关重要的。
量化因子e k 选择过大,系统超调较大,过渡过程较长;ec k 选择过大,系统超调较小,但是响应速度变慢;比例因子u k 选择过大导致系统振荡,过小时系统响应过程变长。
3、在模糊控制和PID 控制中分别加死区、饱和特性以及对时滞大小加以改变。
1)加死区非线性响应曲线比较(如图1-5) 死区参数为(-0.5 0.5)图1-5 PID与模糊控制加死区后的响应曲线比较比较结果可见,模型控制没有PID控制的好2)加饱和非线性响应曲线比较(如图1-6)图1-6 PID与模糊控制加饱和后的响应曲线比较3)改变时滞大小响应曲线比较(如图1-7)图1-7改变时滞大小的PID与模糊控制响应曲线比较由以上两图可知,改变时滞大小以后,PID 控制的控制效果明显变差,而模糊控制的控制效果则相对较好,说明模糊控制较PID 控制有更好的抗时滞能力。
神经网络控制部分大作业已知()0.525123s G e s ss -=+++,分别设计PID 控制与神经网络控制器,使系统达到较好性能,并比较两种方法的结果。
具体要求:1、采用编程实现神经网络控制器。
2、分析神经网络层数和神经元个数对神经网络控制器控制性能的影响。
3、分析系统在神经网络控制和PID 控制作用下的抗干扰能力(加噪声干扰)、抗非线性能力(加死区和饱和特性)以及抗时滞的能力(对时滞大小加以改变)。
4、为系统设计神经网络PID 控制器。
首先设计PID 控制器实现对已知系统的控制,然后利用PID 控制器的采样样本对神经网络进行训练,用训练好的神经网络来控制系统。
然后对加入非线性环节,以验证神经网络控制器的鲁棒性能。
1、PID 控制这里采用模型与模糊控制中的PID 控制模型相同,只是将参数改变了一下,即取27.0=p K ,23.0=i K ,1.0=d K ,单位阶跃响应仿真结果如图2-1所示图2-1 PID控制单位阶跃响应2、神经网络控制利用采集的样本,采用BP算法进行神经网络训练。
训练程序为:p=r';t=u';net=newff([-1 1],[ 20 10 1],{ 'tansig''tansig''purelin'}); net.trainparam.epochs=1000;net.trainparam.goal=0.0001;net=train(net,p,t);gensim(net,-1)利用得到的神经网络控制器进行仿真,控制模型如下图所示:图2-2 神经网络控制模型框图训练结果如下:0 Array图2-3 神经网络训练曲线和模块化描述仿真结果如图2-3所示。
3、增加非线性的仿真结果1)分别在神经网络控制和PID控制系统中加死区非线性进行仿真,如图2-5所示。
