fluent湍流设置
湍流模型及其在FLUENT软件中的应用
湍流模型及其在FLUENT软件中的应用一、本文概述湍流，作为流体动力学中的一个核心概念，广泛存在于自然界和工程实践中，如大气流动、水流、管道输送等。
由于其高度的复杂性和非线性特性，湍流一直是流体力学领域的研究重点和难点。
随着计算流体力学（CFD）技术的快速发展，数值模拟已成为研究湍流问题的重要手段。
其中，湍流模型的选择和应用对于CFD模拟结果的准确性和可靠性具有决定性的影响。
本文旨在深入探讨湍流模型的基本理论及其在FLUENT软件中的应用。
我们将简要回顾湍流的基本概念、特性和分类，为后续的模型介绍和应用奠定基础。
接着，我们将详细介绍几种常用的湍流模型，包括雷诺平均模型（RANS）、大涡模拟（LES）和直接数值模拟（DNS）等，并重点分析它们的适用范围和优缺点。
在此基础上，我们将重点关注FLUENT软件在湍流模拟方面的应用。
FLUENT作为一款功能强大的CFD软件，提供了丰富的湍流模型供用户选择。
我们将通过具体案例，展示如何在FLUENT中设置和应用不同的湍流模型，以及如何通过参数调整和结果分析来优化模拟效果。
我们还将探讨湍流模型选择的影响因素和最佳实践，以帮助读者更好地理解和应用湍流模型。
本文将对湍流模型在FLUENT软件中的应用进行总结和展望，分析当前存在的问题和挑战，并探讨未来的发展趋势和应用前景。
通过本文的阅读，读者可以全面了解湍流模型的基本理论及其在FLUENT 软件中的应用方法，为实际工程问题的解决提供有力的理论支持和技术指导。
二、湍流基本理论湍流，亦被称为乱流或紊流，是一种流体动力学现象，其特点是流体质点做极不规则而又连续的随机运动，同时伴随有能量的传递和耗散。
湍流与层流相对应，是自然界和工程实践中广泛存在的流动状态。
湍流流动的基本特征是流体微团运动的随机性和脉动性，即流体微团除有沿平均运动方向的运动外，还有垂直于平均运动方向的脉动运动。
这种脉动运动使得流体微团在运动中不断混合，流速、压力等物理量在空间和时间上均呈现随机性质的脉动和涨落。
FLUENT中湍流参数的定义
FLUENT中湍流参数的定义在流体力学中，湍流是流体运动的一种状态，以其非线性、混沌、无规律等特点而闻名。
湍流在自然界和工程实践中普遍存在，如河流、大气流动和燃烧等过程都包含湍流现象。
湍流参数是用来描述湍流特性的一组物理量，可以帮助我们理解和预测湍流行为。
在FLUENT中，湍流参数包括湍流模型、湍流能量方程和湍流模型的特定参数。
湍流模型是湍流参数的核心部分，用来计算湍流流场中湍流分量的方程。
在FLUENT中，常用的湍流模型有：可压缩流的RANS（雷诺平均纳维-斯托克斯）模型、不可压缩流的LES（大涡模拟）模型和复杂流场的RSM （雷诺应力模型）等。
这些模型基于不同的假设和数学表达式，有不同的适用范围和精度。
用户可以根据流体流动的特点选择最适合的湍流模型。
湍流能量方程是湍流模型的重要组成部分，用来描述流体运动中湍流能量的传输和转换。
其方程形式包括湍流能量方程和湍流耗散率方程。
湍流能量方程考虑了湍流动能的输送、湍流耗散和湍流扩散等过程，可以通过求解这个方程来获得湍流解。
湍流耗散率方程则用来描述湍流能量的耗散速率，是湍流的产生和湍流尺度变化的基础。
湍流模型的特定参数是湍流参数的额外细节，用来调整湍流模型中的一些假设。
这些参数包括湍流粘度、湍流剪切应力和湍流耗散率等。
调整这些参数可以改变湍流模型的精度和适用范围，但需要经验和实验数据的支持。
在FLUENT中，用户可以根据需要自行设置这些参数，以获得更精确的湍流预测结果。
总之，湍流参数是FLUENT软件中用于描述湍流行为的一组物理量，包括湍流模型、湍流能量方程和湍流模型的特定参数。
通过使用这些参数，用户可以研究和模拟各种湍流流动现象，如流体流动、湍流传热和湍流搅拌等。
在工程实践中，准确预测和控制湍流行为对于提高流体系统的效率和性能至关重要。
FLUENT提供了一套完善的湍流模拟工具，帮助用户解决湍流相关问题。
fluent自然对流关键设置
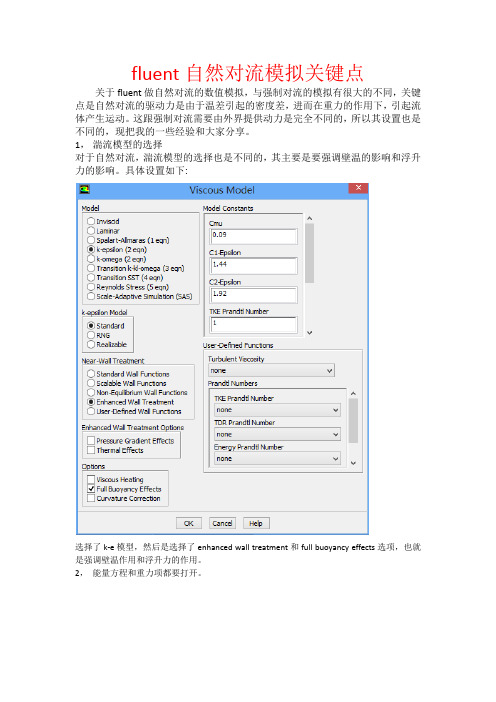
fluent自然对流模拟关键点关于fluent做自然对流的数值模拟，与强制对流的模拟有很大的不同，关键点是自然对流的驱动力是由于温差引起的密度差，进而在重力的作用下，引起流体产生运动。
这跟强制对流需要由外界提供动力是完全不同的，所以其设置也是不同的，现把我的一些经验和大家分享。
1，湍流模型的选择对于自然对流，湍流模型的选择也是不同的，其主要是要强调壁温的影响和浮升力的影响。
具体设置如下:选择了k-e模型，然后是选择了enhanced wall treatment和full buoyancy effects选项，也就是强调壁温作用和浮升力的作用。
2，能量方程和重力项都要打开。
3，材料的设置（1）密度采用Boussinesq假设，然后需要设置流体的密度为一个定值，还要设置流体的热膨胀系数。
关于流体的热膨胀系数需要查资料了。
如下（2）选用不可压缩理想流体假设就是流体按不可压缩理想流体对待，其含义是，流体的密度是变化的，其变化是由温度变化引起的，而不是由压力变化引起的，如下所示，流体密度项选择incompressible ideal gas选项。
（3）对上述两种选择的解释首先，Boussinesq假设比incompressible ideal gas假设，更易收敛。
一般情况下选择这个假设即可。
其次，对于Boussinesq假设有其适用范围，因为其假设流体密度是个定值，所以其主要用于流体密度变化小于20%的情况，也就是两壁面温差较小的情况，那么温差值有没有一个经验数据呢？有的，一般如果壁温与流体温度相差在200K以上，Boussinesq假设就不适用了。
第三，incompressible ideal gas假设，其把流体密度看做随温度的变化而变化，所以其适用范围较广，对于Boussinesq假设不能适用的，就用这个假设。
4，solution method设置对于求解方法的设置，主要是对压力离散方法的选择，要选择PRESTO!或body force weighted 选项。
(整理)FLUENT边界条件(2)—湍流设置.
FLUENT边界条件（2）—湍流设置（fluent教材—fluent入门与进阶教程于勇第九章）Fluent：湍流指定方法（Turbulence Specification Method）2009-09-16 20:50使用Fluent时，对于velocity inlet边界，涉及到湍流指定方法（Turbulence Specification Method），其中一项是Intensity and Hydraulic Diameter （强度和水利直径），本文对其进行论述。
其下参数共两项，（1）是Turbulence Intensity，确定方法如下：I=0.16/Re_DH^0.125 (1)其中Re_DH是Hydraulic Diameter（水力直径）的意思，即式(1)中的雷诺数是以水力直径为特征长度求出的。
雷诺数Re_DH=u×DH/υ(2)u为流速，DH为水利直径，υ为运动粘度。
水利直径见（2）。
（2）水利直径水力直径是水力半径的二倍，水力半径是总流过流断面面积与湿周之比。
水力半径R＝A/X (3)其中，A为截面积（管子的截面积）＝流量/流速X为湿周(字面理解水流过各种形状管子外圈湿一周的周长)例如：方形管的水利半径R=ab/2(a+b)水利直径DH=2×R (4)举例如下：如果水流速度u=10m/s，圆形管路直径2cm，水的运动粘度为1×10-6 m2/s。
则DH=2×3.14*r^2/(2*3.14*r)=2*3.14*0.01^2/(3.14*0.02)=0.01 r为圆管半径Re_DH=u×DH/υ=10*0.02/10e-6=20000I=0.16/Re_DH^0.125=0.16/20000^0.125=0.0463971424017634≈5%水力半径：润湿周长横截面积=h r ， 水力直径：h h r 4D =对圆管而言，管道直径和水力直径是一回事。
fluent湍流设置
fluent湍流设置湍流边界条件设置在流场的入口、出口和远场边界上，用户需要定义流场的湍流参数。
在FLUENT 中可以使用的湍流模型有很多种。
在使用各种湍流模型时，哪些变量需要设定，哪些不需要设定以及如何给定这些变量的具体数值，都是经常困扰用户的问题。
本小节只讨论在边界上设置均匀湍流参数的方法，湍流参数在边界上不是均匀分布的情况可以用型函数和UDF（用户自定义函数）来定义，具体方法请参见相关章节的叙述。
在大多数情况下，湍流是在入口后面一段距离经过转捩形成的，因此在边界上设置均匀湍流条件是一种可以接受的选择。
特别是在不知道湍流参量的分布规律时，在边界上采用均匀湍流条件可以简化模型的设置。
在设置边界条件时，首先应该定性地对流动进行分析，以便边界条件的设置不违背物理规律。
违背物理规律的参数设置往往导致错误的计算结果，甚至使计算发散而无法进行下去。
在Turbulence Specification Method （湍流定义方法）下拉列表中，可以简单地用一个常数来定义湍流参数，即通过给定湍流强度、湍流粘度比、水力直径或湍流特征长在边界上的值来定义流场边界上的湍流。
下面具体讨论这些湍流参数的含义，以保证在设置模型时不出现违背流动规律的错误设置：（1）湍流强度（Turbulence Intensity）湍流强度I的定义为：I=Sqrt(u’*u’+v’*v’+w’*w’)/u_avg(8-1)上式中u',v' 和w' 是速度脉动量，u_avg是平均速度。
湍流强度小于1％时，可以认为湍流强度是比较低的，而在湍流强度大于10％时，则可以认为湍流强度是比较高的。
在来流为层流时，湍流强度可以用绕流物体的几何特征粗略地估算出来。
比如在模拟风洞试验的计算中，自由流的湍流强度可以用风洞的特征长度估计出来。
在现代的低湍流度风洞中，自由流的湍流强度通常低于0.05%。
内流问题进口处的湍流强度取决于上游流动状态。
FLUENT中湍流参数的定义
FLUENT 中湍流参数的定义2011-07-28 10:46:03| 分类：默认分类|举报|字号订阅流场的入口、出口和远场边界上，用户需要定义流场的湍流参数。
在FLUENT 中可以使用的湍流模型有很多种。
在使用各种湍流模型时，哪些变量需要设定，哪些不需要设定以及如何给定这些变量的具体数值，都是经常困扰用户的问题。
本小节只讨论在边界上设置均匀湍流参数的方法，湍流参数在边界上不是均匀分布的情况可以用型函数和UDF（用户自定义函数）来定义，具体方法请参见相关章节的叙述。
在大多数情况下，湍流是在入口后面一段距离经过转捩形成的，因此在边界上设置均匀湍流条件是一种可以接受的选择。
特别是在不知道湍流参量的分布规律时，在边界上采用均匀湍流条件可以简化模型的设置。
在设置边界条件时，首先应该定性地对流动进行分析，以便边界条件的设置不违背物理规律。
违背物理规律的参数设置往往导致错误的计算结果，甚至使计算发散而无法进行下去。
在Turbulence Specification Method （湍流定义方法）下拉列表中，可以简单地用一个常数来定义湍流参数，即通过给定湍流强度、湍流粘度比、水力直径或湍流特征长在边界上的值来定义流场边界上的湍流。
下面具体讨论这些湍流参数的含义，以保证在设置模型时不出现违背流动规律的错误设置：（1）湍流强度（Turbulence Intensity）湍流强度I的定义为：I=Sqrt(u’*u’+v’*v’+w’*w’)/u_avg(8-1)上式中u',v' 和w' 是速度脉动量，u_avg是平均速度。
湍流强度小于1％时，可以认为湍流强度是比较低的，而在湍流强度大于10％时，则可以认为湍流强度是比较高的。
在来流为层流时，湍流强度可以用绕流物体的几何特征粗略地估算出来。
比如在模拟风洞试验的计算中，自由流的湍流强度可以用风洞的特征长度估计出来。
在现代的低湍流度风洞中，自由流的湍流强度通常低于0.05%。
fluent中湍流参数的定义
FLUENT 中湍流参数的定义2011-07-28 10:46:03| 分类：默认分类|举报|字号订阅流场的入口、出口和远场边界上，用户需要定义流场的湍流参数。
在FLUENT 中可以使用的湍流模型有很多种。
在使用各种湍流模型时，哪些变量需要设定，哪些不需要设定以及如何给定这些变量的具体数值，都是经常困扰用户的问题。
本小节只讨论在边界上设置均匀湍流参数的方法，湍流参数在边界上不是均匀分布的情况可以用型函数和UDF （用户自定义函数）来定义，具体方法请参见相关章节的叙述。
在大多数情况下，湍流是在入口后面一段距离经过转捩形成的，因此在边界上设置均匀湍流条件是一种可以接受的选择。
特别是在不知道湍流参量的分布规律时，在边界上采用均匀湍流条件可以简化模型的设置。
在设置边界条件时，首先应该定性地对流动进行分析，以便边界条件的设置不违背物理规律。
违背物理规律的参数设置往往导致错误的计算结果，甚至使计算发散而无法进行下去。
在Turbulence Specification Method （湍流定义方法）下拉列表中，可以简单地用一个常数来定义湍流参数，即通过给定湍流强度、湍流粘度比、水力直径或湍流特征长在边界上的值来定义流场边界上的湍流。
下面具体讨论这些湍流参数的含义，以保证在设置模型时不出现违背流动规律的错误设置：（1）湍流强度（Turbulence Intensity）湍流强度I的定义为：I=Sqrt(u’*u’+v’*v’+w’*w’)/u_avg(8-1)上式中u',v' 和w' 是速度脉动量，u_avg是平均速度。
湍流强度小于1％时，可以认为湍流强度是比较低的，而在湍流强度大于10％时，则可以认为湍流强度是比较高的。
在来流为层流时，湍流强度可以用绕流物体的几何特征粗略地估算出来。
比如在模拟风洞试验的计算中，自由流的湍流强度可以用风洞的特征长度估计出来。
在现代的低湍流度风洞中，自由流的湍流强度通常低于%。
fluent初始化湍流动能和湍流耗散率
fluent初始化湍流动能和湍流耗散率摘要：一、引言二、fluent湍流模型的初始化三、湍流动能和湍流耗散率的定义四、fluent中湍流动能和湍流耗散率的设置五、总结正文：一、引言在流体力学中，湍流是一种普遍存在的现象，尤其在高速、高温的流体运动中。
为了更准确地模拟和预测湍流现象，fluent提供了多种湍流模型供用户选择。
在开始模拟前，我们需要对湍流动能和湍流耗散率进行初始化，以保证模型的准确性。
二、fluent湍流模型的初始化fluent中湍流模型的初始化主要包括以下几个步骤：1.选择湍流模型：fluent提供了k-ε、k-ω、SST、大涡模拟（LES）等多种湍流模型供用户选择。
2.设置湍流参数：根据所选湍流模型，设置相应的湍流参数，如湍流粘度、湍流耗散率等。
3.初始化湍流动能和湍流耗散率：根据所选湍流模型和湍流参数，对湍流动能和湍流耗散率进行初始化。
三、湍流动能和湍流耗散率的定义湍流动能和湍流耗散率是描述湍流特性的两个重要参数。
1.湍流动能：表示湍流运动的能量大小，通常用k表示。
湍流动能是湍流模型的基础参数之一，影响湍流模型的计算结果。
2.湍流耗散率：表示单位时间、单位体积内湍流动能的耗散量，通常用ε表示。
湍流耗散率是湍流模型中的一个重要参数，影响湍流模型的计算精度和计算速度。
四、fluent中湍流动能和湍流耗散率的设置在fluent中，我们可以通过以下步骤设置湍流动能和湍流耗散率：1.打开fluent软件，创建或打开一个模型。
2.在模型设置中，找到湍流模型的设置选项。
3.根据所选湍流模型，设置相应的湍流参数，如湍流粘度、湍流耗散率等。
4.完成设置后，点击“确定”按钮，保存设置并退出设置界面。
五、总结fluent初始化湍流动能和湍流耗散率是进行湍流模拟的重要步骤。
fluent udf 湍流参数
fluent udf 湍流参数湍流参数是湍流模拟中的一个重要概念，它决定了模拟结果的准确性和可靠性。
在Fluent UDF中，我们可以通过定义和调整湍流参数来改善模拟结果，使其更符合实际情况。
本文将介绍几个常见的湍流参数，并探讨它们对模拟结果的影响。
一、湍流模型选择在Fluent UDF中，我们可以选择不同的湍流模型来描述流体中的湍流运动。
常见的湍流模型有k-ε模型、k-ω模型、SST模型等。
每种模型都有其适用的领域和局限性。
在选择湍流模型时，需要根据具体应用场景和模拟目标来进行选择。
二、湍流粘度湍流粘度是一个重要的湍流参数，它决定了流体中湍流运动的强度。
在Fluent UDF中，我们可以通过调整湍流粘度来改变湍流模拟的结果。
一般情况下，湍流粘度越大，湍流运动越强烈；湍流粘度越小，湍流运动越弱。
三、湍流能量和湍流耗散率湍流能量和湍流耗散率是描述湍流运动特征的两个重要参数。
在Fluent UDF中，我们可以通过调整湍流能量和湍流耗散率来改变湍流模拟的结果。
湍流能量越大，湍流运动越强烈；湍流耗散率越大，湍流运动越剧烈。
四、湍流涡粘度比湍流涡粘度比是湍流模拟中的一个重要参数，它描述了湍流涡的扩散和耗散特性。
在Fluent UDF中，我们可以通过调整湍流涡粘度比来改变湍流模拟的结果。
湍流涡粘度比越大，湍流涡的扩散和耗散越强；湍流涡粘度比越小，湍流涡的扩散和耗散越弱。
五、湍流时间尺度湍流时间尺度是描述湍流运动时间特征的一个重要参数。
在Fluent UDF中，我们可以通过调整湍流时间尺度来改变湍流模拟的结果。
湍流时间尺度越小，湍流运动的时间特征越短暂；湍流时间尺度越大，湍流运动的时间特征越持久。
六、湍流强度湍流强度是描述湍流运动强度的一个重要参数。
在Fluent UDF中，我们可以通过调整湍流强度来改变湍流模拟的结果。
湍流强度越大，湍流运动越强烈；湍流强度越小，湍流运动越弱。
七、湍流长度尺度湍流长度尺度是描述湍流涡的空间特征的一个重要参数。
FLUENT 中湍流参数的定义
FLUENT 中湍流参数的定义2011-07-28 10:46:03| 分类：默认分类|举报|字号订阅流场的入口、出口和远场边界上，用户需要定义流场的湍流参数。
在FLUENT 中可以使用的湍流模型有很多种。
在使用各种湍流模型时，哪些变量需要设定，哪些不需要设定以及如何给定这些变量的具体数值，都是经常困扰用户的问题。
本小节只讨论在边界上设置均匀湍流参数的方法，湍流参数在边界上不是均匀分布的情况可以用型函数和UDF（用户自定义函数）来定义，具体方法请参见相关章节的叙述。
在大多数情况下，湍流是在入口后面一段距离经过转捩形成的，因此在边界上设置均匀湍流条件是一种可以接受的选择。
特别是在不知道湍流参量的分布规律时，在边界上采用均匀湍流条件可以简化模型的设置。
在设置边界条件时，首先应该定性地对流动进行分析，以便边界条件的设置不违背物理规律。
违背物理规律的参数设置往往导致错误的计算结果，甚至使计算发散而无法进行下去。
在Turbulence Specification Method （湍流定义方法）下拉列表中，可以简单地用一个常数来定义湍流参数，即通过给定湍流强度、湍流粘度比、水力直径或湍流特征长在边界上的值来定义流场边界上的湍流。
下面具体讨论这些湍流参数的含义，以保证在设置模型时不出现违背流动规律的错误设置：（1）湍流强度（Turbulence Intensity）湍流强度I的定义为：I=Sqrt(u’*u’+v’*v’+w’*w’)/u_avg( 8-1)上式中u',v' 和w' 是速度脉动量，u_avg是平均速度。
湍流强度小于1％时，可以认为湍流强度是比较低的，而在湍流强度大于10％时，则可以认为湍流强度是比较高的。
在来流为层流时，湍流强度可以用绕流物体的几何特征粗略地估算出来。
比如在模拟风洞试验的计算中，自由流的湍流强度可以用风洞的特征长度估计出来。
在现代的低湍流度风洞中，自由流的湍流强度通常低于0.05%。
fluent的空气湍流模型
fluent的空气湍流模型摘要：一、Fluent 空气湍流模型的概述二、湍流模型的类型及选择三、设置湍流模型的步骤四、影响湍流模型的因素五、如何获取较好的湍流模型模拟结果正文：Fluent 是一款广泛应用于流体动力学模拟的软件，其中的空气湍流模型是解决实际工程问题的重要工具。
本文将详细介绍Fluent 中的空气湍流模型，包括模型的类型、设置方法以及影响模拟结果的因素。
一、Fluent 空气湍流模型的概述在Fluent 中，空气湍流模型主要分为以下几种：k-ε 模型、k-ω 模型、SST 模型、大涡模拟（LES）等。
这些模型都是基于实际湍流特性进行数学建模，用以预测和分析流体流动中的复杂现象。
二、湍流模型的类型及选择在选择湍流模型时，需要考虑流动特性、雷诺数、模拟精度等因素。
例如，k-ε 模型适用于广泛范围内的流动问题，但其精度相对较低；而k-ω 模型则适用于高速、大涡占主导的流动场合。
具体模型的选择可根据实际情况和需求进行。
三、设置湍流模型的步骤在Fluent 中设置湍流模型主要包括以下步骤：1.打开Fluent 软件，创建或导入计算模型。
2.在“Meshing”模块中，设置网格类型、尺寸和数量。
3.在“Boundary Conditions”模块中，设置进口、出口、壁面等边界条件。
4.在“Turbulence”模块中，选择合适的湍流模型，并设置模型参数。
5.设置其他物理参数，如压力、速度、密度等。
6.进行模拟计算。
四、影响湍流模型的因素湍流模型的选择和设置不仅取决于流动特性，还受到以下因素的影响：1.雷诺数：雷诺数是判断流动状态的重要参数，不同湍流模型适用于不同雷诺数的流动场合。
2.边界条件：边界条件的设置会影响湍流模型的表现，尤其是壁面边界层的影响。
3.网格质量：网格质量直接影响数值模拟的准确性和稳定性，选用合适的网格类型和尺寸至关重要。
五、如何获取较好的湍流模型模拟结果1.选择合适的湍流模型：根据实际流动特性和需求，选择适合的湍流模型。
fluent 湍流模型
10.10.1 湍流选项湍流模型可用的不同的选项在10.3到10.7节已经详细的介绍过了。
这里将提供这些选项的用法。
如果你选择的是Spalart-Allmaras 模型，下列选项是有用的：● Vorticity-based production （基于漩涡的产出）● Strain/vorticity-based production （基于应变/漩涡的产出）● Viscous heating （对耦合算法总是激活）如果你选择的是标准的ε-k 模型或是可实行的ε-k 模型，下列选项是有用的： ● Viscous heating （对耦合算法总是激活）● Inclusion of buoyancy effects on ε（包含浮力对ε的影响）如果你选择的是RNG ε-k 模型，下列选项是有用的：● Differential viscosity model （微分粘性模型）● Swirl modification （涡动修正）● Viscous heating （对耦合算法总是激活）● Inclusion of buoyancy effects on ε（包含浮力对ε的影响）如果你选择的是标准的ω-k 模型，下列选项是有用的：● Transitional flows● Shear flow corrections● Viscous heating （对耦合算法总是激活）如果你选择的是剪切-应力传输ω-k 模型，下列选项是有用的：● Transitional flows （过渡流）● Viscous heating （对耦合算法总是激活）如果你选择的是雷诺应力模型（RSM ），下列选项是有用的：● Wall reflection effects on Reynolds stresses （壁面反射对雷诺应力的影响） ● Wall boundary conditions for the Reynolds stresses from the k equation （雷诺应力的壁面边界条件来自k 方程）● Quadratic pressure-strain model （二次的压力－应变模型）● Viscous heating （对耦合算法总是激活）● Inclusion of buoyancy effects on ε（包含浮力对ε的影响）如果你选择的是增强壁面处理（对ω-k 模型和雷诺应力模型可用），下列选项是有用的：● Pressure gradient effects （压力梯度的影响）● Thermal effects （热影响）如果你选择的是大漩涡模拟（LES ），下列选项是有用的：● Smagorinsky-Lilly model for the subgrid-scale viscosity● RNG model for the subgrid-scale viscosity● Viscous heating （对耦合算法总是激活）10．2．4 The Spalart-Allmaras 模型Spalart-Allmaras模型是设计用于航空领域的，主要是墙壁束缚流动。
fluent水力半径和湍动强度的设置
fluent水力半径和湍动强度的设置摘要：一、Fluent 水力半径和湍动强度的设置概述二、水力半径的设置方法及其对模拟结果的影响三、湍动强度的设置方法及其对模拟结果的影响四、总结正文：一、Fluent 水力半径和湍动强度的设置概述在Fluent 中，水力半径和湍动强度是两个重要的设置参数，对于模拟流体动力学问题有着重要的影响。
水力半径主要用于描述管道的粗糙程度，而湍动强度则用于描述流体运动的混乱程度。
这两个参数的设置会直接影响到模拟结果的准确性和可靠性。
二、水力半径的设置方法及其对模拟结果的影响水力半径的设置主要可以通过以下几个步骤完成：1.确定管道的长度和形状。
管道的长度和形状会影响到水力半径的计算。
一般来说，管道越长，水力半径越大；管道越粗，水力半径越大。
2.确定管道的粗糙程度。
管道的粗糙程度可以通过实验测量得到，也可以通过经验公式计算。
一般来说，管道越粗糙，水力半径越大。
3.输入Fluent 中的水力半径参数。
在Fluent 中，可以通过设定zone 属性来输入水力半径参数。
水力半径的设置对模拟结果的影响主要体现在以下几个方面：1.影响流体的摩擦阻力。
水力半径越大，流体的摩擦阻力越大，从而影响到流体的流速和压力分布。
2.影响热传递。
水力半径越大，热传递的效率越高，因为流体与管道壁之间的温差越小。
三、湍动强度的设置方法及其对模拟结果的影响湍动强度的设置主要可以通过以下几个步骤完成：1.确定湍流模型。
在Fluent 中，有多种湍流模型可供选择，如k-ε模型、k-ω模型等。
不同的湍流模型对湍动强度的计算方法不同，因此需要先确定湍流模型。
2.输入湍动强度的参数。
在Fluent 中，可以通过设定material 属性或者zone 属性来输入湍动强度参数。
3.调整湍动强度的边界条件。
在Fluent 中，可以通过设定boundary condition 来调整湍动强度的边界条件。
湍动强度的设置对模拟结果的影响主要体现在以下几个方面：1.影响流体的混合程度。
fluent水力半径和湍动强度的设置
在Fluent中，湍流强度和水力半径的设置主要涉及到湍流模型的选取和参数设定。
以下是具体步骤：
1. 湍流强度：可以通过Re数和湍流强度I来估算。
对于内部流，如果上游的气流没有充分发展，没有受到干扰，可以使用低湍流强度。
所谓低湍流强度是指湍流强度小于或等于1%，而大于10%的湍流强度被称为高湍流强度。
默认的湍流强度为5%。
我们设置这个参数时，可以先大概估算出工况的雷诺数，进而估算出湍流强度。
或者自己能够确定工况湍流水平的高低，然后大概给出湍流强度即可。
2. 水力半径：完全发展的管内流动中，湍流长度尺度l与管道的物理尺寸之间存在近似关系，其中L为特征长度，与管道尺寸相关，Cμ是k-e湍流模型的一个常数项系数，一般默认值为0.09。
此系数可在Fluent k-e湍流模型中查询到。
以上信息仅供参考，建议咨询专业人士获取更准确的信息。
FLUENT边界条件2—湍流设置
FLUENT边界条件（2）—湍流设置（fluent教材—fluent入门与进阶教程于勇第九章）Fluent：湍流指定方法（Turbulence Specification Method）2009-09-16 20:50使用Fluent时，对于velocity inlet边界，涉及到湍流指定方法（Turbulence Specification Method），其中一项是Intensity and Hydraulic Diameter （强度和水利直径），本文对其进行论述。
其下参数共两项，（1）是Turbulence Intensity，确定方法如下：I=0.16/Re_DH^0.125 (1)其中Re_DH是Hydraulic Diameter（水力直径）的意思，即式(1)中的雷诺数是以水力直径为特征长度求出的。
雷诺数Re_DH=u×DH/υ(2)u为流速，DH为水利直径，υ为运动粘度。
水利直径见（2）。
（2）水利直径水力直径是水力半径的二倍，水力半径是总流过流断面面积与湿周之比。
水力半径R＝A/X (3)其中，A为截面积（管子的截面积）＝流量/流速X为湿周(字面理解水流过各种形状管子外圈湿一周的周长)例如：方形管的水利半径R=ab/2(a+b)水利直径DH=2×R (4)举例如下：如果水流速度u=10m/s，圆形管路直径2cm，水的运动粘度为1×10-6 m2/s。
则DH=2×3.14*r^2/(2*3.14*r)=2*3.14*0.01^2/(3.14*0.02)=0.01 r为圆管半径Re_DH=u×DH/υ=10*0.02/10e-6=20000I=0.16/Re_DH^0.125=0.16/20000^0.125=0.0463971424017634≈5%水力半径：润湿周长横截面积=h r ， 水力直径：h h r 4D =对圆管而言，管道直径和水力直径是一回事。
fluent圆管仿真湍流参数设置
一、概述在工程领域中，流体力学仿真是一项十分重要的工作。
在进行流体力学仿真时，对于湍流参数的设置尤为关键。
本文主要讨论在使用fluent软件进行圆管湍流仿真时，如何设置参数以获得准确可靠的结果。
二、湍流模型的选择1. 简介在进行圆管湍流仿真时，首先需要选择合适的湍流模型。
目前常用的湍流模型包括k-ε模型、k-ω模型、SST湍流模型等。
每种湍流模型都有其适用的范围和局限性。
2. 参数设置在fluent软件中，进行湍流模型选择时需要考虑雷诺数、流场特性等因素。
根据具体情况选择合适的湍流模型，并对相应的参数进行设置。
三、网格划分1. 网格类型在进行圆管湍流仿真时，合适的网格划分也是至关重要的。
常见的网格类型包括结构化网格、非结构化网格等。
2. 网格密度对于圆管湍流仿真，网格的密度对结果的准确性有着直接的影响。
在fluent软件中，可以通过设置不同的网格密度来进行网格划分。
四、边界条件设置1. 入口边界条件对于圆管湍流仿真，入口边界条件的设置对结果有着重要的影响。
在fluent软件中，可以通过设定入口速度、湍流强度等参数来进行设置。
2. 出口边界条件出口边界条件的设置同样十分重要。
在fluent软件中，需要考虑出口压力、流速等参数。
五、求解器设置1. 时间步长在进行湍流仿真时，时间步长的选择对结果的精度有着很大的影响。
需要根据具体情况进行合理的设置。
2. 收敛准则在fluent软件中，收敛准则的设置也是必不可少的。
通过调整收敛准则的值来保证计算结果的准确性。
六、计算结果分析1. 流场分布通过fluent软件进行湍流仿真后，可以获得流场的分布情况。
需要对结果进行仔细的分析和比对。
2. 压降计算在圆管湍流仿真中，压降是一个重要的参数。
需要对压降进行精确的计算和分析。
七、总结圆管湍流仿真是流体力学仿真中的重要内容。
在使用fluent软件进行仿真时，正确的参数设置和合理的操作流程至关重要。
通过本文的讨论，相信读者对圆管湍流仿真的参数设置有了更清晰的认识，能够在实际工程中取得更好的仿真结果。
FLUENT 中湍流参数的定义
FLUENT 中湍流参数的定义2011-07-28 10:46:03| 分类：默认分类|举报|字号订阅流场的入口、出口和远场边界上，用户需要定义流场的湍流参数。
在FLUENT 中可以使用的湍流模型有很多种。
在使用各种湍流模型时，哪些变量需要设定，哪些不需要设定以及如何给定这些变量的具体数值，都是经常困扰用户的问题。
本小节只讨论在边界上设置均匀湍流参数的方法，湍流参数在边界上不是均匀分布的情况可以用型函数和UDF（用户自定义函数）来定义，具体方法请参见相关章节的叙述。
在大多数情况下，湍流是在入口后面一段距离经过转捩形成的，因此在边界上设置均匀湍流条件是一种可以接受的选择。
特别是在不知道湍流参量的分布规律时，在边界上采用均匀湍流条件可以简化模型的设置。
在设置边界条件时，首先应该定性地对流动进行分析，以便边界条件的设置不违背物理规律。
违背物理规律的参数设置往往导致错误的计算结果，甚至使计算发散而无法进行下去。
在Turbulence Specification Method （湍流定义方法）下拉列表中，可以简单地用一个常数来定义湍流参数，即通过给定湍流强度、湍流粘度比、水力直径或湍流特征长在边界上的值来定义流场边界上的湍流。
下面具体讨论这些湍流参数的含义，以保证在设置模型时不出现违背流动规律的错误设置：（1）湍流强度（Turbulence Intensity）湍流强度I的定义为：I=Sqrt(u’*u’+v’*v’+w’*w’)/u_avg(8-1)上式中u',v' 和w' 是速度脉动量，u_avg是平均速度。
湍流强度小于1％时，可以认为湍流强度是比较低的，而在湍流强度大于10％时，则可以认为湍流强度是比较高的。
在来流为层流时，湍流强度可以用绕流物体的几何特征粗略地估算出来。
比如在模拟风洞试验的计算中，自由流的湍流强度可以用风洞的特征长度估计出来。
在现代的低湍流度风洞中，自由流的湍流强度通常低于0.05%。
3.6.5在FLUENT中设定湍流模型[共3页]
![3.6.5在FLUENT中设定湍流模型[共3页]](https://img.taocdn.com/s3/m/a132459070fe910ef12d2af90242a8956becaa3c.png)
3.6.5在FLUENT中设定湍流模型[共3页]118精通CFD ⼯程仿真与案例实战—— FLUENT GAMBIT ICEM CFD Tecplot（第2版）表3-3⼏种壁⾯处理⽅法的⽐较优点缺点标准壁⾯函数法应⽤较多，计算量⼩，有较⾼的精度适合⾼雷诺数流动，对低雷诺数流动问题，有压⼒梯度、⾼度蒸腾和⼤的体积⼒、低雷诺数和⾼速三维流动问题不合适⾮平衡壁⾯函数法考虑了压⼒梯度，可以计算分离，再附着以及撞击问题对低雷诺数流动问题，有较强压⼒梯度、强体积⼒及强三维性问题不适合增强壁⾯处理不依赖壁⾯法则，对于复杂流动，特别是低雷诺数流动很适合要求⽹格密，因⽽要求计算机处理时间长，内存⼤ 3.6.5 在FLUENT 中设定湍流模型在FLUENT 中设定湍流模型的过程如下。
在Viscous Model 对话框中选中Inviscid （⽆粘）选项，FLUENT 会将流体视为没有黏性的理想流体，此时⽆须指定其他参数，如图3-8所⽰。
在Viscous Model 对话框中选中Laminar （层流）选项，FLUENT 会将流体视为层流流动求解，如图3-9所⽰。
若勾选Low-Pressure Boundary Slip 复选框，将考虑压⼒较低时速度和温度滑移边界条件对流动的影响，⽐如半导体制造装置的模拟。
图3-8 在Viscous 模型对话框中选择⽆粘流动图3-9 在Viscous 模型对话框中选择层流流动在Viscous Model 对话框（见图3-10）内选中Spalart-Allmaras (1 eqn)选项，即选择了Spalart-Allmaras 模型。
Spalart-Allmaras Production 选项组中的V orticity-Based （基于涡的⽣成）选项和Strain/V orticity-Based （基于应变/涡的⽣成）选项为两种计算变形张量的⽅法。
包含涡和应变张量能更精确地预测湍流涡旋的影响，因⽽⼀般结果更为可靠。
fluent初始化湍流动能和湍流耗散率
fluent初始化湍流动能和湍流耗散率（原创实用版）目录1.湍流动能和湍流耗散率的概念2.湍流动能和湍流耗散率的初始化设置方法3.湍流系数计算器的使用4.总结正文一、湍流动能和湍流耗散率的概念湍流动能和湍流耗散率是数值计算中湍流模型的两个重要参数。
湍流动能是湍流运动的能量，它的大小和分布影响到湍流模型的计算精度。
湍流耗散率则是描述湍流扩散能力的参数，它决定了湍流场中物质的扩散速度。
二、湍流动能和湍流耗散率的初始化设置方法在 Fluent 软件中，湍流动能和湍流耗散率的初始值需要根据实际工况进行设置。
一般来说，可以根据工况的速度、尺寸等因素进行计算。
有两种常用的计算方法：1.参考陶文铨院士的《数值传热学》一书中的计算方法，根据流速、特征长度等参数进行计算。
2.使用湍流系数计算器或 k-e 经验系数计算器，输入流速、特征长度等参数，可以得到湍流动能和耗散率的初始值推荐值。
三、湍流系数计算器的使用湍流系数计算器是一种便捷的工具，可以帮助用户快速计算湍流系数。
使用时，只需输入流速、特征长度等参数，即可得到湍流动能和耗散率的初始值推荐值。
例如，假设流速为 1m/s，特征长度为 1mm，则可以使用如下公式计算湍流系数：k = 0.47 * (1/1) ^ 0.25 * (1/1000) ^ 0.75其中，0.47 为陶文铨系数，(1/1) ^ 0.25 表示流速的平方根，(1/1000) ^ 0.75 表示特征长度的倒数。
计算得到湍流系数 k 后，可以根据 k 值和流速、特征长度等参数计算湍流动能和湍流耗散率的初始值。
四、总结在 Fluent 中初始化湍流动能和湍流耗散率时，需要根据实际工况进行设置。
可以通过计算或使用湍流系数计算器等工具得到合适的初始值。
fluent初始化湍流动能和湍流耗散率
fluent初始化湍流动能和湍流耗散率摘要：I.简介- 介绍Fluent软件- 介绍湍流动能和湍流耗散率的概念II.初始化湍流动能和湍流耗散率的重要性- 分析湍流动能和湍流耗散率在Fluent模拟中的作用- 讲解初始化参数对模拟结果的影响III.Fluent中湍流动能和湍流耗散率的设置- 详细说明在Fluent中如何设置湍流动能和湍流耗散率- 阐述设置参数的物理意义及计算方法IV.实例分析- 通过实例分析，讲解如何根据实际情况合理设置初始化参数- 比较不同设置下模拟结果的差异V.总结- 回顾初始化湍流动能和湍流耗散率的重要性- 总结文章中的主要观点和结论正文：Fluent是一款广泛应用于流体动力学模拟的软件，通过数值计算的方法，模拟流体在各种工程问题中的运动和变化。
在Fluent中，湍流动能和湍流耗散率是两个重要的参数，它们的合理设置能够提高模拟的准确性和稳定性。
湍流动能和湍流耗散率在Fluent模拟中的作用主要体现在：它们是湍流模型中的关键参数，影响湍流模型的计算结果；同时，它们还直接影响到流体的内部能量和湍流结构的分布。
因此，在Fluent模拟中，合理设置湍流动能和湍流耗散率是非常重要的。
在Fluent中，湍流动能和湍流耗散率的设置可以通过以下步骤完成：首先，在Fluent的“Define”界面中，选择“Turbulence”选项卡，然后分别设置“Ek”和“k”的值。
其中，“Ek”表示湍流动能，单位为m/s；“k”表示湍流耗散率，单位为m/s。
在设置参数时，需要根据实际问题的特点和模拟需求，合理选择参数值。
一般来说，可以通过查阅相关资料或者使用经验公式来确定参数的取值范围。
通过实例分析，我们可以更好地理解初始化参数对Fluent模拟结果的影响。
例如，在模拟一个流体流动问题时，如果我们设置的湍流动能和湍流耗散率参数不合理，可能会导致模拟结果出现较大误差。
通过调整这些参数，我们可以获得更准确的模拟结果。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
湍流边界条件设置在流场的入口、出口和远场边界上，用户需要定义流场的湍流参数。
在FLUENT 中可以使用的湍流模型有很多种。
在使用各种湍流模型时，哪些变量需要设定，哪些不需要设定以及如何给定这些变量的具体数值，都是经常困扰用户的问题。
本小节只讨论在边界上设置均匀湍流参数的方法，湍流参数在边界上不是均匀分布的情况可以用型函数和UDF（用户自定义函数）来定义，具体方法请参见相关章节的叙述。
在大多数情况下，湍流是在入口后面一段距离经过转捩形成的，因此在边界上设置均匀湍流条件是一种可以接受的选择。
特别是在不知道湍流参量的分布规律时，在边界上采用均匀湍流条件可以简化模型的设置。
在设置边界条件时，首先应该定性地对流动进行分析，以便边界条件的设置不违背物理规律。
违背物理规律的参数设置往往导致错误的计算结果，甚至使计算发散而无法进行下去。
在Turbulence Specification Method （湍流定义方法）下拉列表中，可以简单地用一个常数来定义湍流参数，即通过给定湍流强度、湍流粘度比、水力直径或湍流特征长在边界上的值来定义流场边界上的湍流。
下面具体讨论这些湍流参数的含义，以保证在设置模型时不出现违背流动规律的错误设置：（1）湍流强度（Turbulence Intensity）湍流强度I的定义为：I=Sqrt(u’*u’+v’*v’+w’*w’)/u_avg(8-1)上式中u',v' 和w' 是速度脉动量，u_avg是平均速度。
湍流强度小于1％时，可以认为湍流强度是比较低的，而在湍流强度大于10％时，则可以认为湍流强度是比较高的。
在来流为层流时，湍流强度可以用绕流物体的几何特征粗略地估算出来。
比如在模拟风洞试验的计算中，自由流的湍流强度可以用风洞的特征长度估计出来。
在现代的低湍流度风洞中，自由流的湍流强度通常低于%。
内流问题进口处的湍流强度取决于上游流动状态。
如果上游是没有充分发展的未受扰流动，则进口处可以使用低湍流强度。
如果上游是充分发展的湍流，则进口处湍流强度可以达到几个百分点。
如果管道中的流动是充分发展的湍流，则湍流强度可以用公式(8-2)计算得到，这个公式是从管流经验公式得到的：I=u’/u_avg=*Re_DH^(8-2)其中Re_DH是Hydraulic Diameter（水力直径）的意思，即式(8-2)中的雷诺数是以水力直径为特征长度求出的。
（2）湍流的长度尺度与水力直径湍流能量主要集中在大涡结构中，而湍流长度尺度l则是与大涡结构相关的物理量。
在充分发展的管流中，因为漩涡尺度不可能大于管道直径，所以l 是受到管道尺寸制约的几何量。
湍流长度尺度l 与管道物理尺寸L关系可以表示为：l=(8-3)式中的比例因子是充分发展管流中混合长的最大值，而L则是管道直径。
在管道截面不是圆形时，L可以取为管道的水力直径。
湍流的特征长取决于对湍流发展具有决定性影响的几何尺度。
在上面的讨论中，管道直径是决定湍流发展过程的唯一长度量。
如果在流动中还存在其他对流动影响更大的物体，比如在管道中存在一个障碍物，而障碍物对湍流的发生和发展过程起着重要的干扰作用。
在这种情况下，湍流特征长就应该取为障碍物的特征长度。
从上面的分析可知，虽然式(8-2)对于大多数管道流动是适用的，但并不是普遍适用的，在某些情况下可以进行调整。
在FLUENT 中选择特征长L或湍流长度尺度l的方法如下：1）对于充分发展的内流，可以用Intensity and Hydraulic Diameter（湍流强度与水力直径）方法定义湍流，其中湍流特征长度就是Hydraulic Diameter（水力直径）HD。
2）对于导向叶片或分流板下游的流场，可以用Intensity and Hydraulic Diameter（湍流强度与水力直径）定义湍流，并在Hydraulic Diameter（水力直径）中将导向叶片或分流板的开口部分的长度L 定义为特征长度。
3）如果进口处的流动为受到壁面限制且带有湍流边界层的流动，可以在Intensity and Length Scale 面板中用边界层厚度delta_99 通过公式l=*delta_99计算得到湍流长度尺度l。
最后在Turbulence Length Scale（湍流长度尺度）中输入l的值。
（3）湍流粘度比湍流粘度比mu_t/mu与湍流雷诺数Re_t成正比。
湍流雷诺数的定义为：Re_t=k*k /(Epsilon*nu)(8-4)在高雷诺数边界层、剪切层和充分发展的管道流动中的数值较大，其量级大约在100 到1000 之间。
而在大多数外部流动的自由流边界上，湍流粘度比的值很小。
在典型情况下，其值在1 到10 之间。
（4）推导湍流变量时采用的关系式为了从前面讲到的湍流强度I，湍流长度尺度L和湍流粘度比mu_t/mu 求出其他湍流变量，必须采用几个经验关系式。
在FLUENT 中使用的经验关系式主要包括下面几种：1）从湍流强度和长度尺度求出修正的湍流粘度在使用Spalart-Allmaras 模型时，可以用湍流强度I和长度尺度l求出修正的湍流粘度，具体公式如下：nu~= Sqrt*u_avg*I*L(8-5)在使用FLUENT 时，如果在Spalart-Allmaras 模型中选择Intensity and Hydraulic Diameter（湍流强度与水力直径）选项，则修正的湍流粘度就用这个公式求出。
其中的长度尺度l则用式(8-3)求出。
2）用湍流强度求出湍流动能湍流动能k与湍流强度I的关系如下：k=*(u_avg*I)^2(8-6)如果在使用FLUENT 时没有直接输入湍流动能k和湍流耗散率Epsilon的值，则可以使用Intensity and Hydraulic Diameter（湍流强度与水力直径）、Intensity and Length Scale （湍流强度与长度尺度）或Intensity and Viscosity Ratio（湍流强度与粘度比）等方法确定湍流动能，而确定的办法就是使用上面的公式(8-6)。
3）用长度尺度求出湍流耗散率长度尺度l与湍流耗散率之间的关系为：epsilon=C_mu^*k^l(8-7)式中C_mu为湍流模型中的一个经验常数，其值约等于。
在没有直接输入湍流动能k和湍流耗散率epsilon的情况下，可以用Intensity and Hydraulic Diameter（湍流强度与水力直径）或Intensity and Length Scale（湍流强度与长度尺度）等办法，利用上述公式确定湍流耗散率epsilon。
4）用湍流粘度比求出湍流耗散率湍流耗散率epsilon与湍流粘度比mu_t/mu 和湍流动能k的关系如下：epsilon=rho* C_mu*k^2/mu*(mu_t/mu)^-1 (8-8)式中C_mu为湍流模型中的一个经验常数，其值约等于。
在没有直接输入湍流动能k 和湍流耗散率epsilon的情况下，可以用Intensity andViscosityRatio（湍流强度与粘度比）定义湍流变量，实际上就是利用上述公式算出湍流耗散率epsilon。
5）湍流衰减过程中湍流耗散率的计算如果计算风洞阻尼网下游试验段中的流场，可以用下式求出湍流耗散率Epsilon：epsilon=delta_k*U_farfield/L_farfield(8-9)式中delta_k是湍流动能k 的衰减量，比如可以设为入口处k 值的10％，U_farfield是自由流速度，L_farfield是自由流区域的长度。
(8-9)式是对高雷诺数各向同性湍流衰减指数律的线性近似，其理论基础是衰减湍流中湍流动能k的方程：U*(partial derivative of U with respect to x)= -epsilon (8-10)如果用这种方法计算epsilon，还需要用（8－8）式检验计算结果，以保证湍流粘度比mu_t/mu 不过大。
虽然这种方法在FLUENT 中没有使用，但是可以用这种方法估算出自由流中的湍流耗散率epsilon，然后再用（8－6）式确定k，最后在Turbulence Specification Method （湍流定义方法）下拉列表中选择K and Epsilon（ k 和Epsilon ）并k和Epsilon的计算结果输入到相应的栏目中。
6）用长度尺度计算比耗散率如果知道湍流长度尺度l，可以用下式确定omega:omega=k^(C_mu^*l)(8-11)式中C_mu和长度尺度l的取法与前面段落中所述相同。
在使用Intensity and Hydraulic Diameter（湍流强度与水力直径）或Intensity and Length Scale（湍流强度与长度尺度）定义湍流时，FLUENT 用的就是这种方法。
7）用湍流粘度比计算比耗散率omega的值还可以用mu_t/mu 和k通过下式计算得出：omega=rho*k/mu*(mu_t/mu)^-1(8-12)在使用Intensity and Viscosity Ratio（湍流强度与粘度比）方法定义湍流时，FLUENT 就是使用上述关系式对湍流进行定义的。
8）用湍流动能定义雷诺应力分量在使用RSM（雷诺应力模型）时，如果用户没有在Reynolds-Stess Specification Method （雷诺应力定义方法）的Reynolds-Stress Components（雷诺应力分量）选项中直接定义雷诺应力的值，则雷诺应力的值将由给定的k值计算得出。
假定湍流是各向同性的，即：Average(u’_i*u’_j)=0(8-13)且：Average(u ’_aphla*u’_aphla)=2k/3(8-14)如果用户在Reynolds-Stress Specification Method（雷诺应力定义方法）下拉列表中选择K or Turbulence Intensity（k或湍流强度I）时，FLUENT就用这种方法定义湍流。
（5）在大涡模拟方法（LES）中定义进口湍流在使用速度进口条件时，可以将湍流强度作为对LES 进口速度场的扰动定义在边界条件中。
在实际计算中，根据湍流强度求出的随机扰动速度分量与速度场叠加后形成LES 算法边界上的、随机变化的速度场。
在FLUENT 中选择特征长L或湍流长度尺度l的方法如下：。