湖南科技大学信号处理习题库(2017)
数字信号处理习题及答案

==============================绪论==============================1. A/D 8bit 5V 00000000 0V 00000001 20mV 00000010 40mV 00011101 29mV==================第一章 时域离散时间信号与系统==================1.①写出图示序列的表达式答:3)1.5δ(n 2)2δ(n 1)δ(n 2δ(n)1)δ(n x(n)-+---+++= ②用δ(n) 表示y (n )={2,7,19,28,29,15}2. ①求下列周期)54sin()8sin()4()51cos()3()54sin()2()8sin()1(n n n n n ππππ-②判断下面的序列是否是周期的; 若是周期的, 确定其周期。
(1)A是常数 8ππn 73Acos x(n)⎪⎪⎭⎫ ⎝⎛-= (2))81(j e )(π-=n n x 解: (1) 因为ω=73π, 所以314π2=ω, 这是有理数, 因此是周期序列, 周期T =14。
(2) 因为ω=81, 所以ωπ2=16π, 这是无理数, 因此是非周期序列。
③序列)Acos(nw x(n)0ϕ+=是周期序列的条件是是有理数2π/w 0。
3.加法乘法序列{2,3,2,1}与序列{2,3,5,2,1}相加为__{4,6,7,3,1}__,相乘为___{4,9,10,2} 。
移位翻转:①已知x(n)波形,画出x(-n)的波形图。
②尺度变换:已知x(n)波形,画出x(2n)及x(n/2)波形图。
卷积和:①h(n)*求x(n),其他02n 0n 3,h(n)其他03n 0n/2设x(n) 例、⎩⎨⎧≤≤-=⎩⎨⎧≤≤=}23,4,7,4,23{0,h(n)*答案:x(n)=②已知x (n )={1,2,4,3},h (n )={2,3,5}, 求y (n )=x (n )*h (n )x (m )={1,2,4,3},h (m )={2,3,5},则h (-m )={5,3,2}(Step1:翻转)解得y (n )={2,7,19,28,29,15}③(n)x *(n)x 3),求x(n)u(n u(n)x 2),2δ(n 1)3δ(n δ(n)2、已知x 2121=--=-+-+=}{1,4,6,5,2答案:x(n)=4. 如果输入信号为,求下述系统的输出信号。
信号分析与处理技术习题册

第一章 时域离散信号与离散系统1-1 给定信号:⎪⎩⎪⎨⎧≤≤-≤≤-+=其它,040,614,52)(n n n n x(1) 画出x(n)序列的波形,标上各序列值;(2) 试用延迟的单位脉冲序列及其加权和表示x(n)序列; (3) 令x 1(n)=2x(n-2),试画出x 1(n)波形; (4) 令x 2(n)=2x(n+2),试画出x 2(n)波形; (5) 令x 3(n)=x(2-n),试画出x 3(n)波形。
1-2 有序列如下图所示请计算x e (n)=[x(n)+x(-n)]/2,并画出波形。
1-3 试判断 (1)∑-∞==nm m x n y )()((2)y(n)=[x(n)]2 (3))792sin()()(ππ+=n n x n y是否线性系统,并判断(2)、(3)是否移不变系统。
1-4设线性时不变系统的单位脉冲响应h(n)和输入序列x(n)如图所示,要求画出y(n)的波形。
1-5 已知线性移不变系统的输入为x(n)=δ(n)-δ(n-2),系统的单位抽样响应为h(n)=0.5n R3(n),试求系统的输出y(n)1-6 设有一系统,其输入输出关系由以下差分方程确定:y(n)-0.5y(n-1)=x(n)+0.5x(n-1)设系统是因果性的。
(1)利用递推法求系统的单位抽样响应;(2)由(1)的结果,利用卷积和求输入x(n)=e jwn u(n)的响应。
第二章时域离散信号与系统的频域分析2-1 试求如下序列的傅立叶变换:(1)x1(n)=R5(n)(2)x2(n)=u(n+3)-u(n-4)2-2 设⎩⎨⎧==其它,01,0,1)(n n x ,将x(n)以4为周期进行周期延拓,形成周期序列~)(n x ,画出x(n)和~)(n x 的波形,求出~)(n x 的离散傅立叶级数~)(k X 和傅立叶变换。
2-3 设如图所示的序列x(n)的FT 用X(e jw )表示,不直接求出X(e jw ),确定并画出傅立叶变换实部Re[X(e jw )]的时间序列x e (n)2-4 求序列-2-n u(-n-1)的Z 变换及收敛域:2-5 已知)(2||5.02523)(211n x z zzz z X 对应的原序列,求收敛<<+--=---2-6 分别用长除法、部分分式法求以下X(z)的反变换:21||,411311)(21>--=--z zz z X2-7 用Z 变换法解下列差分方程:y(n)-0.9y(n-1)=0.05u(n),y(-1)=1,y(n)=0,n<-12-8 研究一个输入为x(n)和输出为y(n)的时域线性离散移不变系统,已知它满足)()1()(310)1(n x n y n y n y =++--,并已知系统是稳定的,试求其单位抽样响应。
数字信号处理实验答案湖南大学经典

实验二 DFT 和FFT一、实验目的1)认真复习周期序列 DFS、有限长序列DFT 的概念、旋转因子的定义、以及DFS 和DFT的性质等有关内容;复习基2-FFT 的基本算法,混合基-FFT 的基本算法、Chirp-Z 变换的算法等快速傅立叶变换的方法。
2)掌握有限长序列的循环移位、循环卷积的方法,对序列共轭对称性的含义和相关内容加深理解和掌握,掌握利用DFT 分析序列的频谱特性的基本方法。
3)掌握 FFT 算法的基本原理和方法、Chirp-Z 变换的基本原理和方法,掌握利用FFT 分析序列的频谱特性的方法。
4)熟悉利用 MATLAB 进行序列的DFT、FFT 的分析方法。
二、实验内容1)设周期序列( ) { xn =……,0,1,2,3,0,1,2,3,0,1,2,3,……},求该序列的离散傅立叶级数X (k) = DFS[x(n)],并画出DFS 的幅度特性。
主程序:clc;N=4;n=0:N-1;k=0:N-1;xn=[0 1 2 3];Xk=xn*exp(-j*2*pi/N).^(n'*k);stem(k, abs(Xk));xlabel('k');gtext('|X(k)|');分析:由定义可知,对于周期序列,根据离散傅里叶级数公式即可求出,此实验中显示了一个周期的傅里叶级数。
2)设周期方波序列为其中 N 为基波周期,L/N 是占空比。
(1) 用L 和N求| X(k) |的表达式;(2) 当L 和N 分别为:L=5,N=20;L=5,N=40;L=5,N=60 以及L=7,N=60 时画出DFS 的幅度谱;(3) 对以上结果进行讨论,总结其特点和规律。
主程序:L=5,N=20时clc;N=20;xn=[ones(1,5),zeros(1,15)];xn=[xn,xn,xn];n=0:3*N-1;k=0:3*N-1;Xk=xn*exp(-j*2*pi/N).^(n'*k)stem(k,abs(Xk));xlabel('k');title('L=5,N=20时DFS幅度谱');结果:(修改代码中的L和N(x(n)),可以得到其他占空比时DFS的幅度谱)分析:由四组图对比可知,N越大,其频域抽样间隔越小,N为频域的重复周期。
信号处理技术_习题
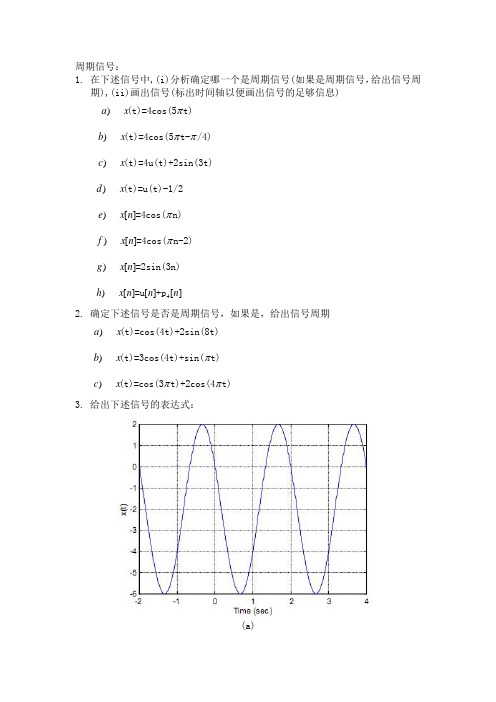
周期信号:1. 在下述信号中,(i)分析确定哪一个是周期信号(如果是周期信号,给出信号周期),(ii)画出信号(标出时间轴以便画出信号的足够信息))a x π(t)=4cos(5t) )b x ππ(t)=4cos(5t-/4) )c x (t)=4u(t)+2sin(3t) )d x (t)=u(t)-1/2 )[]e x n π=4cos(n) )[]f x n π=4cos(n-2) )[]g x n =2sin(3n)4)[][][]h x n n n =u +p2. 确定下述信号是否是周期信号,如果是,给出信号周期)a x (t)=cos(4t)+2sin(8t) )b x π(t)=3cos(4t)+sin(t) )c x ππ(t)=cos(3t)+2cos(4t)3. 给出下述信号的表达式:(a)(b)a) 给出x (t)的表达式b) 画出dx/dt4. 下述信号是否为周期信号?如果是,给出信号周期。
)a x ππ(t)=4cos(3t+/4)+u(t) )[]b x n ππ=4cos(0.5n+/4))c x πππ(t)=4cos(3t+/4)+2cos(4t) )[]20d x n n =12cos()111)e x (t)=cos(2Wt)+cos(3Wt) 这里W 为特定频率 f )x ππππ(t)=4cos(3t+/2)+2cos(8t+/2) )g x πππ(t)=2cos(3t+/2)+4cos(10t-/2) )[]2(8)h x n n π=10cos() )[]8i x n n =10cos()画出信号:1. 画出以下信号a) 04()2if -4323if t x t t t t if t <-⎧⎪=+≤<⎨⎪-≥⎩b) ()(1)y t x t =-,这里x(t)为a)中所定义c) 02[]242444if n x n n ifn n if n <⎧⎪=-≤<⎨⎪-≥⎩d) [][1]y n x n =+,这里x[n]为c)中所定义2.用MATLAB 编码画出问题1中的信号。
数字信号处理期末试卷(含答案)

一、填空题(每题2分,共10题)1、 1、 对模拟信号(一维信号,是时间的函数)进行采样后,就是 信号,再进行幅度量化后就是 信号。
2、 2、 )()]([ωj e X n x FT =,用)(n x 求出)](Re[ωj e X 对应的序列为 。
3、序列)(n x 的N 点DFT 是)(n x 的Z 变换在 的N 点等间隔采样。
4、)()(5241n R x n R x ==,只有当循环卷积长度L 时,二者的循环卷积等于线性卷积。
5、用来计算N =16点DFT ,直接计算需要_________ 次复乘法,采用基2FFT 算法,需要________ 次复乘法,运算效率为__ _ 。
6、FFT 利用 来减少运算量。
7、数字信号处理的三种基本运算是: 。
8、FIR 滤波器的单位取样响应)(n h 是圆周偶对称的,N=6, 3)3()2(2)4()1(5.1)5()0(======h h h h h h ,其幅度特性有什么特性? ,相位有何特性? 。
9、数字滤波网络系统函数为∑=--=NK kk z a z H 111)(,该网络中共有 条反馈支路。
10、用脉冲响应不变法将)(s H a 转换为)(Z H ,若)(s H a 只有单极点k s ,则系统)(Z H 稳定的条件是 (取s T 1.0=)。
二、选择题(每题3分,共6题)1、 1、 )63()(π-=n j en x ,该序列是 。
A.非周期序列 B.周期6π=NC.周期π6=ND. 周期π2=N2、 2、 序列)1()(---=n u a n x n,则)(Z X 的收敛域为 。
A.a Z <B.a Z ≤C.a Z >D.a Z ≥3、 3、 对)70()(≤≤n n x 和)190()(≤≤n n y 分别作20点DFT ,得)(k X 和)(k Y ,19,1,0),()()( =⋅=k k Y k X k F ,19,1,0)],([)( ==n k F IDFT n f ,n 在 范围内时,)(n f 是)(n x 和)(n y 的线性卷积。
数字信号处理习题集

一、单项选择题1.数字信号的特征是( )A.时间离散、幅值连续B.时间离散、幅值量化C.时间连续、幅值量化D.时间连续、幅值连续2.若一线性移不变系统当输入为x(n)=δ(n)时,输出为y(n)=R 2(n),则当输入为u(n)-u(n-2)时,输出为( )A.R 2(n)-R 2(n-2)B.R 2(n)+R 2(n-2)C.R 2(n)-R 2(n-1)D.R 2(n)+R 2(n-1)3.下列序列中z 变换收敛域包括|z|=∞的是( )A.u(n+1)-u(n)B.u(n)-u(n-1)C.u(n)-u(n+1)D.u(n)+u(n+1)4.下列对离散傅里叶变换(DFT )的性质论述中错误的是( )A.DFT 是一种线性变换B.DFT 具有隐含周期性C.DFT 可以看作是序列z 变换在单位圆上的抽样D.利用DFT 可以对连续信号频谱进行精确分析5.若序列的长度为M ,要能够由频域抽样信号X(k)恢复原序列,而不发生时域混叠现象,则频域抽样点数N 需满足的条件是( )A.N ≥MB.N ≤MC.N ≥M/2D.N ≤M/26.基-2 FFT 算法的基本运算单元为( )A.蝶形运算B.卷积运算C.相关运算D.延时运算7.以下对有限长单位冲激响应(FIR )滤波器特点的论述中错误的是( )A.FIR 滤波器容易设计成线性相位特性B.FIR 滤波器的单位冲激抽样响应h(n)在有限个n 值处不为零C.系统函数H(z)的极点都在z=0处D.实现结构只能是非递归结构8.下列结构中不属于IIR 滤波器基本结构的是( )A.直接型B.级联型C.并联型D.频率抽样型9.下列关于用冲激响应不变法设计IIR 滤波器的说法中错误的是( )A.数字频率与模拟频率之间呈线性关系B.能将稳定的模拟滤波器映射为一个稳定的数字滤波器C.使用的变换是s 平面到z 平面的多值映射D.可以用于设计低通、高通和带阻等各类滤波器10.离散时间序列x (n )=cos(n 73π-8π)的周期是( ) A.7 B.14/3 C.14 D.非周期11.下列系统(其中y(n)是输出序列,x(n)是输入序列)中______属于线性系统。
(完整版)数字信号处理题库(附答案).doc

数字信号处理复习题一、选择题1、某系统 y(n) g( n) x(n), g( n) 有界,则该系统(A )。
A. 因果稳定B.非因果稳定C.因果不稳定D. 非因果不稳定2、一个离散系统(D)。
A. 若因果必稳定B. 若稳定必因果C.因果与稳定有关D. 因果与稳定无关3、某系统 y(n) nx(n), 则该系统(A )。
A. 线性时变B. 线性非时变C. 非线性非时变D. 非线性时变 4.因果稳定系统的系统函数 H ( z) 的收敛域是( D)。
A. z 0.9B. z 1.1C. z1.1D.z 0.95. x 1 (n) 3sin(0.5 n) 的周期( A)。
A.4B.3C.2D.16.某系统的单位脉冲响应h(n) ( 1) nu(n), 则该系统(C )。
2A. 因果不稳定B.非因果稳定C.因果稳定D. 非因果不稳定7.某系统 y(n) x(n) 5 ,则该系统(B )。
A. 因果稳定B.非因果稳定C.因果不稳定D. 非因果不稳定8.序列 x(n) a n u( n 1), 在 X ( z) 的收敛域为( A)。
A. z aB. zaC.z a D. z a9.序列 x(n)(1) nu(n) ( 1)n u( n 1), 则 X (z) 的收敛域为( D )。
1 3 12 1 1 1B. zC. z zA. z3 2 D. 223 10.关于序列 x( n) 的 DTFT X (ej) ,下列说法正确的是(C )。
A. 非周期连续函数B.非周期离散函数C.周期连续函数,周期为 2D.周期离散函数,周期为211.以下序列中( D )的周期为 5。
A. x( n)cos( 3n)B. x(n)sin( 3 n)5 588C. x( n) e j ( 2n)x(n)j (2n) 58D. e 5812. x(n)ej (n)3 6,该序列是( A )。
A. 非周期序列B.周期 N6C.周期 N6D.周期N 213. ((4)) 4 ________ 。
数字信号处理习题库选择题附加答案

数字信号处理习题库选择题附加答案第1章选择题1.信号通常是时间的函数,数字信号的主要特征是:信号幅度取;时间取 B 。
A.离散值;连续值B.离散值;离散值C.连续值;离散值D.连续值;连续值2.数字信号的特征是( B )A .时间离散、幅值连续B .时间离散、幅值量化C .时间连续、幅值量化D .时间连续、幅值连续3.下列序列中属周期序列的为( D )A .x(n) = δ(n)B .x(n) = u(n)C .x(n) = R 4(n)D .x(n) = 14.序列x(n)=sinn 311的周期为( D ) A .3B .6C .11D .∞ 5. 离散时间序列x (n )=cos(n 73π-8π)的周期是 ( C )A. 7B. 14/3C. 14D. ⾮周期6.以下序列中( D )的周期为5。
A .)853cos()(ππ+=n n x B. )853sin()(ππ+=n n x C. )852()(π+=n j e n x D. )852()(ππ+=n j e n x 7.下列四个离散信号中,是周期信号的是( C )。
A .sin100n B. n j e 2C. n n ππ30sin cos +D. n j n j e e5431π- 8.以下序列中 D 的周期为5。
A.)853cos()(π+=n n x B.)853sin()(π+=n n x C.)852()(π+=n j e n x D.)852()(ππ+=n j en x 9.离散时间序列x (n )=cos+353ππn 的周期是( C ) A.5B.10/3C.10D.⾮周期10.离散时间序列x(n)=sin (5n 31π+)的周期是( D ) A.3B.6C.6πD.⾮周期 11.序列x (n )=cos ?n 5π3的周期为( C )A.3B.5C.10D.∞12.下列关系正确的为( C ) A .u(n)=∑=nk 0δ (n)B .u(n)=∑∞=0k δ (n)C .u(n)=∑-∞=n k δ (n)D .u(n)=∞-∞=k δ (n)13.设系统的单位抽样响应为h(n),则系统因果的充要条件为( C )A .当n>0时,h(n)=0B .当n>0时,h(n)≠0C .当n<0时,h(n)=0D .当n<0时,h(n)≠014.下列系统(其中y(n)是输出序列,x(n)是输⼊序列)中______属于线性系统。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 1章
习
题
二、判断题(用√或×表示)
1、信号的时域描述与频域描述包含相同的信息量。(
2、非周期信号的频谱一定是连续的。( ) ) )
)
3、具有离散频谱的信号一定是周期信号。 (
4、 单位脉冲函数的函数值等于无穷大,强度为1。( 5、若 x (t ) 的频谱为X ( f ) ,则 X (t ) 的频谱为 X ( f ) 。(
B. D.
x(t 0 )
x(t t0 )
第 1章
习
题
t 5、 若 x(t ) 的频谱为 X ( f ) ,则 x( a ) 的频谱 为 。(a为常数) ( D ) 1 f f X( ) A. aX ( ) B. a a a 1 f C. X ( ) D. aX (af ) a a 6、 若x(t ) 的频谱为 X ( f ) ,则的 (t ) * x(t ) 的 频谱为 B
二、判断对错题(用√或×表示)
1、传递函数相同的各种装置,其频率响应函数与脉冲响应 函数亦相同。( )
2、幅频特性是指系统输出与输入信号的幅值比与频率的关
系。( )
3、相频特性是指系统输出与输入信号的相位比与频率的关 系。 ( )
4、各系统串联时,总的相频特性等于各组成系统相频特性 的乘积。( )
)
第 1章 三、单选题
习
题
1、描述周期信号的数学工具是( B )
A.相关函数
B.傅氏级数 C.拉氏级数 D.傅氏变化
2、已知 x(t ) 10sin t , (t ) 为单位冲击函数,则积分
x(t ) (t 2 )dt 的函数值为( C) A. 5 B. 0 C. 10 D. 任意值
H ( )
1 1 j 0.005
A( )
1 1 (0.005 )
2
( ) arctan( 0.005 )
令,y1 (t ) Y1 cos(10t 1 )
y2 (t ) Y2 cos(100t 2 )
Y1 1 A(1 ) A(10) Y1 0.499 0.5 1 (0.005 10)2
试判断哪一个齿轮轴存在质量不平衡问题?
第 1章
习
题
分析:转子不平衡的典型故障特征为工频突出。 齿数为40的大齿轮为输入轴,转频600r/min,即工 频为10Hz;根据相互啮合的齿轮转速与齿数成反 比的关系,可知齿数为20的中齿轮,工频为20Hz; 齿数为10的小齿轮,工频为40Hz。由频谱图可知, 40Hz的频率成分最为突出,故小齿轮轴存在转子 不平衡的问题。
6、什么是各态历经随机过程? 答:若平稳随机过程任一样本函数的时间平均统计特性等于 该过程的集合平均统计特性,则称该 随机过程是各态历经 的(遍历性)。
第 1章
习
题
思考题:图示为一存在质量不平衡的 齿轮传动系统,大、中、小齿轮的齿 数分别为40,20,10。大齿轮为输入轴, 转速为600r/min,若在齿轮箱机壳上 测得的振动信号频谱如下所示:
4、周期信号频谱的特点是 离散性、谐波性、收敛性 ; 瞬变非周期信号频谱的特点是 连续性 。
5、信号的有效值又称为 均方根值 ,它表示信号的 平均能量 。
6、绘制周期信号 x (t ) 的单边频谱图,依据的数学表达式是 傅里叶级数的三角函数展式 ,双边频谱图的依据数学表
达式是 傅里叶级数的复指数函数展式。
3、设某力传感器可作为二阶系统处理。已知传感器的固有 频率为800Hz,阻尼比为0.14,问使用该传感器测频率 为400Hz正弦力时,其幅值比和相位差各是多少?若将
阻尼比改为0.7,则幅值比和相位差作何变化?
按题意,当 =400 2,n 800 2 时,
四、分析计算题 1、某测试装置为一线性系统,其传递函数为:
1 H ( s) 0.005s 1
求其对周期信号 x(t ) 0.5cos10t 0.2cos(100t 45) 的稳态响应y(t)。
线性系统具有叠加性和频率保持特性。
解:已知 则: 即:
H ( s)
1 1 0.005s
第 1章 五、简答题
习
题
1、简要说明信号的分类及描述方法。
第 1章
习
题
2、什么是信号的时域描述和频域描述?两者有何区别? 解:直接观测或记录到的信号,一般是以时间为独立变量的, 称其为时域描述。信号时域描述能反映信号幅值随时间的 变化关系,而不能明确信号的频率组成关系。把信号的时 域描述通过适当方法可变成信号的频域描述。
5、频率保持特性指的是任何测试装置输出信号的频率总等 于输入信号的频率。( ) 6、一阶系统时间常数τ越小越好。( 7、二阶系统阻尼比 越小越好。( ) )
8、测试装置进行不失真测试的条件是其幅频特性为常数, 相频特性为零( )
三、单项选择题
1、传感器的静态特性中,单位输出所需要的输入量,称为 (C ) A.线性度 B.灵敏度 C.分辨力 D.回程误差
2、关于传递函数的特点,下列叙述正确的是。( B )
A.与具体的物理结构有关 B.反映系统的传输和响应特性
C.与输入有关
D.不能反映了测试系统的动态特性
3、线性度表示静态标定曲线 A.接近真值 C.正反行程的不重合
B
的程度。
B.偏离理想曲线 D. 输出比输入
4、测试装置的频响函数是装置动态特性在
A.幅值域 B.时域 C.频率域
5、描述测试装置动态特性的数学模型有
传递函数H(s)
、
脉冲响应函数 h(t) 频率响应函数H(ω) 、 述。
6、输入、输出,装置的脉冲响应函数,它们三者间 的关系是 y(t)=x(t)*h(t) 。 7、测试装置在稳态下,其输出信号的变化量与其输 入信号的变化量之比值,称为 灵敏度 。 8、相同测试条件下,当输入量由小增大和由大减小 时,所得输出量最大差值称为 回程误差 。 9、一阶系统的主要特征参数有 时间常数τ 。 10.二阶系统的主要特征参数有固有频率 n和阻尼比 。
课后习题1-5
已知信号如图所示:
cos 0 t x( t ) 0
求其傅立叶变换。
tT tT
解:x(t ) w(t ) cos(2 f 0t )
w(t)为矩形脉冲信号
W ( f ) 2T sinc(2 Tf )
1 j 2 f 0t cos(2 f 0t ) e e j 2 f 0t 2 1 1 j 2 f 0t x(t ) w(t )e w(t )e j 2 f0t 2 2
1 1 0 (1 ) arctan(0.005 10) 2.86。
Y2 1 A(2 ) A(100) Y2 0.179 0.2 1 (0.005 100) 2
2 -(-45。 ) arctan(0.005 100) 2 71.57。
第 1章
习
j 2 ft0
题
4、什么是时移特性?它反映了什么规律?
x(t t0 ) X ( f )e
信号在时域中平移,频域中幅频谱不变,相频谱(相位) 会变化。 5、简述单位脉冲函数的采样性质和卷积性质。
如果 函数与某一连续函数f (t )相乘,显然其乘积仅在 t 0处为f (0) (t ), 其余各点(t 0)之乘积均为0。 函数x(t )和 函数的卷积结果,就是在 函数的坐标位置 上简单地将( x t)重新作图。
2
当系统做200Hz信号测试时,有:
=1=1-
1 1 ( ) 2 1
2 1 (2 200 5.23 104) =16.4%
() =-arctan(-2 f )=-arctan(2 3.14 200 5.23 104 )
=-33.4
四、分析计算题
• 绪论作业: 简述测试系统的组成及应用。
第一节 信号的分类与描述
第二节 周期信号与离散频谱
第三节 瞬变非周期信号与连续频谱 第四节 随机信号
重点:周期信号傅里叶级数展开分析方法;非周期信号傅 里叶变换分析方法;二者的频谱特征的区别和联系;
第 1章 一、填空题
习
题
1、信号一般分为 确定性信号 和 随机信号 两类。 2、信号的描述方法常用的有 时域描述 和 频域描述 两种。 3、周期信号用 傅里叶级数 展开到频域描述; 瞬变非周期信号用 傅里叶变换 展开到频域描述。
3、什么是时间尺度改变特性?其对测试工作有何意义? 解:时域压缩,频域扩展,幅值降低;时域扩展,频域压缩, 幅值升高。时域压缩,提高了处理信号的效率。但频域 信号频带加宽,对仪器设备通频带的要求也提高了。反 过来,时域扩展,处理信号的效率会下降,但频域信号 频带变窄,对仪器设备通频带的要求也降低了。
C 中的描述。
D.复数域
5、时间函数为的一阶装置,输入频率为 号,则其输出与输入间的相位差是 B A. 0 º B. -45º C.-90º
1 = 的正弦信 。
D.-180º
6、测试装置的脉冲响应函数与它的频率响应函数间的关系 A 是 。 A.傅氏变换对 B. 卷积 C.拉氏变换对 D.微分。
x(t) 1
-T
0
T
t
-1
w(t) 1
-T
0 图1-26 被截断的余弦函数
T
t
根据频移特性和叠加性得:
1 1 X ( f ) W ( f f0 ) W ( f f0 ) 2 2 T sinc[2 T ( f f 0 )] T sinc[2 T ( f f 0 )]
A. ( f )
B. X ( f )
C. ( f ) * X ( f )
D. X (0)
第 1章 四、分析计算题
