位置随动系统建模与分析--自控课设教材
位置随动系统的分析与设计
位置随动系统的分析与设计1.系统需求分析-实时追踪目标位置：系统需要能够实时获取目标的位置信息，可以通过各种传感器如GPS、惯性测量单元等进行实现。
-实时控制移动对象：系统需要能够根据目标位置进行实时控制移动对象，例如调整机器人的航向、调整无人驾驶汽车的速度等。
-高精度定位：系统需要能够实现高精度的目标定位，以保证位置随动控制的准确性。
-快速响应：系统需要能够快速响应目标位置的变化，并及时调整移动对象的控制策略，以保持目标与移动对象之间的距离恒定。
-可靠性与鲁棒性：系统需要具备高可靠性和鲁棒性，能够应对传感器误差、环境变化等因素的影响。
2.系统设计-目标追踪模块：该模块用于实时获取目标的位置信息。
可以采用多种传感器，如GPS、激光测距仪等。
目标追踪模块需要具备高精度定位和高响应速度的特点，以确保位置信息的准确性和实时性。
-控制算法模块：该模块根据目标位置信息计算出移动对象的控制策略。
控制算法可以根据实际需求选择不同的模型，例如PID控制、模糊控制、最优控制等。
控制算法需要具备良好的控制性能和鲁棒性，以保证位置随动控制的稳定性和可靠性。
-控制器模块：该模块负责将控制策略转化为实际的控制指令，并对移动对象进行实时控制。
控制器可以采用硬件控制器或软件控制器的方式实现，也可以使用现有的控制器模块或定制开发控制器模块。
-反馈系统：该系统用于实时获取移动对象的状态信息，如位置、速度、加速度等。
反馈系统可以采用传感器进行实现，例如编码器、惯性测量单元等。
反馈系统可以为控制算法提供实时的状态反馈信息，以便对控制指令进行调整和优化。
3.系统实现位置随动系统的实现需要进行系统建模、算法设计和软硬件集成等工作。
在系统建模过程中，可以使用系统分析和系统设计方法，如UML建模、数据流图、状态转换图等，对系统进行建模和分析。
在算法设计过程中，可以根据系统需求和设计目标选择合适的算法，并进行仿真验证和优化调整。
在软硬件集成过程中，可以使用现有的软硬件平台，如嵌入式系统、机器人操作系统等，将设计好的算法和控制器模块集成到实际的系统中，并进行测试和调试。
《自动控制原理》课程设计位置随动系统的超前校正
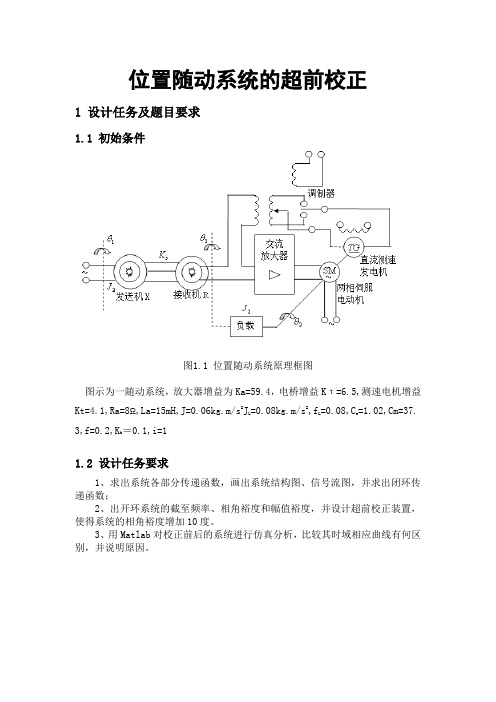
位置随动系统的超前校正1 设计任务及题目要求1.1 初始条件图1.1 位置随动系统原理框图图示为一随动系统，放大器增益为Ka=59.4，电桥增益Kτ=6.5,测速电机增益Kt=4.1,Ra=8Ω,La=15mH,J=0.06kg.m/s2JL =0.08kg.m/s2,fL=0.08,Ce=1.02,Cm=37.3,f=0.2,Kb＝0.1,i=11.2 设计任务要求1、求出系统各部分传递函数，画出系统结构图、信号流图，并求出闭环传递函数；2、出开环系统的截至频率、相角裕度和幅值裕度，并设计超前校正装置，使得系统的相角裕度增加10度。
3、用Matlab对校正前后的系统进行仿真分析，比较其时域相应曲线有何区别，并说明原因。
2 位置随动系统原理2.1 位置随动系统工作原理工作原理：该系统为一自整角机位置随动系统，用一对自整角机作为位置检测元件，并形成比较电路。
发送自整角机的转自与给定轴相连；接收自整角机的转子与负载轴（从动轴）相连。
TX 与TR 组成角差测量线路。
若发送自整角机的转子离开平衡位置转过一个角度1θ，则在接收自整角机转子的单相绕组上将感应出一个偏差电压e u ，它是一个振幅为em u 、频率与发送自整角机激励频率相同的交流调制电压，即sin e em u u t ω=⋅在一定范围内，em u 正比于12θθ-，即12[]em e u k θθ=-，所以可得12[]sin e e u k t θθω=-这就是随动系统中接收自整角机所产生的偏差电压的表达式，它是一个振幅随偏差（12θθ-）的改变而变化的交流电压。
因此，e u 经过交流放大器放大，放大后的交流信号作用在两相伺服电动机两端。
电动机带动负载和接收自整角机的转子旋转，实现12θθ=，以达到跟随的目的。
为了使电动机转速恒定、平稳，引入了测速负反馈。
系统的被控对象是负载轴，被控量是负载轴转角2θ，电动机施执行机构，功率放大器起信号放大作用，调制器负责将交流电调制为直流电供给直流测速发电机工作电压，测速发电机是检测反馈元件。
自动控制原理与系统第九章 位置随动系统
2、直流伺服电动机的结构特点
由于上述的要求，因此直流伺服电动机与普通 直流电动机相比，其电枢形状较细较长(惯量小)， 磁极与电枢间的气隙较小，加工精度与机械配合要 求高，铁心材料好。
直流伺服电动机按照其励磁方式的不同，又可 分为电磁式(即他励式)(型号为SZ)，(见图9-7a)和 永磁式(即其磁极为永久磁钢)(型号为SY)(见图9-b) 。
位置随动系统有开环控制系统，如由单片机控 制的、步进电动机驱动的位置随动系统，开环控制 精度较低，目前已有精度达10000step/r以上的步进 随动系统。
对跟随精度要求较高而且驱动力矩较大的场合 ，多采用闭环控制系统，它们多采用交流(或直流) 伺服电动机驱动。典型位置随动系统的组成框图如 图9-1所示。
（9-2） （9-3）
四、交流伺服电动机
1、交流伺服电动机的结构特点
交流伺服电动机也是自动控制系统中一种常用 的执行元件。它实质上是一个两相感应电动机。它 的定子装有两个在空间上相差90°的绕组：励磁绕 组A和控制绕组B。运行时，励磁绕组A始终加上一 定的交流励磁电压(其频率通常有50Hz或400Hz等几 种)；控制绕组B则接上交流控制电压。常用的一种
如图可见，系统有位置环、速度环和电流环三 个反馈回路。其中位置环为主环（外环），主要消 除位置偏差的作用；速度环和电流环均为副环（内 环），速度环起稳定转速的作用，电流环起稳定电 流与限制电流过大的作用。其中位置环是必需的， 位置随动系统主要依靠位置负反馈来减小并最后消 除位置偏差。
图9-1 典型位置随动系统的组成框图
由图可见，在低速时，它们近似为一簇直线，而交 流伺服电动机较少用于高速，因此有时近似作线性 特性处理。这样，交流伺服电动机的传递函数也可 近似以式(9-2)与式(9-3)表示。
自动控制原理课程设计位置随动系统
，从而拖动负载运动。
~5~
重庆邮电大学自动化学院自动控制原理课程设计
直流电动机：微分方程式为 ：
Tm
d M dt
m K mua K c M c
式中 Tm ， K m ， K c 及 M c 是考虑减速器和负载后，折算到电动机轴上的等效值。
测速发电机
是用于测量角速度并且将角速度转换成电压量的装置， 本设计中是永磁式直流测速 发电机。测速发电机的转子与带测量的轴相连接，在点电枢两端输出与转子角速度成正 比的直流电压，即 U T KT ， 式中 K T 是测速发电机的比例系数。是测速发电机的输 出斜率，表示单位角速度的输出电压。
重庆邮电大学自动化学院自动控制原理课程设计
目录
一、设计题目 ....................................................................................................................... 2 1.1 设计目的 ............................................................................................................ 2 1.2 设计内容与任务 ............................................................................................... 2 二、报告正文 ....................................................................................................................... 3 2.1 任务一的分析与求解 ........................................................................................ 4 2.1.1 系统原理图 ..................................................................................................... 4 2.1.2 系统工作原理 ................................................................................................. 4 2.1.3 系统结构框图 ................................................................................................. 4 2.1.4 系统各环节传递函数..................................................................................... 5 2.2 任务二的分析与求解 ........................................................................................ 7 2.2.1 时域分析 ......................................................................................................... 7 2.2.2 频域分析 ....................................................................................................... 10 2.3 任务三的分析及求解 ...................................................................................... 11 2.3.1 校正要求 ...................................................................................................... 11 2.3.2 校正系统的函数的求解 ............................................................................... 12 2.3.3 通过 Matlab 仿真得到校正后传递函数的频域曲线特性 ............................ 12 三、设计总结及体会 .......................................................................................................... 15 3.1 总结 ................................................................................................................ 15 3.2 体会 ................................................................................................................. 15 四、参考文献： ................................................................................................................. 16 五、附录 ............................................................................................................................. 17 MATLAB 仿真函数 ............................................................................................... 17
自动控制原理课程设计——位置随动系统
自动控制原理课程设计——位置随动系统
在工业自动化领域，位置随动系统扮演着重要的角色。
它能够使驱动装置根据指令精确地移动到指定位置，并保持稳定。
位置随动系统的核心是自动控制系统，该系统通过反馈机制实时监测和调整驱动装置的位置。
在位置随动系统中，通常采用步进电机或伺服电机作为驱动装置。
这些电机能够根据控制系统的指令精确地转动一定的角度，从而实现位置的精确控制。
为了确保系统的稳定性，通常会采用闭环控制，即通过位置传感器实时监测电机的位置，并将位置信息反馈给控制系统。
在自动控制原理课程设计中，学生需要了解并掌握位置随动系统的基本原理、组成和实现方法。
学生需要自行设计并实现一个简单的位置随动系统，通过实验验证系统的性能和稳定性。
在设计过程中，学生需要考虑系统的硬件组成、控制算法的选择和实现、传感器选择和校准、系统调试和优化等方面的问题。
学生需要通过理论分析和实验验证相结合的方法，不断优化和完善系统设计。
通过这个课程设计，学生可以深入了解自动控制原理在实际应用中的重要性，提高自己的动手能力和解决问题的能力。
同时，这个课程设计也可以为学生未来的学习和工作打下坚实的基础。
位置随动系统的分析与设计_自动控制原理课程设计
《自动控制原理》课程设计（简明）任务书——供09级电气工程与自动化专业学生用引言：《自动控制原理》课程设计是该课程地一个重要教案环节，既有别于毕业设计，更不同于课堂教案.它主要是培养学生统筹运用自动控制原理课程中所学地理论知识，掌握反馈控制系统地基本理论和基本方法，对工程实际系统进行完整地全面分析和综合. 一、设计题目：位置随动系统地分析与设计 二、系统说明：该系统结构如下图所示其中：放大器增益为Ka=15，电桥增益6K ε=,测速电机增益2t k =，Ra=7Ω,La=10mH,J=0.005kg.m/s2,JL=0.03kg.m/s2,fL=0.08,Ce=1,Cm=3,f=0.1,Kb ＝0.2,i=0.02三、系统参量： 系统输入信号：）（t 1θ 系统输出信号：）（t 2θ 四、设计指标：设定：输入为r(t)=a+bt （其中：a=10， b=5） 在保证静态指标（ess≤0.3）地前提下， 要求动态期望指标：σ p ﹪≤15﹪；ts≤5sec ；五、基本要求：1. 建立系统数学模型——传递函数；2. 利用根轨迹方法分析系统：（1）作原系统地根轨迹草图；（2）分析原系统地性能，当原系统地性能不满足设计要求时，则进行系统校正.3.利用根轨迹方法综合系统：（1）画出串联校正结构图，分析并选择串联校正地类型（微分、积分和微分-积分校正）；（2）确定校正装置传递函数地参数；（3）画出校正后地系统地根轨迹图，并校验系统性能；若不满足，则重新确定校正装置地参数.4.完成系统综合前后地有源物理模拟电路；六、课程设计报告：1、课程设计计算说明书一份；2、原系统组成结构原理图一张（自绘）；3、系统分析，综合用根轨迹图一张；4、系统综合前后地模拟图各一张；5、总结（包括课程设计过程中地学习体会与收获、对本次课程设计地认识等内容）；6、提供参考资料及文献；7、排版格式完整、报告语句通顺、封面装帧成册摘要随动系统是指系统地输出以一定地精度和速度跟踪输入地自动控制系统，并且输入量是随机地，不可预知地.在很多情况下，随动系统特制被控量是机械位移地比还控制系统 .控制技术地发展，使随动系统得到了广泛地应用.位置随动系统是反馈控制系统，是闭环控制，调速系统地给定量是恒值，希望输出量能稳定，因此系统地抗干扰能力往往显得十分重要.而位置随动系统中地位置指令是经常变化地，要求输出量准确跟随给定量地变化，输出响应地快速性、灵活性和准确性成了位置随动系统地主要特征.简言之，调速系统地动态指标以抗干扰性能为主，随动系统地动态指标以跟随性能为主.在控制系统地分析和设计中，首先要建立系统地数学模型.控制系统地数学模型是描述系统内部物理量（或变量）之间关系地数学表达式.在自动控制理论中，数学模型有多种形式.时域中常用地数学模型有微分方程、差分方程和状态方程；复数域中有传递函数、结构图；频域中有频率特.本次课程设计研究地是位置随动系统地滞后校正，并对其进行分析.关键字：随动系统性能分析digestServo system is to point to the output of the system with a certain the precision and speed of tracking input of the automatic control system, and is the input of random, unpredictable. In many cases, servo system special was charged with volume is mechanical displacement control system than also. Control the development of technology, make servo systems have been widely used.Position servo system is feedback control system, is the closed-loop control and speed regulation system for the quantitative value is constant, want to output quantity can stable, so the anti-interference ability of the system often become very important. And with the position of the position servo system instructions are often changes, requirement output accurate quantitative change to follow, the response of the output, flexibility and accuracy position servo system became the main features. In short, speed regulation system in dynamic index to anti-jamming performance is given priority to, servo system dynamic index to follow performance primarily.In the control system of the analysis and design, the first to establish the mathematical model of the system. The mathematical model of the control system is to describe the system internal parameters (or variables) of the relationship between the mathematical expressions. In automatic control theory, the mathematical model has a variety of forms. Commonly used in time domain of mathematical model of the ordinary differential equations, difference equation and state equation。
位置随动系统的分析与设计自动控制原理课程设计627036讲课教案
《自动控制原理》课程设计（简明）任务书引言：《自动控制原理》课程设计是该课程的一个重要教学环节，既有别于毕业设计，更不同于课堂教学。
它主要是培养学生统筹运用自动控制原理课程中所学的理论知识，掌握反馈控制系统的基本理论和基本方法，对工程实际系统进行完整的全面分析和综合。
一、设计题目：位置随动系统的分析与设计二、系统说明： 该系统结构如下图所示BSTBSR相敏电流功率放大SM负载TG减速器θ1θ2K εuaun其中：放大器增益为Ka=15，电桥增益6K ε=,测速电机增益2t k =，Ra=7Ω,La=10mH,J=0.005kg.m/s 2,J L =0.03kg.m/s 2,f L =0.08,C e =1,Cm=3,f=0.1,K b ＝0.2,i=0.02三、系统参量：系统输入信号：）（t 1θ 系统输出信号：）（t 2θ 四、设计指标：设定：输入为r(t)=a+bt （其中：a=10， b=5） 在保证静态指标（ess ≤0.3）的前提下，要求动态期望指标：σp ﹪≤15﹪；ts≤5sec；五、基本要求：1.建立系统数学模型——传递函数；2.利用根轨迹方法分析系统：（1）作原系统的根轨迹草图；（2）分析原系统的性能，当原系统的性能不满足设计要求时，则进行系统校正。
3.利用根轨迹方法综合系统：（1）画出串联校正结构图，分析并选择串联校正的类型（微分、积分和微分-积分校正）；（2）确定校正装置传递函数的参数；（3）画出校正后的系统的根轨迹图，并校验系统性能；若不满足，则重新确定校正装置的参数。
4.完成系统综合前后的有源物理模拟电路；六、课程设计报告：1、课程设计计算说明书一份；2、原系统组成结构原理图一张（自绘）；3、系统分析，综合用根轨迹图一张；4、系统综合前后的模拟图各一张；5、总结（包括课程设计过程中的学习体会与收获、对本次课程设计的认识等内容）；6、提供参考资料及文献；7、排版格式完整、报告语句通顺、封面装帧成册摘要随动系统是指系统的输出以一定的精度和速度跟踪输入的自动控制系统，并且输入量是随机的，不可预知的。
自动控制原理与系统第6章 位置随动系统性能分析
6.1.5 执行机构 1．直流伺服电动机
直流伺服电动机的作用是将控制电压信号转换成转轴上的 角位移或角速度输出，通过改变控制电压的极性和大小，就能 改变电动机的转向和转速，实质上是一台他励式直流电动机。 优点是效率高、控制性能好(控制电压为零时，可自行停转)、 具有宽广的调速范围，功率范围较大，适用于中、大功率随动 系统。
5．系统的校正设计
（1）采用串联校正 有如下结论：降低增益，将使系统的稳定性改善， 但使系统的快速性和稳态精度变差。PD校正将使系统 的稳定性和快速性改善，但是抗高频干扰能力明显下 降。PI校正将使系统的稳态性能得到明显的改善，但 使系统的稳定性变差。PID校正兼顾了系统稳态性能 和动态性能的改善，因此在要求较高的场合多采用 PID)校正。
所以，位置单环随动系统仅适用于负载小、非 线性因素不强、扰动不大的场合。
2．位置转速负反馈双环系统
3．复合控制随动系统
利用前馈和反馈相结合的方法，构成复合 控制随动系统，可以有效地提高系统精度和 动态品质，因此也得到广泛应用。
6.2.2 位置随动系统的基本类型
1．按控制方式 （1）误差控制的随动系统——系统运动的快慢取决于误差的大小， 误差为零时，系统相对静止。 （2）复合控制系统——按输入信号微分和系统误差综合控制的系统 。特点是系统的运动取决于输入信号的变化率(速度或加速度)和系统误 差信号的综合作用。 2．按组成系统元件的物理性质 （1）电气随动系统一一除机械部件外，均为电气元件。包括直流随 动系统和交流随动系统。 （2）电气一液压随动系统——误差测量和放大部分是电气的，系统 的功率放大和执行机构则是液压系统。 3．按系统信号特点： （1）连续随动系统——系统中传递的电信号是连续的，属于模拟式 控制。 （2）数字随动系统——系统中传递的电信号有离散的脉冲数字信号 ，系统的运动靠数字量控制。系统中必须有A/D，D/A转换器。 （3）脉冲一相位随动系统——系统的输入、输出均为方波脉冲，按 输入、输出方波脉冲的相位差来控制系统的运动。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
课程设计任务书学生姓名： 专业班级： 指导教师： 工作单位： 自动化学院题 目: 位置随动系统建模与分析 初始条件：图示为一位置随动系统，放大器增益为8=a k ，电桥增益2=εk ,测速电机增 益15.0=t k V.s ，Ω=5.7a R ，La=14.25mH ，J=0.0006kg .m 2， C e =Cm=0.4N.m/A, f=0.2N.m.s, 减速比i=10 。
要求完成的主要任务: （包括课程设计工作量及其技术要求，以及说明书撰写等具体要求）1、 求出系统各部分传递函数，画出系统结构图、信号流图，并求出闭环传递函数；2、 当Ka 由0到∞变化时，用Matlab 画出其根轨迹。
3、 Ka ＝10时，用Matlab 画出此时的单位阶跃响应曲线、求出超调量、超调时间、 调节时间及稳态误差。
4、 求出阻尼比为0.7时的Ka ，求出此时的性能指标与前面的结果进行对比分析。
时间安排：指导教师签名：年月日系主任（或责任教师）签名：年月日目录1 位置随动系统原理 (3)１.1 位置随动系统原理框图 (3)１.2 元件结构图分析 (3)1.3 位置随动系统各元件传递函数 (5)1.4 位置随动系统的结构框图 (5)1.5 位置随动系统的信号流图 (6)1.6 相关函数的计算 (6)2根轨迹曲线 (7)2.1参数根轨迹转换 (7)2.2绘制根轨迹 (7)3单位阶跃响应分析 (8)3.1单位阶跃响应曲线 (8)3.2单位阶跃响应的时域分析 (9)4系统性能对比分析 (11)4.1 新系统性能指标计算 (11)4.2 系统性能指标对比分析 (11)5 总结体会 (12)参考文献 (13)位置随动系统建模与分析1 位置随动系统原理１.1 位置随动系统原理框图图1.1位置随动系统原理框图工作原理：用一对电位器作为位置检测元件，并形成比较电路。
两个电位器分别将系统的输入和输出位置信号转换成与位置比例的电压信号，并做出比较。
当发送电位器的转角r θ和接受电位器的转角c θ相等时，对应的电压亦相等，因而电动机处于静止状态。
假设是发送电位器的转角按逆时针方向增加一个角度，而接受电位器没有同时旋转这样一个角度，则两者之间将产生角度偏差εθ，通过电桥产生一个偏差电压εu ，与测速机反馈回电压比较后得到电压u ，然后经放大器放大到电压a u ，供给直流电动机，使其带动负载和接受电位器的动笔一起旋转，直到两角度相等为止，即完成反馈。
１.2 元件结构图分析1.电桥：电桥作为角位移传感器，在位置随动系统中是成对使用的。
作为常用的位置检测装置，它的作用是将角位移或者直线位移转换成模拟电压信号的幅值或相位。
指令轴相连的是发送机，与系统输出轴相连的是接收机。
该元件微分方程是：()()()[]()t k t t k t u c r εεεεθθθ=-=；在零初始条件下，其拉氏变换为)()(s k s u εεεθ=；结构框图如图1.2.1所示。
图1.2.1 电桥2.放大器：放大器的作用将微弱的电流信号或者电压信号放大，该元件的微分方程是：()()t u k t u a a =；结构框图如图1.2.2所示。
图1.2.2 放大器3.直流电机：直流电机是一个转动装置，在差压u 的作用下带动负载和接收电位器的动笔一起旋转，该元件的微分方程是：)()()(22t u k dtt d dt t d T a m m m m =+θθ （1）在零初始条件下，其拉氏变换为2()()()m m m a T s s s k u s θ+=；结构框图如图1.2.3所示。
图1.2.3 直流电机4.测速电机：使用测速机在整个系统中构成PD 控制器，反映m θ的变化趋势，产生有效的早期修正信号，改善了系统的稳定性，该元件的微分方程是：()()m t t d t u t k dtθ= （2）在零初始条件下，其拉氏变换为()()t t m u s k s s θ=；结构框图如图1.2.4所示。
图1.2.4 测速电机5.减速器：减速器将直流电机的速度降下来以加在接收电位器上，其中i 为元件总减速比，该元件的微分方程式：21()()m t t i θθ= （3）在零初始条件下，其拉氏变换为21()()m s s iθθ=；结构框图如图1.2.5所示。
图 1.2.5 减速器1.3 位置随动系统各元件传递函数电桥1()()()u s G s k s εεεθ== （4） 放大器2()()()a a u s G s k u s == （5） 测速机3()()()t t m u s G s k s s θ== （6）电机4()()()(1)m ma m s k G s u s s T s θ==+ （7）减速器25()1()()m s G s s iθθ== （8）1.4 位置随动系统的结构框图图1.4 结构框图1.5 位置随动系统的信号流图图1.5 信号流图1.6 相关函数的计算各元件传递函数消去中间变量，得到系统闭环传递函数如下：mma m tm a mma r c iT k k k s T k k k s iT k k k s s s εεθθ+++==Φ)1()()()(2 （9）开环传递函数如下：2()()1m mm t mk k k iT G s H s k k k s s T εαα=++ （10）其中 me a a m C C fR JgR T +=是电动机机电时间常数;me a mm C C fR C k +=是电动机传递系数（a L 很小，忽略不计）。
代入常数计算可得，闭环传递函数：15.142875.4715.1428)(2++=Φs s s （11） sθk εcθ1i mk u a um θ2根轨迹曲线2.1参数根轨迹转换根据参数根轨迹的的定义，将系统的开环传递函数2()()1m mm t mk k k iT G s H s k k k s s T εαα=++代入常数转化为：12(0.036 4.82)()0.027as K G s s s+=+2.2绘制根轨迹用MATLAB 绘制出开环传递函数的根轨迹代码如下： num=[0.036 4.82];den=[0.027 1 0];rlocus(num,den); title(‘根轨迹图’)用MATLAB 绘制出开环传递函数的根轨迹如图2.1所示。
图2.1 根轨迹图3单位阶跃响应分析3.1单位阶跃响应曲线当10a k =代入式（9）中得到闭环传递函数19.178537.5019.1785)(2++=Φs s s 用MATLAB 做出其阶跃响应曲线代码如下：num=1785.19 den=[1,50.37,1785.19]sys=tf(num,den) %系统表示法 t1=0:0.005:0.35 y1=step(num,den,t1) plot(t1,y1) grid用MATLAB 做出其阶跃响应曲线如图3.1所示。
图3.1 单位阶跃响应曲线3.2单位阶跃响应的时域分析当10a k =代入式（9）中得到闭环传递函数19.178537.5019.1785)(2++=Φs s s 根据闭环传递函数算出此二阶系统的阻尼比6.0=ξ,自然频率)/(25.42s rad n =ω 欠阻尼情况下二阶系统的单位阶跃响应为:0,111)()sin(2≥--=+-t e t h t t d n βωξωξ (12)式中，ξβarccos =。
1.上升时间r t 的计算在式(12)中，令()1=r t h ，求得011)sin(2=-+-βωξωξr d r n t t e (13)由于0≠-r n t e ξω，所以有:s t n dr 065.012=--=-=ξωβωβππ2.超调量%σ的计算因为超调量发生在峰值时间上，所以将峰值时间21ξωπ-=n p t得输出量的最大值21/2111)(ξπξξ----=e t h p按照超调量的定义式%100)()()(%⨯∞∞-=h h t h p σ，并考虑到1)(=∞h ，求得:%48.9%100%21/=⨯=--ξπξσe3.调节时间s t 的计算由教材可知，调节时间与闭环极点的实部数值成反比，选取05.0=∆，可以得到结论n s t ξω/5.3≤，在分析问题时常取:s t ns 138.05.35.3===σξω4.稳态误差)(∞ss e 的计算影响系统稳态误差的因素有：系统的型别，开环增益，输入信号幅值和形式等，该系统开环增益19.1785=p K ，阶跃输入幅值1=R ，则系统稳态误差为:40() 5.6101lim ()()1ss ps R Re G s H s K -→∞===⨯++4系统性能对比分析4.1 新系统性能指标计算若a k 未知，系统的闭环传递函数整理为：aa ak s k s k s 5.178027.0036.015.178)(2+++=Φ (13)由式(13)可以得到a n k 5.178=ω，aak k 5.178054.0036.01+=ξ令7.0'=ξ，代入解得69.5'=a k ，得到此时系统的闭环传递函数为：67.101562.4467.1015)(2++=Φs s s上升时间：s t n r 033.01'2=--=ξωβπ超调量：%59.4%100%'21/=⨯=--ξπξσe调节时间：s t ns 157.05.3'==ξω (取误差带05.0=∆)稳态误差：40()'9.8101lim ()()1ss ps R Re G s H s K -→∞===⨯++4.2 系统性能指标对比分析通常，用r t 评价系统的响应速度，用%σ评价系统的阻尼程度，而s t 是同时反映响应速度和阻尼程度的综合性指标。
阻尼比ξ由0.6增大到0.7，系统的性能指标发生变化，表1为前后结果的对照：表1 系统性能指标对照表前后结果对比分析，得出以下结论：上升时间变短，系统响应变快；阻尼比变大，超调量变小；稳态误差变大，说明系统抗扰动能力下降。
5 总结体会为期两周的《自动控制原理》课程设计就要结束了。
回想两周的课程设计，虽然有不少辛苦，然而在辛苦背后更多的还是欢乐与收获。
对于本次课程设计，我是本着检验自己的原则，在紧张与期待中开始的。
整个课程设计分为四个部分，随动系统建模、传递函数的求解、根轨迹绘制、系统性能比较。
每一部分的完成，都需要我们下一番功夫。
在随动系统的建模上，经过讨论、分析、仿真，找出了符合要求的随动系统模型。
同时根据课设的初始条件，选择参数，计算传递函数。
在模型建立好，参数选择合适的前提下，传递函数的计算还是比较简单。
在根轨迹的绘制过程中，由于课本知识掌握得不是很扎实，经过几次资料的查阅，才明白了解题方法，最后绘制出了正确的根轨迹图。