流动类型与雷诺准数
1.3_流体流动的基本概念

注意:这里定义的是截面上的平均流速,而非点速度
ws = ρVs = uAρ = GA
选管?
四、定态与非定态流动 (P40)
定态
T ρ u p…=f (x,y,z)
仅与空间坐标有关 与空间和时间都有关
非定态 T ρ u p…=f (x,y,z,θ)
计算:
进口段长度:
层流:
x0
d
0.0575Re
湍流:
x0
d
Hale Waihona Puke 40 ~ 50Re 越大,湍动程度越高,层流内层厚度越薄。
讨论_continued
流体进入圆管后在入口处形成边界层,随着流体向前流动,边界 层厚度逐渐增加,直至一段距离(进口段)后,边界层在管中心 汇合,占据整个管截面,其厚度不变,等于圆管的半径,管内各 截面速度分布曲线形状也保持不变,此为完全发展了的流动。 对于管流, 只在进口段内才有边界层内外之分。在边界层汇合处, 若边界层内流动是层流,则以后的管内流动为层流;若在汇合之 前边界层内的流动已经发展成湍流,则以后的管内流动为湍流。
边界层分离的必要条件:
流体具有粘性;
流动过程中存在逆压梯度。
边界层分离的后果: 产生大量旋涡; 造成较大的能量损失。
减小或避免边界层分离的措施:调解流速,选择适宜 的流速,改变固体的形体。
如汽车、飞机、桥墩都是流线型。
3
边界层的分离
A点:驻点(u=0)动能转化为 静压能,P最大,迫使流体改变 方向,绕柱而行
A---B:面积减小,u↑,P↓(一部 分静压能转化为动能,一部分 克服摩擦阻力而消耗掉) B: u最大,P最小 B----C 面积增大,u↓,P↑(动能一 部分转化为静压能,另一部分 克服阻力而消耗) C: u=0, P最大。由于惯性,后 继来的高压液体离开壁面,形 成分离,C点的下游形成空白区。 CC′以下:边界层脱离固体壁面, 而后倒流回来,形成涡流,出 现边界层分离。
雷诺试验 层流和湍流

§1.4.2流动类型与雷诺准数现在开始介绍流体流动的内部结构。
流动的内部结构是流体流动规律的一个重要方面。
因为化工生产中的许多过程都和流动的内部结构密切联系。
例如实际流体流动时的阻力就与流动结构紧密相关。
其它许多过程,如流体的热量传递和质量传递也都如此。
流动的内部结构是个极为复杂的问题,涉及面广。
以下紧接着的内容只作简单的介绍,因而在许多方面只能限于定性的阐述。
1、流动类型——层流和湍流1883年著名的雷诺实验揭示出流动的两种截然不同的型态。
雷诺实验装置如图所示:在水箱内装有溢流装置,以维持水位稳定,水箱的底部安装一个带喇叭型进口的直径相同的玻璃管,管出口处装有一个阀门用来调节流量,水箱上方安装有内有颜料的小瓶,有色液体可经过细管子注入玻璃管内。
在水流经过玻璃管的过程中,同时把有色液体送到玻璃管以后的管中心位置上。
雷诺实验观察到:⑴、水流速度不大时,有色细流成一直线,与水不混合。
此现象表明:玻璃管内的水的质点是沿着与管轴平行的方向作直线运动。
即流体分层流动,层次分明,彼此互不混杂,掺和(唯其如此,才能使有色液体保持直线)这种流型叫层流或滞流。
⑵、水流速度增大到某临界值时,有色细流开始抖动,弯曲,继而断裂,细流消失,与水完全混合在一起,整根玻璃管呈均匀颜色,此现象表明,玻璃管内的水的质点除了沿着管道向前运动外,各质点还作不规则的,杂乱的运动,且彼此间相互碰撞,相互混合,质点速度的大小和方向随时发生变化,这种流型叫湍流或紊流。
2、流型的判据—雷诺准数对管流而言,影响流型的因素有,流道的几何尺寸(管径d)流动的平均速度u 和流体的物理性质(密度ρ和粘度μ)。
雷诺发现,可以将这些影响因素综合成一个无因次数群duρ/μ,作为流型的判据。
此数群称为雷诺(Reynolds)数,以R e表示,即:R e=duρ/μ雷诺指出:Ⅰ、当R e≤2000,必定出现层流,称为层流区;Ⅱ、当R e>4000,必定出现湍流,称为湍流区;Ⅲ、当2000<R e<4000,或出现层流,或出现湍流,依赖于环境(如管道直径和方向改变,外来的轻微振动都易促成湍流的产生),此为过度区;在此要说明一点,以R e为判据将流动划分为三个区:层流区,过度区,湍流区。
化工原理流体流动2
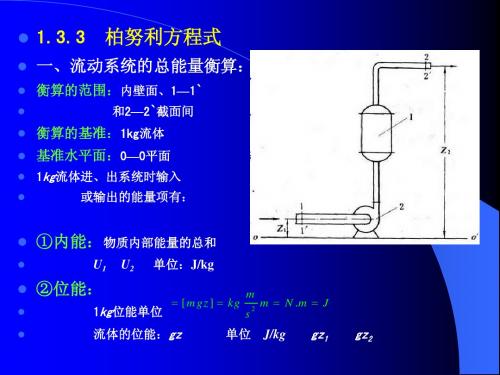
2 1
表示单位质量流体所具有的能量. ②上式中各项单位为 J/kg ,表示单位质量流体所具有的能量.
应注意区别: 应注意区别:
gz
u2 2
是指某截面上流体本身所具有的能量p Nhomakorabeaρ
指流体在两截面之间所获得和所消耗的能量
We
Wf
We是输送设备对单位质量流体所做的有效功, 是决定流体输送设备 是输送设备对单位质量流体所做的有效功, 是输送设备对单位质量流体所做的有效功 的 重要数据, 表示有效功率( 重要数据, 设Ne表示有效功率(单位时间输送设备所做的有效功) 表示有效功率 单位时间输送设备所做的有效功) 单位 J s 或W ③对于可压缩流体的流动 p1 p 2 < 20% p1 可以使用上式; 若 ,可以使用上式; 对于不稳定流动系统的任一瞬间,上式仍成立. 对于不稳定流动系统的任一瞬间,上式仍成立.
令: U = U 2 U 1
g z = gz2 gz1 2 u2 u2 u 2 1 ( pv ) = p2 v2 p1v1 = 2 2 2 2 有增量形式: 有增量形式: U + g z + u + ( pv ) = Qe + We 2
二,流动系统的机械能衡算与柏努利方程式
在流体输送过程中,主要考虑各种形式机械能的转换,为便于应用, 在流体输送过程中,主要考虑各种形式机械能的转换,为便于应用, 消去. 要把式中的 U 和Qe消去. 消去 根据热力学第一定律: 根据热力学第一定律:
表示单位重量流体所具有的机械能, 表示单位重量流体所具有的机械能,可以把自身从基准水平面升举的 高度. 高度.
B:以单位体积流体为衡算基准,各项乘以ρ : 以单位体积流体为衡算基准,
化工原理流体流动3

mmH 2 o
mmHg
注意: 是截然不同的概念: 注意: pf 与 p是截然不同的概念:
u 2 p gz + + ρ = We W f 2 2
r 相邻流体层所产生的内摩擦应力为
τ
由牛顿粘性定律得: 由牛顿粘性定律得:
du r τr = dr
(负号表示u沿半径r增加的方向而减小,作用在流体柱上的阻力为: 负号表示u沿半径r增加的方向而减小,作用在流体柱上的阻力为:
du r du r τ rs = ( 2π rl ) = 2π rl dr dr
32 lu pf = d2
ρu 2 比较
2
2 ∫0 2πur rdr = R 2 pf 2 R r 2 ) rdr = 8l
R
1 u= 2 πR
∫
R
0
u r rdr
上式与 pf = ρhf = λ l d 得
λ=
64 64 64 = = Re du ρ du ρ
当r=0时,管中心处流速为: r=0 管中心处流速为:
λ 用光滑管于Re =3×103--3×105范围内,作实验得出的关系式: = --3 范围内,作实验得出的关系式: 用光滑管于
0.3164 Re 0.25
只有当流体在一段无外功加入,直径又相同的水平管内流动时: 只有当流体在一段无外功加入,直径又相同的水平管内流动时:
u p = p2 p1 = ρWe ρgz ρ ρWf 2
u2 得 We= 0 , z = 0 , = 0 2
化工原理第一章第四节流体流动现象
任意截面的总机械能是相等的,即:
3000
6 6'
E1 E2 E3 E4 E5 E6 E
2 2'
2 2 u12 p1 u2 p2 u3 p3 E gz1 gz2 gz3 2 2 2 2 2 2 u4 p4 u5 p5 u6 p6 gz4 gz5 gz6 2 2 2
式中:
2 1
2
1 h 2
1
u2 2 m
s
2 2
2
d2 184 而u1 u2 2 6.7712m s 100 d1
hf1-2=11.38J/kg
Hale Waihona Puke u u p1 z1g p2 z2 g h f 12 2 2
2 2
2 2' 24m
2m 1 1'
u1 p1 u2 p2 gz1 we gz2 h f 12 2 2
由已知: Z1=0,
Z2=24+2=26m,
P1=0(表) u10
P2= 6.15×104Pa(表压)
hf1-2= 160J/kg
Vs 34.5 u2 2.49 m s 2 2 d 0.07 3600 4 4
1000 500
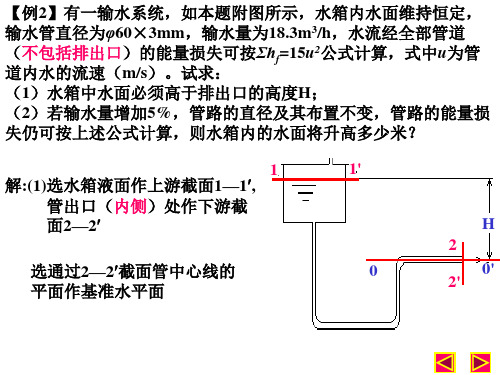
【例4】水在本题附图所示的虹吸管内作定态流动,管路直 径没有变化,水流经管路的能量损失可以忽略不计,试计 算管内截面2-2 、3-3、4-4 、5-5 处的压强。大气压强为 1.0133×105Pa。图中所标注的尺寸均以mm计。 4 解: 选择2-2 截面做基准水平面 4' 3 3' 理想流体,没有外部能量加入, 1 1' 5 5' 因此,根据理想流体柏努利方程,
流体力学(上)实验——11级食科2班105宿舍出版资料

一、流体流动形态的观察与测定(雷诺实验)实验任务:流型及其判断方法;层流、湍流、层流时流速分布曲线1、雷诺准数Re=duρ/μ2、流动类型及判断Re<2100为层流,Re>4000为湍流, 2100<Re<4000为过渡流。
3、转子流量计原理及安装原理:在不同的流量下,要保持转子上下端之间具有相同的静压差,转子与玻璃管环隙间的截面积必须发生改变。
在不同的流量下,转子会停留在玻璃管内不同的高度处,因此转子在不同高度处的刻度就可只是流体的流量。
安装:(1)垂直安装(2)进出口应有5倍管道直径以上的直管段(3)安装在没有振动、便于观察和维修的场所(4)小口径的仪表,应在仪表上游装一个过滤器(5)在转子流量计的进出口装有截止阀和配置旁通阀4、思考题(1)影响流体流动型态的因素有哪些?答:影响流体流动形态的因素有4点:管径d、流速u、流体密度ρ、流体黏度μ。
(2)如果管子不是透明的,不能直接观察来判断管中的流体流动型态,你认为可以用什么办法来判断?答:①若不借助外用工具,如果管子是软的可以摸摸就能感觉,也可以用听来判断;如果只硬的管子,就只能用听来判断。
②用雷诺数判断:Re<2100为层流,Re>4000为湍流, 2100<Re<4000为过渡流。
(3)有人说可以只用流速来判断管中流体流动型态,流速低于某一具体数值时是层流,否则是湍流,你认为这种看法对否?在什么条件下可以由流速的数值来判断流动型态?答:不对。
流体流动型态不仅包括层流、湍流,还有过渡流。
条件:水槽液位高度保持不变,液面绝对平静,墨水粗细合理,水中无杂质,温度、气压和管径保持不变。
(4)在实验中,连续注入水以爆出水槽液面高度不变的目的是什么?答:①由于是通过转子流量计来测量水管中水流的流速,如果水槽中液面高度不能恒定在画线处的话,转子流量计的指示值就不准确,雷诺数的计算值就有较大误差。
②有P=ρgh可知,保持水槽液面高度h不变,就是保持水槽出水口出的压强P不变。
流动类型与雷诺准数

注意:在计算非圆形管内流体的流速u时,应使用真实的 截面积A计算,u =qv/A。不能使用de计算截面积。
例题:温度为400C的水以8m3/h的流量流过套管换热器的环隙通道。套管
换热器由直径Φ57mm×3mm与Φ32mm×2.5mm的无缝钢管同心组装而成, 试求水流过环隙时每米管长因克服流动阻力而引起的压力降。取钢管的粗 糙度为0.1mm。
0.00000 0.000001
0.09 0.08 0.07 0.06 0.05
0.04 Re
0.03 0.025
0.02
0.015
0.01
d 0.009u
0.008
2
103
Re,
d
d
4 68 2 104
u
4 68 2 4 68 2
105
du106
层雷诺流数R底e 层
0.0322 )
1.795m
/
s
Re deu 0.019 1.795 992 .3 51584 4000
65.6 10 5
流型属于湍流
0.1103 0.00526
de 0.019
Re = 51584
查图1-28, λ=0.025
p f
R
(
l de
u2 2
)
0.025
992 .21.795 2
3.2 流动类型与雷诺准数
3.2.1 实验现象及流动类型 流体质点只有轴向运动(层流或滞流)
流体质点除有轴向运动外,还有径向运动。 (过渡流)
流体质点除有轴向运动和径向运动外, 还相互碰撞和混合。 (湍流或紊流)
3.2.2 雷诺准数(雷诺数)(Reynolds Number)
流体力学基本原理

p1 u12 p2 u22
22
1
p1
p2
u22
u12 2
u22 2
1
A2 A1
2
p2
2 0
R
孔板流量计
u2
1
1 A2
A1 2
2 p1 p2
A1u1 A2u2 A0u0 (孔口)
用 A0 代替 A2, 再考虑到机械能损失
4)测速管安装于管路中,装置头部和垂直引出部分都将对管道内流 体的流动产生影响,从而造成测量误差。因此,除选好测点位置,尽量 减少对流动的干扰外,一般应选取皮托管的直径小于管径的1/50。
优点:结构简单、阻力小、使用方便,尤其适用于测量气体管道内的流速。 缺点:不能直接测出平均速度,且压差计读数小,常须放大才能读得准确。
对于连续稳定系统:
1
2
1’ 2’
m1 = m2 m =V = uA
u1 A1 1= u2 A2 2=常数
对于不可压缩性流体,密度可视为不变
u1 A1= u2 A2
------连续性方程
圆形管道 : u1 /u2 = (d2/d1)2
二、流动类型与雷诺准数
1、雷诺实验
2、雷诺数Re
Re du
7)
um 0.82umax (n 7)
du dy
一、测速管:又称皮托(Pitot)管
1、测速管的结构和原理
对于某水平管路,测速管的内管A点测得的
是管口所在位置的局部流体动压头与静压头之和
,称为冲压头 。
hA
u2 2g
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.2.1 实验现象及流动类型 流体质点只有轴向运动(层流或滞流)
流体质点除有轴向运动外,还有径向运动。 (过渡流)
流体质点除有轴向运动和径向运动外, 还相互碰撞和混合。 (湍流或紊流)
3.2.2 雷诺准数(雷诺数)(Reynolds Number)
雷诺数
du
Re
Re
管 粗糙管:钢管、铸铁管等
2.绝对粗糙度:粗糙面凸出部分的平均高度,,m。 3.相对粗糙度:ε/d,无量纲(因次)。 4.层流时,ε(粗糙度)对λ(摩擦系数)没有影响。 5.湍流时
(1) δ>ε,没有影响,光滑管流动 (δ-层流底层厚度) (2) δ< ε ,有影响 ;当Re一定, ε越大,流体的摩擦阻力损失 越大。
机械能损失及压头损失(摩擦阻力损失、摩擦损失、阻 力损失)
4.1.2 阻力的分类
直管阻力Skin friction:流体流经直管时,由于流体流动产生的 内摩擦力而引起的 ΣR 局部阻力Form friction :流体流经管件、阀门等,由于改变 方向产生漩涡而引起的。
4.1.3水平直管阻力Friction of Straight Pipe
在直管中任取一段流动流体。如图所设,
1
2
则由 得 又由x方向上的力平衡
u
d
p1
l
p2 x
得
所以
R l u2
d2
4.1.4 非水平直管阻力Friction of Non-straight Pipe
以垂直直管阻力为例:
则由
得
由y方向上的力平衡,得
R 4l l u 2 d d 2
结论注意:
1.11 10 5
>4000
流体流动类型属湍流,此时泊谡叶方程不适用,所以不能用
其计算管路两截面间的压差。需注意:由于泊谡叶方程在推导过程
中引入了牛顿粘性定律,而只有在层流(滞流)时内摩擦应力才服从牛顿 粘性定律,所以它仅适用于滞流时的流动阻力计算。
(2)对于垂直管,尽管流动类型可能为滞流,但由泊谡叶方
长径比,无因次
R
l u2
d2
----- 直管摩擦阻力计算通式, 对湍流与层流均适用,
摩擦系数
动能 称为范宁公式
4.2 层流摩擦系数
ur
p f
4l
(R2
r2)
流体在圆管内层 流流动时的速 度分布式
l
R
r
p1
ur
p2
x
p f
R
l d
u 2
2
p f
32lu
d2
流体在圆管内作层流(滞流)流动 时直管阻力的计算式,称为哈根 -泊谡叶(Hagon-Poiseuille)公 式
1. 对于同一根直管,不管是垂直或水平安装, 所得的摩擦阻力损失应该相同。
2. 只有水平安装的等直径管路,摩擦损失等于 两截面上的静压能之差。
本题还说明,流动阻力的大小与管段排列方式无关,但压差却与 管段排列方式有关。这是因为管段两端的压力差不仅要克服流 动阻力,还要克服位头的变化,所以液体自下而上流动时,压 差大于水平管。
该关系见图。该图可分为四个区域:
(1) 层流区[Re≤2000],
(2) 过渡流区(2000Re4000),流动条件好时,仍可以是层流; 为安全起见,一般按湍流计算。
表1
某些工业管材的绝对粗糙度约值
管道类别
绝对粗糙度,mm
管道类别
绝对粗糙度,mm
无缝黄铜管、钢管、铅管 金 新的无缝钢管、镀锌铁管
新的铸铁管 属
具有轻度腐蚀的无缝钢管
管 具有显著腐蚀的无缝钢管 旧的铸铁管
0.010.05 0.10.2
0.3 0.20.3 0.5 以上 0.85 以上
干净玻璃管
非
橡皮软管
程算出的仅是摩擦阻力损失项,而垂直管路两截面的压差还要 受位能的影响,所以也不能用泊谡叶方程直接计算两截面的压 差。
长径比,无因次
R
l u2
d2
----- 直管摩擦损失计算通式, 对湍流与层流均适用,
摩擦系数
动能 称为范宁公式
(1)层流时的
32lu
p f d 2
p f R
64
Re
Re du /
分析:此题核心在于上述两种情况下,用泊谡叶方程算出的压力降与管路 两截面的压力差在数值上是否相同。
由柏努利方程式
g
u 2 2
p
We
R
p
p2
p1
We
gZ
u 2 2
R
其中ρ ΣR是指单位体积流体流动时所损失的机械能,以Δpf 表 示,即:Δpf = ρ ΣR , 单位为[Pa], 故常称Δpf 为因流动阻力而引 起的压力降。 (Δpf = ρ ΣR)
(2)湍流时的
主要依靠实验研究
因次分析法:
通过因次分析法,可得到某一物理过程的无因次数 群的个数及形式。
只是一种数学分析方法,它不能代替实验。
因次分析过程:
du
(1)通过实验找到所有影响因素:
R f d,l,u,,,
管壁绝对粗糙度
管壁粗糙度Roughness of Pipe Walls
1.管的分类 光滑管:玻璃管、铜管、塑料管等
思考题-3
下面两种情况,可不可以用泊谡叶方程
p f
32lu
d2
直接计算管路两端的压力差?
= (1)水平管,管内径为50mm,流体的密度为
996kg/m3,粘度为0.894mPa.s,流速为2m/s。
(2)垂直管,管内径为100mm,流体的相对密度为 0.85,粘度为20mPa.s,流速为0.4m/s。
金
木管道
属
陶土排水管
很好整平的水泥管 管
石棉水泥管
0.00150.01 0.010.03 0.251.25 0.456.0 0.33 0.030.8
4.3 湍流摩擦系数
湍流摩擦系数
λ与Re和ε/d的函数关系由实验确定。 λ与Re和ε/d的关联图
R l u2
d2
与Re的关系The friction-factor chart
而两截面间的压力差Δp是由多方面因素引起的,如各种不同 形式机械能的相互转化均会使两截面压力差发生变化。
在一般情况下,Δp 与 Δpf 在数值上是不等的,只有流体在一 段无外功加入,直径相同的水平管内流动时,才能得出压力差
Δp 与 压力降Δpf 在绝对数值上相等。
ห้องสมุดไป่ตู้
(1)
Re
du
50 10 3 2 996 0.894 10 3
du
m N
m s s
kg
m3 m2
m 0 kg 0 s 0
无因次
3.2.3 流体质点的运动方式
流型的判别
直管内流动时,Re2000
层流
Re=20004000 过渡区
Re>4000
湍流
第四节 流体流动阻力
FLUID-FLOW FRICTION
4.1.1 阻力的含义
机械能损失 R和压头损失 Hf
