棋盘覆盖算法
棋盘覆盖算法C#

一、实验目的:用ABCD四个字母代替四种L型骨牌,覆盖于2^kX2^k大小的棋盘中二、实验内容:在一个2^k×2^k (k≥0)个方格组成的棋盘中,恰有一个方格与其他方格不同,称该方格为特殊方格。
显然,特殊方格在棋盘中可能出现的位置有4^k种,因而有4k种不同的棋盘,图4.10(a)所示是k=2时16种棋盘中的一个。
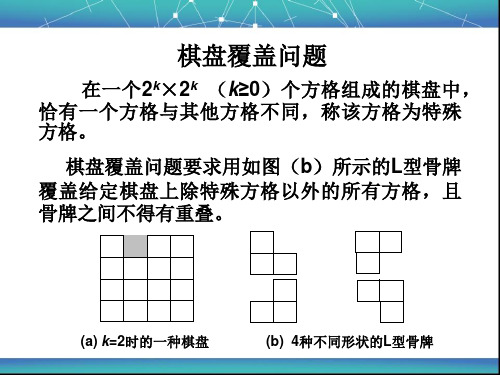
棋盘覆盖问题(chess cover problem)要求用图4.10(b)所示的4种不同形状的L型骨牌覆盖给定棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖。
三、程序设计说明:(算法设计思路)主要思路是利用递归处理棋盘,先确定每个棋盘的特殊骨牌,然后由骨牌位置确定所摆放L型骨牌的型号,依次递归所有棋盘即得其解四、程序代码(经调试正确的源程序)using System;using System.Collections.Generic;using System.Linq;using System.Text;namespace ConsoleApplication4{class Program{static void Main(string[] args){char[,] chessboard = new char[1000,1000];int startU = 1;int endU = 4;//在这里输入棋盘的大小int startV = 1;int endV = endU;int specialU =2;int specialV = 3;setblock(startU, endU, startV, endV, chessboard, specialU, specialV);printchessboard(startU, endU, startV, endV,specialU,specialV, chessboard);Console.ReadLine();//************1、算法没问题,程序实现有问题,增加了L型方块编码ABCD,无形中增加了难度和代码长度,全部抛弃,无法实现,虽然很蛋疼,前后花了十几个小时//************2、问题为:递归进入某函数之后无法返回跳转到上一级函数,同一级别的棋盘递归处理之后无法处理另一同级别棋盘//************3、经过逐步执行得知程序中有一处小错误,调试之后能初步输出正确答案,在4*4规模下完全正确,在8*8规模下少一块L骨牌覆盖,说明递归还是不完全//*****经过处理已经毫无错误}public static void setblock(int startU,int endU,int startV,int endV,char[,] chessboard,int specialU,int specialV ){int style;int sizeU = endU - startU + 1;int sizeV = endV - startV + 1;if(sizeU==1) return;int midU=startU+sizeU/2-1;int midV = startV + sizeV / 2 - 1;if (specialU > midU && specialV <= midV){markSpecialBlock1style1(midU, midV, chessboard, startU, endU, startV, endV);markSpecialBlock2style1(midU, midV, chessboard, startU, endU, startV, endV);markSpecialBlock3style1(midU, midV, chessboard, startU, endU, startV, endV);setblock(midU + 1, endU, startV, midV, chessboard, specialU, specialV);//在这里尝试修改,原始数据(midU+1, endU, midV+1, endV, chessboard, specialU, specialV),改为(midU + 1, endU, startV, midV, chessboard, specialU, specialV)//haha 终于找到了哈哈原来BUG在这里在这个判断上哈哈现在问题规模不管为多大都可以了只要不超过数组大小界限return;}if (specialU <= midU && specialV <= midV){markSpecialBlock1style2(midU, midV, chessboard, startU, endU, startV, endV);markSpecialBlock2style2(midU, midV, chessboard, startU,endU, startV, endV);markSpecialBlock3style2(midU, midV, chessboard, startU, endU, startV, endV);setblock(startU, midU,startV, midV, chessboard, specialU, specialV);return;}if (specialU <= midU && specialV > midV){markSpecialBlock1style3(midU, midV, chessboard, startU, endU, startV, endV);markSpecialBlock2style3(midU, midV, chessboard, startU, endU, startV, endV);markSpecialBlock3style3(midU, midV, chessboard, startU, endU, startV, endV);setblock(startU, midU, midV + 1, endV, chessboard, specialU, specialV);return;}if (specialU > midU && specialV > midV){markSpecialBlock1style4(midU, midV, chessboard, startU,endU, startV, endV);markSpecialBlock2style4(midU, midV, chessboard, startU, endU, startV, endV);markSpecialBlock3style4(midU, midV, chessboard, startU, endU, startV, endV);setblock(midU + 1, endU, midV + 1, endV, chessboard, specialU, specialV);return;}}/*public static void isWhatStyle(int specialU,int specialV,int midU,int midV,out int style){if (specialU > midU && specialV <= midV)style = 1;else if (specialU <= midU && specialV <= midV)style = 2;else if (specialU <= midU && specialV > midV)style = 3;elsestyle = 4;return;}*///********define style1public static void markSpecialBlock1style1(int midU, int midV, char[,] chessboard, int startU, int endU, int startV, int endV){int specialU = midU;int specialV = midV;if (chessboard[specialU, specialV] != 0) return;//防止在棋盘中进行无限制的覆盖if (specialU >= startU && specialU <= midU && specialV >= startV && specialV <= midV)//{chessboard[specialU, specialV] = 'A';startU = startU;endU = midU;startV = startV;endV = midV;setblock(startU,endU,startV, endV, chessboard, specialU, specialV);}}public static void markSpecialBlock2style1(int midU, int midV, char[,] chessboard, int startU, int endU, int startV, int endV){int specialU = midU;int specialV = midV+1;if (chessboard[specialU, specialV] != 0) return;if (specialU >= startU && specialU <= midU && specialV >= midV + 1 && specialV <= endV){chessboard[specialU, specialV] = 'A';startU = startU;endU = midU;startV = midV+1;endV = endV;setblock(startU, endU, startV, endV, chessboard, specialU, specialV);}}public static void markSpecialBlock3style1(int midU, int midV, char[,] chessboard, int startU, int endU, int startV, int endV){int specialU = midU + 1;int specialV = midV + 1;if (chessboard[specialU, specialV] != 0) return;if(specialU >= midU + 1 && specialU <= endU && specialV >= midV + 1 && specialV <= endV){chessboard[specialU, specialV] = 'A';startU = midU+1;endU = endU;startV = midV + 1;endV = endV;setblock(startU, endU, startV, endV, chessboard, specialU, specialV);}}//********define style2public static void markSpecialBlock1style2(int midU, int midV, char[,] chessboard, int startU, int endU, int startV, int endV){int specialU = midU+1;int specialV = midV;if (chessboard[specialU, specialV] != 0) return;if (specialU >= midU + 1 && specialU <= endU && specialV >= startV && specialV <= midV){chessboard[specialU, specialV] = 'B';startU = midU+1;endU = endU;startV = startV;endV = midV;setblock(startU, endU, startV, endV, chessboard, specialU, specialV);}}public static void markSpecialBlock2style2(int midU, int midV, char[,] chessboard, int startU, int endU, int startV, int endV){int specialU = midU;int specialV = midV + 1;if (chessboard[specialU, specialV] != 0) return;if (specialU >= startU && specialU <= midU && specialV >= midV + 1 && specialV <= endV){chessboard[specialU, specialV] = 'B';startU = startU;endU = midU;startV = midV + 1;endV = endV;setblock(startU, endU, startV, endV, chessboard, specialU, specialV);}}public static void markSpecialBlock3style2(int midU, int midV, char[,] chessboard, int startU, int endU, int startV, int endV){int specialU = midU + 1;int specialV = midV + 1;if (chessboard[specialU, specialV] != 0) return;if (specialU >= midU + 1 && specialU <= endU && specialV >= midV + 1 && specialV <= endV){chessboard[specialU, specialV] = 'B';startU = midU + 1;endU = endU;startV = midV + 1;endV = endV;setblock(startU, endU, startV, endV, chessboard, specialU, specialV);}}//********define style3public static void markSpecialBlock1style3(int midU, int midV, char[,] chessboard, int startU, int endU, int startV, int endV){int specialU = midU;int specialV = midV;if (chessboard[specialU, specialV] != 0) return;if (specialU >= startU && specialU <= midU && specialV >= startV && specialV <= midV){chessboard[specialU, specialV] = 'C';startU = startU;endU = midU;startV = startV;endV = midV;setblock(startU, endU, startV, endV, chessboard, specialU, specialV);}}public static void markSpecialBlock2style3(int midU, int midV, char[,] chessboard, int startU, int endU, int startV, int endV){int specialU = midU + 1;int specialV = midV;if (chessboard[specialU, specialV] != 0) return;if (specialU >= midU + 1 && specialU <= endU && specialV >= startV && specialV <= midV){chessboard[specialU, specialV] = 'C';startU = midU+1;endU = endU;startV = startV;endV = midV;setblock(startU, endU, startV, endV, chessboard, specialU, specialV);}}public static void markSpecialBlock3style3(int midU, int midV, char[,] chessboard, int startU, int endU, int startV, int endV){int specialU = midU + 1;int specialV = midV + 1;if (chessboard[specialU, specialV] != 0) return;if (specialU >= midU + 1 && specialU <= endU && specialV >= midV + 1 && specialV <= endV){chessboard[specialU, specialV] = 'C';startU = midU + 1;endU = endU;startV = midV + 1;endV = endV;setblock(startU, endU, startV, endV, chessboard, specialU, specialV);}}//********define style4public static void markSpecialBlock1style4(int midU, int midV, char[,] chessboard, int startU, int endU, int startV, int endV){int specialU = midU;int specialV = midV;if (chessboard[specialU, specialV] != 0) return;if (specialU >= startU && specialU <= midU && specialV >= startV && specialV <= midV){chessboard[specialU, specialV] = 'D';startU = startU;endU = midU;startV = startV;endV = midV;setblock(startU, endU, startV, endV, chessboard, specialU,specialV);}}public static void markSpecialBlock2style4(int midU, int midV, char[,] chessboard, int startU, int endU, int startV, int endV){int specialU = midU;int specialV = midV + 1;if (chessboard[specialU, specialV] != 0) return;if (specialU >= startU && specialU <= midU && specialV >= midV + 1 && specialV <= endV){chessboard[specialU, specialV] = 'D';startU = startU;endU = midU;startV = midV + 1;endV = endV;setblock(startU, endU, startV, endV, chessboard, specialU, specialV);}}public static void markSpecialBlock3style4(int midU, int midV, char[,] chessboard, int startU, int endU, int startV, int endV){int specialU = midU + 1;int specialV = midV;if (chessboard[specialU, specialV] != 0) return;if (specialU >= midU + 1 && specialU <= endU && specialV >= startV && specialV <= midV){chessboard[specialU, specialV] = 'D';startU = midU + 1;endU = endU;startV = startV;endV = midV;setblock(startU, endU, startV, endV, chessboard, specialU, specialV);}}//*********print chessboardpublic static void printchessboard(int startU,int endU,int startV,int endV,int specialU,int specialV,char[,] chessboard){for (int i = startV; i <= endV; i++){for (int j = startU; j <= endU; j++){if(j==specialU&&i==specialV)Console.Write('S'+" ");elseConsole.Write(chessboard[j, i]+" ");}Console.WriteLine();}}}}五.程序运行结果(测试数据和运行结果)。
棋盘覆盖问题(Tromino谜题)
tc
tr
dc
dr
size
棋盘覆盖问题中的数据结构
算法——棋盘覆盖
void ChessBoard(int tr, int tc, int dr, int dc, int size)
// tr和tc是棋盘左上角的下标,dr和dc是特殊方格的下标,
// size是棋盘的大小,t已初始化为0
{
if (size = = 1) return; //棋盘只有一个方格且是特殊方格
{
int s;
if(size==1) return;
if(size>1)
{
s=size/2;
if(dr<=(tr+s-1)&&dc<=(tc+s-1))
/*特殊方块在左上部分
*/
{
a[tr+s-1][tc+s]=t;
a[tr+s][tc+s]=t;
a[tr+s][tc+s-1]=t;
t++;
Tromino(a,dr,dc,tr,tc,s);
board[tr + s - 1][tc + s - 1] = t;
ChessBoΒιβλιοθήκη rd(tr, tc, tr+s-1, tc+s-1, s);
}
// 覆盖右上角子棋盘
if (dr < tr + s && dc >= tc + s) // 特殊方格在右上角子棋盘中
ChessBoard(tr, tc+s, dr, dc, s);
for(j=0;j<N;j++) printf("%-4d",a[i][j]);
棋盘8x8的覆盖问题,其中一个点已经被覆盖,用l型模块将其余完全覆盖的分治策略.约

棋盘8x8的覆盖问题,其中一个点已经被覆盖,用l型模块将其余完全覆盖的分治策略.约【算法】分治策略之棋盘覆盖问题
问题:
在一个{2}^{k}*{2}^{k}个方格组成的棋盘中,恰有一个方格与其他方格不同,称该方格为一特殊方格,且称该棋盘为一特殊棋盘。
在棋盘覆盖问题中,要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖。
策略:
将棋盘分割成四个大小相等的子棋盘,则特殊方格必位于4个较小子棋盘之一中,其余三个无特殊方格。
为了将这3个子棋盘转化为特殊棋盘,可以用一个L
形骨牌覆盖这三个较小棋盘的汇合处,这三个子棋盘被骨牌覆盖的方格就成为该棋盘上的特殊方格,从而将问题转化为四个较小规模的棋盘覆盖问题。
递归地分割棋盘,直到简化为1*1的棋盘。
棋盘覆盖问题的求解

棋盘覆盖问题的求解棋盘覆盖问题是一个经典的数学问题,它引发了人们对于数学中的逻辑思维和问题解决能力的思考。
在这篇文章中,我将为大家详细介绍棋盘覆盖问题的求解方法,并希望能够帮助中学生和他们的父母更好地理解和应用这一问题。
棋盘覆盖问题是指如何用特殊形状的骨牌将一个2^n × 2^n的棋盘完全覆盖的问题。
其中,骨牌的形状分为4种,分别为L型、反L型、凸型和凹型。
在求解这个问题时,我们需要遵循以下几个步骤。
首先,我们需要将给定的棋盘划分为四个相等的小棋盘。
这样,我们就可以将问题分解为四个子问题,分别是将四个小棋盘覆盖完整。
接下来,我们就可以通过递归的方式来解决每个子问题。
在解决子问题时,我们需要根据骨牌的形状来选择放置的位置。
以L型骨牌为例,我们可以将其放置在左上角、左下角或者右上角。
通过不同的放置位置,我们可以将子问题进一步分解为更小的子问题。
同样地,我们可以使用相同的方法来解决反L型、凸型和凹型骨牌。
在每个子问题中,我们需要注意两个关键点。
首先,我们需要保证每个小棋盘上的骨牌能够完全覆盖。
这就要求我们在放置骨牌时,需要选择合适的位置和方向。
其次,我们需要保证四个小棋盘的边缘能够对齐。
这样,才能保证最终的结果是一个完整的棋盘。
通过不断地递归求解子问题,我们最终可以将整个棋盘完全覆盖。
这个过程中,我们需要注意边界条件的处理,以及递归函数的设计。
同时,我们还可以通过剪枝等优化方法来提高算法的效率。
棋盘覆盖问题的求解方法不仅仅是一个数学问题,更是一个思维训练的过程。
通过解决这个问题,我们可以培养自己的逻辑思维能力、问题解决能力和创新思维。
同时,这个问题也具有一定的实用性,可以用于解决一些实际问题,如图像处理、计算机视觉等领域。
总结一下,棋盘覆盖问题是一个经典的数学问题,通过将棋盘划分为四个小棋盘,我们可以通过递归的方式来解决每个子问题。
在解决子问题时,我们需要选择合适的骨牌形状和放置位置,同时保证边缘对齐和完全覆盖。
棋盘覆盖问题c语言

// 覆盖本子棋盘中的其余方格
ChessBoard(tr,tc,tr+s-1,tc+s-1,s);
}
//覆盖右上角子棋盘
if(dr<tr+s&&dc>=tc+s)
// 特殊方格在此棋盘中
ChessBoard(tr,tc,dr,dc,s);
else
{//特此棋盘中无特殊方格 ,t号L型骨牌覆盖左下角
{//此棋盘中无特殊方格 ,t号L型骨牌覆盖左上角
board[tr+s][tc+s]=t;
// 覆盖本子棋盘中的其余方格
ChessBoard(tr+s,tc+s,tr+s,tc+s,s);
}
}
int main()
{
int size,r,c,row,col;
printf("输入棋盘大小:\n");
scanf("%d",&size);//输入棋盘大小
{
for (c = 0; c < size; c++)
{
printf("%d ",board[r][c]);
}
printf("\n");
}
return 0;
}
运行效果:
实验报告成绩
老师
注:1)专业班级按打印课表中名称填写;2)课程名称按课表中名称填写,不能简写;
3)实验日期格式示例:)实验时间格式示例:“第三大节”5)实验情况包括任务(或题目)、解决方案(或者代码)、结果等;6)实验报告成绩按五级标准评分;精心搜集整理,只为你的需要
棋盘覆盖问题算法思路

棋盘覆盖问题算法思路
棋盘覆盖问题是一道经典的分治算法问题,通常用于介绍分治算法的思想。
其基本思路是将棋盘分成若干个小块,然后在其中一个小块上放置一块特殊的骨牌,然后将剩下的小块按照同样的方式继续分成更小的块,并在其中一个小块上放置另一块骨牌,以此类推,直到整个棋盘被覆盖。
具体的实现过程可以采用递归的方式,将棋盘不断地分成四个部分,然后在其中一个部分上放置一块骨牌,再递归求解另外三个部分。
在实现过程中,需要注意处理边界条件和特殊情况,例如棋盘大小为1x1或者存在特殊方块无法覆盖等情况。
该算法的时间复杂度为O(2^n),其中n为棋盘大小的指数。
虽然时间复杂度较高,但是由于该问题特殊的递归性质使得其能够被高效地并行化,因此在实际应用中仍有广泛的应用。
分治法棋盘覆盖问题算法原理
分治法棋盘覆盖问题算法原理
分治法棋盘覆盖问题算法是一种基于分治策略的算法,用于解决棋盘覆盖问题。
该算法的基本原理是将一个复杂的问题分解为若干个较小的子问题,然后分别求解这些子问题,最后将子问题的解合并为原问题的解。
在棋盘覆盖问题中,给定一个n×n的棋盘,要求用最少的1×2骨牌覆盖整个棋盘。
分治法棋盘覆盖问题算法通过将棋盘不断划分,将问题规模逐渐减小,最终将问题转化为若干个1×1的棋盘覆盖问题,从而使得问题得以解决。
具体来说,该算法首先将棋盘划分为四个相等的子棋盘,然后判断哪个子棋盘中包含特殊方格。
对于不包含特殊方格的子棋盘,用L型骨牌覆盖其会合处,将其转化为特殊棋盘。
然后递归地使用这种划分策略,直至将棋盘分割为1×1的子棋盘。
通过这种分治策略,算法可以将问题规模不断减小,直到每个子问题都能够被直接解决。
最终,所有子问题的解将被合并为原问题的解。
这种算法不仅具有高效性,而且能够将复杂的问题分解为若干个简单的子问题,使得问题的解决更加容易。
棋盘覆盖算法
棋盘覆盖算法
棋盘覆盖算法是一种使用分治策略来覆盖一个给定的棋盘的算法。
其基本思想是将棋盘划分成四个等分的子棋盘,然后从中选择一个作为特殊方格,并在其它三个子棋盘上递归执行该算法。
这个过程会一直递归下去,直到棋盘被完全覆盖。
在实际应用中,棋盘覆盖算法可以用来解决一些与棋盘相关的问题,例如:在一个棋盘上,如何用L型骨牌覆盖所有格子?如何在一个棋盘上放置n个皇后,使得它们不互相攻击?
棋盘覆盖算法的时间复杂度为O(2^n),因此在处理大规模的棋盘问题时,可能会存在效率问题。
为了提高算法的效率,可以考虑使用一些优化技巧,例如:使用启发式搜索来减少搜索空间,或者使用记忆化搜索来避免重复计算。
总之,棋盘覆盖算法是一种十分有用的算法,在许多棋盘相关的问题中都能够得到应用。
- 1 -。
棋盘覆盖问题算法思路
棋盘覆盖问题算法思路棋盘覆盖问题是一个经典的递归问题,其原始问题定义如下:给定一个2^n*2^n的棋盘,其中一个方格被标记,将该棋盘分割成4个2^(n-1)*2^(n-1)的小棋盘,同时以递归的方式,将标记方格分割到4个小棋盘之一,并覆盖其他方格。
重复此过程,直到达到基本情况,即当棋盘大小为2*2,无需分割。
我们可以使用分治法来解决这个问题,即将一个大问题分解为多个小问题,并最终将它们的解组合起来得到原问题的解。
下面是一个算法思路:1.定义一个棋盘的类,表示一个棋盘对象。
其中包括棋盘的大小、标记方格的位置坐标等信息。
2. 定义一个递归函数cover(board, size, tr, tc, dr, dc),其中board表示当前的棋盘对象,size表示当前棋盘的大小,(tr, tc)表示当前棋盘左上角方格的坐标,(dr, dc)表示标记方格的坐标。
3.首先检查当前棋盘大小是否为2*2,如果是,则直接将标记方格的位置填充到其他3个方格,并返回。
4. 否则,将当前棋盘的大小减半,计算出当前棋盘分割后4个小棋盘的左上角方格坐标和标记方格的位置坐标(nt, nl, nr, nc)。
5. 然后分别递归调用cover函数对4个小棋盘进行覆盖,需要注意传递的参数:a. 对于第一个小棋盘,其大小为size / 2,左上角坐标为(tr, tc),标记方格的坐标为(nt, nl)。
b. 对于第二个小棋盘,其大小为size / 2,左上角坐标为(tr, tc + size / 2),标记方格的坐标为(nr, nc)。
c. 对于第三个小棋盘,其大小为size / 2,左上角坐标为(tr + size / 2, tc),标记方格的坐标为(nr, nc)。
d. 对于第四个小棋盘,其大小为size / 2,左上角坐标为(tr + size / 2, tc + size / 2),标记方格的坐标为(nt, nl)。
6.最后,将4个小棋盘的覆盖结果组合起来得到原问题的解,并将该结果填充到当前棋盘。
棋盘覆盖算法
棋盘覆盖算法棋盘覆盖算法(Tiling Puzzle)是用小的拼图块填满一个大的棋盘的问题,这些拼图块称作多米诺骨牌,每一块都覆盖两个格子,而棋盘的大小为2的n次方×2的n次方,其中n是整数。
在一个棋盘和一组多米诺骨牌下,棋盘恰好可以被所有的多米诺骨牌覆盖,且每个多米诺骨牌恰好覆盖两个格子。
棋盘覆盖算法是一个NP难问题,它需要在指数时间内找到最佳解决方案。
但是,对于许多小规模的问题,我们可以使用回溯算法来得到最佳解决方案。
回溯算法是一种试探性算法,最初解答第一个问题,可进一步解答其他问题。
该算法探讨所有可能的解决方案,直到找到正确的方案。
如果没有正确的解决方案,那么回溯算法将返回到较早的步骤并尝试其他方案。
因此,我们可以使用回溯算法来解决这个问题。
当我们覆盖一个多米诺骨牌时,我们可以检查是否存在其他多米诺骨牌可以覆盖未覆盖的部分,并将这些多米诺骨牌添加到棋盘的布局中。
如果我们在棋盘上填好所有的多米诺骨牌,那么我们就找到了正确的解决方案。
步骤:1. 首先在棋盘上选择一个没有被覆盖的格子。
2. 从所有可以放置在这个格子上的多米诺骨牌中,选择一个多米诺骨牌放到这个位置上。
3. 如果这个多米诺骨牌可以被放置在棋盘上的其他未被覆盖的位置上,那么就在这个位置上放置。
4. 重复步骤2和3,一直到所有的多米诺骨牌都被放置在棋盘上。
5. 如果无法放置更多的多米诺骨牌了,那么我们就找到了一个正确的解决方案。
如果仍有多米诺骨牌没有被放置,那么我们就返回步骤2,并尝试用其他的多米诺骨牌进行覆盖。
6. 最终,我们找到的正确的解决方案就是把所有多米诺骨牌都放置在位置上的布局。
总之,棋盘覆盖算法是一个重要的问题,它在计算机科学领域中具有广泛的应用。
在实际应用中,我们可以使用计算机来解决这个问题,例如利用回溯算法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用Visual C++实现棋盘覆盖分治算法
一、问题描述
在一个k k 22⨯个方格组成的棋盘中,恰有一个方格与其他方格不同,称该方格为一特殊方格,且称该棋盘唯一特殊棋盘。
在棋盘覆盖问题中,要用4种不同形态的L 型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格,且任何2个L 型骨牌不得重叠覆盖。
当0k >时,将k k 22⨯棋盘分割为4个1-k 1-k 22⨯子棋盘,特殊方格必位于4个较小子棋盘之一中,将其余3个子棋盘中无特殊方格。
为了将这3个无特殊方格子棋盘转化为特殊棋盘,可以用一个L 型骨牌覆盖着3个较小棋盘的会合处,从而将原问题转化为4个较小规模的棋盘覆盖问题。
递归的使用这种分割,直至棋盘转化为棋盘11⨯。
二、程序
(1)新建一个基于对话框的工程Ex0420Chess 。
(2)打开类视图,为CEx0420ChessDlg 类添加以下成员变量和函数:
int tile; //当前方块
int **board;
//指向棋盘的指针 int m_dw; //棋盘每一格的宽度
void chessBoard(int tr, int tc, int dr, int dc, int size); //棋盘覆盖算法
void DrawSubBoard(int x, int y, int w, int c); //画棋盘的x行,y列的方块,w表示宽度,c表示颜色值
(3)在对话框上增加三个编辑框,ID分别IDC_K、IDC_DR和IDC_DC,并为他们分别关联一个int型的变量m_k、m_dr和m_dc。
然后添加三个按钮,ID分别为IDC_DRAW、IDC_DRAWBOAR和DIDC_CLEAR,标题分别为画棋盘、覆盖和清空。
256 ,k值越大,方格越(4)本实验棋盘的大小固定为256
多,这时每个方格的尺寸越小。
为给每个L型骨牌填充不同的颜色,程序中将title的值转换成颜色值,画一个方格的函数DrawSubBoard()的定义如下:
void CEx0420ChessDlg::DrawSubBoard(int x ,int y ,int w, int c)
{
CClientDC dc(this);
COLORREF clr;
clr= RGB(c*c/256,c*c*c/256,c*c*c*c/256); //将c值转换成颜色值
CBrush br(clr);
CRect r;
=10+x*m_dw;
=+m_dw;
=10+y*m_dw;
=+m_dw;
(&r,&br);
}
使用分治算法覆盖棋盘,为清楚看到覆盖棋盘的顺序,每次覆盖完一个L型骨牌后停顿秒,chessBoard()函数源程序如下:
void CEx0420ChessDlg::chessBoard(int tr, int tc, int dr, int dc, int size)
{
if (size == 1) return;
Sleep(500);
int t = this->tile++; // L型骨牌号
int s = size/2; // 分割棋盘
// 覆盖左上角子棋盘
if (dr < tr + s && dc < tc + s) // 特殊方格在此棋盘中chessBoard(tr, tc, dr, dc, s);
else
{// 此棋盘中无特殊方格用t 号L型骨牌覆盖右下角
board[tr + s - 1][tc + s - 1] = t; // 覆盖其余方格
chessBoard(tr, tc, tr+s-1, tc+s-1, s);
this->DrawSubBoard(tr+s-1, tc+s-1,m_dw,t); //递归过程中,此子棋盘中没有特殊方格,调用DrawSubBoard()函数画一个方
格,并填充颜色
}
// 覆盖右上角子棋盘
if (dr < tr + s && dc >= tc + s)
// 特殊方格在此棋盘中
chessBoard(tr, tc+s, dr, dc, s);
else// 此棋盘中无特殊方格
{// 用t 号L型骨牌覆盖左下角
board[tr + s - 1][tc + s] = t;
// 覆盖其余方格
chessBoard(tr, tc+s, tr+s-1, tc+s, s);
this->DrawSubBoard(tr+s-1, tc+s,m_dw,t); }
// 覆盖左下角子棋盘
if (dr >= tr + s && dc < tc + s)
// 特殊方格在此棋盘中
chessBoard(tr+s, tc, dr, dc, s);
else
{// 用t 号L型骨牌覆盖右上角
board[tr + s][tc + s - 1] = t;
// 覆盖其余方格
chessBoard(tr+s, tc, tr+s, tc+s-1, s);
this->DrawSubBoard(tr+s, tc+s-1,m_dw,t);
}
// 覆盖右下角子棋盘
if (dr >= tr + s && dc >= tc + s)
// 特殊方格在此棋盘中
chessBoard(tr+s, tc+s, dr, dc, s);
else
{// 用t 号L型骨牌覆盖左上角
board[tr + s][tc + s] = t;
// 覆盖其余方格
chessBoard(tr+s, tc+s, tr+s, tc+s, s);
this->DrawSubBoard(tr+s, tc+s,m_dw,t);
}
}
(5)为三个按钮分别添加消息响应函数
//点击“画棋盘”按钮消息响应函数
void CEx0420ChessDlg::OnDraw()
{
UpdateData(); //更新编辑框中的数据,重要
if(m_k>5)
this->MessageBox("为了方便演示,建议输入1-5的整数");
else{
this->OnClear();
CClientDC dc(this); //当输入一个新的k值时,清空原有图形
int k=this->m_k;
this->m_dw=256/(int)pow(2,k);//棋盘区域大小固定为256*256,根据k值计算方格宽度
for(int i=10;i<267;i+=m_dw) //画棋盘
{
(10,i);
(267,i);
(i,10;
(i,267);
}
}
}
//点击“覆盖”按钮消息响应函数
Void CEx0420ChessDlg::Ondrawboard()
{
UpdateData();
if(m_dr>=(int)pow(2,m_k)||m_dc>=(int)pow(2,m_k)||m_dr<0|| m_dc<0)
//判断dr,dc中数据是否溢出
this->MessageBox("特殊方格行号或列号错误,请重新输入!");
else{
this->OnClear();
this->OnDraw();
CClientDC dc(this);
COLORREF clr;
clr = RGB(0,0,0);
CBrush br(clr);
CRect r;
int w = 256/(int)pow(2,m_k);
= 10+m_dr*w;
= +w;
= 10+m_dc*w;
= +w;
(&r,&br);
Sleep(1000);
this->chessBoard(0,0,this->m_dr,this->m_dc,(int)pow(2,this->m_k));
}
}
void CEx0420ChessDlg::Onclear()
{
CClientDC dc(this);
(10,10,267,267);
}
二,注意
本程序定义了一个指向指针的指针**board,在使用时必须进行初始化,初始化的方法为:
board = new int *[50];
for(int i=0;i<50;i++)
board[i]=new int[50];。
