NOIP2018-初赛-提高组
NOIP2018初赛提高组Pascal试题

NOIP2018初赛提高组Pascal试题第二十四届全国青少年信息学奥林匹克联赛初赛提高组Pascal语言试题竞赛时间:2018年10月13日14:30~16:30选手注意:●试题纸共有10页,答题纸共有2页,满分100分。
请在答题纸上作答,写在试题纸上的一律无效。
●不得使用任何电子设备(如计算器、手机、电子词典等)或查阅任何书籍资料。
一、单项选择题(共10题,每题2分,共计20分;每题有且仅有一个正确选项)1.下列四个不同进制的数中,与其它三项数值上不相等的是()。
A. (269)16B. (617)10C. (1151)8D. (1001101011)22.下列属于解释执行的程序设计语言是()。
A. CB. C++C. PascalD. Python3.中国计算机学会于()年创办全国青少年计算机程序设计竞赛。
A. 1983B. 1984C. 1985D. 19864.设根节点深度为0,一棵深度为h的满k(k>1)叉树,即除最后一层无任何子节点外,每一层上的所有结点都有k个子结点的树,共有()个结点。
A. (k h+1 - 1) / (k - 1)B. k h-1C. k hD. (k h-1) / (k - 1)5.设某算法的时间复杂度函数的递推方程是T(n) = T(n - 1) + n (n为正整数)及T(0) = 1,则该算法的时间复杂度为()。
A. O(log n)B. O(n log n)C. O(n)D. O(n2)6.表达式a * d - b * c的前缀形式是()。
A. a d * b c * -B. - * a d * b cC. a * d - b * cD. - * * a d b c7.在一条长度为1的线段上随机取两个点,则以这两个点为端点的线段的期望长度是()。
A. 1 / 2B. 1 / 3C. 2 / 3D. 3 / 58.关于Catalan数Cn = (2n)! / (n + 1)! / n!,下列说法中错误的是()。
2018年第二十四届全国青少年信息学奥林匹克联赛初赛提高组含问题详解(WORD重新整理排版)

第二十四届全国青少年信息学奥林匹克联赛初赛提高组 C++语言试题竞赛时间:2018 年 10 月 13 日 14:30~16:30(WORD重新整理排版)选手注意:●试题纸共有 9 页,答题纸共有 2 页,满分 100 分。
请在答题纸上作答,写在试题纸上的一律无效。
●不得使用任何电子设备(如计算器、手机、电子词典等)或查阅任何书籍资料。
一、单项选择题(共 10 题,每题 2 分,共计 20 分;每题有且仅有一个正确选项)1. 下列四个不同进制的数中,与其它三项数值上不相等的是()。
A. (269)16B. (617)10C. (1151)8D. (1001101011)22. 下列属于解释执行的程序设计语言是()。
A. CB. C++C. PascalD. Python3. 中国计算机学会于()年创办全国青少年计算机程序设计竞赛。
A. 1983B. 1984C. 1985D. 19864. 设根节点深度为 0,一棵深度为 h 的满 k(k>1)叉树,即除最后一层无任何子节点外,每一层上的所有结点都有 k 个子结点的树,共有()个结点。
A. (k h+1 - 1) / (k - 1)B. k h-1C. k hD. (k h-1 ) / (k - 1)5. 设某算法的时间复杂度函数的递推方程是 T(n) = T(n - 1) + n(n 为正整数)及 T(0) = 1,则该算法的时间复杂度为()。
A. O(log n)B. O(n log n)C. O(n)D. O(n2 )6. 表达式 a * d - b * c 的前缀形式是()。
A. a d * b c * -B. - * a d * b cC. a * d - b * cD. - * * a d b c7. 在一条长度为 1 的线段上随机取两个点,则以这两个点为端点的线段的期望长度是()。
A. 1 / 2B. 1 / 3C. 2 / 3D. 3 / 58. 关于 Catalan 数 Cn = (2n)! / (n + 1)! / n!,下列说法中错误的是()。
2018 NOIP广东省提高组复赛排名
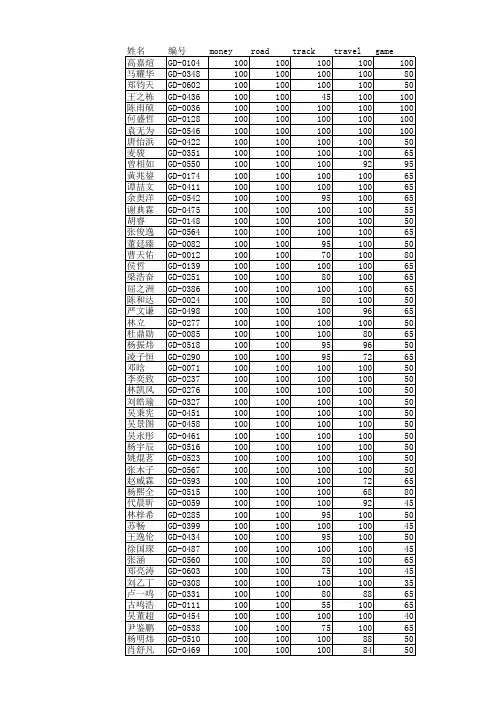
40 30 50 45 40 35 50 55 25 55 80 70 55 55 100 40 50 45 40 50 70 95 55 40 95 20 40 25 20 55 75 35 30 100 70 100 70 80 55 100 95 35 70 35 100 65 40 20 80 20 35 45 45 80
100 95 80 100 90 100 55 95 95 100 55 50 100 95 100 95 100 100 60 45 45 70 55 100 65 100 55 55 70 100 45 55 40 55 100 35 100 80 55 90 75 50 45 55 100 80 100 40 70 40 70 80 35 40
李晗 周魏 邓翔玮 冯烨聪 徐子博 孙文韬 杨佳杰 肖毅帆 杨鸿飞 陈子聪 谢俊 叶汇亘 陈奕林 李泽刚 李子扬 冼昊明 冯飞扬 麦隽绅 文荫华 罗富文 丁畅 孟涵宇 钟迪 冒泓希 冯启豫 刘天弘 贺睿杰 郑嘉佑 高诗豪 潘浩然 朱博凯 黄心悦 邹俊豪 颜星汉 何泓豪 刘澈 刘昊言 洪浩林 林家扬 杨烽 钟思哲 刘俊杰 刘钦玺 陈炜翀 李昊轩 姚敏清 赵艺博 冯英杰 黄致博 刘裕阳 郑少怀 邓植仁 李牧野 萧子若
罗以彬 洪云 周方远 苏静琦 李轩宇 卢凯宾 欧闻博 刘宇林 詹方榕 张家瑞 谢文龙 韩凯儒 丁其安 程司哲 刘森元 唐楷杰 张子扬 杨沁伟 池彦宽 蔡祺峰 尚崇轩 黄晓蓝 刘元昊 赵肖睿 覃浩芸 黄靖元 雷浩云 汪子杰 郑宇城 雷哲涵 谭泽晖 梁佩琪 潘昊翔 金典 苏律硕 杨睿轩 杨天行 陈漫璟 方展鸿 周楷文 覃天 何珈玮 黄凯佳 梁蕴誉 黄正 古智锋 胡晟智 李思博 刘青山 杨培源 詹哲轩 贺卓宇 李明翰 邓熙
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100
NOIP2018_day2
输出文件名为travel.out。
输出文件包含一行,! n 个整数,表示字典序最小的序列。相邻两个整数之间用一 个空格分隔。
【输入输出样例1】
travel.in
65 13 23 25 34 46
travel.out 132546
见选手目录下的travel/travel1.in和travel/travel1.ans。
● 在城市里驻扎军队会产生花费,在编号为!i的城市中驻扎军队的花费是p! i。 小Z很快就规划出了一种驻扎军队的方案,使总花费最小。但是国王又给小Z提出
了m! 个要求,每个要求规定了其中两座城市是否驻扎军队。小Z需要针对每个要求逐一 给出回答。具体而言,如果国王提出的第j! 个要求能够满足上述驻扎条件(不需要考虑 第j个要求之外的其它要求),则需要给出在此要求前提下驻扎军队的最小开销。如果
过这些道路从一个城市前往另一个城市。
小Y的旅行方案是这样的:任意选定一个城市作为起点,然后从起点开始,每次可 以选择一条与当前城市相连的道路,走向一个没有去过的城市,或者沿着第一次访问 该城市时经过的道路后退到上一个城市。当小Y回到起点时,她可以选择结束这次旅行 或继续旅行。需要注意的是,小Y要求在旅行方案中,每个城市都被访问到。
小Y是一个爱好旅行的OIer。她来到X国,打算将各个城市都玩一遍。
小Y了解到,X国的! n 个城市之间有! m 条双向道路。每条双向道路连接两个城 市。不存在两条连接同一对城市的道路,也不存在一条连接一个城市和它本身的道路。
并且,从任意一个城市出发,通过这些道路都可以到达任意一个其他城市。小Y只能通
fpc defense.pas
注意事项:
1、文件名(程序名和输入输出文件名)必须使用英文小写。 2、C/C++中函数main()的返回值类型必须是int,程序正常结束时的返回值必须是0。 3、全国统一评测时采用的机器配置为:Intel(R) Core(TM) i7-8700K CPU @ 3.70GHz,内存
NOIP2018提高组参考答案

第二十四届全国青少年信息学奥林匹克联赛初赛
提高组参考答案
一、单项选择题(共10题,每题2分,共计20分)
1 2 3 4 5 6 7 8 9 10
D D B A D B B A D B
二、不定项选择题(共5题,每题2分,共计10分;每题有一个或多个正确选项,没有部分分)
1 2 3 4 5
AB CD ABD ABD BCD
三、问题求解(共2题,每题5分,共计10分)
1.去了没去没去没下雨(第4空2分,其余1分)
2.454
四、阅读程序写结果(共4题,每题8分,共计32分)
1. 4
2. 6
3.16
4.输出1:2 1 3 5 6 4(3分)输出2:3 2 5 6 1 4(5分)
五、完善程序(共计28分,以下各程序填空可能还有一些等价的写法,由各省赛区组织本省专家审定及上机验证,可以不上报CCF NOI科学委员会复核)
Pascal语言C++语言C语言分值
1 . (1) a[x] := i a[x] = i 3
(2) i + 1 2
(3) R[a[i]] 3
(4) a[i] 3
(5) R[i] 3 2
2 . (1) a[i] * 0.95 <= b[i] 或b[i] >= a[i] * 0.95 2
(2)
total_a >= threshold 或threshold <= total_a 或total_a >= 50000 或50000 <=
total_a
3
(3) total_a + j + a[i] 3
(4) f[j] + total_b - total_b_prefix 3
(5) f[j - a[i]] 3。
信息学竞赛NOIP2018复赛提高组day2题目解答

全国信息学奥林匹克联赛(NOIP2018)复赛 M z(INF); for(int i=0;i<=1;i++) for(int j=0;j<=1;j++) for(int k=0;k<=1;k++) z.a[i][k]=min(z.a[i][k],a[i][j]+y.a[j][k]); return z; } }; struct lnk { lnk *last; long long x1,x2; lnk *left,*right; M now; lnk() { left=NULL; right=NULL; last=NULL; } void Trans() { now.a[0][0]=INF; now.a[1][0]=x2; now.a[1][1]=x2; now.a[0][1]=x1; if(right!=0) now=now*(right->now); if(left!=0) now=(left->now)*now; }
全国信息学奥林匹克联赛(NOIP2018)复赛 } } int main() { freopen("travel.in","r",stdin); freopen("travel.out","w",stdout); int n, m; scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) { scanf("%d%d",&edge[i].x,&edge[i].y); D[edge[i].x]++; D[edge[i].y]++; } for(int i=1;i<=n;i++) { a[i]=new int[D[i]+1]; a[i][0]=D[i]; } for(int i=1;i<=m;i++) { int x=edge[i].x,y=edge[i].y; a[x][D[x]--]=y; a[y][D[y]--]=x; } for(int i=1;i<=n;i++) sort(a[i]+1,a[i]+a[i][0]+1); if(m==n) { ans[1]=2;
全国青少年信息学奥林匹克竞赛联赛-广东计算机学会
2018年第二十四届全国青少年信息学奥林匹克联赛(NOIP 2018)广东赛区成绩公告2018年第二十四届全国青少年信息学奥林匹克联赛(NOIP 2018)广东赛区初赛实际参加人数为5201人(其中提高组1984人,普及组3217人),参赛学校337所。
复赛实际参赛人数为1469人(提高组647人,普及组822人), 有资格参加复赛的学校有139所。
本届参赛选手程序全部由全国统一测评,其中提高组一等奖按分配名额划线,结果提高组317名同学(含初二21人,初三52人)获联赛一等奖。
今届广东省获提高组联赛一等奖分数线高出全国基准分数线65分,分数线在全国排第五,获奖人数在全国排第二,表明广东省信息学竞赛不仅普及面而且尖子层人数也在全国前列。
35年的实践表明,GDOI(广东省青少年信息学(计算机)奥林匹克竞赛活动)是培养我们国家、我省计算机优秀后备人才的成功之路。
今年提高组一、二、三等奖及普及组一、二、三等奖均由全国划定基准分数线及获奖比例,最后确认:提高组一、二、三等奖分数线分别为310、160、120,普及组一、二、三等奖分数线分别为215、100、70。
今年全国提高组一等奖分数线按初、复参赛人数及平均分计算,各省分数线差别很大,广东一等奖奖项大幅度地高于全国的基准分数线,同时,广东提高组平均分在296分以上,高于全国21个省的一等奖分数线。
按照广东省信息学竞赛评委会制定的评估方法,综合测评省内各校在开展计算机教学和科技活动中取得的成绩,从全省参加复赛的学校中评出成绩优异的前60所学校,其中校团体一等奖10所,二等奖20所,三等奖30所。
在个人奖方面,NOIP2018广东赛区复赛分数线按照中国计算机学会规定划定一、二、三等奖,边界同分同奖的规则。
获奖统计情况如下表所列:参赛人数省一等省二等省三等获奖总数提高647317人(占49%)234人(占36.17%)32人(占4.95%)583人(占90.11%)普及822214人(占26.03%)544人(占66.18%)10人(占1.22%)768人(占93.43%)总数1469531人(占36.15%)778人(占52.96%)42人(占2.86%)1351人(占91.97%)其中,提高组获奖人数(583人)占复赛90.11%,普及组获奖人数(768人)占复赛93.43%,全省获奖人数(1351人)占复赛总人数91.97%。
NOIP2018提高组复赛试题day2
CCF全国信息学奥林匹克联赛(NOIP2018)复赛提高组 day2(请选手务必仔细阅读本页内容)注意事项:1、文件名(程序名和输入输出文件名)必须使用英文小写。
2、C/C++中函数main()的返回值类型必须是int,程序正常结束时的返回值必须是0。
3、全国统一评测时采用的机器配置为:Intel(R) Core(TM) i7-8700K CPU @ 3.70GHz,内存32GB。
上述时限以此配置为准。
4、只提供Linux格式附加样例文件。
5、特别提醒:评测在当前最新公布的NOI Linux下进行,各语言的编译器版本以其为准。
1.旅行(travel.cpp/c/pas)【问题描述】小Y是一个爱好旅行的OIer。
她来到X国,打算将各个城市都玩一遍。
小Y了解到,X国的 n 个城市之间有 m 条双向道路。
每条双向道路连接两个城市。
不存在两条连接同一对城市的道路,也不存在一条连接一个城市和它本身的道路。
并且,从任意一个城市出发,通过这些道路都可以到达任意一个其他城市。
小Y只能通过这些道路从一个城市前往另一个城市。
小Y的旅行方案是这样的:任意选定一个城市作为起点,然后从起点开始,每次可以选择一条与当前城市相连的道路,走向一个没有去过的城市,或者沿着第一次访问该城市时经过的道路后退到上一个城市。
当小Y回到起点时,她可以选择结束这次旅行或继续旅行。
需要注意的是,小Y要求在旅行方案中,每个城市都被访问到。
为了让自己的旅行更有意义,小Y决定在每到达一个新的城市(包括起点)时,将它的编号记录下来。
她知道这样会形成一个长度为 n 的序列。
她希望这个序列的字典序最小,你能帮帮她吗?对于两个长度均为 n 的序列A和B,当且仅当存在一个正整数x,满足以下条件时,我们说序列A的字典序小于B。
⚫对于任意正整数1≤i<x,序列A的第i个元素A i和序列B的第i个元素B i相同。
⚫序列A的第x个元素的值小于序列B的第x个元素的值。
NOIP2018提高组解题报告
NOIP2018 解题报告师大学附属中学天2018/11/21(此前题目填数游戏算法五部分出现笔误,已更正由于公式编辑器问题,部分数学公式可能无常显示Day 1铺设道路road标签:贪心简化版题意:给定一个非负整数序列,每次操作可选择一段区间使其中的数全部减,求全部减为需要的最少操作次数。
这题做法有很多……主流大概这么几种:算法一:考场上怎么简单粗暴怎么来每次找到最小值然后分治,不交并总数是的时间复杂度,空间复杂度算法二单调栈:头铁就是要写线性和算法一差不多,只不过使用了单调栈维护时间复杂度/空间复杂度算法三差分完正项的和就是答案。
时间复杂度,空间复杂度作为一道送分题,算法三应该是比较正常的思路然而场上甚至有人写了线段树,不知道是不是现在的选手数据结构有点学傻了……货币系统money标签:贪心,dp,背包简化版题意:给定个不同的正整数,求最少需要几个正整数,使得与这个整数在非负整数权线性组合下等价。
这题也很显然吧……首先给出的整数本身肯定是能被表示出来的,因此超过最大值的不用管,因为简化后肯定能用这些整数表示出来。
然后从小到大考虑每个整数是否能被原系统表示,如果不能就不管,如果能但可以被之前加入的更小的数表示也不管,否则就将其加入答案。
贪心的正确性是显然的,因为小于可被原系统表示的最小整数的数必然不能选,而该最小整数如果无法被此前选的数表示,就必须选。
考虑完该数后,将递归地得到一个子问题。
实现也很简单,就是一个裸的完全背包。
在具体实现上的分歧给出了三种算法:算法一老老实实跑完全背包时间复杂度,空间复杂度算法二考虑值只有,可以利用压位加速转移,不过每次直接重复移位多遍效率很低,可以再考虑二进制分组,即每次分别移位后与或原状态取或。
时间复杂度(取决于压位用或手写)空间复杂度这两种算法复杂度看上去比较极限,实际上并不会跑满,加之今年评测机性能极其优秀,完全没有压力。
**进阶算法**背包问题本质上是卷积,可以使用多项式理论对其进行优化。
第十六届全国青少年信息学奥林匹克联赛初赛试题(提高组,C++)
第十六届全国青少年信息学奥林匹克联赛初赛试题(提高组C++语言两小时完成)●●全部试题答案均要求写在答卷纸上,写在试卷纸上一律无效●●一.单项选择题(共 10 题,每题 1.5 分,共计 15 分。
每题有且仅有一个正确选项)1.与十六进制数A1. 2等值的十进制数是()。
A.101.2 B. 111.4 C. 161.125 D. 177.252.一个字节(byte)由()个二进制位组成。
A.8B. 16C. 32D. 以上都有可能3.以下逻辑表达式的值恒为真的是()。
A. P∨ (﹁P∧ Q)∨ (﹁P∧﹁Q)B. Q∨ (﹁P∧ Q)∨ (P∧﹁Q)C. P∨ Q∨ (P∧﹁Q)∨ (﹁P∧ Q)D. P∨﹁Q∨ (P∧﹁Q)∨ (﹁P∧﹁Q)4.Linux下可执行文件的默认扩展名为()。
A. exeB. comC. dllD. 以上都不是5.如果在某个进制下等式7*7=41成立,那么在该进制下等式12*12=( )也成立。
A. 100B. 144C. 164D. 1966.提出“存储程序”的计算机工作原理的是()。
A. 克劳德·香农B. 戈登·摩尔C. 查尔斯·巴比奇D. 冯·诺伊曼7.前缀表达式“+3 * 2 +5 12”的值是()。
A. 23B. 25C. 37D. 658.主存储器的存取速度比中央处理器(CPU)的工作速度慢得多,从而使得后者的效率受到影响。
而根据局部性原理,CPU所访问的存储单元通常都趋于聚集在一个较小的连续区域中。
于是,为了提高系统整体的执行效率,在CPU中引入了()。
A. 寄存器B. 高速缓存C. 闪存D. 外存9.完全二叉树的顺序存储方案,是指将完全二叉树的结点从上至下、从左至右,依次存放到一个顺序结构的数组中。
假定根结点存放在数组的1号位置,则第k号结点的父结点如果存在话,应当存放在数组的()号位置。
A. 2kB. 2k+1C. k/2下取整D. (k+1)/2下取整10.以下竞赛活动中历史最悠久的是()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B. 目前获得该奖项的华人学者只有姚期智教授一人。
C. 其名称取自计算机科学的先驱、英国科学家艾伦·麦席森·图灵。
D. 它是计算机界最负盛名、最崇高的一个奖项,有“计算机界的诺贝尔奖”之称。
三、问题求解(共 2 题,每题 5 分,共计 10 分) 1. 甲乙丙丁四人在考虑周末要不要外出郊游。 已知 1 如果周末下雨,并且乙不去,则甲 一定不去;2 如果乙去,则丁一定去;3 如果丙去,则丁一定不去;4 如果丁不去,而且甲不 去,则丙一定不去。如果周末丙去了,则甲________(去了/没去)(1 分),乙________(去了/ 没去)(1 分),丁________(去了/没去)(1 分),周末________(下雨/ 没下雨)(2 分)。 2. 方程 a*b = (a or b) * (a and b),在 a,b 都取 [0, 31] 中的整数时,共有_____组解。(*表 示乘法;or 表示按位或运算;and 表示按位与运算)
scanf("%d", &a[i]); } for (int i = 1; i <= t; ++i) {
getNext(); } for (int i = 1; i <= n; ++i) {
printf("%d", a[i]); if (i == n) putchar('\n'); else putchar(' '); } return 0; } 输入 1: 6 10 1 6 4 5 3 2 输出 1: _________ (3 分) 输入 2: 6 200 1 5 3 4 2 6 输出 2:_________(5 分)
while (x)
{
ret++;
________;
}
return ret;
}
则空格内要填入的语句是( )。
A. x >>= 1
B. x &= x - 1
C. x |= x >> 1 D. x <<= 1
二、不定项选择题(共 5 题,每题 2 分,共计 10 分;每题有一个或多个正确选项,多选
或少选均不得分)
}
} return false; } void getNext() { for (int i = 1; i <= n; ++i) {
isUse[i] = false; } getPermutation(1); for (int i = 1; i <= n; ++i) {
a[i] = b[i]; } } int main() { scanf("%d%d", &n, &t); for (int i = 1; i <= n; ++i) {
return 0;
}
输入:10 7 1 4 3 2 5 9 8 0 6
输出:_________
3. #include <iostream>
using namespace std;
string s;
long long magic(int l, int r) {
long long ans = 0;
五、完善程序(共 2 题,每题 14 分,共计 28 分) 1. 对于一个 1 到������的排列������(即 1 到������中每一个数在������中出现了恰好一次),令������������ 为 第������个位置 之后第一个比������值更大的位置,如果不存在这样的位置,则������������ = ������+ 1。举例来说,如果������ = 5 且������为 1 5 4 2 3,则������为 2 6 6 5 6。
一层上的所有结点都有 k 个子结点的树,共有( )个结点。
A. (kh+1 - 1) / (k - 1)
B. kh-1
C. kh
D. (kh-1) / (k - 1)
5. 设某算法的时间复杂度函数的递推方程是 T(n) = T(n - 1) + n(n 为正整数) 及 T(0) = 1,
则该算法的时间复杂度为( )。
求小猪买齐所有物品所需最少的总额。
( )。
A. 1 / 2
B. 1 / 3
C. 2 / 3
D. 3 / 5
8. 关于 Catalan 数 Cn = (2n)! / (n + 1)! / n!,下列说法中错误的是( )。
A. Cn 表示有 n + 1 个结点的不同形态的二叉树的个数。
B. Cn 表示含 n 对括号的合法括号序列的个数。
2. 下列属于解释执行的程序设计语言是( )。
A. C
B. C++
C. Pascal
D. Python
3. 中国计算机学会于( )年创办全国青少年计算机程序设计竞赛。
A. 1983
B. 1984
C. 1985
D. 1986
4. 设根节点深度为 0,一棵深度为 h 的满 k(k>1)叉树,即除最后一层无任何子节点外,
cin >> n; for (int i = 1; i <= n; ++i) {
int x; cin >> x;
(1) ; } for (int i = 1; i <= n; ++i) {
R[i] = (2) ; L[i] = i - 1; } for (int i = 1; i <= n; ++i) {
A. O(log n)
B. O(n log n)
C. O(n)
D. O(n2)
6. 表达式 a * d - b * c 的前缀形式是( )。
A. a d * b c * - B. - * a d * b c C. a * d - b * c D. - * * a d b c
7. 在一条长度为 1 的线段上随机取两个点,则以这两个点为端点的线段的期望长度是
C. Cn 表示长度为 n 的入栈序列对应的合法出栈序列个数。
D. Cn 表示通过连接顶点而将 n + 2 边的凸多边形分成三角形的方法个数。
9. 假设一台抽奖机中有红、蓝两色的球,任意时刻按下抽奖按钮,都会等概率获得红球或
蓝球之一。有足够多的人每人都用这台抽奖机抽奖,假如他们的策略均为:抽中蓝球则继续
下列程序读入了排列������,使用双向链表求解了答案。试补全程序。(第二空 2 分,其余 3 分) 数据范围 1 ≤ ������ ≤ 105。
#include <iostream> using namespace std; const int N = 100010; int n; int L[N], R[N], a[N]; int main() {
if (a[i] != b[i]) return a[i] < b[i]; return false; } bool getPermutation(int pos) { if (pos > n) {
return isSmall(); } for (int i = 1; i <= n; ++i) {
if (!isUse[i]) { b[pos] = i; isUse[i] = true; if (getPermutation(pos + 1)) { return true; } isUse[i] = false;
第二十四届全国青少年信息学奥林匹克联赛初赛试题(2018)
一、单项选择题(共 10 题,每题 2 分,共计 20 分;每题有且仅有一个正确选项)
1. 下列四个不同进制的数中,与其它三项数值上不相等的是( )。
A. (269)16
B. (617)10
C. (1151)8
D. (1001101011)2
++res;
}
}
printf("%d", res);
return 0;
}
输入:15
输出:_________
2. #include <cstdio>
int n, d[100];
bool v[100];
int main() {
scanf("%d", &n);
for (int i = 0; i < n; ++i) {
路。D. 当图中不存在负权边时,调用一次 Dijkstra 算法不能用于每对顶点间最短路
计算。
4. 下列说法中,是树的性质的有( )。
A. 无环
B. 任意两个结点之间有且只有一条简单路径
C. 有且只有一个简单环
D. 边的数目恰是顶点数目减 1
5. 下列关于图灵奖的说法中,正确的有( )。
A. 图灵奖是由电气和电子工程师协会(IEEE)设立的。
for (int i = l; i <= r; ++i) {
ans = ans * 4 + s[i] - 'a' + 1;
}
return ans;
}
int main() {
cin >> s;
int len = s.length();
int ans = 0; for (int l1 = 0; l1 < len; ++l1) {
for (int r1 = l1; r1 < len; ++r1) { bool bo = true; for (int l2 = 0; l2 < len; ++l2) { for (int r2 = l2; r2 < len; ++r2) { if (magic(l1, r1) == magic(l2, r2) && (l1 != l2 || r1 != r2)) { bo = false; } } } if (bo) { ans += 1; }
