人工智能05约束满足问题
人工智能的约束满足与规划

人工智能的约束满足与规划人工智能(Artificial Intelligence,简称AI)作为一种能够模拟人类智能和执行智能任务的科技应用,已经拥有了广泛的应用领域,例如机器学习、计算机视觉、自然语言处理等。
然而,尽管人工智能的发展飞跃,但其受到的限制和约束仍然存在。
在人工智能的研究与应用中,约束满足与规划是不可或缺的关键技术和方法。
本文将对进行深入探讨。
人工智能的约束满足指的是在进行决策和行动选择时,遵循一定的限制条件,以满足特定的目标或需求。
这些限制可以是直接的物理约束,如资源的有限性、环境的不确定性等,也可以是间接的条件约束,如伦理规范、法律法规等。
在人类和自然界的决策行为中,约束满足是一种常见的现象。
例如,当人们在制定旅行计划时,他们必须考虑到时间、预算、旅行方式等一系列的限制因素,以确保计划的可行性和实施性。
同样地,人工智能在执行给定任务时,也需要遵循相应的约束条件。
约束满足与规划在人工智能中具有广泛的应用。
其中一个重要的应用领域是智能机器人。
智能机器人作为一种能够完成复杂任务的智能系统,需要在执行任务时考虑到各种约束条件。
例如,在进行路径规划时,智能机器人需要考虑到环境的不确定性和障碍物的存在,以避免发生碰撞或危险。
在进行机器人协作时,智能机器人需要遵守团队合作的规则和任务分配的约束,以保证协同工作的效率和安全性。
此外,智能机器人还需要遵守人类和社会的伦理规范,不得侵犯他人的权益或违反道德准则。
约束满足与规划还在其他领域的人工智能应用中发挥着重要作用。
例如,在自然语言处理领域,人工智能需要遵循语法规则和语义逻辑,以确保产生的文本具有正确的语法和语义。
在人脸识别和计算机视觉中,人工智能需要满足特定的算法要求和模型约束,以实现准确和可靠的识别结果。
在医疗诊断领域,人工智能需要遵循医学知识和临床规范,以确保疾病诊断的准确性和安全性。
为了实现约束满足与规划,人工智能领域提出了一系列的技术和方法。
【浙江省自然科学基金】_约束满足问题_期刊发文热词逐年推荐_20140812
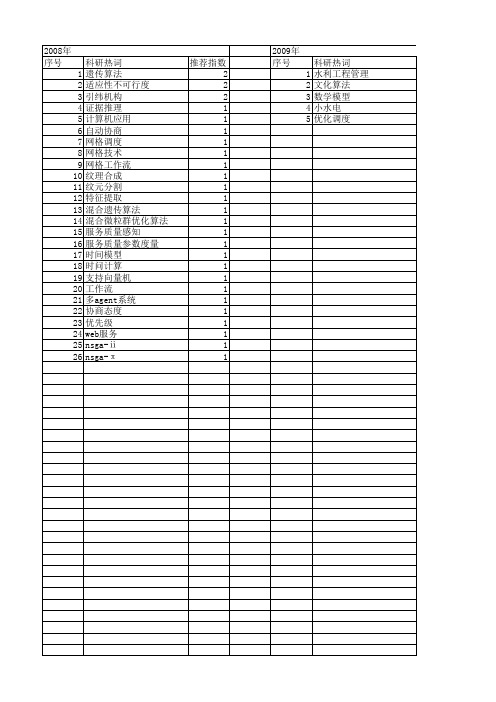
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12
ห้องสมุดไป่ตู้
科研热词 遗传算法 过完备字典 超分辨率 自适应约束传播 约束满足问题 稀疏表示 混流混合 比特位操作 模糊 字典训练 人工智能 云图
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
推荐指数 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
2011年 科研热词 约束满足问题 约束分解技术 知识表示框架 零件分类 迭代逼近 约束满足优先级 田口式三步设计 状态爆炸问题 状态图 模型验证 模型检查 时序逻辑 插值 形式化语义 尺寸变化概率分配 尺寸冲突 容差划分 多目标优化 变型设计 反应系统 参数标定 几何设计 产品变型主模型 交互修改 b-spline曲面 推荐指数 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
科研热词 非均匀分布 随机过程 重建时间 评价指标 蚁群算法 蔬菜钵苗 能量空洞 能量模型 网络编码 绿色评价 绿色计算 约束满足 约束传播 移栽机 模型检测 条件约束 机床 无线传感器 无线mesh网络 护士排班 手术排程 成组调度 多资源约束 启发式搜索 台架试验 取苗机构 参数优化 分布式存储系统 修复带宽 传感器配置 仿真 互模拟 主轴
推荐指数 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
约束满足问题及其求解方法研究

约束满足问题及其求解方法研究随着现代科技的快速发展,人们对各种求解问题的需求日益增长,其中,约束满足问题是一个相对独特却又十分重要的问题类型。
在此,我们将从定义、特点、应用以及求解方法几个方面谈一谈约束满足问题及其求解方法的相关内容。
一、定义约束满足问题(Constraint Satisfaction Problem,CSP)是指在一定约束条件下,满足对变量的限制(约束条件)的数学问题。
因此,CSP可以被定义为一个元组(X,D,C):X 表示所有的变量集合,D 表示每个变量 x ∈ X 的定义域,C 表示x∈X 的约束集合。
二、特点CSP问题通常具有以下几个特点:1、通用性强:CSP问题可以用于描述各种类型的问题,如图着色和行程问题等。
2、规模大:CSP问题通常涉及到大量的变量和约束,其求解过程相对复杂,因此,系统的设计和求解方法是至关重要的。
3、复杂度高:大多数CSP问题属于NP完全问题,无法在多项式时间内精确地解决,同时,这些问题的求解方法也比较困难。
三、应用CSP的应用非常广泛,以下是其中几个代表性的应用领域。
1、人工智能:CSP可以用于优化问题、机器学习、计算机视觉等人工智能任务。
2、排程问题:CSP可以用于作业坊调度、员工排班等任务中。
3、生产问题:CSP可以用于零件生产、工厂排布等任务中。
4、电子设计自动化:CSP可以用于电路自动布局、芯片设计等任务中。
四、求解方法针对CSP问题的复杂性,目前有多种求解方法,这里简要介绍几种主流的方法。
1、基于启发式算法的方法:启发式算法通常针对CSP问题中的子问题进行求解,能够得到比较好的求解结果,但是求解时间可能较长。
2、基于局部搜索的方法:局部搜索算法的优点在于其求解速度较快,但其无法得到全局最优解,可能只能得到局部最优解。
3、基于约束传播的方法:约束传播算法利用限制传播的策略进行求解,能够得到可行解或确定无解,但是在求解大规模问题方面表现相对不足。
5.约束满足问题

– 从Xi向前是无解的 / 从Xi回到某个以前的变量 赋值
– 例如:赋值顺序是WA-NSW-NT-Q-SA(发生错
误)
28
– 每个变量都有一个非空可能值域Di – 每个约束指定了包含若干变量的一
个子集内各变量的赋值范围
• CSP的一个状态—对一些或全部变量的赋值 {Xi=vi, Xj=vj, …}
3
CSP问题的解
• 一个不违反任何约束的对变量的赋值称 为相容赋值或合法赋值
• 对每个变量都进行赋值称为完全赋值 • 一个(一组)既是相容赋值又是完全赋值的
– 考虑U有进位:R={0,2,4,6,8} O={5,……} R=0/O=5(有进位)/T=7/W=6/U=3 解={1530 | 765}
8
例2:密码算术问题(2)
• 四列算式约束
– O+O=R+10*X1
– X1+W+W=U+10*X2
– X2+T+T=O+10*X3
– X3=F
• 对应的约束超图如右
– 当到达Y时,可知回溯到哪个变量
26
后向跳转
• 回溯检验导致失败的变量的赋值—后向 跳转:回溯到冲突集中时间最近(最后赋 值)的变量
• 每个被后向跳转剪枝的分支在前向检验 算法中也被剪枝—简单的后向跳转在前 向检验(弧相容性检验)搜索中是多余的
• 因为都是做取值相容的检测,只要在弧 相容检验时增加一个变量集合记录即可
–当前变量的赋值会对其他未赋值变量产生什 么约束?怎样利用这种约束以提高效率?
–当遇到某个失败的变量赋值时,怎样避免同 样的失败?就是说找到对这种失败起到关键 作用的某个变量赋值
18
人工智能一种现代方法,课后题名词解释

constraint约束:一个约束是对两个或多个变量的可能值的限制。例如,一个约束可能是,当会同B=b时A= a是不允许的。
Backtracking search回溯搜索:回溯搜索是一种形式的深度优先搜索,这种状态有一个单一的表现,即从每个后继获得更新然后必须在查找结束后恢复。
名词解释
Intelligence: 字典中定义为“获取知识和应用知识的能力”或“思考和推理的能力”或“理解和从经验中获益的能力”。这些都是合理的解释,但是如果我们想要量化的定义那就是“为了在一种环境下更好的执行而应用知识的能力”
Artificial intelligence: 智能体程序的研究和构建,对于一个给定的智能体体系,它可以在给定的环境下做正确的事。
state space状态空间:一个状态空间是一个图表,它的结点是所有状态的集合,且它的连接是从一个状态转变为另一状态的行为。
search tree搜索树:搜索树是一棵树(有计划性循环的一个图表),在这棵树里,根结点是开始状态,每个结点的子集由通过采取行动可达到的状态组成。
search node搜索节点:搜索树上的节点
Arc consistent:弧相容指在CSP中从变量A到变量B的一个定向弧,对于当前A值域中的每一个值,在B中存在它的相容值。
Backjumping向后跳转:向后跳转是使回溯搜索更有效的方法,当一个结束点到来时,通过不止一级的向后跳转(使回溯搜索更有效)
Min-conflicts最小冲突:最小冲突是一个在使用本地搜索解决CSP问题时的启发式。启发式的大意是,当给定一个要修改的变量,选择那些与其他变量冲突最少的值。
用CSP(约束满足问题)方法解决八皇后问题

conflictNum++; } } //检查同一列是否有冲突 j=column; for(i=0;i<N;i++) { if((i!=row)&&(queenBoard[i][j]==QUEEN)) {
//如果同一列其它位置有皇后,记录冲突点数 conflictNum++; } } //检查'\'斜线是否有冲突 if(row>column) { i=row-column; j=0; } else { i=0; j=column-row; } for(;(i<N)&&(j<N);i++,j++ ) { if((i!=row)&&(queenBoard[i][j]==QUEEN)) { //如果'\'斜线其它位置有皇后,记录冲突点数 conflictNum++; } } //检查'/'斜线是否有冲突 if((row+column)<N) { i=row+column; j=0; } else { i=N-1; j=row+column-N+1; } for(;(i>=0)&&(j<=N);i --,j++)
该列的每一行中与该位置有冲突的皇后数,选取冲突数最小的位置作为新的该列的皇后位置, 并记录下该列被放置皇后的信息,记录被放置皇后信息的目的是为了避免算法陷入死循环。
为了更清楚地说明该算法,假设算法某一步搜索到的状态如下:
此时按照最小冲突算法,第二列、第六列、第七列和第八列的皇后 有冲突,则当计算第六列 的每一行的与该位置有冲突的皇后数时,结果如下:
人工智能的约束满足和优化问题

人工智能的约束满足和优化问题在当今科技领域已经成为一个热门话题。
随着人工智能技术的不断发展,人们对于如何在人工智能应用中处理约束条件和优化问题提出了更高的要求。
本文将从理论和实践两方面探讨,并就相关应用领域进行案例研究。
首先,我们来介绍人工智能中的约束满足问题。
在人工智能应用中,约束满足是指在一定条件下,使得问题的解满足一定的约束条件。
在一些现实生活中的问题中,约束是必要的,比如在资源分配问题中,约束能够保证资源的合理利用;在生产计划问题中,各种约束条件可以保证生产过程的正常进行。
在人工智能领域,如何解决约束满足问题成为一个重要的挑战。
人工智能中的约束满足问题可以通过多种方式解决,其中较为常见的是约束满足优化问题。
优化问题通过寻找最优解来满足约束条件。
例如,在机器学习中,我们可以使用优化算法来优化模型的目标函数,同时保证模型满足一定的约束条件。
常见的优化算法包括梯度下降算法、遗传算法等。
在实践中,应用广泛。
下面我们以交通流控制和供应链管理两个应用场景进行案例研究。
首先是交通流控制。
在城市交通管理中,如何合理控制交通流量是一个重要的问题。
传统的方法往往采用固定的信号灯控制方案,但是由于交通流量的变化以及路面情况的复杂性,传统的方法容易导致交通堵塞。
可以通过学习交通数据,并使用优化算法来找到最优的信号灯控制方案。
例如,可以使用遗传算法来优化信号灯的配时方案,并考虑交通流量、路况等因素的约束条件,以满足交通流量控制的需求。
通过这种方法,可以提高交通效率,减少交通拥堵。
其次是供应链管理。
在现代供应链管理中,如何有效地调配资源,满足需求,是一个重要的挑战。
传统的供应链管理往往采用固定的生产计划方案,但是由于需求的变化以及供应链各个环节的复杂性,固定方案容易导致资源的浪费或者供应链断裂。
可以通过学习供应链数据,并使用优化算法来找到最优的生产计划方案。
例如,可以使用线性规划算法来优化供应链各个环节的资源分配方案,并考虑需求、生产能力等因素的约束条件,以满足供应链管理的需求。
约束满足问题(CSP)的算法探索

约束满足问题(CSP)的算法探索约束满足问题(Constraint Satisfaction Problem,CSP)是人工智能领域中的一个重要问题类型,涉及到在一组变量上的取值,同时满足一系列约束条件。
CSP在实际生活中有着广泛的应用,比如在排课、时间表安排、资源分配等领域都可以看到CSP的身影。
为了解决CSP问题,人们提出了各种不同的算法,本文将对CSP问题及其相关算法进行探索和介绍。
### 什么是约束满足问题(CSP)?约束满足问题是指一组变量,每个变量有一定的取值范围,同时还有一系列约束条件限制这些变量的取值。
CSP的目标是找到一组取值,使得所有约束条件都得到满足。
通常来说,CSP可以用一个三元组表示:CSP = (X, D, C),其中:- X = {X1, X2, ..., Xn} 表示一组变量;- D = {D1, D2, ..., Dn} 表示每个变量对应的取值范围;- C = {C1, C2, ..., Cm} 表示约束条件的集合。
### CSP的经典问题CSP问题有许多经典的应用场景,下面介绍几个常见的CSP问题:1. **地图着色问题**:给定一张地图和一定数量的颜色,要求每个地区用一种颜色着色,相邻的地区不能使用相同的颜色。
2. **八皇后问题**:在8×8的国际象棋棋盘上放置8个皇后,使得它们互相不能攻击到对方。
3. **数独问题**:填充一个9×9的网格,使得每一行、每一列和每个3×3的子网格中的数字都是1到9且不重复。
### CSP的求解算法为了解决CSP问题,人们提出了多种求解算法,常见的包括回溯算法、约束传播算法和启发式搜索算法等。
下面分别介绍这几种算法: #### 1. 回溯算法回溯算法是解决CSP问题最常用的方法之一。
其基本思想是逐步尝试每个变量的取值,并检查是否满足约束条件,如果不满足则回溯到上一步重新选择取值。
回溯算法的优点是简单易懂,但在处理大规模问题时效率较低。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Example: Map-Coloring
变量 WA, NT, Q, NSW, V, SA, T 值域 Di = {red,green,blue} 约束: adjacent regions must have different colors e.g., WA ≠ NT, or (if the language allows this), or (WA,NT) ∈ {(red,green),(red,blue),(green,red), (green,blue), … }
Degree heuristic(度启发式)
在MRV无法抉择时启动度启发式 度启发式: 通过选择涉及对其它未赋值变量的约束数最大的变 量
提高回溯效率
General-purpose methods can give huge gains in speed:
1. 哪一个变量应该被下一个赋值? 2. 赋值应该以什么样的顺序被尝试?
第五章 约束满足问题
Review: Last Chapter
• Best-first search Heuristic functions estimate costs of shortest paths Good heuristics can dramatically reduce search cost
3. 能更早察觉到不可避免的失败吗?
4. Can we take advantage of problem structure?
Minimum remaining values
Minimum remaining values 最少剩余值(MRV): 选择“合法”取值最少的变量
Why min rather than max? 被称为“最受约束变量” 或“失败优先”启发式
Standard search problem: state is a “black box“ – any old data structure that supports goal test, eval, successor 任何可以由目标测试、评价函数、后继函数访问的数据结构 CSP: state is defined by variables Xi with values from domain(值域)Di goal test is a set of constraints specifying allowable combinations of values for subsets of variables 每个约束包括一些变量的子集,并指定这些子集的值之间允许进行的 合并 Simple example of a formal representation language(形式化表示方法) Allows useful general-purpose(通用的,而不是问题特定的) algorithms with more power than standard search algorithms
Greedy best-first search expands lowest h — incomplete and not always optimal A* search expands lowest g+ h — complete and optimal — also optimally efficient (up to tie-breaks, for forward search)
列举分配
指数时间 dn But complete can we be clever about exponential time algorithms?
形式化描述标准搜索 (incremental增量形式化)
从简单直白的方法开始,状态被定义为已被赋值的变量 • 初始状态: 空的赋值, { } • 后继函数: 给一个未赋值变量赋值使之不与当前状态冲突 → fail 如果没有合法赋值 • 目标测试: 检验当前赋值是否完全 1. This is the same for all CSPs! 2. Every solution appears at depth n with n variables → use depth-first search 3. Path is irrelevant, so can also use complete-state formulation (完全状态形式化) 4. b = (n - l )d at depth l, hence n! ·dn leaves !!!!
Binary CSP: 每个约束与2个变量有关 约束图: 节点是变量, 边是约束
General-purpose CSP algorithms(通用CSP算法) use the graph structure to speed up search. E.g., Tasmania is an independent subproblem!
结合以上启发式来解决1000 queens 是可行的
提高回溯效率
General-purpose methods can give huge gains in speed:
1. 哪一个变量应该被下一个赋值? 2. 赋值应该以什么样的顺序被尝试?
3. 能更早察觉到不可避免的失败吗?
4. Can we take advantage of problem structure?
Example: Map-Coloring
Solutions are assignments satisfying all constraints, e.g., {WA=red, NT =green, Q=red, NSW =green, V =red, SA=blue, T=green}
Constraint graph(约束图)
回溯搜索
Backtracking example
Backtracking example
Backtracking example
Backtracking example
提高回溯效率
General-purpose methods can give huge gains in speed:
1. 哪一个变量应该被下一个赋值? 2. 赋值应该以什么样的顺序被尝试?
Backtracking search回溯搜索
变量赋值具有可交换性 , 也就是说 [ WA = red then NT = green ] same as [ NT = green then WA = red ] 在搜索树的每个节点上只考虑单个变量的可能赋值 b = d and there are dn leaves Depth-first search for CSPs with single-variable assignments is called backtracking search 回溯搜索是处理CSP问题最基础的无信息搜索算法 Can solve n-queens for n ≈ 25
Admissible heuristics can be derived from exact solution of relaxed problems
Review: Last Chapter
Local search algorithms • the path to the goal is irrelevant; the goal state itself is the solution • keep a single "current" state, try to improve it
• 偏好约束 (soft constraints), e.g., red is better than green often representable by a cost for each variable assignment (个体变量赋值的耗散) →约束优化问题
Example: 密码算数
变量: F T U W R O X1 X2 X3 值域: {0,1,2,3,4,5,6,7,8,9} 约束: alldiff (F,T,U,W,R,O) O + O = R + 10 ·X1 X1 + W + W = U + 10 ·X2 X2 + T + T = O + 10 ·X3 X3 = F, T ≠ 0, F ≠ 0
3. 能更早察觉到不可避免的失败吗?
4. Can we take advantage of problem structure?
最少约束值
一个变量被选定, choose the least constraining value(最少约束值) : • 这个选择的值是在约束图中排除邻居变量的可选值最少的 • 需注意的是可能需要经过一些计算来确定这个值
CSP的种类
离散变量 • finite domains 有限值域: n 个变量, 值域大小d → O(dn) 完全赋值 e.g., Boolean CSPs/布尔CSP问题(NP-complete) • infinite domains 无限值域 (integers, strings, etc.) e.g., job scheduling, variables are start/end days for each job 不能通过枚举来描述值域,只能用约束语言 , e.g., 线性约束可解, 非线性约束不可解
本章大纲
• CSP examples
• Backtracking search for CSPs • Problem structure and problem decomposition
• Local search for CSPs
Constraint satisfaction problems (CSPs)
连续值域的变量 e.g., 哈勃望远镜观测的开始、结束时间 线性规划问题linear constraints solvable in polynomial time by linear programming(LP) methods
