(完整版)高中数学选修4-4单元测试题-极坐标与参数方程.docx
高二年数学选修4-4坐标系与参数方程测试(附答案)
高二年数学选修4-4坐标系与参数方程测试班级:__________________ 座号:______ 姓名：___________________成绩：___________ 一、选择题（共12题，每题5分）1、点M的直角坐标是(-，则点M 的极坐标为（ ） A ．(2,)3πB ．(2,)3π-C ．2(2,)3πD ．(2,2),()3k k Z ππ+∈ 2、极坐标系中，下列各点与点P （ρ，θ）（θ≠k π，k ∈Z ）关于极轴所在直线对称的是 （ ）A ．（-ρ，θ）B ．（-ρ，-θ）C ．（ρ，2π-θ）D ．（ρ，2π+θ） 3．已知点P 的极坐标为（1，π），那么过点P 且垂直于极轴的直线的极坐标方程是 （ ）A ．ρ=1B ．ρ=cosθC ．ρ=-θcos 1D ．ρ=θcos 14．以极坐标系中的点（1，1）为圆心，1为半径的圆的方程是 （ ）A ．ρ=2cos(θ-4π) B ．ρ=2sin(θ-4π) C ．ρ=2cos(θ-1) D ．ρ=2sin(θ-1) 5．极坐标方程cos 2sin 2ρθθ=表示的曲线为（ ）A ．一条射线和一个圆B ．两条直线C ．一条直线和一个圆D ．一个圆 6．若直线的参数方程为12()23x tt y t=+⎧⎨=-⎩为参数，则直线的斜率为（ ）A ．23 B ．23- C ．32 D ．32- 7．在极坐标系中，以（2,2πa ）为圆心，2a为半径的圆的方程为（ ）A ．θρcos a =B ．θρsin a =C ．a =θρcosD ．a =θρsin8．曲线的参数方程为⎩⎨⎧-=+=12322t y t x (t 是参数)，则曲线是（ ） A ．线段 B .双曲线的一支 C.圆 D.射线 9、在同一坐标系中，将曲线y=2sin3x 变为曲线y=sinx 的伸缩变换是（ ）A ．⎪⎩⎪⎨⎧==//213y y x xB ．⎪⎩⎪⎨⎧==y y xx 213//C ．⎩⎨⎧==//23y y x xD ．⎩⎨⎧==y y x x 23// 10．下列在曲线sin 2()cos sin x y θθθθ=⎧⎨=+⎩为参数上的点是（ ）A ．1(,2B ．31(,)42- C ． D ．11、直线：3x-4y-9=0与圆：⎩⎨⎧==θθsin 2cos 2y x ，(θ为参数)的位置关系是( )A.相切B.相离C.直线过圆心D.相交但直线不过圆心12、设P(x ，y)是曲线C ：⎩⎨⎧θ=θ+-=sin y ,cos 2x （θ为参数，0≤θ<2π）上任意一点，则yx的取值范围是 （ ）A ．[-3，3]B ．（-∞，3）∪[3，+∞]C ．[-33，33]D ．（-∞，33）∪[33，+∞]二、填空题（共8题，各5分）1、点A 的直角坐标为（1，1，1），则它的球坐标为 ，柱坐标为2、曲线的1cos 3sin --=θθρ直角坐标方程为____________________3、直线3()14x att y t=+⎧⎨=-+⎩为参数过定点_____________4、设()y tx t =为参数则圆2240x y y +-=的参数方程为__________________________。
高中数学选修44极坐标与参数方程试题
高中数学选修44极坐标与参数方程试题————————————————————————————————作者：————————————————————————————————日期：高中数学选修4-4综合试题一、选择题1.直线12+=x y 的参数方程是（ ）A 、⎩⎨⎧+==1222t y t x （t 为参数） B 、⎩⎨⎧+=-=1412t y t x （t 为参数）C 、 ⎩⎨⎧-=-=121t y t x （t 为参数） D 、⎩⎨⎧+==1sin 2sin θθy x （t 为参数） 2.若点(3,)P m 在以点F 为焦点的抛物线24()4x t t y t⎧=⎨=⎩为参数上，则||PF 等于（ ）． A ．2 B ．3 C ．4 D ．53.已知⎪⎭⎫ ⎝⎛-3,5πM ，下列所给出的不能表示点M 的坐标的是( )A 、⎪⎭⎫⎝⎛-3,5π B 、⎪⎭⎫ ⎝⎛34,5πC 、⎪⎭⎫⎝⎛-32,5π D 、⎪⎭⎫ ⎝⎛--35,5π 4.极坐标系中，下列各点与点P （ρ，θ）（θ≠k π，k ∈Z ）关于极轴所在直线对称的是（ ）A ．（-ρ，θ）B ．（-ρ，-θ）C ．（ρ，2π-θ）D ．（ρ，2π+θ）5.点()3,1-P ，则它的极坐标是( )A 、⎪⎭⎫ ⎝⎛3,2πB 、⎪⎭⎫ ⎝⎛34,2πC 、⎪⎭⎫⎝⎛-3,2π D 、⎪⎭⎫ ⎝⎛-34,2π 6.直角坐标系xoy 中，以原点为极点，x 轴的正半轴为极轴建极坐标系，设点A,B 分别在曲线13cos :sin x C y θθ=+⎧⎨=⎩ （θ为参数）和曲线2:1C ρ=上，则AB 的最小值为( ).A.1B.2C.3D.47.参数方程为1()2x t t t y ⎧=+⎪⎨⎪=⎩为参数表示的曲线是（ ）A ．一条直线B ．两条直线C ．一条射线D ．两条射线8.()124123x tt x ky k y t=-⎧+==⎨=+⎩若直线为参数与直线垂直，则常数（ ） A.-6 B.16-C.6D.169.极坐标方程4cos ρθ=化为直角坐标方程是( )A ．22(2)4x y -+= B.224x y += C.22(2)4x y +-= D.22(1)(1)4x y -+-=10.柱坐标（2，32π，1）对应的点的直角坐标是（ ）. A.(1,3,1-) B.(1,3,1-) C.(1,,1,3-) D.(1,1,3-)11.点(1,2)在圆18cos 8sin x y θθ=-+⎧⎨=⎩的（ ）．A ．内部B ．外部C ．圆上D ．与θ的值有关12.曲线24sin()4x πρ=+与曲线12221222x ty t ⎧=-⎪⎪⎨⎪=+⎪⎩的位置关系是（ ）。
(完整版)选修4-4坐标系与参数方程-高考题及答案
x t 3,1、已知在直角坐标系xOy中，直线I的参数方程为_ （t为参数），在极坐标系（与y v3t直角坐标系xOy取相同的长度单位，且以原点0为极点，以x轴正半轴为极轴）中，曲线C 的极坐标方程为2 4 cos 3 0.①求直线I普通方程和曲线C的直角坐标方程；②设点P是曲线C上的一个动点，求它到直线I的距离的取值范围.x = 2cos 0 , 一2、已知曲线C的参数方程是（0为参数），以坐标原点为极点，x轴的正半轴y = 3sin 0 ,为极轴建立极坐标系，曲线C2的极坐标方程是p = 2,正方形ABCD勺顶点都在C2上，且AnB C、D依逆时针次序排列，点A的极坐标为（2 ,—）.3（I ）求点A B C、D的直角坐标；（n ）设P为C上任意一点，求|PA2+ |PB2+ |PC2+ |PD2的取值范围.. . 2 2 . - 2 23、在直角坐标系xOy中，圆C ：x + y = 4,圆C2：(x—2) + y = 4.(I )在以O为极点，x轴正半轴为极轴的极坐标系中，分别写出圆C i, C2的极坐标方程, 并求出圆C，C2的交点坐标(用极坐标表示)；(n)求圆C与C2的公共弦的参数方程.4、在直角坐标系xOy中，直线I的方程为x —y + 4 = 0，曲线C的参数方程为x= ：：：］3cos a ,(a为参数).y= sin a(1)已知在极坐标系(与直角坐标系xOy取相同的长度单位，且以原点O为极点，以xn轴正半轴为极轴)中，点P的极坐标为(4 ,―)，判断点P与直线I的位置关系；(2)设点Q是曲线C上的一个动点，求它到直线I的距离的最小值.X = 2C0S a ,5、在直角坐标系xOy 中，曲线G 的参数方程为( a 为参数).M 是C i 上的y = 2+ 2sin a .动点，P 点满足0F= 20M P 点的轨迹为曲线 C 2.(1)求C 2的方程；(2)在以0为极点，x 轴的正半轴为极轴的极坐标系中，射线 交点为A ,与C 2的异于极点的交点为 B,求|AE |.x = cos e6、已知P 为半圆C:( e 为参数，o w e wn )上的点，点 A 的坐标为(1,0) , Oy = sin en 为坐标原点，点 M 在射线OP 上，线段OM 与C 的弧AP 的长度均为—.(1) 以O 为极点，x 轴的正半轴为极轴建立极坐标系，求点 M 的极坐标;(2) 求直线AM 的参数方程.ne =g 与C 的异于极点的n n .* j 3 7、在极坐标系中，已知圆C经过点P .2，~4，圆心为直线P sin 9—3 =一与极轴的交点，求圆C的极坐标方程.8、在平面直角坐标系中，以坐标原点0为极点，x轴的正半轴为极轴建立极坐标系.已知直线I上两点M, N的极坐标分别为(2,0), 穿,-2，圆C的参数方程为x= 2+ 2cos 9 ,厂(9为参数).y=—3+ 2sin 9(1) 设P为线段MN的中点，求直线OP的平面直角坐标方程；(2) 判断直线l与圆C的位置关系.1、【答案】①直线I 的普通方程为：,3x y 3、、3 0. n n n n nn_nnA (2cos —, 2sin —), B (2cos(-3 + R , 2sin( — + —)) , q2cos( — +n ), 2sin( — +n 3 n n 3 nn )) , D (2cos( — + 〒),2sin( — + 亍)),即 A (1 , 3) , B ( — 3 , 1), Q — 1, — 3) , D ( 3 , — 1). (n )设 P (2cos 0 , 3sin 0 ),令 S =|PA 2+ |PB 2+ |PC 2+ |PD 2 ,则2 2S = 16cos 0 + 36sin 0 + 162=32 + 20sin 0 .因为0W sin 20W 1,所以S 的取值范围是[32 , 52].3、解：(I )圆C 的极坐标方程为p = 2 , 圆G 的极坐标方程p = 4cos 0 .2 解卩,得卩=2, 0=±石,p _ 4cos 03从而p_占.n(1)把极坐标系的点P (4 ,-)化为直角坐标，得 R0,4),满足直线l 的方程x — y + 4_ 0,所以点P 在直线l 上. 故可设点Q 的坐标为曲线C 的直角坐标方程为：x 2y 2②曲线C 的标准方程为(x 2)2 y 2•••圆心C(2,0)到直线I 的距离为：d所以点P 到直线I 的距离的取值范围是2、解：(I )由已知可得2 24x 3 0【或(x 2)2 y 21]1,圆心C(2,0)，半径为1；|2、一 3 0 3.3| 5,32 2故圆C 与圆C 2交点的坐标为(2 ,,(2,—勺.注：极坐标系下点的表示不唯一.x _ p cos 0 ,得圆 y _ p sin 0 (n )法一：由故圆C 与G 的公共弦的参数方程为x_ t 1,-3w t w 3.x _ 1(或参数方程写成 ， —..3 < y w 3)法二：将x = 1代入 cos 0得 p sin 0p cos 0 = 1,于是圆 C 与G 的公共弦的参数方程为x _ 1 y _ tan 0 '4、因为点P 的直角坐标(0,4)⑵因为点Q 在曲线C 上,(.3cos a , sin a ),C 与C 2交点的直角坐标分别为从而点Q 到直线I 的距离=；'2cos( a+ -Q )+ 2 2nl由此得，当cos( a + —) =— 1时，d 取得最小值，且最小值为：2.x y5、⑴设Rx , y )，则由条件知 M ^ 2 .由于M 点在C 上，x=2cos a , 2X = 4cos a ,所以即yy = 4+ 4sin a .2= 2+ 2sin a ,X = 4cos a ,从而C 2的参数方程为(a 为参数)y = 4 + 4sin a .(2)曲线C 的极坐标方程为 p = 4sin 0，曲线C 2的极坐标方程为 p = 8sin 0 .n n射线0 =三与C 的交点A 的极径为 p 1= 4sin —,3 3nn射线0 = y 与G 的交点B 的极径为p 2= 8sin —. 所以 | AB = | p 2— p 1| = 2 '3.nn6、 (1)由已知，M 点的极角为y ，且M 点的极径等于 J ,n n故点M 的极坐标为 ~~ .⑵M 点的直角坐标为n ,二空,A (1,0),故直线AM 的参数方程为6 6nx=1 + 6 — 1t ，(t 为参数).| 3cos a — sina + 4|2cos7t6所以圆C 的圆心坐标为(1,0) 因为圆C经过点P .'2, n,所以圆C的半径PC= 2+ 12—2X 1 x J2cos■—= 1,¥ 4于是圆C 过极点，所以圆 C 的极坐标方程为p = 2cos e .0, ¥8、解：(1)由题意知，M N 的平面直角坐标分别为所以直线l 的平面直角坐标方程为 3x + 3y — 2 3= 0.又圆C 的圆心坐标为(2 , — ,；3)，半径r = 2, 圆心到直线I 的距离d =， ： — ■' =-<r ,故直线l 与圆C 相交.yJ 3 + 9 2又P 为线段MN 勺中点，从而点 P 的平面直角坐标为1,，故直线OP 的平面直角坐标方程为 ⑵因为直线l 上两点M N 的平面直角坐标分别为 (2,0)(2,0)。
(必考题)高中数学高中数学选修4-4第一章《坐标系》检测题(答案解析)
一、选择题1．（理）在极坐标系中,圆2cos ρθ=的垂直于极轴的两条切线方程分别为（ ） A ．0()R θρ=∈ 和cos 2ρθ= B ．()2R πθρ=∈和cos 2ρθ=C ．()2R πθρ=∈和cos 1ρθ= D ．0()R θρ=∈和cos 1ρθ=2．已知曲线C 的极坐标方程为222123cos 4sin ρθθ=+，以极点为原点，极轴为x 轴非负半轴建立平面直角坐标系，则曲线C经过伸缩变换123x x y y ⎧=⎪⎪⎨=''⎪⎪⎩后，得到的曲线是（ ）A ．直线B ．椭圆C ．圆D ．双曲线3．已知圆C 与直线l 的极坐标方程分别为6cos ρθ=，sin 4πρθ⎛⎫+= ⎪⎝⎭C 到直线l 的距离是（ ） A ．1B ．2CD．24．在极坐标系中，点(),ρθ与(),ρπθ--的位置关系为（ ） A ．关于极轴所在直线对称 B ．关于极点对称 C ．重合D ．关于直线()2R πθρ=∈对称5．在极坐标系中，由三条直线0θ=，3πθ=，cos sin 1ρθρθ+=围成的图形的面积为（ ） A ．14BCD ．136．在极坐标系中，曲线1C 的极坐标方程为2sin ρθ=，曲线2C的极坐标方程为ρθ=，若曲线1C 与2C 交于A 、B 两点，则AB 等于（ ）A ．1BC ．2D．7．221x y +=经过伸缩变换23x xy y ''=⎧⎨=⎩后所得图形的焦距（ ）A．B．C ．4D ．68．将2216x y +=的横坐标压缩为原来的12，纵坐标伸长为原来的2倍，则曲线的方程变为（ ）A ．22134x y +=B ．22213x y +=C ．222112x y +=D ．222134x y +=9．已知曲线C 与曲线5ρ=3cos?5sin?θθ-关于极轴对称，则曲线C 的方程为( )A ．10cos ρ=-π-6θ⎛⎫ ⎪⎝⎭ B ．10cos ρ=π-6θ⎛⎫ ⎪⎝⎭ C ．10cos ρ=-π6θ⎛⎫+⎪⎝⎭D ．10cos ρ=π6θ⎛⎫+⎪⎝⎭10．在直角坐标系xOy 中，曲线C 的方程为22162x y+=，以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为cos()36πρθ+=，射线M 的极坐标方程为(0)θαρ=≥.设射线m 与曲线C 、直线l 分别交于A 、B 两点，则2211OAOB+的最大值为（ ） A ．34B ．25C ．23D ．1311．极坐标方程cos ρθ=与1cos 2ρθ=的图形是（ ） A ． B ． C ． D ．12．在同一平面直角坐标系中，将曲线1cos 23y x =按伸缩变换23x x y y ''=⎧⎨=⎩后为（ ）A ．cos y x ''=B ．13cos 2y x ''= C ．12cos3y x ''= D ．1cos32y x ''=二、填空题13．在极坐标系中，曲线C 的方程为28cos 10sin 320ρρθρθ--+=，直线l 的方程为0()R θθρ=∈，0tan 2θ=，若l 与C 交于A ，B 两点，O 为极点，则||||OA OB +=________．14．在极坐标系中，直线sin 24πρθ⎛⎫-= ⎪⎝⎭4ρ=截得的弦长为______.15．（理）在极坐标系中，曲线sin 2ρθ=+与sin 2ρθ=的公共点到极点的距离为_________．16．已知在平面直角坐标系xOy 中，圆C 的参数方程为：2cos 22sin x y ϕϕ=⎧⎨=+⎩（ϕ为参数），以Ox 为极轴建立极坐标系，直线l 30cos sin θθ-=，则圆C截直线l 所得弦长为___________． 17．两条直线sin 20164πρθ⎛⎫+= ⎪⎝⎭，sin 20174πρθ⎛⎫-= ⎪⎝⎭的位置关系是_______ 18．点C 的极坐标是(2,)4π,则点C 的直角坐标为______________ 19．在极坐标系中0,02,ρθπ>≤<，曲线cos 1ρθ=-与曲线=2sin ρθ的交点的极坐标为_______________。
选修4-4极坐标与参数方程试题精选(8套)
极坐标与参数方程单元练习 1一、选择题（每小题 5 分，共25 分）1、已知点M 的极坐标为5，，下列所给出的四个坐标中能表示点M 的坐标是（）。
34 2A. 5，B. 5，C. 5，D.3 3 3 5，532、直线：3x-4y-9=0 与圆：xy2cos2sin，( θ为参数) 的位置关系是( )3、在参数方程xyabttcossin（t 为参数）所表示的曲线上有B、C两点，它们对应的参数值分别为t1、t 2 ，则线段BC的中点M对应的参数值是（）4、曲线的参数方程为xy 3tt222(t 是参数) ，则曲线是（）1A、线段 B 、双曲线的一支C、圆D、射线2 2=6x，则x2 25、实数x、y 满足3x ＋2y ＋ y的最大值为（）A、72B、4 C 、92D 、5二、填空题（每小题 5 分，共30 分）1、点2，2 的极坐标为。
2、若 A 3，，B3 4，，则|AB|=___________，S AOB ___________。
（其中O 是极点）63、极点到直线cos sin 3 的距离是________ _____。
4、极坐标方程 2sin 2 cos 0表示的曲线是_______ _____。
x 2 tan5、圆锥曲线为参数y 3 sec的准线方程是。
6、直线l过点M01,5，倾斜角是3，且与直线x y230交于M，则MM0的长为。
三、解答题（第 1 题14 分，第 2 题16 分，第 3 题15 分；共45 分）1、求圆心为 C 3，，半径为 3 的圆的极坐标方程。
62、已知直线l经过点P(1,1),倾斜角，6（1）写出直线l的参数方程。
（2）设l与圆x2y24相交与两点A、B，求点P到A、B两点的距离之积。
2y 2x3、求椭圆 19 4 上一点P10。
与定点（，）之间距离的最小值极坐标与参数方程单元练习 1 参考答案【试题答案】一、选择题：1、D 2、D 3、B 4、D 5、B二、填空题：1、 2 2，或写成472 ，。
高中数学选修4《极坐标与参数方程》
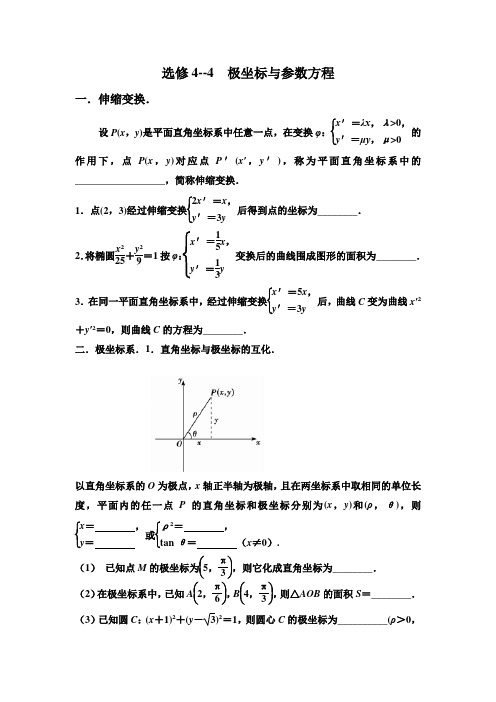
选修4--4 极坐标与参数方程一．伸缩变换．设P (x ，y )是平面直角坐标系中任意一点，在变换φ：⎩⎨⎧x ′＝λx ，λ>0，y ′＝μy ，μ>0的作用下，点P (x ，y )对应点P ′(x ′，y ′)，称为平面直角坐标系中的__________________，简称伸缩变换．1．点(2，3)经过伸缩变换⎩⎨⎧2x ′＝x ，y ′＝3y后得到点的坐标为________．2．将椭圆x 225＋y 29＝1按φ：⎩⎪⎨⎪⎧x ′＝15x ，y ′＝13y 变换后的曲线围成图形的面积为________． 3．在同一平面直角坐标系中，经过伸缩变换⎩⎨⎧x ′＝5x ，y ′＝3y 后，曲线C 变为曲线x ′2＋y ′2＝0，则曲线C 的方程为________． 二．极坐标系．1．直角坐标与极坐标的互化．以直角坐标系的O 为极点，x 轴正半轴为极轴，且在两坐标系中取相同的单位长度，平面内的任一点P 的直角坐标和极坐标分别为(x ，y )和(ρ，θ)，则⎩⎨⎧x ＝ ，y ＝ 或⎩⎨⎧ρ2＝ ，tan θ＝ （x ≠0）. （1） 已知点M 的极坐标为⎝⎛⎭⎪⎫5，π3，则它化成直角坐标为________．（2）在极坐标系中，已知A ⎝ ⎛⎭⎪⎫2，π6，B ⎝ ⎛⎭⎪⎫4，π3，则△AOB 的面积S ＝________．（3）已知圆C ：(x ＋1)2＋(y －3)2＝1，则圆心C 的极坐标为__________(ρ＞0，0≤θ＜2π)．三 圆的参数方程及参数方程与普通方程的互化1．圆x 2＋y 2＝16的参数方程为：____________． 2．圆(x －6)2＋y 2＝4的参数方程为：______________．, 3圆(x －1)2＋y 2＝4上的点可以表示为( )A ．(－1＋cos θ，sin θ)B ．(1＋sin θ，cos θ)C ．(－1＋2cos θ，2sin θ)D ．(1＋2cos θ，2sin θ) 2．3 直线的参数方程1．过定点M 0(x 0，y 0)、倾斜角为α的直线l 的参数方程为__________________，这一形式称为直线参数方程的标准形式，直线上的动点M 到定点M 0的距离等于参数t 的绝对值．当t ＞0时，M 0M →的方向向上；当t ＜0时，M 0M →的方向向下；当点M 与点M 0重合时，t ＝0.1.经过点M 0(1，5)，倾斜角是π3的直线l 的参数方程为：____________________________．2．直线⎩⎪⎨⎪⎧x ＝2＋3t ，y ＝－1＋t (t 为参数)上对应t ＝0，t ＝1两点间的距离是( )A ．1 B.10 C ．10 D ．2 23．曲线C ：⎩⎪⎨⎪⎧x ＝cos θ，y ＝－1＋sin θ(θ为参数)的普通方程为________．如果曲线C 与直线x ＋y ＋a ＝0有公共点，那么a 的取值范围是________． 三、解答题1.曲线C 1的参数方程为x cos ,y sin =θ⎧⎨=θ⎩ (θ为参数),将曲线C 1上所有点的横坐标伸长为原来的2倍,,得到曲线C2.以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:ρ(cosθ-2sinθ)=6.(1)求曲线C2和直线l的普通方程.(2)P为曲线C2上任意一点,求点P到直线l的距离的最值.2. 已知在直角坐标系xOy中,曲线C的参数方程为x14cos,y24sin=+θ⎧⎨=+θ⎩(θ为参数),直线l经过定点P(3,5),倾斜角为3π.(1)写出直线l的参数方程和曲线C的标准方程.(2)设直线l与曲线C相交于A,B两点,求|PA|·|PB|的值.3.在直角坐标系xOy中,直线l经过点P(-1,0),其倾斜角为α,以原点O为极点,以x轴非负半轴为极轴,与直角坐标系xOy取相同的单位长度,建立极坐标系,设曲线C的极坐标方程为ρ2-6ρcosθ+5=0.(1)若直线l与曲线C有公共点,求α的取值范围.(2)设M(x,y)为曲线C上任意一点,求x+y的取值范围.4.已知圆C的极坐标方程为2cosρθ=，直线l的参数方程为1221122x ty t⎧=+⎪⎪⎨⎪=+⎪⎩（t为参数），点A的极坐标为(,)24π，设直线与圆C 交于点P ，Q ． （Ⅰ）写出圆C 的直角坐标方程； （Ⅱ）求||||⋅AP AQ 的值．5. 已知圆()()221:228C x y -+-=和直线:0l x y =. （Ⅰ）求1C 的参数方程以及圆1C 上距离直线l 最远的点P 坐标； （Ⅱ）以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，将圆1C 上除点O 以外所有点绕着O 逆时针旋转3π得到曲线2C ，求曲线2C 的极坐标方程.6.已知极坐标系的极点与直角坐标系的原点重合，极轴与x 轴的正半轴重合，圆C 的极坐标方程为sin a ρθ=，直线l 的参数方程为32545x t y t ⎧=-+⎪⎪⎨⎪=⎪⎩（t 为参数）． （Ⅰ）若2a =，M 是直线l 与x 轴的交点，N 是圆C 上一动点，求||MN 的最大值；（Ⅱ）若直线l 被圆C 截得的弦长等于圆C倍，求a 的值．。
(完整版)高中数学选修4-4习题(含答案)
统考作业题目——4-46.21．在平面直角坐标系中，直线的参数方程为为参数），以原点xOy l 12,(2x t t y t =+⎧⎨=-⎩为极点，以轴非负半轴为极轴建立极坐标系，两坐标系取相同的长度单位。
曲线O x 的极坐标方程为 .C 22cos 4sin 40ρρθρθ+++=（1）求的普通方程和的直角坐标方程；l C （2）已知点是曲线上任一点，求点到直线距离的最大值.M C M l 2．已知极坐标的极点在平面直角坐标系的原点处，极轴与轴的正半轴重合，且长O x 度单位相同。
直线的极坐标方程为：，点，参数l ρ=102sin (θ‒π4)P (2cosα,2sinα+2)．α∈[0,2π]（I ）求点轨迹的直角坐标方程；P （Ⅱ）求点到直线距离的最大值．P l1、【详解】（1）12,2x t y t =+⎧⎨=-⎩10x y ∴+-=因为，222,cos ,sin x y x y ρρθρθ=+==所以，即222440x y x y ++++=22(1)(2)1x y +++=（2）因为圆心到直线，(1,2)--10x y +-==所以点到直线距离的最大值为M l 1.r +=+2、解：（Ⅰ）设，则，且参数，P (x ,y ){x =2cosαy =2sinα+2 α∈[0,2π]消参得：x 2+(y ‒2)2=4所以点的轨迹方程为P x 2+(y ‒2)2=4（Ⅱ）因为ρ=102sin (θ‒π4)所以ρ2sin (θ‒π4)=10所以，ρsinθ‒ρcosθ=10所以直线的直角坐标方程为l x ‒y +10=0法一：由（Ⅰ）点的轨迹方程为P x 2+(y ‒2)2=4圆心为（0,2），半径为2．，d =|1×0‒1×2+10|12+12=42点到直线距离的最大值等于圆心到直线距离与圆的半径之和，P l l 所以点到直线距离的最大值．P l 42+2法二：d =|2cosα‒2sinα‒2+10|12+12=2|cosα‒sinα+4|=2|2cos (α+π4)+4|当时，，即点到直线距离的最大值为．a =74πd max =42+2P l 42+26.33．在平面直角坐标系xOy 中，已知曲线的参数方程为（为参数），曲C 1{x =cosθy =3sinθθ线的参数方程为（，t 为参数）.C 2{x =4‒22ty =4+22tt ∈R(1)求曲线的普通方程和曲线的极坐标方程；C 1C 2(2)设P 为曲线上的动点，求点P 到上点的距离的最小值，并求此时点P 的坐标.C 1C 24．在直角坐标系中曲线的参数方程为（为参数，以坐标原xOy 1C cos x y αα=⎧⎪⎨=⎪⎩α点为极点，以轴的正半轴为极轴，建立极坐标系，曲线的极坐标方程为x 2C .sin 4πρθ⎛⎫+= ⎪⎝⎭（1）写出的普通方程和的直角坐标方程；1C 2C （2）设点在上，点在上，求的最小值及此时的直角坐标.P 1C Q 2C ||PQ P3、【详解】（1）对曲线：，，C 1cos 2θ=x 2sin 2θ=y 23∴曲线的普通方程为．C 1x 2+y 23=1对曲线消去参数可得且C 2t t =(4‒x )×2,t =(y ‒4)×2,∴曲线的直角坐标方程为． C 2x +y ‒8=0又，∵x =ρcosθ,y =ρsinθ∴ρcosθ+ρsinθ‒8=2ρsin (θ+π4)‒8=0从而曲线的极坐标方程为。
极坐标及参数方程
坐标系与参数方程1．直角坐标与极坐标的互化把直角坐标系的原点作为极点，x 轴正半轴作为极轴，且在两坐标 系中取一样的长度单位．如图，设M 是平面内的任意一点，它的直 角坐标、极坐标分别为(x ，y )和(ρ，θ)，那么⎩⎨⎧ x ＝ρcos θy ＝ρsin θ，⎩⎨⎧ρ2＝x 2＋y 2tan θ＝yxx ≠0.2．直线的极坐标方程假设直线过点M (ρ0，θ0)，且极轴到此直线的角为α，那么它的方程为ρsin(θ－α)＝ρ0sin(θ0－α)．几个特殊位置的直线的极坐标方程 (1)直线过极点：θ＝α；(2)直线过点M (a,0)且垂直于极轴：ρcos θ＝a ； (3)直线过点M (b ，π2)且平行于极轴：ρsin θ＝b .3．圆的极坐标方程假设圆心为M (ρ0，θ0)，半径为r 的圆的方程为ρ2－2ρ0ρcos(θ－θ0)＋ρ20－r 2＝0.几个特殊位置的圆的极坐标方程 (1)圆心位于极点，半径为r ：ρ＝r ； (2)圆心位于M (r,0)，半径为r ：ρ＝2r cos θ；(3)圆心位于M (r ，π2)，半径为r ：ρ＝2r sin θ.4．直线的参数方程过定点M (x 0，y 0)，倾斜角为α的直线l 的参数方程为⎩⎨⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(t 为参数)．5．圆的参数方程圆心在点M (x 0，y 0)，半径为r 的圆的参数方程为⎩⎨⎧x ＝x 0＋r cos θ，y ＝y 0＋r sin θ(θ为参数，0≤θ≤2π)．6．圆锥曲线的参数方程(1)椭圆x 2a 2＋y 2b 2＝1的参数方程为⎩⎨⎧x ＝a cos θ，y ＝b sin θ(θ为参数)．(2)抛物线y 2＝2px (p >0)的参数方程为⎩⎨⎧x ＝2pt 2y ＝2pt .真题感悟1．(2021·)曲线C 的极坐标方程为ρ＝2cos θ，以极点为原点，极轴为x 轴的正半轴建立直角坐标系，那么曲线C 的参数方程为________． 2．(2021·)设曲线C 的参数方程为⎩⎨⎧x ＝t y ＝t2(t 为参数)，假设以直角坐标系的原点为极点，x轴的正半轴为极轴建立极坐标系，那么曲线C 的极坐标方程为________．3．(2021·)在直角坐标系xOy 中，椭圆C 的参数方程为⎩⎨⎧x ＝a cos φy ＝b sin φ(φ为参数，a >b >0)，在极坐标系(与直角坐标系xOy 取一样的长度单位，且以原点O 为极点，以x 轴正半轴为极轴)中，直线l 与圆O 的极坐标方程分别为ρsin (θ＋π4)＝22m (m 为非零常数)与ρ＝b .假设直线l 经过椭圆C 的焦点，且与圆O 相切，那么椭圆C 的离心率为________．4．(2021·)在直角坐标系xOy 中，以原点为极点，x 轴的正半轴为极轴建立极坐标系，设点A ，B 分别在曲线C 1：⎩⎨⎧x ＝3＋cos θ，y ＝4＋sin θ(θ为参数)和曲线C 2：ρ＝1上，那么AB 的最小值为________．5．(2021·)在直角坐标系xOy 中，曲线C 1：⎩⎨⎧x ＝t ＋1，y ＝1－2t(t 为参数)与曲线C 2：⎩⎨⎧x ＝a sin θ，y ＝3cos θ(θ为参数，a >0)有一个公共点在x 轴上，那么a ＝________.6.[2021·XX 卷] (坐标系与参数方程选做题)在极坐标系中，曲线C 1与C 2的方程分别为2ρcos 2θ＝sin θ与ρcos θ＝1.以极点为平面直角坐标系的原点，极轴为x 轴的正半轴，建立平面直角坐标系，那么曲线C 1与C 2交点的直角坐标为________．7．[2021·XX 卷] 在平面直角坐标系中，曲线C ：⎩⎪⎨⎪⎧x ＝2＋22t ，y ＝1＋22t (t 为参数)的普通方程为________．8． [2021·XX 卷]C.(坐标系与参数方程选做题)在极坐标系中，点⎝ ⎛⎭⎪⎫2，π6到直线ρsin ⎝ ⎛⎭⎪⎫θ－π6＝1的距离是________．题型与方法题型一 极坐标与直角坐标、参数方程与普通方程的互化例1 直线l 的参数方程：⎩⎨⎧x ＝t ，y ＝1＋2t(t 为参数)和圆C 的极坐标方程：ρ＝22sin ⎝ ⎛⎭⎪⎫θ＋π4 (θ为参数)．(1)将直线l 的参数方程和圆C 的极坐标方程化为直角坐标方程； (2)判断直线l 和圆C 的位置关系．变式训练1 直线l 的参数方程是⎩⎨⎧x ＝2t ，y ＝4t ＋a(t 为参数)，圆C 的极坐标方程为ρ＝4 2cos ⎝ ⎛⎭⎪⎫θ＋π4. (1)将圆C 的极坐标方程化为直角坐标方程；(2)假设圆上有且仅有三个点到直线l 的距离为2，XX 数a 的值．题型二 曲线的极坐标方程例2 在直角坐标系xOy 中，以O 为极点，x 轴正半轴为极轴建立极坐标系．曲线C 的极坐标方程为ρcos ⎝ ⎛⎭⎪⎫θ－π3＝1，M ，N 分别为曲线C 与x 轴，y 轴的交点．(1)写出曲线C 的直角坐标方程，并求M ，N 的极坐标； (2)设M ，N 的中点为P ，求直线OP 的极坐标方程．变式训练2 (2021·)在直角坐标系xOy 中，圆C 1：x 2＋y 2＝4，圆C 2：(x －2)2＋y 2＝4.(1)在以O 为极点，x 轴正半轴为极轴的极坐标系中，分别写出圆C 1，C 2的极坐标方程，并求出圆C 1，C 2的交点坐标(用极坐标表示)； (2)求圆C 1与C 2的公共弦的参数方程．题型三 曲线的参数方程及应用例3 (2021·)在平面直角坐标系中，以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系．直线l 上两点M ，N 的极坐标分别为(2,0)，⎝⎛⎭⎪⎫233，π2，圆C 的参数方程为⎩⎨⎧x ＝2＋2cos θ，y ＝－3＋2sin θ(θ为参数)． (1)设P 为线段MN 的中点，求直线OP 的平面直角坐标方程； (2)判断直线l 与圆C 的位置关系．变式训练3直线l 的参数方程是⎩⎪⎨⎪⎧x ＝22ty ＝22t ＋42(t 是参数)，圆C 的极坐标方程为ρ＝2cos(θ＋π4)．(1)求圆心C 的直角坐标；(2)由直线l 上的点向圆C 引切线，求切线长的最小值．典例 (10分)在直角坐标平面内，以坐标原点O 为极点，x 轴的非负半轴为极轴建立极坐标系，点M 的极坐标为⎝ ⎛⎭⎪⎫42，π4，曲线C 的参数方程为⎩⎨⎧x ＝1＋2cos α，y ＝2sin α(α为参数)．(1)求直线OM 的直角坐标方程；(2)求点M 到曲线C 上的点的距离的最小值． 规X 解答1．圆C 的参数方程为⎩⎨⎧x ＝cos α，y ＝1＋sin α(α为参数)，以原点为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为ρsin θ＝1，那么直线l 与圆C 的交点的直角坐标为________________．2．在直角坐标系xOy 中，曲线C 1的参数方程为⎩⎨⎧x ＝cos α，y ＝1＋sin α(α为参数)．在极坐标系(与直角坐标系xOy 取一样的长度单位，且以原点O 为极点，以x 轴正半轴为极轴)中，曲线C 2的方程为ρ(cos θ－sin θ)＋1＝0，那么C 1与C 2的交点个数为________．3．点P (x ，y )在曲线⎩⎨⎧x ＝－2＋cos θy ＝sin θ(θ为参数，θ∈R )上，那么yx 的取值X 围是________．4．假设直线l 1：⎩⎨⎧x ＝1－2t ，y ＝2＋kt(t 为参数)与直线l 2：⎩⎨⎧x ＝s ，y ＝1－2s(s 为参数)垂直，那么k ＝______.6．(2021·)在平面直角坐标系xOy 中，曲线C 1和C 2的参数方程分别为⎩⎨⎧x ＝t ，y ＝t(t 为参数)和⎩⎪⎨⎪⎧x ＝2cos θ，y ＝2sin θ(θ为参数)，那么曲线C 1与C 2的交点坐标为________．专题限时规X 训练一、填空题1．曲线C ：⎩⎨⎧x ＝－2＋2cos αy ＝2sin α(α为参数)，假设以点O (0,0)为极点，x 轴正半轴为极轴建立极坐标系，那么该曲线的极坐标方程是________．2．两曲线参数方程分别为⎩⎨⎧x ＝5cos θ，y ＝sin θ(0≤θ<π)和⎩⎨⎧x ＝54t 2，y ＝t(t ∈R )，它们的交点坐标为________．3．曲线C 的参数方程是⎩⎨⎧x ＝a cos φy ＝3sin φ(φ为参数，a >0)，直线l 的参数方程是⎩⎨⎧x ＝3＋t y ＝－1－t(t 为参数)，曲线C 与直线l 有一个公共点在x 轴上，那么曲线C 的普通方程为________．4．(2021·)在直角坐标系xOy 中，以原点O 为极点，x 轴的正半轴为极轴建立极坐标系．假设极坐标方程为ρcos θ＝4的直线与曲线⎩⎨⎧x ＝t 2，y ＝t3(t 为参数)相交于A ，B 两点，那么AB＝________.二、解答题5．设直线l 1的参数方程为⎩⎨⎧x ＝1＋t ，y ＝1＋3t(t 为参数)，直线l 2的方程为y ＝3x ＋4，求l 1与l 2间的距离．6．在平面直角坐标系xOy 中，求过椭圆⎩⎨⎧x ＝5cos φ，y ＝3sin φ(φ为参数)的右焦点，且与直线⎩⎨⎧x ＝4－2t ，y ＝3－t (t 为参数)平行的直线的普通方程．7．(2021·)在极坐标系中，圆C 经过点P ⎝ ⎛⎭⎪⎫2，π4，圆心为直线ρsin ⎝ ⎛⎭⎪⎫θ－π3＝－32与极轴的交点，求圆C 的极坐标方程．8．直线的极坐标方程为ρsin ⎝ ⎛⎭⎪⎫θ＋π4＝22，圆M 的参数方程⎩⎨⎧x ＝2cos θ，y ＝－2＋2sin θ(其中θ为参数)，极点在直角坐标原点，极轴与x 轴正半轴重合． (1)将直线的极坐标方程化为直角坐标方程； (2)求圆M 上的点到直线的距离的最小值．9．在直角坐标系中，以原点为极点，x 轴的正半轴为极轴建立坐标系，曲线C ：ρsin 2θ＝2a cosθ(a >0)，过点P (－2，－4)的直线l 的参数方程为⎩⎪⎨⎪⎧x ＝－2＋22t ，y ＝－4＋22t ，直线l 与曲线C 分别交于M ，N 两点．(1)写出曲线C 和直线l 的普通方程；(2)假设PM ，MN ，PN 成等比数列，求a 的值．10．(2021·)在平面直角坐标系中，以坐标原点为极点，x 轴的非负半轴为极轴建立极坐标系，点A 的极坐标为(2，π4)，直线l 的极坐标方程为ρcos(θ－π4)＝a ，且点A 在直线l上．(1)求a 的值及直线l 的直角坐标方程；(2)圆C 的参数方程为⎩⎨⎧x ＝1＋cos α，y ＝sin α(α为参数)，试判断直线l 与圆C 的位置关系．2021、2021年全国高考理科数学试题分类汇编：坐标系与参数方程一、选择题1 ．〔2021年普通高等学校招生统一考试XX 数学〔理〕试题〔纯WORD 版〕〕在极坐标系中,圆=2cos p θ的垂直于极轴的两条切线方程分别为〔 〕A ．=0()cos=2R θρρ∈和B ．=()cos=22R πθρρ∈和C ．=()cos=12R πθρρ∈和 D ．=0()cos=1R θρρ∈和二、填空题2 ．〔2021年普通高等学校招生统一考试XX 数学〔理〕试题〔含答案〕〕圆的极坐标方程为4cos ρθ=, 圆心为C , 点P 的极坐标为4,3π⎛⎫⎪⎝⎭, 那么|CP | = ______.3 ．〔2021年高考XX 卷〔理〕〕在极坐标系中,曲线cos 1ρθ=+与cos 1ρθ=的公共点到极点的距离为__________4 ．〔2021年高考卷〔理〕〕在极坐标系中,点(2,6π)到直线ρsin θ=2的距离等于_________.5 ．〔2021年普通高等学校招生统一考试XX 数学〔理〕试题〔含答案〕〕在直角坐标系xOy 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系.假设极坐标方程为cos 4ρθ=的直线与曲线23x ty t ⎧=⎪⎨=⎪⎩(为参数)相交于,A B 两点,那么______AB = 6 ．〔2021年普通高等学校招生统一考试XX 省数学〔理〕卷〔纯WORD 版〕〕(坐标系与参数方程选讲选做题)曲线C的参数方程为x ty t ⎧=⎪⎨=⎪⎩(为参数),C 在点()1,1处的切线为,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,那么的极坐标方程为_____________.7 ．〔2021年高考XX 卷〔理〕〕C. (坐标系与参数方程选做题) 如图, 以过原点的直线的倾斜角θ为参数, 那么圆220y x x +-=的参数方程为______ .x8 ．〔2021年高考XX 卷〔理〕〕(坐标系与参数方程选做题)设曲线C 的参数方程为2x t y t=⎧⎨=⎩(为参数),假设以直角坐标系的原点为极点,x 轴的正半轴为极轴建立极坐标系,那么曲线c的极坐标方程为__________9 ．〔2021年高考XX 卷〔理〕〕在平面直角坐标系xoy 中,假设,3cos ,:(t )C :2sin x t x l y t a y ϕϕ==⎧⎧⎨⎨=-=⎩⎩为参数过椭圆()ϕ为参数的右顶点,那么常数a 的值为________.10．〔2021年高考XX 卷〔理〕〕在直角坐标系xOy 中,椭圆C 的参数方程为cos sin x a y b θθ=⎧⎨=⎩()0a b ϕ>>为参数，.在极坐标系(与直角坐标系xOy 取一样的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,直线与圆O 的极坐标方程分别为sin 4πρθ⎛⎫+= ⎪⎝⎭()m 为非零常数与b ρ=.假设直线经过椭圆C 的焦点,且与圆O 相切,那么椭圆C 的离心率为___________.三、解答题11．〔2021年普通高等学校招生统一考试新课标Ⅱ卷数学〔理〕〔纯WORD 版含答案〕〕选修4—4;坐标系与参数方程动点,P Q 都在曲线2cos :2sin x C y ββ=⎧⎨=⎩(β为参数上,对应参数分别为βα=与)20(2πααβ<<=,M 为PQ 的中点.(Ⅰ)求M 的轨迹的参数方程;(Ⅱ)将M 到坐标原点的距离d 表示为α的函数,并判断M 的轨迹是否过坐标原点.12．〔2021年普通高等学校招生统一考试XX 数学〔理〕试题〔WORD 版〕〕选修4-4:坐标系与参数方程在直角坐标系xoy 中以O 为极点,x 轴正半轴为极轴建立坐标系.圆1C ,直线2C 的极坐标方程分别为4sin ,cos 4πρθρθ⎛⎫==-= ⎪⎝⎭. (I)求1C 与2C 交点的极坐标;(II)设P 为1C 的圆心,Q 为1C 与2C 交点连线的中点.直线PQ 的参数方程为 ()3312x t a t R b y t ⎧=+⎪∈⎨=+⎪⎩为参数,求,a b 的值.13．〔2021年普通高等学校招生统一考试XX 数学〔理〕试题〔纯WORD 版〕〕坐标系与参数方程:在平面直角坐标系中,以坐标原点为极点,x 轴的非负半轴为极轴建立坐标系.点A 的极坐标为)4π,直线的极坐标方程为cos()4a πρθ-=,且点A 在直线上. (1)求a 的值及直线的直角坐标方程;(2)圆c 的参数方程为1cos sin x y αα=+⎧⎨=⎩,(α为参数),试判断直线与圆的位置关系.14．〔2021年普通高等学校招生全国统一招生考试XX 卷〔数学〕〔已校对纯WORD 版含附加题〕〕C.[选修4-4:坐标系与参数方程]本小题总分值10分.在平面直角坐标系xoy 中,直线的参数方程为⎩⎨⎧=+=t y t x 21 (为参数),曲线C 的参数方程为⎩⎨⎧==θθtan 2tan 22y x (θ为参数),试求直线与曲线C 的普通方程,并求出它们的公共点的坐标.〔2021年高考新课标1〔理〕〕选修4—4:坐标系与参数方程 曲线C 1的参数方程为45cos 55sin x t y t=+⎧⎨=+⎩(为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 2的极坐标方程为2sin ρθ=.(Ⅰ)把C 1的参数方程化为极坐标方程;(Ⅱ)求C 1与C 2交点的极坐标(ρ≥0,0≤θ<2π).[2021·XX 卷] 选修44：坐标系与参数方程将圆x 2＋y 2＝1上每一点的横坐标保持不变，纵坐标变为原来的2倍，得曲线C .(1)写出C 的参数方程；(2)设直线l ：2x ＋y －2＝0与C 的交点为P 1，P 2，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，求过线段P 1P 2的中点且与l 垂直的直线的极坐标方程．[2021·新课标全国卷Ⅱ] 选修44：坐标系与参数方程在直角坐标系xOy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，半圆C 的极坐标方程为ρ＝2cos θ，θ∈⎣⎢⎡⎦⎥⎤0，π2. (1)求C 的参数方程；(2)设点D 在C 上，C 在D 处的切线与直线l ：y ＝3x ＋2垂直，根据(1)中你得到的参数方程，确定D 的坐标．23．[2021·全国新课标卷Ⅰ] 选修4－4：坐标系与参数方程曲线C ：x 24＋y 29＝1，直线l ：⎩⎨⎧x ＝2＋t ，y ＝2－2t (t 为参数)． (1)写出曲线C 的参数方程、直线l 的普通方程；(2)过曲线C 上任意一点P 作与l 夹角为30°的直线，交l 于点A ，求|PA |的最大值与最小值．。
新北师大版高中数学高中数学选修4-4第一章《坐标系》检测(包含答案解析)(2)
一、选择题1．点P 对应的复数为33i -+，以原点为极点，实轴正半轴为极轴建立极坐标系，则点P 的极坐标为（ ） A ．332,4π⎛⎫ ⎪⎝⎭B ．532,4π⎛⎫- ⎪⎝⎭C ．53,4π⎛⎫ ⎪⎝⎭D ．33,4π⎛⎫- ⎪⎝⎭2．在直角坐标系xOy 中，以O 为极点，x 轴正半轴为极轴建立极坐标系，曲线1C 的极坐标方程为2sin 42a πρθ⎛⎫+= ⎪⎝⎭，曲线2C 的参数方程为cos sin x y θθ=⎧⎨=⎩（θ为参数，0θπ）.若1C 与2C 有且只有一个公共点，则实数a 的取值范围是（ ）A ．2±B ．(2,2)-C ．[1,1)-D ．[1,1)-或23．在极坐标系中，点(),ρθ与(),ρπθ--的位置关系为（ ） A ．关于极轴所在直线对称 B ．关于极点对称 C ．重合D ．关于直线()2R πθρ=∈对称4．在极坐标系中，已知A （1，π3），B （2，2π3）两点，则|AB|＝（ ） A ．2B ．3C ．1D ．55．在直角坐标系xOy 中，曲线C 的方程为22162x y +=，以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为cos()36πρθ+=，射线M 的极坐标方程为(0)θαρ=≥.设射线m 与曲线C 、直线l 分别交于A 、B 两点，则2211OAOB+的最大值为（ ） A ．34B ．25C ．23D ．136．()04πθρ=≥表示的图形是( )A ．一条线段B ．一条直线C ．一条射线D ．圆7．在极坐标系中，点到直线的距离是（ ）．A ．B ．C ．D ．8．已知点P 的直角坐标(2,23)--，则它的一个极坐标为（ ）A ．(4，3π) B ．(4，43π) C ．(-4，6π) D ．(4，76π) 9．在平面直角坐标系xOy 中，以O 为极点，x 轴的正半轴为极轴，长度单位不变，建立极坐标系，已知曲线C 的极坐标方程为ρcos(θ－3π)＝1，M ，N 分别为曲线C 与x 轴、y 轴的交点，则MN 的中点的极坐标为（ ）A ．3(1,)3B ．23(,)36πC ．2333π⎛⎫ ⎪ ⎪⎝⎭，D ．2323⎛⎫⎪ ⎪⎝⎭，10．直线πsin 44ρθ⎛⎫+= ⎪⎝⎭与圆π4sin 4ρθ⎛⎫=+ ⎪⎝⎭的位置关系是（ ）． A ．相交但不过圆心B ．相交且过圆心C ．相切D ．相离11．在极坐标系中，两条曲线1πC :ρsin θ14⎛⎫+= ⎪⎝⎭，2C :ρ2=的交点为A,B ，则AB =（ ）A ．4B ．22C ．2D ．112．化极坐标方程2cos 20ρθρ-=为直角坐标方程为（ ） A ．2202x y y +==或 B ．2x =C ．2202x y x +==或D ．2y =二、填空题13．已知圆M 的极坐标方程为242cos()604πρρθ--+=，则ρ的最大值为______.14．将曲线C 按伸缩变换'2'3x x y y=⎧⎨=⎩变换后所得曲线方程为22''1x y +=，则曲线C 的方程为________.15．在极坐标系中，点(2,)3π到直线(cos 3sin )6ρθθ+=的距离为_________．16．在极坐标系中，O 是极点，设点(1,)6A π，(2,)2B π，则OAB ∆的面积是__________．17．在极坐标系中，直线cos sin (0)a a ρθρθ+=>与圆2cos ρθ=相切，则a =__________．18．在平面直角坐标系xOy 中，已知直线l 的参数方程为（t 为参数），以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 的极坐标方程为ρsin 2θ=4cosθ，直线l 与曲线C 交于A ，B 两点，则线段AB 的长为__．19．将曲线221x y +=按伸缩变换公式'2'3x xy y =⎧⎨=⎩变换后得到曲线C ，则曲线C 上的点(,)P m n 到直线:260l x y +-=的距离最小值为_____________.20．过点P (2，4π)并且与极轴垂直的直线的方程是___________________________． 三、解答题21．在平面直角坐标系xOy 中，曲线C 的参数方程为cos 1sin x r y r ϕϕ⎧=⎪⎨=+⎪⎩（0r >，ϕ为参数），以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，直线l 的坐标方程为sin 13πρθ⎛⎫-= ⎪⎝⎭，若直线l 与曲线C 相切. （1）求曲线C 的极坐标方程；（2）在曲线C 上取两点M 、N 于原点O 构成MON ∆，且满足6MON π∠=，求面积MON ∆的最大值.22．在平面直角坐标系中，曲线1C 的参数方程为2cos sin x r y r ϕϕ=+⎧⎨=⎩（0r >，ϕ为参数），以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，曲线1C 经过点6P π⎛⎫⎪⎝⎭，曲线2C 的极坐标方程为()22cos26ρθ+=．（1）求曲线1C 的极坐标方程；（2）若1,6A πρα⎛⎫- ⎪⎝⎭，23,B πρα⎛⎫+ ⎪⎝⎭是曲线2C 上两点，求2211OA OB +的值．23．在平面直角坐标系xOy 中,曲线1C ：222x ax y -+=0(a >0)，曲线2C 的参数方程为cos {1sin x y αα==+(α为参数),以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系；(1)求曲线1C ，2C 的极坐标方程; (2)已知极坐标方程为θ=6π的直线与曲线1C ，2C 分别相交于P ，Q 两点（均异于原点O ），若|PQ|=1，求实数a 的值； 24．(本小题满分12分)在直角坐标系xOy 中,曲线1C 的参数方程为 sin x y αα⎧=⎪⎨=⎪⎩(α为参数),以原点O 为极点,x轴的非负半轴为极轴,建立极坐标系,曲线2C 的极坐标方程πsin 4ρθ⎛⎫+= ⎪⎝⎭（1）求曲线1C 的普通方程和曲线2C 的直角坐标方程;（2）设P 为曲线1C 上的动点,求点P 到曲线2C 上的距离的最小值. 25．在极坐标系下，已知圆C ：2cos 2sin =+和直线:40l x y -+= （1）求圆C 的直角坐标方程和直线l 的极坐标方程； （2）求圆C 上的点到直线l 的最短距离．26．在直角坐标系中，圆1C ：221x y +=经过伸缩变换32x xy y''=⎧⎨=⎩，后得到曲线2C 以坐标原点为极点，x 轴的正半轴为极轴，并在两种坐标系中取相同的单位长度，建立极坐标系，直线l 的极坐标方程为102cos sin θθρ+=()1求曲线2C 的直角坐标方程及直线l 的直角坐标方程；()2在2C 上求一点M ，使点M 到直线l 的距离最小，并求出最小距离．【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【解析】分析：先求出点P 的直角坐标，P 到原点的距离r ，根据点P 的位置和极角的定义求出极角，从而得到点P 的极坐标． 详解：点P 对应的复数为33i -+，则点P 的直角坐标为()3,3-，点P 到原点的距离r =，且点P 第二象限的平分线上，故极角等于34π，故点P 的极坐标为34π⎛⎫ ⎪⎝⎭， 故选A ．点睛：本题考查把直角坐标化为极坐标的方法，复数与复平面内对应点间的关系，求点P 的极角是解题的难点．2．D解析：D 【解析】 【分析】先把曲线1C ，2C 的极坐标方程和参数方程转化为直角坐标方程和一般方程，若1C 与2C 有且只有一个公共点可转化为直线和半圆有一个公共点，数形结合讨论a 的范围即得解.【详解】因为曲线1C 的极坐标方程为2sin ,42a πρθ⎛⎫+= ⎪⎝⎭即222(sin cos )222a ρθθ+= 故曲线1C 的直角坐标方程为：0x y a +-=.消去参数θ可得曲线2C 的一般方程为：221x y +=，由于0θπ，故0y ≥如图所示，若1C 与2C 有且只有一个公共点，直线与半圆相切，或者截距11a -≤< 当直线与半圆相切时122O l d a -==∴=由于为上半圆，故02a a >∴= 综上：实数a 的取值范围是[1,1)-2 故选：D 【点睛】本题考查了极坐标、参数方程与直角坐标方程、一般方程的互化，以及直线和圆的位置关系，考查了学生数形结合，数学运算的能力，属于中档题.3．A解析：A 【分析】由点(),ρπθ--和点(,)ρθ-为同一点. 则比较点(,)ρθ-和点(),ρθ，可推出点(),ρθ与(),ρπθ--的位置关系.【详解】解：点(),ρπθ--与点(),ρθ-是同一个点，(),ρθ-与点(),ρθ关于极轴对称.∴点(),ρθ与(),ρπθ--关于极轴所在直线对称.故选：A. 【点睛】考查极坐标的位置关系.题目较为简单，要掌握极坐标的概念.4．B解析：B 【解析】 【分析】根据题意，由AB 的坐标分析可得|OA |＝1，|OB |＝2，且∠AOB 2333πππ=-=，由余弦定理计算可得答案 【详解】在极坐标系中，已知A （1，π3），B （2，2π3）， 则|OA|＝1，|OB|＝2，且∠AOB 2πππ333=-=， 则|AB|2＝2OA +2OB ﹣2|OA||OB|cos ∠AOB ＝1+4﹣2×1×2×cos π3=3，则|AB|= 故选：B ． 【点睛】本题考查极坐标的应用，涉及余弦定理的应用，属于基础题．5．C解析：C 【解析】分析：先由曲线C 的直角坐标方程得到其极坐标方程为()221+2sin 6ρθ=，设A 、B 两点坐标为()1,ρθ，()2,ρθ，将射线M 的极坐标方程为θα=分别代入曲线C 和直线l 的极坐标方程，得到关于α的三角函数，利用三角函数性质可得结果.详解：∵曲线C 的方程为22162x y +=，即2236x y +=，∴曲线C 的极坐标方程为()221+2sin 6ρθ=设A 、B 两点坐标为()1,ρθ，()2,ρθ，联立()221+2sin 6ρθθα⎧=⎪⎨=⎪⎩，得221112sin 6θρ+=，同理得222cos 163πθρ⎛⎫+ ⎪⎝⎭=， 根据极坐标的几何意义可得22222212cos 111112sin 663OA OBπθθρρ⎛⎫+ ⎪+⎝⎭+=+=+1+1cos 21cos 23sin 23666ππθθθ⎛⎫⎛⎫-+++-+ ⎪ ⎪⎝⎭⎝⎭=，即可得其最大值为23，故选C. 点睛：本题考查两线段的倒数的平方和的求法，考查直角坐标方程、极坐标方程的互化等基础知识，考查运算求解能力，充分理解极坐标中ρ的几何意义以及联立两曲线的极坐标方程得到交点的极坐标是解题的关键，是中档题．6．C解析：C【解析】 【分析】利用极坐标方差化为直角坐标方程即可得出． 【详解】()04πθρ=≥表表示的图形是一条射线：y=x （x≥0）．故选C ． 【点睛】本题考查了射线的极坐标方程，考查了推理能力与计算能力，属于基础题．7．C解析：C 【解析】 点到直线分别化为直角坐标系下的坐标与方程：，直线点到直线的距离，点到直线的距离是，故选C.8．B解析：B 【解析】22(2)(23)4ρ=-+-=，23tan 32θ-==-，3(,)2πθπ∈，所以43πθ=，即极坐标为4(4,)3π．故选B ． 9．B解析：B 【分析】先求出曲线C 的平面直角坐标系的方程，求出M N 、中点在平面直角坐标系的坐标，然后再求出其极坐标 【详解】 由cos 13πρθ⎛⎫-= ⎪⎝⎭可得：13cos sin 122ρθρθ+= ∴曲线C 的直角坐标方程为13122x y +=，即320x -=故点M N 、在平面直角坐标系的坐标为()23200⎛ ⎝⎭，，， ∴点P 坐标为313⎛ ⎝⎭，则极坐标为6P π⎫⎪⎪⎝⎭， 故选B 【点睛】本题主要考查了平面直角坐标系与极坐标之间的转化，只要掌握转化方法然后就可以计算出答案，较为基础．10．C解析：C 【解析】分析：直线πsin 44ρθ⎛⎫+= ⎪⎝⎭化为直角坐标方程，圆π4sin 4ρθ⎛⎫=+ ⎪⎝⎭化为直角坐标方程，求出圆心到直线距离，与半径比较即可得结论. 详解：直线πsin 44ρθ⎛⎫+= ⎪⎝⎭cos 4sin ρθρθ+= ,422x y +=,0y x +-=， 圆π4sin 4ρθ⎛⎫=+⎪⎝⎭可化成2cos sin ρθθ=+,22((4x y -+-=，圆心到直线的距离2d r ===，所以圆与直线相切．故选C ．点睛：利用关系式cos sin x y ρθρθ=⎧⎨=⎩可以把极坐标与直角坐标互化，这类问题一般我们可以先把曲线方程化为直角坐标方程，用直角坐标方程解决相应问题． 11．C解析：C 【解析】联立极坐标方程：π14sin ρθρ⎧⎛⎫+= ⎪⎪⎝⎭⎨⎪=⎩可得：110ρθ⎧=⎪⎨=⎪⎩222ρπθ⎧=⎪⎨=⎪⎩，利用勾股定理可得2AB ==.故选C.12．C解析：C 【解析】由题意得，式子可变形为(cos 2)0ρρθ-=，即0ρ=或cos 20ρθ-=，所以x 2+y 2=0或x=2，选C.【点睛】由直角坐标与极坐标互换公式222cos sin x y x y ρθρθρ=⎧⎪=⎨⎪+=⎩，利用这个公式可以实现直角坐标与极坐标的相互转化． 二、填空题13．【分析】先将原极坐标方程中的三角式利用和角公式化开后再化成直角坐标方程再利用直角坐标方程进行求解到原点的距离最大值即可【详解】将原极坐标方程化为：化成直角坐标方程为：它表示圆心在半径为的圆圆上的点到解析：【分析】先将原极坐标方程中的三角式利用和角公式化开后再化成直角坐标方程，再利用直角坐标方程进行求解到原点的距离最大值即可． 【详解】将原极坐标方程2cos 604πρθ⎛⎫--+= ⎪⎝⎭化为：24+0cos sin ρρθθ-+=（）6 ， 化成直角坐标方程为：2244+60x y x y +--= ， 它表示圆心在22（，）的圆，圆上的点到原点的最远距离是=故答案为 【点睛】本题考查点的极坐标和直角坐标的互化，属基础题.14．【解析】【分析】设曲线上任意一点为与之对应的曲线上的点为将变换公式代入曲线的方程化简即可求解【详解】由题意设曲线上任意一点为与之对应的曲线上的点为将代入曲线方程整理得故答案为：【点睛】本题主要考查了 解析：22491x y +=【解析】 【分析】设曲线C 上任意一点为(,)x y 与之对应的曲线22''1x y +=上的点为(',')x y ，将变换公式，代入曲线的方程，化简即可求解． 【详解】由题意，设曲线C 上任意一点为(,)x y ，与之对应的曲线22''1x y +=上的点为(',')x y ，将'2'3x xy y=⎧⎨=⎩,代入曲线方程22''1x y +=，整理得22491x y +=， 故答案为：22491x y +=． 【点睛】本题主要考查了伸缩变换公式的应用，其中解答中理解变换的公式，代入准确运算是解答的关键，着重考查了推理与运算能力，属于基础题．15．1【解析】由极坐标与直角坐标的互化关系可得点直线由点到直线的距离公式可得应填答案解析：1 【解析】由极坐标与直角坐标的互化关系cos ,sin x y ρθρθ==可得点P ，直线60x +-=，由点到直线的距离公式可得1d ==，应填答案1． 16．【解析】分析：由题意结合三角形面积公式整理计算即可求得三角形的面积详解：的面积点睛：本题主要考查三角形面积公式的应用极坐标的几何意义等知识意在考查学生的转化能力和计算求解能力解析：2【解析】分析：由题意结合三角形面积公式整理计算即可求得三角形的面积.详解：OAB 的面积11sin 1223222OABSOA OB π=⨯⨯⨯=⨯⨯⨯= 点睛：本题主要考查三角形面积公式的应用，极坐标的几何意义等知识，意在考查学生的转化能力和计算求解能力.17．【分析】根据将直线与圆极坐标方程化为直角坐标方程再根据圆心到直线距离等于半径解出【详解】因为由得由得即即因为直线与圆相切所以【点睛】（1）直角坐标方程化为极坐标方程只要运用公式及直接代入并化简即可；解析：1【分析】根据222,cos ,sin x y x y ρρθρθ=+==将直线与圆极坐标方程化为直角坐标方程，再根据圆心到直线距离等于半径解出a . 【详解】因为222,cos ,sin x y x y ρρθρθ=+==， 由cos sin (0)a a ρθρθ+=>，得(0)x y a a +=>，由2cos ρθ=，得2=2cos ρρθ，即22=2x y x +，即22(1)1x y -+=，1101a a a =∴=±>∴=+，，【点睛】（1）直角坐标方程化为极坐标方程，只要运用公式cos x ρθ=及sin y ρθ=直接代入并化简即可；（2）极坐标方程化为直角坐标方程时常通过变形，构造形如2cos ,sin ,ρθρθρ的形式，进行整体代换.其中方程的两边同乘以(或同除以)ρ及方程两边平方是常用的变形方法.但对方程进行变形时，方程必须同解，因此应注意对变形过程的检验.18．8【解析】分析：先根据加减消元法得直线的普通方程再根据将曲线C 的极坐标方程化为直角坐标方程联立方程组解得交点坐标最后根据两点间距离公式求结果详解：由得或因此点睛：(1)直角坐标方程化为极坐标方程只要解析：【解析】分析：先根据加减消元法得直线l 的普通方程，再根据222,cos ,sin x y x y ρρθρθ=+== 将曲线C 的极坐标方程化为直角坐标方程，联立方程组解得交点坐标，最后根据两点间距离公式求结果.详解：12322x tx y y t ⎧=-⎪⎪∴+=⎨⎪=+⎪⎩2222sin 4cos sin 4cos 4y x ρθθρθρθ=∴=∴= ， 由234x y y x +=⎧⎨=⎩ 得12x y =⎧⎨=⎩或96x y =⎧⎨=-⎩，因此AB =点睛：(1)直角坐标方程化为极坐标方程，只要运用公式cos x ρθ=及sin y ρθ=直接代入并化简即可； (2)极坐标方程化为直角坐标方程时常通过变形，构造形如2cos ,sin ,ρθρθρ的形式，进行整体代换.其中方程的两边同乘以(或同除以)ρ及方程两边平方是常用的变形方法.但对方程进行变形时，方程必须同解，因此应注意对变形过程的检验.19．【解析】伸缩变换即：则伸缩变换之后曲线设曲线上点的坐标为：结合点到直线距离公式有：结合三角函数的性质可得当时距离取得最小值【解析】伸缩变换即：'2'3x x y y ⎧=⎪⎪⎨⎪=⎪⎩，则伸缩变换之后曲线22:149x y C +=， 设曲线上点的坐标为：()2cos 3sin P θθ,，结合点到直线距离公式有：d ==，结合三角函数的性质可得，当()sin 1θϕ+=时，距离取得最小值min d =20．【解析】设是直线上任意一点如图由于所以应填答案 解析：cos ρθ=【解析】设(,)M ρθ是直线上任意一点，如图，由于2OH ==，所以cosOH ρθ==cos ρθ= 三、解答题21．（1）4sin 3πρθ⎛⎫=+ ⎪⎝⎭； （2）2+. 【分析】（1）求出直线l 的直角坐标方程为y =+2，曲线C 1），半径为r 的圆，直线l 与曲线C 相切，求出r ＝2，曲线C 的普通方程为（x 2+（y ﹣1）2＝4，由此能求出曲线C 的极坐标方程． （2）设M （ρ1，θ），N （ρ2，6πθ+），（ρ1＞0，ρ2＞0），由126MONSOM ON sin π==2sin （23πθ+）△MON 面积的最大值． 【详解】（1）由题意可知将直线l 的直角坐标方程为2y =+，曲线C 是圆心为)，半径为r 的圆，直线l 与曲线C相切，可得：2r ==；可知曲线C 的方程为(()2214x y -+-=，∴曲线C 的极坐标方程为2cos 2sin 0ρθρθ--=，即4sin 3πρθ⎛⎫=+⎪⎝⎭. （2）由（1）不妨设()1,M ρθ，2,6N πρθ⎛⎫+⎪⎝⎭，()120,0ρρ>>21211sin ?4sin ?sin 2sin cos26432MON S OM ONπππρρθθθθθ∆⎛⎫⎛⎫===++=+ ⎪ ⎪⎝⎭⎝⎭sin22sin 23πθθθ⎛⎫=++=++ ⎪⎝⎭当12πθ=时，2MON S ∆≤MON ∴∆面积的最大值为2.【点睛】本题考查曲线的极坐标方程的求法，考查三角形的面积的最大值的求法，考查参数方程、极坐标方程、直角坐标方程的互化等基础知识，考查运算求解能力，考查函数与方程思想，是中档题．22．（1）4cos ρθ=；（2）23【分析】（1）将1C 首先化为普通方程，再化为极坐标方程，代入点6P π⎛⎫⎪⎝⎭可求得2r ，整理可得所求的极坐标方程；（2）将,A B 代入2C 方程，从而将2212,ρρ代入2222121111OAOBρρ+=+整理可得结果. 【详解】（1）将1C 的参数方程化为普通方程得：()2222x y r -+=由cos x ρθ=，siny ρθ=得1C 的极坐标方程为：224cos 40r ρρθ-+-=将点6P π⎛⎫⎪⎝⎭代入1C 中得：212406r π-+-=，解得：24r =代入1C 的极坐标方程整理可得：4cos ρθ=1C ∴的极坐标方程为：4cos ρθ=（2）将点1,6A πρα⎛⎫-⎪⎝⎭，23,B πρα⎛⎫+⎪⎝⎭代入曲线2C 的极坐标方程得： 212cos 263πρα⎡⎤⎛⎫+-= ⎪⎢⎥⎝⎭⎣⎦，222222cos 22cos 2633ππραρα⎡⎤⎡⎤⎛⎫⎛⎫++=--= ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦2222122cos 22cos 2111123363OA OBππααρρ⎛⎫⎛⎫+-+-- ⎪ ⎪⎝⎭⎝⎭∴+=+== 【点睛】本题考查极坐标方程的求解、极坐标中ρ的几何意义的应用，关键是根据几何意义将所求的2211OAOB+变为221211ρρ+，从而使问题得以求解.23．(1)2cos ,2sin a ρθρθ== (2)2 【解析】 【分析】（1）直接利用转换关系，把参数方程直角坐标方程和极坐标方程之间进行转换．（2）利用（1）的结论，进一步利用极径求出参数的值． 【详解】（1）在平面直角坐标系xOy 中，曲线C 1：x 2﹣2ax+y 2=0（a ＞0）， 转换为极坐标方程为：ρ2=2aρcosθ， 即：ρ=2acosθ． 曲线C 2的参数方程为（α为参数），转换为直角坐标方程为：x 2+（y ﹣1）2=1， 转换为极坐标方程为：ρ=2cosθ． （2）已知极坐标方程为θ=的直线与曲线C 1，C 2分别相交于P ，Q 两点， 由，得到：P （），Q （）， 由于：|PQ|=2﹣1，所以：，解得：a=2． 【点睛】本题考查参数方程直角坐标方程和极坐标方程之间的转换，极径的应用，主要考查学生的运算能力和转化能力．24．(1) 221,2x y +=6x y +=.(2) 6322. 【解析】试题分析：（1）1C 消参数即可得普通方程，2C 利用极坐标化为直角坐标公式化为普通方程；（2）根据点到直线距离公式及三角函数有界性可求出最小值. 试题（1）由曲线1:x C y sin αα⎧=⎪⎨=⎪⎩（α为参数），曲线1C 的普通方程为：2212x y +=，由曲线2:sin 4C πρθ⎛⎫+= ⎪⎝⎭)sin cos 2ρθθ⨯+= 化为：6x y +=.（2）椭圆上的点),sin Pαα到直线O 的距离为d ==tan ϕ=所以当()sin 1αϕ+=时，P 的最小值为.25．（1）()()22112x y -+-=，cos sin 40ρθρθ-+=；（2. 【分析】（1）根据圆C ：2cos 2sin =+，直线:40l x y -+=，利用222,cos ,sin x y x y =+==求解.（2）先求得圆心到到直线l 的距离，再利用圆C 上的点到直线l 的最短距离为d r -求解. 【详解】（1）因为圆C ：2cos 2sin =+，所以22cos 2sin =+ρρθρθ，所以2222x y x y +=+，即()()22112x y -+-=.因为直线:40l x y -+=， 所以cos sin 40ρθρθ-+=.（2）因为圆心到到直线l 的距离为d ==．所以求圆C 上的点到直线l 的最短距离d r -= 【点睛】本题主要考查极坐标方程，直角坐标方程的转化以及直线与圆的位置关系，还考查了运算求解的能力，属于中档题.26．（1）22194x y += 2100x y +-=； （2【分析】（1）由'3'2x x y y =⎧⎨=⎩后得到曲线C 2，可得：1'31'2x x y y ⎧=⎪⎪⎨⎪=⎪⎩，代入圆C 1：x 2+y 2=1，化简可得曲线C 2的直角坐标方程，将直线l 的极坐标方程为cosθ+2sinθ=10ρ化为：ρcosθ+2ρsinθ=10，进而可得直线l 的直角坐标方程.（2）将直线x+2y ﹣10=0平移与C 2相切时，则第一象限内的切点M 满足条件，联立方程求出M 点的坐标，进而可得答案. 【详解】 （1）因为32x xy y''=⎧⎨=⎩后得到曲线2C ， 1'31'2x x y y ⎧=⎪⎪∴⎨⎪=⎪⎩，代入圆1C ：221x y +=得：'2'2194x y +=，故曲线2C 的直角坐标方程为22194x y +=；直线l 的极坐标方程为102cos sin θθρ+=．即210cos sin ρθρθ+=，即2100x y +-=.()2将直线2100x y +-=平移与2C 相切时，则第一象限内的切点M 满足条件，设过M 的直线为20x y C ++=，则由2220194x y C x y ++=⎧⎪⎨+=⎪⎩得：222599360424x Cx C ++-=， 由229259()4360244C C ⎛⎫=-⨯⨯-= ⎪⎝⎭得：52C =±， 故95x =，或95x =-，(舍去)， 则85y =，即M 点的坐标为98,55⎛⎫ ⎪⎝⎭， 则点M 到直线l 的距离d ==【点睛】本题考查的知识点是简单的极坐标方程，直线与圆锥曲线的关系，难度中档．。
(典型题)高中数学高中数学选修4-4第二章《参数方程》测试(有答案解析)
一、选择题1．在直角坐标系xOy 中，曲线C ：22x ty t⎧=⎪⎨=⎪⎩（t 为参数）上的点到直线l ：230x y -+=的距离的最小值为（ ）A ．23B ．223C ．233D ．22．直线2413x t y t =-+⎧⎨=--⎩（t 为参数）被圆25cos 15sin x y θθ=+⎧⎨=+⎩（θ为参数）所截得的弦长为（ ） A ．6B ．5C ．8D ．7 3．已知点是曲线：（为参数，）上一点，点，则的取值范围是 A ．B ．C ．D ．4．在方程sin {cos 2x y θθ==（θ为参数）所表示的曲线上的点是 （ ）A ．(2,7)B ．12(,)33C ．(1,0)D ．11(,)225．若曲线2sin301sin30x t y t =-︒⎧⎨=-+︒⎩（t 为参数）与曲线22ρ=相交于B ，C 两点，则BC 的值为（ ）A ．27B ．60C ．72D ．306．在平面直角坐标系中以原点为极点，以x 轴正方向为极轴建立的极坐标系中，直线:20l y kx ++=与曲线2:cos C ρθ=相交，则k 的取值范围是( )A ．k ∈RB ．34k ≥-C ．34k <-D ．k ∈R 但0k ≠7．过()0,2P -，倾斜角为60︒的直线与曲线232y x x =-+交于A B 、两点，则PA PB ⋅= ( )A ．623+B ．16C ．8D ．623-8．点M 的直角坐标是()3,1--，则点M 的极坐标为（ ） A ．52,6π⎛⎫ ⎪⎝⎭B ．72,6π⎛⎫ ⎪⎝⎭C ．112,6π⎛⎫ ⎪⎝⎭D ．2,6π⎛⎫⎪⎝⎭9．极坐标系中，由三条曲线围成的图形的面积是（ ）A ．B ．C ．D ．10．极坐标cos ρθ=和参数方程12x ty t =--⎧⎨=+⎩（t 为参数）所表示的图形分别是A ．直线、直线B ．直线、圆C ．圆、圆D ．圆、直线11．已知在平面直角坐标系xOy 中，以O 为极点，x 轴的正半轴为极轴，建立极坐标系.曲线1C 的极坐标方程为4cos ρθ=，直线251:51x l y ⎧=⎪⎪⎨⎪=⎪⎩(t 为参数).若曲线2C 的参数方程为2cos sin x y αα=⎧⎨=⎩(α为参数)，曲线1C 上点P 的极角为4π，Q 为曲线2C 上的动点，求PQ 的中点M 到直线l 距离的最大值为（ ）A ．2B 63+C 31D 10 12．椭圆221169x y +=上的点到直线34132x y += ）A ．0B ．25C ．52D ．241325- 二、填空题13．已知点(,)P x y 在曲线2cos sin x y θθ=-+⎧⎨=⎩，（θ为参数）上，则yx 的取值范围为_____.14．以直角坐标系的原点为极点，x 轴的正半轴为极轴，并在两种坐标系中取相同的长度单位，已知直线的极坐标方程为()4R πθρ=∈，它与曲线1222x cos y sin αα=+⎧⎨=+⎩（α为参数）,相交于两点A 和 B ，则AB =__________． 15．直线170{?270x tsin y tcos =+=+（t 为参数）的倾斜角为_________16．在直角坐标系xOy 中，直线l 的参数方程为22212x y ⎧=⎪⎪⎨⎪=+⎪⎩（t 为参数），以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 的极坐标方程为2cos 4sin ρθθ=，l与C 交于,A B 两点，则AB =_______.17．在平面直角坐标系xOy 中，曲线C的参数方程为,sin ,x y φφ⎧=⎪⎨=⎪⎩（φ为参数），直线l 的方程为40x y +-=，则曲线C 上的点到直线l 的距离的最大值为__________． 18．曲线4cos 2sin x y θθ=⎧⎨=⎩上的点到直线20x y +=的最大距离为__________．19．曲线1C 的极坐标方程2cos sin ρθθ=，曲线2C 的参数方程为31x t y t =-⎧⎨=-⎩，以极点为原点，极轴为x 轴正半轴建立直角坐标系，则曲线1C 上的点与曲线2C 上的点最近的距离为__________．20．已知直线12:(22x l t y t⎧=--⎪⎪⎨⎪=+⎪⎩为参数）与曲线:(x cos C y θθθ=⎧⎪⎨=⎪⎩为参数）交于,A B 两点，则点()1,2M -与,A B 两点的距离之积MA MB ⋅=______.三、解答题21．在平面直角坐标系xOy 中，直线l的参数方程为4x aty ⎧=⎪⎨=+⎪⎩（其中t 为参数），以坐标原点O 为极点，x 轴的正半轴为极轴的极坐标系中，点A 的极坐标为2,6π⎛⎫⎪⎝⎭，直线l 经过点A ．曲线C 的极坐标方程为2sin 4cos ρθθ=． （1）求直线l 的普通方程与曲线C 的直角坐标方程； （2）过点)P作直线l 的垂线交曲线C 于D ，E 两点（D 在x 轴上方），求11PD PE-的值． 22．已知纵坐标系的极点在直角坐标系的原点处，极轴与x 轴的正半轴重合，直线l 的参数方程为：112x y t ⎧=-⎪⎪⎨⎪=⎪⎩（t 为参数），曲线C 的极坐标方程为：4cos ρθ=． （1）写出C 的直角坐标方程，并指出C 是什么曲线． （2）设直线l 与曲线C 相交于P ，Q 两点，求PQ 值．23．曲线1C ：2121x t y t =+⎧⎨=-⎩(其中t 为参数)，以原点为极点，x 轴的正半轴为极轴，取相同的单位长度建立极坐标系，曲线2C ：()2cos 0a a ρθ=>关于1C 对称.（1）求曲线1C 的普通方程，曲线2C 直角坐标方程；（2）将2C 向左平移2个单位长度，按照12x x y y ⎧=⎪⎪⎨=''⎪⎪⎩变换得到3C ，点P 为3C 上任意一点，求点P 到曲线1C 距离的最大值. 24．[选修4-4：坐标系与参数方程]（10分）在极坐标系中，圆C 的极坐标方程为()24cos sin 3ρρθθ=+-，若以极点O 为原点，极轴为x 轴的正半轴建立平面直角坐标系. （1）求圆C 的一个参数方程；（2）在平面直角坐标系中，(),P x y 是圆C 上的动点，试求2x y +的最大值，并求出此时点P 的直角坐标.25．在平面直角坐标系中，以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系．已知直线l 上两点M ，N 的极坐标分别为（2，0），（32π，），圆C的参数方程222x cos y sin θθ=+⎧⎪⎨=⎪⎩（θ为参数）． （Ⅰ）设P 为线段MN 的中点，求直线OP 的平面直角坐标方程； （Ⅱ）判断直线l 与圆C 的位置关系．26．已知曲线C 的参数方程为32cos 12sin x y αα=+⎧⎨=+⎩ (α为参数),以直角坐标系原点为极点,以x轴正半轴为极轴并取相同的单位长度建立极坐标系. （1）求曲线C 的极坐标方程,并说明其表示什么轨迹；（2）若直线l 的极坐标方程为1sin 2cos θθρ-=,求曲线C 上的点到直线l 的最大距离.【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【分析】设曲线C上点的坐标为()2t ，利用点到直线的距离公式表示出距离，即可求出最小值. 【详解】设曲线C 上点的坐标为()2,2t t ， 则C 上的点到直线l 的距离2223(1)2233333t t t d -+-+===， 即C 上的点到直线1的距离的最小值为23． 故选：C. 【点睛】本题考查参数方程的应用，属于基础题.2．A解析：A 【分析】把直线和圆的参数方程化为普通方程，结合点到直线的距离公式和利用圆的弦长公式，即可求解. 【详解】由题意，直线2413x ty t =-+⎧⎨=--⎩（t 为参数）可得直线的方程为34100x y ++=，圆25cos 15sin x y θθ=+⎧⎨=+⎩（θ为参数）的普通方程为22(2)(1)25x y -+-=， 可得圆心(2,1)C ，半径为=5r ，所以圆心到直线34100x y ++=的距离为226410434d ++==+，由圆的弦长公式可得，弦长222222546L r d =-=-=. 故选：A. 【点睛】本题主要考查了参数方程与普通方程的互化，以及直线与圆的位置关系的应用，其中解答中把参数方程化为普通方程，结合圆的弦长公式求解是解答的关键，着重考查推理与运算能力.3．D解析：D 【解析】 【分析】将曲线的参数方程化为普通方程，可知曲线是圆的上半圆，再利用数形结合思想求出的最大值和最小值。
高中数学选修4-4《坐标系与参数方程》练习题(答案)
数学选修4-4 坐标系与参数方程一、 选择题1．化极坐标方程2cos 0ρθρ-=为直角坐标方程为（ ）A ．201y y +==2x 或B ．1x =C ．201y +==2x 或xD ．1y =2．极坐标方程cos 2sin 2ρθθ=表示的曲线为（ ）A ．一条射线和一个圆B ．两条直线C ．一条直线和一个圆D ．一个圆3．点M的直角坐标是(1-，则点M 的极坐标为（ ）A ．(2,)3πB ．(2,)3π-C ．2(2,)3πD ．(2,2),()3k k Z ππ+∈4．圆5cos ρθθ=-的圆心坐标是（ ）A ．4(5,)3π-- B ．(5,)3π- C ．(5,)3π D ．5(5,)3π-5．若直线的参数方程为12()23x tt y t =+⎧⎨=-⎩为参数，则直线的斜率为（ ）A ．23B ．23-C ．32D ．32-6．直线l 的参数方程为()x a tt y b t =+⎧⎨=+⎩为参数，l 上的点1P 对应的参数是1t ，则点1P 与(,)P a b 之间的距离是（）A ．1tB ．12t C1 D17．直线112()2x tt y ⎧=+⎪⎪⎨⎪=-⎪⎩为参数和圆2216x y +=交于,A B 两点，则AB 的中点坐标为（ ）A ．(3,3)- B．( C．3)- D．(3,8．与参数方程为)x t y ⎧=⎪⎨=⎪⎩为参数等价的普通方程为（ ）A ．214y +=2x B ．21(01)4y x +=≤≤2xC ．21(02)4y y +=≤≤2xD ．21(01,02)4y x y +=≤≤≤≤2x9．直线2()1x t t y t=-+⎧⎨=-⎩为参数被圆22(3)(1)25x y -++=所截得的弦长为（ ） AB ．1404 CD10．下列在曲线sin 2()cos sin x y θθθθ=⎧⎨=+⎩为参数上的点是（ ）A．1(,2B ．31(,)42- C． D． 11．将参数方程222sin ()sin x y θθθ⎧=+⎪⎨=⎪⎩为参数化为普通方程为（ ） A ．2y x =- B ．2y x =+ C ．2(23)y x x =-≤≤ D ．2(01)y x y =+≤≤12．极坐标方程cos 20ρθ=表示的曲线为（ ） A ．极点 B ．极轴 C ．一条直线 D ．两条相交直线二、填空题13．直线34()45x t t y t=+⎧⎨=-⎩为参数的斜率为______________________。
高二数学选修4-4《极坐标与参数方程》测试题
高二数学选修4-4《极坐标与参数方程》测试题（时间：120分钟，总分：150分） 姓名： 学号:一．选择题（每小题5分，共50分）1.曲线的极坐标方程θρsin 4=化为直角坐标为（ ）。
A.4)2(22=++y xB. 4)2(22=-+y xC. 4)2(22=+-y xD. 4)2(22=++y x 2.已知点P 的极坐标是（1，π），则过点P 且垂直极轴的直线方程是（ ）。
A.1=ρ B. θρcos = C. θρcos 1-= D. θρcos 1= 3.直线12+=x y 的参数方程是（ ）。
A.⎩⎨⎧+==1222t y t x B.⎩⎨⎧+=-=1412t y t x C. ⎩⎨⎧-=-=121t y t x D. ⎩⎨⎧+==1sin 2sin θθy x 4.方程⎪⎩⎪⎨⎧=+=21y t t x 表示的曲线是（ ）。
A.一条直线 B.两条射线 C.一条线段 D.抛物线的一部分5.参数方程⎩⎨⎧+-=+=θθ2cos 1sin 22y x （θ为参数）化为普通方程是（ ）。
A.042=+-y xB. 042=-+y xC. 042=+-y x ]3,2[∈xD. 042=-+y x]3,2[∈x6.设点P 对应的复数为-3+3i ，以原点为极点，实轴正半轴为极轴建立极坐标系，则点P 的极坐标为（ ） A.(23，π43) B. (23-，π45) C. (3，π45) D. (-3，π43) 7.直线l ：02=++kx y 与曲线C ：θρcos 2=相交，则k 的取值范围是（ ）。
A.43-≤k B. 43-≥k C. R k ∈ D. R k ∈但0≠k 8.在极坐标系中，曲线)3sin(4πθρ-=关于（ ）。
A.直线3πθ=对称 B.直线65πθ=对称 C.点(2，3π)中心对称 D.极点中心对称9.若圆的方程为⎩⎨⎧+=+-=θθsin 23cos 21y x ，直线的方程为⎩⎨⎧-=-=1612t y t x ，则直线与圆的位置关系是（ ）。
选修4-4 极坐标与参数方程(极坐标)01
)
1.
（1）求点
(4,
4
)
的直角坐标系下的坐标与直线的普通方程；
（2）求点
(4,
4
)
到直线
sin(
4
)
1的距离.
【练 1】坐标系与参数方程
在直角坐标系 xOy 中，以 O 为极点， x 轴正半轴为极轴建立极坐标系，圆 C1 ,直线 C2 的极坐标方程分别为
4sin ,
cos
N
，求 C2MN
的面积.
【练
4】已知曲线
C1
的参数方程为
x y
4 5
5 5
cos t sin t
,
（
t
为参数），以坐标原点为极点，
x
轴的正半轴为极轴建立
极坐标系，曲线 C2 的极坐标方程为 ＝2 sin ．
（1）把 C1 的参数方程化为极坐标方程；
（2）求 C1 与 C2 交点的极坐标（ 0, 0 ＜2 ）．
4
2
2.
（1） 求 C1 与 C2 交点的极坐标;
x t3 a
（2）设
P
为
C1
的圆心，
Q
为
C1
与
C2
交点连线的中点，已知直线
PQ
的参数方程为
y
b 2
t3
(t 1
R
为，参
数) 求 a, b 的值.
试卷第 2 页，总 14 页
【练 2】坐标系与参数方程
y2
4
人教版高二数学选修4-4单元测试题二及答案
高二数学（文科）选修4-4单元测试题（二）班级______________姓名______________1．在直角坐标系xOy 中，曲线C 的参数方程为⎩⎨⎧+==ααsin 1cos y x （α为参数），以O 为极点，x 轴的正半轴为极轴建立极坐标系，则曲线C 的极坐标方程为 ．2．在平面直角坐标系中，已知直线l 与曲线C 的参数方程分别为l ：1,1x s y s=+⎧⎨=-⎩（s 为参数）和C ：22,x t y t =+⎧⎨=⎩（t 为参数），若l 与C 相交于A 、B 两点，则AB = ．3．在直角坐标系xoy 中, 以坐标原点为极点, x 轴正半轴为极轴建立极坐标系,则直线2()1x t t y t=-+⎧⎨=-⎩为参数截圆22cos 30ρρθ+-=的弦长等于__________．4．化参数方程⎪⎩⎪⎨⎧==ty tx 22sin cos ，0(∈t ，]2π为普通方程为 ．5．直线2()1x tt y t=-+⎧⎨=-⎩为参数被圆35cos 15sin x y θθ=+⎧⎨=-+⎩ ()θθπ∈为参数,[0,2)所截得的 弦长为 ．6．已知直线l ：40x y -+=与圆C ：12cos 12sin x y θθ=+⎧⎨=+⎩（θ为参数），则C 上各点到l 的距离的最小值为___________.7.已知直线112:2x tl y kt=-⎧⎨=+⎩（t 为参数），2,:12.x s l y s =⎧⎨=-⎩（s 为参数），若1l //2l ，则k = ；若12l l ⊥，则k = ．8.直线3470x y +-=截曲线cos ,1sin x y αα=⎧⎨=+⎩（α为参数）的弦长为___________．9.已知两曲线参数方程分别为()πθθθ<≤⎩⎨⎧==0sin cos 5y x 和 ⎪⎩⎪⎨⎧==ty tx 245（t R ∈），它们的交点坐标为 ．10.已知直线314x aty t=+⎧⎨=-+⎩（t 为参数），则该直线恒过定点__________.11.两直线2)4sin(=+πθρ与1)4sin(=-πθρ的位置关系是 .12. 球坐标(2,,)63ππ对应的点的直角坐标是 ___，对应点的柱坐标是 _ __.13.自极点O 向直线l 作垂线，垂足为(2,)3H π，则直线l 的极坐标方程是 .14.极坐标方程 24sin 3θ= 化为直角坐标方程是 ；它表示的图形是 .15.在极坐标系中，曲线4sin ρθ=-和cos 1ρθ=相交于点,A B 两点，则线段AB 的长度 为 ．16.在直角坐标系中圆C 的参数方程为⎩⎨⎧+==θθsin 22cos 2y x （θ为参数），则圆C 的普通方程为 __ __，以原点O 为极点，以x 轴正半轴为极轴建立极坐标系，则 圆C 的圆心极坐标为 __ _．17.参数方程⎩⎨⎧-==αα2cos 2cos 2y x (α是参数)表示的曲线的普通方程是_________________．18.参数方程sin cos sin 2x y θθθ=-⎧⎨=⎩(θ为参数)化为普通方程是 ．19.若直线340x y m ++=与圆⎩⎨⎧+-=+=θθsin 2cos 1y x （θ为参数）相切，则实数m 的值是 ．20.已知曲线sin (11cos 222y x θθθ=⎧⎪⎨=-⎪⎩为参数)与直线x a =有两个不同的公共点，则实数a 的取值范围是_________________.21．已知圆C 的参数方程为cos 1sin x y θθ=+⎧⎨=⎩(θ为参数), 则点()4,4P 与圆C 上的点的最远距离是 ．22.在直角坐标系中，曲线1C 的参数方程为],0[sin ,cos πθθθ∈⎩⎨⎧==y x ，以x 轴的正半轴为极轴建立极坐标系，曲线2C 在极坐标系中的方程为θθρcos sin -=b．若曲线1C 与2C 有两个不同的交点，则实数b 的取值范围是 ．23．已知圆锥曲线2cos x y θθ=⎧⎪⎨=⎪⎩(θ是参数)和定点A(0)，F 1、F 2是圆锥曲线的左、右焦点,以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，则直线AF 2的极坐标方程为__________________________．24.若直线⎩⎨⎧+=-=,32,21t y t x （t 为参数）与直线14=+ky x 垂直，则常数k =__ __.25.已知椭圆:C cos ,()2sin x y θθθ=⎧∈⎨=⎩R 经过点1(,)2m ，则m =______，离心率e =______.26. (2012深圳二模文）在极坐标系中，直线:cos l t ρθ=（常数0)t >）与曲线:2sin C ρθ=相切，则t = ．27. (2012深圳二模理）在极坐标系中，已知直线l ：(sin cos )a ρθθ-=把曲线C ：2cos ρθ= 所围成的区域分成面积相等的两部分，则常数a 的值是 ．28. (2012广州二模文、理）在极坐标系中，若等边三角形ABC (顶点A ，B ，C 按 顺时针方向排列)的顶点A ，B 的极坐标分别为(2，6π)，(2，76π)，则顶点C 的极 坐标为 ．参考答案1．θρsin 2=2 3．44．1=+y x （10≤≤x ）56．2 7．4；1- 8．1659．(1,510．(3,1)- 11．垂直12．1(2；(1,3π13．cos()23πρθ-=14．x y 3±=(或223x y =) ； 两条直线（或两条相交直线） 15．3216．22(2)4x y +-=； )2,2(π17．322+-=x y (2||≤x )18．21,x y x ⎡=-∈⎣19．10或0 20．01a <≤ 21．622．1b ≤<23．sin cos ρθθ=24．－625．415±，226．1 27．1-28．2)3π；或))(232,32(Z k k ∈+ππ。
北师大版高中数学选修4-4极坐标与参数方程练习精选(一)
极坐标与参数方程练习精选（一）班级 姓名 座号（满分150分）一、选择题（每小题5分，共140分）（ ）1、已知点1P 的球坐标是)4,,32(1πϕP ,2P 的柱坐标是)1,,5(2θP ,=21P PA ．2B ．3C ．22D ．22 （ ）2、已知⎪⎭⎫ ⎝⎛-3,5πM ，下列所给出的不能表示点的坐标的是 A ．⎪⎭⎫ ⎝⎛-3,5π B ．⎪⎭⎫ ⎝⎛34,5π C ．⎪⎭⎫ ⎝⎛-32,5π D ．⎪⎭⎫ ⎝⎛--35,5π （ ）3、已知点M 的极坐标为⎪⎭⎫⎝⎛35π，，下列所给出的四个坐标中能表示点M 的坐标的是 A. 53，-⎛⎝ ⎫⎭⎪π B. 543，π⎛⎝ ⎫⎭⎪ C. 523，-⎛⎝ ⎫⎭⎪π D. ⎪⎭⎫ ⎝⎛-355π， （ ）4、极坐标方程⎪⎭⎫ ⎝⎛-=θπρ4cos 表示的曲线是 A ．双曲线 B ．椭圆 C ．抛物线 D ．圆（ ）5、圆)sin (cos 2θθρ+=的圆心坐标是 A ．⎪⎭⎫ ⎝⎛4,1π B ．⎪⎭⎫ ⎝⎛4,21π C ．⎪⎭⎫ ⎝⎛4,2π D ．⎪⎭⎫ ⎝⎛4,2π （ ）6、直线αθ=与1)cos(=-αθρ的位置关系是A 、平行B 、垂直C 、相交不垂直D 、与有关，不确定 （ ）7、两圆θρcos 2=,θρsin 2=的公共部分面积是 A.214-πB.2-πC.12-πD.2π （ ）8、极坐标方程cos 2sin 2ρθθ=表示的曲线为A ．一条射线和一个圆B ．两条直线C ．一条直线和一个圆D ．一个圆 （ ）9、圆5cos 53sin ρθθ=-的圆心坐标是。
(压轴题)高中数学高中数学选修4-4第一章《坐标系》检测卷(含答案解析)(4)
一、选择题1．已知点P 的极坐标是1,2π⎛⎫⎪⎝⎭，则过点P 且垂直极轴的直线方程是（ ） A ．12ρ=B ．1cos 2ρθ=C ．12cos ρθ=-D ．2cos ρθ=-2．以平面直角坐标系的原点为极点，以x 轴的正半轴为极轴，建立极坐标系，则曲线3cos sin x y αα⎧=⎪⎨=⎪⎩（α为参数）上的点到曲线cos sin 4ρθρθ+=的最短距离是（ ）. A ．1B ．2C ．22D ．323．在极坐标系中，由三条直线0θ=，3πθ=，cos sin 1ρθρθ+=围成的图形的面积为（ ） A ．14B ．334- C ．234- D ．134．在极坐标系中，曲线1C 的极坐标方程为2sin ρθ=，曲线2C 的极坐标方程为2cos ρθ=。
若射线3πθ=与曲线1C 和曲线2C 分别交于,A B 两点（除极点外），则AB 等于（ ）A ．31-B ．31+C ．1D ．35．如图所示，极坐标方程sin (0)a a ρθ=>所表示的曲线是（ ）A ．B ．C ．D ．6．在极坐标系中，曲线46sin πρθ⎛⎫=+ ⎪⎝⎭关于( ) A ．直线23πθ=对称 B ．直线56πθ=对称 C ．点2,3π⎛⎫⎪⎝⎭中心对称 D ．极点中心对称7．已知点P 的极坐标是π2,6⎛⎫⎪⎝⎭，则过点P 且平行极轴的直线方程是( ) A ．ρ1=B ．ρsin θ=C ．1ρsin θ=-D ．1ρsin θ=8．将直角坐标方程y x =转化为极坐标方程，可以是( ) A ．1ρ=B ．ρθ=C ．1()R θρ=∈D ．()4R πθρ=∈9．在极坐标系中，点到直线的距离是（ ）．A ．B ．C ．D ．10．化极坐标方程ρ2cos θ－ρ＝0为直角坐标方程为( ) A ．x 2＋y 2＝0或y ＝1 B ．x ＝1 C ．x 2＋y 2＝0或x ＝1 D ．y ＝111．已知曲线C 的极坐标方程为2cos ρθ=，则曲线C 的直角坐标方程为A ．22(1)4x y -+=B ．22(1)4x y +-=C ．22(1)1x y -+=D ．22(1)1y x +-=12．将曲线22(1sin )2ρθ+=化为直角坐标方程为A ．2212y x +=B ．2212x y +=C ．2221x y +=D ．2221x y +=二、填空题13．已知圆的极坐标方程为4cos ρθ=，圆心为C ，点P 的极坐标为2π2,3⎛⎫⎪⎝⎭，则CP 的长度为______________.14．在极坐标系下，点π(1,)2P 与曲线2cos ρθ=上的动点Q 距离的最小值为_________．15．在极坐标系中，O 为极点，点A 为直线:sin cos 2l ρθρθ=+上一点，则||OA 的最小值为______．16．若直线l 的极坐标方程为ρcos ()324πθ-=C ：ρ＝1上的点到直线l 的距离为d ，则d 的最大值为________．17．在极坐标系中，圆2cos ρθ=的圆心到直线sin 1ρθ=的距离为______. 18．在平面直角坐标系中，倾斜角为4π的直线l 与曲线C ：2cos 1sin x y αα=+⎧⎨=+⎩ (α为参数)交于A ，B 两点，且|AB |＝2.以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，则直线l 的极坐标方程是________．19．在平面直角坐标系xOy 中，已知直线l 的参数方程为（t 为参数），以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 的极坐标方程为ρsin 2θ=4cosθ，直线l 与曲线C 交于A ，B 两点，则线段AB 的长为__． 20．（坐标系与参数方程选做题）已知圆C 的圆心为(6,)2π，半径为5，直线(,)2r πθαθπρ=≤<∈被圆截得的弦长为8，则α=_____．三、解答题21．在直角坐标平面内，以坐标原点O 为极点，x 轴的非负半轴为极轴建立极坐标系.已知点A 、B 的极坐标分别为()2,A π，22,4B π⎛⎫⎪⎝⎭，曲线C 的极坐标方程为2sin ρθ=. （1）求AOB 的面积；（2）求直线AB 被曲线C 截得的弦长. 22．在平面直角坐标系xOy 中，圆C 的参数方程为22cos ,2sin x y αα=+⎧⎨=⎩（α为参数），以点O 为极点，x 轴的正半轴为极轴建立极坐标系. （1）求圆C 的极坐标方程；（2）过极点O 作直线与圆C 交于点A ，求OA 的中点所在曲线的极坐标方程.23．在直角坐标系xOy 中，直线1:1C x =，圆()222:23C x y -+=，以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系 （1）求1C ，2C 的极坐标方程； （2）若直线3C 的极坐标方程为()4R πθρ=∈，设2C ，3C 的交点为,M N ，试求2C MN ∆的面积.24．以平面直角坐标系xOy 的原点为极点，x 轴的正半轴为极轴，建立极坐标系，两种坐标系中取相同的长度单位，C 的极坐标方程为8cos ρθ=. （1）求曲线C 的直角坐标方程；（2）经过点()1,1Q 作直线l 交曲线C 于M ，N 两点，若Q 恰好为线段MN 的中点，求直线l 的方程.25．在平面直角坐标系xOy 中，以O 为极点，x 轴的非负半轴为极轴建立极坐标系．已知曲线M 的参数方程为1cos 1sin x y ϕϕ=+⎧⎨=+⎩(ϕ为参数)，过原点O 且倾斜角为α的直线l 交M 于A 、B 两点．(1)求l 和M 的极坐标方程；(2)当04πα⎛⎤∈ ⎥⎝⎦，时，求OA OB +的取值范围．26．已知在平面直角坐标系xOy 中，直线l的参数方程为4x ty =-⎧⎪⎨=+⎪⎩（t 为参数），曲线1C 的方程为22(1)1y x +-=以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系．（1）求直线l 和曲线1C 的极坐标系方程；（2）曲线2C ：0,02πθαρα⎛⎫=><< ⎪⎝⎭分别交直线l 和曲线1C 交于A 、B ，求22OBOA +的最大值．【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【分析】把极坐标化为直角坐标，求出直线的直角坐标方程，再化为极坐标方程． 【详解】1,2P π⎛⎫⎪⎝⎭的直角坐标是1,02⎛⎫- ⎪⎝⎭，∴过P 且与极轴垂直的直线的直角坐标方程为12x =-，其极坐标方程为1cos 2ρθ=-，即12cos ρθ=-．故选：C ． 【点睛】本题考查求直线的极坐标方程，解题时利用极坐标与直角坐标的互化求解．2．B解析：B 【分析】根据cos ,sin x y ρθρθ==，计算出直线的直角坐标方程，然后假设曲线上任意一点),sin Pαα，根据点到直线的距离公式以及辅助角公式进行计算即可.由cos ,sin x y ρθρθ==，则曲线cos sin 4ρθρθ+=的直角坐标方程为40x y +-=设曲线曲线sin x y αα⎧=⎪⎨=⎪⎩（α为参数）上的任意一点位),sin Pαα则点P到直线的距离位d ==所以当sin 13πα⎛⎫+= ⎪⎝⎭时，min d 故选：B 【点睛】本题考查极坐标方程与普通方程的转化以及使用参数方程来解决点到直线的最值问题，重在计算，考查逻辑推理以及计算能力，属中档题.3．B解析：B 【分析】求出直线0θ=与直线cos sin 1ρθρθ+=交点的极坐标()1,0ρ，直线3πθ=与直线cos sin 1ρθρθ+=交点的极坐标2,3πρ⎛⎫ ⎪⎝⎭，然后利用三角形的面积公式121sin 23S πρρ=可得出结果. 【详解】设直线0θ=与直线cos sin 1ρθρθ+=交点的极坐标()1,0ρ，则1cos01ρ=，得11ρ=. 设直线3πθ=与直线cos sin 1ρθρθ+=交点的极坐标2,3πρ⎛⎫⎪⎝⎭， 则22cossin133ππρρ+=，即22112ρρ=，得21ρ=.因此，三条直线所围成的三角形的面积为)12113sin 1123224S πρρ==⨯⨯⨯=故选B. 【点睛】 本题考查极坐标系中三角形面积的计算，主要确定出交点的极坐标，并利用三角形的面积公式进行计算，考查运算求解能力，属于中等题.4．A【分析】 把3πθ=分别代入2sin ρθ=和2cos ρθ=，求得,A B 的极经，进而求得AB ，得到答案． 【详解】 由题意，把3πθ=代入2sin ρθ=，可得2sin33A πρ==，把3πθ=代入2cos ρθ=，可得2cos13B πρ==，结合图象，可得31A B AB ρρ=-=-，故选A ．【点睛】本题主要考查了简单的极坐标方程的应用，以及数形结合法的解题思想方法，着重考查了推理与运算能力，属于基础题．5．C解析：C 【解析】 【分析】把极坐标方程化为直角坐标方程即可。
北师大版高中数学选修4-4极坐标单元检测题.docx
高中数学学习材料鼎尚图文*整理制作北师大版极坐标单元检测题一．选择题1．已知⎪⎭⎫ ⎝⎛-3,5πM ，下列所给出的不能表示点的坐标的是（ ） A ．⎪⎭⎫ ⎝⎛-3,5π B ．⎪⎭⎫ ⎝⎛34,5π C ．⎪⎭⎫ ⎝⎛-32,5π D ．⎪⎭⎫ ⎝⎛--35,5π 2．下列各点中与极坐标⎪⎭⎫ ⎝⎛-6,2π不表示同一个点的极坐标是（ ） Ａ．⎪⎭⎫ ⎝⎛67,2π Ｂ．⎪⎭⎫ ⎝⎛-67,2π Ｃ．⎪⎭⎫ ⎝⎛--611,2π Ｄ．⎪⎭⎫ ⎝⎛-613,2π 3．点()3,1-P ，则它的极坐标是（ ）A ．⎪⎭⎫ ⎝⎛3,2πB ．⎪⎭⎫ ⎝⎛34,2πC ．⎪⎭⎫ ⎝⎛-3,2πD ．⎪⎭⎫ ⎝⎛-34,2π 4．极坐标方程⎪⎭⎫ ⎝⎛-=θπρ4cos 表示的曲线是（ ） A ．双曲线 B ．椭圆 C ．抛物线 D ．圆5．圆)sin (cos 2θθρ+=的圆心坐标是（ ）A ．⎪⎭⎫ ⎝⎛4,1πB ．⎪⎭⎫ ⎝⎛4,21πC ．⎪⎭⎫ ⎝⎛4,2πD ．⎪⎭⎫ ⎝⎛4,2π6．在极坐标系中，与圆θρsin 4=相切的一条直线方程为（ ）A ．2sin =θρB ．2cos =θρC ．4cos =θρD ．4cos -=θρ7．已知点()0,0,43,2,2,2O B A ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛--ππ则ABO ∆为（ ） A ．正三角形 B ．直角三角形 C ．锐角等腰三角形 D ．直角等腰三角形 8．)0(4≤=ρπθ表示的图形是（ ） A ．一条射线 B ．一条直线 C ．一条线段 D ．圆 9.两圆θρcos 2=,θρsin 2=的公共部分面积是（ ） A.214-πB.2-πC.12-πD.2π 10.曲线的极坐标方程θρsin 4=化为直角坐标为（ ）A.4)2(22=++y xB. 4)2(22=-+y xC. 4)2(22=+-y xD. 4)2(22=++y x11.已知点P 的极坐标是（1，π），则过点P 且垂直极轴的直线方程是（ ）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
高中数学选修 4-4
单元测试题 -- 极坐标与参数方程
班级 :
姓名 :
座号 :
评分 :
一 . 选择题 :( 每小题 5 分，共 40 分 )
1. 已知点 M 的极坐标为 (5,
) ，下列所给出的四个坐标中能表示点 M 的坐标是
( )
3
4
2
5
A.
(5, 3 ) B. (5, )
C. (5,
) D.
(5, )
3
3
3
2. 直线： 3x-4y-9=0 与圆：
x
2 cos
，( θ 为参数 ) 的位置关系是 ( )
y 2 sin
A. 相切
B.
相离
C.
直线过圆心
D.
相交但直线不过圆心
3. 在极坐标系中，点
P( , ) 关于极轴对称的点的一个坐标是
( )
A.
( , )
B.
( , )
C.
( , )
D.
( , )
4. 极坐标方程 4 sin
2
5 表示的曲线是
(
)
2
A. 圆
B.
椭圆 C. 双曲线的一支圆 D. 抛物线
5. 实数 x 、y 满足 3x 2＋2y 2=6x ，则 x 2＋ y 2 的最大值为
( )
A.3.5
B.4
C.4.5
D.5
6. 直线 x 3 t sin 200 (t 为参数 ) 的倾斜角是
( )
y 1 t cos200
A.20 0
B.70
C.110
D.160
7. 曲线 x 5 cos (
为参数 ) 的焦距是
( )
y 4 sin
A.3
B.6
C.10
D.8
x
8t
8. 当 t
R 时，参数方程
t 2
（ t 为参数），表示的图形是
( )
4
4 t 2
y
t 2
4
A. 双曲线
B.椭圆
C.抛物线
D.圆
二 . 填空题 :( 每小题 5分，共 30分 )
9. 点 (2,-2)的极坐标为 :_____________.
10.若A
(3,) ,B (4,) ，则|AB|=___________,S
AOB_____________. （其中 O是极点）34
11.极点到直线cos sin3的距离是 :____________ .
12.x12t(t为参数)与曲线 (y-2)22到弦 AB的距离
-x=1 相交于 A,B 两点 , 则点 M(-1,2)
y 3 4t
是:_____________ , 线段 AB 的中点坐标是 : _______ _____.
13.圆锥曲线x
4sec的准线方程是 :_______. y
为参数
3 tan
14.直线 l 过点M0(1,5) ,倾斜角是，且与直线 x y 2 3 0 交于M，则MM0的长为: __ _.
3
三 . 解答题 :
15.(12分)求圆心为C(3,) ,半径为3的圆的极坐标方程.
6
16.(14分)已知直线l 经过点 P(1,1),倾斜角，(1)写出直线l 的参数方程 .
6
(2) 设 l 与圆x2y 2 4 相交与两点A、 B, 求点 P 到 A、 B 两点的距离之积.
17.(13 分) 参数方程x2cos
,[0,2 ), 判断点 A(1, 3 )和B(2,1)是否在方程的曲线上 . y2sin
18.(14 (1)分 ) 将下列方程化为普通方程：
e t t
x cos sin
e
(为参数 ) (2)
x
(t 为参数 ) 222
1e t t
y sin )
e
(1y
22
19.(13分)设O是直径为 a 的圆上的一点 , 过 0 点任意作直线交圆于眯P, 在射线 OP上取一点 M,
使 MP a ,当点P在圆上移运一周时, 求相应的点M的轨迹方程 .
20.(14分 ) 椭圆x
2
y 21( a b 0) 与x轴正半轴交于点A, 若这个椭圆上存在点P, 使a2b2
OP AP (O为原点),求椭圆的离心率e的取值范围.
高中数学选修4-4 单元测试题 -- 极坐标与参数方程参考答案
1.D
2.D
3.B
4.D
5.B
6.C
7.B
8.B
9.2或写成2710.5， 611.36
，，d
4422
12. 4 5, (4,11
)13.y1614.10 6 3
3335
15. 如下图，设圆上任一点为P（，），则OP ，
POA
，
OA 2 3 6
6
Rt OAP 中， OP
OA cos POA
6cos
2 ) A (0, ) 符合
而点 O(0,
6
3
6
P
A
C
O
x
16. 解： (1) 直线的参数方程是
x
1
3
t,
2 (t 是参数）
1
t;
y
1
2
(2) 因为点 A,B 都在直线 l 上，所以可设它们对应的参数为 t 1 和 t 2, 则点 A,B 的坐标分别为
A(1
3
t 1 ,1
1
t 1 ), B(1
3
t 2 ,1
1
t 2 )
2 2
2 2
以直线 L 的参数方程代入圆的方程 x 2
y 2 4 整理得到 t 2
( 3 1)t 2 0
①
因为 t 1 和 t 2 是方程①的解，从而
t 1t 2＝－ 2 所以 |PA| · |PB|= |t 1t 2|
＝ | －2| ＝ 2
17. 解：把 A 、 B 两点坐标分别代入方程得
1 2 cos 2 2cos
3 (1) ，
(2) ，在 [0,2)
2 sin
1 2sin
内，方程组 (1) 的解是
，而方程组 (2) 无解，故 A 点在方程的曲线上，而 B 点不在方
3
程的曲线上 .
18. 解 :(1)
做 x 2
2
+sin
2
+sin ) － (1+sin ) ＝ 0
2 y
＝ (cos
2
2
x
2
2 y
＝ 0，但由于 x
2 sin(
) ，即 0≤ x ≤ 2 .
4
∴参数方程只表示抛物线的一部分，即
x 2
2y （ ≤ x ≤
2 ）
(2) 解方程组得 x y e t ① ;
x y
e t ② ①×②得 x 2 y 2 ＝ 1
从 x
e t
e t 知 x ≥ 1（提示应用均值定理）
所求的普通方程为 x 2 y 2 ＝ 1 ( x ≥ 1)
2
19. 以 O 为极点 , 水平向右的直线为极轴建立极坐标系
, 则圆的方程为 a cos . 设点案
M ( , ), P( 1 , 1 ), 则
1 , 所以
OP MP
a cos a , 所以点 M 的轨迹方程
是 :
a a cos
20. ( 2
,1)
2。