电路理论基础-第十章-含有耦合电感的电路PPT课件
10章 含有耦合电感的电路
jω L2 (支路 支路3)L ± 同侧取 同侧取“ 支路 3=±M(同侧取“＋”,异 异
R2
侧取“ 侧取“－”) (支路 1’=L1 m M，M前所取符 支路1)L 支路 ， 前所取符 号与L 号与 3中的相反 (支路 2’=L2 m M，M前所取 支路2)L 支路 ， 前所取 符号与L 符号与 3中的相反
反相串联无互感等效电路
R1 u1 u M L1 R1 L1-M u1 R2 u2 L2 u R2 L2-M u2
Z = Z1 + Z 2 = R1 + R2 + jω ( L1 + L2 − 2 M )
R1
L1 u1
2、顺向串联 、 每一耦合电感支路的阻抗为： 每一耦合电感支路的阻抗为：
Z1 = R1 + jω ( L1 + M )
两个耦合线圈的磁通链可表示为： 两个耦合线圈的磁通链可表示为：
ψ 1 = ψ 11 ± ψ 12
= L1i1±Mi2
ψ 2 = ±ψ 21 + ψ 22
= ±Mi1+L2i2 上式表明， 上式表明 ， 耦合线圈中的磁通链与施感电流 线性关系 关系， 成 线性 关系 ， 是各施感电流独立产生的磁通链叠 加的结果。 加的结果。
di di u2 = R2i + ( L2 −M ) dt dt di = R2i + ( L2 − M ) dt
无互感等效电路
R1 u1 u M L1 R1 L1-M u1 R2 u2 L2 u R2 L2-M u2
di u = u1 + u 2 = ( R1 + R2 )i + ( L1 + L2 − 2 M ) dt
L1 N1 L2 N2
(播放版)第10章含有耦合电感的电路PPT课件
27.01.2021
-
7
§10-1 互感
1. 互感的概念
L1 N1
结束
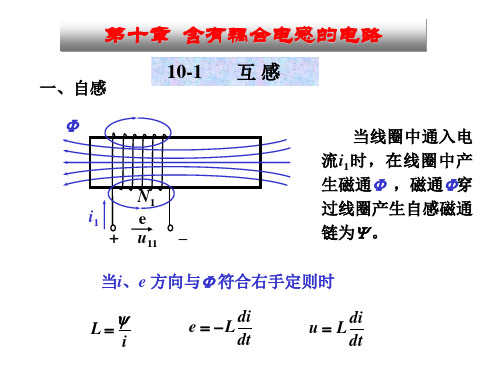
(1)一个线圈的情况
i1产生的磁通为F11
(符合右手螺旋法则 为关联参考方向)。
F11穿越自身线圈时，
产生的自感磁通链
定义为：Y11 = L1i1
当i1变化时，将产生 自感电压u11。
27.01.2021
F11
i1
1' -
u11
实际的互感线圈是封 闭的，看不出绕向
1 + i1
i2 + 2
u1 L1
-
u2
L2 -
1'
2'
M
在电路图中也无法反映绕向
为解决这个问题引入同名端的概念。
27.01.2021
-
15
同名端 当两个电流分别从两个线圈的对应端子同时 结束
流入或流出，若所产生的磁通相互加强时，则这 两个对应端子称为两互感线圈的同名端。
产生磁通F22。磁通链 Y22 = L2 i2 。 F22的一 部分F12也穿过L1。
F11
i1
1' -
u11
1 +
2'
i2 F22
2
当两个线圈都有电流时， 每一线圈的磁链为自磁链 与互磁链的代数和：
载流线圈之间通过彼 此的磁场相互联系的 物理现象称为磁耦合。
Y1=Y11±Y12 Y2=Y22±Y21
第十章 含有耦合电感的电路
结束
学习要点
熟练掌握互感的概念； 具有耦合电感电路的计算方法：
①直接列写方程的支路法或回路法。 ②受控源替代法。 ③互感消去法。 掌握空心变压器和理想变压器的应用。
《电路理论教学课件》第10章 含有耦合电感的电路
L2
2M
) di dt
Ri
L di dt
R R1 R2
L L1 L2 2M
L L1 L2 2M 0
M
1 2
( L1
L2
)
互感不大于两个自感的算术平均值。
在正弦激励下：反串
•
- jM I
•
j M
I R1 • j L1 R2
+
•
U1
+
消互感
–+ •
U
j L2 •
•
U2
–
–
•
U
•
•
Lc = －M La =L1 ＋ M Lb = L2 ＋ M
j La
•
U
R1
–
I2
j Lb R2
三、一般分析法(采用支路法、回路法直接列方程) 支路法、回路法：因为互感电压可以直接计入KVL方程中。
含互感的电路，直接用节点法列写方程不方便。 关键：正确考虑互感电压作用（要注意正负号，不要漏项。）
例 10-3. I1
4
* 全耦合 M L1L2
L L1 L2 2M L1 L2 2 L1 L2 ( L1 L2 )2
当 L1=L2 时 , M=L
4M L=
0
顺接 反接
二、互感线圈的并联
a. 同侧并联
•
•
•
U （R1 jL1）I 1 jM I 2
•
•
•
U （R2 jL2）I 2 jM I 1
已知：R1=3， R2=5
L1 7.5, L2 12.5, M 6
R1
求K闭合后各支路电流
U 500
jM
I2
电工原理之含有耦合电感电路介绍课件
频率响应分析：通过分析频 率响应曲线，可以了解电路 的滤波特性、增益、相位等 参数，从而优化电路设计。
频率响应的应用：耦合电感 电路的频率响应分析在电子 技术、通信工程、电力电子 等领域具有广泛的应用。
3
耦合电感电路 的应用实例
耦合电感电路在滤波器中的应用
01 滤波器类型：低通滤波器、高通 滤波器、带通滤波器等
03
耦合电感的大小与线圈的几何形状、相对位 04
耦合电感在电路中起到能量传递、信号处
置、绕线方式等因素有关。
理等作用。
耦合电感的作用
1
耦合电感是电 路中两个或多 个电感之间的
相互影响
3Байду номын сангаас
耦合电感可以 减小电路的噪
声干扰
2
耦合电感可以 增强电路的滤
波性能
4
耦合电感可以 提高电路的功
率传输效率
耦合电感的分类
电工原理之含有 耦合电感电路介 绍课件
目录
01. 耦合电感电路的基本概念 02. 耦合电感电路的分析方法 03. 耦合电感电路的应用实例
1
耦合电感电路 的基本概念
耦合电感的定义
01
耦合电感是两个或多个电感线圈之间通过
02
耦合电感是电路中一种重要的元件，常用于
磁场相互影响的现象。
滤波、调谐、阻抗匹配等电路中。
自感耦合：两个电感线圈之 间通过磁场相互耦合
变压器耦合：两个电感线圈 之间通过变压器相互耦合
互感耦合：两个电感线圈之 间通过电流相互耦合
电容耦合：两个电感线圈之 间通过电容相互耦合
2
耦合电感电路 的分析方法
电路分析的基本方法
电路图分析：了
1 解电路的结构和 功能
10-23含有耦合电感的电路-PPT课件
同名端的实验测定：
R
+
US -
S
1 i1 *
1'
i
2 *
2'
i2=0
+ V –
图中 US表示直流电源，例如1.5V干电池。V表示高内阻直 流电压表，当开关闭合时，电流由零急剧增加到某一量值，电 流对时间的变化率大于零，即 d i1 0 。 dt d i 如果发现电压表指针正向偏转，说明 u u M 1 0
d i 1 u M 21 21 d t
d i 1 u M 31 31 d t
注意
线圈的同名端必须两两确定。
确定同名端的方法：
(1)当两个线圈中电流同时由同名端流入(或流出)时，两个电 流产生的磁场相互增强。 例 1* 1'
i
*2 2'
* 1 1'
2
3 3'
2'*
(2)当随时间增大的时变电流从一线圈的一端流入时，将会 引起另一线圈相应同名端的电位升高。
4.互感线圈的同名端
对自感电压，当u, i 取关联参考方向，u、i与 符合 右螺旋定则，其表达式为：
d Ψ d Φ d i 11 11 1 u N L 11 1 1 d t d t d t
i1 + u11 –
上式说明，对于自感电压由于电压电流为同一线圈上的， 只要参考方向确定了，其数学描述便可容易地写出，可不 用考虑线圈绕向。
k
ቤተ መጻሕፍቲ ባይዱ
def
M 1 L1L2
11= 21 ，22 =12
2 M M ( Mi )( Mi ) 1 2 12 21 k 1 L L L i L i L L 1 2 1 1 2 2 11 22 1 2
第10章电路邱关源课件PPT
电路第十章含有耦合电感的电路电路§1010--1 1 互互感1121i 111'22'L 2N 2L 1N 1i 222212ΨΨΨ+±=12111ΨΨΨ±=电路22122111i L Mi ΨMi i L Ψ+±=±=1111i L Ψ=2222i L Ψ=21212i M Ψ=12121i M Ψ=**ML 1L 2+−i 1i 2u 1u 2+−11'22'dt di Mdt di L dt d u 21111±=Ψ=dtdi L dt di M dt d u 22122+±=Ψ=ML 1L 2+−i 1i 2u 1u 2+−122122111i L Mi ΨMi i L Ψ+±=±=2111I M j I L j U &&&ωω+=2212I L j I M j U &&&ωω+=Mj Z M ω=121≤=L L Mk 22211112ΨΨΨΨ=k电路§1010--2 2 含有耦合电感电路的计算含有耦合电感电路的计算I L j R U &&)(111ω+=[]I M L L j R R U &&)22121(−+++=ω1R R 1L −+1u −+uM••i 1R R ML −21−+1u −+ui I L j R U &&)(222ω+=[]I M I M j L j R &&)(−=−+11ωω[]I M I M j L j R &&)(−=−+22ωω电路[])22121(M L L j R R U I−+++=ω&&))222111((M M L j R Z L j R Z −−+=+=ωω)22121(M L L j R R Z −+++=ω))222111((M M L j R Z L j R Z ++=++=ωω)22121(M L L j R R Z ++++=ω电路cos10002**12M1R 2+−iu s4522000°∠Z cos 22121×L L ∠2电路1R R 1L −+1u −+uM••i SS 826.05.125.782121=×===L L ML L M k ωωωΩ−∠=−=−+=o46.904.35.03)(111j M L j R Z ωΩ∠=+=−+=o4237.65.45)(222j M L j R Z ωΩ∠=+=+=o57.2694.84821j Z Z Z o &050∠=U57.2659.557.2694.8050−∠=∠∠==oo &&Z U I1212121Z I X jI R I S =+=AV 63.14025.1564237.659.52222⋅+=∠×==j Z I S oAV 12525057.2659.550*⋅+=∠×==j I U S o &&21S S S +=A V .....⋅−=−∠×=631575934690435952j o1R R 2L j ω1L j ω−+U&••I&1I &I &Mj ω2111I j I L j R U M &&&ωω++=)(1R R 2L j ω1L j ω−+U&••I&1I &I &Mj ω22212111)()(I L j R I j U I j I L j R U M M &&&&&&ωωωω++−=−+=2221I L j R I j U M &&&)(ωω++=2112I I I I I I &&&&&&−=−=[]I j I M L j R M &&m ωω±+=111)(1R R ML −1−+U&I&1I &I &ML −21R R ML +1−+U&I&1I &I &ML +222212111)()(I L j R I j U I j I L j R U M M &&&&&&ωωωω++±=±+=[]222I M L j R I j U M &m &&)(ωω++±=)()(1111I I j I L j R U M &&&&−±+=ωω电路410CL =ωH 05.0662410510411===−×××C L ωA87.36025.0240320010)(2111o o &&−∠=+∠=−+−+=j M L M L j R U I AB ωV13.53387.36025.0120)(12o o &&∠=−∠×=−=j I M L j U ED ωW2.0025.03202211=×==I R P电路+−U S500 V o13ΩIR 25Ω1j ωL 2I 1**j ωM+−U S500 V o13ΩIR 25Ω1j (+)ωL M 2I 1()22电路()+−U S500 V o13ΩIR 25Ω1j (+)ωL M 2I 1电路§1010--3 3 空心变压器空心变压器()21111I j I L j R U M &&&ωω++=11Z22Z MZ 2221112221111)(Y M Z U Y Z Z U I M ω+=−=&&&1R 1L j ω••−+1U &1′••2R 2L j ωR ω••2′2221)(0I jX R L j R I j L L M &&++++=ωω1222⋅−=I Z Z I M &1⋅I电路11222111112221112)(Y M jX R L j R U MY j Y Z Z U Y Z I L L M M ωωω++++−=−−=&&&−+1U &222)(Y M ω1I 12221112221111)(Y M Z U Y Z Z U I M ω+=−=&&&Z 2I −+111U MY j &ω1222⋅−=I Z Z I M &电路1R 1L j ω••−+1U &1′••2R 2L j ωR ω••2′Ω==50111j L j Z ωΩ+=++=123222j jX R L j Z L L ωΩ−=+=37.3184.7123400)(222j j Y M ωo &021001∠=U o &&2.675.337.3184.7502/100)(2221111−∠=−+=+=j j Y M Z U I ωo o &&84.12666.51232.675.3202212∠=+−∠×=−=j j Z I M j I ω)84.12610cos(266.5)2.6710cos(25.321oo +=−=t i t i电路cos3142115**+−u sa i 112L 1L 2R LM电路+−a b422Ω−Ωj189U 1I 1电路§1010--3 3 理想变压器理想变压器1N ••1−+1u ••2N ••−+u 21i n −••1−+1••11u n 2211N u N u =12211=+i N i N 122211=+i u i u 1N N电路11N ••1−+1u ••2N ••−+u 21in ••1−+1••11u n −22211nu u N N u −=−=212112ii i n N N ==电路11N ••1−+1u ••2N ••Z ••1−+1u 11I U Z in &&=1N ••1−+1u ••2N ••Z Ln in Z n I U n I U Z 221211=−==&&&&L n Z n I U n 2212=−=&&电路1−+s u ••Z −+2u −+1u 110:Ω+=+×==300300)33(1022j j Z n Z L in inZ −+sU &1I 13003001000220011j Z R U I in s ++∠=+=&&09.3644.0−∠=211I nI &&−=12I n I &&=A9.364.4−∠=电路21210I nI I &&&==1−+s u ••−+2u −+1u 1n sU U &&=1000221∠==s c U nU &&22I U Z in &&=Ω===1)1(12111R n I n U n &&9.364.433102202−∠=++∠=+=j Z Z U I L in oc &&in−+oc u 2i电路1••iI &−+1U &22••2I &−+2U &−+1u 1:2R 1I &ii I U R &&1=221212)11(1I U R R U R &&&−=++−11U U n &&=)(22112R U U I n I n I i &&&&&−−=−=121U U n &&=i I n R n nR nR U &&=−++)211(2121Ω==381ii I U R &&电路Ω−5j V 4=sU &Ω−=)5(222j n Z in Ω+−=5120141222n j j Y 05120122=+−n j j 22=n 2211Z n Z in =100=Ω=42Z 100421=n 51=n W 04.01004422m ax=×=×=ssUR U P电路)1(21==R R 21122111I L j I M j U I M j I L j U &&&&&&ωωωω+=+=21,1)2(L L M k ==1R 1L j ω••−+1U &1′••2R 2L j ωR ω••2′−+2U&2121u u L L =121212L L L L L L 221212221111I L j I L L j U I L L j I L j U &&&&&&ωωωω+=+=n=电路nL L L =∞→211211i ni −=212111I L L L j U I &&&−=ω2121I L L I &&−=n L L =21)3(221111I L L j I L j U &&&ωω+=电路M j Z L j R Z L j R Z M ωωω=+=+=222111221211I Z I Z U I Z I Z U M M &&&&&&+±=±=U Z Z Z Z Z I MM &m &22121−=U Z Z Z Z Z I MM &m &22112−=U Z Z Z Z Z Z I I I M M &m &&&2212121−+=+=22212111)()(I L j R I j U I j I L j R U M M &&&&&&ωωωω++±=±+=电路。
2019年第10章含耦合电感的电路.ppt
互感 10.1 互感 (mutual inductance )
耦合电感元件属于多端元件，在实际电路中，如收音机、 电视机中的中周线圈、振荡线圈，整流电源里使用的变压器 等都是耦合电感元件，熟悉这类多端元件的特性，掌握包含 这类多端元件的电路问题的分析方法是非常必要的。
11
（2）同名端异侧并联
+
u
L1
di1 dt
R1i1
M
di2 dt
u
u
L2
di2 dt
R2i2
M
di1 dt
i = i1 +i2
–
解得u, i 的关系：
-M
u
M
di dt
(L1
M)
di1 dt
R1i1
+
u
M
di dt
(L2
M)
di2 dt
R2i2
u
M i
* i1
L1
R1
i i1 L1+M
R1
i2 L2 * R2
i2 L2+ M R2
去耦等效电路
–
返回本节 上 页 下 页
3. 受控源等效电路
i1
M
i2
+
**
+
u
L1
L2 u
–
–
I1
+
j L1
U1
+
j
–
M I–2
U1 jL1 I1 jM I 2
10第十章 含有耦合电感的电路PPT课件
图10－1(b)
对于图10－l(b)所示的情况有：
11112L1i1M12i2 22122M21i1L2i2
式中11、22表示电流在本身线圈形成的磁链，称为 自感磁链。12、21表示另一个线圈中电流产生的磁场在
本线圈中形成的磁链，称为互感磁链。也就是说每个线圈
根据以上叙述，定义一种称为耦合电感的双口电路元 件，其元件符号和电压电流关系分别如下所示：
u1
L1
d i1 dt
M
d i2 dt
u2
M
d i1 dt
L2
d i2 dt
u1
L1
d i1 dt
M
d i2 dt
u2
M
d i1 dt
L2
d
i2
d t
u1
L1
d i1 dt
M
d i2 dt
中的总磁链为自感磁链与互感磁链的代数和。
当电流i1和i2随时间变化时，线圈中磁场及其磁链也随 时间变化，将在线圈中产生感应电动势。
图(a)
对于图(a)的情况，根据电磁感应定律可以得到：
u1
d1
dt
d11
dt
d12
dt
L1
di1 dt
Mdi2 dt
u2
d2
dt
d21
dt
d22
dt
Mdi1 dt
L2
最后得到图(a)单口网络的等效电路为5电阻与10H电
感的串联。
§ 10.3 耦合电感的功率
当耦合电感中的施感电流变化时，将出现变化的 磁场，从而产生电场（互感电压），耦合电感通过 变化的电磁场进行电磁能的转换和传输，电磁能从 耦合电感一边传输到另一边。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1st2s 2st
返回 上页 下页
10-2 含有耦合电感电路的计算
1. 耦合电感的串联
M
* i1
* – u21 +
u21
M
di1 dt
返回 上页 下页
例1-1
i1 M i2
+* *+ u_1 L1 L2 _u2
解
u1L1ddit1 Mddit2
u2 Mddit1 L2ddit2
i1 M i2
+*
+
u_1 L1
L2 *
_u2
i1 M i2
+*
+
u_1 L1
L2 *
_u2
u1
L1ddit1
重点
1.互感和互感电压 2.有互感电路的计算 3.变压器和理想变压器原理
返回
10-1 互感
耦合电感元件属于多端元件，在实际电路中， 如收音机、电视机中的中周线圈、振荡线圈，整 流电源里使用的变压器等都是耦合电感元件，熟 悉这类多端元件的特性，掌握包含这类多端元件 的电路问题的分析方法是非常必要的。
为互感磁通。两线圈间有磁的耦合。
定义 ：磁通链 ， =N
返回 上页 下页
空心线圈， 与i 成正比。当只有一个线圈时：
1 = 11=L1i1 L1 为自感系数，单位 H(亨)
当两个线圈都有电流时，每一线圈的磁通链为 自感磁通链与互感磁通链的代数和：
1 = 11 12= L1i1 M12 i2
2 = 22 21= L2i2 M21 i1
L 1L 2 L 1L 2
L 1 i1L 2 i2
1122
注意耦合系数 k 与线圈的结构、相互几何位置、
空间磁介质有关。
返回 上页 下页
互感现象
利用——变压器：信号、功率传递
避免——干扰
克服：合理布置线圈相互位置或增加屏蔽减少互感 作 用。
返回 上页 下页
3. 耦合电感上的电压、电流关系
当i1为时变电流时，磁通也将随时间变化，从 而在线圈两端产生感应电压。
称M12、M21为互感系数， H(亨 单 ) 位
注意 M值与线圈的形状、几何位置、空间媒
质有关，与线圈中的电流无关，满足 M12=M21。 ② L 总为正值，M 值有正有负。
返回 上页 下页
2. 耦合系数
用耦合系数k 表示两个线圈 磁耦合的紧密程度。
k=1 称全耦合
def
k
M
1
L1L2
kMM 2(M 1)M (i2) i 1221 1
例
1*i
*2
•*
1
2
3
1'
2' 1'
2*'
•
3'
(2)当随时间增大的时变电流从一线圈的一端流入 时，将会引起另一线圈相应同名端的电位升高。
返回 上页 下页
同名端的实验测定：
S
1i
+
i *
-
R
1'
2
*
+
V
2'
–
如图电路，当闭合开关 S 时，i 增加，
d dti0, u2'2 M d dti0 电压表正偏。
10 M
i1/A
+ u _
i1 R1 * L1
* R2 + 10
L2
_u2
O
1 2 t/s
解
10V 0t1s
10tA 0t 1s
u2(t)Mddit1
10V1st2s 0 2st
i1 (2010t)A 1s t 2s
0A
2st
(10t 05)0V 0t1s
u(t)R1i1Ld dit1 0 (V 10t 015)V 0
返回 上页 下页
11
0
i1 *• N1
i2 •△N2 i3
N3 *△
+ u11 – + u21 – + u31 –
u21 M 2d 1 d it1
u31 M 3d 1 d it1
注意 线圈的同名端必须两两确定。
返回 上页 下页
确定同名端的方法：
(1)当两个线圈中电流同时由同名端流入(或流出)时， 两个电流产生的磁场相互增强。
返回 上页 下页
对互感电压，因产生该电压的电流在另一线圈 上，因此，要确定其符号，就必须知道两个线圈 的绕向。这在电路分析中显得很不方便。为解决 这个问题引入同名端的概念。
同名端 当两个电流分别从两个线圈的对应端子同时流
入或流出，若所产生的磁通相互加强时，则这 两个对应端子称为两互感线圈的同名端。
当两组线圈装在黑盒里，只引出四个端线组， 要确定其同名端，就可以利用上面的结论来加 以判断。
返回 上页 下页
由同名端及u、i参考方向确定互感线圈的特性方程
有了同名端，表示两个线圈相互作用时，就不
需考虑实际绕向，而只画出同名端及u、i参考方
向即可。
M * i1
互感电压！
* + u21 –
u2
11、u21方向与 符合右手螺旋法则时，
根据电磁感应定律和楞次定律有
u11d dt11L1ddit1
u21d dt21Mddit1
自感电压 互感电压
当两个线圈同时通以电流时，每个线圈两端
的电压均包含自感电压和互感电压。
返回 上页 下页
11 1 1 2L 1 i1 M 1 i2 2
2 2 2 2 1 L 2 i2 M 2 i 1 1
Mdi2 dt
u2
Mdi1 dt
L2ddit2
i1 M i2
+*
-
u_1 L1
L2 *
+u2
写 出 图 示 电 路 电 压、 电 流 关 系 式
返回 上页 下页
已 例1R -21 已1 知 , L 1 知 0 5 H , L 2 2 H , M 1 H 求 u ( t ) 和 u , 2 ( t ) 。
返回 上页 下页
4.互感线圈的同名端
对自感电压，当u, i 取关联参考方向，u、i 与 符合右手螺旋法则，其表达式为
u11 ddt11 N 1dd Φ t11 L 1d dit1
i1 u11
上式说明，对于自感电压由于电压、电流为 同一线圈上的，只要参考方向确定了，其数学描 述便可容易地写出，可不用考虑线圈绕向。
u1
u2
u11 u12
L1
di1 dt
Mdi2 dt
u21 u22
Mdi1 dt
L2
di2 dt
在正弦交流电路中，其相量形式的方程为
U1 jL1I1 jMI2 U2 jMI1 jL2I2
返回 上页 下页
注意
两线圈的自感磁通链和互感磁通链方向一致， 互感电压取正，否则取负。表明互感电压的正、 负： （1）与电流的参考方向有关。 （2）与线圈的相对位置和绕向有关。
返回 上页 下页
变压器
返回 上页 下页
电力变压器
返回 上页 下页
三相电力变压器
返回 上页 下页
小变压器
返回 上页 下页
调压器 牵引电磁铁
整流器
电流互感器
返回 上页 下页
1. 互感
11
21
i1
N1
N2
+ u11 – + u21 –
线圈1中通入电流i1时，在线圈1中产生磁通， 同时，有部分磁通穿过临近线圈2，这部分磁通称