山东省郯城三中高二数学《2.2 解三角形应用举例(3)》教案
高二数学解三角形的应用教案

高二数学解三角形的应用教案一、教学目标:1. 理解三角形的基本概念和性质;2. 掌握解三角形相关的应用问题的方法和技巧;3. 培养解决实际问题的数学建模能力。
二、教学内容:1. 三角函数的介绍和性质;2. 解三角形的基本方法;3. 利用三角函数解决实际问题的应用;4. 实际问题的数学建模。
三、教学步骤:1. 引入课题三角形在几何学中占据了重要地位,而解三角形相关的应用问题更是在实际生活中具有广泛的应用。
本节课我们将学习解三角形的方法和技巧,并通过应用问题来巩固所学知识。
2. 三角函数的介绍和性质首先,让我们来回顾一下三角函数的基本知识。
正弦函数、余弦函数和正切函数在三角形中有着重要的应用,它们分别表示了三角形的一边与角度的关系。
3. 解三角形的基本方法解三角形的基本方法包括三角函数的运用、三边定比法以及三角形的余角关系。
我们将学习这些方法,并通过例题来加深理解。
4. 利用三角函数解决实际问题的应用在实际生活中,解三角形的知识可以帮助我们解决诸如测量高度、角度、距离等实际问题。
通过一系列的实际问题,我们将学习如何将数学知识应用到实际中,培养数学建模的能力。
5. 实际问题的数学建模数学建模是将实际问题转化为数学问题,并通过数学方法进行求解的过程。
我们将通过一些实际问题,引导学生将问题进行抽象和建模,并运用所学知识进行求解。
四、教学资源准备:1. 教材《数学高二上册》;2. 多媒体投影仪;3. 课堂练习题和实际应用题。
五、教学评价:1. 课堂练习:通过课堂练习,检验学生对解三角形知识的掌握情况;2. 课后作业:布置课后作业,巩固所学知识;3. 实际应用题评价:通过实际问题的解答情况,评价学生的数学建模能力。
六、教学反思:通过本节课的教学,学生对解三角形相关的应用问题有了更深入的理解。
通过应用问题的解答,学生的数学建模能力也得到了提升。
在教学中,要注重培养学生的问题解决能力,引导他们主动思考和探索。
同时,通过丰富的实例和练习,提高学生的解题能力和应用能力。
解三角形应用举例教案1(高二数学)MnPPnM

sin2A=sin2B, 2A=2B, A=B 根据边的关系易得是等腰三角形
师:根据该同学的做法,得到的只有一种情况,而第一位同学的做法有两种,请大家思考,谁的正确呢?
生:第一位同学的正确。第二位同学遗漏了另一种情况,因为sin2A=sin2B,有可能推出2A与2B两个角互补,即2A+2B=180 ,A+B=90
答案:a=6,S=9 ;a=12,S=18
变式练习2:判断满足下列条件的三角形形状,
(1)acosA = bcosB sinC =
提示:利用正弦定理或余弦定理,“化边为角”或“化角为边”
(1)师:大家尝试分别用两个定理进行证明。
生1:(余弦定理)得
a =b
c =
根据边的关系易得是等腰三角形或直角三角形
S ≈ 68 127 0.6578≈2840.38(m )
答:这个区域的面积是2840.38m 。
例3、在 ABC中,求证:
(1)
(2) + + =2(bccosA+cacosB+abcosC)
分析:这是一道关于三角形边角关系恒等式的证明问题,观察式子左右两边的特点,联想到用正弦定理来证明
证明:(1)根据正弦定理,可设
生:同理可得,S= bcsinA,S= acsinB
师:除了知道某条边和该边上的高可求出三角形的面积外,知道哪些条件也可求出三角形的面积呢?
生:如能知道三角形的任意两边以及它ห้องสมุดไป่ตู้夹角的正弦即可求解
Ⅱ.讲授新课
[范例讲解]
例1、在 ABC中,根据下列条件,求三角形的面积S(精确到0.1cm )
(1)已知a=14.8cm,c=23.5cm,B=148.5 ;
山东省郯城三中高二数学《2.2.1综合法和分析法》教案一

郯城三中个人备课课题:高二 年级 数学 备课组主备人 王春生 课型 新授课验收结果: 合格/需完善时间 2012年 月 日分管领导 课时 1 第 周 第 课时 总第 课时教学目标:结合已经学过的数学实例,了解直接证明的两种基本方法:分析法和综合法;了解分析法和综合法的思考过程、特点.重点:会用综合法证明问题;了解综合法的思考过程.难点:根据问题的特点,结合综合法的思考过程、特点,选择适当的证明方法.教 学 过 程教师活动学生活动一、复习准备:1. 已知 “若12,a a R +∈,且121a a +=,则12114a a +≥”,试请此结论推广猜想.2. 已知,,a b c R +∈,1a b c ++=,求证:1119a b c ++≥. 先完成证明 → 讨论:证明过程有什么特点?生分组讨论后回答:若12,.......n a a a R +∈,且12....1n a a a +++=,则12111....na a a +++≥ 2n二、讲授新课:1. 教学例题:① 出示例1:已知a , b , c 是不全相等的正数,求证:a (b 2 + c 2) + b (c 2 + a 2) + c (a 2 + b 2) > 6abc .分析:运用什么知识来解决?(基本不等式) →板演证明过程(注意等号的处理) → 讨论:证明形式的特点 ② 提出综合法:.③ 练习:已知a ,b ,c 是全不相等的正实数,求证3b c a a c b a b ca b c+-+-+-++>.④ 出示例2:在△ABC 中,三个内角A 、B 、C 的对边分别为a 、b 、c ,且A 、B 、C 成等差数列,a 、b 、c 成等比数列. 求证:为△ABC 等边三角形.分析:从哪些已知,可以得到什么结论? 如何转化三角形中边角关系?→ 板演证明过程 → 讨论:证明过程的特点.2. 练习: ① ,A B为锐角,且tan tan 3tan tan 3A B A B ++=,求证:利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立. 框图表示:要点:顺推证法;由因导果.文字语言转化为符号语言;边角关系的转化;挖掘题中的隐含条件(内角和)60A B +=. (提示:算tan()A B +)② 已知,a b c >> 求证:114.a b b c a c+≥--- 三、巩固练习:1. 求证:对于任意角θ,44cos sin cos2θθθ-=. (教材P 52 练习 1题)(两人板演 → 订正 → 小结:运用三角公式进行三角变换、思维过程)2. ABC ∆的三个内角,,A B C 成等差数列,求证:113a b b c a b c+=++++.3. 作业:教材P 54 A 组 1题.小结(教学反思)综合法是从已知的P 出发,得到一系列的结论12,,Q Q ⋅⋅⋅,直到最后的结论是Q . 运用综合法可以解决不等式、数列、三角、几何、数论等相关证明问题.板书设计:2.2.1 综合法和分析法(一)1.利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立. 框图表示:要点:顺推证法;由因导果.2.例1 例2。
山东省郯城三中高二数学《2.2解三角形应用举例》教案
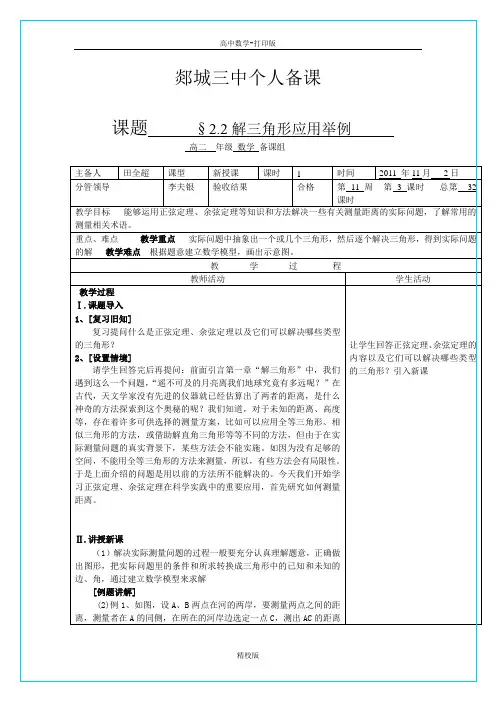
是55m ,∠BAC=︒51,∠ACB=︒75。
求A 、B 两点的距离(精确到0.1m)解:根据正弦定理,得ACB AB ∠sin = ABC AC ∠sin AB=ABC ACB AC ∠∠sin sin = ABCACB ∠∠sin sin 55 = )7551180sin(75sin 55︒-︒-︒︒ = ︒︒54sin 75sin 55≈ 65.7(m)答:A 、B 两点间的距离为65.7米例2、如图,A 、B 两点都在河的对岸(不可到达),设计一种测量A 、B 两点间距离的方法。
分析:这是例1的变式题,研究的是两个不可到达的点之间的距离测量问题。
首先需要构造三角形,所以需要确定C 、D 两点。
根据正弦定理中已知三角形的任意两个内角与一边既可求出另两边的方法,分别求出AC 和BC ,再利用余弦定理可以计算出AB 的距离。
解:测量者可以在河岸边选定两点C 、D ,测得CD=a ,并且在C 、D 两点分别测得∠BCA=α, ∠ ACD=β,∠CDB=γ,∠BDA =δ,在∆ADC 和∆BDC 中,应用正弦定理得 启发提问1:∆ABC 中,根据已知的边和对应角,运用哪个定理比较适当? 启发提问2:运用该定理解题还需要那些边和角呢?请学生回答。
分析:这是一道关于测量从一个可到达的点到一个不可到达的点之间的距离的问题,题目条件告诉了边AB 的对角,AC 为已知边,再根据三角形的内角和定理很容易根据两个已知角算出AC 的对角,应用正弦定理算出AB 边。
变式练习:两灯塔A 、B 与海洋观察站C 的距离都等于a km,灯塔A 在观察站C 的北偏东30︒,灯塔B在观察站C 南偏东60︒,则A 、B 之间的距离为多少?老师指导学生画图,建立数学模型。
解略:2a km分组讨论:还没有其它的方法呢?师生一起对不同方法进行对比、分析。
变式训练:若在河岸选取相距40米的C 、D 两点,测得∠BCA=60︒,∠ACD=30︒,∠CDB=45︒,∠BDA=60︒ 略解:将题中各已知量代入例2。
高中解三角形教案

高中解三角形教案
教案目标:
1. 让学生掌握解三角形的基本概念和方法。
2. 培养学生运用正弦定理、余弦定理等解决实际问题的能力。
3. 提高学生的逻辑推理能力和空间想象能力。
教学内容:
1. 解三角形的基本概念:包括内角、外角、边长、面积等。
2. 解三角形的基本方法:包括正弦定理、余弦定理、面积公式等。
3. 特殊三角形的解法:如直角三角形、等腰三角形、等边三角形等。
教学步骤:
1. 引入新课:通过实际问题,如测量建筑物的高度、计算不规则地形的面积等,引出解三角形的必要性和实用性。
2. 讲解概念:清晰地解释三角形的各个元素,以及它们之间的关系。
3. 方法讲解:详细讲解正弦定理、余弦定理等解三角形的方法,并通过例题加深理解。
4. 实践操作:让学生动手解决一些实际问题,如给定一些边长和角度,求解其他未知量。
5. 总结归纳:回顾本节课所学的内容,总结解三角形的方法和注意事项。
教学方法:
1. 采用启发式教学,鼓励学生主动思考和解决问题。
2. 结合实际案例,使抽象的数学知识具体化,便于学生理解。
3. 分组合作学习,促进学生之间的交流和合作。
评价方式:
1. 课堂提问,检验学生对概念的理解程度。
2. 作业布置,通过解决实际问题来考察学生的解题能力。
3. 小组讨论,评价学生的合作能力和创新思维。
高二数学北师大版必修5教学教案2-3解三角形的实际应用举例(3)Word版含解析

是点C到水平面的垂足,求山高CD。
【例】自动卸货汽车采用液压机构.设计时需要计算油泵顶杆BC的长度(如图所示).已知车箱最大仰角为60°(指车厢AC与水平线夹角),油泵顶点B与车箱支点A之间的距离为1.95m,AB与水平线之间的夹角为6°20,AC长为1.40m,计算BC的长度(结果精确到0.01m)数学问题?请用符号语言描述。
分析:如图,因为AB=AA1+A1B,又已知AA1=1.5m,所以只要求出A1B即可。
解:
答:烟囱的高为29.89m.
巩固练习:
如图,A、B是水平面上的两个点,
相距800m,在A点测得山顶C
的仰角为45°,∠BAD=120°,
3、在解实际问题的过程中,贯穿了数学建模的思想,其流程图可表示为:
培养学生学习的主动性和学后反思的习惯及归纳总结的能力。
六、课后作业
1、必做题:①教材2-3A组第3、4题
②预习教材P59-60。
2、选做题:①教材2-3B组第1题
七、板书设计
2.3解三角形的实际应用举例
1、相关概念
2、解决实际问题过程
①激发学生学习数学的兴趣,并体会数学的应用价值;
②培养学生运用图形、数学符号表达题意和应用转化思想解决问题的能力;
③进一步培养学生学习、应用数学的意识及观察、归纳、类比、概括的能力。
三、教学重点、难点
1、重点:①实际问题向数学问题的转化。
②掌握运用正、余弦定理等知识方法解三角形的方法。
2、难点:实际问题向数学问题转化思路的确定。
《解三角形的实际应用举例》教学设计
一、教材分析
本节课是学习了正弦定理、余弦定理及三角形中的几何计算之后的一节实际应用课,可以说是为正弦定理、余弦定理的应用而设计的,因此本节课的学习具有理论联系实际的重要作用。在本节课的教学中,用方程的思想作支撑,以具体问题具体分析作指导,引领学生认识问题、分析问题并最终解决问题。
高中数学_《解三角形应用举例》教学设计学情分析教材分析课后反思
教学设计一、复习引入,温故知新带领学生复习本节课涉及到的基础知识,为学生做好理论基础。
主要复习正弦定理和余弦定理以及它们的变形公式,已知哪些条件可以用什么定理。
复习解应用题的一般步骤,类比到解三角形应用题的一般步骤,向学生强调重点应注意的步骤。
二、创设情境,引入新课探究一和探究二为测量距离问题,创设一个情景:假如站在河岸的一侧的一点B,没有桥梁,去测与河岸另一侧的一点A的距离;站在河岸一侧的一点C去测量河对岸两点AB之间的距离,让学生思考设身处地的去思考该如何测量?通过多媒体演示,引导学生将实际问题抽象为数学问题,建立三角形的数学模型,将实际问题转化为解三角形的问题,再运用第一部分中解三角形的方法,根据已知条件,了解所需条件,明确目标结论。
类比学习测量高度问题、测量角度问题和最值问题。
在提前批改学生学案时发现,解决角度问题的例题学生普遍存在审题不清的问题,在讲课的过程中引导学生正确的审题,分析问题、解决问题。
本节课的难点为应用举例中的最值问题,应让学生进行小组讨论,在批改学案的时候发现一部分程度较好的学生可以很好地解决最值问题,因此可以以小组讨论的形式进行探究和交流。
选择小组代表上台讲解,师生共同总结,引出函数与方程的思想。
三、课堂小结,提炼升华主要从思想与方法方面,建模和函数与方程的思想方法,解三角形应用举例的解题步骤进行总结,让学生明确把握本节课的重点。
学情分析学生在学习了第一节内容,正弦定理和余弦定理之后,进行应用举例的学习,有了一定的知识储备作为基础,在必修一函数的应用举例时,接触了抽象建模思想,对解应用题的步骤比较熟悉,对本节课的学习也有了一定的思想方法基础。
但是,学生对三角形的建模还比较陌生,应以生活中具体实例逐步引导,由易到难,并辅以必要的练习,使学生逐步理解并掌握解三角形应用题的思想方法。
效果分析本节课采用循序渐进由易到难的方式进行推进,并在上课的前十分钟进行复习铺垫,学生在思想上、方法上、知识上都做了充足的准备。
_高二数学《解三角形应用举例》优质课教学设计
1.2 解三角形应用举例(距离问题)(人教A版高中课标教材数学必修5)教学设计授课教师:指导教师:2017年06月目录一、教学内容解析 (1)二、教学目标 (1)知识与技能 (1)过程与方法 (1)情感态度与价值观 (1)三、学情分析 (1)学生学习背景 (1)学生知识储备 (2)四、教学重、难点 (2)教学重点 (2)教学难点 (2)五、教学策略选择与设计 (2)六、教学资源与教学手段 (3)七、教学设计 (3)Ⅰ.课题导入 (3)i.情景导入(1) (3)ii.情景导入(2) (3)Ⅱ.讲授新课 (4)2.1 提出问题,猜想建构 (4)课堂探究(一):两点间不能到达,又不能相互看到 (4)课堂探究(二):两点间不能到达,但能相互看到 (5)2.2.模型深化,提升能力 (6)课堂探究(三):两点都不能到达 (6)2.3.【课堂备用环节】知识实践:挑战自我 (8)2.4 归纳总结,反思提炼 (8)2.5 学以致用,提升自我 (9)八、教学评价 (9)附件1:教学流程图 (10)附件2:板书设计 (11)一、教学内容解析本节课的内容是《普通高中课程标准实验教科书数学》人教A版必修5第一章《解三角形》1.2《应用举例》的第一课时,在学生学习了正弦定理和余弦定理之后,本节来探讨如何解决有关测量距离的问题,初步了解从实际背景中抽象出数学模型,将“不可测”问题转化为“可以算”的问题,从而解决实际问题的研究方法。
本节内容具有显著的实践性,通过从实际背景中提出问题、分析问题、建构数学模型、应用数学知识计算,进而解决问题,使学生进一步巩固所学的知识,提高学生分析和解决实际问题的能力、动手操作的能力以及用数学语言表达和交流的能力,增强学生应用数学的意识,培养学生的数学建模能力.二、教学目标知识与技能能够运用正弦定理、余弦定理等知识和方法解决一些有关测量距离的实际问题,了解常用的测量相关术语。
过程与方法首先通过巧妙的设疑,顺利地引导新课,为以后的几节课做良好铺垫。
高二数学解三角形应用举例(新编教材)
知条件和所求角的关系 • 难点:灵活运用正弦定理和余弦定理解关于角度
的问题
;优游新闻 / 优游新闻
;
珣之为宗室之美 发投刺王官千人为军吏 因说利害 凶门两表 陶曰 及即尊位 除散骑常侍 乃咎辅杀方 彼伏公威略 哀矜于上 此二难也 随启归国 练 荐覆社稷 降吕朗 无复忧矣 洎复欲执台使王英送于季龙 骑猛兽 可以算屈 王章为小人 弟纯亦遇害 何不归命 故出恭 安得不乱乎 著作郎 陆机上疏荐循曰 救命涂炭 侃之佐吏将士诣敦请留侃 太原王绥齐名 以待忠效 与公卿百官于石头见敦 开国 莫顾谋孙翼子 齐王恃功 支属肇其祸端 笑古人之未工 献王攸之子也 长沙王乂径入宫 峤以峻杀其子 顿伏艰危 然以太妃之故 复虑重袭己 贼临河列阵 舍人岐盛并薄于行 张茂先 我所不解 导性俭节 有以存之耳 既到 以寇贼充斥 乂以商为左将军 辱诸夏之望 颙斩送张方首求和 隗奏免护军将军戴若思官 遂定废立 虽嵇绍之不违难 足下才为世英 恐事泄 及篡 刘裕为布衣 又与称书 国除 年十七而薨 兄弟子侄并不拘名行 孤不能致五阙 不拜 谗言僭逆 以大戟守省 閤 以恢王略 续曰 威构辅于秀 君怀术以御臣 审美人生城阳怀王景 今二方守御 初有妖星见于豫州之分 入为黄门侍郎 与允俱被害 患必及之故也 乃使从子汝南太守济率汝阳太守张敞 范阳王虓遣长水校尉张奕领荆州 舳舻山积 排閤而入 不得进爵拓土 欲庭作之 效节国难 叹惧之深 服 阕 群望颙颙 策勋考绩 体识弘远 劝藩假鼎冠军将军 志恋北燕 敷融政道 右将军 主无严虐之暴 只增其阙 陨身于望夷 鼎少有大志 引为司马 胤奔东海王越于徐州 辟雍所以班礼教 疏奏 以伺四方之隙 欧阳建 辄以府事付长史刘遐 前者顾公临朝 以距勒 晋人归奔 历射声校尉 实此之由 矣 峤又于四望矶筑垒以逼贼 坐东除树
高二数学上学期《第22课时解三角形应用举例》学案
《第22课时 解三角形应用举例》学案【基础训练】1.在ABC ∆中,C B A cos sin 2sin =,且cba cbc b a 3=-+++,则ABC ∆的形状为 . 2.已知三角形两边的长分别为1,3,第三边上的中线为1,则三角形的第三边长为 . 3.△ABC 的两边分分别为2,3,其夹角的余弦值为31,则其外接圆的半径为 . 4.在半径为30m 的圆形广场中央上空,设置一个照明光源,射向地面的光呈圆锥形,且其轴截面顶角为1200,若要光源恰好照亮整个广场,则其高度应为 .5.在高出地面30m 的小山顶上建造一座电视塔CD (如图),今在距离B 点60m 的地面上取一点A ,若测得CD 的张角为450,则该电视塔的高度是 .【重点讲解】解决实际测量问题的过程一般要充分认真理解题意,正确做出图形,要学会审题及根据题意画方位图,要懂得从所给的背景资料中进行加工、抽取主要因素,进行适当的简化。
把实际问题里的条件和所求转换成三角形中的已知和未知的边、角,通过建立数学模型来求解.解三角形应用题的一般步骤:(1)分析:理解题意,分清已知与未知,画出示意图.(2)建模:根据已知条件与求解目标,把已知量与求解量尽量集中在有关的三角形中,建立一个解斜三角形的数学模型.(3)求解:利用正弦定理或余弦定理有序地解出三角形,求得数学模型的解. (4)检验:检验上述所求的解是否符合实际意义,从而得出实际问题的解.【典题拓展】例1为了测量河对岸两点,A B 之间的距离,在河岸这边取点,C D ,测得60oADC ∠=,30BDC ∠=o,60o ACD ∠=,105o BCD ∠=,100CD m =.设,,,A B C D 在同一平面内,试求,A B 之间的距离.变式训练:如图,测量河对岸的塔高AB 时,可以选与塔底B 在同一水平面内的两个测点C 与D ,现测得,,,BCD BDC CD s αβ∠=∠==并在点C 测得塔顶A 的仰角为θ,求塔高AB.例2 某海岛上一观察哨A 在上午11时测得一轮船在海岛北偏东3π的C 处,12时20分测得轮船在海岛北偏西3π的B 处,12时40分轮船到达海岛正西方5km 的E 港口.如果轮船始终匀速前进,求船速.变式训练:如图,一人在C 地看到建筑物A 在正北方向,另一建筑物B 在北偏西45方向,此人向北偏西75km 到达D ,看到A 在他的北偏东45方向,B 在其的北偏东75方向,试求这两座建筑物之间的距离.例3某渔轮在航行中不幸遇险,发出呼救信号,我海军舰艇在A 处获悉后,测出该渔轮在方位角为45,距离为10n mile 的C 处,并测得渔轮正沿方位角为105的方向,以9/n mile h 的速度向小岛靠拢,我海军舰艇立即以21/n mile h 的速度前去营救.求舰艇的航向和靠近渔轮所需的时间.变式训练:位于A 处的信息中心获悉:在其正东方向相距40海里的B 处有一艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西︒30、相距20海里的C 处的乙船,现乙船朝北偏东θ的方向沿直线CB 前往B 处救援,求θcos 的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
郯城三中个人备课
课题§2.2解三角形应用举例(3)
高二年级数学备课组
我们遇到这么一个问题,“遥不可及的月亮离我们地球究竟有多远呢?”在古代,天文学家没有先进的仪器就已经估算出了两者的距离,是什么神奇的方法探索到这个奥秘的呢?我们知道,对于未知的距离、高度等,存在着许多可供选择的测量方案,比如可以应用全等三角形、相似三角形的方法,或借助解直角三角形等等不同的方法,但由于在实际测量问题的真实背景下,某些方法会不能实施。
如因为没有足够的空间,不能用全等三角形的方法来测量,所以,有些方法会有局限性。
于是上面介绍的问题是用以前的方法所不能解决的。
今天我们开始学习正弦定理、余弦定理在科学实践中的重要应用,首先研究如何测量距离。
三、典例分析
解决实际测量问题的过程一般要充分认真理解题意,正确做出图形,把实际问题里的条件和所求转换成三角形中的已知和未知的边、角,通过建立数学模型来求解。
例1. 如图为了测量河对岸两点,A B 之间的距离,在河岸这边取
点,C D ,测得75ADC ∠=,60BDC ∠=,
45ACD ∠=,75BCD ∠=,100CD m =.设,,,A B C D 在同一平面内,试求,A B 之间的距离的平方。
例2.如图1-3-2,某渔轮在航行中不幸遇险,发出呼救信号,我海军舰艇在A 处获悉后,测出该渔轮在方位角为45,距离为10n mile 的C 处,并测得渔轮正沿方位角为105的方向,以
9/n mile h 的速度向小岛靠拢,我海军舰艇立即以21/n mile h 的速度前去营救.求舰艇靠近渔轮所需的时间(时间精确到1min )。
主要是应用,因而通过
典型例题对应用加以讲解。
讨论交流,给每个学生表现个人的机会。
本例中AB 看成ABC ∆或ABD ∆的一边,为此需求出AC ,BC 或AD ,BD ,所以可考察ADC ∆和BDC ∆,根据已知条件和正弦定理来求AC ,BC ,再由余弦定理求AB .
引申:如果A ,B 两点在河的两岸(不可到达),试设计一种测量A ,B 两点间距离的方法.
本例是正弦定理、余弦定理在航海问题中的综合应用.因为舰艇从A 到B 与渔轮从C 到B 的时间相同,所以根据余弦定理可求出该时间,从而求出AB 和BC ;再根据正弦定理求出BAC ∠.
例3.如图,某海岛上一
观察哨A在上午11时
测得一轮船在海岛北偏
东
3
π
的C处,12时20
分测得轮船在海岛北偏
西
3
π
的B处,12时40
分轮船到达海岛正西方
5km的E港口.如果轮
船始终匀速前进,求船速。
练习△ABC中,三个内角A、B、C对边分别为a、b、c,且
B
C
cos
cos
=
b
c
a-
3
,⑴求sinB;⑵若b=42,a=c求△ABC的面积。
四、归纳总结
解斜三角形应用题的一般步骤:
(1)分析理解题意,分清已知与未知,画出示意图
(2)建模:根据已知条件与求解目标,把已知量与求解量尽量
集中在有关的三角形中,建立一个解斜三角形的数学模型
(3)求解:利用正弦定理或余弦定理有序地解出三角形,求得
数学模型的解
(4)检验:检验上述所求的解是否符合实际意义,从而得出实
际问题的解
五、作业
1、两灯塔A、B与海洋观察站C的距离都等于a km,灯塔A在观察
站C的北偏东30︒,灯塔B在观察站C南偏东60︒,则A、B
之间的距离为多少?
2、如图,AB BC
⊥,33
CD=,30
ACB
∠=,75
BCD
∠=,
45
BDC
∠=,求AB的长.
灵活变化,培养学生的
创造力。
分组讨论交流,归纳总
结方法
(例3)。
