广东省江门市普通高中2017_2018学年高一数学10月月考试题04
广东省江门市2017-2018学年高一上数学10月月考试题(11)含答案
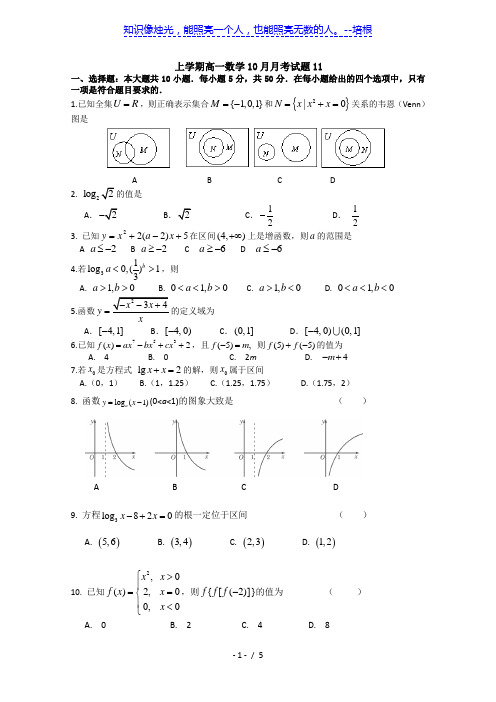
上学期高一数学10月月考试题11一、选择题:本大题共10小题.每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集U R=,则正确表示集合{1,0,1}M=-和{}2|0N x x x=+=关系的韦恩(Venn)图是A B C D2.2log2的值是A.2-B.2C.12-D.123. 已知5)2(22+-+=xaxy在区间(4,)+∞上是增函数,则a的范围是A 2a≤- B 2a≥- C 6-≥a D 6-≤a4.若31log0,()13ba<>,则A. 1,0a b>> B. 01,0a b<<> C. 1,0a b>< D. 01,0a b<<<5.函数234x xy--+=的定义域为A.[4,1]-B.[4,0)-C.(0,1]D.[4,0)(0,1]-6.已知753()2f x ax bx cx=-++,且(5),f m-=则(5)(5)f f+-的值为A. 4B. 0C. 2mD. 4m-+7.若x是方程式lg2x x+=的解,则x属于区间A.(0,1)B.(1,1.25)C.(1.25,1.75)D.(1.75,2)8.函数log(1)ay x=-(0<a<1)的图象大致是()A B C D9.方程3log820x x-+=的根一定位于区间()A. ()5,6 B. ()3,4 C. ()2,3 D. ()1,210.已知2,0()2,00,0x xf x xx⎧>⎪==⎨⎪<⎩,则)]}2([{-fff的值为()A. 0B. 2C. 4D. 8二、填空题:(本大题5个小题,每小题5分,共25分)11.若幂函数()f x 的图象过点2,2⎛ ⎝⎭,则()9f = .12.函数2()ln f x x=的定义域为 .13.若函数f (x )=(2a -1)x +b 在R 上是减函数,则a 的取值范围是________. .14.已知集合{}3log (1)2A x x =-<,1()33x B x ⎧⎫=>⎨⎬⎩⎭则R AC B =_____ .15. 集合M ={1,2,3}的子集的个数为________.三、解答题:(本大题5个小题,共75分)各题解答必须答在答题卡上,必须写出必要的文字说明、演算步骤或推理过程.16. (本题满分10分)已知集合A ={x |3≤x <7},B ={x |2<x <10},求∁R (A ∪B ),A ∩B .17.(本题满分12分)已知函数()f x =A ,函数()lg(2)g x x =-的定义域是集合B. (1)求集合A 、B ;(2)若A B B ⋃=,求实数a 的取值范围.18. (本小题满分14分) 计算求值(I ) 1100.753270.064()160.258---++ (II ) 22lg 5lg 5lg 4lg 2+⋅+19. (本小题满分12分)已知),0(56>-=a a x求xx xx aa a a ----33的值。
广东省江门市普通高中2017-2018学年高一数学10月月考试题07

上学期高一数学10月月考试题07一、选择题(本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的)1.在“①高一数学课本中的难题;②所有的正三角形; ③方程220x +=的实数解”中,能够表示成集合的是( )A. ②B. ③C. ②③D. ①②③ 2.与函数1y x =+相同的函数是( )A .211x y x -=- B .1y t =+ C .y = D .2y =3.函数1()1f x x=+-( ) A. [1,)-+∞ B. [1,1)(1,)-⋃+∞ C. (1,)+∞ D. (,)-∞+∞4.设A={x|20≤≤x },B={y|12≤≤y },下列图形表示集合A 到集合B 的函数图形的是( )5.下列所给出的函数中是幂函数的是( ) A. 3x y -= B.3-=xy C. 22x y = D.13-=x y6.设a >l ,则0.20.2log 0.2、、a a a 的大小关系是( ) A .0.20.2log 0.2a a a << B .0.20.2log 0.2a a a<<C .0.20.20.2log a a a <<D .0.20.20.2log a a a<<7.函数1()f x x x=-的图象关于( ) A .y 轴对称B .直线y x =对称 C .坐标原点对称 D .直线y x =-对称8.若二次函数b x a x y +-+=)1(232在区间(,1]-∞上为减函数,那么( ) A .4a ≥ B .2a ≥- C .4a ≤ D .2-≤a9.已知函数()⎩⎨⎧≤>=.0,2,0,log 3x x x x f x 则⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛91f f 的值为( )A.41 B.4 C.2 D. 21 10. 如果指数函数y=(2)x a -在x ∈R 上是减函数,则a 的取值范围是( )A.a >2B.a <3C.2<a <3D.a >311.定义在R 上的偶函数()f x 满足:对任意的1212,[0,)()x x x x ∈+∞≠,有2121()()0f x f x x x -<-.则 ( )A.(3)(1)(2)f f f <<-B.(1)(2)(3)f f f <-<C.(2)(1)(3)f f f -<<D.(3)(2)(1)f f f <-< 12.设)(123)(R x a x f x∈+-=是奇函数,则( )A .23=a ,且)(x f 为增函数 B .1-=a ,且)(x f 为增函数 C .23=a ,且)(x f 为减函数 D .1-=a ,且)(x f 为减函数二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上) 13. 若集合A={1,2,3},则集合A 的真子集共有 个 14.不等式2511x x --+>的解集为15.设函数()()()()4242x x f x x f x ⎧≥⎪=⎨<+⎪⎩,则()2log 3f =16.用{}min ,a b 表示,a b 两个数中的较小值.设1()min{21,}(0)f x x x x=->,则()f x 的最大值为三、解答题(共6道大题,总计70分) 17.(本小题满分10分)已知全集U=R ,A ={x |x ≥2},B={x |-1<x ≤4}(Ⅰ)求集合A ∪B 、A ∩B ;(Ⅱ)求)()(B C A C U U ⋃18.计算下列各题(本小题满分10分):(1) ()0.7522310.25816--⎛⎫+- ⎪⎝⎭-lg25-2lg2(2)19.(本小题满分12分)已知函数()f x 是定义在R 上的偶函数,已知当0x ≤时,2()43f x x x =++.(1)求函数()f x 的解析式;(2)画出函数()f x 的图象,并写出函数()f x 的单调递增区间; (直接画图,不用列表)20.(本小题满分12分)已知函数f (x )=log 412x -log 41x +5,x ∈[2,4],求f (x )的最大值及最小值.21.(本小题满分12分) 已知函数()b f x ax x=+,且(1)2f =,5(2)2f =(1)求a 、b 的值;(2)判断函数()f x 的奇偶性;(3)判断()f x 在(1,)+∞上的单调性并用单调性定义证明。
广东省江门市2017-2018学年高一上数学10月月考试题(8)含答案

上学期高一数学10月月考试题08共150分;时间120分钟第Ⅰ卷(选择题共60分)一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共60分).1.设全集为R ,{}{}|22|1)R M x x N x x M N =-≤≤=<⋂=则(C ( ){}{}|2|21A x x B x x <--<< {}{}|1|21C x x D x x <-≤<2.下列四组函数,表示同一函数的是( )A .f (x )=2x ,g (x )=x B .f (x )=x ,g (x )=2x x C .2(),()2ln f x lnx g x x == D .33()log (),()x a f x a a g x x =>0,α≠1=3.设已知函数21,0(),0x x f x x x +≥⎧=⎨<⎩,则f [f (2-)]的值为( ). A .1- B 2 C. 4 D.54.下列函数中,是奇函数是( )A .2x y = B. x y lg = C.3y x = D.1+=x y5. 当0<a <1时,在同一坐标系中,函数x y a -=与log a y x =的图象是( )6.下列函数中,在区间)2,0(上递增的是( )A xy 1= B x y -= C 1-=x y D 122++=x x y 7.令0.760.76,0.7,log 6a b c ===,则三个数a 、b 、c 的大小顺序是( )A .b <c <aB .b <a <cC .c <a <bD .c <b <a8.{}=|1A x x ≤已知集合{}|,B x x a A B R a =≥⋃=且则实数的取值范围是 ( )A 1a <B 1a ≤C 1a >D 1a ≥9.幂函数y=f(x)的图象经过点1(2,)8--,则满足f(x)=27的x 的值为( ) A 13 B 3 C -3 D 1210. 若2log 31x =,则39x x +的值为( )A .6B .3C .52D .1211. [)[)22,1,,1,x x a x x x++∈+∞∈+∞已知函数f(x)=若对于,f(x)>0恒成立,则a 的取值范围( )A 3a >-B 3a ≥-C 1a >D 1a ≥12.()f x =已知 (23)1,1log , 1x a a x x x --<⎧⎨-≥⎩是R 上的增函数,则实数a 的取值范围为( ) A 203a << B 1a<13≤ C 213a << D 1233a ≤< 第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题,每小题5分,共20分)。
广东省江门市2017-2018学年高一上数学10月月考试题(1)(含答案)

上学期高一数学10月月考试题01第I 卷(选择题)一、选择题:1.设全集U ={1,2,3,4,5},集合A ={1,2},B ={2,3},则A ∩C U B = A .{4,5} B .{2,3} C .{1} D .{2} 2.下列表述中错误的是( ) A .若A B A B A =⊆ 则, B .若B A B B A ⊆=,则C .)(B A A )(B AD .()()()B C A C B A C U U U =3.符号{}a ⊂≠{,,}P a b c ⊆的集合P 的个数是 ( )A. 2B. 3C. 4D. 54.若集合2{440,}A x kx x x R =++=∈中只有一个元素,则实数k 的值为 ( )A.0B. 1C. 0或1D. 1k <5.若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“孪生函数”,那么函数解析式为y =2x 2+1,值域为{3,9}的“孪生函数”共有( ) A .10个 B .9个 C .8个 D .7个6.设⎩⎨⎧<+≥-=)10x ()],6x (f [f )10x (,2x )x (f 则)5(f 的值为( ) A. 10 B. 11C. 12D. 137.已知a 是实数,则下列函数中,定义域和值域都有可能是R 的是( )A .f(x)=x 2+aB .f(x)=ax 2+1C .f(x)=ax 2+x +1D .f(x)=x 2+ax +1 8.下列两个函数相等的是( )A .y y =xB .y y =|x|C .y =|x|与yD .y y =x x29.定义在R 上的函数()f x 满足(6)()f x f x +=.当31x -≤<-时,2()(2)f x x =-+,当13x -≤<时,()f x x =。
则(1)(2)(3)(2012)f f f f +++⋅⋅⋅=( )A .335B .338C .1678D .201210.下列函数中,既是奇函数又是增函数的为( ) A .1y x =+ B .2y x =- C .1y x= D .||y x x =11.函数y =x ( )A .有最小值12,无最大值 B .有最大值12,无最小值C .有最小值12,最大值2D .无最大值,也无最小值 12.(05福建卷))(x f 是定义在R 上的以3为周期的偶函数,且0)2(=f , 则方程)(x f =0在区间(0,6)内解的个数的最小值是 ( ) A .5B .4C .3D .2第II 卷(非选择题)二、填空题(题型注释)13.设集合{211}A x x x =-<<->或,{},B x a x b =≤≤若{2},A B x x ⋃=>-{13}A B x x ⋂=<≤,则a = ,b =14.已知集合}023|{2=+-=x ax x A 至多有一个元素,则a 的取值范围 ;若至少有一个元素,则a 的取值范围 。
【配套K12】广东省江门市普通高中2017-2018学年高一数学10月月考试题06

上学期高一数学10月月考试题06一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一个是符合题目要求的.1. 已知集合{}1,2A =, {}1,0,1B =-, 则AB 等于 ( )A .{}1 B. {}1,0,2- C. {}1,0,1,2- D. ∅ 2. cos120︒的值是 ( )A . 2-B. 12- C. 12 D. 2 3. 函数sin 2y x =是 ( )A . 最小正周期为2π的偶函数 B. 最小正周期为2π的奇函数 C. 最小正周期为π的偶函数 D. 最小正周期为π的奇函数 4.已知函数 2()log (1),f x x =+若()1,f α= α=( ) A 、 0B 、1C 、2D 、35. 若向量a =(1,1),b =(2,5),c =(3,x)满足条件(8a —b )·c =30,则x=( ) A .6 B .5 C .4 D .3 6、设函数()23,(2)()f x x g x f x =++=,则()g x 的表达式是( ) A 21x + B 21x - C 23x - D 27x + 7. 函数f(x)=23xx +的零点所在的一个区间是( )(A)(-2,-1) (B)(-1,0) (C)(0,1) (D)(1,2) 8.设0abc >,二次函数()2f x ax bx c =++的图象可能是( )9、函数)(x f y =的图象如图所示,则)(x f y =的解析式为( )A.y=sin2x-2B.13cos 2-=x yC.1)52sin(--=πx y D. )52sin(1π--=x y10. 定义平面向量之间的一种运算“⊙”如下,对任意的a=(m,n),b p,q)=(,令a ⊙b mq np =-,下面说法错误的是( ) A.若a 与b 共线,则a ⊙b 0= B. a ⊙b = b ⊙a C.对任意的R λ∈,有()a λ⊙b = (a λ⊙)b D. (a ⊙b )2222()a b a b +⋅= 二、填空题:本大题共4小题,每小题5分,满分20分. 11. 函数()ln 21y x =-的定义域是 .12. 已知向量(2,1),(1,),(1,2)a b m c =-=-=- ,若()a b +∥c , 则m =_____________.13、如果a x x x f ++=2)(在[1,1]-上的最大值是2,那么()f x 在[1,1]-上的最小值是_____ 14、在平面内,A 点的坐标为(2,4),B 点的坐标为(-1,0),则AB 两点间的距离为__________ 三.解答题(本题共6小题,共80分)15、(本题12分)(1)设α为第四象限角,其终边上一个点为()5,-x ,且x 42cos =α,求αsin 。
广东省江门市2017-2018学年高一上数学10月月考试题(7)含答案(数学试卷新课标人教版)

上学期高一数学10月月考试题07、选择题(本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的)1.在“①高一数学课本中的难题;②所有的正三角形;③方程x2^0的实数解”中,能够表示成集合的是()A.②B.③C.②③D.①②③2. 与函数y = x • 1相同的函数是()A. y =—-B. y = t 1C. y = . x2 2x 1D. y = ( x 1)2x —13. 函数f (x)—, x 1的定义域是()1 —XA. [ -1,二)B. [一1,1) - (1, ::)C. (1, ::)D.(一匚」,::)4. 设A二{x|o沙曲} ,B={y|1曲乞2},下列图形表示集合A到集合B的函数图形的是()5. 下列所给出的函数中是幕函数的是()A . y = -x3B . y = x:C . y = 2x2D . y = x3-16. 设a >1,则Iog0.2a0.2a、a0.2的大小关系是()A. log0.2a< 0.2a£a0.2B. log0.2a< a0.2£0.2aC. 0.2a< log0.2a< a0.2D. 0.2a v a0.2£log0.2a7. 函数f(x)的图象关于()xA. y轴对称B.直线y二x对称C .坐标原点对称D.直线y二-x对称8. 若二次函数y =3x2• 2(a T)x • b在区间(」:,1]上为减函数,那么()x贝y f (x)的最大值为A. a 兰 4B .ax/.a 兰4D.a 兰—29.已知函数f (x ) =*w 0 则 ff -i ;l 的值为 ()2 , xEO.] l 9丿一A. 1B.4C.2D .1 4210.如果指数函数 y=(a —2)x在x € R 上是减函数,则a 的取值范围是( )A.a > 2B.a v 3C.2 v a v 3D.a >311. 定义在R 上的偶函数f(x)满足:对任意的XM • [0, •::)(为=x 2),有f(X 2)—f (X i )z.则()X 2「捲A. f (3) ::: f (1)::: f(—2)B. f(1)::: f(—2) ::: f (3) C . f (—2) c f ⑴ c f(3)D. f( 3)cf(—2)cf(1)12. 设 f (x) =ax3(X * R )是奇函数,则()2 +1A . a=3,且f(x)为增函数 B. a 「1,且f (x)为增函数 2C. a = 3,且f (x)为减函数D . a - -1,且f (x)为减函数二、填空题(本大题共4小题,每小题5分,共20分•把答案填在题中横线上)13. 若集合A 二{1,2,3},则集合A 的真子集共有 _____________ 个 14. 不等式|x -2卜x +5 >11的解集为 _______________ 15. 设函数 f x 二'X-4,则 f log o 3 =」(x +2)(x <4)'16. 用mi n :a,b ;表示a,b 两个数中的较小值.设 f (x)二mi n {2x-1」}(x 0),三、解答题(共6道大题,总计70分)17. (本小题满分10分)已知全集U=R A={x|x> 2}, B=x卜1v x< 4} (I)求集合A U B、A H B;(n)求(C u A) (QB)18. 计算下列各题(本小题满分10分):2 / 1 Z75(1)0.25 工8空-丄-Ig25-2lg2116丿已知当19. (本小题满分12分)已知函数f(x)是定义在R上的偶函数, x 三0 时,f (x) = x2 4x 3.(1)求函数f(x)的解析式;(2)画出函数f(x)的图象,并写出函数f(x)的单调递增区间;(直接画图,不用列表)20. (本小题满分12分)已知函数f(x) = log/x—log丄x+5, x€ :2, 4],4 4求f(x)的最大值及最小值.21. (本小题满分12分)已知函数 f (x)二ax b,且f(1) = 2 , f (2)x 2(1)求a、b的值;(2)判断函数f(x)的奇偶性;(3)判断f(x)在(1「:)上的单调性并用单调性定义证明22. (本小题满分14分)已知函数f (x),当x、y€ R时,恒有f (x) - f (y) = f (x-y).(I)求证:f (x)是奇函数;(H)如果x v 0时,f (x)> 0,并且f (2)二1,试求f (x)在区间[T2,6]上的最值;(皿)在(H)的条件下,对任意x€ [-2,6],不等式f(x)>m2+am-5 对任意a€ [-1,1]恒成立,求实数m的取值范围.答案题 1 号23 4 5678910 11 12答 C案B B D B ACD A C D A二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)13. 若集合A={1,2,3},则集合A的真子集共有7 ________ 个14. ________________________________ 不等式x-2-x+5>11的解集为015. 设函数 f x = ,x_4,则f log23 = 48f x 2 x :::416. 用min^ab表示a,b两个数中的较小值.设f(x)=min{2x-1」}(x 0),则f(x)的最大值为 1 x三、解答题(共6道大题,总计70分)17. (本小题满分10分)已知全集U=R A={x|x> 2}, B=x卜1v x< 4}(I)求集合A U B、A H B;18. 计算下列各题(本(1) (0.糾2(2) log 4 Jlog 3jog 6512 =0 19. (本小题满分12分)已知函数f(x)是定义在R 上的偶函数,已知当x 乞0时,2f (x) x 4x 3.(1) 求函数f (x)的解析式;(2) 画出函数f(x)的图象,并写出函数f(x)的单调递增区间; (直接画图,不用列表)解(1):函数f(x)是定义在R 上的偶函数 •••对任意的R 都有f(-x)二f(x)成立 •••当 x 0 时,-x <0 即f(x)二 f (谚汝x )3 吏(.和 3=x 1 2 3 4 5--f (X )2(2) 图形如右图所示/函数f(x)的单调递增区间为[-2,0]和[2「)(写成开区间 也可以) 20. (本小题满分 12 分)已知函数 f(x) = log1 2x — log 1 x+5, x €[2, 4],求 f(x) 的最大值及最小值. 1 N令 t = log 1 x ■/ x €[2, 4], log 1 4<1。
广东省江门市普通高中2017_2018学年高一数学10月月考试题10201712090110

上学期高一数学10月月考试题10第Ⅰ卷客观卷(共48分)一、选择题(每小题4分,共48分)1.设集合U {x N0x 8},S {1,2,3,4,5},T {3,5,7},则( )S C TU A.{1,2,4}B.{1,2,3,4,5,7}C.{1,2}D.{1,2,4,5,6,8}2.三个数0.32,log0.3,20.3的大小顺序是( )2A. < <B. < <log0.320.30.320.32log0.320.322C. < <D. < <log0.30.3220.30.3220.3log0.3223.已知幂函数f(x)x (为常数)的图象过(2,1),则的单调递减区间是()f(x)2A.,0B.,C.,00,D.,0,0,4.下列函数中,值域是0,的是()A. y x23x 1B. y 2x 1C. y x2x1 D. y1x25.设是方程的解,则属于区间()x ln x x 4x00A. 0,1B. 1,2 C. 2,3 D. 3,46.若函数f x 的定义域是2,4,则gx fx f x的定义域是()A .4,4 B. 2,2 C. 4,2 D. 2,47.已知函数y x22x 3在区间0,m上的最大值为3,最小值为2,则m的取值范围是()A .1,B .0,2C .1,2D.,20.2- 1 -9.已知定义域为 R 的函数 fx在区间8,上为减函数,且函数 yf x 8为偶函数,则( )A . f 6 f 7B . f 6 f 9C . f 7f9D . f7f1010.已知 fx是奇函数,且当 x0 时, f xx x 2 ,则 x 0 时, fx的表达式为( )A . f x x x 2B . f x x x 2C . fxx x 2D . fxx x 211.为了得到函数 ylg x 的图象,只需把函数lg 3 的图象上所有的点( )x y10A .向左平移 3个单位长度,再向上平移 1个单位长度B .向右平移 3个单位长度,再向上平移 1个单位长度C .向左平移 3个单位长度,再向下平移 1个单位长度D .向右平移 3个单位长度,再向下平移 1个单位长度a12.已知函数 f (x )log (x4) (a 0, 且 a 1) 的值域为 R ,则实数 a 的取值范围是(ax)A.0,11, 2B.2,C.4,D.0,11, 4第 II 卷 主观卷(共 52分)二、填空题(每小题 4分,共 16分)211 1313.计算14.函数y log(x26x5)的单调增区间是1315.已知集合,若,则实数A x x23x100,B x m1x2m1A B A m- 2 -的取值范围是a,a b16.对a、b R,记max a,b,max1,2的最小值f x x x x Rb,a b是三、解答题17.(8分) 已知集合A x x a x b,集合,满足2120B x x2ax b0C A B24A CB U Ra,b ,,,求实数的值.U U18.(8分) 作出函数y x x4x的图象根据图象写出函数的单调区间以及在每一单调区间上的函数是增函数还是减函数.19.(8分) f(x)是定义在0,上的增函数,且f x f(x)f(y)y(1) 求f(1)的值.(2) 若f(6)1,解不等式f(x3)f(1)2.xa1x20.(12分) 已知函数.f(x)(a1)a1x(1) 判断函数f(x)的奇偶性(2) 求f(x)的值域(3) 用定义证明f(x)在,上的单调性- 3 -参考答案。
广东省江门市2017-2018学年高一上数学10月月考试题(11)含答案

上学期高一数学10月月考试题11一、选择题:本大题共10小题.每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集U R =,则正确表示集合{1,0,1}M =-和{}2|0N x x x =+=关系的韦恩(Venn )图是A B C D2. 2log 的值是A. BC .12-D . 123. 已知5)2(22+-+=x a x y 在区间(4,)+∞上是增函数,则a 的范围是 A 2a ≤- B 2a ≥- C 6-≥a D 6-≤a4.若31log 0,()13b a <>,则A. 1,0a b >>B. 01,0a b <<>C. 1,0a b ><D. 01,0a b <<<5.函数y =的定义域为A .[4,1]-B .[4,0)-C .(0,1]D .[4,0)(0,1]-6.已知753()2f x ax bx cx =-++,且(5),f m -= 则(5)(5)f f +-的值为A. 4B. 0C. 2mD. 4m -+ 7.若0x 是方程式 lg 2x x +=的解,则0x 属于区间A.(0,1)B.(1,1.25)C.(1.25,1.75)D.(1.75,2) 8. 函数log (1)a y x =-(0<a <1)的图象大致是 ( )A B C D9. 方程3log 820x x -+=的根一定位于区间 ( )A. ()5,6B. ()3,4C. ()2,3D. ()1,210. 已知2,0()2,00,0x x f x x x ⎧>⎪==⎨⎪<⎩,则)]}2([{-f f f 的值为 ( )A. 0B. 2C. 4D. 8二、填空题:(本大题5个小题,每小题5分,共25分)11.若幂函数()f x 的图象过点2,2⎛⎫⎪ ⎪⎝⎭,则()9f = .12.函数2()ln f x x=的定义域为 .13.若函数f (x )=(2a -1)x +b 在R 上是减函数,则a 的取值范围是________. .14.已知集合{}3log (1)2A x x =-<,1()33x B x ⎧⎫=>⎨⎬⎩⎭则R AC B =_____ .15. 集合M ={1,2,3}的子集的个数为________.三、解答题:(本大题5个小题,共75分)各题解答必须答在答题卡上,必须写出必要的文字说明、演算步骤或推理过程.16. (本题满分10分)已知集合A ={x |3≤x <7},B ={x |2<x <10},求∁R (A ∪B ),A ∩B .17.(本题满分12分)已知函数()f x A ,函数()lg(2)g x x =-的定义域是集合B. (1)求集合A 、B ;(2)若A B B ⋃=,求实数a 的取值范围.18. (本小题满分14分) 计算求值(I ) 1100.753270.064()160.258---++ (II ) 22lg 5lg 5lg 4lg 2+⋅+19. (本小题满分12分)已知),0(56>-=a a x求xx xx aa a a ----33的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上学期高一数学10月月考试题04
一、选择题(每小题3分,共36分) 1、︒420sin 的值是 ( ) A 、-
21 B 、 21 C 、-23 D 、2
3
2、下列集合中,不同于另外三个集合的是 ( ) A 、{}1 B 、{}
2
(1)0y R y ∈-=
C 、{}1x =
D 、{}
10x x -= 3、函数)6
52cos(
3π
-=x y 的最小正周期是 ( ) A 、52π B 、2
5π C 、π2 D 、π5
4、函数
33()2
x x f x --=
是 ( ) A 、奇函数,在(0,+∞)上是减函数 B 、偶函数,在(0,+∞)上是减函数 C 、奇函数,在(0,+∞)上是增函数 D 、偶函数,在(0,+∞)上是增函数 5、设()83l o g
3
-+=x x x f ,用二分法求方程083log 3=-+x x 在区间()1,3内的近似解中,
取区间中点02x =,则下一个区间为 ( )
A 、(1,2)或(2,3)
B 、[1,2]
C 、(1,2)
D 、(2,3)
6、若函数)sin()(ϕω+=x x f 的图象(部分)如图所示,则ϕω和的取值是( ) A 、6,21πϕω==
B 、6
,21π
ϕω-== C 、3,1π
ϕω=
= D 、 3,1π
ϕω-
==
7、若⎩⎨⎧≥<+=-)2(,
2)
2(),2()(x x x f x f x , 则)1(f 的值为 ( )
A 、8
B 、8
1 C 、
2 D 、21
8、已知
sin 2cos 53sin 5cos αα
αα
-=-+,则=αtan ( ).
A 、-2
B 、2
C 、1623
D 、-16
23
9、在△ABC 中,5
1
cos sin =
+A A ,则=A tan ( ) A 、34 B 、34- C 、43 D 、4
3
-
10、函数x
x
x x x x y tan tan cos cos sin sin ++=的值域是( ) A 、{}3,1,0,1- B 、{}3,0,1- C 、{}3,1- D 、{}1,1- 11、若
2
4π
απ
<
<则 ( )
A 、αααtan cos sin >>
B 、αααsin tan cos >>
C 、αααcos tan sin >>
D 、αααcos sin tan >>
12、已知1A ,2A ,…n A 为凸多边形的内角,且0sin lg sin lg sin lg 21=+++n A A A ,则这个多边形是( )
A 、正六边形
B 、梯形
C 、矩形
D 、有一个角是锐角的菱形 二、填空题(每小题3分,共12分)
13、半径为πcm ,中心角为120o 的弧长为 14、计算=-++-e ln 25
802
13
2π
15、)(x f y =是定义在R 上的函数,)()2(x f x f =+,当20≤≤x 时,x x f x
3log 2)(+=,
则=)3(f .
16、已知函数)(x f y =的图象上的每一点的纵坐标扩大到原来的4倍,横坐标扩大到原来的
2倍,然后把所得的图象沿x 轴向左平移
2
π
,这样得到的曲线和x y sin 2=的图象相同,则已知函数)(x f y =的解析式为_______________________________. 三、解答题:(共52分,解答题应写出文字说明、证明过程或演算步骤)
17、(8分)(1)化简:sin(2)sin()cos()sin(3)cos()
παπαπαπαπα-+----
(2)求证:cos 1sin 1sin cos x x
x x
+=-
18、(8分)已知函数)6
2sin(2π
-
=x y .
(1)写出它的振幅、周期、频率和初相; (2)求这个函数的单调递减区间;
(3)求出使这个函数取得最大值时,自变量x 的取值集合,并写出最大值。
19、(8分)已知,3
1
cos =α求,tan ,sin αα
20、(8分)已知函数()2
x x
a a f x -+=(0,1,a a a >≠为常数,x ∈R ).
(1)若()6f m =,求()f m -的值; (2)若(1)3f =,求(2)f 及)2
1(f 的值。
21、(10分)已知函数)4
21cos(
2π+=x y (1)用“五点法”作出这个函数在一个周期内的图象;
(2)函数x y cos =图象经过怎样的变换可以得到)4
21cos(2π
+=x y 的图象? 解:
(2)
O
x
y
22、(10分)为了预防流感,某学校对教室用药熏消毒法进行消毒。
已知药物释放过程中,室
内每立方米空气中的含药量y (毫克)与时间t (小时)成正比;药物释放完毕后,y 与t 的函数关系式为为常数)a y a
t ()16
1(
-=,如图所示。
(1)请写出从药物释放开始,每立方米空气中的含药量y (毫克)与时间t (小时)之间
的函数关系式;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室。
那
么,从药物释放开始,至少需要经过多少小时后,学生才能回到教室。
答案:
1、 D
2、C
3、D
4、C
5、D
6、A
7、B
8、D
9、B 10、C 11、D 12、C
13、2
1
3
π 14、21/5 15、2 16、
17、(1)sin α (2)略(必修四)19页例题。
18、(1)振幅A=2,周期T=π,频率1
f π
=
,初相6
π
ϕ=-
(2)单调递减区间5,()36k k k z ππππ⎡⎤
++∈⎢⎥⎣⎦
.
(3)当,3
x k k z π
π=
+∈,函数有最大值2y =
19、当α
在第一象限时,sin α=
,tan α= 当α
在第四象限时,sin α=
,tan α=-20、
21、 解:(1)列表
【注:列表每行1分,该行必须全对才得分;图象五点对得1分,图象趋势错扣1分】
(2)把x y co s =的图象向左平移
4
π个单位得到)4cos(π
+=x y 的图象,再把
)4cos(π+=x y 的图象纵坐标不变,横坐标变为原来的2倍得到)4
21cos(π
+=x y 的图象,
y
O
x
最后把)4
2
1c o s (π
+
=x y 的图象横坐标不变,纵坐标变为原来的2倍,得到
)4
21cos(2π
+=x y 的图象。
………10分.
【注:对1步得2分,对2步得3分,只有3步全对才得5分】 22、解:(1)依题意,当
,可设y 与t 的函数关系式为y =kt ,
易求得k =10,∴ y =10t ,
∴ 含药量y 与时间t 的函数关系式为…5分
(2)由图像可知y 与t 的关系是先增后减的,在时,y 从0增加到1;
然后时,y 从1开始递减。
∴,解得t =0.6,
∴至少经过0.6小时,学生才能回到教室 ………10分。
