平行四边形存在性问题公式
【常考压轴题】平行四边形存在性问题—2023-2024学年八年级数学下册(浙教版) (解析版)

平行四边形存在性问题【知识储备】①平行四边形是中心对称图形②中心对称图形的性质:对称中心平分中心对称图形内通过该点的任意线段,且使中心对称图形的面积被平分③中点公式: 类型一 几何背景下的平行四边形存在性问题【典题练习】1.(2023•河北二模)如图,在四边形ABCD 中,∠A =∠B =90°,AD =8cm ,BC =6cm ,点P 从点D 出发,以1cm /s 的速度向点A 运动,点M 从点B 同时出发,以相同的速度向点C 运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P 的运动时间为t (单位:s ),下列结论正确的是( )A .当t =3s 时,四边形ABMP 为矩形B .当t =4s 时,四边形CDPM 为平行四边形C .当CD =PM 时,t =3sD .当CD =PM 时,t =3s 或5s【分析】根据题意,表示出DP ,BM ,AP 和CM 的长,当四边形ABMP 为矩形时,根据AP =BM ,列方程求解即可;当四边形CDPM 为平行四边形,根据DP =CM ,列方程求解即可;当CD =PM 时,分两种情况:①四边形CDPM 是平行四边形,②四边形CDPM 是等腰梯形,分别列方程求解即可.【解答】解:根据题意,可得DP =t cm ,BM =t cm ,∵AD =8cm ,BC =6cm ,∴AP =(8﹣t )cm ,CM =(6﹣t )cm ,当四边形ABMP 为矩形时,AP =BM ,即8﹣t =t ,解得t =4,故A 选项不符合题意;当四边形CDPM 为平行四边形,DP =CM ,)2,2),(),,(21212211y y x x P y x B y x A ++坐标为(,则其中点若即t=6﹣t,解得t=3,故B选项不符合题意;当CD=PM时,分两种情况:①四边形CDPM是平行四边形,此时CM=PD,即6﹣t=t,解得t=3,②四边形CDPM是等腰梯形,过点M作MG⊥AD于点G,过点C作CH⊥AD于点H,如图所示:则∠MGP=∠CHD=90°,∵PM=CD,GM=HC,∴△MGP≌△CHD(HL),∴GP=HD,∵AG=AP+GP=8﹣t+,又∵BM=t,∴8﹣t+=t,解得t=5,综上,当CD=PM时,t=3s或5s,故C选项不符合题意,D选项符合题意,故选:D.2.(2023春•盱眙县期末)如图,在▱ABCD中,AB=6cm,AD=10cm,点P在AD边上以每秒1cm的速度从点A向点D运动.点Q在BC边上以每秒4cm的速度从点C出发,在CB之间往返运动.两个点同时出发,当点P到达点D时停止(同时点Q也停止运动),设运动时间为t秒.当5<t<10时,运动时间t为何值时,以P、D、Q、B为顶点的四边形是平行四边形()A.B.8C.4或D.或8【分析】根据P的速度为每秒1cm,可得AP=t cm,从而得到PD=(10﹣t)cm,由四边形ABCD为平行四边形可得出PD∥BQ,结合平行四边形的判定定理可得出当PD=BQ时以P、D、Q、B四点组成的四边形为平行四边形,当5<t<10时,分两种情况考虑,在每种情况中由PD=BQ即可列出关于t的一元一次方程,解之即可得出结论.【解答】解:∵四边形ABCD为平行四边形,∴PD∥BQ.若要以P、D、Q、B四点组成的四边形为平行四边形,则PD=BQ.当5<t≤时,AP=t cm,PD=(10﹣t)cm,CQ=(4t﹣20)cm,BQ=(30﹣4t)cm,∴10﹣t=30﹣4t,解得:t=;当<t≤10时,AP=t cm,PD=(10﹣t)cm,BQ=(4t﹣30)cm,∴10﹣t=4t﹣30,解得:t=8综上所述:当运动时间为秒或8秒时,以P、D、Q、B四点组成的四边形为平行四边形.故选:D.3.(2022春•曹县期中)如图,在平行四边形ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/秒的速度从点A出发,沿AD向点F 运动:点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动,点P运动到F点时停止运动,点Q 也同时停止运动,当点P运动()秒时,以点P、Q、E、F为顶点的四边形是平行四边形.A.2B.3C.3或5D.4或5【分析】由平行四边形的性质可得AD∥BC,AD=BC,由平行线的性质可得BF=DF=12cm,可得AD =AF+DF=18cm=BC,由平行四边形的性质可得PF=EQ,列出方程可求解.【解答】解:∵四边形ABCD是平行四边形∴AD∥BC,AD=BC∴∠ADB=∠MBC,且∠FBM=∠MBC∠ADB=∠FBM∴BF=DF=12cm∴AD=AF+DF=18cm=BC,∵点E是BC的中点∴EC=BC=9cm,∵以点P、Q、E、F为顶点的四边形是平行四边形∴PF=EQ∴6﹣t=9﹣2t,或6﹣t=2t﹣9∴t=3或5故选:C.4.(2023春•大竹县校级期末)如图,平行四边形ABCD的对角线AC,BD相交于点O,BD=12cm,AC=6cm,点E在线段BO上从点B以1cm/s的速度运动,点F在线段OD上从点O以2cm/s的速度运动.若点E,F同时运动,设运动时间为t秒,当t=时,四边形AECF是平行四边形.【分析】先根据平行四边形的性质求出OB的长,从而得到OE的长,再由平行四边形的性质得到OE=OF进而得到关于t的方程,解方程即可.【解答】解:由题意得OE=OB﹣BE=OB﹣t,OF=2t,∵四边形ABCD是平行四边形,BD=12cm,∴OB=OD=6cm,∴OE=6﹣t,∵四边形AECF是平行四边形,∴OE=OF,∴6﹣t=2t,∴t=2,∴当t=2时,四边形AECF是平行四边形,故答案为:2.5.(2023秋•红山区校级月考)如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度向点C运动,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,点P,Q分别从点B,A同时出发,当点P运动到点C时,点Q随之停止运动,设运动的时间t(秒).(1)求DQ、PC的代数表达式;(2)当t为何值时,四边形PQDC是平行四边形;(3)是否存在点P,使△PQD是等腰三角形?若存在,请求出所有满足要求的t的值;若不存在,请说明理由.【分析】(1)根据题意,写出代数表达式即可;(2)根据平行四边形的性质知DQ=CP,分当P从B运动到C时,当P从C运动到B时,两种情况进行求解即可;(3)分PQ=QD、PQ=PD、QD=PD三种情况讨论求出t值即可.【解答】解:(1)根据题意,DQ=(16﹣t)cm,PC=(21﹣2t)cm;(2)∵四边形PQDC是平行四边形,∴DQ=CP,当P从B运动到C时,∵DQ=AD﹣AQ=16﹣t,CP=21﹣2t,∴16﹣t=21﹣2t,解得:t=5,∴当t=5秒时,四边形PQDC是平行四边形;(3)当PQ=PD时,作PH⊥AD于H,则HQ=HD,∵cm,AH=BP,∴,∴.当PQ=QD时,QH=AH﹣AQ=BP﹣AQ=2t﹣t=t cm,QD=(16﹣t)cm,∵QD2=PQ2=t2+122,∴(16﹣t)2=122+t2,解得.当QD=PD时,DH=AD﹣AH=AD﹣BP=16﹣2t,∵QD2=PD2=PH2+HD2=122+16﹣2t)2,∴(16﹣t)2=122+(16﹣2t)2,即3t2﹣32t+144=0,∵Δ=(﹣32)2﹣4×3×144=﹣704<0,∴方程无实根,综上可知,当秒或秒时,△PQD是等腰三角形.6.(2023春•和平区校级月考)已知▱ABCD中,一动点P在AD边上,以每秒1cm的速度从点A向点D 运动.(1)如图1,运动过程中,若BP平分∠ABC,且满足AB=BP,求∠ABC的度数.(2)如图2,在(1)的条件下,连结CP并延长,与AB的延长线交于点F,连结DF,若CD=2cm,直接写出:△DPF的面积为cm2.(3)如图3,另一动点Q在BC边上,以每秒4cm的速度从点C出发,在BC间往返运动,两个点同时出发,当点P停止运动时Q点也停止,设运动时间为t(t>0),若AD=12cm,则t=秒时,以P、D、Q、B为顶点的四边形是平行四边形.【分析】(1)可证AB=AP,从而可证AB=BP=AP,即可求解;(2)设边CD上的高为h1,边BC上的高为h2,,可得S△DPF=S△P AB,即可求解;(3)当PD=BQ时,四边形PDBQ是平行四边形,进行分类讨论:①当12﹣t=12﹣4t时,②当12﹣t =24﹣4t时,③当12﹣t=4t﹣12时,④当12﹣t=4t﹣24时,⑤当12﹣t=36﹣4t时,⑥当12﹣t=4t﹣36时,即可求解.【解答】解:(1)∵四边形ABCD是平行四边形,∴AD∥BC,∴∠APB=∠CBP,∵BP平分∠ABC,∴∠ABP=∠CBP,∴∠ABP=∠APB,∴AB=AP,∵AB=BP,∴AB=BP=AP,∴△ABP是等边三角形,∴∠ABP=60°,∴∠ABC=120°.(2)如图,设边CD上的高为h1,边BC上的高为h2,,∵四边形ABCD是平行四边形,∴S△CDF=•CD=S▱ABCD,S△PBC=h2•BC=S▱ABCD,∴S△PBC=S△CDF=S▱ABCD,∴S△PCD+S△DPF=S▱ABCD,∴S△P AB+S△PCD=S▱ABCD,∴S△PCD+S△DPF=S△P AB+S△PCD,∴S△DPF=S△P AB,∵△ABP是等边三角形,∴S△DPF=S△P AB==3,故答案为:;(3)∵PD∥BQ,∴当PD=BQ时,四边形PDBQ是平行四边形,∵(s),∴0≤t<12,①当12﹣t=12﹣4t时,解得:t=0(不合题意,舍去);此时当P与A重合,Q与C重合;②当12﹣t=24﹣4t时,解得:t=4;③当12﹣t=4t﹣12时,解得:t=4.8;④当12﹣t=4t﹣24时,解得:t=7.2;⑤当12﹣t=36﹣4t时,解得:t=8;⑥当12﹣t=4t﹣36时,解得:t=9.6;综上所述:t为4秒或4.8秒或7.2秒或8秒或9.6秒.类型二“三定一动”求平行四边形的顶点坐标当平面直角坐标系中有3个定点,找第4个点形成平行四边形时:①设第4个点的坐标②以3个定点组成的3条线段为对角线分类讨论③以中心对称图形的性质为等量关系列式求解例,如图所示,平面直角坐标系内有A、B、C三点,在平面内找第4个点,构成平行四边形;【典题练习】7.(2022春•西双版纳期末)在平面直角坐标系中,点A、B、C的坐标分别是A(0,1),B(1,0),C(3,1),若以A,B,C,D为顶点的四边形是平行四边形,那么点D的坐标是.【分析】分三种情况:①BC为对角线时,②AB为对角线时,③AC为对角线时;由平行四边形的性质容易得出点D的坐标.【解答】解:分三种情况:①BC为对角线时,点D的坐标为(4,0);②AB为对角线时,点D的坐标为(﹣2,0)③AC为对角线时,点D的坐标为(2,2)综上所述,点D的坐标是(﹣2,0)或(4,0)或(2,2);故答案为:(4,0)或(﹣2,0)或(2,2).8.(2018春•大邑县期末)如图,在平面直角坐标系中,A(﹣2,3),B(﹣5,1),C(﹣1,0).(1)在图中作出△ABC关于x轴的对称图形△A1B1C1;(2)在图中作出△ABC关于y轴的对称图形△A2B2C2;(3)若以点A,B,C,D为顶点的四边形为平行四边形时,请直接写出满足条件的点D的坐标.【分析】(1)根据关于x轴对称的点的坐标特征写出A1、B1、C1的坐标,然后描点即可得到△A1B1C1;(2)根据关于y轴对称的点的坐标特征写出A2、B2、C2的坐标,然后描点即可得到△A2B2C2;(3)分别以AB、BC、AC为对角线画平行四边形可得到D点坐标.【解答】解:(1)如图,△A11C1为所作;(2如图,△A2B2C2为所作;(3)满足条件的点D的坐标为(2,2)或(﹣4,﹣2)或(﹣6,4).9.(2023春•凤山县期末)如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA,OB分别在x轴的负半轴和y轴的正半轴上,且OA,OB的长满足|OA﹣8|+(OB﹣6)2=0,∠ABO的平分线交x轴于点C,过点C作AB的垂线,垂足为点D,交y轴于点E.(1)求直线AB的解析式;(2)若△ABC的面积为15,求点C的坐标;(3)在(2)的条件下,在坐标平面内是否存在点P,使以O,C,E,P为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.【分析】(1)根据绝对值和完全平方式的非负性得出OA和OB的值,然后确定A点和B点的坐标,用待定系数法求出直线AB的解析式即可;(2)根据△ABC的面积为15,得出AC的长,确定C点的坐标即可;(3)分情况根据平行四边形的性质分别求出P点的坐标即可.【解答】解:(1)∵|OA﹣8|+(OB﹣6)2=0,∴OA=8,OB=6,∴A(﹣8,0),B(0,6),设直线AB的解析式为y=kx+b,代入A点和B点的坐标得,解得,∴直线AB的解析式为y=;(2)∵△ABC的面积为15,∴AC•OB=15,即AC×6=15,∴AC=5,∵OA=8,∴OC=OA﹣AC=8﹣5=3,即C(﹣3,0);(3)存在,∵D点在直线AB上,设D(a,a+6),∵BC平分∠ABO,∴CD=OC,即=3,解得a=﹣,∴D(﹣,),设直线DE的解析式为y=sx+t,∴,解得,∴直线DE的解析式为y=﹣x﹣4,∴E(0,﹣4),设点P的坐标为(m,n),①以CE为对角线时,此时以O,C,E,P为顶点的四边形是矩形,∵O(0,0),C(﹣3,0),E(0,﹣4),∴P(﹣3,﹣4);②以OE为对角线时,由平行四边形对角线互相平分可知,,解得,即P'(3,﹣4);③以OC为对角线时,由平行四边形对角线互相平分可知,,解得,即P''(﹣3,4);综上所述,符合条件的P点坐标为(﹣3,﹣4)或(3,﹣4)或(﹣3,4).类型三“两定两动”求平行四边形的顶点坐标当坐标系中有2个定点,且另外两个动点均在特殊的位置上时,方法策略同类型二。
一次函数之平行四边形存在性问题

一次函数与平行四边形1.线段中点公式平面直角坐标系中,点A 坐标为(x 1,y 1),点B 坐标为(x 2,y 2),则线段AB 的中点P 的坐标为 (2,22121y y x x ++) 例:如图,已知点A (-2,1),B (4,3),则线段AB 的中点P 的坐标是________.2.线段的平移平面内,线段AB 平移得到线段A'B' ,则①AB ∥A'B' ,AB =A'B' ;②AA'∥BB',AA'= BB'. 如图,线段AB 平移得到线段A'B' ,已知点A (-2,2),B (-3,-1), B' (3,1),则点A'的坐标是________.%例:如图,在平面直角坐标系中,□ABCD 的顶点坐标分别为A (x 1,y 1)、B (x 2,y 2)、C (x 3,y 3)、D (x 4,y 4),已知其中3个顶点的坐标,如何确定第4个顶点的坐标"例:如图,已知□ABCD 中A (-2,2),B (-3,-1), C (3,1),则点D 的坐标是________. 方法一:利用线段平移总结:x 1-x 2= x 4-x 3,y 1-y 2= y 4-y 3 或者 x 4-x 1= x 3-x 2,y 4-y 1= y 3-y 2 等方法二:利用中点公式总结:x 1+x 3= x 2+x 4,y 1+y 3= y 2+y 4类型一:三定一动例1 、如图,平面直角坐标中,已知中A(-1,0),B(1,-2),C (3,1),点D是平面内一动点,若以点A、B、C、D为顶点的四边形是平行四边形,则点D的坐标是_________________________________.*总结:三定一动问题,可以通过构造中点三角形得以解决.说明:若题中四边形ABCD是平行四边形,则点D的坐标只有一个结果________【例1】.一次函数y =x +3与y =﹣x +q 的图象都过点A (m ,0),且与y 轴分别交于点B 、C .(1)试求△ABC 的面积;(2)点D 是平面直角坐标系内的一点,且以点A 、C 、B 、D 为顶点的四边形是平行四边形,请直接写出点D 的坐标;(3)过△ABC 的顶点能否画一条直线,使它能平分△ABC 的面积若能,求出直线的函数关系式,若不能,说明理由.【解答】解:(1)将点A (m ,0)代入y =x +3中,得$m +3=0,解得m =﹣3,即点A (﹣3,0),将点A (﹣3,0)代入y =﹣x +q 中,得q =﹣3,∴点B (0,3)、C (0,﹣3),故S =12×BC ×AO =9;(2)满足条件的D 点坐标为D (﹣3,6)、D (﹣3,﹣6)、D (3,0);(3)若过点A ,则得直线l :y =0;若过点C ,则得直线l :y =﹣3x ﹣3;@若过点B ,则得直线l :y =3x +3.例2.如图,在平面直角坐标系xOy 中,已知直线PA 是一次函数y =x +m (m >0)的图象,直线PB 是一次函数y =﹣3x +n (n >m )的图象,点P 是两直线的交点,点A 、B 、C 、Q 分别是两条直线与坐标轴的交点.(1)用m 、n 分别表示点A 、B 、P 的坐标及∠PAB 的度数;(2)若四边形PQOB 的面积是112,且CQ :AO =1:2,试求点P 的坐标,并求出直线PA 与PB的函数表达式;(3)在(2)的条件下,是否存在一点D ,使以A 、B 、P 、D 为顶点的四边形是平行四边形若存在,求出点D 的坐标;若不存在,请说明理由.【解答】解:(1)在直线y =x +m 中,令y =0,得x =﹣m .∴点A (﹣m ,0).…在直线y =﹣3x +n 中,令y =0,得x =x 3. ∴点B (x 3,0). 由{x =x +x x =−3x +x ,得{x =x −x 4x =x +3x 4,∴点P (x −x 4,x +3x 4). 在直线y =x +m 中,令x =0,得y =m ,∴|﹣m |=|m |,即有AO =QO .又∵∠AOQ =90°,∴△AOQ 是等腰直角三角形,∴∠PAB =45°.(2)∵CQ :AO =1:2,,∴(n ﹣m ):m =1:2,整理得3m =2n ,∴n =32m , ∴x +3x 4=32x +3x 4=98m , 而S 四边形PQOB =S △PAB ﹣S △AOQ =12(x 3+m )×(98m )−12×m ×m =1132m 2=112, 解得m =±4,∵m >0,∴m =4,∴n =32m =6,∴P (12,92). !∴PA 的函数表达式为y =x +4,PB 的函数表达式为y =﹣3x +6.(3)存在.过点P 作直线PM 平行于x 轴,过点B 作AP 的平行线交PM 于点D 1,过点A 作BP 的平行线交PM 于点D 2,过点A 、B 分别作BP 、AP 的平行线交于点D 3.①∵PD 1∥AB 且BD 1∥AP ,∴PABD 1是平行四边形.此时PD 1=AB ,易得x 1(132,92); ②∵PD 2∥AB 且AD 2∥BP ,∴PBAD 2是平行四边形.此时PD 2=AB ,易得x 2(−112,92);③∵BD 3∥AP 且AD 3∥BP ,此时BPAD 3是平行四边形.】∵BD 3∥AP 且B (2,0),∴y BD 3=x ﹣2.同理可得y AD 3=﹣3x ﹣12{x =x −2x =−3x −12, 得{x =−52x =−92,∴x 3(−52,−92).3.如图,在等边△ABC 中,BC =8cm ,射线AG ∥BC ,点E 从点A 出发沿射线AG 以1cm /s 的速度运动,同时点F 从点B 出发沿射线BC 以2cm /s 的速度运动,设运动时间为t (s ).(1)连接EF ,当EF 经过AC 边的中点D 时,求证:△ADE ≌△CDF ;(2)填空:#①当t 为 s 时,以A 、F 、C 、E 为顶点的四边形是平行四边形;②当t 为 s 时,四边形ACFE 是菱形.【解答】(1)证明:∵AG ∥BC ,∴∠EAD =∠DCF ,∠AED =∠DFC ,∵D 为AC 的中点,∴AD =CD ,∵在△ADE 和△CDF 中,{∠xxx =∠xxx∠xxx =∠xxx xx =xx,∴△ADE ≌△CDF (AAS );(2)解:①当点F 在C 的左侧时,根据题意得:AE =tcm ,BF =2tcm ,·则CF =BC ﹣BF =6﹣2t (cm ),∵AG ∥BC ,∴当AE =CF 时,四边形AECF 是平行四边形,即t =8﹣2t ,解得:t =83; 当点F 在C 的右侧时,根据题意得:AE =tcm ,BF =2tcm ,则CF =BF ﹣BC =2t ﹣8(cm ),∵AG ∥BC ,∴当AE =CF 时,四边形AEFC 是平行四边形,即t =2t ﹣8,]解得:t =8;综上可得:当t =83或8s 时,以A 、C 、E 、F 为顶点四边形是平行四边形.②若四边形ACFE 是菱形,则有CF =AC =AE =8,则此时的时间t =8÷1=8(s );故答案是:83或8;8.|4.已知,Rt △OAB 的两直角边OA 、OB 分别在x 轴和y 轴上,如图1,A ,B 坐标分别为(﹣2,0),(0,4),将△OAB 绕O 点顺时针旋转90°得△OCD ,连接AC 、BD 交于点E .(1)求证:△ABE ≌△DCE .(2)M 为直线BD 上动点,N 为x 轴上的点,若以A ,C ,M ,N 四点为顶点的四边形是平行四边形,求出所有符合条件的M 点的坐标.(3)如图2,过E 点作y 轴的平行线交x 轴于点F ,在直线EF 上找一点P ,使△PAC 的周长最小,求P 点坐标和周长的最小值.【分析】(1)由A 、B 的坐标可求得AO 和OB 的长,由旋转的性质可求得OC 、OD 的长,从而可求得∠AEB =90°,再由勾股定理可求得CD 和AB 的长,可求得AB =CD ,可证得△ABE ≌△DCE ;(2)由B 、D 坐标可求得直线BD 解析式,当M 点在x 轴上方时,则有CM ∥AN ,则可求得M 点纵坐标,代入直线BD 解析式可求得M 点坐标,当M 点在x 轴下方时,同理可求得M 点纵坐标,则可求得M 点坐标;)(3)由AE =DE 可知A 、D 关于EF 对称,连接CD 交EF 于点P ,则P 点即为满足条件的点,由C 、D 坐标可求得直线CD 的解析式,则可求得P 点坐标,利用勾股定理可分别求得AC 和CD 的长,则可求得此时△PAC 的周长.【解答】解:(1)∵A (﹣2,0),B (0,4),∴OA =2,OB =4,∵将△OAB 绕O 点顺时针旋转90°得△OCD ,∴OC =OA =2,OD =OB =4,AB =CD ,∴∠ACO =∠ECB =∠CBE =45°,∴∠CEB =90°,∴∠AEB =∠CED ,且CE =BE ,在Rt △ABE 和Rt △DCE 中:{xx =xx xx =xx∴Rt △ABE ≌Rt △DCE (HL );(2)由(1)可知D (4,0),且B (0,4),∴直线BD 解析式为y =﹣x +4,当M 点在x 轴上方时,则有CM ∥AN ,即CM ∥x 轴,∴M 点到x 轴的距离等于C 点到x 轴的距离,∴M 点的纵坐标为2,在y =﹣x +4中,令y =2可得x =2,∴M (2,2);当M 点在x 轴下方时,同理可得M 点的纵坐标为﹣2,(在y =﹣x +4中,令y =﹣2可求得x =6,∴M 点的坐标为(6,﹣2);综上可知M 点的坐标为(2,2)或(6,﹣2);(3)由(1)可知AE =DE ,∴A 、D 关于直线EF 对称,连接CD 交EF 于点P ,则PA =PD , ∴PA +PC =PD +PC =CD ,∴满足△PAC 的周长最小,∵C (0,2),D (4,0),∴可设直线CD 解析式为y =kx +2,∴4k +2=0,解得k =−12, ∴直线CD 解析式为y =−12x +2,∵A (﹣2,0),D (4,0),∴F (1,0),即直线EF 解析式为x =1,在y =−12x +2中,令x =1可得y =32, ∴P (1,32), 在Rt △AOC 中,由勾股定理可求得AC =2√2, 在Rt △COD 中,由勾股定理可求得CD =√22+42=2√5, ∴PA +PC +AC =CD +AC =2√5+2√2, 即△PAC 的周长最小值为2√5+2√2.。
学生版:一招解决二函与平行四边形存在性问题

一招解决二函与平行四边形存在性问题 1.平行四边形的性质与判定平行四边形的性质 1.两组对边分别平行且相等2.两组对角分别相等3.对角线互相平分平行四边形的判定 1.两组对边分别平行的四边形是平行四边形2.两组对边分别相等的四边形是平行四边形3.一组对边平行且相等的四边形是平行四边形4.两组对角分别相等的四边形是平行四边形5.对角线互相平分的四边形是平行四边形3.坐标系中的平行四边形顶点坐标关系如图平行四边形 ABCD , A (x A , y A ) ,B (x B , y B ) ,C (x C , y C ) ,D (x D , y D ) ,对角线 AC ,BD 相交于点 M (x M , y M ) .y CDM BAO x结论:由中点坐标公式可得:① M ( x A + x c , y A + y c ) ; M ( x B + x D , y B + y D)22 2 2 ② x A + x C = x B + x D ; y A + y C = y B + y D知识讲解1.题目可以分为①三定一动②二定两动③一定三动.一般动点越多,难度越大;2.符合题意的平行四边形一般不唯一,往往需要分类讨论;3.熟练掌握平行四边形的性质与判定、中点坐标公式及两点间距离公式等;4.数形结合动态思考,利用平行四边形的性质作出符合题意图形,保证不重不漏.【例1】(1)如图①,若A、C点的坐标分别为A(−1,3) 、C(3, −1) ,求AC中点M的坐标。
(2)如图②,在平面直角坐标系中,平行四边形ABCD的顶点A、B、C 的坐标分别为(−1,5) 、(−2,2) 、(3,3) ,求点D的坐标。
【例2】已知抛物线y = x2 − 2x− 3 与x轴交于A,C两点,与y轴交于B点.点P为抛物线对称轴上一动点,点Q为x轴上一动点,当点A,B,P,Q构成以AB为边的平行四边形时,求点P的坐标.典型例题【例3】已知抛物线y = x2 − 2x− 3 与x轴交于A,C两点,与y轴交于B点.点P为抛物线对称轴上一动点,点Q为抛物线上一动点,当点B,C,P,Q构成平行四边形时,求点Q的坐标.【例4】如图,已知二次函数y = (x + 2)2的图象与x轴交于点A,与y轴交于点B.P 在抛物线对称轴上,以P、A、O、B 为顶点的四边形为平行四边形,则点P 的坐标为()A.(-2 ,4)B.(-2 ,-4 )C.(-2 ,4)或(-2 ,-4 )D.(-2 ,4)或(-2 ,2)。
平行四边形存在性问题
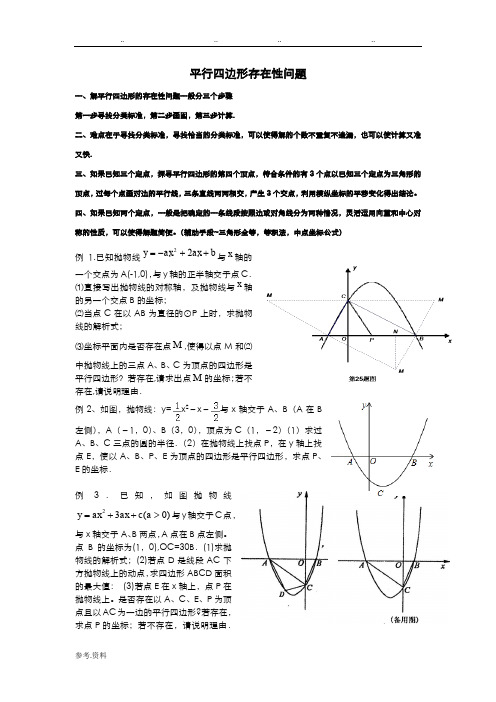
平行四边形存在性问题一、解平行四边形的存在性问题一般分三个步骤 第一步寻找分类标准,第二步画图,第三步计算.二、难点在于寻找分类标准,寻找恰当的分类标准,可以使得解的个数不重复不遗漏,也可以使计算又准又快.三、如果已知三个定点,探寻平行四边形的第四个顶点,符合条件的有3个点以已知三个定点为三角形的顶点,过每个点画对边的平行线,三条直线两两相交,产生3个交点,利用横纵坐标的平移变化得出结论。
四、如果已知两个定点,一般是把确定的一条线段按照边或对角线分为两种情况,灵活运用向量和中心对称的性质,可以使得解题简便。
(辅助手段~三角形全等,等积法,中点坐标公式)例1.已知抛物线b ax ax y ++-=22与x 轴的一个交点为A(-1,0),与y 轴的正半轴交于点C .⑴直接写出抛物线的对称轴,及抛物线与x 轴的另一个交点B 的坐标;⑵当点C 在以AB 为直径的⊙P 上时,求抛物线的解析式;⑶坐标平面内是否存在点M ,使得以点M 和⑵中抛物线上的三点A 、B 、C 为顶点的四边形是平行四边形?若存在,请求出点M 的坐标;若不存在,请说明理由.例2、如图,抛物线:y=x 2﹣x ﹣与x 轴交于A 、B (A 在B左侧),A (﹣1,0)、B (3,0),顶点为C (1,﹣2)(1)求过A 、B 、C 三点的圆的半径.(2)在抛物线上找点P ,在y 轴上找点E ,使以A 、B 、P 、E 为顶点的四边形是平行四边形,求点P 、E 的坐标.例3.已知,如图抛物线23(0)y ax ax c a =++>与y 轴交于C 点,与x 轴交于A 、B 两点,A 点在B 点左侧。
点B 的坐标为(1,0),OC=30B .(1)求抛物线的解析式;(2)若点D 是线段AC 下方抛物线上的动点,求四边形ABCD 面积的最大值: (3)若点E 在x 轴上,点P 在抛物线上。
是否存在以A 、C 、E 、P 为顶点且以AC 为一边的平行四边形?若存在,求点P 的坐标;若不存在,请说明理由.例4.已知抛物线:x x y 22121+-= (1)求抛物线1y 的顶点坐标.(2)将抛物线1y 向右平移2个单位,再向上平移1个单位,得到抛物线2y ,求抛物线2y 的解析式.(3)如下图,抛物线2y 的顶点为P ,x 轴上有一动点M ,在1y 、2y 这两条抛物线上是否存在点N ,使O (原点)、P 、M 、N 四点构成以OP 为一边的平行四边形,若存在,求出N 点的坐标;若不存在,请说明理由.例5.如图,抛物线223y x x =--与x 轴交A 、B 两点(A点在B 点左侧),直线l 与抛物线交于A 、C 两点,其中C 点的横坐标为2.(1)求A 、B 两点的坐标及直线AC 的函数表达式;(2)P 是线段AC 上的一个动点,过P 点作y 轴的平行线交抛物线于E 点,求线段PE 长度的最大值; (3)点G 抛物线上的动点,在x 轴上是否存在点F ,使A 、C 、F 、G 这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F 点坐标;如果不存在,请说明理由.练习1、已知抛物线 c bx ax y ++=2经过A (-3,0),B(1,0),C(0,3)三点.(1)求抛物线的解析式;(2)P 为抛物线的顶点,M 为坐标平面内的点,若以A,C,P,M 为顶点的四边形为平行四边形,求点M 的坐标.2、在平面直角坐标系中,已知抛物线经过A )0,4(-,B )4,0(-,C )0,2(三点.(1)求抛物线的解析式;(2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S .求S 关于m 的函数关系式,并求出S 的最大值. (3)若点P 是抛物线上的动点,点Q 是直线x y -=上的动点,判断有几个位置能够使得点P 、Q 、B 、O 为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标.2的⊙C与x轴3、如图,在平面直角坐标系中,半径为5交于点A(-1,0),B(3,0)两点,且点C在x轴的上方.(1)求圆心C的坐标;(2)已知一个二次函数的图象经过点A,B,C,求这个二次函数的解析式;(3)设点P在y轴上,点M在(2)的二次函数图象上,如果以点P,M,A,B为顶点的四边形是平行四边形,请你直接写出点M的坐标.4、已知二次函数图象的顶点坐标为M(1,0),直线y=x+m与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在y轴上.(1)求m的值及这个二次函数的解析式;(2)在x轴上找一点Q,使△QAB的周长最小,并求出此时Q点坐标;(3)若P(a,0)是x轴上的一个动点,过P作x轴的垂线分别与直线AB和二次函数的图象交于D、E两点.①设线段DE的长为h,当0<a<3时,求h与a之间的函数关系式;②若直线AB与抛物线的对称轴交点为N,问是否存在一点P,使以M、N、D、E为顶点的四边形是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.5.如图,已知抛物线y=-x2-2x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,顶点为P.若以A、C、P、M为顶点的四边形是平行四边形,求点M的坐标.6、如图1,在平面直角坐标系中,抛物线y=ax2+bx-3a经过A(-1,0)、B(0,3)两点,与x轴交于另一点C,顶点为D.(1)求该抛物线的解析式及点C、D的坐标;(2)经过点B、D两点的直线与x轴交于点E,若点F是抛物线上一点,以A、B、E、F 为顶点的四边形是平行四边形,求点F的坐标;(3)如图2,P(2,3)是抛物线上的点,Q是直线AP上方的抛物线上一动点,求△APQ 的最大面积和此时Q点的坐标.7、已知平面直角坐标系xOy (如图),一次函数334y x =+的图像与y 轴交于点A ,点M在正比例函数32y x =的图像上,且MO =MA .二次函数y =x 2+bx +c 的图像经过点A 、M . (1)求线段AM 的长; (2)求这个二次函数的解析式;(3)如果点B 在y 轴上,且位于点A 下方,点C 在上述二次函数的图像上,点D 在一次函数334y x =+的图像上,且四边形ABCD 是菱形,求点C 的坐标.8.如图,在平面直角坐标系xOy 中,△ABC 的A 、B 两个顶点在x 轴上,顶点C 在y 轴的负半轴上.已知|OA |∶|OB |=1∶5,|OB |=|OC |,△ABC 的面积S △ABC =15,抛物线y =ax 2+bx +c (a ≠0)经过A 、B 、C 三点. (1)求此抛物线的函数表达式;(2)设E 是y 轴右侧抛物线上异于点B 的一个动点,过点E 作x 轴的平行线交抛物线于另一点F ,过点F 作FG 垂直于x 轴于点G ,再过点E 作EH 垂直于x 轴于点H ,得到矩形EFGH .则在点E 的运动过程中,当矩形EFGH 为正方形时,求出该正方形的边长;(3)在抛物线上是否存在异于B 、C 的点M ,使△MBC 中BC 边上的高为求出点M 的坐标;若不存在,请说明理由.9、将抛物线c1:2y =x 轴翻折,得到抛物线c 2,如图所示.现将抛物线c 1向左平移m 个单位长度,平移后得到新抛物线的顶点为M ,与x 轴的交点从左到右依次为A 、B ;将抛物线c 2向右也平移m 个单位长度,平移后得到新抛物线的顶点为N ,与x 轴的交点从左到右依次为D 、E .在平移过程中,是否存在以点A 、N 、E 、M 为顶点的四边形是矩形的情形?若存在,请求出此时m 的值;若不存在,请说明理由.。
平行四边形的存在性——平移坐标法

m1 n1
0 (舍去) 1
m2 -2
n
2
-1
E(-1,0)
第二步情况3平行四边形AECF
F(,m22m3)
C(0,3)
A(1,0)
n01m
030m22m3
E(n,0)
m1 n1
0 (舍去) 1
m2 -2
凤凰中学
——刘远义
平行四边形的存在性
——平移坐标法
平移坐标性质 平移坐标法
平移坐标性质
线段的平移,各个点横坐标的变化对应相同,纵坐标的变化 对应相同。A (a,b) ,B (c,d),若C(c+m,d+n),则D(a+m,b+n)
例:
二次函数为:yx22x3,抛物线交x轴与
A,与y轴交于C。若E点在x轴上,F点在抛物 线上,如果A、C、E、F构成平行四边形,写 出点E的坐标 .
例:
第一步确定点的坐标及设点坐标
( 0 ,3 )
E(n,0)
F(m,m22m3)
(1,0 )
二次函数为:yx22x3,抛物线交x轴与
A,与y轴交于C。若E点在x轴上,F点在抛物 线上,如果A、C、E、F构成平行四边形,写 出点E的坐标 .
例:
第一步确定点的坐标及设点坐标
F(m,m22m3) ( 0 ,3 )
E(n,0)
(1,0 )
E(n,0)
C(0,3)
F(m,m22m3) A(1,0)
第二步分类平行四边形的情况
A(1,0)
C(0,3)
E(n,0)
F(m,m22m3)
第二步情况1平行四边形ACEF
巧解二次函数中平行四边形存在性问题

图 2 图 3 图1 巧解二次函数中平行四边形存在性问题以二次函数为载体的平行四边形存在性问题是近年来中考的热点,其图形复杂,知识覆盖面广,综合性较强,对学生分析问题和解决问题的能力要求高.对这类题,常规解法是先画出平行四边形,再依据“平行四边形的一组对边平行且相等”或“平行四边形的对角线互相平分”来解决.由于先要画出草图,若考虑不周,很容易漏解.为此,借助探究平行四边形顶点坐标公式来解决这一类题.1 两个结论,解题的切入点数学课标,现行初中数学教材中没有线段的中点坐标公式,也没有平行四边形的顶点坐标公式,我们可帮助学生来探究,这可作为解题的切入点。
1.1 线段中点坐标公式平面直角坐标系中,点A 坐标为(x 1,y 1),点B 坐标为(x 2,y 2),则线段AB 的中点坐标为(221x x +,221y y +). 证明 : 如图1,设AB 中点P 的坐标为(x P ,y P ).由x P -x 1=x 2-x P ,得x P =221x x +,同理y P =221y y +,所以线段AB 的中点坐标为(221x x +,221y y +).1.2 平行四边形顶点坐标公式 □ABCD 的顶点坐标分别为A (x A ,y A )、B (x B ,y B )、C (x C ,y C )、D (x D ,y D ),则:x A +x C =x B +x D ;y A +y C =y B +y D .证明: 如图2,连接AC 、BD ,相交于点E .∵点E 为AC 的中点,∴E 点坐标为(2C A x x +,2C A y y +). 又∵点E 为BD 的中点, ∴E 点坐标为(2D B x x +,2D B y y +). ∴x A +x C =x B +x D ;y A +y C =y B +y D .即平行四边形对角线两端点的横坐标、纵坐标之和分别相等.2 一个基本事实,解题的预备知识如图3,已知不在同一直线上的三点A 、B 、C ,在平面内另找一个点D ,使以A 、B 、C 、D 为顶点的四边形是平行四边形.答案有三种:以AB 为对角线的□ACBD 1,以AC 为对角线的□ABCD 2,以BC 为对角线的□ABD 3C .3 两类存在性问题解题策略例析与反思3.1 三个定点、一个动点,探究平行四边形的存在性问题图4例1 已知抛物线y=x 2-2x+a (a <0)与y 轴相交于点A ,顶点为M .直线y=21x-a 分别与x 轴、y 轴相交于B 、C 两点,并且与直线AM 相交于点N .(1)填空:试用含a 的代数式分别表示点M 与N 的坐标,则M ( ), N ( );(2)如图4,将△NAC 沿y 轴翻折,若点N 的对应点N ′恰好落在抛物线上,AN ′与x 轴交于点D ,连接CD ,求a 的值和四边形ADCN 的面积;(3)在抛物线y=x 2-2x+a (a <0)上是否存在一点P ,使得以P 、A 、C 、N 为顶点的四边形是平行四边形?若存在,求出点P 的坐标;若不存在,试说明理由.解:(1)M (1,a-1),N (a 34,-a 31);(2)a=-49;S 四边形ADCN =16189; (3)由已知条件易得A (0,a )、C (0,-a )、N (a 34,-a 31).设P (m ,m 2-2m +a ). ①当以AC 为对角线时,由平行四边形顶点坐标公式(解题时熟练推导出),得:⎪⎪⎩⎪⎪⎨⎧+-+-=-+=+a m m a a a m a 23134002,∴⎪⎪⎩⎪⎪⎨⎧-==81525a m . ∴P 1(25,-85); ②当以AN 为对角线时,得:⎪⎪⎩⎪⎪⎨⎧+-+-=-+=+a m m a a a m a 23103402,∴⎪⎪⎩⎪⎪⎨⎧==81525a m (不合题意,舍去). ③当以CN 为对角线时,得:⎪⎪⎩⎪⎪⎨⎧+-+=--+=+a m m a a a m a 23103402,∴⎪⎪⎩⎪⎪⎨⎧-=-=8321a m . ∴P 2(-21,87). ∴在抛物线上存在点P 1(25,-85)和P 2(-21,87),使得以P 、A 、C 、N 为顶点的四边形是平行四边形.反思:已知三个定点的坐标,可设出抛物线上第四个顶点的坐标,运用平行四边形顶点坐标公式列方程(组)求解.这种题型由于三个定点构成的三条线段中哪条为对角线不清楚,往往要以这三条线段分别为对角线分类,分三种情况讨论.图53.2 两个定点、两个动点,探究平行四边形存在性问题例2 如图5,在平面直角坐标系中,抛物线A (-1,0),B (3,0),C (0,-1)三点.(1)求该抛物线的表达式;(2)点Q 在y 轴上,点P 在抛物线上,要使以点Q 、P 、A 、B 为顶点的四边形是平行四边形,求所有满足条件点P 的坐标.解 :(1)易求抛物线的表达式为y=132312--x x ; (2)由题意知点Q 在y 轴上,设点Q 坐标为(0,t );点P 在抛物线上,设点P 坐标为(m ,132312--m m ). 尽管点Q 在y 轴上,也是个动点,但可理解成一个定点,这样就转化为三定一动了. ①当以AQ 为对角线时,由四个顶点的横坐标公式得:-1+0=3+m ,∴m=-4,∴P 1(-4,7);②当以BQ 为对角线时,得:-1+m=3+0,∴m=4,∴P 2(4,35); ③当以AB 为对角线时,得:-1+3=m+0,∴m=2,∴P 3(2,-1).综上,满足条件的点P 为P 1(-4,7)、P 2(4,35)、P 3(2,-1). 反思:这种题型往往特殊,一个动点在抛物线上,另一个动点在x 轴(y 轴)或对称轴或某一定直线上.设出抛物线上的动点坐标,另一个动点若在x 轴上,纵坐标为0,则用平行四边形顶点纵坐标公式;若在y 轴上,横坐标为0,则用平行四边形顶点横坐标公式.该动点哪个坐标已知就用与该坐标有关的公式.本例中点Q 的纵坐标t 没有用上,可以不设.另外,把在定直线上的动点看成一个定点,这样就转化为三定一动了,分别以三个定点构成的三条线段为对角线分类,分三种情况讨论.图 6例3 如图6,在平面直角坐标系中,已知抛物线经过A (-4,0),B (0,-4),C (2,0)三点.(1)求抛物线的解析式;(2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S .求S 关于m 的函数关系式,并求出S 的最大值;(3)若点P 是抛物线上的动点,点Q 是直线y =-x 上的动点,判断有几个位置能使以点P 、Q 、B 、O 为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标.解:(1)易求抛物线的解析式为y=21x 2+x-4; (2)s=-m 2-4m (-4<m <0);s 最大=4(过程略);(3)尽管是直接写出点Q 的坐标,这里也写出过程.由题意知O (0,0)、B (0,-4). 由于点Q 是直线y=-x 上的动点,设Q (s ,-s ),把Q 看做定点;设P (m ,21m 2+m -4). ①当以OQ 为对角线时,⎪⎩⎪⎨⎧-++-=-+=+42140002m m s m s ∴s=-252±.∴Q 1(-2+52,2-52),Q 2(-2-52,2+52);②当以BQ 为对角线时,⎪⎩⎪⎨⎧--=-+++=+s m m s m 44210002 ∴s 1=-4,s 2=0(舍).∴Q 3(-4,4);③当以OB 为对角线时,⎪⎩⎪⎨⎧-++-=-+=+42140002m m s m s ∴s 1=4,s 2=0(舍).∴Q 4(4,-4).综上,满足条件的点Q 为Q 1(-2+52,2-52)、Q 2(-2-52,2+52)、Q 3(-4,4)、Q 4(4,-4).反思:该题中的点Q 是直线y =-x 上的动点,设动点Q 的坐标为(s ,-s ),把Q 看做定点,就可根据平行四边形顶点坐标公式列方程组了.4 问题总结这种题型,关键是合理有序分类:无论是三定一动,还是两定两动,统统把抛物线上的动点作为第四个动点,其余三个作为定点,分别以这三个定点构成的三条线段为对角线分类,分三种情况讨论,然后运用平行四边形顶点坐标公式转化为方程(组).这种解法,不必画出平行四边形草图,只要合理分类,有序组合,从对角线入手不会漏解,条理清楚,而且适用范围广.其本质是用代数的方法解决几何问题,体现的是分类讨论思想、数形结合的思想.。
中点坐标公式与二次函数中平行四边形存在性问题

图2图 3 图1二次函数中平行四边形存在性问题 以二次函数为载体的平行四边形存在性问题是近年来中考的热点,其图形复杂,知识覆盖面广,综合性较强,对学生分析问题和解决问题的能力要求高.对这类题,常规解法是先画出平行四边形,再依据“平行四边形的一组对边平行且相等”或“平行四边形的对角线互相平分”来解决.由于先要画出草图,若考虑不周,很容易漏解.为此,笔者另辟蹊径,借助探究平行四边形顶点坐标公式来解决这一类题.1 两个结论,解题的切入点数学课标,现行初中数学教材中没有线段的中点坐标公式,也没有平行四边形的顶点坐标公式,我们可帮助学生来探究,这可作为解题的切入点。
1.1 线段中点坐标公式平面直角坐标系中,点A 坐标为(x 1,y 1),点B 坐标为(x 2,y 2),则线段AB 的中点坐标为(221x x +,221y y +). 证明 : 如图1,设AB 中点P 的坐标为(x P ,y P ).由x P -x 1=x 2-x P ,得x P =221x x +,同理y P =221y y +,所以线段AB 的中点坐标为(221x x +,221y y +). 1.2 平行四边形顶点坐标公式□ABCD 的顶点坐标分别为A (x A ,y A )、B (x B ,y B )、C (x C ,y C )、D (x D ,y D ),则:x A +x C =x B +x D ;y A +y C =y B +y D . 证明: 如图2,连接AC 、BD ,相交于点E .∵点E 为AC 的中点,∴E 点坐标为(2C A x x +,2C A y y +). 又∵点E 为BD 的中点,∴E 点坐标为(2D B x x +,2D B y y +). ∴x A +x C =x B +x D ;y A +y C =y B +y D .即平行四边形对角线两端点的横坐标、纵坐标之和分别相等.2 一个基本事实,解题的预备知识如图3,已知不在同一直线上的三点A 、B 、C ,在平面内另找一个点D ,使以A 、B 、C 、D 为顶点的四边形是平行四边形.答案有三种:以AB 为对角线的□ACBD 1,以AC 为对角线的□ABCD 2,以BC 为对角线的□ABD 3C . 3 两类存在性问题解题策略例析与反思3.1 三个定点、一个动点,探究平行四边形的存在性问题例1 已知抛物线y=x 2-2x+a (a <0)与y 轴相交于点A ,顶点为M .直线y=21x-a 分别与x 轴、y 轴相交于B 、C 两点,并且与直线AM 相交于点N .(1)填空:试用含a 的代数式分别表示点M 与N 的坐标,则M ( ), N ( );图 4图5(2)如图4,将△NAC 沿y 轴翻折,若点N 的对应点N ′恰好落在抛物线上,AN ′与x 轴交于点D ,连接CD ,求a 的值和四边形ADCN 的面积;(3)在抛物线y=x 2-2x+a (a <0)上是否存在一点P ,使得以P 、A 、C 、N 为顶点的四边形是平行四边形?若存在,求出点P 的坐标;若不存在,试说明理由.解:(1)M (1,a-1),N (a 34,-a 31);(2)a=-49;S 四边形ADCN =16189; (3)由已知条件易得A (0,a )、C (0,-a )、N (a 34,-a 31).设P (m ,m 2-2m +a ). ①当以AC 为对角线时,由平行四边形顶点坐标公式(解题时熟练推导出),得:⎪⎪⎩⎪⎪⎨⎧+-+-=-+=+a m m a a a m a 23134002,∴⎪⎪⎩⎪⎪⎨⎧-==81525a m . ∴P 1(25,-85); ②当以AN 为对角线时,得:⎪⎪⎩⎪⎪⎨⎧+-+-=-+=+a m m a a a m a 23103402,∴⎪⎪⎩⎪⎪⎨⎧==81525a m (不合题意,舍去). ③当以CN 为对角线时,得:⎪⎪⎩⎪⎪⎨⎧+-+=--+=+a m m a a a m a 23103402,∴⎪⎪⎩⎪⎪⎨⎧-=-=8321a m . ∴P 2(-21,87). ∴在抛物线上存在点P 1(25,-85)和P 2(-21,87),使得以P 、A 、C 、N 为顶点的四边形是平行四边形. 反思:已知三个定点的坐标,可设出抛物线上第四个顶点的坐标,运用平行四边形顶点坐标公式列方程(组)求解.这种题型由于三个定点构成的三条线段中哪条为对角线不清楚,往往要以这三条线段分别为对角线分类,分三种情况讨论.3.2 两个定点、两个动点,探究平行四边形存在性问题例2 如图5,在平面直角坐标系中,抛物线A (-1,0),B (3,0),C (0,-1)三点.(1)求该抛物线的表达式;(2)点Q 在y 轴上,点P 在抛物线上,要使以点Q 、P 、A 、B 为顶点的四边形是平行四边形,求所有满足条件点P 的坐标.解 :(1)易求抛物线的表达式为y=132312--x x ; (2)由题意知点Q 在y 轴上,设点Q 坐标为(0,t );点P 在抛物线上,图6 设点P 坐标为(m ,132312--m m ). 尽管点Q 在y 轴上,也是个动点,但可理解成一个定点,这样就转化为三定一动了.①当以AQ 为对角线时,由四个顶点的横坐标公式得:-1+0=3+m ,∴m=-4,∴P 1(-4,7);②当以BQ 为对角线时,得:-1+m=3+0,∴m=4,∴P 2(4,35); ③当以AB 为对角线时,得:-1+3=m+0,∴m=2,∴P 3(2,-1).综上,满足条件的点P 为P 1(-4,7)、P 2(4,35)、P 3(2,-1). 反思:这种题型往往特殊,一个动点在抛物线上,另一个动点在x 轴(y 轴)或对称轴或某一定直线上.设出抛物线上的动点坐标,另一个动点若在x 轴上,纵坐标为0,则用平行四边形顶点纵坐标公式;若在y 轴上,横坐标为0,则用平行四边形顶点横坐标公式.该动点哪个坐标已知就用与该坐标有关的公式.本例中点Q 的纵坐标t 没有用上,可以不设.另外,把在定直线上的动点看成一个定点,这样就转化为三定一动了,分别以三个定点构成的三条线段为对角线分类,分三种情况讨论.例3 如图6,在平面直角坐标系中,已知抛物线经过A (-4,0),B (0,-4),C (2,0)三点.(1)求抛物线的解析式;(2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S .求S 关于m 的函数关系式,并求出S 的最大值;(3)若点P 是抛物线上的动点,点Q 是直线y =-x 上的动点,判断有几个位置能使以点P 、Q 、B 、O 为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标.解:(1)易求抛物线的解析式为y=21x 2+x-4; (2)s=-m 2-4m (-4<m <0);s 最大=4(过程略);(3)尽管是直接写出点Q 的坐标,这里也写出过程.由题意知O (0,0)、B (0,-4).由于点Q 是直线y=-x 上的动点,设Q (s ,-s ),把Q 看做定点;设P (m ,21m 2+m -4). ①当以OQ 为对角线时,∴s=-252±.∴Q 1(-2+52,2-52),Q 2(-2-52,2+52);②当以BQ 为对角线时,∴s 1=-4,s 2=0(舍).∴Q 3(-4,4);③当以OB 为对角线时,∴s1=4,s2=0(舍).∴Q4(4,-4).综上,满足条件的点Q为Q1(-2+52)、Q3(-4,4)、Q4(4,-4).2,2+52,2-52)、Q2(-2-5反思:该题中的点Q是直线y=-x上的动点,设动点Q的坐标为(s,-s),把Q看做定点,就可根据平行四边形顶点坐标公式列方程组了.4 问题总结这种题型,关键是合理有序分类:无论是三定一动,还是两定两动,统统把抛物线上的动点作为第四个动点,其余三个作为定点,分别以这三个定点构成的三条线段为对角线分类,分三种情况讨论,然后运用平行四边形顶点坐标公式转化为方程(组).这种解法,不必画出平行四边形草图,只要合理分类,有序组合,从对角线入手不会漏解,条理清楚,而且适用范围广.其本质是用代数的方法解决几何问题,体现的是分类讨论思想、数形结合的思想.。
指数对数函数平行四边形存在性问题例题

指数对数函数平行四边形存在性问题例题本文将介绍一个关于指数对数函数的平行四边形存在性问题的例题,并给出详细的解答过程。
通过解答这个例题,我们将了解到如何应用指数对数函数的性质判断平行四边形的存在性。
题目描述已知函数 f(x) = a^x 和 g(x) = loga x,其中 a 是正实数。
问题:对于 a 的取值范围,存在一个正实数 b,使得线段 A(0, f(b)) 和线段 B(1, g(b)) 平行吗?如果存在,给出一个满足条件的实数 b 的取值范围。
解答过程首先,我们需要判断函数 f(x) = a^x 和 g(x) = loga x 是否存在一个公共的斜率。
如果存在,则线段 A 和线段 B 平行。
为了寻找可能的共线条件,我们可以对函数 f(x) 和 g(x) 进行求导。
1. 对函数 f(x) 进行求导:f'(x) = a^x * ln(a)2. 对函数 g(x) 进行求导:g'(x) = 1 / (x * ln(a))根据导数的定义,如果两条函数曲线上某一点处的斜率相等,则这两条函数是共线的。
设存在一个正实数 b,使得 f'(b) = g'(b)。
将 f'(x) 和 g'(x) 的表达式代入,得到以下方程:a^b * ln(a) = 1 / (b * ln(a))通过移项和分式求解,我们可以得到 b 的解的范围。
ln(a^b) = 1 / (b * ln(a))ln(a^b) = ln(a)^(-b)将等式两边都取指数,得到以下方程:a^b = a^(-b)根据指数函数的性质,上述方程成立的条件是 b = 0 或 b = 1。
当 b = 0 时,线段 A 和线段 B 的起点和终点相同,即 A(0, f(0)) 和 B(1, g(0))。
此时,线段 A 和线段 B 重合,因此平行。
当 b = 1 时,线段 A 和线段 B 的起点和终点分别是 A(0, f(1))和 B(1, g(1))。
