概率论与数理统计试题AB两卷及答案

合集下载

概率论与数理统计期末考试试题及参考答案

概率论与数理统计期末考试试题及参考答案一、选择题（每题2分，共20分）1. 设A、B为两个事件，且P(A) = 0.5，P(B) = 0.6，则P(A∪B)等于（）A. 0.1B. 0.3C. 0.5D. 0.7参考答案：D2. 设随机变量X的分布函数为F(x)，若F(x)是严格单调增加的，则X的数学期望（）A. 存在且大于0B. 存在且小于0C. 存在且等于0D. 不存在参考答案：A3. 设X～N(0,1)，以下哪个结论是正确的（）A. P(X<0) = 0.5B. P(X>0) = 0.5C. P(X=0) = 0.5D. P(X≠0) = 0.5参考答案：A4. 在伯努利试验中，每次试验成功的概率为p，失败的概率为1-p，则连续n次试验成功的概率为（）A. p^nB. (1-p)^nC. npD. n(1-p)参考答案：A5. 设随机变量X～B(n,p)，则X的二阶矩E(X^2)等于（）A. np(1-p)B. npC. np^2D. n^2p^2参考答案：A二、填空题（每题3分，共15分）1. 设随机变量X～N(μ,σ^2)，则X的数学期望E(X) = _______。

参考答案：μ2. 若随机变量X、Y相互独立，且X～N(0,1)，Y～N(0,1)，则X+Y的概率密度函数f(x) = _______。

参考答案：f(x) = (1/√(2πσ^2))exp(-x^2/(2σ^2))3. 设随机变量X、Y相互独立，且X～B(n,p)，Y～B(m,p)，则X+Y～_______。

参考答案：B(n+m,p)4. 设随机变量X、Y的协方差Cov(X,Y) = 0，则X、Y的相关系数ρ = _______。

参考答案：ρ = 05. 设随机变量X～χ^2(n)，则X的期望E(X) = _______，方差Var(X) = _______。

参考答案：E(X) = n，Var(X) = 2n三、计算题（每题10分，共40分）1. 设随机变量X、Y相互独立，且X～N(0,1)，Y～N(0,1)，求X+Y的概率密度函数f(x)。

概率论与数理统计期末考试试题(答案)

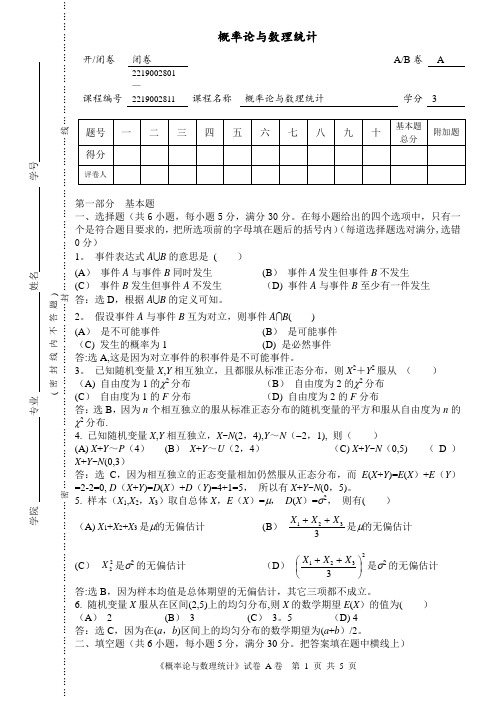
概率论与数理统计开/闭卷闭卷A/B 卷 A课程编号 2219002801—2219002811课程名称概率论与数理统计学分 3基本题6小题，每小题5分，满分30分。

在每小题给出的四个选项中，只有一把所选项前的字母填在题后的括号内）（每道选择题选对满分,选错分）。

事件表达式A B 的意思是 ( ））事件A 与事件B 同时发生 (B ）事件A 发生但事件B 不发生）事件B 发生但事件A 不发生（D) 事件A 与事件B 至少有一件发生D ，根据A B 的定义可知。

假设事件A 与事件B 互为对立，则事件A B ( )）是不可能事件 (B ）是可能事件 C) 发生的概率为1 (D) 是必然事件 :选A,这是因为对立事件的积事件是不可能事件。

已知随机变量X ,Y 相互独立，且都服从标准正态分布，则X 2＋Y 2服从（） A) 自由度为1的χ2分布（B ）自由度为2的χ2分布）自由度为1的F 分布（D) 自由度为2的F 分布选B ，因为n 个相互独立的服从标准正态分布的随机变量的平方和服从自由度为n 的2分布.已知随机变量X ,Y 相互独立，X ~N (2，4),Y ～N （-2，1), 则（） X +Y ～P （4） (B ） X +Y ～U （2，4）（C) X +Y ~N （0,5) （D ） +Y ~N (0,3）C ，因为相互独立的正态变量相加仍然服从正态分布，而E (X +Y )=E (X ）+E （Y ）D （X +Y )=D (X ）+D （Y )=4+1=5，所以有X +Y ~N (0，5)。

样本（X 1,X 2，X 3）取自总体X ，E （X ）=μ， D (X ）=σ2，则有( ） A) X 1+X 2+X 3是μ的无偏估计(B ）1233X X X ++是μ的无偏估计） 22X 是σ2的无偏估计（D ） 21233X X X ++⎛⎫ ⎪⎝⎭是σ2的无偏估计:选B ，因为样本均值是总体期望的无偏估计，其它三项都不成立。

概率论与数理统计试题AB两卷及答案

概率论与数理统计试题考试时间：120分钟试卷总分100分一、填空题（满分15分）1.已知3.0)(=B P ,7.0)(=⋃B A P ,且A 与B 相互独立，则=)(A P 。

2.设随机变量X 服从参数为λ的泊松分布，且31}0{==X P ，则=λ 。

3.设),2(~2σN X ,且2.0}42{=<<X P ，则=<}0{X P4.已知DX=2，DY=1，且X 和Y 相互独立，则D(X-2Y)＝5.设2S 是从)1,0(N 中抽取容量为16的样本方差，则=)(2S D 二、选择题（满分15分）1.已知事件A ，B 满足)()(B A P AB P =，且4.0)(=A P ，则=)(B P 。

（A ）0.4，（B ）0.5，（C ）0.6，（D ）0.7 2.有γ个球，随机地放在n 个盒子中（γ≤n），则某指定的γ个盒子中各有一球的概率为。

（A ）γγn!（B ）γγnC rn!（C ）nn γ!(D) nnn C γγ!3.设随机变量X 的概率密度为||)(x ce x f -=，则c ＝。

（A ）－21 （B ）0 （C ）21（D ）14.掷一颗骰子600次，求“一点” 出现次数的均值为。

（A ）50 （B ）100 （C ）120 （D ）1505.设总体X 在),(ρμρμ+-上服从均匀分布，则参数μ的矩估计量为。

（A ）x1 （B ）∑=-n i i X n 111 （C ）∑=-ni i X n 1211 （D ）x 三、计算题（满分60分）1.某商店拥有某产品共计12件，其中4件次品，已经售出2件，现从剩下的10件产品中任取一件，求这件是正品的概率。

2.设某种电子元件的寿命服从正态分布N （40，100），随机地取5个元件，求恰有两个元件寿命小于50的概率。

（8413.0)1(=Φ，9772.0)2(=Φ）3.在区间（0，1）中随机地取两个数，求事件“两数之和小于56”的概率。

概率论与数理统计试题与答案完整版

概率论与数理统计试题与答案HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】概率论与数理统计试题与答案(2012-2013-1)概率统计模拟题一一、填空题（本题满分18分，每题3分）1、设,3.0)(,7.0)(=-=B A P A P 则)(AB P = 。

2、设随机变量p)B(3,~Y p),B(2,~X ，若95)1(=≥X p ，则=≥)1(Y p 。

3、设X 与Y 相互独立，1,2==DY DX ，则=+-)543(Y X D 。

4、设随机变量X 的方差为2，则根据契比雪夫不等式有≤≥}2EX -X {P 。

5、设)X ,,X ,(X n 21 为来自总体)10(2χ的样本，则统计量∑==n1i i X Y 服从分布。

6、设正态总体),(2σμN ，2σ未知，则μ的置信度为α-1的置信区间的长度=L 。

（按下侧分位数）二、选择题（本题满分15分，每题3分）1、若A 与自身独立，则（）(A)0)(=A P ； (B) 1)(=A P ；(C) 1)(0<<A P ； (D) 0)(=A P 或1)(=A P2、下列数列中，是概率分布的是（）(A) 4,3,2,1,0,15)(==x xx p ； (B) 3,2,1,0,65)(2=-=x x x p (C) 6,5,4,3,41)(==x x p ； (D) 5,4,3,2,1,251)(=+=x x x p 3、设),(~p n B X ，则有（）(A) np X E 2)12(=- (B) )1(4)12(p np X D -=-(C) 14)12(+=+np X E (D) 1)1(4)12(+-=+p np X D4、设随机变量),(~2σμN X ，则随着σ的增大，概率()σμ<-X P （）。

(A)单调增大 (B)单调减小 (C)保持不变 (D)增减不定5、设),,,(21n X X X 是来自总体),(~2σμN X 的一个样本，X 与2S 分别为样本均值与样本方差，则下列结果错误．．的是（）。

概率论与数理统计答案完整版

概率论与数理统计答案 Company number：【0089WT-8898YT-W8CCB-BUUT-202108】习题答案第1章三、解答题1．设P (AB ) = 0，则下列说法哪些是正确的 (1) A 和B 不相容； (2) A 和B 相容； (3) AB 是不可能事件； (4) AB 不一定是不可能事件； (5) P (A ) = 0或P (B ) = 0 (6) P (A – B ) = P (A ) 解：(4) (6)正确.2．设A ，B 是两事件，且P (A ) = ，P (B ) = ，问： (1) 在什么条件下P (AB )取到最大值，最大值是多少 (2) 在什么条件下P (AB )取到最小值，最小值是多少解：因为)()()()(B A P B P A P AB P -+≤，又因为)()(B A P B P ≤即.0)()(≤-B A P B P 所以(1) 当)()(B A P B P =时P (AB )取到最大值，最大值是)()(A P AB P ==.(2) 1)(=B A P 时P (AB )取到最小值，最小值是P (AB )=+=. 3．已知事件A ，B 满足)()(B A P AB P =，记P (A ) = p ，试求P (B )．解：因为)()(B A P AB P =，即)()()(1)(1)()(AB P B P A P B A P B A P AB P +--=-== ，所以 .1)(1)(p A P B P -=-=4．已知P (A ) = ，P (A – B ) = ，试求)(AB P ．解：因为P (A – B ) = ，所以P (A )– P(AB ) = , P(AB ) = P (A )– , 又因为P (A ) = ，所以P(AB ) =– =，6.0)(1)(=-=AB P AB P .5．从5双不同的鞋子种任取4只，问这4只鞋子中至少有两只配成一双的概率是多少解：显然总取法有410C n=种，以下求至少有两只配成一双的取法k ：法一：分两种情况考虑：15C k=24C 212)(C +25C 其中：2122415)(C C C 为恰有1双配对的方法数法二：分两种情况考虑：!2161815C C C k ⋅⋅=+25C其中：!2161815C C C ⋅⋅为恰有1双配对的方法数法三：分两种情况考虑：)(142815C C C k-=+25C其中：)(142815C C C -为恰有1双配对的方法数法四：先满足有1双配对再除去重复部分：2815C C k=-25C法五：考虑对立事件：410C k=-45C 412)(C其中：45C 412)(C 为没有一双配对的方法数法六：考虑对立事件：!4141618110410C C C C C k ⋅⋅⋅-=其中：!4141618110C C C C ⋅⋅⋅为没有一双配对的方法数所求概率为.2113410==C k p6．在房间里有10个人，分别佩戴从1号到10号的纪念章，任取3人记录其纪念章的号码．求： (1) 求最小号码为5的概率； (2) 求最大号码为5的概率．解：(1) 法一：12131025==C C p ，法二：1213102513==A A C p (2) 法二：20131024==C C p ，法二：2013102413==A A C p 7．将3个球随机地放入4个杯子中去，求杯子中球的最大个数分别为1，2，3的概率．解：设M 1, M 2, M 3表示杯子中球的最大个数分别为1，2，3的事件，则834)(3341==A M P , 1694)(324232=⨯=A C M P , 1614)(3143==C M P8．设5个产品中有3个合格品，2个不合格品，从中不返回地任取2个，求取出的2个中全是合格品，仅有一个合格品和没有合格品的概率各为多少解：设M 2, M 1, M 0分别事件表示取出的2个球全是合格品，仅有一个合格品和没有合格品，则3.0)(25232==C C M P ,6.0)(2512131==C C C M P ,1.0)(25221==C C M P 9．口袋中有5个白球，3个黑球，从中任取两个，求取到的两个球颜色相同的概率．解：设M 1=“取到两个球颜色相同”，M 1=“取到两个球均为白球”，M 2=“取到两个球均为黑球”，则φ==2121M M M M M 且.所以.2813C C C C )()()()(282328252121=+=+==M P M P M M P M P10．若在区间(0，1)内任取两个数，求事件“两数之和小于6/5”的概率．解：这是一个几何概型问题．以x 和y 表示任取两个数，在平面上建立xOy 直角坐标系，如图. 任取两个数的所有结果构成样本空间 = {(x ，y )：0 x ，y 1} 事件A =“两数之和小于6/5”= {(x ，y ) ： x + y 6/5} 因此2517154211)(2=⎪⎭⎫ ⎝⎛⨯-=Ω=的面积的面积A A P ．图11．随机地向半圆220x ax y -<<（a 为常数）内掷一点，点落在半圆内任何区域的概率与区域的面积成正比，求原点和该点的连线与x 轴的夹角小于4π的概率．解：这是一个几何概型问题．以x 和y 表示随机地向半圆内掷一点的坐标，表示原点和该点的连线与x 轴的夹角，在平面上建立xOy 直角坐标系，如图.随机地向半圆内掷一点的所有结果构成样本空间 ={(x ，y )：220,20x ax y a x -<<<<}事件A =“原点和该点的连线与x 轴的夹角小于4π” ={(x ，y )：40,20,202πθ<<-<<<<x ax y a x }因此211214121)(222+=+=Ω=πππa aa A A P 的面积的面积．12．已知21)(,31)(,41)(===B A P A B P A P ，求)(B A P ．解：,1213141)()()(=⨯==A B P A P AB P ,6121121)|()()(=÷==B A P AB P B P 13．设10件产品中有4件不合格品，从中任取两件，已知所取两件产品中有一件是不合格品，则另一件也是不合格品的概率是多少解：题中要求的“已知所取两件产品中有一件是不合格品，则另一件也是不合格品的概率”应理解为求“已知所取两件产品中至少有一件是不合格品，则两件均为不合格品的概率”。

(完整版)概率论与数理统计试题及答案.doc

2008－ 2009 学年第1学期概率论与数理统计(46 学时 ) A一、单项选择题（本大题共 5 小题，每小题 3 分，共 15 分）。

1、 A、 B 为两个随机事件，若P( AB)0 ，则（ A） A、 B 一定是互不相容的；（B）AB一定是不可能事件；（C） AB 不一定是不可能事件；（D）P( A)0或 P(B)0 .Y 0 1 22、二维离散型随机变量( X ,Y)的分布律为X1 1/6 1/3 02 1/4 1/6 1/12F ( x, y) 为 ( X ,Y) 的联合分布函数，则F (1.5,1.5)等于（A）1/6 ；（B）1/2 ；（C）1/3 ；（ D）1/4.3、 X、 Y 是两个随机变量，下列结果正确的是（A）若E( XY)EXEY ,则X、Y独立；（B）若 X、Y 不独立 , 则 X、Y 一定相关；（C）若 X、Y 相关, 则 X、Y 一定不独立；（D）若D(X Y) DX DY ,则X、Y独立.4、总体 X ~ N ( , 2 ), , 2均未知， X 1, X 2 ,L , X n 为来自 X 的一个简单样本，X 为样本均值， S 2 为样本方差。

若的置信度为 0.98的置信区间为 (X c S n , X c S n ) ，则常数 c 为（ A ）t 0.01 (n 1) ；（） 0.01 (n) ；B t（ C ）t0.02(n 1) ；（）(n) .D t 0.025、随机变量 X 1, X 2 ,L , X n 独立且都服从 N (2,4)__1 n分布，则 XX i 服从n i1（A ） N (0,1) ；（B ） N (2,4 n) ；（C ） N (2 n, 4n) ；（D ） N(2, 4) .n二、填空题（本大题共 5 小题，每小题 3 分，共 15 分）。

6、已知 A 、 B 为两个随机事件，若 P( A) 0.6, P( AB) 0.1,则 P( A | AB) =1.7、已知随机变量 X 服从区间 (0, 2) 上的均匀分布，则 E(2X) =（）.8、已知连续型随机变量 X 的概率密度函数为 f (x)2 x,0 x 1，则概率 P(| X | 1 2) =0,其它（） .9、随机变量 X : b(3, 1 ), Y : b(3, 2 ) ,且 X ,Y 独立，则 D(X Y) =（） .3310 、已知随机变量 X i , i 1,2,3 相互独立，且都服从 N(0,9)分布，若随机变量Y a( X 12X 22 X 32) :2(3) ，则常数 a =（）.三、解答题（本大题共 6 小题，每小题 10 分，共 60 分）。

概率论与数理统计问题及答案AB卷

概率论与数理统计问题及答案AB卷一、选择题1. 事件A和事件B是互斥事件，它们的概率分别为P(A) = 0.3和P(B) = 0.4，求事件“A或B”的概率P(A∪B)。

答案：根据概率的加法公式，事件"A或B"的概率等于事件A的概率加上事件B的概率减去它们的交集的概率。

因为事件A和事件B是互斥事件，所以它们的交集概率为0。

因此，P(A∪B) =P(A) + P(B) - P(A∩B) = P(A) + P(B) = 0.3 + 0.4 = 0.7。

2. 一批产品中有10%的次品，现从中随机抽取3个进行检测，求恰好有1个次品的概率。

答案：这是一个二项分布问题。

设p为单个产品为次品的概率，则单个产品为良品的概率为1-p。

根据二项分布的公式，恰好有1个次品的概率为C(3, 1) * p * (1-p)^2。

代入p=0.1，可计算得出恰好有1个次品的概率。

3. 某城市一年的降水量服从正态分布，平均降水量为800毫米，标准差为50毫米。

则该城市一年降水量在700毫米到900毫米之间的概率是多少？答案：根据正态分布的性质，平均降水量加减1个标准差的范围内约有68%的概率，加减2个标准差的范围内约有95%的概率，加减3个标准差的范围内约有99.7%的概率。

所以，一年降水量在700毫米到900毫米之间的概率为95%。

二、计算题1. 设A、B、C为三个事件，已知P(A) = 0.3，P(B) = 0.5，P(C) = 0.4，且P(A∩B∩C) = 0.1，求以下概率：a) P(A∪B)b) P(A'∩B)c) P(A∪B∪C')答案：a) 根据概率的加法公式，P(A∪B) = P(A) + P(B) - P(A∩B)。

代入已知概率可计算得出P(A∪B)。

b) 求A的补集A'，即事件A不发生的概率。

然后求A'∩B的概率，即事件A不发生且事件B发生的概率。

根据事件的互斥性，可推出P(A'∩B) = P(B) - P(A∩B)。

概率论与数理统计试题及答案 (2)

一.选择题（18分，每题3分）1. 如果 1)()(>+B P A P ，则事件A 与B 必定（）)(A 独立； )(B 不独立； )(C 相容； )(D 不相容.2. 已知人的血型为 O 、A 、B 、AB 的概率分别是0.4； 0.3；0.2；0.1。

现任选4人，则4人血型全不相同的概率为：（）)(A 0.0024； )(B 40024.0； )(C 0. 24； )(D 224.0.3. 设~),(Y X ⎩⎨⎧<+=.,0,1,/1),(22他其y x y x f π 则X 与Y 为（）)(A 独立同分布的随机变量； )(B 独立不同分布的随机变量；)(C 不独立同分布的随机变量；)(D 不独立也不同分布的随机变量. 4. 某人射击直到中靶为止,已知每次射击中靶的概率为0.75. 则射击次数的数学期望与方差分别为（）)(A 4934与； )(B 16934与； )(C 4941与； (D) 9434与．5. 设321,,X X X 是取自N (,)μ1的样本，以下μ的四个估计量中最有效的是（）)(A 32112110351ˆX X X ++=μ； )(B 3212949231ˆX X X ++=μ； )(C 3213216131ˆX X X ++=μ； )(D 32141254131ˆX X X ++=μ． 6. 检验假设222201:10,:10H H σσ≤>时，取统计量)(~10)(22212n Xini χμχ-=∑=，其拒域为（1.0=α）（）)(A )(21.02n χχ≤；)(B )(21.02n χχ≥；)(C )(205.02n χχ≤；)(D )(205.02n χχ≥.二. 填空题（15分，每题3分）1. 已知事件A ，B 有概率4.0)(=A P ，5.0)(=B P ，条件概率3.0)|(=A B P ，则=⋃)(B A P ．2. 设随机变量X 的分布律为⎪⎪⎭⎫⎝⎛-+c b a 4.01.02.04321，则常数c b a ,,应满足的条件为 .3. 已知二维随机变量),(Y X 的联合分布函数为),(y x F ，试用),(y x F 表示概率=>>),(b Y a X P .4. 设随机变量)2,2(~-U X ，Y 表示作独立重复m 次试验中事件)0(>X 发生的次数，则=)(Y E ，=)(Y D . 5．设),,,(21n X X X 是从正态总体),(~2σμN X 中抽取的样本，则概率 =≤-≤∑=)76.1)(37.0(222012012σσX XP ii .5. 设n X X X ,,,21 为正态总体),(2σμN （2σ未知）的一个样本，则μ的置信度为1α－的单侧置信区间的下限为 . 三. 计算题（54分，每题9分）1．自动包装机把白色和淡黄色的乒乓球混装入盒子，每盒装12只，已知每盒内装有的白球的个数是等可能的。

概率论与数理统计试题试卷及答案AB卷

概率论与数理统计（A ）姓名：学年学期：学号：考试时间：班级：u 0.975=1.96，u 0.95=1.645t 0.995(18)=2.88， t 0.975(5)=2.57，t 0.975(4)=2.776, t 0.975(12)=2.1788F 0.95(2,37)=3.28，F 0.995(9,9)=6.54, F 0.95(1,4)=7.71, F 0.95(2,12)=3.89, F 0.99(2,12)=6.93一、选择题（从下列各题四个备选答案中选出正确答案，并将其代号写在答题纸相应位置处。

答案错选或未选者，该题不得分。

每小题3分，共15分。

） 1.设â是未知参数a 的无偏估计量，且D(â)>0,则[ ](A) â2不是a 2的无偏估计量；(B) â2是a 2的无偏估计量;(B) â2不一定是a 2的无偏估计量；(D) â2不是a 2的估计量.2. 设X~N(μ,σ2), μ,σ2为未知参数，X 1, X 2,…, X n 是来自X 的样本，则作μ的估计时，下列统计量中（）是最有效的.(A)3X -2X 1；(B)X ; (C)X 1；(D) n X X X )6/1()3/2()2/1(21-+3. 设X~N(μ,σ2), X 1, X 2,…, X n 是来自X 的样本，则σ2的极大似然估计量是（）4.. 设X~N(μ,σ2), X 1, X 2,…, X n 是来自X 的样本，X 为样本均值，记则下列统计量中( )服从t(n-1)分布.5.假设检验中，显著性水平α表示 ( )(A)P(接受H 0|H 0为假)；(B) P(拒绝H 0|H 0为真);(C)P(拒绝H 0|H 0为假)；(D) 无具体含义.二、填空题（将下列各题的一个或多个正确答案写在答题纸相应位置处。

答案写错的，该题不得分。

每小题3分，共15分。

《概率论与数理统计》练习题及答案

《概率论与数理统计》练习题一、单项选择题1. A 、B 为两事件，则B A ⋃=（）A ．B A ⋃ B ．A ∪BC ．A BD ．A ∩B 2.对任意的事件A 、B ，有（）A ．0)(=AB P ，则AB 不可能事件 B ．1)(=⋃B A P ，则B A ⋃为必然事件C ．)()()(B P A P B A P -=-D ．)()()(AB P A P B A P -=⋂ 3.事件A 、B 互不相容，则（）A ．1)(=⋃B A P B ．1)(=⋂B A PC ．)()()(B P A P AB P =D ．)(1)(AB P A P -= 4．设A 为随机事件，则下列命题中错误．．的是（） A ．A 与A 互为对立事件 B ．A 与A 互不相容 C ．Ω=⋃A AD ．A A =5.任意抛一个均匀的骰子两次，则这两次出现的点数之和为8的概率为（） A ．363 B ．364 C ．365 D ．3626.已知A 、B 、C 两两独立，21)()()(===C P B P A P ，51)(=ABC P ，则)(C AB P 等于（）A ．401 B ．201 C ．101 D ．417.事件A 、B 互为对立事件等价于（）（1）A 、B 互不相容（2）A 、B 相互独立（3）Ω=⋃B A （4）A 、B 构成对样本空间的一个剖分 8.A 、B 为两个事件，则)(B A P -=（）A ．)()(B P A P - B ．)()(AB P A P -C ．)()(B P A P -D ．)(A B P - 9.1A 、2A 、3A 为三个事件，则（）A ．若321,,A A A 相互独立，则321,,A A A 两两独立；B ．若321,,A A A 两两独立，则321,,A A A 相互独立；C ．若)()()()(321321A P A P A P A A A P =，则321,,A A A 相互独立；D ．若1A 与2A 独立，2A 与3A 独立，则1A 与3A 独立10．设A 与B 相互独立，2.0)(=A P ，4.0)(=B P ，则=)(B A P （） A ．0.2B ．0.4C ．0.6D ．0.811．同时抛掷3枚均匀的硬币，则恰好三枚均为正面朝上的概率为（） A.0.125 B.0.25 C.0.375 D.0.5 12．设A 、B 为任意两个事件，则有（）A.（A ∪B ）-B=AB.(A-B)∪B=AC.(A ∪B)-B ⊂AD.(A-B)∪B ⊂A 13．设A ，B 为两个互不相容事件，则下列各式错误．．的是（） A ．P （AB ）=0B ．P （A ∪B ）=P （A ）+P （B ）C ．P （AB ）=P （A ）P （B ）D ．P （B-A ）=P （B ）14．设事件A ，B 相互独立，且P （A ）=31，P （B ）>0，则P （A|B ）=（）A ．151B ．51C ．154D ．3115．设事件A 与B 互不相容，且P (A )>0，P (B ) >0，则有（） A ．P (AB )=lB ．P (A )=1-P (B )C ．P (AB )=P (A )P (B )D ．P (A ∪B )=116．设A 、B 相互独立，且P (A )>0，P (B )>0，则下列等式成立的是（） A ．P (AB )=0 B ．P (A -B )=P (A )P (B ) C ．P (A )+P (B )=1D ．P (A |B )=017．同时抛掷3枚均匀的硬币，则恰好有两枚正面朝上的概率为（） A ．0.125 B ．0.25C ．0.375D ．0.5018．某射手向一目标射击两次，A i 表示事件“第i 次射击命中目标”，i =1，2，B 表示事件“仅第一次射击命中目标”，则B =（）A ．A 1A 2B ．21A AC ．21A AD ．21A A19．某人每次射击命中目标的概率为p (0<p <1)，他向目标连续射击，则第一次未中第二次命中的概率为（）A ．p 2B ．(1-p )2C ．1-2pD ．p (1-p )20．已知P (A )=0.4，P (B )=0.5，且A ⊂B ，则P (A |B )=（）A ．0B ．0.4C ．0.8D ．121．一批产品中有5%不合格品，而合格品中一等品占60%，从这批产品中任取一件，则该件产品是一等品的概率为（）A ．0.20B ．0.30C ．0.38D ．0.5722．X 的密度为⎩⎨⎧∈=其它,0],0[,2)(A x x x f ，则A=（）A ．41 B ．21 C ．1 D ．223．离散型随机变量X 的分布列为其分布函数为)(x F ,则=)3(F ( ) A ． 0 B ．3.0 C ．8.0 D ．1 24．随机变量X 的密度函数⎩⎨⎧∈=其它]1,0[)(4x cx x f 则常数c =（）A ．51 B ．41 C ．4 D ．525．离散型随机变量X 的分布列为其分布函数为)(x F ，则=)1(F ( ) A ．4.0 B ．2.0 C ．6.0 D ．126．设随机变量X 服从参数为3的指数分布，其分布函数记为)(x F ，则=)31(F （）A ．e31 B ．3eC ．11--eD ．1311--e27．设随机变量X 的概率密度为⎩⎨⎧≤≤=,,0,10,)(3其他x ax x f 则常数=a （）A ．41 B ．31C ．3D ．428．设随机变量X 与Y 独立同分布，它们取-1，1两个值的概率分别为41，43，则{}=-=1XY P （）C ．41 D ．8329．设三维随机变量),(Y X 的分布函数为),(y x F ，则=∞+),(x F （） A ．0 B ．)(x F X C ．)(y F YD ．130．设随机变量X 和Y 相互独立，且)4,3(~N X ，)9,2(~N Y ，则~3Y X Z -=（） A ．)21,7(N B ．)27,7(N C ．)45,7(ND ．)45,11(N31．设随机变量X 的概率密度为f(x)=⎪⎩⎪⎨⎧≤<-≤<.,0;2x 1,x 2;1x 0,x 其它则P{0.2<X<1.2}的值是（）A ．5.0B ．6.0C ．66.0D ．7.032．某人射击三次，其命中率为0.7，则三次中至多击中一次的概率为（） A.027.0 B.081.0 C.0.189 D.0.21633．设二维随机变量(X,Y)的联合分布函数为F(x,y). 其联合概率分布为（）则F （0,1）=( )A.2.0B.6.0C.7.0D.0.834．设二维随机变量（X ，Y ）的联合概率密度为f(x,y)=⎩⎨⎧≤≤≤≤+.,0;1y 0,2x 0),y x (k 其它则k=（）A.41 B.31C.21 D.3235．设随机变量X 在[-1，2]上服从均匀分布，则随机变量X 的概率密度f （x ）为（）A ．⎪⎩⎪⎨⎧≤≤-=.,0;21,31)(其他x x fB ．⎩⎨⎧≤≤-=.,0;21,3)(其他x x fC ．⎩⎨⎧≤≤-=.,0;21,1)(其他x x fD ． ⎪⎩⎪⎨⎧≤≤--=.,0;21,31)(其他x x f36．设随机变量X ~ B ⎪⎭⎫ ⎝⎛31,3，则P{X ≥1}=（）C ．2719D ．272637．设二维随机变量（X ，Y ）的分布律为Y X1231 2101 103102 101102 101则P{XY=2}=（） A ．51 B ．103 C ．21D ．5338．设二维随机变量（X ，Y ）的概率密度为 ⎩⎨⎧≤≤≤≤=,,0;10,10,4),(其他y x xy y x f则当0≤y ≤1时，（X ，Y ）关于Y 的边缘概率密度为f Y （ y ）= （） A ．x 21 B ．2x C ．y21D ．2y39．设函数f (x )在[a ，b ]上等于sin x ，在此区间外等于零，若f (x )可以作为某连续型随机变量的概率密度，则区间[a ，b ]应为（）A ．[0,2π-] B ．[2π,0] C ．]π,0[D ．[23π,0]40．设随机变量X 的概率密度为f (x )=⎪⎩⎪⎨⎧≤<-≤<其它21210x xx x ，则P (0.2<X<1.2)=（） A ．0.5 B ．0.6 C ．0.66 D ．0.741．设在三次独立重复试验中，事件A 出现的概率都相等，若已知A 至少出现一次的概率为19／27，则事件A 在一次试验中出现的概率为（）A ．61 B ．41 C ．31D ．2142．设随机变量X ，Y 相互独立，其联合分布为则有（） A ．92,91==βα B ．91,92==βα C ．32,31==βαD ．31,32==βα43．设随机变量X 的分布律为X 0 1 2 P0.3 0.2 0.5则P {X <1}=（）A ．0B ．0.2C ．0.3D ．0.544．下列函数中可作为某随机变量的概率密度的是（）A ．⎪⎩⎪⎨⎧≤>100,0,100,1002x x x B ．⎪⎩⎪⎨⎧≤>0,0,0,10x x xC ．⎩⎨⎧≤≤-其他,0,20,1xD ．⎪⎩⎪⎨⎧≤≤其他,0,232121x ，45.随机变量X 服从二项分布)2.0,10(B ，则（） A ．==DX EX 2 B ．==DX EX 6.1C ．=EX 2，=DX 6.1D ．=EX 6.1，=DX 246.X 可取无穷多个值 ,2,1,0，其概率分布为普阿松分布)3(P ，则（） A ．DX EX ==3 B ．DX EX ==31 C ．EX =3，DX =31 D ．EX =31，DX =9147.随机向量),(Y X 有25,36==DY DX ,协方差12=XYσ，则)()(=-Y X DA ．1B ．37C ．61D ．8548.设X~B(10, 31), 则=)X (E )X (D （）A.31 B.32 C.1D.31049．已知随机变量X 的分布函数为F(x)=⎩⎨⎧>--.;0x e 1x2其它则X 的均值和方差分别为（）A.E(X)=2, D(X)=4B.E(X)=4, D(x)=2C.E(X)=41,D(X)=21D.E(X)=21, D(X)=4150．设随机变量X 的E （X ）=μ,D(X)=2σ，用切比雪夫不等式估计≥σ≤-)3|)X (E X (|P （） A.91 B.31C.98D.151．设二维随机变量（X ，Y ）的分布律为Y X 010 131 3131则E （XY ）=（） A ．91- B ．0 C ．91D ．3152．已知随机变量X 服从参数为2的泊松分布，则随机变量X 的方差为（） A ．-2 B ．0 C ．21 D ．253．设n μ是n 次独立重复试验中事件A 出现的次数，P 是事件A 在每次试验中发生的概率，则对于任意的0>ε，均有}|{|lim εμ>-∞→p nP n n （）A ．=0B ．=1C ．> 0D ．不存在54．设随机变量X 与Y 相互独立，X 服从参数为2的指数分布，Y ～B (6，21)，则E(X-Y)=（）A ．25- B ．21C ．2D ．555．设二维随机变量(X ，Y )的协方差Cov(X ，Y )=61，且D (X )=4，D (Y )=9，则X 与Y 的相关系数XY ρ为（）A ．2161B ．361C ．61 D ．156.设总体X 服从),(2σμN ，n X X X ,,21为其样本，则SX n Y )(μ-=服从（）)(.)1(.)1,0(.)1(.2n t D n t C N B n x A --57.设总体X 服从),(2σμN ，,,21X X …n X ,为其样本，则∑=-=n i iXY 122)(1μσ服从（）)(.)1(.)(.)1(.22n t D n t C n x B n x A --58．设总体X 的分布律为{}p X P ==1，{}p X P -==10，其中10<<p .设n X X X ,,,21 为来自总体的样本，则样本均值X 的标准差为（）A ．np p )1(- B ．np p )1(-C ．)1(p np -D ．)1(p np -59．设随机变量)1,0(~,)1,0(~N Y N X ，且X 与Y 相互独立，则~22YX +（）A ．)2,0(NB ．)2(2χC ．)2(tD ．)1,1(F60.记F 1-α(m,n)为自由度m 与n 的F 分布的1-α分位数，则有（） A.)n ,m (F 1)m ,n (F 1α-α=B.)n ,m (F 1)m ,n (F 11α-α-=C.)n ,m (F 1)m ,n (F αα=D.)m ,n (F 1)m ,n (F 1α-α=61．设x 1, x 2, …, x 100为来自总体X ~ N （0，42）的一个样本，以x 表示样本均值，则x ~（） A ．N （0，16） B ．N （0，0.16） C ．N （0，0.04）D ．N （0，1.6）62．设总体X ～N (2,σμ)，X 1，X 2，…，X 10为来自总体X 的样本，X 为样本均值，则X ～（）A ．)10(2σμ，N B ．)(2σμ，NC ．)10(2σμ，N D ．)10(2σμ，N63．设X 1，X 2，…，X n 为来自总体X 的样本，X 为样本均值，则样本方差S 2=（） A ．∑=-ni iX X n12)(1B ．∑=--ni iX X n 12)(11C ．∑=-ni iX X n12)(1D ．∑=--ni iX X n 12)(1164．设总体n X X X N X ,,,),,(~212 σμ为来自总体X 的样本，2,σμ均未知，则2σ的无偏估计是（）A ．∑=--ni iX X n 12)(11B ．∑=--ni iX n 12)(11μC ．∑=-ni iX X n12)(1D ．∑=-+ni iX n 12)(11μ65．设总体X ~ N （2,σμ），其中μ未知，x 1，x 2，x 3，x 4为来自总体X 的一个样本，则以下关于μ的四个估计：)(41ˆ43211x x x x +++=μ，3212515151ˆx x x ++=μ，2136261ˆx x +=μ，1471ˆx =μ中，哪一个是无偏估计？（）A ．1ˆμB ．2ˆμC ．3ˆμD ．4ˆμ 66.总体X 服从)(λP ，其中0>λ为未知参数,n X X X ,,21为样本,则下面说法错误的是( ) A ．X 是E X 的无偏估计量 B ．X 是DX 的无偏估计量 C ．X 是EX 的矩估计量 D ．X 是2λ的无偏估计量 67．矩估计必然是（）(1)无偏估计 (2)总体矩的函数 (3)样本矩的函数 (4)极大似然估计 68．设θˆ是未知参数θ的一个估计量，若θθ=)ˆ(E ，则θˆ是θ的（） A ．极大似然估计 B ．矩估计 C ．无偏估计 D ．有偏估计二、填空题1. A 、B 为两事件，8.0)(=⋃B A P ，2.0)(=A P ，4.0)(=B P ，则=-)(A B P 。

概率论与数理统计试题试卷及答案AB卷

答案错选或未选者，该题不得分。

每小题3分，共15分。

答案写错的，该题不得分。

每小题3分，共15分。

概率论与数理统计期末考试试题及参考答案(最终)

概率论与数理统计复习题〔一〕一. 选择题：1、假设两个事件 A 和B 同时呈现的概率P(AB)= 0, 那么以下结论正确的选项是( ).(A) A 和B 互不相容.(C) AB 未必是不成能事件. 解此题答案应选(C).2x, x [0, c], (B) AB 是不成能事件.(D) P(A )=0 或P(B)=0.2、设f ( x) 如果c=( ), 那么f (x) 是某一随机变量的概率0, x [0, c].密度函数.1 1 3(A) . (B) . (C) 1. (D) .3 2 2c解由概率密度函数的性质 f ( x)dx 1可得 2 xdx 1, 于是c 1,故本题应选(C ).3、设X ~ N (0,1), 又常数c 满足P{ X≥c} P{ X c} , 那么c 等于( ).1(A) 1. (B) 0. (C) . (D) - 1.2解因为P{ X≥c} P{ X c} , 所以1 P{ X c} P{ X c} ,即2P{ X c} 1 , 从而P{ X c} ,即(c) , 得c=0. 因此此题应选(B).4、设X 与Y 彼此独立，且都从命N(, 2 ) , 那么有( ).(A) E( X Y) E(X ) E(Y) .(C) D( X Y)D(X) D (Y) .(B) E( X Y) 2 .(D) D(X Y) 2 2 .解注意到E(X Y) E(X)E(Y ) 0.由于X 与Y 彼此独立,所以D( X Y)D(X) D(Y) 2 2 . 选(D).25、设总体X 的均值μ与方差σ都存在但未知, 而X , X ,L , X 为来自X 的样1 2 n本, 那么均值μ与方差σ2 的矩估计量别离是() . 1nn(A) X 和S2. (B) X 和(D) X 和2(X ) .ii 1n1(C) μ和σ2. 解选(D).2( X i X ) . n i 1二、在三个箱子中, 第一箱装有4个黑球, 1个白球; 第二箱装有3个黑球, 3 个白球; 第三箱装有 3 个黑球, 5 个白球. 现任取一箱, 再从该箱中任取一球。