构建三层BP网络 神经网络控制课件(第三版)
BP神经网络Simulink模型设计 神经网络控制课件(第三版)

第一个值没完全显示
第一个值完全显示
隐层阈值 10
BP神经网络Simulink模型设计
Simulink模型仿真
分别点击 网络输出层结构
11
BP神经网络Simulink模型设计
Simulink模型仿真
第一个值没完全显示
第一个值完全显示
输出层权值 12
BP神经网络Simulink模型设计
Simulink模型仿真
例 2-11-2MS BP神经网络 Simulink模型设计
1
BP神经网络Simulink模型设计
应用函数 Gensim( ) : 将例2-5-3M BP网络生成Simulink模型的网络
2
BP神经网络Simulink模型设计
Matlab程序:ms2b2.m
3
BP神经网络Simulink模型设计
输出层阈值 13
BP神经网络Simulink模型设计
思考与练习
画出设计的BP网络的结构
14
结束
15
Simulink模型仿真
点击
6
BP神经网络Simulink模型设计
Simulink模型仿真
点击
网络隐层结构
7
BP神经网络Simulink模型设计
Simulink模型仿真
分别点击
8
BP神经网络Simulink模型设计
Simulink模型仿真
隐层权值 9
BP神经网络Simulink模型设计
Simulink模型仿真
构建三层BP网络 神经网络控制课件(第三版)

结束
16
3 网络仿真函数:
a=sim(net,p)
或
y=sim(net,u)
8
构建三层BP网络
构建:BPNN2,3,1
9
构建三层BP网络
Matlab程序: m251a.m
10
构建三层BP网络
m251a.m某次执行结果
Command Window:
w1= 1.6158 -0.0302 -0.9155 0.7994 0.6102 0.8982
Command Window:
见数据
w1 b1 w2 b2 u y= 1.1982
-0.2372
14
构建三层BP网络
思考与练习
1. m252a、b程序中,隐层、输出层各用了什么作用函数? 为何说是“某次”执行结果?
2. 由m252a、b程序及执行结果的数据,画出网络结构图。 3. 编写构建N2,5,1结构的BP网络程序,执行程序,检验结果的正确性。
构建的BP神经网络权值、阈值均为随机数。
7
构建三层BP网络
2 设置权值、阈值函数为常值及随机数函数:
常值
net.iw{1,1}
net.b{1}
net.lm{2,1}
net.b{2}
随机数 w=net.inputweights{1,1}.initFcn=‘rands’ ?
b=net.biases{1} .initFcn=‘rands’
b1 =-3.1573 -1.5408 -0.1257
w2 = -0.0871 -0.9630 0.6428 b2 = -0.1106 u =1
2 y= 1.2684
11
构建三层BP网络
构建:BPNN3,4,2
BP神经网络bp设计PPT课件

--误差反传(BP)算法的改进 与BP网络设计
3.4 基于BP算法的多层前馈网络模型
三层BP网络
o1 W1○
…
ok Wk○
…
ol
输出层
Wl
○
…
y1○ V1
y2○
…
○ yj
○ym
Vm
隐层
○
x1
○
x2
…
○
xi
…
○
xn-1
○
xn
输入层
数学表达
模型的数学表达
输入向量: X=(x1,x2,…,xi,…,xn)T 隐层输出向量: Y=(y1,y2,…,yj,…,ym)T
利用算法使得权值在更新的过程中,‘走’合适的路径,
比如跳出平坦区来提高收敛速度,跳出局部最小点等等
如何操作?
需要在进入平坦区或局部最小点时进行一些判断,通过
改变某些参数来使得权值的调整更为合理。
标准的BP算法内在的缺陷:
⑴ 易形成局部极小而得不到全局最优; ⑵ 训练次数多使得学习效率低,收敛速度慢; ⑶ 隐节点的选取缺乏理论指导; ⑷ 训练时学习新样本有遗忘旧样本的趋势。
输出层与隐层之间的连接权值调整
E w jk w jk
j=0,1,2,…,m; k=1,2,…,l (3.4.9a)
隐层和输入层之间的连接权值调整
E vij vij
i=0,1,2,…,n; j=1,2,…,m
(3.4.9b)
式中负号表示梯度下降,常数η∈(0,1)表示比例系数,反映了 训练速率。可以看出BP算法属于δ学习规则类,这类算法常被 称为误差的梯度下降(Gradient Descent)算法。
3 BP神经网络
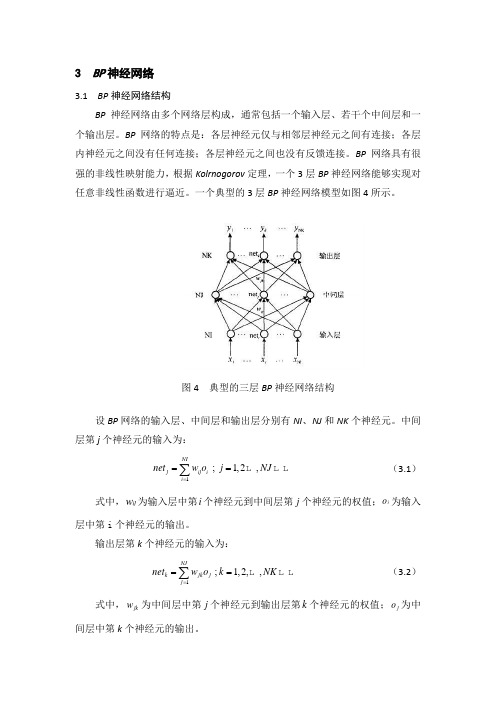
3 BP 神经网络3.1 BP 神经网络结构BP 神经网络由多个网络层构成,通常包括一个输入层、若干个中间层和一个输出层。
BP 网络的特点是:各层神经元仅与相邻层神经元之间有连接;各层内神经元之间没有任何连接;各层神经元之间也没有反馈连接。
BP 网络具有很强的非线性映射能力,根据Kolrnogorov 定理,一个3层BP 神经网络能够实现对任意非线性函数进行逼近。
一个典型的3层BP 神经网络模型如图4所示。
图4 典型的三层BP 神经网络结构设BP 网络的输入层、中间层和输出层分别有NI 、NJ 和NK 个神经元。
中间层第j 个神经元的输入为:1;1,2,NIj ij i i net w o j NJ ===∑ (3.1)式中,ij w 为输入层中第i 个神经元到中间层第j 个神经元的权值;i o 为输入层中第i 个神经元的输出。
输出层第k 个神经元的输入为:1;1,2,,NJk jk j j net w o k NK ===∑ (3.2)式中,jk w 为中间层中第j 个神经元到输出层第k 个神经元的权值;j o 为中间层中第k 个神经元的输出。
输入层、中间层和输出层的输出分别为:i i i o net x ==(3.3)()1(,)1j j j j j j net o f net eθ--==+(3.4) ()1(,)1k k k k k k k net y o f net e θθ--===+(3.5)式中j θ和k θ分别为中间层第j 个神经元和输出层第k 个神经元的阈值。
BP 网络的训练采用基于梯度法的δ学习律,其目标是使网络输出与训练样本的均方误差最小。
设训练样本为P 个,其中输入向量为12,,,p x x x ;输出向量为12,,,p y y y ;相应的教师值(样本)向量为12,,,p t t t 。
则第P 个样本的均方误差为:211()2NK ppp k k k E t y ==-∑(3.6)式中,p k t 和p k y 分别为第k 个输出神经元第p 个样本的教师值和实际输出值。
BP神经网络详解和实例ppt课件

• 图1飞蠓的触角长和翼长
• 思路:作一直线将两类飞蠓分开
• 例如;取A=(1.44,2.10)和 B=(1.10,1.16), 过A B两点作一条直线:
•
y= 1.47x - 0.017
• 其中X表示触角长;y表示翼长.
• 分类规则:设一个蚊子的数据为(x, y) • 如果y≥1.47x - 0.017,则判断蚊子属Apf类; • 如果y<1.47x - 0.017;则判断蚊子属Af类.
算法的目的:根据实际的输入与输出数据,计算模型的参 数(权系数) 1.简单网络的B-P算法
图6 简单网络
• 假设有P个训练样本,即有P个输入输出对 • (Ip, Tp),p=1,…,P, 其中
输入向量为 :
I p (i p1 ,...,i pm )T
目标输出向量为(实际上的):
Tp (t p1 ,...,t pn )T
神经网络研究的两个方面
• 从生理上、解剖学上进行研究 • 从工程技术上、算法上进行研究
脑神经信息活动的特征
(1)巨量并行性。 (2)信息处理和存储单元结合在一起。 (3)自组织自学习功能。
神经网络基本模型
电脉冲
输 入
树 突
细胞体 形成 轴突
突
输
触
出
信息处理
传输
图 12.2 生物神经元功能模型
• 神经元的数学模型
cqk
… … c1 Wp1
W1j cj Wpj
W1q cq
输出层LC
W11 Wi1
Wij
Wiq Wpq W
… b1 Vn1
Vh1 V11
V1i bi Vhi
… Vni
V1p bp Vhp Vnp
BP神经网络PPTppt课件

B .非 线 性 斜 面 函 数 (R am p F unction):
b
f
net
k
net
b
net net net
b 0为 常 数 , 称 饱 和 值 , 是 该 神 经 单 元 的 最 大 输 出 ;
输出函数值限制在 b,b范围内。
可编辑课件PPT
13
C(.2符) 号输出函函数数f
k 1,..., c
隐含层单元 可表达更为复杂的非线性函数
激活函数 不一定为符号函数 常要求激活函数是连续可微的
输出层与隐含层的激活函数可以不同,并且输出层
各单元的激活函数可有所区别
可编辑课件PPT
26
2 多层网络的表达能力
按照Kolmogorov定理,任何一个判决均可用 前式所示的三层神经网络实现。
理
解
为
函
数
逼
近
回 归
状
态
预
测
可 应 用 到 众 多 领 域 ,如 :
优化计算;信号处理;智能控制;
模式识别;机器视觉;等等。
可编辑课件PPT
18
主要内容
• 人工神经网络基本知识 二. 前馈神经网络、多层感知器、及非线性分类
三. BP神经网络 四. 数据处理及神经网络结 构的选择 五. 应用
可编辑课件PPT
将可能的无线域变换到指定的有限范围输出。
单 调 增 函 数 , 通 常 为 "非 线 性 函 数 "
网 络 输 入
net W
x
n
ixi
i 1
--神 经 元 的 输 入 兴 奋 总 量 是 多 个 输 入 的 代 数 和
其
中
智能控制(第三版)chap9-神经网络控制
第9章 神经网络控制
9.1 概述
神经网络是一种具有高度非线性的连续时间动力 系统,它有着很强的自学习功能和对非线性系统的强 大映射能力,已广泛应用于复杂对象的控制中。
神经网络的硬件实现愈趋方便。大规模集成电路 技术的发展为神经网络的硬件实现提供了技术手段。
2
神经网络控制所取得的进展为: (1) 基于神经网络的系统辨识:可在已知常规模型结构 的情况下,估计模型的参数;或利用神经网络的非线 性特性,建立非线性系统的静态、动态、逆动态及预 测模型;
图9-2(a) 神经网络直接逆控制 14
(2)神经网络间接自校正控制:使用常规控制器, 神经网络估计器需要较高的建模精度。假设控制对象: y(t) = f(yt) + g(yt)u(t),其结构如图9-3所示。
图9-3 神经网络间接自校正控制
15
假设被控对象为如下单变量仿射非线性系统:
y(t)fytgytu(t)
第9章 神经网络控制
9.1 概述 9.2 神经网络控制结构 9.3 单神经元网络控制 9.4 RBF网络监督控制 9.5 RBF网络自校正控制 9.6 基于RBF网络直接模型参考自适应控制 9.7 一种简单的RBF网络自适应控制
9.8 基于不确定逼近的RBF网络自适应控制 9.9 基于模型整体逼近的机器人RBF网络自适应控制 9.10 神经网络数字控制
11
9.2.3 神经网络自适应控制
①与传统自适应控制相同,神经网络自适应控制也分 为神经网络自校正控制和神经网络模型参考自适应 控制两种。
②自校正控制根据系统正向或逆向模型的结果来调节 控制器内部参数,使系统满足给定的指标。
③而在模型参考自适应控制中,闭环控制系统的期望 性能由一个稳定的参考模型来描述。
神经网络理论基础 神经网络控制课件(第三版)
神经网络理论基础
人脑
人的思维由脑完成
人脑约由10^11~10^12个神经元组成,每个神经 元约与10^4~10^5个神经元连接,能接受并处理 信息。因此,人脑是复杂的信息并行加工处理 巨系统。
人脑
可通过自组织、自学习,不断适应外界环境的 变化。其自组织、自学习性来源于神经网络结 构的可塑性,主要反映在神经元之间连接强度 的可变性上。
基础
神经网络理论基础
• 引言
• 生物神经元与人工神经元模型 • 感知器 • 线性神经网络 • 多层前馈网络与BP学习算法 • 径向基函数神经网络 • 小脑模型神经网络 • PID神经网络 • 局部递归型神经网络 • 连续型Hopfield网络 • 应用Simulink设计神经网络 • 应用GUI设计网络 • 小结
静态与动态网络 2. 按连接方式分:前馈型与反馈型 3.按逼近特性分:全局逼近型与局部逼近型 4.按学习方式分:有导师的学习;无导师的学习;
再励学习三种 从总的方面讲,一般将神经网络分为: 前馈、反馈、 介绍模拟生物神经元的人工神经元模型 2. 阐述控制中常用的前馈型与反馈型网络的理论
人工神经网络
人工神经网络 是从微观结构与功能上模拟人脑神经系统而建 立的一类模型,是模拟人的智能的一条途径。
人工神经网络 信息处理由人工神经元间的相互作用来实现, 由连接权来传递,具有学习能力、自适应性、 联接强度的可变性。
神经网络的分类
神经网络的不同分类: 1. 按性能分:连续型与离散型;确定型与随机型;
BP神经网络模型PPT课件
激活函数: f()
误差函数:e
1 2
q o1
(do (k )
yoo (k ))2
BP网络的标准学习算法
第一步,网络初始化 给各连接权值分别赋一个区间(-1,1) 内的随机数,设定误差函数e,给定计 算精度值 和最大学习次数M。
第二步,随机选取第 k个输入样本及对应 期望输出
修正各单元权 值
误差的反向传播
BP网络的标准学习算法-学习过程
正向传播:
输入样本---输入层---各隐层---输出层
判断是否转入反向传播阶段:
若输出层的实际输出与期望的输出(教师信号)不 符
误差反传
误差以某种形式在各层表示----修正各层单元 的权值
网络输出的误差减少到可接受的程度 进行到预先设定的学习次数为止
x(k) x1(k), x2(k), , xn(k)
do (k) d1(k),d2(k), ,dq(k)
BP网络的标准学习算法
第三步,计算隐含层各神经元的输入和
输出
n
hih (k ) wih xi (k ) bh
i 1
h 1, 2, , p
hoh (k) f(hih (k)) h 1, 2, , p
f(
yio (k)))2)
hoh (k)
hoh (k)
hih (k)
( 1 2
q
((do (k)
o1
p
f(
h1
whohoh (k)
bo )2 ))
hoh (k)
hoh (k)
hih (k)
q o1
(do (k )
神经网络BP网络课堂PPT
输出量为0到1之间的连续量,它可实现从输入 6 到输出的任意的非线性映射
.
2.1 BP网络简介
BP网络主要用于下述方面 函数逼近:用输入矢量和相应的输出矢量训练一个 网络逼近一个函数 模式识别和分类:用一个特定的输出矢量将它与输 入矢量联系起来;把输入矢量以所定义的合适方式 进行分类; 数据压缩:减少输出矢量维数以便于传输或存储
利用梯度下降法求权值变化及误差的反向传播
– 输出层的权值变化
• 其中 • 同理可得
16
.
2.3 学习规则
利用梯度下降法求权值变化及误差的反向传播
– 隐含层权值变化
• 其中
• 同理可得
17
.
2.3 学习规则
对于f1为对数S型激活函数,
对于f2为线性激活函数
18 .
2.4 误差反向传播图形解释
之间的误差修改其权值,使Am与期望的Tm,(m=l,…,q) 尽可能接近
12
.
2.3 学习规则
BP算法是由两部分组成,信息的正向传递与误差 的反向传播
– 正向传播过程中,输入信息从输入层经隐含层逐层计 算传向输出层,每一层神经元的状态只影响下一层神 经元的状态
– 如果在输出层未得到期望的输出,则计算输出层的误 差变化值,然后转向反向传播,通过网络将误差信号 沿原来的连接通路反传回来修改各层神经元的权值直 至达到期望目标
38
.
4.2 附加动量法
带有附加动量因子的权值调节公式
其中k为训练次数,mc为动量因子,一般取0.95左右
附加动量法的实质是将最后一次权值变化的影响,通 过一个动量因子来传递。
当动量因子取值为零时,权值变化仅根据梯度下降法产生
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7
构建三层BP网络
2 设置权值、阈值函数为常值及随机数函数:
常值
net.iw{1,1}
net.b{1}
net.lm{2,1}
net.b{2}
随机数 w=net.inputweights{1,1}.initFcn=‘rands’ ?
b=net.biases{1} .initFcn=‘rands’
15
结束
16
3 网络仿真函数:
a=sim(net,p)
或
y=sim(net,u)
8
构建三层BP网络
构建:BPNN2,3,1
9
构建三层BP网络
Matlab程序: m251a.m
10
构建三层BP网络
m251a.m某次执行结果
Command Window:
w1= 1.6158 -0.0302 -0.9155 0.7994 0.6102 0.8982
例 2-5-1M
构建 三层BP网络
1
构建 三层BP网络
用Matlab函数 构建三层BP网络
2
BP网络神经元
结构 与 模型
3
三层BP网络
结构 与 模型
输入层
隐层
输出层
典 Matlab 型 用结
p iw1,1
R 1 S1 R
1
n1
+
S11
a1 S21
1
lw 2,1
S2 S1
n2
+
S21
a2 S21
Command Window:
见数据
w1 b1 w2 b2 u y= 1.1982
-0.2372
14
构建三层BP网络
思考与练习
1. m252a、b程序中,隐层、输出层各用了什么作用函数? 为何说是“某次”执行结果?
2. 由m252a、b程序及执行结果的数据,画出网络结构图。 3. 编写构建N2,5,1结构的BP网络程序,执行程序,检验结果的正确性。
b1 =-3.1573 -1.5408 -0.1257
w2 = -0.0871 -0.9630 0.6428 b2 = -0.1106 u =1
2 y= 1.2684
11
构建三层ห้องสมุดไป่ตู้P网络
构建:BPNN3,4,2
12
构建三层BP网络
Matlab程序: m251b.m
13
构建三层BP网络
m251b.m某次执行结果
符构
b1
b2
R
S21
S21
号一
例
书用符号 u
M用符号
p
对应
xo o
n1 a1
xy
n2 a2
n m1s m 1W
2W
θ1
θ2
R S1 S2 iw1,1(IW1,1) lw2,1(LW2,1) b1 b2
6
构建三层BP网络
1 构建函数:
new (a,fb,fc,d)
()中,为构建需的四个条件: a. R2 维矩阵, 由R维输入样本的最大最小值组成; b. 二 、 三层节点个数; c. 各层节点作用函数; d. 训练用函数,若BP算法为:Traingd。
