小学五年级数学思维训练解方程
小学五年级数学思维训练 解方程

小学五年级数学思维训练解方程(一)【例1】解方程:(1)x+63= 100 (2)x-127=2.7 (3)9x=6.3 (4)x÷5=120【巩固】解方程:(1)x-7.4=8 (2)3+x=18 (3)0.4x=2.4 (4)x÷5=0.016【例2】解方程:(1)x+3x=664 (2)4x-x=72 (3)x+7x-4x+x=(15-5)×4 【拓展】解方程:(1)3x+5-2x=13 (2)5x-8x+6x-10x=15【3】解方程:(1)8x-15=3x+5 (2)15x+3=28+14x (3)3x-3=2x+2【巩固】解方程:(1)12x-4=7x+6 (2)15x+5=8x+40 (3)0.1x+0.75=3-0.125x【拓展】解方程:(1)x+3x+5+2x+1=840 (2)5x-8+6x=10x+15(3)11x+42-2x=100-9x-22 (4)8x-3+2x+1=7x+6-5x【例4】解方程:(1)4x+48=6x-8 (2)46-5x=x-6+4【拓展】解方程:(1)2x+35-3x=15x-39 (2)0.4x-0.08+1.5=0.7x-0.38【课后练习】1、解方程:(1)x-0.52=1.3 (2)x+2.7=14.2(3)0.5x=3.9 (4)x÷2.5=42、解方程:(1)x+3x=160 (2)4x-x=249 (3)3x-2x+x=(11-3)×43、解方程:(1)3.4x-1.02=0.2x+16.9 (2)2x+5=25-8x4、解方程:(1)x+3x+14=134 (2)x+3x+2+3+2=1275、解方程:(1)1.5x+0.5=2.5x-0.5 (2)6x-59=10x-756、解方程:(1)60x-40=(60+20)×(x-5)(2)32x+32×0.5-25x+64x=24x+496-49x第二讲解方程(二)【知识梳理】1、解方程的依据:(1)方程等号的两边同时加上或减去同一个数,方程仍然成立;(2)方程等式两边同时乘以或除以一个不为零的数,方程等式成立。
小学五年级数学思维训练--解方程

小学五年级数学思维训练解方程(一)【例1】解方程:(1)x+63= 100 (2)x-127=2.7 (3)9x=6.3 (4)x÷5=120【巩固】解方程:(1)x-7.4=8 (2)3+x=18 (3)0.4x=2.4 (4)x÷5=0.016【例2】解方程:(1)x+3x=664 (2)4x-x=72 (3)x+7x-4x+x=(15-5)×4【拓展】解方程:(1)3x+5-2x=13 (2)5x-8x+6x-10x=15【3】解方程:(1)8x-15=3x+5 (2)15x+3=28+14x (3)3x-3=2x+2【巩固】解方程:(1)12x-4=7x+6 (2)15x+5=8x+40 (3)0.1x+0.75=3-0.125x【拓展】解方程:(1)x+3x+5+2x+1=840 (2)5x-8+6x=10x+15(3)11x+42-2x=100-9x-22 (4)8x-3+2x+1=7x+6-5x【例4】解方程:(1)4x+48=6x-8 (2)46-5x=x-6+4【拓展】解方程:(1)2x+35-3x=15x-39 (2)0.4x-0.08+1.5=0.7x-0.38【课后练习】1、解方程:(1)x-0.52=1.3 (2)x+2.7=14.2(3)0.5x=3.9 (4)x÷2.5=42、解方程:(1)x+3x=160 (2)4x-x=249 (3)3x-2x+x=(11-3)×43、解方程:(1)3.4x-1.02=0.2x+16.9 (2)2x+5=25-8x4、解方程:(1)x+3x+14=134 (2)x+3x+2+3+2=1275、解方程:(1)1.5x+0.5=2.5x-0.5 (2)6x-59=10x-756、解方程:(1)60x-40=(60+20)×(x-5)(2)32x+32×0.5-25x+64x=24x+496-49x第二讲解方程(二)【知识梳理】1、解方程的依据:(1)方程等号的两边同时加上或减去同一个数,方程仍然成立;(2)方程等式两边同时乘以或除以一个不为零的数,方程等式成立。
思维拓展第三讲:解方程-数学五年级上册含参考答案

思维拓展第三讲:解方程-数学五年级上册1.解方程。
6x-4x=20.25x-3×11=42(12+x)×9=1622.解方程。
6.2x-x=8.32 3.5+0.5x=6 2.7×8-5x=133.解方程。
5(x+4.4)=612x-12+3=264.解方程。
8(x-6.2)=41.6x-0.36x=165.解方程。
x÷1.6=5 5.4x-x=8.86.解方程。
60.9 4.5−=x 3.8 1.57.4x += 2.350.6x ÷=7.解方程。
3x -7=62 3(x +2.1)=10.58.解方程。
3 6.820.2x −= 1.4 2.6120x x += ()126 4.5x −×=9.解方程。
5x +6x =24.22.5x +4=16 4x -8×7=4010.解方程。
5.18.6x +=2411.5x ÷= 8 1.347.6x −×=11.解方程。
2.510x +=3 1.5 3.6x −=12.解方程。
2 1.6516x−×=2438310x÷=x x+=0.3215 17.列式计算。
18.列综合算式并计算。
一个数的4倍比1.7多0.1,这个数是多少?19.列式计算。
一个数的2.5倍比12.7少5.2,这个数是多少?参考答案:1.x=10.1;x=15;x=6【分析】(1)先计算方程的左边,把原方程化为2x=20.2,再根据等式的性质,在方程两边同时除以2即可;(2)先计算方程的左边,把原方程化为5x-33=42,再根据等式的性质,在方程两边同时加上33,再同时除以5即可;(3)根据等式的性质,先在方程两边同时除以9,再同时减去12即可。
【详解】6x-4x=20.2解:2x=20.22x÷2=20.2÷2x=10.15x-3×11=42解:5x-33=425x-33+33=42+335x=755x÷5=75÷5x=15(12+x)×9=162解:(12+x)×9÷9=162÷912+x=1812+x-12=18-12x=62.x=1.6;x=5;x=1.72【分析】根据等式的性质解方程。
五年级数学思维训练《列方程解图形题》专题训练
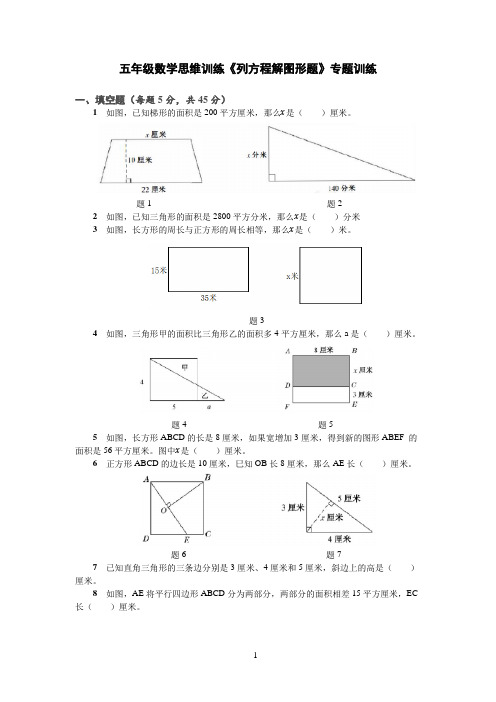
五年级数学思维训练《列方程解图形题》专题训练一、填空题(每题5分,共45分)1如图,已知梯形的面积是200平方厘米,那么x是()厘米。
题1 题22如图,已知三角形的面积是2800平方分米,那么x是()分米3如图,长方形的周长与正方形的周长相等,那么x是()米。
题34如图,三角形甲的面积比三角形乙的面积多4平方厘米,那么a是()厘米。
题4 题55如图,长方形ABCD的长是8厘米,如果宽增加3厘米,得到新的图形ABEF 的面积是56平方厘米。
图中x是()厘米。
6正方形ABCD的边长是10厘米,巳知OB长8厘米,那么AE长()厘米。
题6 题77已知直角三角形的三条边分别是3厘米、4厘米和5厘米,斜边上的高是()厘米。
8如图,AE将平行四边形ABCD分为两部分,两部分的面积相差15平方厘米,EC 长()厘米。
题8 题99如图,两个正方形的面积分别为20平方米和12平方米,两阴影部分的面积分别为a和b(a>b),如图所示,则a-b=( )平方米。
二、解答题(笫10题15分,笫ll~13题20分,共75分)10平行四边形ABCD的周长为75厘米,以CD为底时,高是16厘米,以BC为底时,高是14厘米,则平行四边形的面积是多少平方厘米?11在长方形ABCD中,放入6个形状、大小相同的小长方形(如图),每个小长方形的长和宽分别是多少厘米?12如图,用8块相同的长方形地砖拼成一个矩形,则每个长方形地砖的面积是多少平方厘米?13四个相同的长方形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是144平方厘米,小正方形的面积是4平方厘米,若用x,y表示长方形的长和宽,则x和y 分别是多少厘米?三、选做题(每题15分,共30分)14 把四张形状大小完全相同的小长方形卡片(如图1),分两种不同形式不重叠地放在一个底面长为m,宽为n的长方形盒子底面(如图2、图3),盒子底面未被卡片覆盖的部分用阴影表示。
(1)求图2中阴影部分图形的周长。
五年级数学思维列方程解应用题

例1 今年李老师年龄是王东的2倍,李老师10年前的年龄和王东8年后的年龄相等,今年李老师和王东各是多少岁?解:设今年王东的年龄为x岁,李老师的年龄为2x岁,可列方程2x-10=x+82x-x=10+8x=182x=36答:李老师今年36岁,王东今年18岁。
例2 今年姐姐的年龄比弟弟年龄的3倍多1岁,弟弟5年后年龄比3年前姐姐的年龄大1岁,姐弟俩现在各多少岁?解:设弟弟今年x岁,那么姐姐今年(3x+1)岁,可列方程x+5=3x+1-3+1x+5=3x-16=2xx=33x+1=3×3+1=10答:姐姐今年10岁,弟弟今年3岁。
例3 小学学生乘汽车去春游,如果每辆车上从45人,那么有30人没有座位;如果每辆车上多坐5人,那么可以多出1辆汽车,问原计划准备多少辆汽车?学校共有学生多少人?解:设原计划准备x辆汽车,可列方程45x+30=(45+5) (x-1)45x+30=50x-5080=5xx=16学生有45×16+30=750(人)或50×(16-1)=750(人)答:原计划准备16辆汽车,学校共有学生750人。
例4 小明用一根绳子测量井有多深,他把绳子三折后垂入井底,井外余4米,把绳子四折后垂入井底,井外余1米,那么,井深和绳长各是多少米?解:设井深x米。
可列方程3(x+4)=4(x+1)3x+12=4x+4x=8绳的长度是3(x+4)=3×(8+4)=36(米)答:井深8米,绳长36米。
例5 果园有桃树和杏树一共180棵,已知杏树比桃树的3倍少8棵,桃树和杏树各有多少棵?解:设桃树有x棵,那么杏树有(3x-8)棵。
可列方程x+3x-8 =1804x=188x=47杏树有3×47-8=133(棵)答:桃树有47棵,杏树有133棵。
例6 李大爷给承包的麦田施化肥,若每亩施6千克,则缺少化肥300千克;若每亩施5千克,则余下化肥200千克,那么李大爷共承包了麦田多少亩?这批化肥有多少千克?解:设麦田x亩,化肥有6x-300千克。
(完整版)小学五年级数学思维训练解方程

小学五年级数学思维训练解方程(一) 【例1】解方程:(1) x+63二 100 (2) x-127= 2.7 (3) 9x=6.3 (4) x-5=120【巩固】解方程:( 1) x-7.4=8 (2)3+x=18(3) 0.4x=2.4 (4)x -5=0.016【例2】解方程:(1) x+3x= 664 (2) 4x-x=72 (3)x+7x-4x+x= (15-5) X 4【拓展】解方程:( 1) 3x+5-2x=13 (2)5x-8x+6x-10x=15【3】解方程:(1)8x-15=3x+5(2)15x+3=28+14x(3)3x-3=2x+2【巩固】解方程:(1)12x-4=7x+6 (2)15x+5=8x+40 (3)0.1x+0.75=3-0.125x【拓展】解方程:(1) x+3x+5+2x+1=840 (2)5x-8+6x=10x+15(3)11x+42-2x=100-9x-22 (4)8x-3+2x+1=7x+6-5x 【例4】解方程:(1)4x+48=6x-8 (2)46-5x=x-6+4【【课后练习】1、解方程: ( 1) x-0.52=1.3 (2)x+2.7=14.2(3)0.5x=3.9(4)x - 2.5=421?方程:(1)x+3x=160 (2)4x-x=249 (3)3x-2x+x=(11-3) 拓X4展】解方程:(1)2x+35-3x=15x-39(2)0.4x-0.08+1.5=0.7x-0.383、解方程:(1)3.4x-1.02=0.2x+16.9(2) 2x+5=25-8x4 解方程:(1)x+3x+14=134 ⑵x+3x+2+3+2=1275 解方程:(1)1.5x+0.5= 2.5x- 0.56、解方程:(1)60x-40=(60+20) X (x-5)(2)32x+32X 0.5-25x+64x=24x+496-49X26x-59=10x-75 (第二讲解方程(二)【知识梳理】1 、解方程的依据:( 1 )方程等号的两边同时加上或减去同一个数,方程仍然成立;( 2)方程等式两边同时乘以或除以一个不为零的数,方程等式成立。
小学五年级下册数学思维训练(奥数) 《列方程解应用题(行程问题)》(含答案)

小学五年级下册数学思维训练(奥数) 《列方程解应用题(行程问题)》(含答案)列方程解应用题(行程问题)相遇是行程问题的基本类型,在相遇问题中可以用速度×时间=路程的公式求解全程。
下面我们来看几个例子。
例1:AB两地相距352千米。
甲乙两辆汽车从A、B两地相对开出。
甲车每小时行36千米,乙车每小时行44千米。
乙车因有事,在甲车开出32千米后才出发。
求出两车相遇需要多少小时?分析解答:为了求出两车相遇的时间,需要找到速度和、时间和和总路程之间的关系式。
根据已知条件,可以设相遇时间为X小时,列出方程:36+44)×x+32=352解方程得到X=4,因此两车相遇需要4小时。
练题:甲乙两地相距300千米,客车从甲地开往乙地,每小时行40千米。
1小时后,货车从乙地开往甲地,每小时行60千米。
货车出发几小时后与客车相遇?例2:甲乙两人从A、B两地相向而行,甲每分钟行52米,乙每分钟行48米。
两人走了10分钟后交叉而过,且相距64米。
甲从A地到B地需要多少分钟?分析解答:为了求出甲从A地到B地需要的时间,需要知道A、B两地的路程和甲的速度。
设A、B两地相距X米,则可以列出方程:52+48)×10-X=64解方程得到X=936,因此甲从A地到B地需要18分钟。
练题:从A地到B地,水路比公路近40千米。
上午8时,一艘轮船从A地驶向B地,3小时后一辆汽车从A地到B地,它们同时到达B地。
轮船的速度是每小时24千米,汽车的速度是每小时40千米。
求A地到B地水路、公路是多少千米?例3:XXX和XXX分别从一座桥的两端同时相向出发,往返于两端之间。
XXX每分钟走60米,XXX每分钟走75米。
经过6分钟两人第二次相遇,这座桥长多少米?分析解答:第一次相遇就是行了一个全程,第二次相遇就是行了三个全程。
设这座桥长X米,则可以列出方程:3X=(60+75)×6解方程得到X=270,因此这座桥长270米。
小学五年级数学思维训练(奥数)《巧解方程》讲解及练习题(含答案)

巧解方程专题简析:学习解方程。
首先,我们要对方程进行观察,将能够先计算的部分先计算或合并,使其化简,然后再求出x的值。
例1:解方程:6x+9x-13=17分析与解答方程左边的6x与9x可以合并为15x,因此,可以将原方程转化成15x-13=17,从而顺利地求出方程的解。
解:6x+9x-13=17,15x-13=1715x=30x= 2随堂练习:解方程7.5x-4.1x+1.8=12例2 解方程:8x-16=4x分析与解答方程胡两边都有X,运用等式的性质,我们先将方程两边同时减去4x,然后再方程两边同时加上16变为8x-4x=16.8x-16=4x解:8x-4x=164x= 16x=4随堂练习:解方程10x-7=4.5x+20.5 16-2x=6x例3 解方程:4(4x-11)=3(22-2x)分析与解答第一步先运用乘法分配律去掉括号;第二步,运用等式的性质,便未知数和已知数分别在等号的两边;第三步把等号两边的未知数与数合并;第四步求出方程的解4(4x-11)=3(22-2x)解:16x-44=66-6x 去括号16x+6x=66+44 等式的性质22x=110x=5随堂练习解方程7(2x-6)=84 15(22-x)+2=68x例4 解方程:x÷3=(2x-11) ÷5分析与解答我们先根据等式的性质,在方程的两边同时乘3和5的最小公倍数,然后再运用前面的方法进行求解。
解:x÷3×15=(2x-11)÷5×155x=3(2x-11)5x=6x-33x=33随堂练习:解方程:2x÷3=(2x-5)÷2 (3x-0.5)÷2=2x÷3拓展应用1、解方程5x+0.7x-3x=10-1.92、解方程7(2x-6)=843、解方程5(x-8)=3x4、解方程5.9x-9=4.2x+2.95、解方程9(2x-3)-2=5(2x-1)6、解方程:x÷5+0.5=x÷47、在下面的□内填入相同的数,使等式成立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学五年级数学思维训练解方程(一)【例 1】解方程:(1)x+63= 100(2)x-127=2.7(3)9x=6.3(4)x÷5=120【巩固】解方程:(1)x-7.4=8 (2)3+x=18(3)0.4x=2.4(4)x÷5=0.016【例 2】解方程:(1)x+3x =664(2)4x-x=72 (3)x+7x-4x+x=(15-5) ×4【拓展】解方程:(1)3x+5-2x=13(2)5x-8x+6x-10x=15【 3 】解方程: (1)8x-15=3x+5(2)15x+3=28+14x(3)3x-3=2x+2【巩固】解方程:(1)12x-4=7x+6 (2)15x+5=8x+40(3)0.1x+0.75=3-0.125x【拓展】解方程:(1 )x+3x+5+2x+1=840(2)5x-8+6x=10x+15(3)11x+42-2x=100-9x-22(4)8x-3+2x+1=7x+6-5x【例 4】解方程: (1)4x+48=6x-8(2)46-5x=x-6+4【拓展】解方程: (1)2x+35-3x=15x-39 (2)0.4x-0.08+1.5=0.7x-0.38【课后练习】1、解方程:(1)x-0.52=1.3(2)x+2.7=14.2(3)0.5x=3.9(4)x÷2.5=42、解方程: (1)x+3x=160 (2)4x-x=249(3)3x-2x+x=(11-3)×43、解方程:(1)3.4x-1.02=0.2x+16.9(2)2x+5=25-8x4、解方程: (1)x+3x+14=134(2)x+3x+2+3+2=1275、解方程: (1)1.5x+0.5=2.5x-0.5(2)6x-59=10x-756、解方程: (1)60x-40=(60+20)×(x-5)(2)32x+32×0.5-25x+64x=24x+496-49x第二讲解方程(二)【知识梳理】1、解方程的依据:(1)方程等号的两边同时加上或减去同一个数,方程仍然成立;(2)方程等式两边同时乘以或除以一个不为零的数,方程等式成立。
2、解方程的步骤:(1)有括号就先去掉;(2)移项:将含未知数的项移到左边,常数项移到右边;(3)合并同类项:使方程变形为单项式;(4)方程两边同时除以未知数的系数得未知数的值。
【例题精讲】【例 1】解方程: 3x=(x+1200) ÷2800〖巩固〗解方程: (1)x+(3x+14)=134(2)x+(3x+5)+(2x+1)=840【例 2】解方程: (1)3(x-60)=x+20(2)2(x+6)=x+22〖巩固〗解方程:(1)2(5x-60 )=x+60 (2)4(x+2)=6x+2〖拓展〗解方程: (1)0.4 ×(x-0.2)+1.5=0.7x-0.38(2)x ÷3+(100—x) ×2=100【例 3】解方程:(1)4×( 5x-9 )=15×(x+3)(2)9(x -4)=7(4 -x)〖拓展〗解方程:(1)5(3x-7)-4=2x+(35-3x) (2)15-(4-5x)=2x+(35-3x)【例 4】解方程: 4(2x-7)-2(x-1)=3(x-1)-2〖拓展〗解方程:(2)15-(4-5x)=8(1-x)-(x-39)【例 5】解方程: x+(x+200)-1400=9800-[x+(x+200)]〖巩固〗解方程:(1)2[ (x-10 )+15]=7(x-10)+15 (2)[(x+6)+6]+[(5x+6)+6]=78【课后练习】1、解方程:(1)x+(3x+2)+3+2=127(2)x+(3x-40)-7602、解方程: (1)x-2=(104-x)+2(2)4(x-62)=x-38(3)4+6 ×(3x-2)=16x3、解方程: (1)(x+10)+(x-15)=280-x (2)x+15=3×(109-x)4、解方程:(1)5(3x-1.4)=2(6x-0.5)(2)3(x+0.9)=5(x-1.7)5 、解方程: (1)13x-4(2x+5)=17(x-2)-4(2x-1)(2)(13x+8) ÷3=5x-16、解方程: (1)x-60=2[(3561-x)+100]+1(2)(x+9)+12=2[(x-9)-12]第三讲列方程解应用题(一)【知识梳理】列方程解应用题是运用方程知识来解决的一类实际问题,有些稍复杂的应用题需要逆向思维,运用算术方法有一定困难,列方程解答就比较容易。
列方程解应用题的步聚是:(1)理解题意,找出一个适当的未知数,用字母 X 表示,把所设的未知数当做已知数来用。
(2)找出题目中的等量关系式。
这个关系应是题目中最主要的、最明显的关系式,要能尽量含有其中的已知量和未知量。
(3)根据等量关系列出方程,但尽量不用算术方法解题的思路。
(4)解方程并检验,写答语。
【例题精讲】【例 1】笔记本和练习本共99本,笔记本的本数是练习本的 4.5 倍,笔记本和练习本各有多少本?【巩固】一个书架,上层放的书是下层放的书本的数的 4 倍,上层比下层多 27 本,两层书架上各有多少本书?【例 2】两块钢块共重73千克,第一块的重量比第二块的2倍还多 4 千克,这两块钢块各重多少千克?〖巩固〗书架上、下两层共有图书 109 本,如果把新买的 15 本放入上层,那么上层的书正好是下层的 3 倍。
两层原来各有书多少本?【例 3】甲、乙两个建筑队,甲队存水泥 64 袋,乙队存水泥 114 袋,以后甲队每天运进 18 袋,乙队每天运进 8 袋。
几天后,甲队的水泥袋数是乙队的 2 倍?〖巩固〗小胖和小巧买同样的练习本 10 本和 14 本,小胖比小巧少付1.08 元,每本练习本多少元?两人各付了多少元?〖拓展〗有 9 筐重量相等的蔬菜,如果从每筐里取出 15 千克, 9 个筐里剩下蔬菜的重量等于原来 4 筐的重量。
原来每筐蔬菜重多少千克?【例 3】今年爸爸的岁数是小华的5倍,2年后是小华的4倍,小华今年多少岁?〖巩固〗有甲、乙两艘货船,甲船所载货物是乙船的 3 倍,若甲船增加货物 1200 吨,乙船增加货物900 吨,则甲船所载货物是乙船的2倍,甲船原载货物多少吨?〖拓展〗某校学生参加数学竞赛,考了两场试,第一场及格的人数比不及格的人数的 4 倍还多 2 人。
第二场及格的人数增加 2 人,这时及格的人数正好是不及格的人数的 6 倍。
这次参赛的总数有多少人?【课后练习】1、少先队员种柳树和杨树共 134 棵,杨树的棵数比柳树棵数的 3 倍还多 14 棵,两种树各有多少棵?2、父亲现年 50 岁,女儿现年 14 岁,问几年前父亲的年龄是女儿年龄的 5倍?3、妈妈去买水果,所带的钱正好能买 18 千克苹果或 25 千克的梨,已知每千克梨比每千克苹果便宜 0.7 元,妈妈一共带了多少钱?4、甲班有图书 120 本,乙班有图书 30 本,甲班给乙班多少本,甲班的图书是乙班图书的 2 倍?5、有两筐水果,甲筐的个数是乙筐的 3 倍,如果从乙筐中拿出 5 个放进甲筐,这时甲筐的个数恰好是乙筐的 5 倍,原来两筐各有多少个水果?6、某牧场有绵羊和山羊共3561 只,如果绵羊减少60 只而山羊增加100 只,那么绵羊只数比山羊的 2 倍还多 1 只。
原来两种羊各有多少只?第四讲列方程解应用题(二)【知识梳理】列方程解应用题是运用方程知识来解决的一类实际问题,有些稍复杂的应用题需要逆向思维,运用算术方法有一定困难,列方程解答就比较容易。
列方程解应用题的步骤是:(1)理解题意,找出一个适当的未知数,用字母 X 表示,把所设的未知数当做已知数来用。
(2)找出题目中的等量关系式。
这个关系应是题目中最主要的、最明显的关系式,要能尽量含有其中的已知量和未知量。
(3)根据等量关系列出方程,但尽量不用算术方法解题的思路。
(4)解方程并检验,写答语。
【例题精讲】【例 1】有一个班的同学去划船,他们算了一下,如果增加一条船,正好每条船坐 6 人;如果减少一条船,正好每条船坐9 人。
这个班共有多少学生?〖巩固〗学校规定上午8 时到校,小明去上学,如果每分钟走60 米,可提早10 分钟到校;如果每分钟走50 米,可提早8 分钟到校,求小明几时几分离家刚好 8 时到校?由家到学校的路程是多少?〖拓展〗三年级一班少先队员参加学校搬砖劳动,如果每人搬 4 块砖,还剩 7 块;如果每人搬 5 块,则少 2 块砖。
这个班少先队有几个人?要搬的砖共有多少块?【例 2】学校为新生分配宿舍。
每个房间住 3 人,则多出 23 人;每个房间住 5 人,则空出 3 个房间。
问宿舍有多少间?新生有多少人?〖拓展〗少先队员去植树,如果每人种 5 棵,还有 3 棵没人种;如果其中2 人各种4 棵,其余的人各种6 棵,这些树苗正好种完。
问有多少少先队员参加植树,一共种多少树苗?【例 3】鸡与兔共有 100 只,鸡的脚比兔的脚多80 只,问鸡与兔各多少只?〖巩固〗刘老师带了 41 名同学去北海公园划船,共租了 10 条船。
每条大船坐 6 人,每条小船坐 4 人,问大船、小船各租几条?12〖拓展〗鸡、兔共有脚140 只,若将鸡换成兔,兔换成鸡,则共有160只。
问:原有鸡、兔各几只?【例 4】现有大、小桶50 个,每个大桶装油 4 千克,每个小桶装油2 千克,而所有大桶比所有小桶共多装20 千克。
求大、小桶各有多少个?【课后练习】1、小强由家里到学校,如果每分钟走 50 米,上课就要迟到 3 分钟;如果每分钟走 60 米,就可以比上课时间提前 2 分钟到校。
小强家到学校的路程是多少米?2、鸡兔同笼共有头176 只,已知鸡脚总数比兔脚总数多214 只,求鸡、兔各有多少只?3、红英小学三年级有 3 个班共 135 人,二班比一班多 5 人,三班比二班少 7 人,三个班各有多少人?4、某运输队为商店运暖瓶500 箱,每箱6 个。
已知10 个暖瓶的运费为5.5 元,如果损坏一个,不仅该只暖瓶运费没有,而且还要赔偿成本 11.5 元,结果运完后运输队共得运费 1553.6 元。
求共损坏了多少个暖瓶?5、妈妈买回一筐苹果,按计划吃的天数算了一下,如果每天吃 4 个,要多出 48 个苹果;如果每天吃 6 个,则又少 8 个苹果。
那么妈妈买回的苹果有多少个?计划吃多少天?6、红山小学学生乘汽车到香山春游。
如果每车坐65 人,则有5 人不能乘上车;如果每车多坐 5 人,恰多余了一辆车,问一共有几辆汽车,有多少学生?。
