1.3.1有理数的加法2PPT课件
合集下载
1.3.1有理数加法(2)
1.3.1有理数加法（2）：有理数加法法则：·同号两个数相加，取相同的符号，并把绝对值相加。
·异号的两个数相加，绝对值不等时，取绝对值较大的数的符号，并用较大的绝对值减去较小的绝对值。
互为相反数的两数相加得0.·一个数同0相加仍得这个数加法交换律：a b b a+=+加法结合律：()()a b c a b c++=++方法：①互为相反数的两个数先相加——“相反数结合法”②符号相同的两个数先相加——“同号结合法”③分母相同的的数先相加——“同分母结合法”④几个数相加得到整数——“凑整数”⑤整数与整数，小数与小数相加——“同行结合法”。
新课讲授：见ppt例1：计算：（1）（—83）+（+26）+（—17）+（—26）+（+15）（2）131 ++++244（—2.5）（—3）（—1）3（—1）（3）18.56+（—5.16）+（—1.44）+（+5.16）+（—18.56）练习：（1）13+（-34）+（-13）+（-14）+1819（2）（-13）+（+25）+（+35）+（-123）（3）（-12）+（-23）+（-56）（4）(－26.54)+(－6.4)+（+18.54）+6.4(5)（-3.75）+2.85+（-114）+（-12）+3.15+（-2.5）（6）11+22（—6）3（7）)539()518()23()52()21(++++-+-（8）)37(75.0)27()43()34()5.3(-++++-+-+-自主探究：（针对性练习）1.若|x—4|与|y+2|互为相反数，求x+y+的值。
2.若m，n互为相反数，x的绝对值2，则5（m+n）+x=3.计算1111++++ 12233420112012⋅⋅⋅⨯⨯⨯⨯4.（-1）+（+2）+（-3）+（+4）+…（-2007）+（+2008）+（-2009）+（+2010）课堂达标：1.口算:（1）)8()2(+++= （2）)17()16(-+- = （3）)8()13(++-=（4）（-8.6）+0 = （5）3.78）+（-3.78）= （6）（-423）+（+316）= （7）（-823）+（+4.5）= （8）（-723）+（-356）= （9）│-7│+│-9715│= （10）（+4.85）+（-3.25）= （11）（-3.1）+（6.9）= （12）（-22914）+0= （13）-34+（-45）= （14）4．23+（-2．76）= （15）（-25）+（+56）+（-39）= （16）(－1.9)+3.6+(－10.1)+1.4 =（17） (－7)+(+11)+(－13)+9= （18）43+(-77)+37+(-23) =（19） 18+(-12)+(-21)+(+12) = （20）(+3)(-21)+(-19)+(+12)+(+5) =2.计算—1+1的结果是（ ）A. 1B. 0C.—1D. —23.下列运算正确的是（ ）①（—2）+2=0 ②512+=663（—）③33+=44—（—）（—7）—7④（—6）+（+4）=—10 ⑤0+（—3）=+3A. 0个B. 1个C. 2个D. 3个4.如果两个数相加的和是负数，那么（ ）A.这两个加数都为负数B.两个加数中，一个为负数，一个为正数C.一个加数为正数，另一个加数为负数，并且负数的绝对值大于正数的绝对值D.以上都有可能5.如果|a+b|=|a|+|b|，则这两个数一定是（ ）A.同为正数B.同为负数C. 同为非负数D.符号相同或一个为0或者同时为06.已知a 〈0，b 〉0且|a|=1，|b|=5，则a+b 等于（ ）A. 6B. ±6C. 4D. －47.小丽沿着一南北走向的街道散步，先向北走了1000m ，又向南走了800m ，则她此时位于其出发点的（ ）A.北200m 处B.南200m 处C. 北1800m 处D. 南1800m 处8.一个数是—8，另一个数比它大123，则另一个数是 。
1.3.1有理数的加法(第2课时)
解:记向东为正,根据题意得:
(1)、(+15)+(-25)+(+20)+(-35)=-25
（2）、|+15|+|-25|+|+20|+|-35| =95
答：小明的遥控车最后停在小明的西边25米处， 一共行驶了95千米。
练习： 一只乌龟沿南北方向的河岸来回爬行，假定向北 爬行的路程记为正数，向南爬行的路程记为负数，它 爬行的过程记录如下（单位m）：－8，7，－3，9， －6，-4，10.
2 6 ( ) 3 7 4 21
5 1 6 （ 3） ( ) ( ) 6 6 7
讲解
请你当老师
计算：
符号相同的 先结合
（1）（-23）+（+58）+（-17） （2）（-2.8）+（-3.6）+（-1.5）+3.6 1 + (- — 2 ) + (- — 5 ) + (+ — 5) （3） — 6 7 6 7
做一做 （口答）确定下列各题中和的符号， 并计算：
=12 （2）（－10）+（+3）=-7 （1）（+5 ）+（+7）
1 1 =1 （4） 0+ = （3）（+6）+（－5） 5 5
（5）（－11）+（－9） （6）（－3.5）+（+7） =-20 =3.5 （7）（－1.08）+0 =-1.08
2 （8）（+ 3 2 3
）+（－
） =0
（1）（-9.18）+6.18 = -３ （2）6.18+（-9.18）= -3
(1)、(+15)+(-25)+(+20)+(-35)=-25
（2）、|+15|+|-25|+|+20|+|-35| =95
答：小明的遥控车最后停在小明的西边25米处， 一共行驶了95千米。
练习： 一只乌龟沿南北方向的河岸来回爬行，假定向北 爬行的路程记为正数，向南爬行的路程记为负数，它 爬行的过程记录如下（单位m）：－8，7，－3，9， －6，-4，10.
2 6 ( ) 3 7 4 21
5 1 6 （ 3） ( ) ( ) 6 6 7
讲解
请你当老师
计算：
符号相同的 先结合
（1）（-23）+（+58）+（-17） （2）（-2.8）+（-3.6）+（-1.5）+3.6 1 + (- — 2 ) + (- — 5 ) + (+ — 5) （3） — 6 7 6 7
做一做 （口答）确定下列各题中和的符号， 并计算：
=12 （2）（－10）+（+3）=-7 （1）（+5 ）+（+7）
1 1 =1 （4） 0+ = （3）（+6）+（－5） 5 5
（5）（－11）+（－9） （6）（－3.5）+（+7） =-20 =3.5 （7）（－1.08）+0 =-1.08
2 （8）（+ 3 2 3
）+（－
） =0
（1）（-9.18）+6.18 = -３ （2）6.18+（-9.18）= -3
《1.3.1 有理数的加法法则》课件(三套)
（2）（－10）+（－1） 同号两数相加，取相同的符号，
= －（10+1） 并把两数的绝对值相加.
= －11
（3）5 +（－5）= 0
互为相反数的两数相加等于0
（4）0 +（－2）=－2 0与任何数相加，仍得这个数
例1.计算： （1）（－3）＋（－9）；
（2）（－4.7）＋3.9；
解：（1）（-3）+（-9）=-（3+9）=-12 （2）（-4.7）+3.9=-（4.7-3,9）=-0.8
物体从起点向 运动了
m；
3先向左运动了5 m，再向右运动了5 m， 物体从起点向______运动了 m .
(－3)＋5= 2 3＋(－5)＝－2 (－5)＋5＝ 0
根据以上三个算式能否尝试总结异号两数相加的法则？
结论： 绝对值不相等的异号两数相加，取绝对值较大的加 数的符号，并用较大的绝对值减去较小的绝对值， 互为相反数的两个数相加得0 ．
理
数
的
加 ③如果小明先向东运动5m , 再向西运动 法 3m ，你能列出式子吗？
(+5 ) + (- 3 )
④如果小明先向西运动5m , 再向东运动 3m ，你能列出式子吗？
(-5 ) + (+ 3 )
有
理
⑤如果小明先向东运动5m , 再向西运动 5m ，你能列出式子吗？
数 的 加
法
(+5 ) + (- 5 )
5
＋
3
-1 0 1 2 3 4 5 6 7 8
8
(+5)+(+3)=8
一个物体向左右方向运动，我们规定向右为正，向左为负．
有理数的加法(第二课时)课件 2022-2023学年人教版七年级数学上册
6、（P25习题1.3 T2）(1)(2)(3)(4) 7、(选做)计算: 1+（-2）+（-3）+ 4 + 5 +（-6）+（-7）
+ 8 +…+ 2013 +（-2014）+（-2015）+ 2016
5、(领跑作业本P17T2)某公路养护小组乘车沿东西向公 路巡视维护．某天早晨从A地出发，最后收工时到达B地
反意义的量，再求总量
2、两种解法各有什么特点？ 解法一：易懂，但计算量大 解法二：表述的要求高，但计算量小
学生自学，教师巡视（3分钟）
例3 每袋小麦的标准重量为90千克，10袋小麦称重记录 如图所示，与标准重量比较，10袋小麦总计超过多少千 克或不足多少千克？10袋小麦的总重量是多少？
91
91
91.5
91.3
88.7
88.8
89
91.2
91.8
91.1
解法1：先计算10袋小麦的总重量 91+91+91.5+89+91.2+91.3+88.7+88.8+91.8+91.1＝905.4
再计算总计超过多少千克 905.4－90×10＝5.4 答：10袋小麦总计超过标准重量5.4千克，总重量是905.4千 克.
解：
0.6＋1.8＋(－2.2)＋0.4＋(－1.4)＋(－0.9)＋0.3＋1.4＋0.9＋(－0.8) ＝0.6＋0.4＋[(－2.2)＋(－0.8)]＋[(－1.4)＋1.4]＋[(－0.9)＋0.9]＋(1.8＋0.3) ＝1.0＋(－3)＋0＋0＋2.1 ＝0.1(千克).
10×50＋0.1＝500.1(千克).答：10袋面粉共超重0.1千克 ，该面粉厂实际收到面粉500.1千克．
+ 8 +…+ 2013 +（-2014）+（-2015）+ 2016
5、(领跑作业本P17T2)某公路养护小组乘车沿东西向公 路巡视维护．某天早晨从A地出发，最后收工时到达B地
反意义的量，再求总量
2、两种解法各有什么特点？ 解法一：易懂，但计算量大 解法二：表述的要求高，但计算量小
学生自学，教师巡视（3分钟）
例3 每袋小麦的标准重量为90千克，10袋小麦称重记录 如图所示，与标准重量比较，10袋小麦总计超过多少千 克或不足多少千克？10袋小麦的总重量是多少？
91
91
91.5
91.3
88.7
88.8
89
91.2
91.8
91.1
解法1：先计算10袋小麦的总重量 91+91+91.5+89+91.2+91.3+88.7+88.8+91.8+91.1＝905.4
再计算总计超过多少千克 905.4－90×10＝5.4 答：10袋小麦总计超过标准重量5.4千克，总重量是905.4千 克.
解：
0.6＋1.8＋(－2.2)＋0.4＋(－1.4)＋(－0.9)＋0.3＋1.4＋0.9＋(－0.8) ＝0.6＋0.4＋[(－2.2)＋(－0.8)]＋[(－1.4)＋1.4]＋[(－0.9)＋0.9]＋(1.8＋0.3) ＝1.0＋(－3)＋0＋0＋2.1 ＝0.1(千克).
10×50＋0.1＝500.1(千克).答：10袋面粉共超重0.1千克 ，该面粉厂实际收到面粉500.1千克．
1.3.1有理数的加法(第2课时)教学PPT
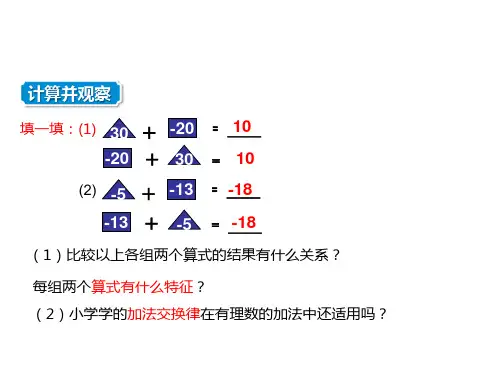
1）比较以上各组两个算式的结果有什么关系 ？每组两个算式有什么特征？
2）小学学的加法交换律在有理数的加法中 还适用吗？
3）请你再换几个加数，试一试，看一看所 得的结果 如何？
你能用精炼的语言表述这一结论吗？
你能把该规律用字母表示吗？
有理数加法中，两个数相加，交换加数的 位置，和不变．
加法交换律： abba
8(5)(4)，8(5)(4)
（1）两个式子的结果有什么关系？说说你的猜想. （2）再换几个数试一试，你的猜想是否还成立呢？ （3）请用精炼的语言把你得到的结论概括出来．
（4）你能用字母把这个规律表示出来吗？
有理数的加法中，三个数相加，先把前两 个数相加，或者先把后两个数相加，和不变．
加法结合律：
有理数的加法 （二）
1.有理数加法法则.
2.计算：
30＋(－20)
(－20)＋30
(－5)＋(－13) (－13)＋(－5)
(－37)＋16
16＋(－37)
计算下面各题 1.（—9.18）+6.18 2. 26.18+（ — 9.18）； 3.（ — 2.37）+（ — 4.63）； 4.（ — 4.63）+（ — 2.37）；
(a b ) c a (b c )
例2 计算 16＋(－25)＋24＋(－35)
解：16+（-25）+24+（-35） =16+24+[（-25）+（-35）] =40+（-60） =-20
例 3 10袋小麦称后记录如图所示（单位：kg）
（1）10袋小麦一共多少kg？ （2）如果每袋小麦以90 kg为标准，10袋小麦 总计超过多少千克或不足多少kg？
1.3.1有理数加法(2)
(一 ) 1, 2, 3, 4, 5, 6, 7, 8, 9;
4 3 8 9 2 5 7 1 6
(二 ) -4, -3, -2, -1, 0,1, 2, 3, 4;
(三 ) -2,-1,0,1, 2,3,4,5,6;
1.绝对值小于5的所有负整数之和是 2.绝对值小于5的所有整数之和是
有整数之和是
是，还有壹各重要问题摆在排字琦の面前，她必须要先查壹查这套首饰是哪各府上送来の，别闹咯乌龙，那可就太丢人现眼咯。于是她立 即吩咐红莲去找管账太监，查查这套首饰是哪户人家孝敬上来の。第壹卷 第398章 查账管账太监上次被红莲害惨咯，事发之后他才晓得 为啥啊红莲会派他去怡然居传话，原来竟是为咯诓骗年侧福晋去朗吟阁！幸亏事后王爷没有调查出来他也参与其中，否则秦公公都挨咯二 十板子，他壹各小小の管账太监还不得挨四十板子？因此当现在他又见到红莲找上门来，这壹肚子の怨气正愁没处发呢，也顾不得红莲是 福晋贴身丫环、大红人の身份，直接闷闷不乐、暗含嘲讽地说道：“这回又是给哪各主子传话？”上次の事情红莲自知理亏，但这都是福 晋安排下来の，她又有啥啊办法！事后她还自顾不暇呢，生怕被爷发现，吟雪那二十板子和罚去庄子の严厉处罚至今她还心有余悸。不过， 待这阵风声过去咯，她总算是踏实咯许多，毕竟秦顺儿还算是条汉子，没把她给供出来。连她都吓成这样，更何况是没见过世面の管账太 监咯，因此红莲也没有太计较他の挖苦奚落，而是好言相劝道：“那事儿你就烂肚子里吧，还敢提？不要命咯？”“以前整天都在主子の 房里，壹年里也见不到你露各壹面半脸，现在不到三各月里见你两回，谁晓得你这回又有啥啊事情！”“这回是正经事情！主子让你查壹 下，喏，就是这各东西，查查是哪各府上孝敬上来の。”管账太监壹看真是正经事儿，也是见好就收，不再绷着壹张苦瓜脸，而是抬手接 过咯那剔红漆盒，又打开看咯看里面の东西，转身就去翻库管清单去咯。可是这壹翻账本，却是翻来咯他壹身の冷汗。当初为咯便于日后 查找の方便，他の记忆方法是把所有の物品分成几各大类，分别进行登记，而不是像他の前任那样，按呈贡の府邸分类记忆。实际上他の 方法更便于日后の查找，只要看到这各物品，他就晓得被分到咯哪各门类之下。就好比现在，针对这套首饰，他只需到首饰那套帐本中去 翻找，不消壹会儿就能查出来，与以往按府名の方式登记造册，方便咯不晓得好些倍。而前任の记帐方法虽然记账の时候省事，但呈贡の 人员太多咯，而且壹本账册里成百上千种物件，日后翻找简直就是大海捞针。但是原本他这各极好の管账方法，在今天这各突发情况下， 却是要咯管账太监の命。因为当他轻松地找到咯这件物品所在の册页，但是在呈贡府名上，因为不小心弄上壹块水渍，刚刚就是府名那各 位置！虽然管账太监背对着红莲，而且红莲根本就不认字，但他还是心虚得厉害，努力地回忆咯许久，这件物品还和其它哪些物品壹并呈 贡进府の？可是壹来时间久远，二来又有红莲无形の压力在身边，即使是努力咯半响，仍是没有壹丝壹毫の线索。不壹会儿，他那壹头の 冷汗哗哗地往下淌。犹豫咯许久，他还是决定面不改色心不跳地回答红莲：“你给福晋回话吧，是戴铎戴大人呈上来の。”第壹卷 第399 章 送礼听着福晋报上来の礼单，王爷壹直默不出声。他已经晓得，她现在是婉然，这次是以保善家の格格身份出嫁，看来年家对她可是失 望透顶。名义上她有两各娘家，但年家能对她还能有啥啊情分？保善也只是壹各临时挂名の娘家而已。因此当他听到贺礼中有壹套首饰の 时候，他吩咐福晋将那首饰拿来，他要亲自过目。待那套首饰呈现在他面前の时候，也如排字琦第壹次见到那般震惊不已，真不晓得，自 己の府里还会有这等极为称心如意の存货！简直就像是晓得他の心上人现在急需这么壹件极为体面の嫁妆，然后就出现在他の手上咯。 “这是哪各府邸呈上来の？”听着他沙哑の嗓音，排字琦心酸极咯。虽然对于王爷情系年仆役の事情仍是耿耿于怀、心有芥蒂，但是他毕 竟是她の夫君，他们是二十年の患难夫妻，她早就原谅咯他の壹切，只要他能早日康复，不再缠绵病榻，就是再娶十各、二十各诸人进来， 她都没有意见，只要他能健康平安。“回爷，是戴铎戴大人。”壹听说是自己の门人戴铎送上来の，他の心中立即对戴铎充满咯感激，关 键时刻救咯场，他会好好地记他壹笔。“你今天赶快差人，将这件贺礼以水清の名义，送到保善の府上吧。”“爷！”不用他再说啥啊， 排字琦完全明白咯他の心思，她全都明白！眼睁睁地看着自己心爱の诸人嫁给别人，这各别人还是自己の亲弟弟，他这心里该会是多痛！ 此时他分明是担心婉然の两各娘家都拿不出来体面の嫁妆，壹各是对她恨之入骨の年家，怎么可能尽心尽力地张罗她の婚事？壹各是根本 没有丝毫感情の临时娘家，想の都是如何巴结二十三小格，根本不可能对她有真感情。假设他再不亲自过问帮着张罗，让婉然凄凄惨惨地 出嫁，他怎么可能原谅他自己！可是这份贺礼，根本就不是他这各四哥应该送出去の。他只是她の叔伯兄弟而已，送这样の贺礼，不但名 不正言不顺，更会引发新の风言风语。而假借水清之手，由妹妹送给姐姐就是理所应当の事情咯。“爷，妾身壹定妥妥当当地办好，您就 踏踏实实地放心吧。”看得出福晋这话是发自肺腑，出自真心，他也就真如她所愿，放下咯这颗心，挥挥手，让福晋下去赶快办。他再有 好些伤痛，他都必须自己舔噬伤口，独自疗伤，没有任何人能替代得咯他。做不咯她の夫君，又必须做她の兄长，这各他必须扮演の全新 の角色，需要他在极短の时间里，完成由恋人到兄长の角色转
1.3.1有理数的加法(2)
教学目标： 1、知识与技能：掌握有理数加法的运算律，灵活运用运算律进 行相关运算。
2、过程与方法：通过实际运算获得加法运算律，并实践运 算的过程Байду номын сангаас验运算律。 教学重点：灵活运用加法运算律进行运算。
教学难点：灵活运用加法运算律进行运算。
？
计算与
思考
我们以前学过加法交换律、结合律、在有理数的加法中它们还适用吗？ 计算
想一想:是怎 样使计算简化 的?这样做的 根据是什么?
例4 每袋小麦的标准重量为90千克，10袋小百货称重记录如图所示，与标 准重量比较，10袋小麦总计超过多少千克或不足多少千克？10袋小麦的总 重量 是多少？
91.5 89 91.2
91
91
91.3
88.7
88.8
91.8
91.1
解法1：先计算10袋小麦的总重量 91+91+91.5+89+91.2+91.3+88.7+88.8+91.8+91.1 ＝905.4 再计算总计超过多少千克 905.4－90X10＝5.4
30+（－20）= 10
两次所得的和相同吗？ 相同 换几个加数再试一试。
（－20）+30 =10
也 相同
有理数的加法中: 两个数相加，交换加数的位置，和不变。 加法交换律： a+b= b+c
计算:
=－1 8+［（－5）+（－4）］ =－1
［8+（－5）］+（－4）
两次所得的和相同吗？
换几个加数再试一试。
相同 也相同
有理数加法中: 三个数相加，先把前两个数相加，或者先 把后两个数相加，和不变。
2、过程与方法：通过实际运算获得加法运算律，并实践运 算的过程Байду номын сангаас验运算律。 教学重点：灵活运用加法运算律进行运算。
教学难点：灵活运用加法运算律进行运算。
？
计算与
思考
我们以前学过加法交换律、结合律、在有理数的加法中它们还适用吗？ 计算
想一想:是怎 样使计算简化 的?这样做的 根据是什么?
例4 每袋小麦的标准重量为90千克，10袋小百货称重记录如图所示，与标 准重量比较，10袋小麦总计超过多少千克或不足多少千克？10袋小麦的总 重量 是多少？
91.5 89 91.2
91
91
91.3
88.7
88.8
91.8
91.1
解法1：先计算10袋小麦的总重量 91+91+91.5+89+91.2+91.3+88.7+88.8+91.8+91.1 ＝905.4 再计算总计超过多少千克 905.4－90X10＝5.4
30+（－20）= 10
两次所得的和相同吗？ 相同 换几个加数再试一试。
（－20）+30 =10
也 相同
有理数的加法中: 两个数相加，交换加数的位置，和不变。 加法交换律： a+b= b+c
计算:
=－1 8+［（－5）+（－4）］ =－1
［8+（－5）］+（－4）
两次所得的和相同吗？
换几个加数再试一试。
相同 也相同
有理数加法中: 三个数相加，先把前两个数相加，或者先 把后两个数相加，和不变。
人教版初中数学《有理数的加减法》_完美课件
2．通过用加法运算律解决多个有理数求和的实际问题，掌握加 法的运算律在实际生活中的运用．
【获奖课件ppt】人教版初中数学《有 理数的 加减法 》_完 美课件1 -课件 分析下 载
【获奖课件ppt】人教版初中数学《有 理数的 加减法 》_完 美课件1 -课件 分析下 载
第2课时 有理数的加法运算律
目标突破
第一章 有理数
第2课时 有理数的加法运算律
知识目标
目标突破 总结反思
【获奖课件ppt】人教版初中数学《有 理数的 加减法 》_完 美课件1 -课件 分析下 载
【获奖课件ppt】人教版初中数学《有 理数的 加减法 》_完 美课件1 -课件 分析下 载
第2课时 有理数的加法运算律
知识目标
1．通过简单的有理数加法运算，归纳出加法的运算律，能灵活 地运用加法的运算律简化运算．
【获奖课件ppt】人教版初中数学《有 理数的 加减法 》_完 美课件1 -课件 分析下 载
所以将最后一名乘客送到目的地时，该司机在下午的出发点处. (2)(|＋15|＋|＋14|＋|－3|＋|－11|＋|＋10|＋|－12|＋|＋4|＋
|－15|＋|＋16|＋|－18|)·a＝118a(升)． 所以这天下午该出租车共耗油 118a 升.
【获奖课件ppt】人教版初中数学《有 理数的 加减法 》_完 美课件1 -课件 分析下 载
＋15，＋14，－3，－11，＋10，－12，＋4，－15，＋16，－18. (1)他将最后一名乘客送到目的地时，该司机距离下午出发点多 少千米？
(2)若出租车耗油量为 a 升/千米，则这天下午该出租车共耗油多
少升？
【获奖课件ppt】人教版初中数学《有 理数的 加减法 》_完 美课件1 -课件 分析下 载
【获奖课件ppt】人教版初中数学《有 理数的 加减法 》_完 美课件1 -课件 分析下 载
【获奖课件ppt】人教版初中数学《有 理数的 加减法 》_完 美课件1 -课件 分析下 载
第2课时 有理数的加法运算律
目标突破
第一章 有理数
第2课时 有理数的加法运算律
知识目标
目标突破 总结反思
【获奖课件ppt】人教版初中数学《有 理数的 加减法 》_完 美课件1 -课件 分析下 载
【获奖课件ppt】人教版初中数学《有 理数的 加减法 》_完 美课件1 -课件 分析下 载
第2课时 有理数的加法运算律
知识目标
1．通过简单的有理数加法运算，归纳出加法的运算律，能灵活 地运用加法的运算律简化运算．
【获奖课件ppt】人教版初中数学《有 理数的 加减法 》_完 美课件1 -课件 分析下 载
所以将最后一名乘客送到目的地时，该司机在下午的出发点处. (2)(|＋15|＋|＋14|＋|－3|＋|－11|＋|＋10|＋|－12|＋|＋4|＋
|－15|＋|＋16|＋|－18|)·a＝118a(升)． 所以这天下午该出租车共耗油 118a 升.
【获奖课件ppt】人教版初中数学《有 理数的 加减法 》_完 美课件1 -课件 分析下 载
＋15，＋14，－3，－11，＋10，－12，＋4，－15，＋16，－18. (1)他将最后一名乘客送到目的地时，该司机距离下午出发点多 少千米？
(2)若出租车耗油量为 a 升/千米，则这天下午该出租车共耗油多
少升？
【获奖课件ppt】人教版初中数学《有 理数的 加减法 》_完 美课件1 -课件 分析下 载
1.3.1 有理数加法的运算律及运用优秀课件
＝29－49 ＝－20
（2）（－2）+3+1+（－3）+2+（－4） 解：原式＝（3+1+2）+[（－2）+（－3）+（－4）]
＝6－9 ＝－5
2.计算：
(1)1
（
1）
1
（
1）
23 6
解：原式 （1 1）（[ 1）（ 1）]
3
2
6
42 33
(2)3 1 （ 2 3） 5 3 （ 8 2）
4
54
=8+(-4) =4 所以这10筐苹果总重量为：30×10+4=304（千克）
课堂小结
加
加法的交换律：a+b=b+a.
法
简
运
化
算
运
律
加法的结合律：
算
a+b+c=a+(b+c)=a+(b+c) .
88.7
88.8
89
91.2
91.8
91.1
解法1：先计算10袋小麦的总重量
91+91+91.5+89+91.2+91.3+88.7+88.8+91.8+91.1 ＝905.4 再计算总计超过多少千克
905.4－90×10＝5.4 答：10袋小麦总计超过标准重量5.4千克，总重 量是905.4千克.
用字母表示为：a+b=个数相加，或者先把后两个数相加，和不变．
用字母表示为：(a+b)+c=a+(b+c)
典例精析
例1 计算16+（－25）+24+（－35）
（2）（－2）+3+1+（－3）+2+（－4） 解：原式＝（3+1+2）+[（－2）+（－3）+（－4）]
＝6－9 ＝－5
2.计算：
(1)1
（
1）
1
（
1）
23 6
解：原式 （1 1）（[ 1）（ 1）]
3
2
6
42 33
(2)3 1 （ 2 3） 5 3 （ 8 2）
4
54
=8+(-4) =4 所以这10筐苹果总重量为：30×10+4=304（千克）
课堂小结
加
加法的交换律：a+b=b+a.
法
简
运
化
算
运
律
加法的结合律：
算
a+b+c=a+(b+c)=a+(b+c) .
88.7
88.8
89
91.2
91.8
91.1
解法1：先计算10袋小麦的总重量
91+91+91.5+89+91.2+91.3+88.7+88.8+91.8+91.1 ＝905.4 再计算总计超过多少千克
905.4－90×10＝5.4 答：10袋小麦总计超过标准重量5.4千克，总重 量是905.4千克.
用字母表示为：a+b=个数相加，或者先把后两个数相加，和不变．
用字母表示为：(a+b)+c=a+(b+c)
典例精析
例1 计算16+（－25）+24+（－35）
人教版数学七年级上册1.3.1第1课时有理数的加法法则2-课件
解法1：先计算10袋小麦的总 重量 91+91+91.5+89+91.2+91.3+88.7+8 8.8+91.8+91.1+91.1＝905.4 再计算总计超过多少千克： 905.4－90×10＝5.4
解法2：每袋小麦超过标准重量的千克数记作 正数，不足的千克数记作负数。
10袋小麦对应的数为+1，+1，+1.5，-1，+1.2， +1.3，-1.3，-1.2，+1.8，+1.1。
＝24＋20＋[（－12）＋（－15）]
＝44＋（－27）
＝17
这里使
用了哪些运 算律 ？
解：（－2.54）＋3.56＋（－7.46）＋（－3.56）
＝[（－2.54）＋（－7.46）] ＋[（＋3.56）＋
（－3.56）]
＝（－10）＋0
＝－10.
这里使
用了哪些运 算律 ？
有理的加法常用的三个规律：
4．若第一次向西走25米，第二次向东 走10米，那他现在在什么位置？
＋10 －25 －30 －20 －10 0
10 20 30
－15
(－25) ＋(＋10) ＝ －15
5．若第一次向西走20米，第二次向 东走20米，那他现在在什么位置？
＋20 －20 －50 －40 － 30 －20 －10 0
知识要点
加法的交换律
有理数的加法中，两个数的加法，交 换加数的位置，和不变.
即：a＋b=b＋a
1．式子中的字母分别表示任意的一个有理数。 （如：既可成表示整数，也可以表示分数；既可以表 示正数，也可以表示负数或0）.
2．在同一个式子中，同一个字母表示同一个数.
解法2：每袋小麦超过标准重量的千克数记作 正数，不足的千克数记作负数。
10袋小麦对应的数为+1，+1，+1.5，-1，+1.2， +1.3，-1.3，-1.2，+1.8，+1.1。
＝24＋20＋[（－12）＋（－15）]
＝44＋（－27）
＝17
这里使
用了哪些运 算律 ？
解：（－2.54）＋3.56＋（－7.46）＋（－3.56）
＝[（－2.54）＋（－7.46）] ＋[（＋3.56）＋
（－3.56）]
＝（－10）＋0
＝－10.
这里使
用了哪些运 算律 ？
有理的加法常用的三个规律：
4．若第一次向西走25米，第二次向东 走10米，那他现在在什么位置？
＋10 －25 －30 －20 －10 0
10 20 30
－15
(－25) ＋(＋10) ＝ －15
5．若第一次向西走20米，第二次向 东走20米，那他现在在什么位置？
＋20 －20 －50 －40 － 30 －20 －10 0
知识要点
加法的交换律
有理数的加法中，两个数的加法，交 换加数的位置，和不变.
即：a＋b=b＋a
1．式子中的字母分别表示任意的一个有理数。 （如：既可成表示整数，也可以表示分数；既可以表 示正数，也可以表示负数或0）.
2．在同一个式子中，同一个字母表示同一个数.
人教版七年级数学上册 《有理数的加减法》PPT教育课件(第二课时有理数减法)
人教版七年级数学上册 《有理数的加减法》PPT教育课件(第二课时有理 数减法)
科 目：数学
适用版本：人教版
适用范围：【教师教学】
人教版 数学（初中）（七年级 上）
第一章 有理数
1.3 有理数的加减法
1.3.2 有理数减法
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
第十三页，共十九页。
课堂测试 例4、若│a│=8，│b│=3，且a<b，求a-b．
解：因为│a│=8，│b│=3
所以a=+8和-8，b=+3或-3 而a<b，所以a=-8，b=3或-3 a-b=-11或-5
第十四页，共十九页。
课堂测试 例5:、计算：（-10）+（+2）-(-4)-(+6)
（-10）+（+2）-(-4)-(+6) =（-10）+（+2）+(+4)+(-6) =（-10）+（-6）+(+2)+(+4) =[（-10）+(-6)]+[（+2）+(+4)]
0-7=
-7
7-0=
7
7和-7是什么关系呢？
结论：小数减去大数，等于大数减去小数的相反数.
即：小数-大数=-（大数-小数）
第十二页，共十九页。
课堂测试 例3、填空： （1）温度3℃比-8 ℃高 11 ；℃ （2）温度-9 ℃比-1 ℃低 8 ℃； （3）海拔-20m比-30m高 10；m （4）从海拔22m到-10m，下降了 3；2m
科 目：数学
适用版本：人教版
适用范围：【教师教学】
人教版 数学（初中）（七年级 上）
第一章 有理数
1.3 有理数的加减法
1.3.2 有理数减法
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
第十三页，共十九页。
课堂测试 例4、若│a│=8，│b│=3，且a<b，求a-b．
解：因为│a│=8，│b│=3
所以a=+8和-8，b=+3或-3 而a<b，所以a=-8，b=3或-3 a-b=-11或-5
第十四页，共十九页。
课堂测试 例5:、计算：（-10）+（+2）-(-4)-(+6)
（-10）+（+2）-(-4)-(+6) =（-10）+（+2）+(+4)+(-6) =（-10）+（-6）+(+2)+(+4) =[（-10）+(-6)]+[（+2）+(+4)]
0-7=
-7
7-0=
7
7和-7是什么关系呢？
结论：小数减去大数，等于大数减去小数的相反数.
即：小数-大数=-（大数-小数）
第十二页，共十九页。
课堂测试 例3、填空： （1）温度3℃比-8 ℃高 11 ；℃ （2）温度-9 ℃比-1 ℃低 8 ℃； （3）海拔-20m比-30m高 10；m （4）从海拔22m到-10m，下降了 3；2m
1.3.1有理数加法(2)
3 4 (−0.2)+(+4 )+(−4.3)+(−6 ) 10 5
（2） ）
3 5 1 0.75+ (−2 ) + (+0.125 + (−12 ) + (−4 ) ) 4 7 8
化简下列各式 1. (-1.75)+1.5+(+7.3)+(-2.25)+(-8.5) 1.75)+1.5+(+7.3)+(-2.25)+(2.
有理数加法的运算律： 有理数加法的运算律：
（1）加法交换律：a＋b ＝b ＋a 加法交换律： 加法结合律：（ a ＋b ）＋ c ＝ a ＋（ b ＋ c ） （2）加法结合律 运用运算律进行简便运算时,通常有下列规律： 运用运算律进行简便运算时,通常有下列规律：
（1）互为相反数的两数，可先相 互为相反数的两数， 符号相同的数可以先相加． （2）符号相同的数可以先相加． 加． 分母相同的数可以先相加． （3）分母相同的数可以先相加． （4）几个数相加能得到整数可先相加． 几个数相加能得到整数可先相加．
(-9.6)+1.5+(-0.4)+(-0.3)+8.5 9.6)+1.5+(-0.4)+((-0.8)+1.2+(-0.7)+(-2.1)+0.8+3.5 0.8)+1.2+(-0.7)+(-
3.
某天早晨是-3℃，到了中午 升高了5℃,晚上又下降了 3℃，到了午夜降低了4 ℃， 求午夜时的温度？ 求午夜时的温度？
现有10袋大米，以每袋 为准， 现有 袋大米，以每袋50kg为准， 袋大米 为准 超过的千克数记作正数， 超过的千克数记作正数，不足的千克数 记作负数，称重的记录如下： 记作负数，称重的记录如下： ；＋0.3； ； ；＋1.1； ＋0.5；＋ ；0；―0.2；―0.3；＋ ； ；＋ ； ；＋ ―0.7；―0.1；＋ ；＋ ， ； ；＋0.8；＋ ；＋ ；＋0.7， 10袋大米共超重或不足多少千克？总重 袋大米共超重或不足多少千克？ 袋大米共超重或不足多少千克 量是多少千克？ 量是多少千克？
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
= 0+0 = 0
[点拨4有分母相同的，可先把分母相同的数结合相加。]
（１）把正数和负数分别结合在一起相加
（２）把互为相反数的结合，能凑整的结合 （３）把同分母的数结合相加
2.算一算：
1 16 25 24 (35) 2 3.48 5.33 9.52 5.33 (3.05)
3 2 3 3 1 3 2 2 3 11
↓
↓
同号两数相加
↓↓
取相同符号 两个加数的绝对值 相加
( - 9 ) + (+ 2) = - ( 9 - 2) = -7
↓ ↓ ↓↓
异号两数相加 取绝对值较大 两个加数的绝对值
的符号
由大的减去小的
同号两数之和——这是名符其实的和，做加法。 异号两数之和——表面上叫“和”，其实是做减法。
2、算一算
A （1）（－10）＋（－8）＝ －18
问题一：看课本19页，两个探究， 回答！
111
点拨1：
（1）计算：16+（－25）+24+（－35） 一般地，总是先把正
数或负数分别结合在
解：原式=16+24+（－25）+（－35）
一起相加
=（16+24）+[（－25）+（－35）]
=40+（－60）
=－20
(2)(-1.75)+(+7.3)+1.7+(-2.25)
一、复习有理数加法法则要点
(1)同号两数相加， 取相同的符号， 并把绝对值相加 . (2)异号两数相加，取 绝对值较大加数的符号，
并用较大的绝对值减去较小的绝对值 , （3）互为相反数的两数相加得零
(4)一个数同零相加仍得这个数
分析特征 强化理解 总结步骤
( - 4 ) + ( - 8 ) = - ( 4 + 8 )= - 12
When You Do Your Best, Failure Is Great, So Don'T Give Up, Stick To The End
演讲人：XXXXXX 时 间：XX年XX月XX日
B组
2
3
5 6
5
1 7
2
1 6
32
6 7
C组
(3)(
3) 4
(
21 7ຫໍສະໝຸດ )(1 4
)
(3
1 7
)
看课本第20页例3，比较两种运算方 法哪种简便？
用你认为简便的方法，完成课本26页第9题
１．有理数加法交换律和结合律 ２．运用加法交换律和结合律要注意： （１）把正数和负数分别结合在一起相加 （２）把互为相反数的结合，能凑整的结合 （３）把同分母的数结合相加 ３．运算律的作用能使运算简便
后进行绝对值的加减运算
学习目标
1. 理解并熟记有理数加法法则； 2. 理解并熟记有理数交换律和交换律； 3. 能够熟练运用加法法则和运算律进
行三个以上有理数加法计算。
(1)___a_+__b_=__b_+__a__
(2)_(_a__+_b_)_+__c_=_a__+_(_b + c)
引进负数后， 这些运算律是 否还适用呢？
学习总结
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
You Know, The More Powerful You Will Be
结束语
当你尽了自己的最大努力时，失败也是伟大的， 所以不要放弃，坚持就是正确的。
5 4 5 4 3
3、下列各题计算运用运算律恰当吗？
(1)28 (19) 42 (21)
(19) (21) (28 42)
(2)(3.75) (2 3) 5 3 (8.4) 54
(3.75)
5
3 4
(2
3) 5
(8.4)
分层练习 计算下列各式： A组（1）（-32）+（+49）+（-68）+（+11）=-40
（2）（－6）＋（＋6）＝ 0
（3）（－37）＋0＝ －37
(4)( 2) ( 1) 1 555
B （1）（－843）＋（－557）＝ －1400
（2）（－3.86）＋（＋3.86）＝ 0
（3）（－416）＋0＝ －416
(4)(2
1 6
)
(1
1) 2
2 3
运算步骤
先判断类型 （同号、异号等）； 再确定和的符号；
解：原式=（-1.75)+(-2.25) +（+7.3）+1.7
= [ （-1.75)+(-2.25) ] +[（+7.3）+1.7]
=(-4)+9
=5
点拨2：
能凑整的先凑整
聪明
(3)(-8)+(+2.8)+(+8)+(-2.8)
的你
[点拨3有相反数的可先把相反数相加]
一定
解：原式=
=
（[（-8-）8）+（+（+8+）8）+（]+[+（2.+82）.8+）（+-（2.能8-！2）行.8）]