大学物理习题及解答10
大学普通物理复习题(10套)带答案

普通物理试题1-10试题1一、填空题11. 7.在与匀强磁场B垂直的平面,有一长为L 的铜杆OP ,以角速度 绕端点O 作逆时针匀角速转动,如图13—11,则OP 间的电势差为 P O U U (221L B )。
3. 3.光程差 与相位差 的关系是(2 )25. 1.单色光在水中传播时,与在真空中传播比较:频率(不变 );波长( 变小 );传播速度( 变小 )。
(选填:变大、变小、不变。
)68.17-5. 波长为 的平行单色光斜入射向一平行放置的双缝,如图所示,已知入射角为θ缝宽为a ,双缝距离为b ,产生夫琅和费衍射,第二级衍射条纹出现的角位置是(sin 2sin 1b。
33. 9. 单色平行光垂直照射在薄膜上.经上下两表面反射的两束光发生干涉、如图所示, 若薄膜的厚度为e .且321n n n ,1 为入射光在1n 中的波长,则两束反射光的光程差为 ( 22112 n e n)。
二、选择题6. 2. 如图示,在一无限长的长直载流导线旁,有一形单匝线圈,导线与线圈一侧平行并在同一平面,问:下列几种情况中,它们的互感产生变化的有( B ,C ,D )(该题可有多个选择)(A) 直导线中电流不变,线圈平行直导线移动; (B) 直导线中电流不变,线圈垂直于直导线移动;(C) 直导线中电流不变,线圈绕AB 轴转动; (D) 直导线中电流变化,线圈不动12.16-1.折射率为n 1的媒质中,有两个相干光源.发出的光分别经r 1和r 2到达P 点.在r 2路径上有一块厚度为d ,折射率为n 2的透明媒质,如图所示,则这两条光线到达P 点所经过的光程是( C )。
(A )12r r(B ) d n n r r 2112(C ) d n n n r r 12112 (D ) d n n r r 1211283. 7.用白光垂直照射一平面衍射光栅、发现除中心亮纹(0 k )之外,其它各级均展开成一光谱.在同一级衍射光谱中.偏离中心亮纹较远的是( A )。
大学物理课后题答案10

过 点作一圆柱体垂直穿过无限大带电平板,由高斯定理
两底面上各点的场强大小相等,因此
即
由于平板外一点的场强与距平板的距离无关
(2)板内P点处的场强由左右两边薄板的场强在该点叠加产生
(3)若电场强度为0,则
所以
10-14半径为R、线电荷密度为 的均匀带电圆环,在其轴线上放一长为l、线电荷密度为 的均匀带电直线,该线段的一端处于圆心处,如图所示。求该直线段受到的电场力。
[解]在细棒上距O点x处取一线元dx,所带电量为
均匀带电圆环在dx处产生的场强为
dq在带电圆环的电场中所受到的电场力的大小为
所以
整个带电细棒所受的电场力为
在 处取电荷元 ,它受到的左棒的电场力为
所以右棒受的总电场力为
[解二]直接求电荷元间的库仑力,再积分求整个带电体的受力。
在两带电细棒上各取一微元 、 ,它们之间的距离为 。根据库仑定律, 受 的库仑力为
F方向为x正向,左棒受右棒库仑力
10-4用绝缘细线弯成的半圆环,半径为R,其上均匀地带有正电荷Q,试求圆心处点O的场强。
[证明二]在静电场中作一矩形闭合回线abcd,根据场强与电力线密度的关系式 ,可知ab线上各点场强 ,cd线上各点场强 各自相等。所以
这违反静电场中E的环流定律 。所以在静电场中,若电场线平行必然是等间距的,即均匀场可用平行等间距的场线表示。
10-26假如静电场中某一区域电场线的形状是以点O为中心的同心圆弧,如图所示。试证明:该区域各点的电场强度的大小都应与该点离O点的距离成反比。
[解]电荷连续分布带电体产生的场应用点电荷场强公式积分求解。
大学物理习题十答案

10-1 质量为10×10-3 kg 的小球与轻弹簧组成的系统,按20.1cos(8)3x t ππ=+(SI)的规律做谐振动,求: (1)振动的周期、振幅、初位相及速度与加速度的最大值;(2)最大的回复力、振动能量、平均动能和平均势能,在哪些位置上动能与势能相等?(3)t2=5 s 与t1=1 s 两个时刻的位相差.解:(1)设谐振动的标准方程为)cos(0φω+=t A x ,则知:3/2,s 412,8,m 1.00πφωππω===∴==T A又 πω8.0==A v m 1s m -⋅ 51.2=1s m -⋅2.632==A a m ω2s m -⋅(2) N 63.0==m m a FJ 1016.32122-⨯==m mv E J 1058.1212-⨯===E E E k p 当p k E E =时,有p E E 2=,即 )21(212122kA kx ⋅=∴ m 20222±=±=A x(3) ππωφ32)15(8)(12=-=-=∆t t10-2 一个沿x 轴做简谐振动的弹簧振子,振幅为A ,周期为T ,其振动方程用余弦函数表出.如果t =0时质点的状态分别是:(1)x0=-A ;(2)过平衡位置向正向运动;(3)过2Ax =处向负向运动; (4)过x =处向正向运动. 试求出相应的初位相,并写出振动方程.解:因为 ⎩⎨⎧-==0000sin cos φωφA v A x将以上初值条件代入上式,使两式同时成立之值即为该条件下的初位相.故有)2cos(1πππφ+==t T A x )232cos(232πππφ+==t T A x )32cos(33πππφ+==t T A x)452cos(454πππφ+==t T A x10-3 一质量为10×10-3 kg 的物体做谐振动,振幅为24 cm ,周期为4.0 s ,当t =0时位移为+24 cm.求:(1)t =0.5 s 时,物体所在的位置及此时所受力的大小和方向;(2)由起始位置运动到x =12 cm 处所需的最短时间;(3)在x =12 cm 处物体的总能量.解:由题已知 s 0.4,m 10242=⨯=-T A ∴ 1s rad 5.02-⋅==ππωT又,0=t 时,0,00=∴+=φA x故振动方程为m )5.0cos(10242t x π-⨯=(1)将s 5.0=t 代入得0.17m m )5.0cos(102425.0=⨯=-t x πN 102.417.0)2(10103232--⨯-=⨯⨯⨯-=-=-=πωxm ma F方向指向坐标原点,即沿x 轴负向. (2)由题知,0=t 时,00=φ, t t =时 3,0,20πφ=<+=t v A x 故且∴ s 322/3==∆=ππωφt(3)由于谐振动中能量守恒,故在任一位置处或任一时刻的系统的总能量均为J 101.7)24.0()2(10102121214223222--⨯=⨯⨯⨯===πωA m kA E10-4 题10-4图为两个谐振动的x -t 曲线,试分别写出其谐振动方程.题10-4图解:由题10-4图(a),∵0=t 时,s 2,cm 10,,23,0,0000===∴>=T A v x 又πφ即 1s rad 2-⋅==ππωT故 m )23cos(1.0ππ+=t x a由题10-4图(b)∵0=t 时,35,0,2000πφ=∴>=v A x 01=t 时,22,0,0111ππφ+=∴<=v x又 ππωφ253511=+⨯= ∴ πω65=故 m t x b )3565cos(1.0ππ+=11-4 已知波源在原点的一列平面简谐波,波动方程为y =Acos (Bt -Cx),其中A ,B ,C 为正值恒量.求:(1)波的振幅、波速、频率、周期与波长;(2)写出传播方向上距离波源为l 处一点的振动方程;(3)任一时刻,在波的传播方向上相距为d 的两点的位相差.解: (1)已知平面简谐波的波动方程)cos(Cx Bt A y -= (0≥x )将上式与波动方程的标准形式)22cos(λππυx t A y -= 比较,可知: 波振幅为A ,频率πυ2B =, 波长C πλ2=,波速C B u ==λυ, 波动周期B T πυ21==. (2)将l x =代入波动方程即可得到该点的振动方程)cos(Cl Bt A y -=(3)因任一时刻t 同一波线上两点之间的位相差为)(212x x -=∆λπφ 将d x x =-12,及C πλ2=代入上式,即得Cd =∆φ.11-5 沿绳子传播的平面简谐波的波动方程为y =0.05cos(10πt -4πx),式中x ,y 以m 计,t 以s 计.求:(1)波的波速、频率和波长;(2)绳子上各质点振动时的最大速度和最大加速度;(3)求x =0.2 m 处质点在t =1 s 时的位相,它是原点在哪一时刻的位相?这一位相所代表的运动状态在t =1.25 s 时刻到达哪一点?解: (1)将题给方程与标准式)22cos(x t A y λππυ-= 相比,得振幅05.0=A m ,频率5=υ1-s ,波长5.0=λm ,波速5.2==λυu 1s m -⋅.(2)绳上各点的最大振速,最大加速度分别为ππω5.005.010max =⨯==A v 1s m -⋅222max 505.0)10(ππω=⨯==A a 2s m -⋅(3)2.0=x m 处的振动比原点落后的时间为08.05.22.0==u x s 故2.0=x m ,1=t s 时的位相就是原点(0=x ),在92.008.010=-=t s 时的位相,即 2.9=φπ.设这一位相所代表的运动状态在25.1=t s 时刻到达x 点,则825.0)0.125.1(5.22.0)(11=-+=-+=t t u x x m。
大学物理第10章题解

习题10.1 两平行金属板A 、B ,带有等量异号电荷,相距为5.0mm,两板的面积都是150cm 2,电荷量的大小都是2.66×10-8C ,A 板带正电荷并接地,设地的电势为零,并忽略边缘效应,求B 板的电势及A B 间离A 板1.0mm 处的电势。
解:因平行板间电荷的散布的电场是匀强电场,有由高斯定理得)(100.20.50.1100.10.1,)(100.11015010854.8100.51066.201)1(23341238V V Ed Ed U mm A B A V V Q d d B QPB p PA BABAA B U sU U s⨯-=⨯⨯-=-=-=-=⨯-=⨯⨯⨯⨯⨯⨯-=︒-=E -=⋅E -=︒=︒=E ⎰⎰⎰-----处的电势为:板间离板的电势为:)得由(εεεσ 10.2 如下图,三块平行的金属板A 、B 和C ,面积都为200 cm 2,A 、B 相距4.0mm ,A 、C 相距2.0mm, B 和C 都接地。
若是使A 板带+ 3.0×10-7的电荷,略去边缘效应,问B 、C 两板上的感应电荷各是多少?以地的电势为零,A 板的电势为多少?解:因B ,C 两板都接地,故知B ,C 两板上只有向着A 的那里有感应电荷,设电荷的面密度别离为)(103.21020010854.8100.4100.1)(100.2)100.1(24)(100.1100.324210410987,,6e e e 5e 4320103412370077770E E V V sA C C C C C AB AC A B A B A C B A d Qd d E U QQd ddQ Q dd Qddd d d UU d d QQQ QQ ABBAB BABABAC AACABACBBACABCBAC AB C AB B AB AB AC C CBAC AB CAC AC ABABACBACABCBAB BACCAC AB C B⨯=⨯⨯⨯⨯⨯⨯==-=⋅=⨯-=⨯-⨯=⨯-=⨯⨯+-=+===∴-==-==-==-=+--=+∴=+=+--------εεσσσεσεσεσεεεσσσσσσσσσσσσσ板的电势为:)联立得:),(由()(两边乘以板的面积即得)()(得)(,则由间的距离为间的距离为,设)()(间的电场强度为:,指向量,从为垂直于板面的单位矢式中)(间的电场强度为:,由高斯定理得)(的关系为:得三块板上电荷量两间两边乘以鞭的面积,便)()()(理得,则由对称性和高斯定和则由度分别为的两面上电荷量的面密和板向着,和10.3 半径为10cm 的金属球A 带电1.0×10-8C 。
《大学物理》 第二版 课后习题答案 第十章

习题精解10-1 在平面简谐波的波射线上,A,B,C,D 各点离波源的距离分别是3,,,424λλλλ。
设振源的振动方程为cos 2y A t πω⎛⎫=+ ⎪⎝⎭ ,振动周期为T.(1)这4点与振源的振动相位差各为多少?(2)这4点的初相位各为多少?(3)这4点开始运动的时刻比振源落后多少? 解 (1) 122,2,2xxπϕπϕππλλ∆∆∆==∆==3432,222x x πϕπϕππλλ∆∆∆==∆== (2)112233440,,2223,222πππϕϕϕϕππϕϕπϕϕπ=-∆==-∆=-=-∆=-=-∆=-(3) 1212343411,,,24223,,,242t T T t T T t T T t T Tϕϕππϕϕππ∆∆∆==∆==∆∆∆==∆==10-2 波源做谐振动,周期为0.01s ,振幅为21.010m -⨯,经平衡位置向y 轴正方向运动时,作为计时起点,设此振动以1400u m s -=∙的速度沿x 轴的正方向传播,试写出波动方程。
解 根据题意可知,波源振动的相位为32ϕπ= 2122200, 1.010,4000.01A m u m s T ππωπ--====⨯=∙ 波动方程231.010cos 2004002x y t m ππ-⎡⎤⎛⎫=⨯-+ ⎪⎢⎥⎝⎭⎣⎦10-3 一平面简谐波的波动方程为()0.05cos 410y x t m ππ=-,求(1)此波的频率、周期、波长、波速和振幅;(2)求x 轴上各质元振动的最大速度和最大加速度。
解 (1)比较系数法 将波动方程改写成0.05cos10 2.5x y t m π⎛⎫=-⎪⎝⎭与cos x y A t u ω⎛⎫=-⎪⎝⎭比较得1120.05;10;0.21015; 2.5;0.5A m T s v s u m s u T m Tπωππλ--=======∙=∙=(2)各质元的速度为()10.0510sin 410v x t m s πππ-=⨯-∙ 所以1max 0.0510 1.57()v m s π-=⨯=∙ 各质元的加速度为()220.05(10)cos 410a x t m s πππ-=-⨯-∙ 所以22max 0.05(10)49.3()a m s π-=⨯=∙10-4 设在某一时刻的横波波形曲线的一部分如图10.1所示。
大学物理学-习题解答-习题10

第十章10-1 无限长直线电流的磁感应强度公式为B =μ0I2πa,当场点无限接近于导线时(即a →0),磁感应强度B →∞,这个结论正确吗?如何解释?答:结论不正确。
公式a IB πμ20=只对理想线电流适用,忽略了导线粗细,当a →0,导线的尺寸不能忽略,电流就不能称为线电流,此公式不适用。
10-2 如图所示,过一个圆形电流I 附近的P 点,作一个同心共面圆形环路L ,由于电流分布的轴对称,L 上各点的B 大小相等,应用安培环路定理,可得∮L B ·d l =0,是否可由此得出结论,L 上各点的B 均为零?为什么? 答:L 上各点的B 不为零. 由安培环路定理∑⎰=⋅ii I l d B 0μρρ得 0=⋅⎰l d B ρρ,说明圆形环路L 内的电流代数和为零,并不是说圆形环路L 上B 一定为零。
10-3 设题10-3图中两导线中的电流均为8A ,对图示的三条闭合曲线a ,b ,c ,分别写出安培环路定理等式右边电流的代数和.并讨论:(1)在各条闭合曲线上,各点的磁感应强度B ϖ的大小是否相等? (2)在闭合曲线c 上各点的B ϖ是否为零?为什么? 解: ⎰μ=⋅al B 08d ϖϖ⎰μ=⋅bal B 08d ϖϖ⎰=⋅cl B 0d ϖϖ(1)在各条闭合曲线上,各点B ϖ的大小不相等.(2)在闭合曲线C 上各点B ϖ不为零.只是B ϖ的环路积分为零而非每点0=B ϖ.习题10-2图题10-3图10-4 图示为相互垂直的两个电流元,它们之间的相互作用力是否等值、反向?由此可得出什么结论?答:两个垂直的电流元之间相互作用力不是等值、反向的。
B l Id F d ρρρ⨯= 20ˆ4r r l Id B d ⨯=ϖϖπμ2212122110221212201112)ˆ(4ˆ4r rl d I l d I r r l d I l d I F d ⨯⨯=⨯⨯=ϖρϖρρπμπμ 2121211220212121102212)ˆ(4ˆ4r rl d I l d I r r l d I l d I F d ⨯⨯=⨯⨯=ϖρϖρρπμπμ ))ˆ()ˆ((4212121221************r r l d l d r r l d l d I I F d F d ⨯⨯+⨯⨯-=+ϖρϖρρρπμ 2122112210212112221212102112)(ˆ4))ˆ()ˆ((4r l d l d r I I r l d r l d l d r l d I I F d F d ϖρϖρϖρρρ⨯⨯=⋅-⋅=+πμπμ 一般情况下 02112≠+F d F d ρρ由此可得出两电流元(运动电荷)之间相互作用力一般不满足牛顿第三定律。
大学物理(第四版)课后习题及答案磁场
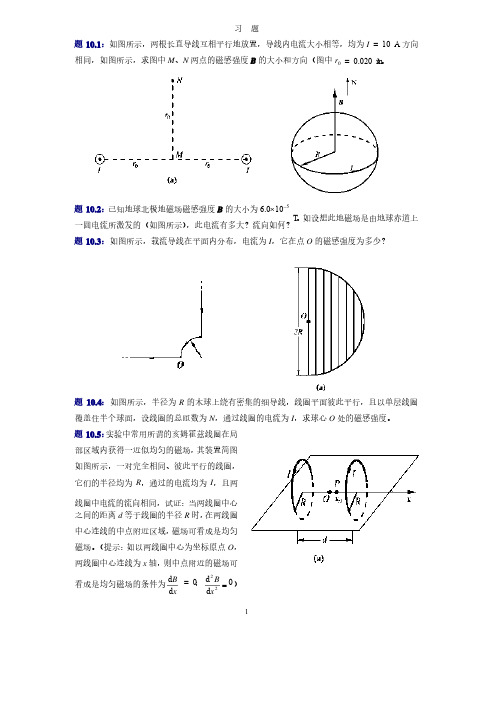
1 习题题10.1:如图所示,两根长直导线互相平行地放置,导线内电流大小相等,均为I = 10 A ,方向,方向相同,如图所示,求图中M 、N 两点的磁感强度B 的大小和方向(图中r 0 = 0.020 m )。
题10.2:已知地球北极地磁场磁感强度B 的大小为6.0´10-5 T 。
如设想此地磁场是由地球赤道上一圆电流所激发的(如图所示),此电流有多大?流向如何?题10.3:如图所示,载流导线在平面内分布,电流为I ,它在点O 的磁感强度为多少?题10.4:如图所示,半径为R 的木球上绕有密集的细导线,线圈平面彼此平行,且以单层线圈覆盖住半个球面,设线圈的总匝数为N ,通过线圈的电流为I ,求球心O 处的磁感强度。
题10.5:实验中常用所谓的亥姆霍兹线圈在局部区域内获得一近似均匀的磁场,其装置简图如图所示,一对完全相同、彼此平行的线圈,它们的半径均为R ,通过的电流均为I ,且两线圈中电流的流向相同,试证:当两线圈中心之间的距离d 等于线圈的半径R 时,在两线圈中心连线的中点附近区域,磁场可看成是均匀磁场。
(提示:如以两线圈中心为坐标原点O ,两线圈中心连线为x 轴,则中点附近的磁场可看成是均匀磁场的条件为x B d d = 0;0d d 22=x B )题10.6:如图所示,载流长直导线的电流为I ,试求通过矩形面积的磁通量。
,试求通过矩形面积的磁通量。
题10.7:如图所示,在磁感强度为B 的均匀磁场中,有一半径为R 的半球面,B 与半球面轴线的夹角为a ,求通过该半球面的磁通量。
,求通过该半球面的磁通量。
题10.8:已知10 10 mmmm 2裸铜线允许通过50 50 A A 电流而不会使导线过热。
电流在导线横截面上均匀分布。
求:(1)导线内、外磁感强度的分布;(2)导线表面的磁感强度。
)导线表面的磁感强度。
题10.9:有一同轴电缆,其尺寸如图所示,两导体中的电流均为I ,但电流的流向相反,导体的磁性可不考虑。
大学物理学 第10章_静电场 习题解答 [王玉国 康山林 赵宝群]
![大学物理学 第10章_静电场 习题解答 [王玉国 康山林 赵宝群]](https://img.taocdn.com/s3/m/d8d02e12650e52ea55189898.png)
q 6 0 q ;如果它包含 q 所在 24 0
2 2
对于边长 a 的正方形,如果它不包含 q 所在的顶点,则 e 顶点则 e 0 .
(3) 因为通过半径为 R 的圆平面的电通量等于通过半径为 R x 的球冠面的电通 量,而球冠面积*
S 2π( R 2 x 2 )[1
P R q r P'
2q a O a 3q a
+Q q a
R
d
∞
题 10-10 图
题 10-11 图
题 10-12 图
10-12 如图所示.试验电荷 q , 在点电荷 Q 产生的电场中,沿半径为 R 的整个圆弧 的 3/4 圆弧轨道由 a 点移到 d 点的过程中电场力做功多大?从 d 点移到无穷远处的过程中, 电场力做功为多少? 解:因为在点电荷 Q 产生的电场中, U a U d 。故试验电荷 q 在点电荷 Q 产生的电 场中, 沿半径为 R 的整个圆弧的 3/4 圆弧轨道由 a 点移到 d 点的过程中电场力做功 Aad 0 ; 从 d 点移到无穷远处的过程中,电场力做功为
q0 2.0 105 C .试求该点电荷所受的电场力。
点电荷所在处产生场强为: d E
dx
4 0 d x
2 l
。整个杆上电荷在该点的场强为:
E
4 0
d x
0
dxLeabharlann 2l4 0 d d l
点电荷 q0 所受的电场力大小为:
F
方向:沿 x 轴负向
A q U d U qU d
[或另解: A
qQ 4 0 R
]
R
qE d r
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0 ( I 2 I1 ) B dl ____________,
L1
3. 如图所示,两根无限长载流 直导线相互平行,通过的电流分 别为I1和I2。则
2
0 nI
L2
I1
I2
L1
大学物理 牟群英主讲 大学物理 刘凌虹主讲
4. 如图所示,正电荷q在磁场中运 动,速度沿x轴正方向。若电荷q不 受力,则外磁场的方向是______; 平行于x轴 若电荷q受到沿y轴正方向的力,且 受到的力为最大值,则外磁场的方 向为__________。 沿z轴的反方向 5. 如图所示,ABCD是无限长导线 ,通以电流I,BC段被弯成半径为R 的半圆环,CD段垂直于半圆环所在 的平面,AB的延长线通过圆心O和C 点。则圆心O处的磁感应强度大小为 0 I 1 2 _______________。 1 ( ) 4R
I1
P
l I1
r1
r2
r3
大学物理 牟群英主讲 大学物理 刘凌虹主讲
解:(1)两导线电流的P点激 发的磁感强度分别为
d
B1
0 I1
2 (r1 1 r2 ) 2
B2
0 I 2
I1
P
l I1
2 (r1 1 r2 ) 2
r1
P点的磁感强度为
B B1 B2 2
r2
答:D
大学物理 牟群英主讲 大学物理 刘凌虹主讲
4. 两个载有相等电流I的半径为R的圆线圈一个处于水 平位置,一个处于竖直位置,两个线圈的圆心重合, 则在圆心o处的磁感应强度大小为多少? (A)0; (C) (B) ; (D) ; 0 I / 2 R
20 I / 2 R
0 I / R。
I
答:C
R2 I1 I R1 R2
B
I
R1 I2 I R1 R2
O
A
两段铁环的电流在O点处激发的 磁感强度大小分别为
大学物理 牟群英主讲 大学物理 刘凌虹主讲
0 I1 1 0 I R2 1 B1 2 R 2 2 R R1 R2 2
0 I 2 2 0 I R1 2 B2 2 R 2 2 R R1 R2 2
I2
B
I
2
O
1
A
l r 根据电阻定律 R S S 可知 R1 1 所以 B1 B2 R2 2
R2
I1 R1
O点处的磁感强度大小为
B B1 B2 0
大学物理 牟群英主讲 大学物理 刘凌虹主讲
3、如图所示,用毕奥——萨伐尔定律计算图中O 点的磁感强度。 I B A N M R O 0 Idl r 解: dB
y
40cm
b 30cm e
B
a
30cm
o
50cm
f
x
z
d
大学物理 牟群英主讲 大学物理 刘凌虹主讲
2. 真空中一载有电流I的长直螺线管,单位长度的 线圈匝数为n,管内中段部分的磁感应强度为 ________,端点部分的磁感应强度为________。 1 0
nI
B dl __________。 I1 ) 0 (I 2
r3
0 I1
2 (r1 1 r2 ) 2
4 10 7 20 2 4 10 5 (T ) 2 0.20
方向垂直于纸面向外。
大学物理 牟群英主讲 大学物理 刘凌虹主讲
(2)在矩形面上,距离左边导线电流为r处取长度 为l宽度为dr的矩形面元,电流I1激发的磁场,通过 矩形面元的磁通量为 d
z
o x
v
R
y q
C
D
I
B
A
O
大学物理 牟群英主讲 大学物理 刘凌虹主讲
三、计算题:
1.两平行长直导线相距d=40cm,通过导线的电流 I1=I2=20A,电流流向如图所示。求 (1)两导线所在平面内与两导线等距的一点P处的磁 感应强度。 (2)通过图中斜线所示面积的磁通量(r1=r3=10cm, l=25cm)。 d
MA段: B 0 I 1 sin d d 4 a 0 I B1 (cos 1 cos 2 ) 4a 0 I B1 (1 sin ) 4R cos
4 r3
a R cos 1 0 2 2
大学物理 牟群英主讲 大学物理 刘凌虹主讲通量为
2 1 2.2 106 (Wb)
大学物理 牟群英主讲 大学物理 刘凌虹主讲
2.两根长直导线沿半径方向引到铁环上的A、B两 点,并与很远的电源相连,如图所示,求环中心O的 磁感应强度。
解:设两段铁环的电阻分别为R1和R2, 则通过这两段铁环的电流分别为
0 I1 d1 B1dS ldr 2r
dr
r
I1
P
电流激发的磁场,通过矩形面积的磁 通量为 r1 r2 I 0 1 1 d1 ldr r1 2r 0 I1l r1 r2 6 ln 1.110 (Wb) 2 r1 同理可得 2 1
答:A
大学物理 牟群英主讲 大学物理 刘凌虹主讲
3. 如图所示,在无限长载流直导线附近作一球形闭 合曲面S,当曲面S向长直导线靠近时,穿过曲面S的 磁通量和面上各点的磁感应强度B将如何变化? [ ] I (A)增大,B也增大; S (B)不变,B也不变; (C)增大,B不变; (D)不变,B增大。
B B1 B2 B3 0 I 0 I B (1 sin ) 2R cos 2 R
大学物理 牟群英主讲 大学物理 刘凌虹主讲
4、如图,一根很长的长直圆管形导体的横切面,内、 外半径分别为a、b,导体内载有沿轴线方向的电流I, 且I均匀分布在管的横切面上。设导体的磁导率 。 试求导体内部各点的磁感应强度分布规律。 0
解: a< r < b时,
B dl 2r B 0 I
L
I I (r a ) 2 2 (b a ) 2 2 0 I r a B 2 . 2 2r b a
2 2
答案: B
大学物理 牟群英主讲 大学物理 刘凌虹主讲
2.磁场的高斯定理说明了下面的哪些叙述是正确 的? [ ] a 穿入闭合曲面的磁感应线条数必然等于穿出的 磁感应线条数; b 穿入闭合曲面的磁感应线条数不等于穿出的磁 感应线条数; c 一根磁感应线可以终止在闭合曲面内; d 一根磁感应线可以完全处于闭合曲面内。 (A)ad; (B)ac; (C)cd; (D)ab。
大学物理 牟群英主讲 大学物理 刘凌虹主讲
2007级大学物理作业十 参考解答 一、选择题:
1、一匀强磁场,其磁感应强度方向垂直于纸面, 而带电粒子在该磁场中的运动轨迹如图所示,则: (A)两粒子的电荷必然同号。 . . . . (B)粒子的电荷可以同号也可以异号。 . . . . (C)两粒子的动量大小必然不同。 . . . . (D)两粒子的运动周期必然不同。 . . . . . . . .
0 I 1 BN段:dB sin d 4 a 0 I B2 (cos 1 cos 2 ) 4a 0 I B2 (1 sin ) 4R cos
AB段:
a R cos 1 2
2
0 I 1 0 I 1 2 0 I dB d B3 0 d 2 R 4 R 4 R
I
o
大学物理 牟群英主讲 大学物理 刘凌虹主讲
二、填空题:
1. 如图所示,均匀磁场的磁感应强度为B=0.2T, 方向沿x轴正方向,则通过abod面的磁通量为 _________,通过befo面的磁通量为__________,通 0 0.024Wb 过aefd面的磁通量为_______。 0.024Wb
