刚体作业答案
中南-工程力学纸质作业与答案

由钢的强度条件
解得:
由木材强度条件
解得:
所以许可载荷FP为697kN
10.解:
铆钉的剪切强度:每个铆钉的受力图如图
铆钉与板的挤压强度:由于上下板厚度为中间板厚度的1/2,挤压力为中间板的1/2,故铆钉与中间板和盖板的挤压应力相同
钢板的拉伸强度:盖板和中间板的轴力图如图,经分析盖板1-1截面为危险截面
一、填空题
1. 力偶
2. ,0, ,0
3. 力系的主矢、主矩分别等于零
4.弹性阶段、屈服阶段、强化阶段、颈缩阶段
5.26.4%,65.19%,塑性材料
6. ,
7. , ,
8. ,
9.
10.突变,集中力的大小,突变,集中力偶的大小
11.二,二,三
12.
13.C,B,A
14.[σt]/[σc]
15.15MPa
3. 结构如图所示。作用在结构上的力P=10kN,力偶矩m=12kN·m,分布载荷的最大值q=0.4kN/m。求A、B、C处的约束力。
4. 图所示传动轴中,作用于齿轮上的齿合力F推动AB轴作匀速转动。已知皮带上皮带紧边的拉力T1=200N,松边的拉力T2=100N,皮带轮直径D1=160mm,圆柱齿轮的节圆直径D=240mm,压力角α=20o,其它尺寸如图。试确定力F的大小和轴承A、B处的约束力。
二、作图题
1. 分别画出下列各物体的受力及整个系统的受力图,各杆的自重不计。
2. 作下列各梁的剪力和弯矩图。
三、计算题
1.试求梁的支座约束力。
2.图示结构A处为固定端约束,C处为光滑接触,D处为铰链连接。已知F1=F2=400N,M=300N·m,AB=BC=400mm,CD=CE=300mm,α=45o,不计各构件自重,求固定端A处与铰链D处的约束力。
刚体习题和答案

作业5 刚体力学♫刚体:在力的作用下不发生形变的物体⎰=-⇒=210t t dt dtd ωθθθω角速度⎰=-⇒=210t t dt dtd βωωωβ角加速度1、根底训练〔8〕绕定轴转动的飞轮均匀地减速,t =0时角速度为05rad s ω=,t =20s 时角速度为00.8ωω=,那么飞轮的角加速度β= -0.05 rad/s 2 ,t =0到 t =100 s 时间飞轮所转过的角度θ= 250rad . 【解答】飞轮作匀变速转动,据0t ωωβ=+,可得出:200.05rad s tωωβ-==-据2012t t θωβ=+可得结果。
♫定轴转动的转动定律:定轴转动的角加速度与它所受的合外力矩成正比,与刚体的转动惯量成反比.βJ M =质点运动与刚体定轴转动对照[C ]1、根底训练〔2〕一轻绳跨过一具有水平光滑轴、质量为M 的定滑轮,绳的两端分别悬有质量为m 1和m 2的物体(m 1<m 2),如下图.绳与轮之间无相对滑动.假设某时刻滑轮沿逆时针方向转动,那么绳中的力 (A) 处处相等. (B) 左边大于右边. (C) 右边大于左边. (D) 哪边大无法判断. 【解答】逆时针转动时角速度方向垂直于纸面向外, 由于(m 1<m 2),实际上滑轮在作减速转动,角加速m 2m 1 O度方向垂直纸面向,所以,由转动定律21()T T R J β-=可得:21T T >[C ] 2、自测提高〔2〕将细绳绕在一个具有水平光滑轴的飞轮边缘上,现在在绳端挂一质量为m 的重物,飞轮的角加速度为.如果以拉力2mg 代替重物拉绳时,飞轮的角加速度将(A) 小于. (B) 大于,小于2. (C) 大于2. (D) 等于2. 【解答】设飞轮的半径为R ,质量为m ,根据刚体定轴转动定律M J β=,当挂质量为m 的重物是:mg T maTR J a R ββ-=== 所以2mgRJ mRβ=+,当以2F mg =的拉力代替重物拉绳时,有: '2mgR J β=,2'mgRJβ=,比拟二者可得出结论。
第三次作业 牛顿运动定律和刚体力学

J
d d M Fr FN 2[ Fr ( F mg )] M 可得圆盘的角速度变化率 。 2 1 2 dt J mr dt mr 2
(2)以横梁为研究对象,受力平衡: Fl Fr FN 。 对横梁左端和右端,力矩平衡分别为: FN 2aFr aFN 0 和 FN 2aFl aFN 0 。 联立以上各方程解得:
2
可得:
dz r 2 r 2 (r ) 2 ,即 dz tan dr 。两端积分得: z dr g g 2g
mR
2
2
。
解:以转盘中心为转动轴,转盘和夯锤系统角动量(动量矩)守恒,碰撞后瞬间转盘与夯锤绕转盘中心
5
的角速度相同,得 ( J mR 2 ) J 0 ,即
J J R0 0 。则夯锤速度为 v R 2 J mR 2 J mR
[3-19] 如 图 所 示 , 弹 簧 的 劲 度 系 数
[3-26] 在重力场中有一个以匀速度 旋转着的圆筒容器,该容器内盛有密度为 的不可压缩性流 体。试求:(1)液体表面的状态;(2)液体内的压力分布。
解:(1)以圆筒的转轴为 Z 轴,原点位于液面最低处。液面处于平衡状态时,在液面取一质量元 dm , 受到重力 gdm 和其它流体的合力 F 。由于质量元相对液面静止,所以合力 F 的方向沿液面法向, 设 F 与竖直方向的夹角为 ,旋转时 dm 以径向 r 为半径,以 o 为圆心作匀速率圆周运动,向心加 速度为 an r 2 。由牛顿运动定律,有 F sin r dm 和 F cos gdm 。
m1v0 (m1 m2 )v 1 1 1 2 m1v0 (m1 m2 )v 2 kx 2 2 2 2
面向新世纪课程教材大学物理大作业答案——刚体力学作业
L2
−
L1
=
J 2ω2
−
J1ω1
质点的动量定理
dpr
=
r F
⋅
dt
∫ r
I
=
tr F ⋅ dt =
t0
pr − pr0 = mvr − mvr0
三、刚体的角动量守恒定律
1. 角动量守恒定律
∫ 由角动量定理
r M
当
r M外
=
0
时,
外
d
t r
ΔL
= =
Δ 0
r L
r L
=
恒矢量
P.6
1
区分两类冲击摆
(1)
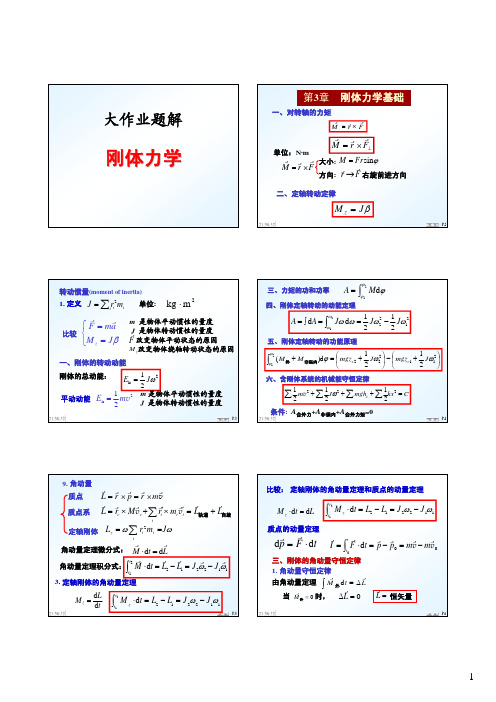
大作业题解
刚体力学
第3章 刚体力学基础
一、对转轴的力矩
r M
=
rr
×
r F
单位:N·m
r M
=
rr
×
r F⊥
r M
=
rr
×
r F
大小: 方向:
M = Frsinϕ
rr
→
r F
右旋前进方向
二、定轴转动定律
M z = Jβ
P.2
转动惯量(moment of inertia)
∑ 1. 定义 J = iri2mi 单位: kg ⋅ m 2
l/4 O
[ A]
mg l = 1 Jω 2 J = 7 ml 2
22
48
⇒ ω = 4 3g 7l
P.11
9.如图所示,一人造卫星到地球中心C的最大距离和
最小距离分别为RA和RB。设人造卫星对应的角动量分
别为LA和LB,动能分别为EkA和EkB,则有
(A) LB > LA,EkB > EkA
建筑力学与结构力学作业答案(高职)讲解

建筑力学与结构、结构力学与建筑构造练习册(宁大专升本)姓名:学号:班级:任课教师:杭州科技职业技术学院作业一、静力学基本概念(一)判断题:1、使物体运动状态发生改变的效应称为力的内效应。
( ⨯ )2、在两个力作用下处于平衡的杆件称为二力杆。
( √ )3、力的可传性原理适用于任何物体。
( ⨯ )4、约束是使物体运动受到限制的周围物体。
( √ )5、画物体受力图时,只需画出该物体所受的全部约束反力即可。
( ⨯ )(二)选择题:1、对刚体来说,力的三要素不包括以下要素( B )。
(A )大小 (B )作用点 (C )方向 (D )作用线2、刚体受不平行的三个力作用而平衡时,此三力的作用线必( C )且汇交于一点。
(A )共点 (B )共线 (C )共面 (D )不能确定3、光滑圆柱铰链约束的约束反力通常有( B )个。
(A )一 (B )二 (C )三 (D )四4、如图所示杆ACB ,其正确的受力图为( A )。
(A )图A (B )图B (C )图C (D )图D成绩D(A )(D )(C )5、下图中刚架中CB 段正确的受力图应为( D )。
(A )图A (B )图B (C )图C (D )图D(三)分析题:1、画出下图所示各物体的受力图,所有接触面均为光滑接触面,未注明者,自重均不计。
解:(a)取球为研究对象,作受力图如下:∙C G(b)60︒(c)F CFB (C)F B∙ABC GAR(b)取刚架为研究对象,作受力图如下:(c)取梁为研究对象,作受力图如下:2、画出下图所示各物体的受力图,所有接触面均为光滑接触面,未注明者,自重均不计。
解:(a)先取AC 杆为研究对象,作受力图如下:(a) AC 杆、BC 杆、整体(b)AC 杆、BC 杆、整体q (c) AB 杆、BC 杆、整体 CAAx F B R F或:BB R60︒ Ay F BF CCx F再取BC 杆为研究对象,作受力图如下:最后取整体为研究对象,作受力图如下:(b) 先取AC 杆为研究对象,作受力图如下:再取BC 杆为研究对象,作受力图如下:最后取整体为研究对象,作受力图如图所示:BF BF CxFF 'T 'BB A F A Ax FAy FB Cx F F 'Bx F By FA Ax FAy FBBx FBy F(c) 先取AB 杆为研究对象,作受力图如下:再取BC 杆为研究对象,作受力图如上:最后取整体为研究对象,作受力图如下:二、平面汇交力系(一)判断题:1、求平面汇交力系合力的几何作图法称为力多边形法。
刚体的平面运动作业参考答案

刚体的平面运动作业参考答案1.图示半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。
如曲柄OA 以等角加速度α 绕O 轴转动,当运动开始时,角速度ω0=0,转角ϕ0=0,求动齿轮以中心A 为基点的平面运动方程。
答案: 2A 22)(21, 2sin)( , 2cos )(t r R rt r R y t r R x A A αϕαα+=+=+=2. 图示平面机构中,曲柄OA =R ,以角速度ω 绕O 轴转动。
齿条AB 与半径为2Rr =的齿轮相啮合,并由曲柄销A 带动。
求当齿条与曲柄的交角θ =60º时,齿轮的角速度。
答案:顺时针 31ωω=提示:可先用速度投影法求出齿条上与齿轮重合点的速度。
3.图中曲柄OA 长150mm ,连杆AB 长200mm ,BD 长300mm 。
设OA ⊥OO 1时,AB ⊥OA ,θ =60º,曲柄OA 的角速度为4rad/s ;求此时机构中点B 和D 的速度以及杆AB 、O 1B 和BD 的角速度。
答案:逆时针顺时针顺时针 rad/s 34 , rad/s 4, rad/s 3 , mm/s 800 , mm/s 34001O =====BD B AB D B v v ωωω提示:在图示瞬时,杆AB 的速度瞬心为点C ,杆BD 的速度瞬心为点E 。
4.图示平面机构中,曲柄长OA =r ,以角速度ω0绕O 轴转动。
某瞬时,摇杆O 1N 在水平位置,而连杆NK 和曲柄OA 在铅垂位置。
连杆上有一点D ,其位置为DK =31NK ,求D 点的速度。
答案:←=320ωr v D 提示:在图示瞬时,杆AB 瞬时平动,杆KN 的速度瞬心为点N 。
5.杆AB 长0.4m ,其端点B 沿与水平成倾角θ =30º的斜面运动,而端点A 沿半径OA =0.6m 的圆弧运动,如图所示。
求当杆AB 水平时,端点B 的速度和加速度。
假设此时OA ⊥AB ,杆OA 的角速度为πrad/s ,角加速度为零。
刚体答案——精选推荐

刚体的定轴转动作业题答案1.{均匀细棒OA可绕通过其一端O而与棒垂直的水平固定光滑轴转动,如图所示.今使棒从水平位置由静止开始自由下落,在棒摆动到竖直位置的过程中,下述说法正确的是()}A.角速度从小到大,角加速度从大到小B.角速度从小到大,角加速度从小到大C.角速度从大到小,角加速度从大到小D.角速度从大到小,角加速度从小到大答案:A题型:单选题2.一轻绳绕在有水平轴的定滑轮上,滑轮的转动惯量为J,绳下端挂一物体.物体所受重力为P,滑轮的角加速度为.若将物体去掉而以与P相等的力直接向下拉绳子,滑轮的角加速度将()A.不变B.变小C.变大D.如何变化无法判断答案:C题型:单选题3.一水平圆盘可绕通过其中心的固定竖直轴转动,盘上站着一个人.把人和圆盘取作系统,当此人在盘上随意走动时,若忽略轴的摩擦,此系统()A.动量守恒B.机械能守恒C.对转轴的角动量守恒D.动量、机械能和角动量都守恒E.动量、机械能和角动量都不守恒答案:C题型:单选题4.一刚体以每分钟60转绕z轴做匀速转动(沿z轴正方向)设某时刻刚体上一点P的位置矢量为,其单位为“10-2m”,若以“10-2m·s-1”为速度单位,则该时刻P点的速度为()A.B.C.D.试题编号:E17549 24678答案:B题型:单选题5.{一轻绳跨过一具有水平光滑轴、质量为M的定滑轮,绳的两端分别悬有质量为m1和m2的物体(m1<m2),如图所示.绳与轮之间无相对滑动.若某时刻滑轮沿逆时针方向转动,则绳中的张力()}A.处处相等B.左边大于右边C.右边大于左边D.哪边大无法判断试题编号:E17549 24680答案:C题型:单选题6.{一圆盘绕过盘心且与盘面垂直的光滑固定轴O以角速度w按图示方向转动.若如图所示的情况那样,将两个大小相等方向相反但不在同一条直线的力F沿盘面同时作用到圆盘上,则圆盘的角速度将()}A.必然增大B.必然减少C.不会改变D.如何变化,不能确定试题编号:E17549 24681答案:A题型:单选题7.两个匀质圆盘A和B的密度分别为和,若>,但两圆盘的质量与厚度相同,如两盘对通过盘心垂直于盘面轴的转动惯量各为J A和J B,则()A.J A>J BB.J B>J AC.J A=J BD.J A、J B哪个大,不能确定试题编号:E17549 24682答案:B题型:单选题8.将细绳绕在一个具有水平光滑轴的飞轮边缘上,现在在绳端挂一质量为m的重物,飞轮的角加速度为.如果以拉力2mg代替重物拉绳时,飞轮的角加速度将()A.小于B.大于,小于C.大于D.等于试题编号:E17549 24684答案:C题型:单选题9.{光滑的水平桌面上有长为、质量为m的匀质细杆,可绕通过其中点O且垂直于桌面的竖直固定轴自由转动,转动惯量为,起初杆静止.有一质量为m的小球在桌面上正对着杆的一端,在垂直于杆长的方向上,以速率v运动,如图所示.当小球与杆端发生碰撞后,就与杆粘在一起随杆转动.则这一系统碰撞后的转动角速度是()}A.B.C.D.试题编号:E17549 24686答案:C题型:单选题10.质量为m的小孩站在半径为R的水平平台边缘上.平台可以绕通过其中心的竖直光滑固定轴自由转动,转动惯量为J.平台和小孩开始时均静止.当小孩突然以相对于地面为v的速率在台边缘沿逆时针转向走动时,则此平台相对地面旋转的角速度和旋转方向分别为()A.,顺时针B.,逆时针C.,顺时针D.,逆时针试题编号:E17549 24687答案:A题型:单选题11.有一半径为R的水平圆转台,可绕通过其中心的竖直固定光滑轴转动,转动惯量为J,开始时转台以匀角速度转动,此时有一质量为m的人站在转台中心.随后人沿半径向外跑去,当人到达转台边缘时,转台的角速度为()A.B.C.D.试题编号:E17549 24688答案:A题型:单选题12.一块方板,可以绕通过其一个水平边的光滑固定轴自由转动.最初板自由下垂.今有一小团粘土,垂直板面撞击方板,并粘在板上.对粘土和方板系统,如果忽略空气阻力,在碰撞中守恒的量是()A.动能B.绕木板转轴的角动量C.机械能D.动量试题编号:E17549 24690答案:B题型:单选题13一个作定轴转动的轮子,对轴的转动惯量J =2.0kg·m2,正以角速度作匀速转动.现对轮子加一恒定的力矩M = -12N·m,经过时间t=8.0s时轮子的角速度=-,则=___.试题编号:E17549 24694答案:24 rad/s题型:填空题14.{有一半径为R的匀质圆形水平转台,可绕通过盘心O且垂直于盘面的竖直固定轴OO'转动,转动惯量为J.台上有一人,质量为m.当他站在离转轴r处时(r<R),转台和人一起以的角速度转动,如图.若转轴处摩擦可以忽略,问当人走到转台边缘时,转台和人一起转动的角速度=___.}试题编号:E17549 24696答案:题型:填空题15.{长为l、质量为M的匀质杆可绕通过杆一端O的水平光滑固定轴转动,转动惯量为,开始时杆竖直下垂,如图所示.有一质量为m的子弹以水平速度射入杆上A点,并嵌在杆中,OA=2l/ 3,则子弹射入后瞬间杆的角速度=___.}试题编号:E17549 24697答案:题型:填空题16.{质量为m、长为l的棒,可绕通过棒中心且与棒垂直的竖直光滑固定轴O在水平面内自由转动(转动惯量J=m l2/ 12).开始时棒静止,现有一子弹,质量也是m,在水平面内以速度v0垂直射入棒端并嵌在其中.则子弹嵌入后棒的角速度=___.}试题编号:E17549 24698答案:3v0/ (2l)题型:填空题17.一个圆柱体质量为M,半径为R,可绕固定的通过其中心轴线的光滑轴转动,原来处于静止.现有一质量为m、速度为v的子弹,沿圆周切线方向射入圆柱体边缘.子弹嵌入圆柱体后的瞬间,圆柱体与子弹一起转动的角速度=___.(已知圆柱体绕固定轴的转动惯量J=)试题编号:E17549 24700答案:题型:填空题18.一飞轮以角速度绕光滑固定轴旋转,飞轮对轴的转动惯量为J1;另一静止飞轮突然和上述转动的飞轮啮合,绕同一转轴转动,该飞轮对轴的转动惯量为前者的二倍.啮合后整个系统的角速度=___.试题编号:E17549 24703答案:题型:填空题19.可绕水平轴转动的飞轮,直径为1.0 m,一条绳子绕在飞轮的外周边缘上.如果飞轮从静止开始做匀角加速运动且在4 s内绳被展开10 m,则飞轮的角加速度为___.试题编号:E17549 24704答案:2.5 rad / s2题型:填空题20.一飞轮作匀减速转动,在5 s内角速度由40rad·s-1减到10rad·s-1,则飞轮在这5 s内总共转过了___圈,飞轮再经___的时间才能停止转动.试题编号:E17549 24705答案:62.5 | 1.67s题型:填空题21.{如图所示,一质量为m、半径为R的薄圆盘,可绕通过其一直径的光滑固定轴转动,转动惯量J=mR2/ 4.该圆盘从静止开始在恒力矩M作用下转动,t秒后位于圆盘边缘上与轴的垂直距离为R的B点的切向加速度a t=___,法向加速度a n=___.}试题编号:E17549 24706答案:4M/ (mR) |题型:填空题22.一长为L的轻质细杆,两端分别固定质量为m和2m的小球,此系统在竖直平面内可绕过中点O且与杆垂直的水平光滑固定轴(O轴)转动.开始时杆与水平成60°角,处于静止状态.无初转速地释放以后,杆球这一刚体系统绕O轴转动.系统绕O轴的转动惯量J=___.释放后,当杆转到水平位置时,刚体受到的合外力矩M=___;角加速度___.试题编号:E17549 24707答案:3mL2/ 4 |mgL |题型:填空题23.{有两位滑冰运动员,质量均为50 kg,沿着距离为3.0 m的两条平行路径相互滑近.他们具有10 m/s的等值反向的速度.第一个运动员手握住一根3.0 m长的刚性轻杆的一端,当第二个运动员与他相距3m时,就抓住杆的另一端.(假设冰面无摩擦)(1)试定量地描述两人被杆连在一起以后的运动.(2)两人通过拉杆而将距离减小为1.0m,问这以后他们怎样运动?}A. (%)试题编号:E17549 24710答案:{解:(1)对两人系统,对于杆中点合外力矩为零,角动量守恒.故 1分1分=2v/=6.67 rad / s∴w0两人将绕轻杆中心O作角速度为6.67 rad/s的转动. 1分(2)在距离缩短的过程中,合外力矩为零,系统的角动量守恒,则J0w0= J1w11分1分即作九倍原有角速度的转动.}题型:计算题题型:计算题24.{一轴承光滑的定滑轮,质量为M=2.00 kg,半径为R=0.100 m,一根不能伸长的轻绳,一端固定在定滑轮上,另一端系有一质量为m=5.00 kg的物体,如图所示.已知定滑轮的转动惯量为J=,其初角速度=10.0 rad/s,方向垂直纸面向里.求:(1)定滑轮的角加速度的大小和方向;(2)定滑轮的角速度变化到0时,物体上升的高度;(3)当物体回到原来位置时,定滑轮的角速度的大小和方向.}A. (%)试题编号:E17549 24712答案:{解:(1) ∵ mg-T=ma 1分TR=J2分a=R1分∴=81.7 rad/s21分方向垂直纸面向外. 1分(2) ∵当=0时,物体上升的高度h=R=6.12×10-2m 2分(3)10.0 rad/s方向垂直纸面向外.2分}题型:计算题25.{一质量均匀分布的圆盘,质量为M,半径为R,放在一粗糙水平面上(圆盘与水平面之间的摩擦系数为),圆盘可绕通过其中心O的竖直固定光滑轴转动.开始时,圆盘静止,一质量为m的子弹以水平速度v0垂直于圆盘半径打入圆盘边缘并嵌在盘边上,求(1)子弹击中圆盘后,盘所获得的角速度.(2)经过多少时间后,圆盘停止转动.(圆盘绕通过O的竖直轴的转动惯量为,忽略子弹重力造成的摩擦阻力矩)}A. (%)试题编号:E17549 24715答案:{解:(1)以子弹和圆盘为系统,在子弹击中圆盘过程中,对轴O的角动量守恒.1分mv0R=(MR2+mR2)2分1分(2)设s表示圆盘单位面积的质量,可求出圆盘所受水平面的摩擦力矩的大小为2分设经过时间圆盘停止转动,则按角动量定理有-M f=0-J=-(MR2+mR2-)=-mv0R 2分∴ 2分}题型:计算题26.{质量为M1=24 kg的圆轮,可绕水平光滑固定轴转动,一轻绳缠绕于轮上,另一端通过质量为M2=5 kg的圆盘形定滑轮悬有m=10 kg的物体.求当重物由静止开始下降了h=0.5 m时,(1)物体的速度;(2)绳中张力.(设绳与定滑轮间无相对滑动,圆轮、定滑轮绕通过轮心且垂直于横截面的水平光滑轴的转动惯量分别为,)}A. (%)试题编号:E17549 24717答案:{解:各物体的受力情况如图所示.图2分由转动定律、牛顿第二定律及运动学方程,可列出以下联立方程:T 1R =J 11=方程各1分共5分T 2r -T 1r =J 22=mg -T 2=ma , a =R 1=r2, v2=2ah求解联立方程,得m/s 2=2 m/s 1分T 2=m(g -a)=58 N 1分T 1==48 N 1分 }题型:计算题 27.{如图所示的阿特伍德机装置中,滑轮和绳子间没有滑动且绳子不可以伸长,轴与轮间有阻力矩,求滑轮两边绳子中的张力.已知m 1=20 kg ,m 2=10 kg .滑轮质量为m 3=5 kg .滑轮半径为r =0.2 m .滑轮可视为均匀圆盘,阻力矩M f =6.6N·m ,已知圆盘对过其中心且与盘面垂直的轴的转动惯量为.}A. (%)试题编号:E17549 24718 答案:{解:对两物体分别应用牛顿第二定律(见图),则有 m 1g -T 1=m 1a ①T 2– m 2g= m 2a ② 2分对滑轮应用转动定律,则有③ 2分对轮缘上任一点,有 a =r ④ 1分又:=T1,=T2⑤则联立上面五个式子可以解出=2 m/s22分T1=m1g-m1a=156 NT2=m2g-m2a=118N 3分}题型:计算题2844.{一匀质细棒长为2L,质量为m,以与棒长方向相垂直的速度v0在光滑水平面内平动时,与前方一固定的光滑支点O发生完全非弹性碰撞.碰撞点位于棒中心的一侧处,如图所示.求棒在碰撞后的瞬时绕O点转动的角速度.(细棒绕通过其端点且与其垂直的轴转动时的转动惯量为,式中的和分别为棒的质量和长度.)}A. (%)试题编号:E17549 24720答案:{解:碰撞前瞬时,杆对O点的角动量为3分式中r为杆的线密度.碰撞后瞬时,杆对O点的角动量为3分因碰撞前后角动量守恒,所以3分∴= 6v0/ (7L) 1分.{一匀质细棒长为2L,质量为m,以与棒长方向相垂直的速度v0在光滑水平面内平动时,与前方一固定的光滑支点O发生完全非弹性碰撞.碰撞点位于棒中心的一侧处,如图所示.求棒在碰撞后的瞬时绕O点转动的角速度.(细棒绕通过其端点且与其垂直的轴转动时的转动惯量为,式中的和分别为棒的质量和长度.)}A. (%)试题编号:E17549 24720答案:{解:碰撞前瞬时,杆对O点的角动量为3分式中r为杆的线密度.碰撞后瞬时,杆对O点的角动量为3分因碰撞前后角动量守恒,所以3分∴= 6v0/ (7L) 1分29.质量为75 kg的人站在半径为2 m的水平转台边缘.转台的固定转轴竖直通过台心且无摩擦.转台绕竖直轴的转动惯量为3000 kg·m2.开始时整个系统静止.现人以相对于地面为1 m·s-1的速率沿转台边缘行走,求:人沿转台边缘行走一周,回到他在转台上的初始位置所用的时间.A. (%)试题编号:E17549 24709答案:解:由人和转台系统的角动量守恒 J11+ J22= 0 2分其中 J1=300 kg·m2,1=v/r=0.5rad / s, J2=3000kg·m2∴2=-J11/J2=-0.05 rad/s 1分人相对于转台的角速度=1-2=0.55 rad/s 1分∴ t=2/=11.4 s 1分。
【大题】工科物理大作业04-刚体定轴转动

【大题】工科物理大作业04-刚体定轴转动 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN0404 刚体定轴转动班号 学号 姓名 成绩一、选择题(在下列各题中,均给出了4个~5个答案,其中有的只有1个是正确答案,有的则有几个是正确答案,请把正确答案的英文字母序号填在题后的括号内)1.某刚体绕定轴作匀变速转动,对刚体上距转轴为r 处的任一质元来说,在下列关于其法向加速度n a 和切向加速度τa 的表述中,正确的是:A .n a 、τa 的大小均随时间变化;B .n a 、τa 的大小均保持不变;C .n a 的大小变化,τa 的大小保持恒定;D .n a 的大小保持恒定,τa 大小变化。
(C )[知识点]刚体匀变速定轴转动特征,角量与线量的关系。
[分析与题解] 刚体中任一质元的法向、切向加速度分别为 r a n 2ω=,r a τβ=当β = 恒量时,t βωω+=0 ,显然r t r a n 202)(βωω+==,其大小随时间而变,ra τβ=的大小恒定不变。
2. 两个均质圆盘A 和B ,密度分别为ρA 和ρB ,且B ρρ>A ,但两圆盘的质量和厚度相同。
若两盘对通过盘心且与盘面垂直的轴的转动惯量分别为A I 和B I ,则 A .B I I >A; B. B I I <A ;C .B I I =A ; D. 不能确定A I 和B I 的相对大小。
(B )[知识点]转动惯量的计算。
[分析与题解] 设A 、B 两盘厚度为d ,半径分别为R A 和R B ,由题意,二者质量相等,即B B A A d R d R ρπρπ22=因为B A ρρ>, 所以22B A R R < 且转动惯量221mR I =,则B A I I <3.在下列关于刚体的表述中,不正确的是:A .刚体作定轴转动时,其上各点的角速度相同,线速度不同;B .刚体定轴转动的转动定律为βI M =,式中β,,I M 均对同一条固定轴而言的,否则该式不成立;C .对给定的刚体而言,它的质量和形状是一定的,则其转动惯量也是唯一确定的;D .刚体的转动动能等于刚体上各质元的动能之和。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、 选择题
[ C ]1、【基础训练2】一轻绳跨过一具有水平光滑轴、质量为M 的定滑轮,绳的两端分别悬有质量为m 1和m 2的物体(m 1<m 2),如图5-7所示.绳与轮之间无相对滑动.若某时刻滑轮沿逆时针方向转动,则绳中的张力
[ D ]2、【基础训练3】如图5-8所示,一质量为m 的匀质细杆AB ,A 端靠在粗糙的竖直墙壁上,B 端置于粗糙水平地面上而静止.杆身与竖直方向成θ角,则A 端对墙壁的压力大 (A) 为
41mg cos θ. (B)为2
1
mg tg θ. (C) 为 mg sin θ. (D) 不能唯一确定
图5-8
个质量相同,速度大小相同,方向相反并在一条直线上的子弹,子弹射入圆盘并且留在盘内,则子弹射入后的瞬间,圆盘的角速度 (A) 增大. (B) 不变. (C) 减小. (D) 不能确定.
【提示】:
把三者看作同一系统时,系统所受合外力矩为零,系统角动量守恒。
m m
图5-11
设L 为每一子弹相对与O 点的角动量大小,ω0为子弹射入前圆盘的角速度,ω为子弹射入后的瞬间与圆盘共同的角速度,J 为圆盘的转动惯量,J 子弹为子弹转动惯量,据角动量守恒定律有:
00
()J L L J J J J J ωω
ωωω+-=+=
<+子弹
子弹
[ C ]4、【自测提高4】光滑的水平桌面上,有一长为2L 、质量为m 的匀质细杆,可绕过其中点且垂直于杆的竖直光滑固定轴O 自由转动,其转动惯量为
3
1mL 2
,起初杆静止.桌面上有两个质量均为m 的小球,各自在垂直于杆的方向上,正对着杆的一端,以相同速率v 相向运动,如图5-19所示.当两小球同时与杆的两个端点发生完全非弹性碰撞后,就与杆粘在一起转动,则这一系统碰撞后的转动角速度应为 (A)
L 32v . (B) L 54v . (C) L 76v . (D) L 98v . (E) L
712v .
图5-19
【提示】:
视两小球与细杆为一系统,碰撞过程中系统所受合外力矩为零,满足角动量守恒条件,所以
2221
[(2)]12
lmv lmv ml ml m l ω+=++
可得答案(C )
[ A ] 5、【自测提高7】质量为m 的小孩站在半径为R 的水平平台边缘上.平台可以绕通过其中心的竖直光滑固定轴自由转动,转动惯量为J .平台和小孩开始时均静止.当小孩突然以相对于地面为v 的速率在台边缘沿逆时针转向走动时,则此平台相对地面旋转的角速度和旋转方向分别为
(A) ⎪⎭⎫
⎝⎛=
R J
mR v 2
ω,顺时针. (B) ⎪⎭⎫ ⎝⎛=R J mR v 2ω,逆时针. (C) ⎪⎭⎫ ⎝⎛+=R mR J mR v 22ω,顺时针. (D) ⎪⎭
⎫
⎝⎛+=R mR J mR v 22ω,逆时针.
【提示】:
二、填空题
1、【基础训练8】绕定轴转动的飞轮均匀地减速,t =0时角速度为05rad ω=,t =20s 时角速度为00.8ωω=,则飞轮的角加速度β= -0.05 rad/s 2 ,t =0到 t =100 s 时间内飞轮所转过的角度θ=
250rad
.
O v 俯视图
2、【基础训练10】如图5-13所示,P 、Q 、R 和S 是附于刚性轻质细杆上的质量分别为4m 、3m 、2m 和m 的四个质点,PQ =QR =RS =l ,则系统对O O '轴的转动惯量为 50ml 2 。
3、【基础训练12】 如图5-14所示,滑块A 、重物B 和滑轮C 的质量分别为m A 、m B 和m C ,滑轮的半径为R ,滑轮对轴的转动惯量J =
2
1
m C R 2.滑块A 与桌面间、滑轮与轴承之间均无摩擦,绳的质量可不计,绳与滑轮之间无相对滑动.滑块A 的加速度
C
B A B m m m g
m a ++=
)(22
4、【自测提高9】一长为l 、质量可以忽略的直杆,两端分别固定有质量为2m 和m 的小球,杆可绕通过其中心O 且与杆垂直的水平光滑固定轴在铅直平面内转动.开始杆与水平方向成某一角度θ,处于静止状态,如图5-21所示.释放后,杆绕O 轴转动.则当杆转到水平位置时,该系统所受到的合外力矩的大小M =/2mgl ,此时该系统角加速度的大小β =
23g l
. 【提示】:
图5-21
5、【自测提高12】一根质量为m 、长为l 的均匀细杆,可在水平桌面上绕通过其一端的竖直固定轴转动.已知细杆与桌面的滑动摩擦系数为μ,则杆转动时受的摩擦力矩的大小为=μmgl /2
三、计算题
1、【基础训练16】一转动惯量为J 的圆盘绕一固定轴转动,起初角速度为0ω,设它所受阻力矩与转动角速度成正比,即M k ω=- (k 为正的常数),求圆盘的角速度从0ω变为0
2
1
ω时所需时间.
2、【基础训练18】如图5-17所示、质量分别为m 和2m 、半径分别为r 和2r 的两个均匀圆盘,同轴地粘在一起,可以绕通过盘心且垂直盘面的水平光滑固定轴转动,对转轴的转动惯量为9mr 2/2,大小圆盘边缘都绕有绳子,绳子下端都挂一质量为m 的重物,求盘的角加速杆可绕水平光滑固定轴O 在竖直面内转动,转轴O 距两端分别为3l 和3
l .轻杆原来静止在竖直位置.今有一质量为m 的小球,以水平速度0v 与杆下端小球m 作对心碰撞,碰后以0
2
1v
的速度返回,试求碰撞后轻杆所获得的角速度.
解:系统所受的合外力矩为零,角动量守恒:
碰前的角动量为:
l mv 3202m
m
2
1
v l
3
2l 3
1
碰后的角动量为:
所以:
得
4、【自测提高17】如图5-25所示,一质量均匀分布的圆盘,质量为0m ,半径为R ,放在一粗糙水平面上(圆盘与水平面之间的摩擦系数为μ),圆盘可绕通过其中心O 的竖直固定光滑轴转动.开始时,圆盘静止,一质量为m 的子弹以水平速度v 0垂直于圆盘半径打入圆盘边缘并嵌在盘边上。
求:(1) 子弹击中圆盘后,盘所获得的角速度.(2) 经过多少时间后,圆盘停止转动.(圆盘绕通过O 的竖直轴的转动惯量为201
2
m R ,
忽略子弹重力造成的摩擦阻力矩)
量为J 0,环的半径为R ,初始时环的角速度为ω0.质量为m 的小球静止在环内最高处A 点,由于某种微小干扰,小球沿环向下滑动,问小球滑到与环心O 在同一高度的B 点和环的最低处的C 点时,环的角速度及小球相对于环的速度各为多大?(设环的内壁和小球都是光滑的,小球可视为质点,环截面半径r <<R.)
解: 选小球和环为系统.运动过程中所受合外力矩为零,故角动量守恒.
即系统起初的角动量J 0ω0与小球滑到B 点时系统角动量相同,
J 0ω0=(J 0+mR 2)ω
所以 00
2
0J J mR ωω=
+ 图5-26
图5-25
ω])3
1
(2)32([3221220l m l m l v m
++-ω])31
(2)32([322132
2200
l m l m l v m l mv ++-=l
v
230
=ω
又因环的内壁和小球都是光滑,只有保守力做功,系统机械能守恒.取过环心的水平面为势能零点,则有
22222000111()222
B J mgR J m R v ωωω+=++
式中v B 表示小球在B 点时相对地面的竖直分速度,也等于它相对于环的速度.代入ω得:
222002J mR R
J gR B ++=ωv
当小球滑到C 点时,由角动量守恒定律,系统的角速度又回复至ω0,又由机械能守恒定律可知,小球在C 的动能完全由在A 点的重力势能转换而来.所以:
()R mg m C 22
12=v , gR C 4=v
四、附加题
1、【基础训练17】在半径为R 的具有光滑竖直固定中心轴的水平圆盘上,有一人静止站立在距转轴为
R 2
1
处,人的质量是圆盘质量的1/10.
开始时盘载人对地以角速度0ω匀速转动,现在此人垂直圆盘半径相对于盘以速率v 沿与盘转动相反方向作圆周运动,如图5-16所示. 已知圆盘对中心轴的转动惯量为
22
1
MR . 图5-16
求:(1) 圆盘对地的角速度.
ω
2、【(自测提高19】一轻绳绕过一定滑轮,滑轮轴光滑,滑轮的半径为R,质量为m/4,均匀分布在其边缘上.绳子的A端有一质量为m的人抓住了绳端,而在绳的另一端B系了一质量为m/2的重物,如图5-27所示。
设人从静止开始相对于绳匀速向上爬时,绳与滑轮间无相对滑动,求B端重物上升的加速度?(已知滑轮对通过滑轮中心且垂直于轮面的轴的转动惯量J=mR2/4)
图5-27。
