多釜串联流动特性的测定
管式反应器流动特性测定实验

管式反应器流动特性测定实验一.实验目的1.了解连续均相管式循环反应器的返混特性; 2.分析观察连续均相管式循环反应器的流动特征; 3.研究不同循环比下的返混程度,计算模型参数n 。
二、实验原理及要点在工业生产上,对某些反应为了控制反应物的合适浓度,以便控制温度、转化率和收率,同时需要使物料在反应器内由足够的停留时间,并具有一定的线速度,而将反应物的一部分物料返回到反应器进口,使其与新鲜的物料混合再进入反应器进行反应。
在连续流动的反应器内,不同停留时间的物料之间的混和称为返混。
对于这种反应器循环与返混之间的关系,需要通过实验来测定。
在连续均相管式循环反应器中,若循环流量等于零,则反应器的返混程度与平推流反应器相近,由于管内流体的速度分布和扩散,会造成较小的返混。
若有循环操作,则反应器出口的流体被强制返回反应器入口,也就是返混。
返混程度的大小与循环流量有关,通常定义循环比R 为:流量离开反应器物料的体积循环物料的体积流量R其中,离开反应器物料的体积流量就等于进料的体积流量循环比R 是连续均相管式循环反应器的重要特征,可自零变至无穷大。
当R=0时,相当于平推流管式反应器; 当R=∞时,相当于全混流反应器。
因此,对于连续均相管式循环反应器,可以通过调节循环比R ,得到不同返混程度的反应系统。
一般情况下,循环比大于20时,系统的返混特性已经非常接近全混流反应器。
返混程度的大小,一般很难直接测定,通常是利用物料停留时间分布的测定来研究。
然而测定不同状态的反应器内停留时间分布时,我们可以发现,相同的停留时间分布可以有不同的返混情况,即返混与停留时间分布不存在一一对应的关系,因此不能用停留时间分布的实验测定数据直接表示返混程度,而要借助于反应器数学模型来间接表达。
停留时间分布的测定方法有脉冲法,阶跃法等,常用的是脉冲法。
当系统达到稳定后,在系统的入口处瞬间注入一定量Q 的示踪物料,同时开始在出口流体中检测示踪物料的浓度变化。
多釜串联

实验报告课程名称: 化工专业实验1 指导老师: 黄灵仙 成绩:__________________ 实验名称: 多釜串联流动特性的测定 实验类型:___________同组学生姓名: 一、实验目的和要求(必填) 二、实验内容和原理(必填) 三、主要仪器设备(必填) 四、操作方法和实验步骤 五、实验数据记录和处理 六、实验结果与分析(必填) 七、讨论、心得一、实验目的1.观察了解多釜串联的流动特性,并与理想流型特性曲线作比较。
2.掌握用脉冲示踪法测定停留时间分布的实验方法及数据处理。
3.根据单个釜的流动特性推测四釜串联的理论流动特性,并与实际测量值进行比较。
二、实验内容和原理1.对于等容积理想全混式多釜串联的流动,如用脉冲示踪法测定其出口浓度变化曲线,经过换算,可得到停留时间分布的密度函数E ( t ),即1()(1)!N Nt N tN t E t eN t t --⎛⎫= ⎪-⎝⎭(1)令-=t t /θ,代入上式 θθθN N Ne N N E ---=1)()!1()( (2)式中 N —釜数t — 整个装置的平均停留时间,(= N(V R )i / v)(V R )i — 每一小釜的体积 v — 流体流量据式(1),(2)可计算一组理想全混式的流动曲线,如图一(a )所示,由于实验测定的是出口浓度变化曲线C ( t ) ~ t ,如图一(b )所示,经下列关系换算,可得E ( t )()()()C t C t E t Co Cdt∞==⎰ 或写成离散型函数1()()nC t E t C t=-∆∑及 1()()()ntC t E tE t C tθ==∆∑ (3)据式(3)可得一组实验测定E ( θ ) ~ θ曲线,可与图一(a )所得到的一组曲线进行拟合比较。
(a )理论值(b )实验值图1 多釜串联的停留时间分布曲线2.计算实测分布曲线的均值(t )和方差2θσ因为 21Nθσ=由上式可计算的模型参数N (釜数)及t ,再与理论值进行比较。
串联流动反应釜停留时间分布的测定

附页:数据处理结果一、单釜实验部分 1, 原始图表2,原始电导率的Origin60作图200400600800100012001400160018000.70.80.91.01.11.21.31.41.5图1 单釜原始图像图2 单釜原始电导率作图3,平滑后原始电导率的Origin60作图200400600800100012001400160018000.70.80.91.01.11.21.31.41.54,浓度与时间的Origin60作图200400600800100012001400160018001020304050图3 单釜平滑后电导率作图 图4 单釜实验KCl 浓度与时间的关系图5,选取数据点计算数学期望、方差及模型参数根据要求,按离散化方法取30个数据点,如表1所示表1 单釜实验选取数据表二、多釜实验部分 1,原始图表2,原始电导率的Origin60作图1002003004005000.81.01.21.41.61.82.0图5 多釜原始图像图6 多釜原始电导率作图3,平滑后原始电导率的Origin60作图1002003004005000.81.01.21.41.61.82.04,浓度与时间的Origin60作图100200300400500010203040506070图7 多釜平滑后电导率作图图8 多釜实验KCl 浓度与时间的关系图5,选取数据点计算数学期望、方差及模型参数根据要求,按离散化方法取30个数据点,如表1—表3所示表2 多釜中釜1的选取数据表。
实验七 多釜串联流动特性的测定

实验报告课程名称: 化工专业实验 指导老师: 成绩:________________实验名称: 多釜串联流动特性的测定 实验类型: 反应工程实验 同组学生姓名: 一、实验目的和要求 二、实验内容和原理 三、主要仪器设备 四、操作方法和实验步骤 五、实验数据记录和处理 六、实验结果与分析 七、讨论、心得一、实验目的1.观察了解多釜串联的流动特性,并与理想流型特性曲线作比较。
2.掌握用脉冲示踪法测定停留时间分布的实验方法及数据处理。
3.根据单个釜的流动特性推测四釜串联的理论流动特性,并与实际测量值进行比较。
二、实验原理1.对于等容积理想全混式多釜串联的流动,如用脉冲示踪法测定其出口浓度变化曲线,经过换算,可得到停留时间分布的密度函数E ( t ),即1()(1)!N Nt N tN t E t eN t t --⎛⎫= ⎪-⎝⎭ (1)()1()(1)!N N N t E N e N t θθθθ--⎛⎫==⎪-⎝⎭…………(2) 式中 N —釜数t — 整个装置的平均停留时间,(= N (V R )i / v ) (V R )i — 每一小釜的体积 v — 流体流量据式(1),(2)可计算一组理想全混式的流动,由于实验测定的是出口浓度变化曲线C ( t ) ~ t ,经下列关系换算,可得E ( t )()()()C t C t E t CoCdt∞==⎰ 或写成离散型函数1()()nC t E t C t=-∆∑及 1()()()ntC t E tE t C tθ==-∆∑ (3)据式(3)可得一组实验测定E ( θ ) ~ θ曲线,可与图1(a)所得到的一组曲线进行拟合比较。
(a)理论值(b)实验值图1 多釜串联的停留时间分布曲线2.计算实测分布曲线的均值(t)和方差2θσ因为21 Nθσ=由上式可计算的模型参数N(釜数)及t,再与理论值进行比较。
三、实验装置及仪器本装置由四个搅拌釜反应器组成,分别装备了不同类型的搅拌桨和挡板,每个搅拌釜反应器可独立操作,也可以串联操作。
应用化工技术专业《多釜串联-图解法》

§4.2.2 图解法
将各釜平均停留时间公式变形为
)()(110
1---=--
=Ai Ai i
A Ai Ai Ai Ai x x c r c c r ττ 利用上两式反响速度是浓度或转化率的函数,可以在坐标图上作出 r A =f(c A )或 r A =f(x A )曲线可以进行图解法计算。
通常在给定了物料的处理量和转化率后需选定锅数和锅的容积时用图解法,往往可以防止复杂动力学方程式代数法求解时的试差,有时测得动力数据不必建立动力学方程可直接进行图解法计算。
图4-5表示的用r A =f(c A ) 关系图解计算程序。
按照以上公式,从横轴上 c AO )1(c -Ai 处出发,作出斜率为)/1(/11i ττ--的直线使之与反响速度曲线相交,交点横坐标即为)(1Ai A c c 。
再从c A1 点出发依次作以后各条操作线求各浓度值,直至c An ,符合工艺最终要求浓度为止,有n 条直线即表示需用n 个釜。
假设各釜容积不等,图上各操作线斜率各异。
假设各釜容积相等,那么各条操作线相互平行。
同理可用r A =f(x A 〕关系图进行求解。
图解法计算的优点是可由实验测得的动力学数据直接作图。
但应注意,仅在反响动力学方程式用反响物之一的浓度函数或转化率函数表示时,且各釜温度相同,体积大小相等时才比拟方便。
否那么相当麻烦。
串联流动反釜停留时间分布测定
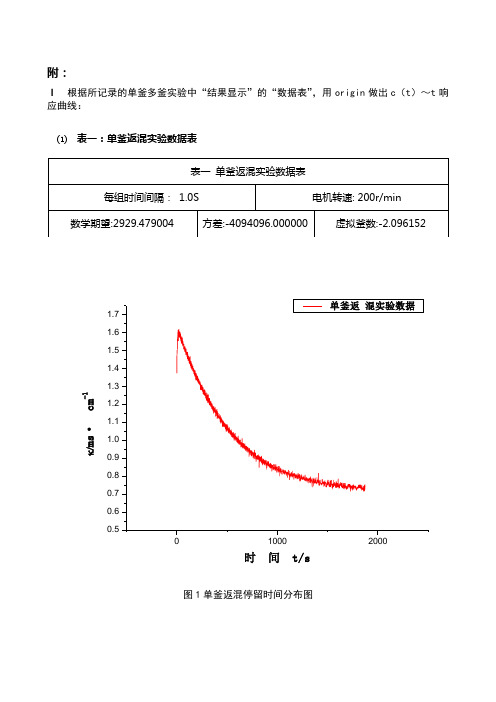
附:Ⅰ 根据所记录的单釜多釜实验中“结果显示”的“数据表”,用origin 做出c (t )~t 响应曲线:⑴ 表一:单釜返混实验数据表100020000.50.60.70.80.91.01.11.21.31.41.51.61.7κ/m s ·c m -1时间t/s图1单釜返混停留时间分布图⑵ 表二:多釜返混实验数据表80016000.50.60.70.80.91.01.11.21.31.41.51.61.71.81.92.0 B C D/m S ·c m -1时间t/s图2 单釜返混停留时间分布图以及模型参数N。
Ⅱ采用离散化方法,间隔取20~30组数据,求出单釜和多釜的t,2t⑴取单釜实验数据如下:表1 单釜实验计算数据824.139s 1824.138759903.22250.18875)()(1800018000≈===∑∑t c t tc t22218001800022s 277861.1923277861.192138759.824903.22000.21919680)()(≈=-=-=∑∑t t c t c tt σ0.409180.409097861387591.8241923.277861222≈===tt σσθ2.44442.4444028680.40909786112≈===θσN⑵ 取多釜实验数据如下:表2 多釜实验计算数据①对于釜1,处理过程如下:表2-1s 766.08050.17400.13406)()(1800018000===∑∑t c t tc t22218001800022s 248417.862080.76650.17500.14617687)()(=-=-=∑∑t t c t c tt σ0.42320.42328665080.766248417.862222≈===tt σσθ362.282.362465240.42328665112≈===θσN② 对于釜2,处理过程如下:表2-2s 796.24521.93517465.625)()(1800018000===∑∑t c t tc t22218001800022s 229293.710245.796935.2117465.625)()(=-=-=∑∑t t c t c tt σ3617.090.36165889245.796229293.710222≈===tt σσθ765.252.7650363490.36165889112≈===θσN③ 对于釜3,处理过程如下:表2-3s 619.27821.79618038.775)()(1800018000===∑∑t c t tc t22218001800022s 216013.944619.827796.212519637465.6)()(=-=-=∑∑t t c t c tt σ3154.00.31537067619.827216013.944222≈===tt σσθ171.313.170871910.31537067112≈===θσN。
实验一 多釜串联连续流动反应器中停留时间分布的测定

实验一 多釜串联连续流动反应器中停留时间分布的测定一、实验目的本实验通过单釜与三釜反应器中停留时间分布的测定,将数据计算结果用多釜串联模型来描述返混程度,从而认识限制返混的措施。
1、掌握停留时间分布的测定方法;2、了解停留时间分布与多釜串联模型的关系;3、掌握多釜串联模型参数N 的物理意义及计算方法。
二、实验原理在连续流动的反应器内,不同停留时间的物料之间的混和称为返混。
返混程度的大小,一般很难直接测定,通常是利用物料停留时间分布的测定来研究。
然而在测定不同状态的反应器内停留时间分布时,可以发现,相同的停留时间分布可以有不同的返混情况,即返混与停留时间分布不存在一一对应的关系,因此不能用停留时间分布的实验测定数据直接表示返混程度,而必须借助于反应器数学模型来间接表达。
物料在反应器内的停留时间完全是一个随机过程,须用概率分布方法来定量描述。
所用的概率分布函数为停留时间分布密度函数E (t)和停留时间分布函数F (t)。
停留时间分布密度函数E (t )的物理意义是:同时进入的N 个流体粒子中,停留时间介于t 到t +dt 间的流体粒子所占的分率dN/N 为E (t )dt 。
停留时间分布函数F (t )的物理意义是:流过系统的物料中停留时间小于t 的物料所占的分率。
停留时间分布的测定方法有脉冲输入法、阶跃输入法等,常用的是脉冲输入法。
当系统达到稳定后,在系统的入口处瞬间注入一定量Q 的示踪物料,同时开始在出口流体中检测示踪物料的浓度变化。
由停留时间分布密度函数的物理含义,可知: E (t )dt =VC (t )/Q (1) ⎰∞=0)(dt t VC Q (2)所以 ⎰⎰∞∞==)()()()()(dtt C t C dtt VC t VC t E (3)由此可见E (t )与示踪剂浓度C (t )成正比。
本实验中用水作为连续流动的物料,以饱和KCl 作示踪剂,在反应器出口处检测溶液的电导值。
在一定范围内,KCl 浓度与电导值成正比,则可用电导值来表达物料的停留时间变化关系,即E (t )∝L (t ),这里L(t)=L t -L ∞,L t 为t 时刻的电导值,L ∞为无示踪剂时电导值。
多釜串联模型的基本假设

多釜串联模型的基本假设多釜串联模型是一种用于描述流体在多个容器中串联流动的模型。
它基于一些基本假设,以简化问题并提供对流体行为的定量描述。
下面将详细介绍多釜串联模型的基本假设。
一、稳态假设多釜串联模型假设系统处于稳态,即流体在各个容器之间的流动速率保持不变。
这意味着系统中不存在时间相关性和变化性,可以通过一组恒定的参数来描述。
二、连续介质假设该模型假设流体是连续不可压缩介质,即认为流体在微观尺度上是连续分布的,并且密度保持不变。
这个假设使得我们可以使用连续性方程来描述流体在各个容器中的质量守恒。
三、均匀混合假设多釜串联模型假设系统中的流体经过每个容器时都能够均匀混合,即认为每个容器内部存在足够强大的搅拌作用使得流体达到均匀分布。
这个假设使得我们可以使用平衡条件来描述各个容器之间的物质交换。
四、忽略摩擦和粘性该模型忽略了流体在容器壁面上的摩擦和粘性效应。
这个假设是为了简化问题并减少计算量,特别适用于处理大容器之间的流体传递。
五、恒定温度假设多釜串联模型假设系统中的温度保持恒定,即认为流体在各个容器之间的温度不发生变化。
这个假设使得我们可以使用热平衡条件来描述各个容器之间的热交换。
六、理想气体状态方程该模型使用理想气体状态方程来描述流体的压力和温度之间的关系。
这个假设适用于低密度和高温度条件下的流体,并且可以简化计算过程。
七、无外部作用力多釜串联模型忽略了外部作用力对系统的影响,如重力、电磁场等。
这个假设是为了简化问题并减少计算量,特别适用于处理小尺寸容器之间的流体传递。
多釜串联模型基于稳态假设、连续介质假设、均匀混合假设、忽略摩擦和粘性、恒定温度假设、理想气体状态方程和无外部作用力等基本假设。
这些假设使得模型简化且易于计算,适用于描述多个容器中流体的串联流动行为。
然而,在实际应用中,我们需要根据具体情况对这些假设进行合理性评估,并在必要时引入更复杂的模型来更准确地描述系统行为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1) 打开蠕动泵,设置流量为最大值,等待其流量稳定,并充满4个釜(充满1个釜约需 6min);
2) 同时将搅拌电机的转速调到设定值,使其达到全混流(推荐值为最大值),等待转速的 稳定;
3) 打开阀门6,将可能残余在管路中的水排净; 4) 关闭阀门6,打开阀门1,让示踪剂充满管路; 5) 等釜出口液体的电导率恒定后(电导率比实验开始的时候有较大的变化,这是因为水的
剂浓度 0.194075 0.193192 0.192521 0.192064 0.191344 0.192201 0.191249 0.191192 0.190493 0.191123 0.190963 0.191138 0.190594 0.190428 0.191120 0.191123 0.190963 0.190909 0.190435 0.191191 0.190646 0.190963
电导率比空气的电导率大),打开阀门2,向釜内脉冲注入示踪剂,记下此时刻t; 6) 脉冲示踪后,注意观察各电导率的读数,等待电导率4的曲线回至走平,此时可以认为4
个釜内的示踪剂被替换完全; 7) 在放大图上选择一区域,满足:开始时刻在t时刻附近,结束时刻在电导率曲线走平的时
刻附近,在这样的一个区域内采集数据,并且将其组名保存为此转速下的电导率值; 8) 停止搅拌桨,停止蠕动泵,将釜内的水排空,关闭电源,结束实验。
总电源,釜式反应器混合特性及流动模式实验研究的远程操作界面如图3所示。蠕动泵将储液槽
中的水打入釜I,从反应器上部流出,依次通过釜II、釜III、釜IV后排出。4个釜的体积均为1
500 mL,各自带有可调速的搅拌电机,分别控制每个釜的搅拌强度,每个釜出口液体浓度由电
导仪测定。
I 蠕动泵 储液槽 1#电磁阀 2# 3# 4# 5# 6# II III IV 搅拌电机 图3 釜式反应器混合特性研究远程实验操作界面
浓度 0.234240 0.226797 0.220768 0.215539 0.211404 0.207762 0.204980 0.202639 0.200987 0.198321 0.197468 0.196124 0.195248 0.195305 0.194781 0.194601 0.193212 0.193272 0.192874 0.192509 0.192695 0.192511
图2 实验流程装置示意图 1-示踪剂高位槽;2-水槽;3-蠕动泵;4-釜式反应器;5-搅拌电机;6-电导槽;7-电导仪;8螺旋式搅拌器;9-纵向挡板;10-浆式搅拌器;11-锚式搅拌器;12~17-电磁阀
4 8 9 12 13 14 15 16 17
利用分配到的实验序号和注册的用户名及密码在客户端上登录,并且点击开始实验,打开
定时,电导率的值基本保持不变,则说明由电导率的值可知釜内流体是 否达到稳定。
2. 根据实验结果,你可得到那些结论?尚存在着哪些问题。 答:由实验结果可知,串联釜数越多就越接近于0,也越接近于平
推流状况达。达到的情况也就越理想。 3. 结合装置特点及操作条件,分析讨论实验值和理论值的偏差原因。
答:本实验全部在电脑的控制下进行,物料的流量基本变化不大, 相对来说也比较稳定,但有些设定值并非输入状态的值,而是由手拖动 鼠标设定的,这使得需设定值相同的几项只是接近,而存在着较大的误 差,从而实验值与理论值偏差较大。
由实验测定的出口浓度与时间的关系数据,经公式(3)变换得到实 验测定
的E(θ)--θ曲线,如下图所示。
由于理论串联数为整数,这使得理论曲线与实际曲线相差很多。
七、思考题
1. 脉冲示踪前怎样根据每个釜出口电导率的变化来判断各釜内流体的 情况? 答:在加脉冲试剂前,由于流体和空气均具有电导率,且当流体稳
令 ,代入上式 (2)
式中 m——釜数 ——整个装置的平均停留时间,(= m(VR)i/v) (VR)i——每一小釜的体积 v ——流体流量
据式(1),(2)可计算一组理想全混流的流动曲线,如图一(a)所示,由于实验测定的是出 口浓度变化曲线C(t)~ t,如图一(b)所示,经下列关系换算,可得E(t)
0.114432124 0.084588424 0.078213663 0.077232977
m计算 值
8.738804836
11.82194864
12.78548992
12.94783709
m实际 取值
9
12
13
13
将得到的m值代入公式(2)即可得到理论曲线,如下图所示。
由于3号4号的m的取值均为13,因此两条曲线重合。
或写成离散型函数
及
(3)
据式(3)可得到一组实验测定E(θ)~θ曲线,可与图一(a)所得到的一组曲线进行拟合比较。
2. 计算实测分布曲线的均值()和方差
图1 多釜串联的停留时间分布曲线
(a)——理论值
(b)——实验值
由上式可计算的模型参数m(釜数)及,再与理论值进行比较。 因为
三、实验装置
四、实验步骤
2700 0.184624 0.179826 0.259084 0.294574
2800 0.687469 0.183554 0.258670 0.296842 2900 0.770193 0.241506 0.260183 0.296312 3000 0.742904 0.272298 0.262006 0.296450 3100 0.712762 0.322428 0.267115 0.295715 3200 0.671123 0.373031 0.275390 0.297756 3300 0.618592 0.438241 0.291310 0.299081 3400 0.563163 0.490534 0.314315 0.302045 3500 0.520588 0.521227 0.334678 0.306920 3600 0.491302 0.541856 0.353894 0.312665 3700 0.442952 0.562696 0.385435 0.322040 3800 0.416383 0.568405 0.406389 0.330897 3900 0.387822 0.569142 0.426877 0.341227 4000 0.357337 0.563349 0.451623 0.355042 4100 0.318318 0.543280 0.480282 0.379758 4200 0.293761 0.519423 0.497896 0.403440 4300 0.270570 0.490487 0.509498 0.426786 4400 0.253488 0.459872 0.513651 0.448181 4500 0.244643 0.440562 0.511625 0.462809 4600 0.236989 0.419587 0.509324 0.471222 4700 0.227946 0.395497 0.502222 0.481970 4800 0.220688 0.373741 0.492510 0.489477 4900 0.215100 0.352639 0.482362 0.493463 5000 0.209692 0.329416 0.466297 0.496320 5100 0.205903 0.312122 0.453327 0.495511 5200 0.202793 0.294016 0.437346 0.493281 5300 0.200154 0.278613 0.420664 0.486226 5400 0.198304 0.264268 0.404391 0.478665 5500 0.196414 0.252961 0.389789 0.469947 5600 0.195282 0.242911 0.376120 0.459207
2.计算结果
项目 1号反应釜 2号反应釜 3号反应釜 4号反应釜 C0 1583.5477 1661.1518 1903.0355 2026.4008 4543.706426 4780.315676 5064.600277 5184.102183
2362481.881 1932965.423 2006194.219 2075629.718
由以上数据绘图可得出口浓度变化曲线C(t)--t,如下图所示。
六、数据处理
1.用梯形法计算各釜流出曲线的面积 以100s为时间间隔,出口浓度为纵坐标计算单个小块的面积,加和即
为各釜流 面积
1号反应釜 2号反应釜 3号反应釜 4号反应釜 1564.836 1642.557 1876.728 1996.327
实验一 多釜串联流动特性的测定
一、实验目的
1. 观察了解多釜串联的流动特性,并与理想流型特性曲线作比较。 2. 掌握用脉冲示踪法测定停留时间分布的实验方法及数据处理。
二、实验原理
1. 对于等容积理想全混流多釜串联的流动,如用脉冲示踪法测定其出口浓度变化曲线,经过 换算,可得到停留时间分布的密度函数E(t),即 (1)
五.原始试验数据记录
原始试验数据表
1号反应釜 2号反应釜 3号反应釜 4号反应釜
时间/s 出口示踪 出口示踪剂 出口示踪 出口示踪剂
剂浓度
浓度
剂浓度
浓度
2500 0.183270 0.179395 0.257960 0.295839
2600 0.185021 0.180598 0.258373 0.295726
浓度 0.448285 0.437075 0.426060 0.414567 0.403667 0.393358 0.383117 0.373708 0.364777 0.356552 0.349832 0.342917 0.337651 0.332439 0.327602 0.323368 0.319798 0.315624 0.312647 0.310863 0.309073 0.305634
