微专题:椭圆中斜率之积为定值的问题探究
微专题:椭圆中斜率之积为定值的问题探究

微专题:解析几何中斜率之积为定值(2221ab k k -=•)的问题探究【教学重点】掌握椭圆中2221ab k k -=•的形成的路径探寻及成果运用理性判断【教学难点】运算的设计和化简活动一:2221ab k k -=•形成的路径探寻1. 若AB 是椭圆)0(12222>>=+b a by a x 上的不过原点的弦,点P 是弦AB 的中点,且直线OP,AB的斜率都存在,求PO ABK K •.【解析】 :设点()0,y x P,()11,y x A ,()22,y x B ,则有;;)2(1)1(1222222221221=+=+bya xb y a x (代点作差)将①式减②式得,,,所以所以,即22ab K K POAB-=•.【结论形成总结】【结论1】 若AB 是椭圆)0(12222>>=+b a by a x 上的非直径的弦,点P 是弦AB 的中点,且直线OP,AB 的斜率都存在,则1222-=-=•e ab K K POAB .2.已知AB 是椭圆)0(12222>>=+b a by a x 上过原点的弦,点P 是椭圆异于A,B 的任意一点,若直线PA,PB 的斜率都存在,记直线PA,PB 的斜率分别为21k k ,.求21k k •的值。
【解法1】:设()0,y x P,()11,y x A 又因为A,B 是关于原点对称,所以点B 的坐标为()11-,-y x B ,所以212021201010101021x x y y x x y y x x y y k k --=++•--=•.又因为点()00,y x P ,()11,y x A 在椭圆上,所以有;;)2(1)1(1221221220220=+=+b y a x b y a x两式相减得,2221202120-ab x x y y =--,所以2221ab k k -=•.【方法小结】本解法从设点入手,利用“点在曲线上”代点作差使用“点差法”。
2020年二轮微专题椭圆中两直线斜率之积为定值的问题

微专题34 椭圆中两直线斜率之积为定值的问题定点定值问题是圆锥曲线中十分重要的研究课题,蕴含着动、静依存的辩证关系,深刻体现了数学的魅力,在高考中常常涉及此类问题且位于中档题的位置.本专题以椭圆中两直线斜率之积为条件,从具体问题入手,通过对解决方法进行总结辨析,使学生能够根据问题的条件寻找与设计更合理、更简捷的运算途径,并引导学生发现这类问题所具有的更一般性规律.过椭圆C :x 24+y 2=1的上顶点A 作互相垂直的直线分别交椭圆于M ,N 两点.求证:直线MN 过定点,并求出该定点坐标.本题考查的是定点问题,由题意可知,题中的两已知直线存在斜率,且斜率之积为-1,利用此结论,结合韦达定理及代数恒等变形,导出动直线可化为点斜式方程,其中所过的点是一个定点,从而证明动直线过定点.在平面直角坐标系xOy 中,椭圆C :x 24+y 23=1的左顶点为A ,P ,Q 是椭圆C 上的两个动点.(1)如图34-1,当P ,O ,Q 三点共线时,直线P A ,QA 分别与y轴交于M ,N 两点,求证:AM →·AN →为定值;(2)设直线AP ,AQ 的斜率分别为k 1,k 2,当k 1·k 2=-1时,求证:直线PQ 经过定点R.图34-1在平面直角坐标系xOy 中,已知椭圆T的方程为x 22+y 2=1.设A ,B ,M 是椭圆T 上的三点(异于椭圆顶点),且存在锐角θ,使OM→=cos θOA →+sin θOB →.(1)求证:直线OA 与OB 的斜率之积为定值;(2)求OA 2+OB 2的值.(江苏卷)如图34-2,在平面直角坐标系xOy 中,已知椭圆x 29+y 25=1的左、右顶点为A ,B ,设过点T (9,m )的直线TA ,TB 与此椭圆分别交于点M (x 1,y 1),N (x 2,y 2),其中m >0,y 1>0,y 2<0.图34-2求证:直线MN必过x轴上的一定点(其坐标与m无关).已知椭圆C:x2a2+y2b2=1(a>b>0)的长轴长为4,两准线间距离为4 2.设A为椭圆C的左顶点,直线l过点D(1,0),且与椭圆C 相交于E,F两点.图34-3(1)求椭圆C的方程;(2)若△AEF的面积为10,求直线l的方程;(3)已知直线AE,AF分别交直线x=3于点M,N,线段MN的中点为Q,设直线l和QD的斜率分别为k(k≠0),k′,求证:k·k′为定值.(本小题满分16分)(2019·南京一模) 已知椭圆C:x2a2+y2b2=1(a>b>0)的两个焦点之间的距离为2,两条准线间的距离为8,直线l:y=k(x-m)(m∈R)与椭圆C相交于P,Q两点.(1)求椭圆C的方程;(2)设椭圆的左顶点为A,记直线AP、AQ的斜率分别为k1、k2.①若m=0,求k1k2的值;②若k 1k 2=-14,求实数m 的值. (1)x 24+y 23=1;(2)①-34;②m =1.因为椭圆C 的两个焦点间距离为2,两准线间的距离为2×a 2c =8,所以a =2,c =1,所以b 2=3,所以椭圆的方程为x 24+y 23=1. …………………………3分(求出椭圆方程)①设P (x 0,y 0),由于m =0,则Q (-x 0,-y 0),由x 204+y 203=1,得y 20=3-3x 204…………………………5分(设出点P (x 0,y 0)求出关系式y 20=3-34x 20)所以k 1k 2=y 0x 0+2·-y 0-x 0+2=y 20x 20-4=3-3x 204x 20-4=-34.…………………………8分(利用上面关系式,推证k 1k 2=定值.) ②由(1)得A (-2,0).设P (x 1,y 1),设直线AP 的方程为AP :y =k 1(x +2),联立⎩⎨⎧ x 24+y 23=1y =k 1(x +2),消去y ,得(3+4k 21)x 2+16k 21x +16k 21-12=0,所以x A ·x 1=16k 21-123+4k 21,…………………………10分(联立方程组,写出韦达定理)所以x 1=6-8k 213+4k 21, 代入y =k 1(x +2)得y 1=12k 13+4k 21, 所以P (6-8k 213+4k 21,12k 13+4k 21).…………………………12分(求出点P 的坐标) 由k 1k 2=-14,得k 2=-14k 1,所以Q (24k 21-21+12k 21,-12k 11+12k 21).…………………………13分(由点P 坐标求得Q 坐标) 设M (m ,0),由P ,Q ,M 三点共线,得PM →=λQM →,即12k 13+4k 21×(24k 21-21+12k 21-m )=-12k 11+12k 21×(6-8k 213+4k 21-m ), 化简得(m -1)(16k 21+4)=0,所以m =1. …………………………16分(由三点共线构建方程,并求出m 的值)设P (x 1,y 1),Q (x 2,y 2),联立⎩⎨⎧ x 24+y 23=1y =k (x -m ),消去y ,得(3+4k 2)x 2-8mk 2x +4m 2k 2-12=0,所以x 1+x 2=8mk 23+4k 2,x 1·x 2=4m 2k 2-123+4k 2…………………………10分 而k 1k 2=y 1x 1+2·y 2x 2+2=k (x 1-m )x 1+2·k (x 2-m )x 2+2=k 2[x 1x 2-m (x 1+x 2)+m 2]x 1x 2+2(x 1+x 2)+4=-14,13分 化简得k 2(3m 2-12)4m 2k 2+16mk 2+16k2=-14,即m 2k 2+mk 2-2k 2=0. 因为k 2≠0,所以m 2+m -2=0,解得m =1或m =-2(舍去). 当m =1时,Δ>0,所以,m =1. …………………………16分答题模板 第一步:求出椭圆方程;第二步:设点P 坐标,推出点P 坐标满足的等式,y 20=3-34x 20;第三步:利用第二步中的等式推出k 1k 2=-34;第四步:联立方程组,写出韦达定理;第五步:写出点P 的坐标;第六步:由条件求出Q 点坐标;第七步:由P ,M ,Q 共线,列出关于m 的方程,并求得解.作业评价已知椭圆x 216+y 24=1的左顶点为A ,过A 作两条弦AM ,AN 分别交椭圆于M ,N 两点,直线AM ,AN 的斜率记为k 1,k 2,满足k 1·k 2=-2,则直线MN 经过的定点为________.已知椭圆C :9x 2+y 2=m 2(m >0),直线l 不过原点O 且不平行于坐标轴,l 与C 有两个交点A ,B ,线段AB 的中点为M .则直线OM 的斜率与l 的斜率的乘积为____________.如图34-4所示,已知椭圆C :x 24+y 2=1的上、下顶点分别为A ,B ,点P 在椭圆上,且异于点A ,B ,直线AP ,BP 与直线l :y =-2分别交于点M ,N .当点P 运动时,以MN 为直径的圆经过的定点是______.图34-4已知椭圆C :x 24+y 22=1的上顶点为A ,直线l :y =kx +m 交椭圆于P ,Q 两点,设直线AP ,AQ 的斜率分别为k 1,k 2.若k 1·k 2=-1,则直线l :y =kx +m 过定点________.(1)求椭圆E 的方程;(2)若点A ,B 分别是椭圆E 的左、右顶点,直线l 经过点B 且垂直于x 轴,点P 是椭圆上异于A ,B 的任意一点,直线AP 交l 于点M .(i )设直线OM 的斜率为k 1,直线BP 的斜率为k 2,求证:k 1k 2为定值;(ii )设过点M 垂直于PB 的直线为m .求证:直线m 过定点,并求出定点的坐标.已知椭圆C :x 2a 2+y 2b 2=1()a >b >0的离心率为12,以原点为圆心,椭圆的短半轴长为半径的圆与直线7x -5y +12=0相切.(1)求椭圆C 的方程;(2)设A ()-4,0,过点R ()3,0作与x 轴不重合的直线l 交椭圆C于P ,Q 两点,连接AP ,AQ 分别交直线x =163于M ,N 两点,若直线MR ,NR 的斜率分别为k 1,k 2,试问:k 1k 2是否为定值?若是,求出该定值,若不是,请说明理由.已知椭圆x2a2+y2b2=1(a>b>0)的离心率为22,且过点P(22,12),记椭圆的左顶点为A.(1)求椭圆的方程;(2)设垂直于y轴的直线l交椭圆于B,C两点,试求△ABC面积的最大值;(3)过点A作两条斜率分别为k1,k2的直线交椭圆于D,E两点,且k1k2=2,求证:直线DE恒过定点.在平面直角坐标系xOy中,已知椭圆x2a2+y2b2=1(a>b>0)的左、右顶点分别为A、B,焦距为2,直线l与椭圆交于C,D两点(均异于椭圆的左、右顶点).当直线l过椭圆的右焦点F且垂直于x轴时,四边形ACBD的面积为6.⑴求椭圆的标准方程;(2)设直线AC,BD的斜率分别为k1,k2.①若k2=3k1,求证:直线l过定点;②若直线l过椭圆的右焦点F,试判断k1k2是否为定值,并说明理由.。
椭圆中斜率之积为定值的问题

椭圆中斜率之积为定值的问题
哎呀,啥是椭圆中斜率之积为定值的问题呀?这对我这个小学生来说,简直就像一个超级大怪兽!
我们先来看看椭圆是啥吧。
椭圆就像一个被压扁的圆,它有两个焦点,就像两个小眼睛盯着你。
那斜率又是什么呢?想象一下,你在山坡上往上爬,山坡的陡峭程度就是斜率。
那在椭圆里,斜率之积为定值,这可太神奇啦!比如说,有两个点在椭圆上,它们连接起来的线的斜率相乘,结果居然是一个不变的数!这难道不像魔法吗?
我就想啊,这和我们平常玩的游戏有啥不一样?比如说跳皮筋,每次跳的高度都不一样,可在椭圆里,这斜率之积居然就固定啦!
老师给我们讲的时候,我瞪大眼睛,心里直犯嘀咕:“这咋就这么难理解呢?”同桌也一脸迷茫,小声跟我说:“这比数学作业还难!”
我们一起努力思考,互相讨论。
我问他:“你说这是不是就像我们跑步,速度和时间的乘积是路程,在椭圆里就是斜率和啥啥的乘积是个定值?”他摇摇头说:“我也不太清楚呢!”
后来,老师又给我们举了好多例子,画了好多图,慢慢地,好像有点懂啦。
我觉得吧,这椭圆中斜率之积为定值的问题,虽然一开始让人头疼,但只要我们不放弃,努力去想,还是能搞明白的。
就像爬山,虽然过程很累,但爬到山顶看到美景的那一刻,一切都值得啦!所以呀,遇到难题别害怕,加油冲就对啦!。
椭圆中斜率乘积为定值引出的直线过定点问题
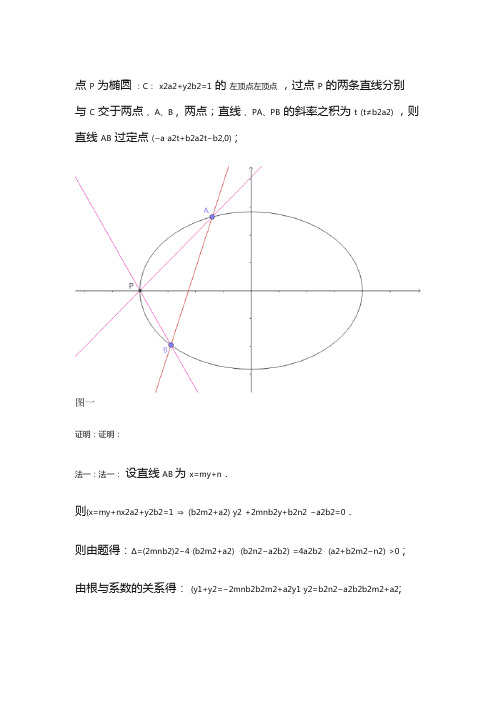
点P为椭圆:C:x2a2+y2b2=1的左顶点左顶点,过点P的两条直线分别与C交于两点、A、B , 两点;直线、PA、PB的斜率之积为t(t≠b2a2),则直线AB过定点(−a⋅a2t+b2a2t−b2,0) ;图一证明:证明:法一:法一:设直线AB为x=my+n .则{x=my+nx2a2+y2b2=1⇒(b2m2+a2)⋅y2+2mnb2y+b2n2−a2b2=0 .则由题得:Δ=(2mnb2)2−4⋅(b2m2+a2)⋅(b2n2−a2b2)=4a2b2⋅(a2+b2m2−n2)>0 ; 由根与系数的关系得:{y1+y2=−2mnb2b2m2+a2y1⋅y2=b2n2−a2b2b2m2+a2;设A(my1+n,y1) , B(my2+n,y2) , 又P(−a,0), kPA⋅kPB=t ,所以kPA⋅kPB=y1−0my1+n+a⋅y2−0my2+n+a=t⇔(tm2−1)⋅y1y2+tm(n+a)⋅(y1+y2)+t(n+a)2=0 ;代入{y1+y2=−2mnb2b2m2+a2y1⋅y2=b2n2−a2b2b2m2+a2得:(tm2−1)⋅b2n2−a2b2b2m2+a2+tm(n+a)⋅(−2mnb2b2m2+a2)+t(n+a)2=0 ,化简得:(a2t−b2)n2+2ta3n+ta4+a2b2=0 ,因式分解得:[(a2t−b2)n+a(a2t+b2)]⋅(n+a)=0 ,(t≠b2a2)解得:n=a⋅b2+a2tb2−a2t ,或者n=−a(此时直线过点,不符合题意,舍去)(此时直线AB过点P,不符合题意,舍去)因此直线AB过定点(−a⋅a2t+b2a2t−b2,0) ;法二:法二:椭圆:C:x2a2+y2b2=1向右平移a个单位长度,即将椭圆C的左顶点P平移到原点O,如图二;图二则此时椭圆方程为(x−a)2a2+y2b2=1 ,化简为x2a2−2xa+y2b2=0;设平移后直线AB为mx+ny=1 .联立{mx+ny=1x2a2−2xa+y2b2=0得:x2a2−2xa⋅(mx+ny)+y2b2=0;化简得:(1a2−2ma)⋅x2−2na⋅xy + +1b2⋅y2=0 ,等式两边同时除以x2齐次化得:1b2⋅(yx)2−2na⋅(yx)+1a2−2ma=0 ;设平移后A(x1,y1) , B(x2,y2) ,又平移后的直线、PA、PB的斜率之积依然为t(t≠b2a2),则kPA⋅kPB=t=y1x1⋅y2x2 .由根与系数的关系得:y1x1⋅y2x2=1a2−2ma1b2=t,解得:m=b2−a2t2ab2 ,所以平移后直线AB为b2−a2t2ab2⋅x+ny=1,过定点(2ab2b2−a2t,0) ,再平移回去即可得原直线过定点(2ab2b2−a2t−a,0) ,化简即可得直线AB过定点(−a⋅a2t+b2a2t−b2,0) ;注:如果点P为椭圆C右顶点右顶点,则直线AB过定点(a⋅a2t+b2a2t−b2,0) ;对于法一法一,因式分解是一个难点,想必到这里会劝退了一波人,不过这里有巧可钻;从图一可知,当点A或点B在无限靠近点P时,直线AB也无限接近点P,所以在解关于n的方程时,必有一增根n=−a;因此在因式分解(a2t−b2)n2+2ta3n+ta4+a2b2=0时,可以借助这一点,利用多项式除法化简即可得[(a2t−b2)n+a(a2t+b2)]⋅(n+a)=0;对于法二法二,则是利用齐次化的方法,对于解决斜率之和与斜率之积问题,齐次化的方法不失为一种简单而又巧妙的方法;。
微专题:椭圆中斜率之积为定值的问题探究

微专题:解析几何中斜率之积为定值(2221ab k k -=•)的问题探究【教学重点】掌握椭圆中2221ab k k -=•的形成的路径探寻及成果运用理性判断【教学难点】运算的设计和化简活动一:2221ab k k -=•形成的路径探寻1. 若AB 是椭圆)0(12222>>=+b a by a x 上的不过原点的弦,点P 是弦AB 的中点,且直线OP,AB的斜率都存在,求PO ABK K •.【解析】 :设点()0,y x P,()11,y x A ,()22,y x B ,则有;;)2(1)1(1222222221221=+=+bya xb y a x (代点作差)将①式减②式得,,,所以所以,即22ab K K POAB-=•.【结论形成总结】【结论1】 若AB 是椭圆)0(12222>>=+b a by a x 上的非直径的弦,点P 是弦AB 的中点,且直线OP,AB 的斜率都存在,则1222-=-=•e ab K K POAB .2.已知AB 是椭圆)0(12222>>=+b a by a x 上过原点的弦,点P 是椭圆异于A,B 的任意一点,若直线PA,PB 的斜率都存在,记直线PA,PB 的斜率分别为21k k ,.求21k k •的值。
【解法1】:设()0,y x P,()11,y x A 又因为A,B 是关于原点对称,所以点B 的坐标为()11-,-y x B ,所以212021201010101021x x y y x x y y x x y y k k --=++•--=•.又因为点()00,y x P ,()11,y x A 在椭圆上,所以有;;)2(1)1(1221221220220=+=+b y a x b y a x两式相减得,2221202120-ab x x y y =--,所以2221ab k k -=•.【方法小结】本解法从设点入手,利用“点在曲线上”代点作差使用“点差法”。
椭圆中两直线斜率积(和)为定值与定点问题专题

椭圆中两直线斜率积(和)为定值与定点问题1.过椭圆C :x 24+y 2=1的上顶点A 作斜率分别为1和-1的直线分别交椭圆于M ,N 两点.则直线MN 与y 轴交点的坐标是________.2.已知椭圆C :9x 2+y 2=m 2(m >0),直线l 不过原点O 且不平行于坐标轴,l 与C 有两个交点A ,B ,线段AB 的中点为M.则直线OM 的斜率与l 的斜率的乘积为________.3.如图,已知椭圆C :x 24+y 2=1的上、下顶点分别为A ,B ,点P 在椭圆上,且异于点A ,B 的直线AP ,BP 与直线l :y =-2分别交于点M ,N.当点P 运动时,以MN 为直径的圆经过的定点是________.4.已知椭圆C :x 24+y 22=1的上顶点为A ,直线l :y =kx +m 交椭圆于P ,Q 两点,设直线AP ,AQ 的斜率分别为k 1,k 2.若k 1·k 2=-1,则直线l :y =kx +m 过定点________.5.已知椭圆x 236+y 24=1上一点M(32,2),过点M 作两直线与椭圆C 分别交于相异两点A ,B ,∠AMB 的平分线与y 轴平行,则直线AB 的斜率为定值________.6.如图,已知椭圆E 1方程为x 2a 2+y 2b 2=1(a >b >0),圆E 2方程为x 2+y 2=a 2,过椭圆的左顶点A 作斜率为k 1的直线的l 1与椭圆E 1和圆E 2分别相交于B ,C.设D 为圆E 2上不同于A 的一点,直线AD 的斜率为k 2,当k 1k 2=b 2a2时,直线BD 过定点________.7.已知椭圆x 23+y 22=1,过点P(1,1)分别作斜率为k 1,k 2的椭圆的动弦AB ,CD ,设M ,N 分别为线段AB ,CD 的中点.若k 1+k 1,求证直线MN 恒过定点,并求出定点坐标.8.已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为63,以原点O 为圆心,椭圆C 的长半轴长为半径的圆与直线2x -2y +6=0相切.(1)求椭圆C 的标准方程;(2)已知点A ,B 为动直线y =k(x -2)(k ≠0)与椭圆C 的两个交点,问:在x 轴上是否存在定点E ,使得EA →2+EA →·AB →为定值?若存在,试求出点E 的坐标和定值;若不存在,请说明理由.1.答案:⎝ ⎛⎭⎪⎫0,-35. 解析:由直线AM ,AN分别和椭圆方程联立,即可求得M 坐标为⎝ ⎛⎭⎪⎫-85,-35和N 坐标为⎝ ⎛⎭⎪⎫85,-35,进而可求得MN 直线方程y =-35,然后求得MN 与y 轴交点的坐标⎝⎛⎭⎪⎫0,-35. 2.答案:-9. 解析:设直线l :y =kx +b (k ≠0,b ≠0),A (x 1,y 1),B (x 2,y 2),M (x M ,y M ).将y =kx +b 代入9x 2+y 2=m 2得(k 2+9)x 2+2kbx +b 2-m 2=0,故x M =x 1+x 22=-kb k 2+9,易得y M =9bk 2+9,从而k OM ·k =-9. 3.答案:()0,-2±23.解析:设点P (x 0,y 0),直线AP ,BP 的斜率分别为k 1,k 2,易得k 1k 2=y 0-1x 0·y 0+1x 0=y 02-1x 02= -14.所以AP 的方程为y =k 1x +1,BP 的方程为y=k 2x -1=-14k 1x -1,所以M ⎝ ⎛⎭⎪⎫-3k 1,-2,N (4k 1,-2),则以MN 为直径的圆的方程为⎝ ⎛⎭⎪⎫x +3k 1(x -4k 1)+(y +2)2=0.即x 2+y 2+⎝ ⎛⎭⎪⎫3k 1-4k 1x +4y -8=0,所以⎩⎪⎨⎪⎧x =0x 2+y 2+4y -8=0.所以MN 为直径的圆过定点(0,-2±23). 4.答案:x 225+y 216=1.解析:设动点M (x ,y ),由题意(x -3)2+y 2⎪⎪⎪⎪⎪⎪253-x =35,化简得x 225+y 216=1,所以动点M 的轨迹方程是x 225+y 216=1.5.答案:13.解析:设直线MA 的斜率为k ,A (x 1,y 1),B (x 2,y 2),由题直线MA 与MB 的斜率互为相反数,直线MB 的斜率为-k ,联立直线MA 与椭圆方程:⎩⎪⎨⎪⎧y =kx +2-32kx 236+y 24=1,整理得(9k 2+1)x 2+182k (1-3k )x +162k 2-108k -18=0,得x 1=182(3k 2-k )9k 2+1-32, 所以x 2=182(3k 2+k )9k 2+1- 32,整理得x 2-x 1=362k 9k 2+1,x 2+x 1=1082k29k 2+1-6 2.又y 2-y 1=-kx 2+2+32k -(kx 2+2-32k )=-k (x 2+x 1)+62k .=-108k 39k 2+1+122k =122k 9k 2+1,所以k AB =y 2-y 1x 2-x 1=122k 9k 2+1362k 9k 2+1=13为定值. 6.答案:直线BD 过定点(a ,0).解法1由⎩⎪⎨⎪⎧y =k 1(x +a ),x 2a2+y2b2=1,得x 2-a 2a 2+k 12(x +a )2b 2=0,所以x=-a ,或x =a (b 2-k 12a 2)b 2+a 2k 12,因为x B ≠-a ,所以x B =a (b 2-k 12a 2)b 2+a 2k 12,则y B =k 1(x B+a )=2ab 2k 1b 2+a 2k 12.由⎩⎪⎨⎪⎧y =k 2(x +a ),x 2+y 2=a 2,得x 2-a 2+k 22(x +a )2=0,得x=-a ,或x =a (1-k 22)1+k 22,同理,得x D =a (1-k 22)1+k 22,y D =2ak 21+k 22,当k 1k 2=b 2a 2时,x B =a ⎝⎛⎭⎪⎫b 2-b 4a 2k 22b 2+b 4a2k 22=a (a 2-b 2k 22)a 2+b 2k 22,y B =2ab 2k 2a 2+b 2k 22, k BD=2ab 2k 2a 2+b 2k 22-2ak 21+k 22a (a 2-b 2k 22)a 2+b 2k 22-a (1-k 22)1+k 22=-1k 2,所以BD ⊥AD ,因为E 2为圆,所以∠ADB 所对圆E 2的弦为直径,从而直线BD 过定点(a ,0).解法2直线BD 过定点(a ,0),证明如下:设P (a ,0),B (x B ,y B ),则x B 2a 2+y B 2b2=1(a >b >0),k AD k PB =a2b 2k 1k PB =a 2b 2·y B x B +a ·y B x B -a =a 2b 2·y B 2x B 2-a 2=a 2b 2⎝ ⎛⎭⎪⎫-b 2a 2=-1,所以PB ⊥AD ,又PD ⊥AD .所以三点P ,B ,D 共线,即直线BD 过定点P (a ,0).7.答案:直线MN 恒过定点,且坐标为⎝ ⎛⎭⎪⎫0,-23. 解析:依题设,k 1≠k 2.设M (x M ,y M ),直线AB 的方程为y -1=k 1(x -1),即y =k 1x +(1-k 1),亦即y =k 1x +k 2,代入椭圆方程并化简得(2+3k 12)x 2+6k 1k 2x +3k 22-6=0.于是,x M =-3k 1k 22+3k 12,y M =2k 22+3k 12.同理,x N =-3k 1k 22+3k 22,y N =2k 12+3k 22.当k 1k 2≠0时,直线MN 的斜率k =y M -y Nx M -x N= 4+6(k 22+k 2k 1+k 12)-9k 2k 1(k 2+k 1)=10-6k 2k 1-9k 2k 1.直线MN 的方程为y -2k 22+3k 12=10-6k 2k 1-9k 2k 1⎝ ⎛⎭⎪⎫x --3k 1k 22+3k 12, 即y =10-6k 2k 1-9k 2k 1x +错误!,亦即y =10-6k 2k 1-9k 2k 1x -23.此时直线过定点⎝ ⎛⎭⎪⎫0,-23.当k 1k 2=0时,直线MN 即为y 轴,此时亦过点⎝⎛⎭⎪⎫0,-23.综上,直线MN 恒过定点,且坐标为⎝⎛⎭⎪⎫0,-23. 8.答案:(1)椭圆C 的标准方程为x 26+y 22=1. (2)在x 轴上存在定点E ⎝ ⎛⎭⎪⎫73,0使得EA →2+EA →·AB →为定值,且定值为-59.解析:(1)由e =63,得c a =63,即c =63a ,①.又以原点O 为圆心,椭圆C 的长半轴长为半径的圆为x 2+y 2=a 2,且该圆与直线2x -2y +6=0相切,所以a =|6|22+(-2)2=6,代入①得c =2,所以b 2=a 2-c 2=1,所以椭圆C 的标准方程为x 26+y 22=1. (2)由⎩⎪⎨⎪⎧x 26+y 22=1,y =k (x -2),得(1+3k 2)x 2-12k 2x +12k 2-6=0.设A (x 1,y 1),B (x 2,y 2),所以x 1+x 2=12k21+3k 2,x 1x 2=12k 2-61+3k2.根据题意,假设x 轴上存在定点E (m ,0),使得EA →2+EA →·AB →=(EA →+AB →)·EA →=EA →·EB →为定值,则EA →·EB →=(x 1-m ,y 1)·(x 2-m ,y 2)=(x 1-m )(x 2-m )+y 1y 2=(k 2+1)x 1x 2-(2k 2+m )(x 1+x 2)+(4k 2+m 2)=错误!,要使上式为定值,即与k 无关,只需3m 2-12m +10=3(m 2-6),解得m =73,此时,EA →2+EA →·AB →=m 2-6=-59,所以在x 轴上存在定点E ⎝ ⎛⎭⎪⎫73,0使得EA →2+EA →·AB →为定值,且定值为-59.。
微专题22 椭圆中两直线斜率积(和)为定值与定点问题

kADkPB=ab22k1kPB=ab22·xBy+B a·xBy-B a=ab22·x2B-y2B a2=ab22-ba22=-1,所以 PB ⊥AD,又 PD⊥AD.所以三点 P,B,D 共线,即直线 BD 过定点 P(a,0).
7.已知椭圆x32+y22=1,过点 P(1,1)分别作斜率为 k1,k2 的椭圆的动弦 AB,CD,设 M,N 分别为线段 AB,CD 的中点.若 k1+k1,求证 直线 MN 恒过定点,并求出定点坐标.
y=kx+ 2-3 2k
3x62 +y42=1
,
整理得(9k2+1)x2+18 2k(1-3k)x+162k2-108k-18=0, 得 x1=18 92k23+k21-k-3 2, 所以 x2=18 92k23+k21+k-3 2, 整理得 x2-x1=93k62+2k1,
x2+x1=190k82+21k2-6 2.
2.已知椭圆 C:9x2+y2=m2(m>0),直线 l 不过原点 O 且不平行于坐
标轴,l 与 C 有两个交点 A,B,线段 AB 的中点为 M.则直线 OM 的
斜率与 l 的斜率的乘积为 -9
.
解析:设直线 l:y=kx+b(k≠0,b≠0),A(x1,y1),B(x2,y2),M(xM, yM). 将 y=kx+b 代入 9x2+y2=m2 得(k2+9)x2+2kbx+b2-m2=0,故 xM
=x1+2 x2=-k2k+b 9,易得 yM=k29+b 9, 从而 kOM·k=-9.
3.如图,已知椭圆 C:x42+y2=1 的上、下顶点分别为 A,B,点 P 在椭
圆上,且异于点 A,B 的直线 AP,BP 与直线 l:y=-2 分别交于点
M,N.当点 P 运动时,以 MN 为直径的圆经过的定点是
椭圆中一类斜率之积为定值 高考数学

主讲人:某某某老师
某某学校
一、教材习题变式构建模型
二、高考解题析游刃有余
试卷讲评课件
椭圆是高考考查的难点之一,椭圆中一类斜率之积问题早有出现.
本文从教材出发,通过一系列的变式,转化和化归达到高考考查要求,
体现出试题源于教材且高于教材的理念,同时,找到在椭圆中一类斜
−′
=
′
=
,则
=
−
= ,则′ = −
−
−
−′
′
−
故,直线与直线的斜率之积为定值− 。
=
........②
′
− ,
........③
试卷讲评课件
x2
[变式3]:已知椭圆Γ: 2
率之积问题的通性.
一、教材习题变式构建模型
试卷讲评课件
典型习题:(人教A版选修2-1)设点A,B的
坐标分别为 −5,0 、 5,0 ,直线AM,BM相交
4
于点M,且他们的斜率之积为− ,求点M的轨
9
迹方程。
试卷讲评课件
解:如图1,设点 , ,由已知得, =
⋅ =
⋅ =
−
故,直线与直线的斜率之积为定值− 。
试卷讲评课件
【评析】此题也属于斜率之积为定值,但此解法与变式1、2、3有所不
同,直线与椭圆有一个交点,联立两直线方程得出点的坐标,继
而得出 ∗ 式,再联立直线方程与椭圆方程,消去其中一个变量,得出
关于另一变量的一元二次方程,再利用一元二次方程有一个实数解
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
微专题:椭圆中斜率之积为定值的问题探究微专题:解析几何中斜率之积为定值的问题探究教学重点】掌握椭圆中斜率之积为定值的运算设计和化简。
教学难点】如何理性判断问题的路径探寻及成果运用。
活动一:斜率之积为定值的路径探寻假设AB是椭圆$x^2/a^2+y^2/b^2=1(a>b>0)$上的一条不过原点的弦,点P是弦AB的中点,且直线OP和AB的斜率都存在,求$K_{AB} \cdot K_{PO}$。
解析】设点$P(x,y)$,$A(x_1,y_1)$,$B(x_2,y_2)$,则有$\frac{1}{2}\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}=\sqrt{a^2-b^2}$(代点作差)。
将$AB$的斜率$k_{AB}$表示为$\frac{y_1-y_2}{x_1-x_2}$,$OP$的斜率$k_{OP}$表示为$\frac{y}{x}$,则有:begin{aligned} K_{AB}&=\frac{y_1-y_2}{x_1-x_2}=\frac{(y_1-y)+(y-y_2)}{(x_1-x)+(x-x_2)} \\ &=\frac{y_1-y}{x_1-x} \cdot \frac{y-y_2}{x-x_2}=-\frac{b^2}{a^2} \cdot\frac{x-x_2}{y-y_2} \\ K_{PO}&=\frac{y}{x}=-\frac{b^2}{a^2} \cdot \frac{x_1-x_2}{y_1-y} \end{aligned}$$因此,$K_{AB} \cdot K_{PO}=\frac{b^4}{a^4} \cdot\frac{(x-x_2)(x_1-x_2)}{(y-y_2)(y_1-y)}=-\frac{b^2}{a^2}=e^2-1$。
结论形成总结】结论1】若$AB$是椭圆$x^2/a^2+y^2/b^2=1(a>b>0)$上的非直径的弦,点$P$是弦$AB$的中点,且直线$OP$和$AB$的斜率都存在,则$K_{AB} \cdot K_{PO}=-\frac{b^2}{a^2}=e^2-1$。
假设$AB$是椭圆$x^2/a^2+y^2/b^2=1(a>b>0)$上过原点的弦,点$P$是椭圆异于$A,B$的任意一点,若直线$PA$和$PB$的斜率都存在,记直线$PA$和$PB$的斜率分别为$k_1$,$k_2$,求$k_1 \cdot k_2$。
解法1】设$P(x,y)$,$A(x_1,y_1)$,$B(-x_1,-y_1)$,则有$k_1 \cdot k_2=\frac{y-y_1}{x-x_1} \cdot\frac{y+y_1}{x+x_1}=\frac{(y^2-y_1^2)(x^2+x_1^2)}{(x^2-x_1^2)(y^2-y_1^2)}=\frac{x^2+x_1^2}{y^2-y_1^2}$。
由椭圆的性质可得$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,代入$k_1 \cdot k_2$中得:k_1 \cdot k_2=\frac{x^2+x_1^2}{y^2-y_1^2}=\frac{a^2+b^2}{b^2-a^2}=-\frac{b^2}{a^2}$$因此,$k_1 \cdot k_2=-\frac{b^2}{a^2}$。
解法2】将椭圆圆化,由圆的结论类比到椭圆中。
2.由题可得 OB = 3,O = 60,因此直线 BD 的倾斜角为120 度,所以直线 BD 的斜率为 K。
根据结论可知 K BD = -3,因此 K CD = -2/33.3.在椭圆 x^2/4 + y^2/9 = 1 上,A、B 分别为椭圆的左右顶点,l2 是椭圆的右准线。
设 P 是椭圆上的动点,直线 AP、BP 分别交 l2 于 M、N,求线段 MN 的最小值。
解法一:设直线 AP 的斜率为 K(k>0),则直线 AP 的方程为 y=k(x+2)。
又 MN 的方程为 x=4,易求 M(4,6K)。
将 M 代入椭圆方程可得 y^2/9 = 1 - x^2/4,解得 y = 2√(1 - x^2/4) 或y = -2√(1 - x^2/4)。
因为 N 在 l2 上,所以 N 的横坐标为 4,代入直线 BP 的方程可得 N 的纵坐标为 -3/(4k)。
因此 MN = 6K + 3/(4K) ≥ 6(当且仅当 K = 1/2 时等号成立)。
解法二:利用中心弦结论 K PA · K PB = -b^2/a^2,设直线 AP 的方程为 y=k(x+2),因为 K PA · K PB = -9/4,所以直线 BP 的方程为 y = -3/(4(x-2))。
易得 M(4,6K)、N(4,-3/(4K)),因此MN = 6K + 3/(4K) ≥ 6(当且仅当 K = 1/2 时等号成立)。
解法三:设M(4,m)(m>0),N(4,n)(n<0),A(-2,0),B(2,0),则 K PA = mn/4,K PB = -6/4,因此 mn = -9.因为 M、N 在椭圆上,所以 (4/2)^2 + m^2/9 = 1,(4/2)^2 + n^2/9 = 1,解得 m = 3√5/5,n = -3√5/5.因此 MN = m - n ≥ 2√(m·n) = 6(当且仅当 m = n = 3/√5 时等号成立)。
方法小结:通过两道小题强化结论的应用,并让学生能够通过图形自主发现中点弦、中心弦的特征,从而合理巧妙地应用结论。
三种解法两个角度:显然从设点和设 K 的角度处理问题结合中心弦的结论能够快速计算找到解题的突破口。
拓展延伸:在椭圆 x^2/4 + y^2/9 = 1 上异于顶点的两点 A、B,若 OA、OB 的斜率之积为 -1,则 AB 的斜率为 2/3 或 -3/2.求证:OA+OB为定值;若OA,OB的斜率之积为-1,证明OA2+OB2为定值。
设A(x1,y1);B(x2,y2),则KOA·KOB=-1,即y1y2=-x1x2.又因为点A,B在椭圆上,所以x1=2-2y1,x2=2-2y2.将x1,x2代入y1y2=-x1x2得4y1y2=x1x2.所以OA2+OB2=x1+y1+x2+y2=4-(y1+y2)=3.求证:线段AB的中点C在某个定椭圆上。
设C(x,y)为AB中点,因为C为AB中点,所以2x=x1+x2,2y=y1+y2.又因为A,B在椭圆上,所以4x2=x12+2x1x2+x22,4y2=y12+2y1y2+y22.将x1=2-2y1,x2=2-2y2代入4x2=x12+2x1x2+x22得4y1y2+x1x2=1.所以4y1y2+2x1x2=3,即2y1y2+x1x2=3/2.所以C(x,y)在椭圆x2/4+y2/2=1/2上。
若OA,OB的斜率之积为-K,证明OA2+OB2=a2+b2.设A(x1,y1);B(x2,y2),则KOA·KOB=-y1/y2=x1/x2=-b2/a2.又因为点A,B在椭圆上,所以b2x1+a2y1=a2b2,b2x2+a2y2=a2b2.将b2x1+a2y1=a2b2代入-y1/y2=x1/x2得y1=-b2x1/a2,将b2x2+a2y2=a2b2代入-y1/y2=x1/x2得y2=b2x2/a2.所以OA2+OB2=x1^2+y1^2+x2^2+y2^2=a2+b2.2-a2)=b4x1x2,因此x1+x2=axxxxxxxx.由此可得:y1+y2=bxxxxxxxx-a2b2.因为OA2+OB2=x1+y1+x2+y2=a2+b2,所以y1+y2=b2-a2,代入上式可得:OA2+OB2=a2+b2.若OA,OB的斜率之积为-2,证明线段AB的中点C在某个定椭圆上。
设C(x,y),因为C为AB中点,所以有4x2=x12+2x1x2+x22.又因为KOA·KOB=y1y2/b2=-x1x2/a2=-2,所以(1)×b2+(2)×a2可得a2y1y2+b2x1x2=a2b2.所以有4b2x2=b2x12+2b2x1x2+b2x22,即4bx+4ay=2ab。
又因为4ay=ay1+2ay1y2+ay2,所以有xy=AB的中点轨迹方程为:x2y2/a2+b2=1.题目中给出的图形描述比较复杂,但是根据题目所求,可以通过计算得到线段AB的中点轨迹方程为:x2y2/a2+b2=1.因此,只需要证明该方程为椭圆即可。
已知椭圆 $E_1:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,$E_2: \frac{(x-b)^2}{a^2}+\frac{y^2}{b^2}=1$,且 $E_1$ 的离心率为$\frac{1}{2}$,点 $P$ 在椭圆 $E_2$ 上,直线 $L$ 经过点$P$ 且与椭圆$E_1$ 交于$A,B$ 两点,且$AP=\lambda AB$,求实数 $\lambda$ 的值。
解析】方法一:设 $P(x,y)$,则 $A(-x,-y)$,$B(x_1,y_1)$,则$C(x,0)$,$k_{PA}=\frac{y}{x}$,$k_{AB}=\frac{b^2}{a^2}\frac{y_1}{x_1}$。
由结论1:$K_{AB}\cdot K_{PB}=-1$,用 $K_{PA}$ 代换 $K_{AB}$ 得$a^2\frac{x_1}{y_1}=-\frac{y}{x}$,解得 $x_1=-\frac{a^2y}{x^2+y^2}$,$y_1=\frac{b^2x}{x^2+y^2}$。
又因为点 $A,B$ 在椭圆 $E_1$ 上,代入可得$x^2+y^2=\frac{5}{4}a^2$,$x_1^2+y_1^2=\frac{5}{4}a^2$。
联立解得 $x=-\frac{a^2}{\sqrt{5}},y=\frac{b^2}{\sqrt{5}}$,$x_1=-\frac{a^2}{\sqrt{5}},y_1=-\frac{2b^2}{\sqrt{5}}$。
设直线 $L$ 的方程为 $y=kx$,则 $k=-\frac{y}{x}=-\sqrt{5}$,$AB$ 的斜率为 $\frac{b^2}{a^2}\frac{y_1}{x_1}=2\sqrt{5}$,$AB$ 的中点坐标为$(0,-\frac{b^2}{\sqrt{5}})$,设其为$N$,则 $ON\parallel PB$,$PA\perp PB$,所以 $PA\perp L$,即$AP$ 在 $AB$ 上的高为 $\frac{b^2}{\sqrt{5}}$,由相似三角形可得 $\lambda=\frac{\sqrt{5}}{2}$。
